CPU and Cache Efficient Management

1 . CPU and Cache Efficient Management of Memory-Resident Databases Holger Pirk # , Florian Funke ∗ , Martin Grund % , Thomas Neumann ∗ , Ulf Leser + , Stefan Manegold # , Alfons Kemper ∗ , Martin Kersten # # ∗ CWI TU M¨unchen Amsterdam, The Netherlands M¨unchen, Germany {first.last}@cwi.nl {first.last}@in.tum.de % + HPI Humboldt Universit¨at zu Berlin Potsdam, Germany Berlin, Germany {first.last}@hpi.uni-potsdam.de {last}@informatik.hu-berlin.de Abstract— Memory-Resident Database Management Systems JiT Processing JiT Processing (MRDBMS) have to be optimized for two resources: CPU cycles CPU Efficiency and memory bandwidth. To optimize for bandwidth in mixed Bulk Processing Partially Decomposed OLTP/OLAP scenarios, the hybrid or Partially Decomposed Storage Storage Model (PDSM) has been proposed. However, in current Decomposed Storage implementations, bandwidth savings achieved by partial decom- ce position come at increased CPU costs. To achieve the aspired an rm bandwidth savings without sacrificing CPU efficiency, we combine r fo partially decomposed storage with Just-in-Time (JiT) compilation Pe of queries, thus eliminating CPU inefficient function calls. Since existing cost based optimization components are not designed for Volcano Processing Partially Decomposed JiT-compiled query execution, we also develop a novel approach Storage to cost modeling and subsequent storage layout optimization. N-ary Storage Our evaluation shows that the JiT-based processor maintains the bandwidth savings of previously presented hybrid query processors but outperforms them by two orders of magnitude Cache Efficiency due to increased CPU efficiency. Fig. 1: Dimensions of Memory-Resident DBMS Performance I. I NTRODUCTION Increasing capacity at decreasing costs of RAM make Memory-Resident Database Management Systems but only cache efficient on data that is stored according to the (MRDBMSs) an interesting alternative to disk-based Decomposed Storage Model (DSM) [12]. The DSM is known solutions [30]. The superior latency and bandwidth of for its good OLAP performance but suffers from bad OLTP RAM can boost many database applications such as Online performance due to poor cache efficiency when (partially) Analytical Processing (OLAP) and Online Transaction reconstructing tuples. To achieve good performance for mixed Processing (OLTP). Unfortunately, the Volcano-style (OLTP & OLAP) workloads, the hybrid or, more accurately, processing model [14] that forms the basis of most disk-based the Partially Decomposed Storage Model (PDSM) has been DBMSs was not designed to support such fast storage devices. proposed [15]. Even though they bulk-process data partition- To process arbitrarily wide tuples with generic operators, at-a-time, current implementations have to handle arbitrarily Volcano-style query processors “configure” the operators wide tuples (within a partition). Just like Volcano, they do using function pointers that are “chased” at execution time. this using function pointers [15]. Therefore, the current PDSM This pointer chasing is highly CPU inefficient [2], [6], but processors yield better cache efficiency than the DSM but acceptable for disk-based systems because disk I/O costs lower CPU efficiency (Figure 1). hide the costs for function calls. Due to its CPU inefficiency, To resolve the conflict between CPU and cache efficient a direct port of the Volcano model to a faster storage query processing we propose to remove the need for func- device often fails to yield the expected performance gain. tion pointers by combining Just-in-Time (JiT) compilation of MRDBMSs performance has a second critical dimension next queries with the PDSM. Specifically, we make the following to I/O (cache) efficiency: CPU efficiency (see Figure 1). contributions: To improve the CPU efficiency of MRDBMSs, the Bulk • We present the design and implementation of a PDSM- Processing model has been proposed [23]. Using this model, based storage component for HyPer, our JiT-based data is processed column-at-a-time which is CPU efficient Database Management System (DBMS). 

2 . • We introduce a novel approach to query cost estima- packing [20], it is possible to efficiently evaluate selections on tion and subsequent storage layout optimization for JiT- multiple attributes in a bulk-manner. However the necessary compiled queries: treating a generic cost model like a compression hurts update performance and decompression “programmable” machine that yields holistic query cost adds to tuple reconstruction costs. estimations using an appropriate instruction set (A-priory) query compilation is advocated by, e.g., the • We conduct an extensive evaluation of our system using VoltDB [17] system as a means to support high performance existing benchmarks and compare our results to those of transaction processing on any storage model. It achieves CPU previously published systems [15] efficiency, i.e., avoids function calls, by statically compiling The remainder of this paper is organized as follows: In queries to machine code and inlining functions. The process- Section II we present related work on CPU and cache efficient ing model supports SQL for query formulation but needs processing of memory resident data. In Section III we asses the a reassembly and restart of the system whenever a query impact of this conflict and describe how we resolve it using is changed or added. It also complicates the optimization JiT-compiled query execution in HyPer [21]. In Section IV of complex queries, because all plans have to be generated we describe the cost model and illustrate its usage for layout without knowledge of the data or parameters of the query. optimization in Section V. In Section VI we present our Both of these factors make it unsuited for OLAP applications evaluation and conclude in Section VII. that involve complex or ad-hoc queries. II. R ELATED W ORK B. Cache Efficient Storage Before illustrating our approach to CPU and cache efficient Having eliminated the function call overhead through one of memory-resident data management, we discuss previous ap- these techniques, memory bandwidth is the next bottleneck [5]. proaches, the encountered problems and inherent tradeoffs. One way to reduce bandwidth consumption is compression A. CPU Efficient Processing in its various forms [33] (dictionary compression, run-length encoding, etc.). However, this is beyond the focus of this In Volcano, relational query plans are constructed from paper and orthogonal to the techniques presented here. In flexible operators. When constructing the physical query plan, this paper, we study (partial) decomposition of database tables the operators are “configured” and connected by injecting to reduce bandwidth waste through suboptimal co-location of function pointers (selection predicates, aggregation functions, relation attributes. Full decomposition, i.e., storage using the etc.). Although variants of this model exist, they face the DSM [12] yields significant bandwidth savings for analytical same fundamental problem: operators that can change their applications on disk-resident databases. Unfortunately, full behavior at runtime are, from a CPU’s point of view, un- decomposition has a negative impact on intra-tuple cache predictable. This is a problem, because many of the perfor- locality and therefore transaction processing performance [1]. mance optimizations of modern CPUs and compilers rely on Consequently, it is suboptimal for applications that generate predictable behavior [19]. Unpredictable behavior circumvents mixed OLTP/OLAP workloads. To improve cache efficiency these optimizations and causes hazards like pipeline flushing, for such applications, the hybrid or, more accurately, the poor instruction cache locality and limited instruction level Partially Decomposed Storage Model (PDSM) has been pro- parallelism [2]. Therefore, flexible operators, as needed in posed [15]. In this model, database schemas are decomposed Volcano-style processing, are usually CPU inefficient. into partitions such that a given workload is supported op- To increase the CPU efficiency of MRDBMS, the database timally. Applications that can benefit from this technique in- research community has proposed a number of techniques [5], clude mixed OLTP/OLAP applications like real-time reporting [35], [20], [17]. The most prominent ones are bulk processing on transactional data, non-indexed search, or the management and a-priory query compilation . The former is geared towards of schemas with tables in which a tuple may describe one of OLAP applications, the later towards OLTP. Both have short- multiple real-life objects. Such schemas may result from, e.g., comings for mixed workloads that we discuss in the following. mapping complex class hierarchies to relations using Object Bulk processing focuses on analytical applications and was Relational Mapping (ORM). pioneered by the MonetDB project [23], [5]. Like in Volcano, complex queries are decomposed into precompiled primitives. III. CPU AND C ACHE E FFICIENT DATA M ANAGEMENT However, Bulk processing primitives are static loops without function calls that materialize all intermediate results [5]. For By definition, partially decomposed data involves at least analytical applications, the resulting materialization costs are one N-ary partition (otherwise we would refer to it as fully outweighed by the savings in CPU efficiency. Efforts to reduce decomposed). As already described, MRDBMS need flexible the materialization costs have led to the vectorized query operators to process arbitrarily wide tuples in a single scan. processing model [35] which constrains materialization to the To achieve such flexibility, current query processors [15] rely CPU cache. Due to the inflexibility of the primitives, however, on function pointers which causes CPU inefficiency. In this bulk processing is only efficient on fully decomposed relations, section we demonstrate the impact of this problem using a which are known to yield poor cache locality for OLTP practical example. Following that, we describe our approach applications. Using tuple clustering, compression and bank that employs JiT compilation to overcome this problem. 

3 . (a) SQL Query: select sum(B), sum(C), sum(D), sum(E) from R where A = $1 Schema: create table R(A int, C int, ..., P int) (b) Relational Algebra (c) C-Implementation on Partially Decomposed Relation 1 v o i d q u e r y ( c o n s t s t r u c t { i n t A[ SIZE ] ; v 4 s i B t o E [ SIZE ] ; Ɣ 2 int F to P [ ] ; } ∗ R, 3 v 4 s i ∗ sums , c o n s t i n t c ) { 4 δ 5 6 f o r ( i n t t i d = 0 ; t i d < SIZE ; ++ t i d ) i f ( R−>A[ t i d ] == c ) 7 ∗ sums += R−>B t o E [ t i d ] ; R 8 } Fig. 2: Representations of the example query The selectivity-dependent advantage of bulk- and JiT- compiled processing is consistent with recent work [32]. The figure also shows that, across all selectivities, our implemen- tation of the JiT-compiled query on partially decomposed data outperforms the other approaches. This observation led us to the following claim: JiT compilation of queries is an essential technique to support efficient query processing on memory-resident databases in N-ary or partially decomposed representation. In the remainder we study how to combine the advantages of PDSM and JiT-compiled queries in a relational Database Fig. 3: Costs of the Example Query on 25 M tuples (1.6GB) Management System (DBMS). B. Partially Decomposed Storage in HyPer A. The Impact of Storage and Processing Model HyPer is our research prototype of a relational MRDBMS. To compete with the bulk processing model in terms of CPU To evaluate the impact of storage and processing model, we efficiency, HyPer relies on JiT-compilation of queries [27]. implemented a typical select-and-aggregate query (Figure 2a) Whilst DBMS compilers have a long history [3], [8], up to in C. We implemented the query to the best of our abilities recently [27], [24], [31], the focus has been flexibility and according to the different processing and storage strategies1 extensibility rather than performance. The idea is to generate and measured the query evaluation time while varying the code that is directly executable on the host system’s CPU. This selectivity of the selection predicate (Figure 3). promises highly optimized code and high CPU efficiency due In our bulk processing implementation, the first operator to the elimination of function call overhead. scans column A and materializes all matching positions. After The code generation process is described in previous that, each of the columns B to E are scanned and all the match- work [27] and out of scope of this paper. To give an im- ing positions materialized. Finally, each of the materialized pression of the generated code, however, Figure 2 illustrates buffers are aggregated. This is CPU efficient but cache ineffi- the translation of the relational algebra plan of the example cient for high selectivities. The Volcano-style implementation query (Figure 2a) to C99-code. The program evaluates the consists or three functions (scan, selection, aggregation), each given query on a partially decomposed relation R. The relation calling the underlying repetitively to produce the next input R, the output buffer sums and the selection criteria c are tuple. The resulting performance (independent of the storage parameters of the function. In this example, every operator model) of the Volcano model indicates that it is, indeed, corresponds to a single line of code (the four aggregations are inappropriate for such a query on memory-resident data. The performed in one line using the vector intrinsic type v4si). JiT-compiled query was implemented according to the HyPer The scan yields a loop to enumerate all tuple ids (Line 5). The compilation model [27] and is displayed in Figure 2c in the selection is evaluated by accessing the appropriate value from version that is executed on the PDSM data. the first partition in an if statement (Line 6). If the condition 1 The partially decomposed representation was hand-optimized holds, the values of the aggregated attributes are added to the 

4 .global sum (Line 7). It is apparent that no overhead in storage CPU or executed code is generated. All operators are merged into Core 1 Core 2 a single for-loop. Values enter the CPU registers once and do Registers Registers not leave them until they are no longer needed. In practice, the compiler does not generate C-code but equivalent LLVM- L1 Cache TLB L1 Cache TLB assembler which is compiled into machine code by the LLVM- compiler library [25]. L2 Cache L2 Cache As demonstrated in previous work [27], the generated code achieves the CPU efficiency of the bulk processing model without the need for expensive intermediate materialization. Last Level (L3) Cache More importantly for our case, however, JiT-compilation on die makes the N-ary storage model viable for memory-resident off die databases. Since the generated code is static, it is very pre- Memory dictable and allows the respective optimizations by the CPU and the compiler. Since HyPer already has an N-ary storage Fig. 4: Memory Structure of an Intel Nehalem System backend, developing a backend for PDSM is straightforward. We extended the catalog to support multiple vertical partitions Notation Description [26] Parameters within a single relation and the compiler to generate accesses R.n The number of tuples, values or tuple fragments stored to the respective partitions rather than the relation. As with in a relation/partition R earlier systems, the main challenge is to determine the appro- R.w The data width of tuple, value or tuple fragment priate decomposition for a given schema and workload. We u The number of data words of a data item that are will discuss our approach to this problem in the next sections. accessed when performing an access pattern (u < R.w) Bi The access granularity (block size) of cache i IV. Q UERY C OST E STIMATION li The block access latency of cache i In addition to the processing model, the query performance Atoms s trav The sequential traversal of a memory region of width on partially decomposed data also depends on the choice of the (R.n,R.w) R.w with unconditional access to every single of the decomposition/layout. Like earlier approaches [15], we focus R.n data items on cost-based optimization to find an appropriate layout for a r trav The traversal of a memory region of width R.w with given workload. Since in memory-resident data processing no (R.n,R.w) unconditional access to every single of the R.n data cost factor clearly dominates, a hardware-conscious cost model items in random order is needed. Since memory-resident bulk processors face similar rr acc The repetitive (r times) access of one of the R.n data (R.n,R.w,r) items of a memory region of width R.w challenges there is already a body of research in hardware- Algebraic Operators conscious cost modeling for main memory databases [26], P1 P2 The concurrent execution of the Access Patterns P1 to [15]. For JiT-compiled queries, however, query evaluation ... Pn Pn is more complicated: as described in Section III-B query P1 ⊕ P2 ⊕ The sequential execution of the Access Patterns P1 to . . . ⊕ Pn Pn operators are interleaved, resulting in complex and irregular Intermediate Metrics memory access. Simply adding the costs of the operators [26] Mis The number of sequential access cache misses induced or neglecting non-scan operators [15] would yield inaccurate on cache i estimates. To achieve more accurate estimates, we developed Mir The number of random access cache misses induced on a “programmable” holistic cost model based on the existing cache i Generic Cost Model [26], using its atoms as instructions. (a) Atoms and Operators In the rest of this section we briefly motivate the need for a access pattern of the example query complex model, introduce the Generic Cost Model [26] as well s trav(26214400,4) rr acc(26214400,16,262144) rr acc(1,16,262144) as our extensions and the use for hardware and storage-layout (b) aware cost estimation of queries. TABLE I: Overview of the Generic cost model A. Cost Factors on modern CPUs To achieve high memory access performance, modern CPUs incorporate a complex memory hierarchy (see Figure 4). Mul- enough, a fetch instruction is issued to the memory system tiple levels of caches and TLBs speed up repetitive accesses and the cache line loaded into a slot of the Last Level Cache to data items (or data items located on the same cache line or (LLC). A correctly prefetched cache line may hide memory TLB-Block). In addition, many CPUs have prefetching units access latency behind the time spent processing the data that speculatively load data items before they are accessed. whilst incorrect prefetching a) causes unnecessary traffic on 1) Prefetching: While transferring and processing a fetched the memory bus and b) may evict a cache line that should cache line in the CPU, the next accessed cache line is have stayed cache-resident. Due to these potentially harmful anticipated by a Prefetching Unit. If the confidence is high effects, prefetching units generally follow a cautious strategy 

5 . R.n × R.w when issuing prefetch instructions. Prefetching strategies: Prefetching strategies vary among R.w CPUs and are often complex and defensive up to not issuing u any prefetch instructions at all. In our model, we assume 1 2 ... an Adjacent Cache Line Prefetching with Stride Detection strategy that is, e.g., implemented in the Intel Core Microar- s 1−s s 1−s chitecture [18]. Using this strategy, a cache line is prefetched whenever the prefetcher anticipates a constant stride. Although Fig. 5: s trav cr this seems a na¨ıve strategy, its simplicity and determinism make it attractive for implementation as well as modeling. 1.00 More complex strategies exist, but usually rely on the (par- tial) data access history of the executed program. These are generally geared towards more complex operations (e.g., high 0.75 dimensional data processing or interleaved access patterns) yet behave similar to the Adjacent Cache Line Prefetcher in simpler cases like relational query processing. 0.50 Predicted Sequential B. The Generic Cost Model Measured Sequential The Generic Cost Model is built around the concept of Measured Random 0.25 Predicted Random Memory Access Patterns, formal yet abstract descriptions of Predicted rr_acc the memory access behavior that an algorithm exposes. The model provides atomic access patterns, an algebra to construct 0 complex patterns and equations to estimate induced costs. 0 0.25 0.5 0.75 1 Although the model is too complex for an in-depth discussion Selectivity (s) here, Table Ia provides a brief description. We refer the Fig. 6: Prediction Accuracy of s trav cr vs. rr acc interested reader to the original work [26] for a detailed description. To illustrate the model’s power, consider the example in first has been hinted at in the last section: the inadequacy Table Ib which is the access pattern of the example query of the model for selective projections. We overcome this (see Figure 2a) on partially decomposed data for a selectivity problem by introducing a new access pattern, the Sequential of 1%. To evaluate the given query, the DBMS scans col- Traversal/Conditional Read. We also report two modifications umn A by performing a sequential traversal of the memory we applied to the model to improve the accuracy of random region that holds the integer-values of a (s trav(A) = access estimation and the impact of prefetching. While an s trav(26214400,4)2 ). Concurrently ( ), whenever the understanding of the new access pattern is crucial for the rest condition holds, the columns B, C, D, E are accessed. This of this paper, the other two are extensions that do not change is modeled as a rr acc on the region with r reflecting the nature of the model. the number of accessed values (r can be derived from the 1) Sequential Traversal/Conditional Read: The example in selectivity). For every matching tuple, the output region has Table Ib already indicated a problem of the cost model: If to be updated which yields the last atom: a rr acc of a a memory region is scanned sequentially but not all tuples region which holds only one tuple but is accessed for every are accessed, most DBMSs expose an access pattern that matching tuple. This algebraic description of the executed cannot be accurately modeled using the atoms in Table Ia. program has proven useful for the prediction of main memory In the example, we resorted to modeling this operation using join performance [26]. a rr acc which is not appropriate because a) the region is One may notice, however, that the access pattern in Table Ib traversed from begin to end without ever going backwards and is not an entirely accurate description of the actual operation: b) no element in the region is accessed more than once. While the rr acc for the access of B, C, D, E is not fully this is not an issue for the original purpose of the cost model, random since the tuple can be assumed to be accessed in order. i.e., join optimization, it severely limits its capabilities for the In the next section, we illustrate our extensions to the model holistic estimation of query costs and subsequent optimization that allow modeling of such behavior. of the storage layout. C. Extensions to the Generic Cost Model We developed an extension to accurately model this behav- When modeling JiT-compiled queries on a modern CPU we ior. A new atom, the Sequential Traversal with Conditional encountered several shortcomings of the original model. The Reads (s trav cr), captures the behavior of selective pro- jections using the same parameters as s trav yet also in- 2 Depending on the context we will use either numeric parameters or corporates the selectivity of the applied conditions s. Figure 5 relation identifiers when denoting atomic access patterns. While using relation identifiers is not strictly speaking correct, the numeric parameters are generally gives a visual impression of this Access Pattern: The Region R easily inferred from the relation identifiers. is traversed sequentially in R.n steps. In every step, u bytes 

6 .are read with probability s and the iterator unconditionally misses using the CPU’s Performance Counters. The Nehalem advances R.w bytes. This extension provides the atomic access CPU Performance Counters only count Demand/Requested pattern that is needed to accurately model the query evaluation L3 cache misses as misses. Misses that are triggered by the of the example in Table Ib: The rr acc([B, C, D, E]) prefetcher are not reported, which allows us to distinguish becomes a s trav cr([B, C, D, E], s) with the se- them when measuring. The sequential misses are simply the lectivity s = 0.01. number of reported L3 accesses minus the reported L3 misses. To estimate the number of cache misses from these param- The random misses are the reported L3 misses. In addition to eters we have to estimate the probability Pi of accessing a the predicted, Figure 6 also shows the measured cache misses. cache line when traversing it. Pi is equal to the probability The Figure shows that the prediction overestimates the number that any of the data items of the cache line is accessed. It is of random misses for mid-range selectivities and underesti- independent of the capacity of the cache but depends on the mates for very high selectivities. However, the general trend width of a cache line (i.e., the block size and thus denoted of the prediction is reasonably close to the measured values. with Bi ). Assuming a uniform distribution of the values over To illustrate the improvement of the model as achieved by the region, Pi can be estimated using Equation 1. For non- this new pattern, the figure also shows the predicted number uniformly distributed data the model can be extended with a of accessed cache lines when modeling the pattern using a different formula. rr acc instead of s trav cr. It shows that a) the rr acc highly underestimates the total number of misses and b) does Pi = 1 − (1 − s) Bi (1) not distinguish random from sequential misses. Especially for low selectivities, the model accuracy has improved greatly. However, to estimate the induced costs, we have to distinguish 2) Prefetching aware Cost Function: In its original form random and sequential misses. Even though not explicitly the Generic cost model [26] distinguishes random and se- stated, we believe that the distinction between random and quential misses (Mir and Mis respectively) and associates sequential cache misses in the original model [26] was in- them with different but constant weights (relative costs) to troduced largely to capture non-prefetched and prefetched determine the final costs. These weights are determined using misses. Thus, we model them as such. Assuming an Adjacent empirical calibration rather than detailed inspection and appro- Cache Line Prefetcher, the probability of a cache line to be a priate modeling. This is sufficient for the original version of sequential, i.e., prefetched, cache miss is the probability of the model because access patterns induce almost exclusively a cache line being accessed with the preceding cache line random or exclusively sequential misses. Since our new atom, being accessed as well. Since these two events are statistically s trav cr, induces both kinds of misses, however, we have independent, the probability of the two events can simply be to distinguish the costs of the different misses more carefully. multiplied which yields Equation 2 for the probability of a For this purpose, we propose an alternative cost function. cache miss being a sequential miss (Pis ). Where Manegold et al. [26] simply add the weighted costs 2 induced at the various layers of memory, we use a more sophis- Bi Pis = 1 − (1 − s) (2) ticated cost function to account for the effects of prefetching. Since the most important (and aggressive) prefetching usually Since any cache miss that is not a sequential miss is a happens at the LLC, we change the cost function to model it random miss, the probability for a cache line to be a random differently. miss Pir can be calculated using Equation 3. Prefetching is essentially only hiding memory access la- 2 tency behind the activity of higher storage and processing Bi Bi Pir = Pi − Pis = 1 − (1 − s) − 1 − (1 − s) layers. Therefore, its benefit highly depends on the time it takes to process a cache line in the faster memory layers. Bi 2Bi = (1 − s) − (1 − s) (3) Following the rationale that execution time is determined by Equipped with the probability of an access to a cache line memory accesses the costs induced at the LLC are reduced we can estimate the number of cache misses per type using by the costs indexed at the faster caches and the processor Equation 4. registers (which we consider just another layer of memory). If processing the values takes longer than the LLC-fetching, R.w × R.n the overall costs are solely determined by the processing costs Mix = Pix × for x ∈ {r, s} (4) Bi and the costs induced at the LLC are 0 — the application Prediction Accuracy: To get an impression of the proba- is CPU-bound. The overall costs for sequential misses in the bility for Pir and Pis with varying s consider Figure 6. The LLC (in our Nehalem system the Level 3 Cache, hence T3s ) percentage of random and sequential misses increases steeply can, thus, be calculated using Equation 5. with the selectivity in the range from 0 < s < 0.05. After that point, the number of random misses declines in favor of more 2 sequential misses. T3s =max 0, M3s · l3 − Mi · li+1 (5) To assess the quality of our prediction, we implemented i=0 a selective projection in C and measured the induced cache Following [26], the costs (in CPU cycles) for an access to 

7 . π level i (i.e., a miss on level i − 1) will be denoted with li . Since we regard the CPU’s registers as just another level of 6 - Pattern Emmitance Point memory, l1 denotes the time it takes to load and process one value and M0 the number of register values that have to be processed. The overall costs TM em are calculated by summing the ⋈ 5 weighted misses of all cache layers except the LLC. The costs 3 ⋈ δ for prefetched LLC misses are calculated using Equation 5 and 2 4 added to the overall costs in Equation 6. 1 2 N TM em = Mi · li+1 + T3s + M3r · l4 + Mi · li+1 (6) i=0 i=4 R1 R2 R3 3) Random Accesses Estimation: To estimate the number of cache misses that are induced by a Repetitive Random Access Fig. 7: Plan Traversal (rr acc), the work of Manegold et al. includes an equation to estimate the number of unique accessed cache lines (I) from Operation Emitted Pattern the number of access operations (r) and the number of tuples Select s trav cr(s, [attributes]) in a region (R.n). While mathematically correct, this equation Join (Push) r trav([ht attributes]) ⊕ Hash-Build is hard to compute due to heavy usage of binomial coefficients Join (Push) rr acc([ht attributes]) of very large numbers. This makes the model impractical for Hash-Probe the estimation of operations on large tables. For completeness, Join (Pull) s trav cr(s, [ht attributes]) Hash-Build r trav([ht attributes]) ⊕ we report a different formula that we used here. Join (Pull) s trav cr(s, [ht attributes]) This problem, the problem of distinct record selection, Hash-Probe rr acc([ht attributes]) has been studied extensively (and surprisingly controversial). GroupBy (Pull) s trav cr(s, [group attributes] + [aggr attributes]) Cardenas [7], e.g., gives Equation 7 for to estimate the distinct rr acc([group attributes] + accessed records when accessing one of R.n records r times. [aggr attributes]) Whilst challenged repeatedly for special cases [13], [34], [9], GroupBy (Push) s trav cr(s, [group attributes] + [aggr attributes] - we found the equation yields virtually identical results to [pushed attributes]) the equation from the original cost model while being much rr acc([group attributes] + cheaper to compute. [aggr attributes]) Project (Push) s trav cr(s, [attributes] r - [pushed attributes]) 1 s trav([attributes]) I (r, R.n) = R.n · 1 − 1 − (7) R.n Project (Pull) s trav cr(s, [attributes]) s trav([attributes]) Equipped with a model to infer costs from memory access Sort (Push) s trav cr(s, [attributes] patterns, we can estimate the costs of a relational query by - [pushed attributes]) s trav([attributes]) ⊕ translating it into the memory access pattern algebra. In the rr acc([attributes]) ⊕ rest of this section we will describe this process. Sort (Push) s trav cr(s, [attributes]) s trav([attributes]) ⊕ D. Modeling JiT Query Execution rr acc([attributes]) ⊕ Due to the instruction-like character of the access pattern TABLE II: Operators and their Access Pattern algebra, we can treat it like a programmable machine with each atomic access pattern forming an instruction. Thus, generating the access pattern for a given physical query plan is similar of its two children3 . Thus, they emit patterns twice: once for to generating the actual code to perform the query (see [27] building the internal hashtable and once for probing it. When for a description). To generate the access pattern, the relational emitting patterns, we distinguish pulling and non-pulling op- query plan is traversed in pre-order from its root (see Figure 7) erators. Operators that are within a pipeline fragment that has and the appropriate patterns emitted according to Table II. Just a join on its lower end are non-pulling, others are pulling. like statements in a program, the emitted patterns are appended The rationale behind this is that operators placed above a join to the overall pattern. (e.g., the outer join in Figure 7) do not have to explicitly fetch Note that no operator produces a pattern when entering an their input because join operators essentially push tuples into a operator node for the first time. All operations are performed pipeline fragment as a result of the hash-probing (this effect is when data flows into the operator, i.e., when leaving the explained in detail in [27]). Operators in pull-mode (e.g., the operator in the traversal process. Joins (hash) behave slightly differently since data flows into them twice, once for each 3 n-way joins are represented by n nodes 

8 .selection in Figure 7) have to pull/read their input explicitly. {{A}, {B, C, D, E}, ...} is not considered a reasonable cut As an example, consider the inner join operator in Figure 7: and therefore never considered for decomposition because when entering a subtree rooted at the node, no pattern is the attributes are accessed in the same query. If, however, emitted and the traversal continues with its left child. When the selectivity of the condition was 0, {B, C, D, E} would leaving the left subtree (Mark 1), a pattern is generated that never be accessed and storing them in one partition with A reflects the hash-building phase of the hashjoin. Since its left would hurt scan performance. It is therefore reasonable to child is a base table it has to pull tuples into the hashtable, thus, also consider a partitioning that divides attributes that are it emits a s trav(R1) and a concurrent ( ) r trav(ht) accessed within one query but in different access patterns. of the hashtable. Since the hash-build causes materialization, Thus, we consider what we call Extended Reasonable Cuts it breaks the pipeline and marks that by appending a sequence as potential solutions. These are generated from the access operator ⊕ to the pattern. After that, the processing continues patterns rather than the queries. An extended reasonable cut is with its right child. When leaving the subtree (Mark 2), the made up from all attributes that are accessed together within an hashtable is probed (again in pull-mode) and the tuples pushed atomic pattern or in concurrently ( ) executed atomic access to the next hashtable (Mark 3). The emitted pattern at Mark patterns of the same kind. E.g., s trav(a) s trav(b) 2 is s trav(R2) rr acc(ht). would lead to one cut while s trav(a) r trav(b) Using this procedure, we effectively program the generic would lead to two. For concurrent s trav cr the case is cost model using the access patterns as instructions. While slightly more complicated. Depending on the selectivity s1 being a simple and elegant way to holistically estimate JiT- and s2 in s trav cr(a,s1 ) s trav cr(b,s2 ) , the compiled query costs, it also allows us to estimate the impact values of a and b may or may not be accessed together. If, of a change in the storage layout. In the next section, we will e.g., s1 = s2 = 1, the traversed attributes are always accessed use this to optimize the storage layout for a given workload. together and do not have to be considered for decomposition. If the selectivity is less than 1, we have to consider all possible V. S CHEMA D ECOMPOSITION cuts: {{{A}, ...}, {{B}, ...}, {{A, B}, ...}}. Finding the optimal schema decomposition is an optimiza- Based on the solution space of all reasonable cuts, BPi tion problem in the space of all vertical partitionings with employs a Branch and Bound strategy to reduce the search the estimated costs as objective function. Since the number space. The schema is iteratively cut according to a (randomly) of vertical partitionings of a schema grows exponentially with selected cut. This cut is considered for inclusion in the solution the size of the tables, attribute-based partitioning algorithms by estimating its cost improvement. If the improvement is like the one used in the Data Morphing Approach [16] are above a user defined threshold, the cut is considered for impractical due to the high optimization effort (linear with inclusion and the algorithm branches into two cases: including the number of partitionings, thus exponential with the number or excluding the cut in the solution. If the cost improvement is of attributes). Instead we apply an algorithm that takes the below that threshold the cut is not considered for inclusion and queries of the workload as hints on potential partitionings of the subtree pruned. While sacrificing optimality this reduces the schema. Chu et al. [10] proposed two such algorithms. The the search space and thus the optimization costs. first, OBP, yields optimal solutions but has exponential effort VI. E VALUATION with regard to the number of considered queries. The second, BPi only approaches the optimal solution but has reduced costs The benefits of cache-conscious storage do not only depend (depending on a selectable threshold down to linear). We will on the query processing model but also on characteristics of apply the BPi algorithm to approach the optimal solution. the workload, schema and the data itself. It is, therefore, not enough to evaluate the approach only on a single application. A. Binary Partitioning We expect wider tables and more diverse queries to benefit OBP and BPi generate potential solutions by iteratively par- more from partial decomposition than specialized queries on titioning a table according to what is called a reasonable cut. narrow tables. To support this claim we evaluated using three In the original work, every query yields one reasonable cut for very different benchmarks. every accessed table. The cut is a set of two distinct attribute 1) The SAP Sales and Distribution Benchmark that was used sets: the ones that are accessed in the query and the ones to benchmark the HYRISE system [15]. We consider the that are not. The query in our initial example (see Figure 2a), schema relatively generic in the sense that it support e.g., would yield the cut {{A, B, C, D, E}, {F, .., P }}. For multiple use cases and covers business operations for workloads with multiple queries, the set of a reasonable cuts enterprises in many different countries with different also contains all cuts that result from cutting the relation regulatory requirements. multiple times. Thus, the solution spaces grows exponential 2) The CH-benchmark [11], a merge between the TPC-C with the number of queries. and TPC-H benchmarks, modeling a very specific use However, this definition of a reasonable cut is oblivious case: the selling and shipping of products from ware- to the actual access pattern of the query. It does not re- houses in one country. flect the fact that different attributes within a query may be 3) A custom set of queries on the CNET product catalog accessed in a different manner. E.g., in the initial example dataset [4] designed to reflect the workload of such 

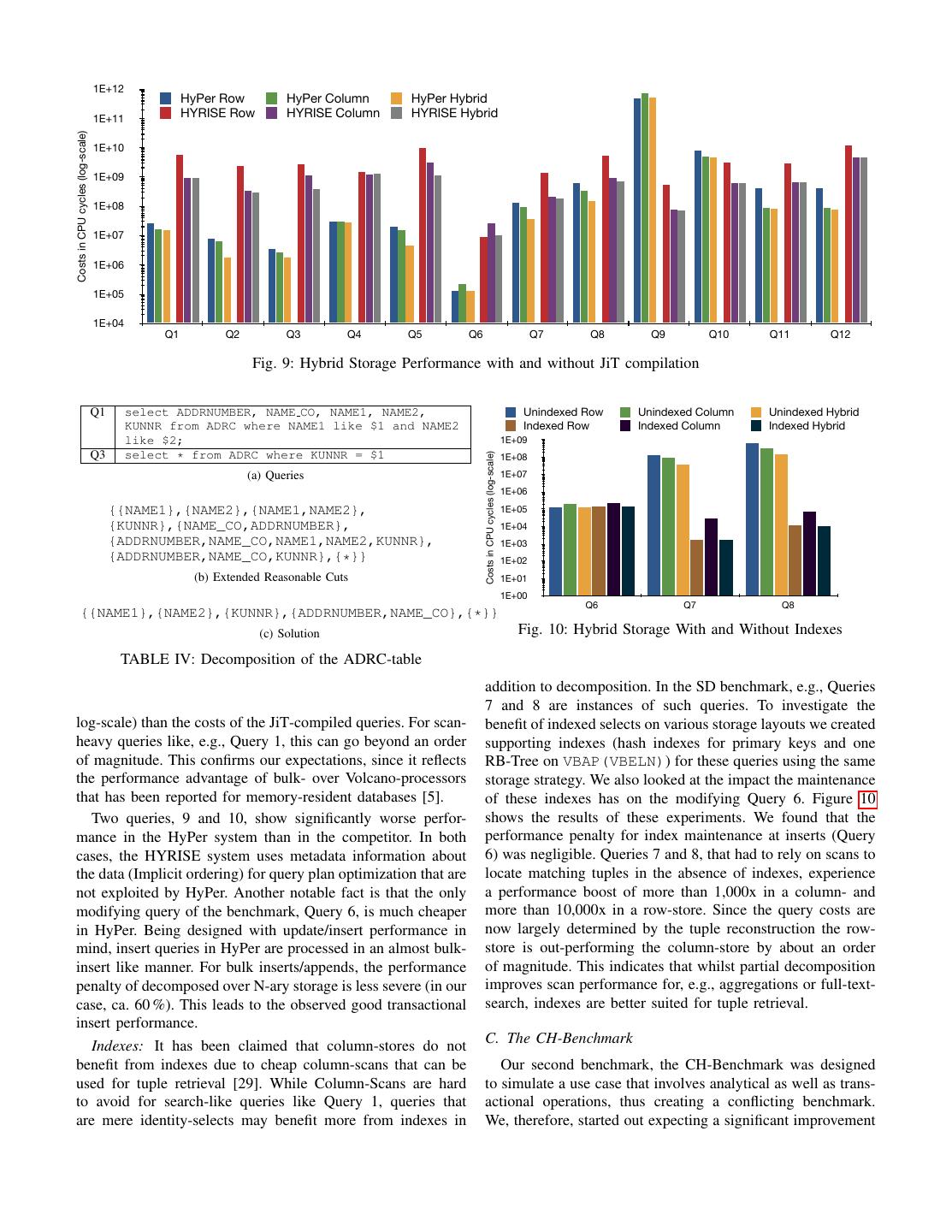
9 . 100 of a memory layer. The latencies can be determined from this CPU cycles per Access (log-scale) graph manually or automatically by fitting the curve to the Experiment Model data points. Table III lists the parameters of the cost model 10 and their values for our system. Besides providing the needed parameters, this experiment illustrates the significance of a hardware-conscious cost model. 1 If we only counted misses on a single layer (e.g., only processed values or only L2-misses) we would underestimate 1K 10K 100K 1000K 10000K 100000K the actual costs. This observation is what triggered the de- Size of Accessed Memory Region (log-scale) velopment of the Generic Cost Model in the first place [26]. Due to space limitations we focus our evaluation on the high Fig. 8: The configuring experiment level impact of partial decomposition rather than the accuracy Level Capacity Blocksize Access Time of the cost model. In addition to the original validation [26], L1 Cache 32 kB 8B 1 Cyc we performed an extensive study of the extended generic cost L2 Cache 256 kB 64 B 3 Cyc model and demonstrated it’s validity on current hardware [28]. TLB 32 kB 4 kB 1 Cyc L3 Cache 8 MB 64 B 8 Cyc We determined an appropriate layout for each of our three Memory 48 GB 64 B 12 Cyc benchmarks using our extended BPi. TABLE III: Parameters used for the model B. The SAP-SD Benchmark The SAP Sales and Distribution (SD) Benchmark was used to evaluate the HYRISE system [15] and illustrates a perfor- a product catalog web application. Due to the variety mance gain of partial decomposition in a moderately generic of attributes of the different products, we consider the case. We consider this benchmark to cover the middle ground schema very generic. between the highly specialized CH-benchmark and the very Since the non-hybrid HyPer system has been shown to generic CNET Products case. We implemented the benchmark be competitive to established DBMSs (VoltDB and Mon- using the reported queries [15] on publicly available schema etDB) [22] we will focus our evaluation on the partial de- information6 . We filled the database with randomly generated composition aspect of the system. data, observing uniqueness constraints where applicable. Decomposition: Due to space limitations, we cannot cover A. Setup the optimization process in detail here7 . To give an impression We evaluated our approach on a system based on the Intel of the optimization process we briefly discuss the decomposi- Nehalem Microarchitecture as depicted in Figure 4 with 48 GB tion of the ADRC table of the SD benchmark (see Table IV). of RAM. The 4 CPUs were identified as “Intel(R) Xeon(R) Query 1 and 3 of the benchmark (see Table IVa) operate CPU X5650 @ 2.67 GHz” running a “Fedora 14 (Laughlin) on that table. Query 1 scans NAME1 and (conditionally) Linux” (Kernel Version: 2.6.35.14-95.fc14.x86 64). Since the NAME2 to evaluate the selection conditions and Query 3 scans model relies on more detailed parameters to predict costs we KUNNR. The extended reasonable cuts that originate from their will discuss how to obtain these in more detail. plans are listed in Table IVb. The optimization yields the Training the Model: The cost estimation relies on parame- decomposition as listed in Table IVc: The first three partitions ters that describe the memory hierarchy of a given system. support the scans of the queries efficiently. Since NAME2 is To a large extent, these parameters can be extracted from only accessed if NAME1 does not match the condition, these the specification or read directly from the CPU using, e.g., are decomposed. KUNNR is stored in the third partition to cpuinfo x864 . The reported information includes the capaci- support Query 3. The fourth partition supports the projection ties and blocksizes of the available memory layers but not of Query 1 and the last partition the projection of Query 3. their respective latency. To determine these experimentally, Results: For reference, we compare the performance of the we, inspired by the Calibrator5 of the Generic Cost Model, JiT-compiled queries to the processing model of the HYRISE implemented the following experiment in C to determine system. HYRISE uses a bulk-oriented model but still relies the latencies: calculate the sum of a constant number of on function calls to process multiple attributes within one values varying the size of the memory region that they are partition. It therefore suffers from the same CPU inefficiency read from (and thus the number of unique accessed values). as the Volcano model. Figure 9 shows the results for queries Figure 8 shows the execution time in cycles per summed value one to twelve of the benchmark. We observed that, in general, as a function of the size of the accessed memory region. JiT-compiled queries have similar relative costs on different The latencies of the different memory layers become visible layouts as volcano processed ones. However, the processing whenever the size of the accessed region exceeds the capacity costs of the HYRISE processor are much higher (note the 4 http://osxbook.com/book/bonus/misc/cpuinfo_x86/ 6 http://www.se80.co.uk, http://msdn.microsoft.com/ cpuinfo_x86.c en-us/library/cc185537(v=bts.10).aspx 5 http://www.cwi.nl/ manegold/Calibrator 7 We are currently working to make the optimizer publicly available. ˜ 

10 . 1E+12 HyPer Row HyPer Column HyPer Hybrid 1E+11 HYRISE Row HYRISE Column HYRISE Hybrid Costs in CPU cycles (log-scale) 1E+10 1E+09 1E+08 1E+07 1E+06 1E+05 1E+04 Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 Q12 Fig. 9: Hybrid Storage Performance with and without JiT compilation Q1 select ADDRNUMBER, NAME CO, NAME1, NAME2, Unindexed Row Unindexed Column Unindexed Hybrid KUNNR from ADRC where NAME1 like $1 and NAME2 Indexed Row Indexed Column Indexed Hybrid like $2; 1E+09 Q3 select * from ADRC where KUNNR = $1 1E+08 Costs in CPU cycles (log-scale) (a) Queries 1E+07 1E+06 {{NAME1},{NAME2},{NAME1,NAME2}, 1E+05 {KUNNR},{NAME_CO,ADDRNUMBER}, 1E+04 {ADDRNUMBER,NAME_CO,NAME1,NAME2,KUNNR}, 1E+03 {ADDRNUMBER,NAME_CO,KUNNR},{*}} 1E+02 (b) Extended Reasonable Cuts 1E+01 1E+00 Q6 Q7 Q8 {{NAME1},{NAME2},{KUNNR},{ADDRNUMBER,NAME_CO},{*}} (c) Solution Fig. 10: Hybrid Storage With and Without Indexes TABLE IV: Decomposition of the ADRC-table addition to decomposition. In the SD benchmark, e.g., Queries 7 and 8 are instances of such queries. To investigate the log-scale) than the costs of the JiT-compiled queries. For scan- benefit of indexed selects on various storage layouts we created heavy queries like, e.g., Query 1, this can go beyond an order supporting indexes (hash indexes for primary keys and one of magnitude. This confirms our expectations, since it reflects RB-Tree on VBAP(VBELN)) for these queries using the same the performance advantage of bulk- over Volcano-processors storage strategy. We also looked at the impact the maintenance that has been reported for memory-resident databases [5]. of these indexes has on the modifying Query 6. Figure 10 Two queries, 9 and 10, show significantly worse perfor- shows the results of these experiments. We found that the mance in the HyPer system than in the competitor. In both performance penalty for index maintenance at inserts (Query cases, the HYRISE system uses metadata information about 6) was negligible. Queries 7 and 8, that had to rely on scans to the data (Implicit ordering) for query plan optimization that are locate matching tuples in the absence of indexes, experience not exploited by HyPer. Another notable fact is that the only a performance boost of more than 1,000x in a column- and modifying query of the benchmark, Query 6, is much cheaper more than 10,000x in a row-store. Since the query costs are in HyPer. Being designed with update/insert performance in now largely determined by the tuple reconstruction the row- mind, insert queries in HyPer are processed in an almost bulk- store is out-performing the column-store by about an order insert like manner. For bulk inserts/appends, the performance of magnitude. This indicates that whilst partial decomposition penalty of decomposed over N-ary storage is less severe (in our improves scan performance for, e.g., aggregations or full-text- case, ca. 60 %). This leads to the observed good transactional search, indexes are better suited for tuple retrieval. insert performance. Indexes: It has been claimed that column-stores do not C. The CH-Benchmark benefit from indexes due to cheap column-scans that can be Our second benchmark, the CH-Benchmark was designed used for tuple retrieval [29]. While Column-Scans are hard to simulate a use case that involves analytical as well as trans- to avoid for search-like queries like Query 1, queries that actional operations, thus creating a conflicting benchmark. are mere identity-selects may benefit more from indexes in We, therefore, started out expecting a significant improvement 

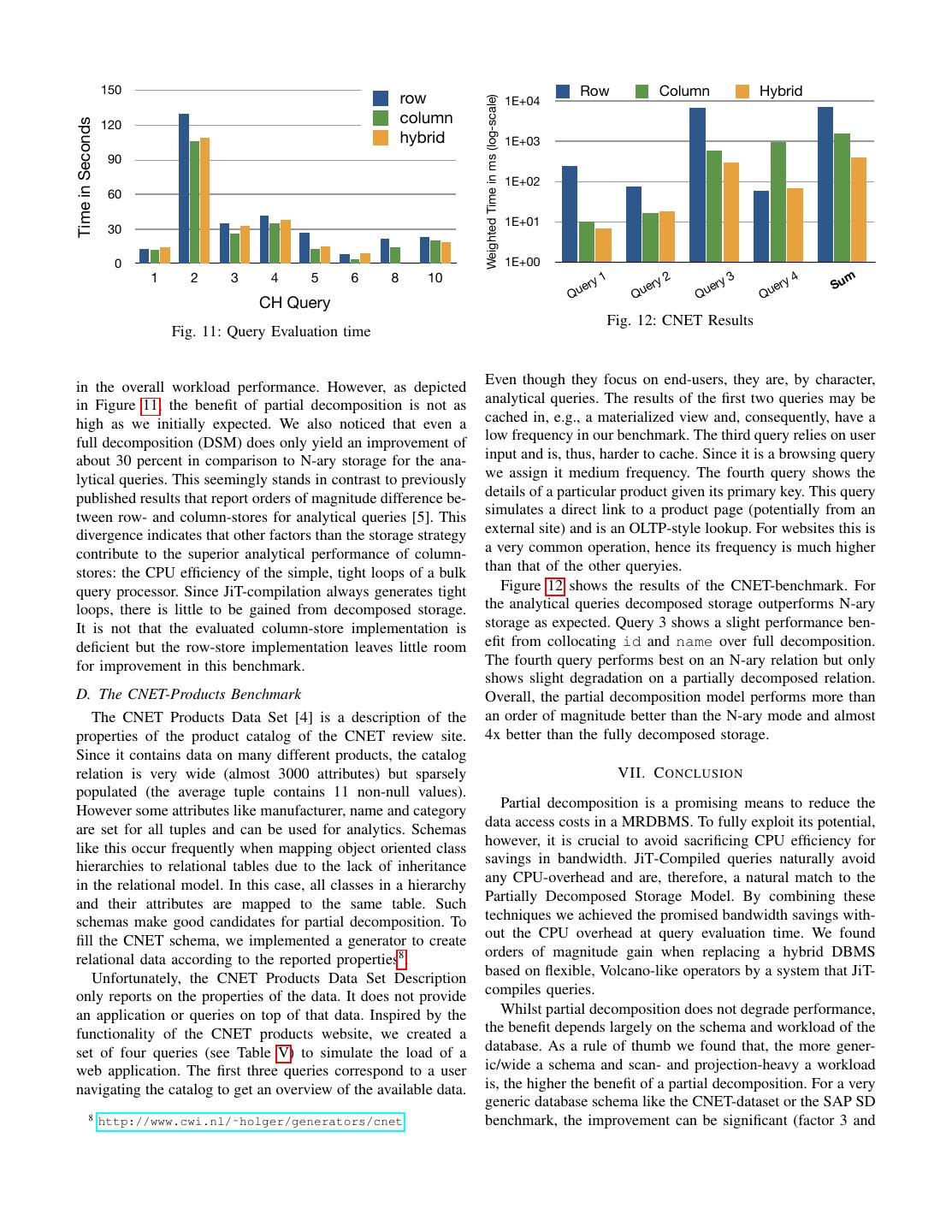
11 . 150 Row Column Hybrid row 1E+04 Weighted Time in ms (log-scale) 120 column Time in Seconds hybrid 1E+03 90 1E+02 60 1E+01 30 0 1E+00 1 2 3 4 5 6 8 10 1 2 3 4 m ery ery ery ery Su Qu Qu Qu Qu CH Query Fig. 12: CNET Results Fig. 11: Query Evaluation time in the overall workload performance. However, as depicted Even though they focus on end-users, they are, by character, in Figure 11, the benefit of partial decomposition is not as analytical queries. The results of the first two queries may be high as we initially expected. We also noticed that even a cached in, e.g., a materialized view and, consequently, have a full decomposition (DSM) does only yield an improvement of low frequency in our benchmark. The third query relies on user about 30 percent in comparison to N-ary storage for the ana- input and is, thus, harder to cache. Since it is a browsing query lytical queries. This seemingly stands in contrast to previously we assign it medium frequency. The fourth query shows the published results that report orders of magnitude difference be- details of a particular product given its primary key. This query tween row- and column-stores for analytical queries [5]. This simulates a direct link to a product page (potentially from an divergence indicates that other factors than the storage strategy external site) and is an OLTP-style lookup. For websites this is contribute to the superior analytical performance of column- a very common operation, hence its frequency is much higher stores: the CPU efficiency of the simple, tight loops of a bulk than that of the other queryies. query processor. Since JiT-compilation always generates tight Figure 12 shows the results of the CNET-benchmark. For loops, there is little to be gained from decomposed storage. the analytical queries decomposed storage outperforms N-ary It is not that the evaluated column-store implementation is storage as expected. Query 3 shows a slight performance ben- deficient but the row-store implementation leaves little room efit from collocating id and name over full decomposition. for improvement in this benchmark. The fourth query performs best on an N-ary relation but only shows slight degradation on a partially decomposed relation. D. The CNET-Products Benchmark Overall, the partial decomposition model performs more than The CNET Products Data Set [4] is a description of the an order of magnitude better than the N-ary mode and almost properties of the product catalog of the CNET review site. 4x better than the fully decomposed storage. Since it contains data on many different products, the catalog relation is very wide (almost 3000 attributes) but sparsely VII. C ONCLUSION populated (the average tuple contains 11 non-null values). However some attributes like manufacturer, name and category Partial decomposition is a promising means to reduce the are set for all tuples and can be used for analytics. Schemas data access costs in a MRDBMS. To fully exploit its potential, like this occur frequently when mapping object oriented class however, it is crucial to avoid sacrificing CPU efficiency for hierarchies to relational tables due to the lack of inheritance savings in bandwidth. JiT-Compiled queries naturally avoid in the relational model. In this case, all classes in a hierarchy any CPU-overhead and are, therefore, a natural match to the and their attributes are mapped to the same table. Such Partially Decomposed Storage Model. By combining these schemas make good candidates for partial decomposition. To techniques we achieved the promised bandwidth savings with- fill the CNET schema, we implemented a generator to create out the CPU overhead at query evaluation time. We found relational data according to the reported properties8 . orders of magnitude gain when replacing a hybrid DBMS Unfortunately, the CNET Products Data Set Description based on flexible, Volcano-like operators by a system that JiT- only reports on the properties of the data. It does not provide compiles queries. an application or queries on top of that data. Inspired by the Whilst partial decomposition does not degrade performance, functionality of the CNET products website, we created a the benefit depends largely on the schema and workload of the set of four queries (see Table V) to simulate the load of a database. As a rule of thumb we found that, the more gener- web application. The first three queries correspond to a user ic/wide a schema and scan- and projection-heavy a workload navigating the catalog to get an overview of the available data. is, the higher the benefit of a partial decomposition. For a very generic database schema like the CNET-dataset or the SAP SD 8 http://www.cwi.nl/˜holger/generators/cnet benchmark, the improvement can be significant (factor 3 and 

12 . Query Frequency Description select category, count(*) from products group by category 1 Give overview of all categories with product counts select (price from/10)*10 as price, count(*) from products 1 Drill down to a category and show price where category = $1 group by price order by price; ranges select id, name from products where category=$1 and 100 Show a Listing of all products in a category (price from/10)*10 = $2 for the selected price range select * from products where id=$1 10,000 Show available Details of a selected Product TABLE V: The Queries on the CNET Product Catalog more). We therefore believe that workload-conscious storage [13] G. Diehr and A. Saharia. Estimating block accesses in database optimization is an interesting field for further research. organizations. IEEE TKDE, Jan 1994. [14] G. Graefe. Volcano-an extensible and parallel query evaluation system. Beyond schema decomposition there are a number of other IEEE TKDE, 6(1):120–135, 1994. workload-conscious storage optimizations. Especially with the [15] M. Grund, J. Kr¨uger, H. Plattner, A. Zeier, P. Cudre-Mauroux, and S. Madden. Hyrise: a main memory hybrid storage engine. VLDB focus on sparse data the storage as dense key-value lists is ’10, 4(2):105–116, 2010. an option that may save storage space and processing effort. [16] R. Hankins and J. Patel. Data morphing: An adaptive, cache-conscious We also expect such a key-value storage to be easier to storage technique. In VLDB ’03, pages 417–428. VLDB Endowment, 2003. integrate into existing column-stores than a new processing [17] S. Harizopoulos, D. Abadi, S. Madden, and M. Stonebraker. Oltp model like JiT. Partial compression may work well when data through the looking glass, and what we found there. In ACM SIGMOD is not sparse but has a small domain and might be a good ’08, pages 981–992. ACM, 2008. [18] R. Hedge. Optimizing application performance on Intel Core microar- application for our hardware-conscious cost model. Another chitecture using hardware-implemented prefetchers, 2007. area is online/adaptive reorganization of the decomposition [19] J. Hennessy and D. Patterson. Computer architecture: a quantitative strategy and Query-Layout-Co-Optimization. approach. Morgan Kaufmann Pub, 2011. [20] R. Johnson, V. Raman, R. Sidle, and G. Swart. Row-wise parallel ACKNOWLEDGMENTS predicate evaluation. VLDB ’08, 1(1):622–634, 2008. [21] A. Kemper and T. Neumann. HyPer: A hybrid OLTP&OLAP main The work reported here has partly been funded by the EU- memory database system based on virtual memory snapshots. In ICDE FP7-ICT project TELEIOS. ’11, pages 195–206, 2011. [22] A. Kemper and T. Neumann. One size fits all, again! the architecture R EFERENCES of the hybrid oltp&olap database management system hyper. Enabling Real-Time Business Intelligence, pages 7–23, 2011. [1] D. Abadi, D. Myers, D. DeWitt, and S. Madden. Materialization [23] M. Kersten, S. Plomp, and C. Berg. Object storage management in strategies in a column-oriented dbms. In ICDE ’07, pages 466–475. goblin. IWDOM ’92, 1992. IEEE, 2007. [24] K. Krikellas, S. Viglas, and M. Cintra. Generating code for holistic [2] A. Ailamaki, D. DeWitt, M. Hill, and D. Wood. Dbmss on a modern query evaluation. In ICDE ’10, pages 613–624. IEEE, 2010. processor: Where does time go? In VLDB ’99, pages 266–277, 1999. [25] C. Lattner and V. Adve. The llvm instruction set and compilation [3] D. Batory. Concepts for a database system compiler. In Proceedings of strategy. CS Dept., Univ. of Illinois at Urbana-Champaign, Tech. Report the seventh ACM SIGACT-SIGMOD-SIGART symposium on Principles UIUCDCS, 2002. of database systems, pages 184–192. ACM, 1988. [26] S. Manegold, P. Boncz, and M. L. Kersten. Generic database cost models [4] J. Beckham. The cnet e-commerce data set. University of Wisconsin, for hierarchical memory systems. In VLDB ’02, pages 191–202. VLDB Madison, Tech. Report, 2005. Endowment, 2002. [5] P. Boncz, S. Manegold, and M. Kersten. Database architecture optimized [27] T. Neumann. Efficiently compiling efficient query plans for modern for the new bottleneck: Memory access. In VLDB ’99, pages 54–65, hardware. In VLDB ’11, VLDB, 2011. VLDB, VLDB Endowment. 1999. [28] H. Pirk. Cache conscious data layouting for in-memory databases. [6] P. Boncz, M. Zukowski, and N. Nes. Monetdb/x100: Hyper-pipelining Master’s thesis, Humboldt-Universit¨at zu Berlin, available at query execution. In CIDR ’05, pages 225–237, 2005. http://oai.cwi.nl/oai/asset/19993/19993B.pdf, 2010. [7] A. C´ardenas. Analysis and performance of inverted data base structures. [29] H. Plattner. A common database approach for oltp and olap using an Communications of the ACM, 18(5), May 1975. in-memory column database. In ACM SIGMOD ’09, pages 1–2. ACM, [8] D. Chamberlin, M. Astrahan, M. Blasgen, J. Gray, W. King, B. Lindsay, 2009. R. Lorie, J. Mehl, T. Price, F. Putzolu, et al. A history and evaluation [30] H. Plattner and A. Zeier. In-memory data management, 2011. of system r. Communications of the ACM, 24(10):632–646, 1981. [31] J. Rao, H. Pirahesh, C. Mohan, and G. Lohman. Compiled query [9] T.-Y. Cheung. Estimating block accesses and number of records in file execution engine using jvm. In ICDE’06, pages 23–23. Ieee, 2006. management. Communications of the ACM, 25(7), Jul 1982. [32] J. Sompolski, M. Zukowski, and P. Boncz. Vectorization vs. compilation [10] W. Chu and I. Ieong. A transaction-based approach to vertical partition- in query execution. In DaMoN ’11, pages 33–40. ACM, 2011. ing for relational database systems. IEEE TSE, 19(8):804–812, 1993. [33] T. Westmann, D. Kossmann, S. Helmer, and G. Moerkotte. The imple- [11] R. Cole, F. Funke, L. Giakoumakis, W. Guy, A. Kemper, S. Krompass, mentation and performance of compressed databases. ACM SIGMOD H. Kuno, R. Nambiar, T. Neumann, M. Poess, et al. The mixed workload Record, 29(3):55–67, 2000. ch-benchmark. In DBTest ’11, page 8. ACM, 2011. [34] S. Yao. Approximating block accesses in database organizations. [12] G. P. Copeland and S. N. Khoshafian. A decomposition storage model. Communications of the ACM, 20(4), Apr 1977. In ACM SIGMOD ’85, pages 268–279, New York, NY, USA, 1985. [35] M. Zukowski, P. A. Boncz, N. Nes, and S. H´eman. MonetDB/X100 - A ACM. DBMS In The CPU Cache. IEEE Data Engineering Bulletin, 28(2):17– 22, June 2005.