Bitmap Index Design and Evaluation

1 . Bitmap Index Design and Evaluation Chee-Yong Chan Yannis E. Ioannidis* t Departmentof ComputerSciences Departmentof Computer Sciences University of Wisconsin-Madison University of Wisconsin-Madison cychan@cs.wisc.edu yannis@cs.wisc.edu Abstract dominated by complex adhoc queries that have high selectivity fac- tors (i.e., large foundsets). Bitmap indexing has been touted as a promising approach for pro- A promising approach to process complex queries in DSS is cessing complex adhoc queries in read-mostly environments, like the use of bitmap indexing [8, 9, lo]. Bitmap manipulation tech- those of decision support systems. Nevertheless, only few possible niques have already been used in some commercial products [12] bitmap schemes have been proposed in the past and very little is to speed up query processing: a notable example is Model 204, known about the space-time tradeoff that they offer. In this paper, a pre-relational DBMS from Computer Corporation of America we present a general framework to study the design space of bitmap [S]. More recently, various DBMS vendors, including Oracle, Red- indexes for selection queries and examine the disk-space and time Brick, and Sybase, have introduced bitmap indexes into their prod- characteristics that the various alternative index choices offer. In ucts to meet the performance requirements of DSS applications particular, we draw a parallel between bitmap indexing and num- [5, 61. In its simplest form, a bitmap index on an indexed attribute ber representation in different number systems, and define a space consists of one vector of bits (i.e., bitmap) per attribute value, where of two orthogonal dimensions that captures a wide array of bitmap the size of each bitmap is equal to the cardinalit of the indexed re- indexes, both old and new. Within that space, we identify (analyt- lation The bitmaps are encoded such that the it x record has a value ically or experimentally) the following interesting points: (1) the of TJin the indexed attribute if and only if the ith bit in the bitmap time-optimal bitmap index; (2) the space-optimal bitmap index; (3) associated with the attribute value IJ is set to 1, and the it’” bit in the bitmap index with the optimal space-time tradeoff (knee); and each of the other bitmaps is set to 0. This is called a Value-List (4) the time-optimal bitmap index under a given disk-space con- index [lo]. An example of a Value-List index for a 12-record re- straint. Finally, we examine the impact of bitmap compression and lation R is shown in Figure 1, where each column in Figure l(b) bitmap buffering on the space-time tradeoffs among those indexes. represents a bitmap B” associated with an attribute value ‘u. As part of this work, we also describe a bitmap-index-based evalua- tion algorithm for selection queries that represents an improvement over earlier proposals. We believe that this study offers a useful XA (RI B* 8’ B6 B5 B4 B3 B2 B’ B” first set of guidelines for physical database design using bitmap in- I 3 0 0 0 0 0 I 0 0 0 2 2 0 0 0 0 0 0 1 0 0 dexes. 3 I 0 0 0 0 0 0 0 I 0 4 2 0 0 0 0 0 0 1 0 0 5 8 1 0 0 0 0 0 0 0 0 1 Introduction 6 2 0 0 0 0 0 0 I 0 0 I 2 0 0 0 0 0 0 I 0 0 While the query performance issues of on-line transaction process- 8 0 0 0 0 0 0 0 0 0 I ing (OLTP) systems have been extensively studied [7] and are pretty 9 7 0 I 0 0 0 0 0 0 0 IO 5 0 0 0 I 0 0 0 0 0 much well-understood, the state-of-the-art for Decision Support II 6 0 0 0 0 0 0 0 0 Systems (DSS) is still evolving as indicated by the growing ac- 12 0 0 :, 0 0 0 0 0 tive research in this area [3]. Current database systems, which are -+ ($ optimized mainly for OLTP applications, are not suitable for DSS applications due to their different requirements and workload [6]. In particular, DSS operate in read-mostly environments, which are Figure 1: Example of a Value-List Index. (a) Projection of indexed attribute values with duplicates preserved. (b) Value-List Index. ‘Partially supported by the Narional Science Foundation under Grant IRI-9157368 (PYI Award) and by grants from DEC. IBM, HP, AT&T, Oracle, and Informix. ‘Author’s present address: Department of Informatics, University of Athens, Hel- Consider a high-selectivity-factor query with selection predi- Ias (Greece). cates on two different attributes. A conventional OLTP optimizer would generate one of the following three query plans: (Pl) a full Permission to make digital or hard copies of all or part of thic work for relation scan, (P2) an index scan (using the predicate with lower personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advsn- selectivity factor) followed by a partial relation scan to filter out tags and that copies bear this notice and the full citation on the first page. the non-qualifying tuples, or (P3) an index scan for each selection To copy otherwise, to republish, to post on servers or to predicate, followed by a “merge” of the results from the two in- redistribute to lists, requires prior specific permission and/or a fee. dex scans. Due to the compact sizes of bitmaps (especially for SIGMOD ‘98 Seattle, WA, USA attributes with low cardinality) and the efficient hardware support 8 1998 ACM 0-89791-9955/98/006...$5.00 for bitmap operations (AND, OR, XOR, NOT), plan (P3) using bitmap indexes is likely to be more efficient than a plan that re- 355 

2 .quires a partial or full relation scan (plans (PI) and (P2)). A simple cost analysis shows that evaluating plan (P3) with bitmap indexes is more efficient than using the conventional RID-list based indexes for queries with selectivity factor above some threshold. Let N and n be the relation and query result cardinalities, respectively. As- sume that each RID is 4 bytes long and that one bitmap is scanned per predicate. In terms of the number of bytes read, using bitmap indexes for Ian (P3) is more efficient than using RID-list based indexes if 2KR < 4(2n); i.e., % 2 &. Furthermore, operations on bitmaps are more CPU-efficient than merging RID-lists. Various bitmap indexes [8,9,10, 13, 141have been designed for different query types, including range queries, aggregation queries, and OLAP-style queries. However, as there is no overall best bitmap index over all kinds of queries, maintaining multiple types of bitmap indexes for an attribute may be necessary in order to achieve the de- sired level of performance. While the gains in query performance Figure 2: Space-Time Tradeoff Issues using a multiple-index approach might be offset by the high update cost in OLTP applications, this is not an issue in the read-mostly environment of DSS applications. Indeed, the multiple-index ap- selection queries. Section 3 presents an improved evaluation algo- proach is adopted by Sybase IQ, a DBMS specifically designed for rithm for bitmap indexes, including both analytical and experimen- data warehousing applications, which supports five different types tal performance evaluations. Section 4 presents an analytical cost of bitmap indexes, and requires the database to be fully inverted model for the space-time tradeoff study. Section 5 compares the [l]. Maintaining multiple indexes for an attribute, however, further space-time tradeoff of two basic bitmap encoding schemes. In Sec- increases the disk space requirement of data warehouse applica- tion 6, we examine the space-optimal (point (A)) and time-optimal tions. Understanding the space-time tradeoff of the various bitmap (point (D)) bitmap indexes. In Section 7, we characterize the knee indexes is therefore essential for a good physical database design. of the space-time tradeoff graph of bitmap indexes (point (C)). Sec- In this paper, we study the space-time tradeoff of bitmap in- tion 8 presents an optimal as well as a heuristic approach to find dexes for the class of selection queries, i.e., queries with predi- the time-optimal bitmap index under space constraint (point (B)). cates of the form “A op u”, where A refers to the indexed attribute, In Section 9, we present an experimental study of the impact of op is one of six comparison operators { I,>, <, >, =, #}, and ‘u bitmap compression on the space-time tradeoff issues. Section 10 is the predicate constant. We refer to selection predicates where presents an analytical study of the effect of bitmap buffering on the op E {=, #} as equality predicates, and to selection predicates space-time tradeoff issues. Finally, we summarize our results in where op E { 5, 2, <, >} as range predicates. Information on Section 11. bitmap indexes for other types of queries (e.g., star-join and group- For the rest of this paper, we use the term index to refer to a by queries) can be found elsewhere [9, IO]. bitmap index. Due to lack of space, the derivations of analytical The main contributions in this paper are as follows: results and the proofs of theorems and algorithms’ correctness are omitted from this paper; full details are given elsewhere [2]. l The presentation of a general framework to study the design space of bitmap indexes for selection queries. The frame- work not only captures the existing proposed ideas but re- 2 Design Space of Bitmap Indexes for Selection Queries veals several other design alternatives as well. In this section, we present a framework to examine the design space l An analysis of the space-time tradeoff of bitmap indexes; of indexes for selection queries. The framework has been inspired in particular, we identify analytically or experimentally four by the work of Wong et. al. [13, 141. interesting points in a typical space-time tradeoff graph, as Let C denote the attribute cardinality; i.e., the number of dis- shown in Figure 2: tinct actual values of the indexed attribute. The attribute cardinality is generally smaller than the cardinality of the attribute domain; i.e., (A) The space-optimal bitmap index. the number of all possible values of the indexed attribute. Without (B) The time-optimal bitmap index under a given space con- loss of generality and to keep the presentation simple, we assume straint. in this paper that the actual attribute values are consecutive integer (C) The bitmap index with the optimal space-time tradeoff, values from 0 to C - 1. For the general case where the actual at- i.e., the knee of the space-time tradeoff graph. tribute values are not necessarily consecutive, a bitmap index can be built either on the entire attribute domain, or on C consecu- (D) The time-optimal bitmap index. tive values by mapping each actual attribute value to its rank via a l An experimental study of the effects of bitmap compression lookup table. As described in Section 1, the Value-List index is a set of bitmaps, on the space-time tradeoff issues. one per attribute value. In other words, if one views this set as l An analytical study of the effects of bitmap buffering on the a two-dimensional bit matrix (Figure l(b)), the focus is on the space-time tradeoff issues. columns. If the focus moves on the rows, however, then the in- dex can be seen as the list of attribute values represented in some l The proposal of a more efficient evaluation algorithm for particular way. As there is a large number of possible representa- bitmap indexes. The new algorithm reduces the number of tions for attribute values (integers in this case), this clearly opens bitmap operations by about 50% and incurs one less bitmap up the way for defining a whole host of bitmap indexing schemes. scan for a range predicate evaluation. In classifying all these representations, we identify two major or- thogonal parameters that define the overall space of alternatives. The rest of this paper is organized as follows. In Section 2, we In particular, considering the Value-List index again, we observe present a framework to study the design space of bitmap indexes for that each attribute value is represented as a single digit (in base-C 356 

3 .arithmetic), this digit being encoded in bits by turning exactly one (2) Bitmap Encoding Scheme Consider the ith component of out of C bits on. The arithmetic we choose for the value repre- an index with attribute cardinality bi. There are essentially two sentation, i.e., the decomposition of the value in digits according to major schemes to directly encode the corresponding values v; (0 5 some base, and the encoding scheme of each digit in bits are the 5 bi - 1) in bits’: two dimensions of the space and are analyzed below. (1) Attribute Value Decomposition Consider an attribute value l Equality Encoding: There are bi bits, one for each possible vandasequenceof(n-l)numbers< b,-l,b,-2, . . ..bl >. Fur- value. The representation of value ‘ui has all bits set to 0, ex- cept for the bit corresponding to v;, which is set to 1. Clearly, thermore, define b, = an equality-encoded component consists of bi bitmaps. l Range Encoding: There are b; bits again, one for each possi- =Vl ?J = fib1 fvl ble value. The representation of value U; has the vi rightmost bits set to 0 and the remaining bits (starting from the one cor- responding to o; and to the left) set to 1 Intuitively, each bitmap ByI has 1 in all the records whose ith component = &(bzbl) + vzbl + v~ value is less than or equal to ‘ui. Since the bitmap Bf’-’ has = K(bxbzbl) + vs(bzbl) + vzbl + vl all bits set to 1, it does not need to be stored, so a range- = encoded component consists of (bi - 1) bitmaps. /n-l \ /z-l \ Figures 4(b) and (c) show the range-encoded indexes correspond- = w, (Ebj) +...+v, (gb3) +...+vzbl+vl, ing to the equality-encoded indexes in Figure 1 and Figure 3, re- spectively. where v; = V; mod bi, V; = 2 , 1 < i 5 n, and each digit L 1 ~a(@ 8’ B6 B5 B4 B3 8’ B’ B” vz is in the range 0 5 wi < b,. I I 1 I I 1 0 0 0 Based on the above, each choice of n and sequence < b,, b,-1 , 2 I I I I I I 0 0 3 1 I I I I I 1 0 bl > gives a different representation of attribute values, and 4 I I I I I I 0 0 the;efore a different index. An index is well-dejned if bi 2 2, 5 0 0 0 0 0 0 0 0 1 <i <TX. Thesequence< b,,b,-l,...,bl >isthebaseof 6 I I 1 I 1 I 0 0 the-index, which is in turn called a base-< b,, b,,-1, . . . , bl > 7 I 1 I I 1 I 0 0 index, If b, = b,-1 = = bl z b, then the base is called 8 1 I I I I I 1 I 9 I 0 0 0 0 0 0 0 uniform and the index is called base-b for short. The index consists IO I I I 0 0 0 0 0 of n components, i.e., one component per digit. Each component II I 1 0 0 0 0 0 0 individually is now a collection of bitmaps, constituting essentially 12 I I I I 0 0 0 0 a base-bj index. (b) Let ni denote the number of bitmaps in the ith component of an index and {B” - ‘, BrZ -‘, . , BP} denote the collection of ni bitmaps that form the ith component. Figure 3 shows a base- < 3,3 > Value-List index (based on the same 12-record relation in Figure 1). By decomposing a single-component index into a 2- component index. the number of bitmaps has been reduced from 9 to 6. na(R) B; B; B!j Bf B; By 1x3+0 I 3 - 0 I 0 0 0 I 0X3+2 2 2 - 0 0 I I 0 0 0x3+1 3 I - 0 0 I 0 I 0 Figure 4: Examples of Range-Encoded Bitmap Indexes. (a) Projec- 0x3+2 tion of indexed attribute values with duplicates preserved. (b) Sin- 4 2 - 0 0 I I 0 0 2x3+2 gle Component, Base-9 Range-Encoded Bitmap Index. (c) Base- 5 8 I 0 0 I 0 0 < 3,3 > Range-Encoded Bitmap Index. 0x3+2 6 2 - 0 0 I I 0 0 0x3+2 7 2 - 0 0 I I 0 0 Figure 5 shows the two-dimensional design space of indexes 0x3+0 for selection queries, with the two existing alternatives, namely, 8 0 - 0 0 I 0 0 I 2x3+1 the Value-List index and the Bit-Sliced index [lo], classified as 9 I I 0 0 0 I 0 shown, The Value-List index, which is the simplest index and is 1.X3+2 IO 5 - 0 I 0 I 0 0 the most commonly implemented, has a single component and is 2x3+0 equality-encoded. The Bit-Sliced index [lo] has a uniform base II 6 I 0 0 0 0 1 1x3+1 and is range-encoded. A base-10 Bit-Sliced index has been used 12 0 I 0 0 I 0 in MODEL 204 for evaluating range predicates [8]. The Bit-Sliced index is also used in Sybase IQ for evaluating range predicates and 1 We have excluded the third “basic” encoding scheme (the binary encoding Figure 3: Example of a 2-Component Value-List Index (a) Pro- scheme) discussed in [13, 141, as it can be characterized in our framework asa base-2 jection of indexed attribute values with duplicates preserved. (b) decomposition with one of the two encodings we do present. ‘Clearly, a symmetric scheme exists as well, where the roles of right and left are Base-< 3,3 > Value-List Index. exchanged. 357 

4 . BITMAP ENCODING SCHEME 4 bitmap operations and 5 bitmap scans, compared to Algorithm RangeEval, which incurs 10 bitmap operations and 6 bitmap scans. Moreover, while efficient processing of Algorithm BSRange- Opt requires buffering for only one bitmap (the intermediate/final result), efficient processing of Algorithm RangeEval requires buffer- ing for two bitmaps (for BEQ and BGT/BLT). VALUE DECOMPOSITION c + ’ h, ’ Figure 5: Design Space of Bitmap Indexes for Selection Queries. performing aggregation [lo]. In this paper, we consider all well- defined decompositions, and just the two encoding schemes pre- sented above, which are used in practice. 3 An Improved Evaluation Algorithm for Range-Encoded Bitmap Indexes An evaluation algorithm for selection queries based on range-encoded indexes has been proposed by O’Neil and Quass (Algorithm 4.3 in [IO]), which we referred to as Algorithm RangeEval. In this section, we present an improved evaluation algorithm (Algorithm RangeEval-Opt) that reduces the number of bitmap operations by about 50% and requires one less bitmap scan for a range pred- Figure 7: Comparison of Evaluation Strategies for Selection Predi- icate evaluation, Given this, in the rest of the paper, the improved cate “A 5 864” using a 3-Component, Base-10 Range-Encoded evaluation algorithm is used as the basis for the time analysis of Bitmap Index. (a) Algorithm RangeEval. (b) Algorithm range-encoded indexes. Both evaluation algorithms are shown in RangeEval-Opt. Figure 6. Let Bc and Di denote bitmaps with all bits set to 0 and 1, re- spectively. Also let A, V, and @ denote the logical AND, OR, and 3.1 Analytical Comparison of Evaluation Algorithms for XOR operations, respectively, and B denote the complement of a Range-Encoded Bitmap Index bitmap B. Depending on the input predicate operator (op), Algo- rithm RangeEval evaluates each range predicate by computing two bitmaps: the BEQ bitmap and either the &T or BLT bitmap. Number of Bitmap Operations For example, if the predicate is “<‘I, then the result bitmap BLE is obtained by computing the bitmaps BEQ and BLT; steps that involved BGT, BGE, or BNE are not required. The final result bitmap that is returned is either BLT, BLE. BGT, BGE, BEQ, or BNE, corresponding to the predicate operator “<‘I, “I”, ‘I>“, “2”. “=“, or “#“, respectively. As we show below, such an evaluation strategy not only costs more bitmap operations to incrementally build the two intermediate bitmaps, but also incurs more bitmap RanaeEval-Oot scans since the evaluation of the bitmap BEQ, which corresponds to an equality predicate evaluation, is the most expensive predicate in terms of bitmap scans. Algorithm RangeEval-Opt avoids the intermediate equal- ity predicate evaluation by evaluating each range query in terms Aft 11 n 1 0 ( 1 1 n I2n+l 11 2; of only the “5” predicate based on the following three identities: (1) A < v z A 2 v - 1, (2) A > v = A 5 v, (3) A 2 v E A 5 v - 1. Furthermore, the evaluation of the “I” predi- Table 1: Worst Case Analysis of Evaluation Algorithms; n is the cate itself does not require an equality predicate evaluation. Con- number of index components. sequently, Algorithm RangeEval-Opt requires the computation of only one bitmap B for any predicate evaluation, as opposed to Table 1 shows the worst case analysis of the performance of the two bitmaps (BEQ and either BLT or BGT) required in Algorithm evaluation algorithms in terms of the number of bitmap operations RangeEval. and scans. For Algorithm RangeEval, since each range pred- Figure 7 compares the two algorithms for evaluating the pred- icate evaluation entails an equality predicate evaluation (for BEQ icate “A 2 864” using a 3-component base-10 index. Clearly, bitmap), the number of bitmap operations of a range predicate eval- Algorithm RangeEval-Opt is more efficient as it requires only uation is at least twice that of the “=” predicate evaluation. By us- ing a more direct evaluation strategy, Algorithm RangeEval-Opt 358 

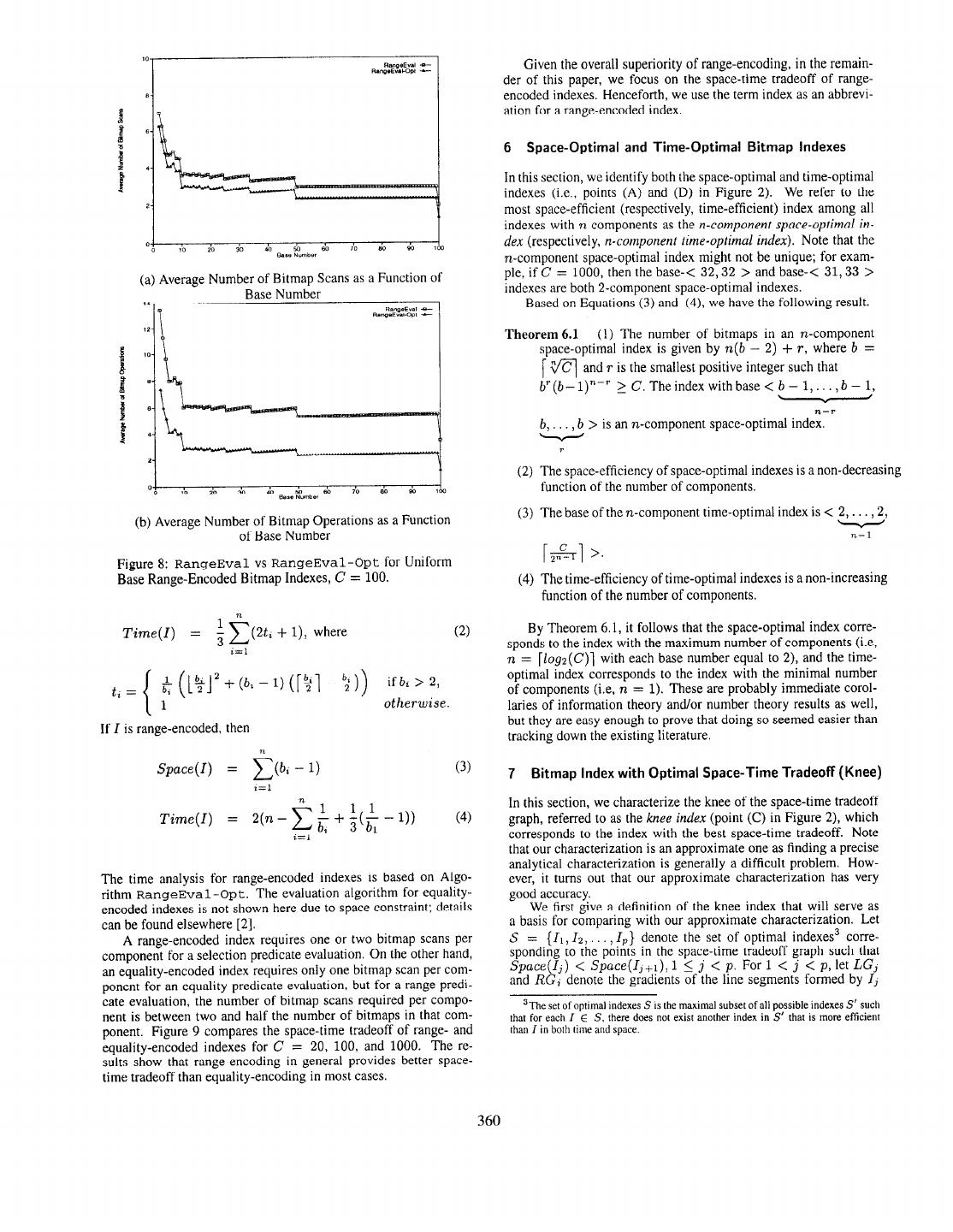
5 . Evaluation Algorithms for Selection Queries Using Range-Encoded Bitmap Indexes. Input: n is the number of components in the range-encoded index. <bn,bn-I,..., bl > is the base of the index. op is the predicate operator, op E {<, >, <,>, =, #}. II is the predicate value. B,, is a bitmap representing the set of records with non-null values for the indexed attribute. Output: A bitmap representation of the set of records that satisfies the predicate “A op v”. Algorithm RangeEval Algorithm RangeEval -Opt I) BGT = BLT = 80; 1) B=B,, 2) BEQ = B,,; 2) if(opE{<,>})thenv=v-1; 3) letv=v,v,-l...vt; 3) let v = 1)~2)~-1 .211; 4) for i = R.downto 1 do 4) if(opE {<,>,<,>})then 5) if (v, > 0) then 5) if (VI < bl - 1) then B = By’ ; BL~ = BLT v (BEG A B;‘-‘); 6) for i = 2 to 71do I;; if (w, < b, - 1) then 7) if (v; # bi - 1) then B = B A By’; 8) BGT = BGT V (BEQ A B1y’); 8) if(ui#O)thenB=BVBY*-‘; BEQ = BEQ A (By’ $ BF’-l); 9) else 9) else 10) for i = 1 to n do 10) 11) if(u;=O)thenB=BABF; 11) BEQ = BEQ A Bf’-‘; 12) else 12) elseif(v;=b;-1)thenB=BAB~‘c2; BGT = BGT V (BEQ A @); 13) elseB=BA(BY’@By’-I); 13) BEQ = BEQ A BP; 14)if(opE {>,>,#})then 14) 15) return % A B,,; 15) BNE = BEQ A B,,; 16) BLE = BLT V BEQ; BGE = BGT V BEQ; 16) else 17) return B,,; 17) return B A B,,,; Figure 6: Algorithms RangeEval and RangeEval-Opt. reduces the number of bitmap operations for range predicate eval- 4 Cost Model for Space-Time Tradeoff Analysis uations by about half; the number of bitmap scans for range pred- icates is reduced by one. Both algorithms have the same cost for Our cost model for the space-time tradeoff analysis uses the fol- an equality predicate evaluation. For both evaluation algorithms, lowing two metrics: the worst case occurs when 0 < w2 < b; - 1, 1 < i 5 n, which corresponds also to the most probable case. l The space metric is in terms of the number of bitmaps stored. l The time metric is in terms of the expected number of bitmap 3.2 Experimental Comparison of Evaluation Algorithms scans for a selection query evaluation, and is based on the as- for Range-Encoded Bitmap Index sumption that the queries in the query space & are uniformly distributed, where Q = {A op IJ : op E (5, 2, <, >, =, # In this section, we compare the performance of the evaluation al- },O 5 w < C}. gorithms in terms of the average number of bitmap scans and the average number of bitmap operations. Indexes with uniform base Note that our time metric incorporates only the I/O cost (i.e., are generated by varying the two main parameters: the attribute number of bitmap scans) and does not include the CPU cost (i.e., cardinality C and the base number b. We experimented with C = number of bitmap operations) as the number of bitmap scans and 50, 100, and 1000; for each value of C, the entire space of base- the number of bitmap operations for a query evaluadon are cor- b range-encoded indexes are generated by varying b from 2 to C. related. We denote the space and time metric of an index I by For each index, we generated a total of 6C selection queries of the Space(l) and Time(l), respectively. form “A op c” by varying the predicate op E { <, 5, >, 2, =, #} and the predicate constant 0 <_ c < C. Each query is evaluated 5 Comparison of Bitmap Encoding Schemes using Algorithm RangeEval and Algorithm RangeEval-Opt. For a given range-encoded index and an evaluation algorithm, the This section compares the performance of the two basic encoding average number of bitmap scans (operations) is computed by tak- schemes, namely, equality encoding and range encoding, for selec- ing the average of the number of bitmap scans (operations) over all tion queries. Our result shows that range encoding provides better 6C queries. space-time tradeoff than equality encoding in most cases. Let I Figure 8 compares the performance of the two evaluation algo- denote an n-component index with base < b,, b,- 1, . . . , bl >. rithms as a function of the base number with C = 100. The graphs Based on the cost model, we have the following result. clearly demonstrate that Algorithm RangeEval-Opt is more ef- ficient than Algorithm RangeEval. Similar trends are obtained for other values of C. Theorem 5.1 If I is equality-encoded, then bi if b; > 2, Space(l) = 25-i, where s; = (1) 1 otherwise. i=l 359 

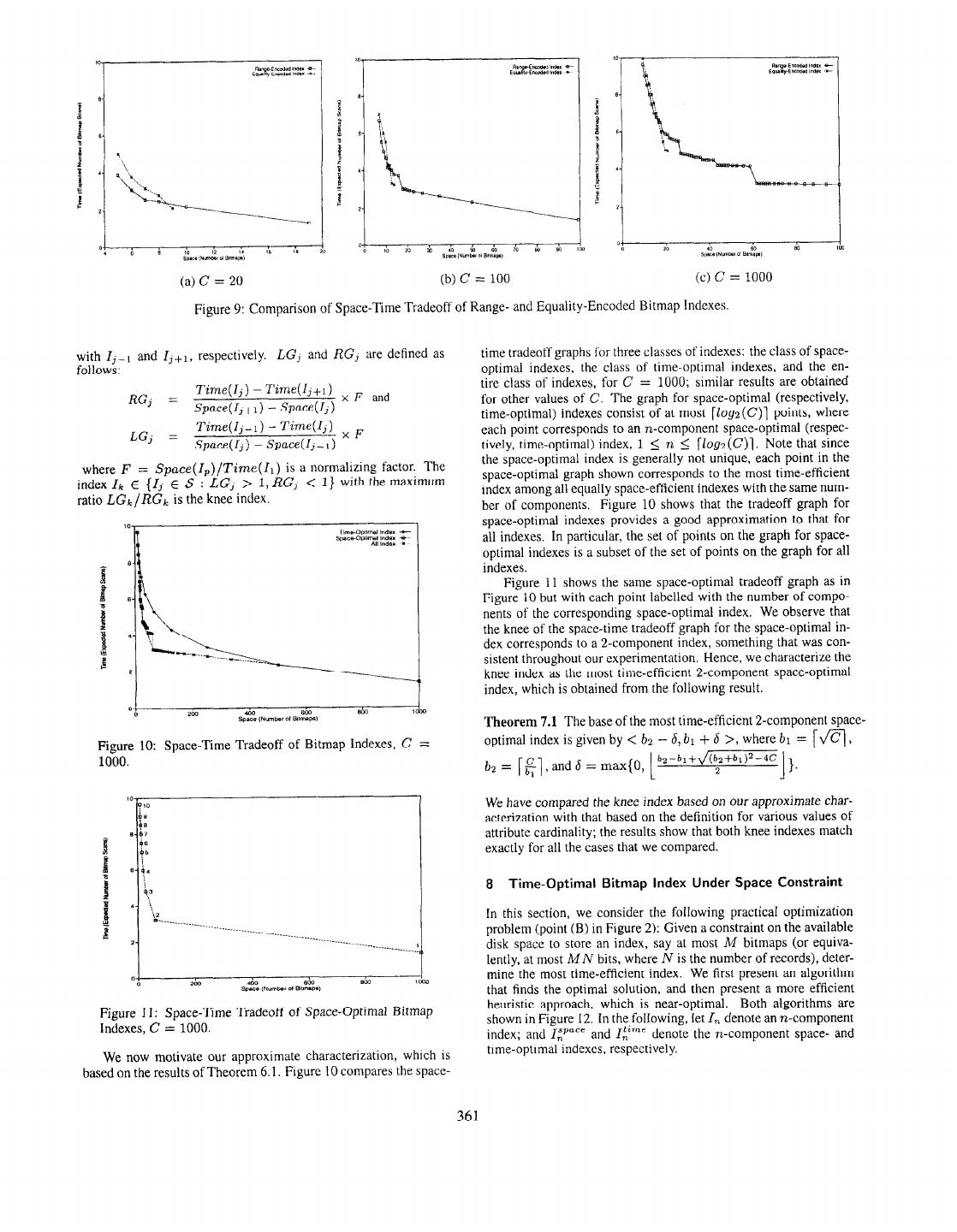
6 . Given the overall superiority of range-encoding, in the remain- der of this paper, we focus on the space-time tradeoff of range- encoded indexes. Henceforth, we use the term index as an abbrevi- ation for a range-encoded index. 6 Space-Optimal and Time-Optimal Bitmap Indexes In this section, we identify both the space-optimal and time-optimal indexes (i.e., points (A) and (D) in Figure 2). We refer to the most space-efficient (respectively, time-efficient) index among all indexes with n components as the n-component space-optimal in- dex (respectively, n-component time-optimal index). Note that the n-component space-optimal index might not be unique; for exam- (a) Average Number of Bitmap Scans as a Function of ple, if C = 1000, then the base-< 32,32 > and base-< 31,33 > Base Number indexes are both 2-component space-optimal indexes. Based on Equations (3) and (4). we have the following result. Theorem 6.1 (1) The number of bitmaps in an n-component space-optimal index is given by n(b - 2) + T, where b = 1q and T is the smallest positive integer such that V(b- l)n-’ 2 C. The index with base < ,b - 1,. ,. , b - l,, lx--T b, . . , b > is an n-component space-optimal index. T (2) The space-efficiency of space-optimal indexes is a non-decreasing 4 Oo I IO I1I.I. 20 30 49 Bale E”,b.. 60 70 I1 80 w I ICC function of the number of components. (3) The base of the n-component time-optimal index is < w (b) Average Number of Bitmap Operations as a Function of Base Number n-1 Figure 8: RangeEval vs RangeEval-Opt for Uniform pi-1 >. Base Range-Encoded Bitmap Indexes, C = 100. (4) The time-efficiency of time-optimal indexes is a non-increasing function of the number of components. Time(l) = 2t, + l), where (2) By Theorem 6.1, it follows that the space-optimal index corre- sponds to the index with the maximum number of components (i.e, n = [logz(C)l with each base number equal to 2), and the time- optimal index corresponds to the index with the minimal number ([+j’+(b,-l)([+l-4)) ifbi>2, of components (i.e. n = 1). These are probably immediate corol- otherwise. laries of information theory and/or number theory results as well, but they are easy enough to prove that doing so seemed easier than If 1 is range-encoded, then tracking down the existing literature. n Space(l) = C(bi - 1) 7 Bitmap Index with Optimal Space-Time Tradeoff (Knee) z=l In this section, we characterize the knee of the space-time tradeoff Time(l) = 2(n - 2 $ + Jj(k - 1)) (4) graph, referred to as the knee index (point (C) in Figure 2), which i=l ’ corresponds to the index with the best space-time tradeoff. Note that our characterization is an approximate one as finding a precise analytical characterization is generally a difficult problem. How- The time analysis for range-encoded indexes is based on Algo- ever, it turns out that our approximate characterization has very rithm RangeEval-Opt. The evaluation algorithm for equality- good accuracy. encoded indexes is not shown here due to space constraint; details We first give a definition of the knee index that will serve as can be found elsewhere [2]. a basis for comparing with our approximate characterization. Let A range-encoded index requires one or two bitmap scans per S = {II, 12, , I,,} denote the set of optimal indexes3 corre- component for a selection predicate evaluation. On the other hand, sponding to the points in the space-time tradeoff graph such that an equality-encoded index requires only one bitmap scan per com- Space(1,) < Space(l,+l), 1 5 j < p. For 1 < j < p, let LGj ponent for an equality predicate evaluation, but for a range predi- and RGj denote the gradients of the line segments formed by I3 cate evaluation, the number of bitmap scans required per compo- 3The set of optimal indexes S is the maximal subset of all possible indexes S’ such nent is between two and half the number of bitmaps in that com- that for each I E S, there does not exist another index in S’ that is more efficient ponent. Figure 9 compares the space-time tradeoff of range- and than I in both time and space. equality-encoded indexes for C = 20, 100, and 1000. The re- sults show that range-encoding in general provides better space- time tradeoff than equality-encoding in most cases. 360 

7 . (c) c (c) c = = 1000 1000 Figure 9: Comparison of Space-Time Tradeoff of Range- and Equality-Encoded Bitmap Indexes. with Ij-r and I,+,, respectively. LG, and RG, are defined as time tradeoff graphs for three classes of indexes: the class of space- follows: optimal indexes, the class of time-optimal indexes, and the en- TiVLe(lj) - ?‘i?TK(lj+l) x F and tire class of indexes, for C = 1000; similar results are obtained RG, = for other values of C. The graph for space-optimal (respectively, SpUCe(lj+l) - Space(l,) time-optimal) indexes consist of at most [logz(C)l points, where Ti77E(lj-1) - Time(lj) x F each point corresponds to an n-component space-optimal (respec- LGj = SpUCe(lj) - Space(l,-1) tively, time-optimal) index, 1 5 n 5 [Zogz(C)l. Note that since the space-optimal index is generally not unique, each point in the where F = Space(l,,)/Time(lr) is a normalizing factor. The space-optimal graph shown corresponds to the most time-efficient index Ik E {I3 E S : LG, > 1, RGj < 1) with the maximum index among all equally space-efficient indexes with the same num- ratio LGk/RGk is the knee index. ber of components, Figure 10 shows that the tradeoff graph for space-optimal indexes provides a good approximation to that for all indexes. In particular, the set of points on the graph for space- optimal indexes is a subset of the set of points on the graph for all indexes. Figure 11 shows the same space-optimal tradeoff graph as in Figure 10 but with each point labelled with the number of compo- nents of the corresponding space-optimal index. We observe that the knee of the space-time tradeoff graph for the space-optimal in- dex corresponds to a 2-component index, something that was con- sistent throughout our experimentation. Hence, we characterize the knee index as the most time-efficient 2-component space-optimal index, which is obtained from the following result. Theorem 7.1 The base of the most time-efficient 2-component space- Figure 10: Space-Time Tradeoff of Bitmap Indexes, C = optimal index is given by < bz - 6, bl + 6 >, where bl = [q, 1000. bz = I$], and 6 = max{O, b2mb1+J(~+b1)2-4C 1). L We have compared the knee index based on our approximate char- acterization with that based on the definition for various values of attribute cardinality; the results show that both knee indexes match exactly for all the cases that we compared. 8 Time-Optimal Bitmap Index Under Space Constraint \2 In this section, we consider the following practical optimization =~--~~---~~-~-~------~-..--...---- .............._.._.__..............~~ ~~ ....-_____-___----_- problem (point (B) in Figure 2): Given a constraint on the available * disk space to store an index, say at most M bitmaps (or equiva- / lently, at most MN bits, where N is the number of records), deter- mine the most time-efficient index. We first present an algorithm that finds the optimal solution, and then present a more efficient heuristic approach, which is near-optimal. Both algorithms are Figure II: Space-Time Tradeoff of Space-Optimal Bitmap shown in Figure 12. In the,following, let I, denote an n-component Indexes, C = 1000. index; and IApace and I:‘,’ denote the n-component space- and time-optimal indexes, respectively. We now motivate our approximate characterization, which is based on the results of Theorem 6.1, Figure 10 compares the space- 361 

8 . Algorithms to Find Time-Optimal Bitmap Index Under Space Constraint. Input: M is the space constraint in terms of the maximum number of bitmaps. C is the attribute cardinality. Output: The time-optimal bitmap index with no more than M bitmaps. Algorithm TimeOptAlg Algorithm TimeOptHeur 1) let n be the smallest number such that Sp~ce(l~~“~“) 5 M; 1) (r&,1)= FindSmallestN(M,C); 2) if (Space(l:lim”) 5 M) then return 12”“; 2) if (Space(lkvL”) 5 ill) then return 1:‘,‘; 3) let n’ be the smallest number such that n’ > n and Spuce(l$“‘) 5 M; 3) return Ref ineIndex(1); 4) let Z = {II, : n < k < n’, Space(lh) 5 M} u {I,!J”“}; 5) return I’ E Z such that Time(1’) 5 Ti,me(l), V I E 1; Figure 12: Algorithms TimeOptAlgandTimeOptHeur 8.1 Optimal Approach Algorithm TimeOptAlg finds the actual optimal solution. By re- sult (2) of Theorem 6.1, the solution must have at least n compo- nents, where n is the smallest number of components such that Spuce(l~Pace ) 5 M. If the n-component time-optimal index satisfies the space constraint (step 2), then by result (4) of Theo- rem 6.1, it is the solution; otherwise, by result (4) of Theorem 6.1, the solution index must have no more than n’ components where n’ 2 n is the smallest number of components such that the n’- component time-optimal index satisfies the space constraint. Fig- ure 13 shows two cases to illustrate the bounds on the number of components of the solution index; each point on the space-time tradeoff graphs shown is labelled with the number of components of the corresponding index. The time complexity of the algorithm is determined by the size of the set of candidate indexes defined by Z (step 4). This search space is large as we need to enumerate for each value of k, n 5 k < n’, all possible /c-component indexes such that n,“=, bi 2 C and Cfzl(bi - 1) < M. F’lgure 14 shows the size of Z as a function of M for C = 1000. 8.2 Heuristic Approach To avoid the costly exhaustive search in the optimal approach (steps 4 and 5), we present in this section a heuristic approach (Algorithm TimeOptHeur in Figure 12) to find an approximate optimal solu- tion. Our experimental results show that the heuristic approach is near-optimal with the optimal index being selected at least 97% of the time. The main idea is to first select a “seed” index that satis- fies the space constraint, and then to improve the time-efficiency of the seed index by adjusting its base numbers. For the seed index, Figure 13: Bounds on Number of Components of Solution Index in our approach uses an n-component index I with Space(l) = M, Algorithm TimeOptAlg. where n is the least number of components such that Space(l~Pace) 5 M. Both n and I are determined by Algorithm FindSmallestN satisfies the space cqnstraint (step Let I:, be another n-component index with base < b’,, b/,-l, .., (Figure 15). Note that if I:,’ b’l > as defined above. Then Time(lL) < Time(1,). 2),then,as in step 2 of Algorithm TimeOptAlg,I$me is the op- timal solution index. Algorithm Ref ineIndex (Figure 15) im- proves the time-efficiency of an index; its correctness is based on Based on Theorem 8.1, Algorithm Ref ineIndex essentially the following result. tries to maximize the number of components with small base num- bers; in particular, step 8 determines the largest possible 6 value for Theorem 8.1 Let I,, be an n-component index with base < 0,) b,- 1, adjusting a pair of base numbers. To illustrate Algorithm Refine- Index,consider a3-component index I withbase < 21,21,22 > . , bl >. Suppose there exists two base numbers b, and b,, and C = 1000. In the first iteration, with b, = b, = 21, S = 19 2 < b, 5 b,, and some integer constant 0 < 6 5 b, - 2, such that n b,--6 ifi=p, and the base is refined to < 2,22,40 >. In the second iteration, b’i 2 C, where b’; = b,+b ifi=q, with b, = 22 and b, = 40, 6 = 12 and the base is refined to II < 2, lo,52 >. After the final refinement step 3, the base of the re- i=l b, otherwise. fined index I’ is < 2,10,50 >. By Equation (3), Space(l) = 61 362 

9 . Algorithm FindSmal les tN: Algorithm to Find the Bitmap Index with Least Number of Components Under Space Constraint. 1 Input: M is the space constraint in terms of the maximum number of bitmaps. C is the attribute cardinality. Output: n, the smallest number of components such that Space(l~Pace) < M, and An n-component index I, with Space(I,,) = M. 1) n=o; // n is the number of components 2) repeat 3) n=n+l; 4) b= +j; 5) r= i M+n)modr~; //r is the number of components with base (b + 1) 6) until ((b + l)Tbn-’ > C); 7) let I, be the n-component bitmap index with base < b, . , b, b + 1,. . . , b + 1 >; -- n--r 7 8) return (n, I,); Algorithm Ref ineIndex: Algorithm to Improve the Time-Efficiency of a Bitmap Index. Input: I, is a ,n-component bitmap index. C is the attribute cardinality. Output: A n-component bitmap index IL such that Time 5 Time(I,) and Space(I:,) I: Space(I,). I) letseqOfBase=<b,,b,-I,...,bl >bethebaseofI,; 2) prodOfBase = fi bi; i=l 3) for i = n downto 2 do 4) let b, be the smallest base number from seqOf Base; 5) delete b, from seqOf Base; 6) if (bp > 2) then 7) let b, be the smallest base number from seq0 f Buse; bb b-b,+&,+bd2-p?,#& 8) let 6 = 2 L J1 9) if (0 < 6 5 b, - 2) then 10) prodOfBase = prodOjBasbep~~-6)(b1+6); 11) b, = b, - 6; 12) b, = b, + 6; 13) b’, = b,; 14) b; = 15) return the n-component bitmap index with base < b’,, b’,- 1, . . , b; >; Figure 15: Algorithms FindSmallestN and Ref ineIndex. and Space(I’) = 59. By Equation (4), Time(I) = 5.08 and Table 2 shows the effectiveness of the heuristic approach for Time(l’) = 4.10. various values of attribute cardinality. The second column shows The time complexities of Algorithms FindSmal les tN and the percentage of solutions selected by the heuristic approach that Ref ineIndex are O(log:,(C)) and O(nlogz(n)), respectively, are optimal for the attribute cardinality value indicated in the first where n is at most [logz(C)l. Therefore, the time complexity of column. For those cases where the optimal and heuristic approaches Algorithm TimeOptHeur is o(logz(C)logz(log:!(C))). differ, the third column shows the maximum difference in the ex- pected number of bitmap scans of their selected indexes. The result indicates that the proposed heuristic approach is near-optimal. Max. Difference in Expected Number 9 Effect of Bitmap Compression on Space-Time Tradeoff 50 500 This section examines the effect of bitmap compression on the 1000 space-time tradeoff of bitmap indexes. [_-I 2000 9.1 Bitmap Index Storage Schemes Table 2: Effectiveness of Heuristic Approach to Select Time- We first investigate different physical organizations for bitmap in- Optimal Bitmap Index under Space Constraint. dexes to identify storage schemes that have good space-time trade- 363 

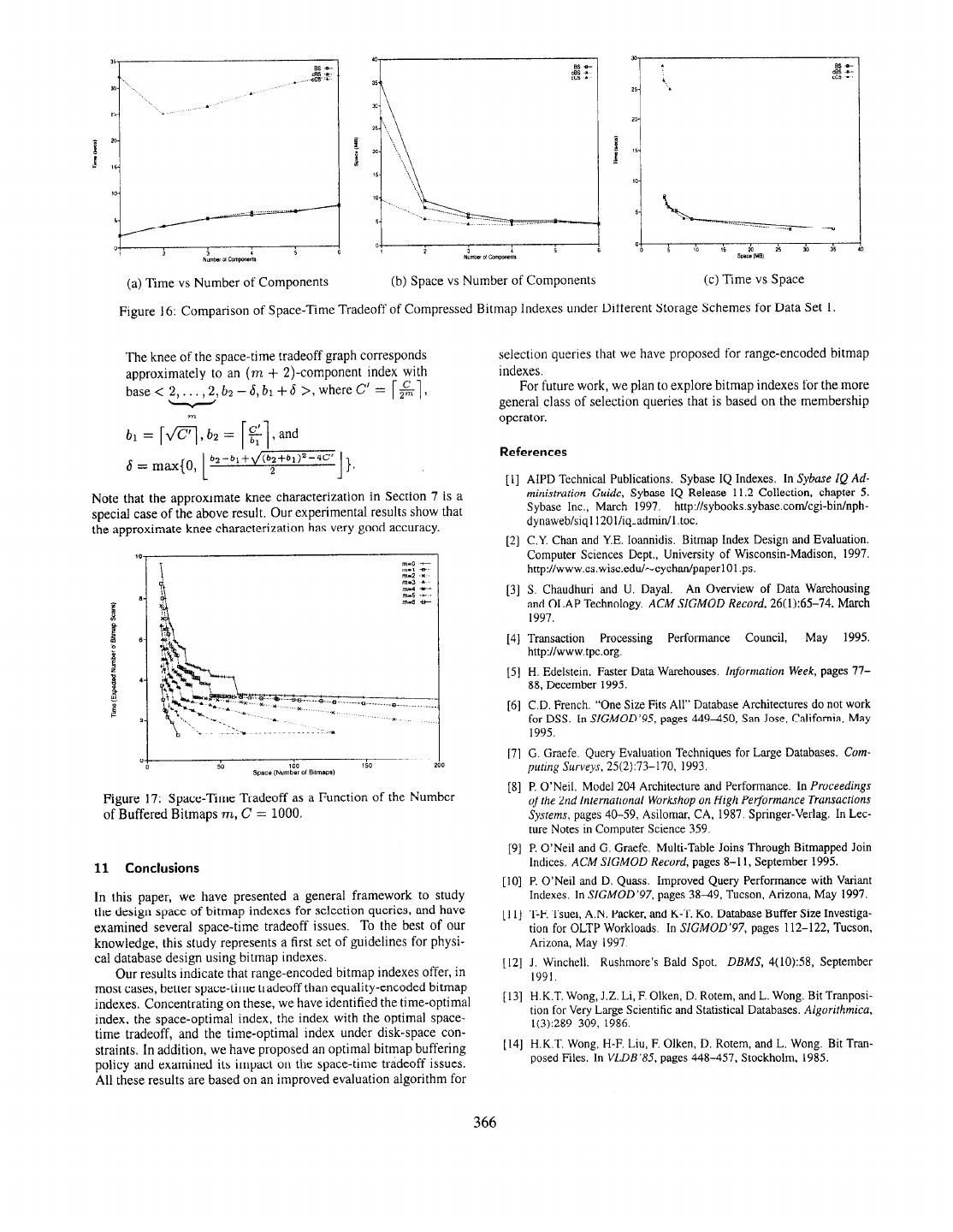
10 . DataSet 1 1 DataSet 2 ‘~~ Table 3: Characteristics of TPC-D Benchmark Data used in Exper- iments to 6; this is motivated by our results in Section 7 which show that the space-time tradeoff of space-optimal indexes provides a good Figure 14: Size of Set of Candidate Bitmap Indexes, 2, as a approximation to the space-time tradeoff of all indexes. The data Function of the Space Constraint A4 for C = 1000. compression code used is from the zlib library5. Table 4 compares the compressibility of the three storage schemes for both data sets. For each n-component index I and each com- off. Consider an k-component bitmap index for a N-record re- pressed storage scheme S, where 1 5 n 5 6 and S E {CBS, cCS, lation, where the z.” index component comprises of 72; bitmaps, clS}, we compute the percentage of the size of I under S to the size of I under BS. For both data sets, the results show that CS- 1 < i 5 lc. Let n = 2 nl. The entire bitmap index is essen- E=l Base Size of I Compressibility of tially a (N x n) bit-matrix, where the ith component is a (N x n;) bit-matrix, and each bitmap is a (N x 1) bit-vector. Based on the above view of a bitmap index, we compare the following three stor- age schemes: Bitmap-Level Storage (BS) Each bitmap is stored individually in a single bitmap file of N bits. Thus, the bitmap index is stored in n N-bit bitmap files. Component-Level Storage (CS) Each index component is stored Base Size of I Compressibility of individually in a row-major order in a single bitmap file of of under BS Storage Scheme (%) (N x ni) bits, 1 < i < Ic. Thus, the bitmap index is stored Index I (in bytes) CBS cCS cIS in k bitmap files. < 2406 > 450,937,500 76.2 2.2 2.2 < 43,56 > 18,187,500 77.6 26.3 28.8 Index-Level Storage (IS) The entire index is stored in a row-major < 11,13,17 > 7,125,OOO 80.7 40.9 48.8 order in a single bitmap file of Nn bits. < 5,7,7,10 > 4,687,500 84.2 60.5 76.8 < 4,5,5,5,5 > 3,562,500 87.7 67.2 87.6 We refer to a bitmap index that is organized using storage scheme < 3,3,3,3,5,6 > 3,187,500 89.7 75.1 93.0 X (without any compression) as a X-index, and refer to a X-index (b) Data Set 2 with all its bitmaps compressed as a cX-index (i.e., c for com- pressed). For a l-component bitmap index, both a CS-index and an IS-index are equivalent. For a bitmap index with the maximum Table 4: Comparison of Compressibility of Different Storage number of components; i.e., each component is of base 2, (1) both Schemes. a BS-index and a CS-index are equivalent, and (2) an IS-index is a projection index4. indexes give the best compression. In a CS-index, each row of a component bit-matrix has either In terms of query evaluation cost, a BS-index requires at most a consecutive stream of 1 bits followed by a consecutive stream of 2 bitmap file scans per index component. On the other hand, both a 0 bits if the index is range-encoded, or exactly one bit set to 1 if CS-index and an IS-index require all the bitmap files to be scanned; the index is equality-encoded. In contrast, in a BS-index, the dis- moreover, they also incur additional CPU overhead to extract the tribution of the bits in each bitmap is dependent on the distribution bits of each relevant bitmap from the component bitmap files (which of the attribute values. Thus, we expect a CS-index to be more are stored in row-major order). Thus, we expect CBS-indexes to compressible than a BS-index. be more time-efficient than cCS- and cIS-indexes; this is indeed supported by our experimental results. For example, consider the 9.2 Experimental Setup base-50 CBS-index; the average size of each compressed bitmap is 36Y7571448xo.776 = 582,118 bytes. Even when two bitmaps (an Our experimental study uses two data sets extracted from the TPC- averag:if 1,164,236 bytes) are scanned to evaluate an equality D Benchmark [4]: data set 1 is for small attribute cardinality, and query, using the CBS-index is still significantly cheaper than us- data set 2 is for large attribute cardinality. Table 3 shows the key ing the cCS-index (or cIS-index), which requires (36,757,448 x characteristics of our experimental data. To limit the number of ex- 0.272) = 9,998,026 bytes to be scanned. periments for each data set, our comparison of the space-time trade- Since CBS-indexes are the most time-efficient and cCS-indexes off is restricted to the class of space-optimal indexes (as a function are the most space-efficient, we shall compare the space-time trade- of the number of index components, n) with n being varied from 1 ‘The zlib library is written by Jean-loup Gdly 4A projection index [IO] on an attribute A in B relation R is simply the projection and Mark Adler (http //www.cdrom,com/pub/infozip/zlib); the compression method of A on R with duplicates preserved and stored in RlD-order. is based on a LZ77 variantcalleddeflation. 364 

11 .offs of only CBS- and cCS-indexes against BS-indexes for the rest into account the amount of main-memory allocated for buffering of this section, Each bitmap index is used to evaluate a set of 2C bitmaps, more optimal indexes with better space-time tradeoff can selection queries & (using Algorithm RangeEval-Opt), where be designed. & = {A op v : op E {<,=},O 5 u < C). The predicate oper- The unit of buffering that we consider here is the number of ator is restricted to “5” (for range queries) and “=” (for equality bitmaps. Consider an n-component index I with base < b,, b,-1, queries) to limit the number of queries. . . , bl >. Let m denote the number of bitmaps that can be buffered The performance of each index is measured in terms of its space- in main-memory, where 1 5 m < Space(l). We denote a m- and time-efficiency. The space metric is in terms of the total space bilmap bujj%l- assignment for I by < f,,, fn-l, . , fl >, where of all its bitmaps (in MBytes), and the time metric is in terms of the f, is the number of bitmaps in the ith component of I that are average predicate evaluation time (in sets) which includes (1) the buffered. A m-bitmap buffer assignment for I is well-defined if time to read the bitmaps, (2) the time for in-memory bitmap decom- 77 pression (for compressed bitmaps), and (3) the time for bitmap op- O<f~<b,,Vl<i~n,and fi =m. c erations The average predicate evaluation time, Tavy, is computed 2=1 C-l In addition to the uniform query distribution assumption stated as follows: T,,q = & c (T> + TT), where Tzp denote the in Section 4, we further assume that the buffer hit rate for each %I=” referenced bitmap is uniformly distributed (i.e., the probabrlity that time to evaluate the predicate “A op v”. a reference to any bitmap in the ith component is a buffer hit is given by A). Then, the expected number of bitmaps scans for 9.3 Experimental Results a selection query evaluation using an n-component index I with a m-bitmap buffer assignment is given by This section presents experimental results for indexes under the storage schemes BS, CBS, and cCS for data set 1; results for data set 2 are not shown due to space limitation. Figure 16(a) compares the Time(I) = 2(n - 2 y + j!($k$ - 1)) (5) time-efficiency of the indexes as a function of the number of index 2=1 z components. Both BS- and CBS-indexes outperform cCS-indexes significantly; in particular, for cCS-indexes, over 70% of the to- We now present an optimal bitmap buffering policy for indexes. tal evaluation time is due to bitmap decompression, The decom- From result (3) of Theorem 6.1 and Theorem 8.1, we know that an pression cost for cCS-indexes generally increases with the number index is more time-efficient if it has more components with smaller of bitmap components since the number of bits to be extracted is base numbers. Since buffering the bitmaps in an index component an increasing function of the number of components. For cCS- effectively reduces the base of that component, it follows that it indexes, since all the compressed bitmap files need to be scanned is more beneficial (in terms of reducing the expected number of for a query evaluation, their I/O cost is a function of the total size of bitmap scans) to buffer a bitmap from a component with a smaller all compressed bitmap files, which generally decreases as the num- base number than from one with a larger base number. The follow- ber of components increases. In contrast, for both BS- and CBS- ing optimal bitmap buffering policy is based on a prioritization of indexes, since the number of bitmaps to be scanned increases with the index components using their base numbers. the number of components, their l/O cost is an increasing function of the number of components. Comparing BS- and CBS-indexes, Theorem 10.1 Consider the following priority assignment to bitmap while CBS-indexes incur a lower I/O cost, this is often offset by components: their bitmap decompression cost; our results show that both BS- and CBS-indexes are almost comparable in their time-efficiency. 1. Partition the components of an index into two disjoint sets Figure 16(b) compares the space-efficiency of the indexes as X and X’ such that X = (1 < i 5 n : b, 5 $bl} and a function of the number of index components. There are two X’=(l<i<n:i#X}. main observations. First, as we already know from Table 4, cCS- 2. Components in X have higher priority than those in X’. indexes are the most space-efficient. Second, the results show that the effectiveness of bitmap compression decreases as the number 3. Within each set (X or X’), components with smaller base of components increases. This can be explained by the fact that numbers have higher priority. the number of bitmaps is a decreasing function of the number of components (result (2) of Theorem 6.1); in particular, there is a Based on the above priority assignment, a bitmap buffering policy significant space reduction when an index is decomposed from one that favors bitmaps from a higher priority component over those to two components. Consequently, the gain of bitmap compression, from a lower priority component is optimal. with respect to space reduction, is only marginal once an index has been decomposed (i.e., n 2 2). Thus, in terms of improving space Based on Equation (5) and the above optimal bitmap buffering efficiency, decomposing an i-component BS-index to an (i + l)- policy, we have the following result. component BS-index could be more effective than compressing the i-component index. Theorem 10.2 If m > 0, the time-optimal index is an m-component Figure 16(c) compares the space-time tradeoff of the indexes. - ,-Y - The result shows that BS- and CBS-indexes have comparable space- >. time tradeoff, which is better than that of cCS-indexes. 10 Effect of Buffering on Space-Time Tradeoff Figure 17 compares the space-time tradeoff of indexes (based on the optimal bitmap buffering policy) as a function of the number This section considers the effect of bitmap buffering on the space- of buffered bitmaps m for C = 1000. As expected, the space- time tradeoff issues that we have addressed. As the typical size of time tradeoff improves as m increases. Based on our experimental buffer space is at least 1 GB in database systems running on SMP observations, we have the following approximate characterization systems for large data warehouse applications [ 111, it is likely that of the knee: a good number of bitmaps can remain memory-resident, By taking 365 

12 . (a) Time vs Number of Components (b) Space vs Number of Components (c) Time vs Space Figure 16: Comparison of Space-Time Tradeoff of Compressed Bitmap Indexes under Different Storage Schemes for Data Set 1. The knee of the space-time tradeoff graph corresponds selection queries that we have proposed for range-encoded bitmap approximately to an (m + 2)-component index with indexes. base<2 ,..., 2,bs--J,bi+S>,whereC’= [$I, For future work, we plan to explore bitmap indexes for the more general class of selection queries that is based on the membership operator. , bz-bl+ (bz+b1)2-4C’ References 6 = max{O, 2 1, [I] AIPD Technical Publications. SybaseIQ Indexes. In Sybuse IQ Ad- Note that the approximate knee characterization in Section 7 is a ministration Guide, Sybase IQ Release 11.2 Collection, chapter 5. special case of the above result. Our experimental results show that Sybase Inc., March 1997. http://sybooks.sybase.com/cgi-bin/nph- dynaweb/siql120l/iq~admin/l.toc. the approximate knee characterization has very good accuracy. [2] C.Y. Chan and Y.E. Ioannidis. Bitmap Index Design and Evaluation. Computer SciencesDept., University of Wisconsin-Madison, 1997. http:Nwww.cs.wisc.edu/~cychan/paperl0l.ps. [3] S. Chaudhuri and U. Dayal. An Overview of Data Warehousing and OLAP Technology. ACM SlGMOD Record, 26( 1):65-74, March 1997. [4] Transaction Processing Performance Council, May 1995. http://www.tpc.org. [5] H. Edelstein. FasterData Warehouses,information Week, pages77- 88, December 1995. [6] C.D. French. “One Size Fits All” DatabaseArchitecturesdo not work for DSS. In SfGMOD’95, pages449-450, San Jose,California, May 1995. [7] G. Graefe. Query Evaluation Techniquesfor Large Databases.Com- puting Surveys, 25(2):73-170, 1993. [8] P.O’Neil. Model 204 Architecture and Performance.In Proceedings Figure 17: Space-Time Tradeoff as a Function of the Number of the 2nd lnlernarional Workshop on High Performance Transactions of Buffered Bitmaps m, C = 1000. Systems, pages40-59, Asilomar, CA, 1987.Springer-Verlag. In Lec- ture Notes in ComputerScience359. [9] P.O’Neil and G. Graefe. Multi-Table Joins Through Bitmapped Join 11 Conclusions Indices. ACM SIGMOD Record, pages8-l 1, September1995. [lo] P. O’Neil and D. Quass. Improved Query Performancewith Variant In this paper, we have presented a general framework to study Indexes. In SlGMOD’97, pages38849,Tucson,Arizona, May 1997. the design space of bitmap indexes for selection queries, and have [ 1l] T-E Tsuei, A.N. Packer,and K-T. Ko. DatabaseBuffer Size Investiga- examined several space-time tradeoff issues. To the best of our tion for OLTP Workloads. In SIGMOD’97, pages 112-122, Tucson, knowledge, this study represents a first set of guidelines for physi- Arizona, May 1997. cal database design using bitmap indexes. [12] J. Winchell. Rushmore’sBald Spot, DBMS, 4(10):58, September Our results indicate that range-encoded bitmap indexes offer, in 1991. most cases, better space-time tradeoff than equality-encoded bitmap indexes. Concentrating on these, we have identified the time-optimal [ 131 H.K.T. Wong,J.Z. Li, F. Olken, D. Rotem,and L. Wong. Bit Tranposi- tion for Very Large Scientific and Statistical Databases.Algarithmica, index, the space-optimal index, the index with the optimal space- 1(3):289-309,1986. time tradeoff, and the time-optimal index under disk-space con- straints. In addition, we have proposed an optimal bitmap buffering [14] H.K.T. Wong, H-F. Liu, F. Olken, D. Rotem, and L. Wong. Bit Tran- policy and examined its impact on the space-time tradeoff issues, posedFiles. In VLDE’85, pages448-457, Stockholm, 1985. All these results are based on an improved evaluation algorithm for 366