Optimizing Data Warehouse Loading Procedures for Enabling Useful

1 . Processing Forecasting Queries Songyun Duan Shivnath Babu∗ Duke University Duke University syduan@cs.duke.edu shivnath@cs.duke.edu ABSTRACT an important role in personal and enterprise-level decision Forecasting future events based on historic data is useful making. For example, inventory planning involves forecast- in many domains like system management, adaptive query ing future sales based on historic data; and day traders processing, environmental monitoring, and financial plan- rapidly buy and sell stocks based on forecasts of stock per- ning. We describe the Fa system where users and appli- formance [21]. cations can pose declarative forecasting queries—both one- In this paper, we describe the Fa1 data-management sys- time queries and continuous queries—and get forecasts in tem where users and applications can pose declarative fore- real-time along with accuracy estimates. Fa supports effi- casting queries. Fa supports efficient algorithms to generate cient algorithms to generate execution plans automatically execution plans for these queries, and returns forecasts and for forecasting queries from a novel plan space comprising accuracy estimates in real-time. A forecasting query is posed operators for transforming data, learning statistical mod- over a multidimensional time-series dataset that represents els from data, and doing inference using the learned mod- historic data, as illustrated by the following example query. els. In addition, Fa supports adaptive query-processing al- Q1 : Select C gorithms that adapt plans for continuous forecasting queries From Usage to the time-varying properties of input data streams. We re- Forecast 1 day port an extensive experimental evaluation of Fa using syn- The full syntax and semantics of forecasting queries will be thetic datasets, datasets collected on a testbed, and two given in Section 2. The From clause in a forecasting query real datasets from production settings. Our experiments specifies the historic time-series data on which the forecast give interesting insights on plans for forecasting queries, and will be based. The query result will contain forecasts for demonstrate the effectiveness and scalability of our plan- the attributes listed in the Select clause, with the forecasts selection algorithms. given for the timestamp(s) specified in the (new) Forecast clause. By default, this timestamp is specified as an interval, 1. INTRODUCTION called lead-time, relative to the maximum timestamp in the Forecasting future events based on historic data is appli- historic data. cable and useful in a range of domains like proactive system The time-series dataset “Usage” in example query Q1 is management, inventory planning, adaptive query process- shown in Figure 1(a). Usage contains daily observations ing, and sensor data management. On-demand computing from Day 5 to Day 17 of the bandwidth used on three links in systems, e.g., Amazon’s Elastic Cloud [9], treat physical re- an Internet Service Provider’s network. Since Q1 specifies a sources like servers and storage as a part of a shared com- lead-time of 1 day, Q1 ’s result will be a forecast of attribute puting infrastructure, and allocate resources dynamically to C for Day 18. Q1 is a one-time query posed over a fixed support changing application demands. These systems ben- dataset, similar to a conventional SQL query posed over re- efit significantly from early and accurate forecasts of work- lations in a database system. Our next example forecasting load surges and potential failures [13]. query Q2 is posed as a continuous query over a windowed Adaptive query processing [3], where query plans and data stream. physical designs adapt to changes in data properties and Q2 : Select cpu util, num io, resp time resource availability, becomes very effective if these changes From PerfMetricStream [Range 300 minutes] can be predicted with reasonable accuracy. Forecasting plays Forecast 15 minutes, 30 minutes ∗ Supported by an NSF CAREER award and gifts from IBM Q2 is expressed in the CQL continuous query language [1] extended with the Forecast clause. Here, “PerfMetricStream” is a continuous stream of performance metrics collected once Permission to copy without fee all or part of this material is granted provided every minute from a production database server. At times- that the copies are not made or distributed for direct commercial advantage, tamp τ (in minutes), Q2 asks for forecasts of CPU utiliza- the VLDB copyright notice and the title of the publication and its date appear, tion, number of I/Os, and response time for all timestamps and notice is given that copying is by permission of the Very Large Data Base Endowment. To copy otherwise, or to republish, to post on servers in [τ + 15, τ + 30]. This forecast should be based on the or to redistribute to lists, requires a fee and/or special permission from the window of data in PerfMetricStream over the most recent publisher, ACM. 300 minutes, i.e., tuples with timestamps in [τ − 299, τ ]. VLDB ‘07, September 23-28, 2007, Vienna, Austria. 1 Copyright 2007 VLDB Endowment, ACM 978-1-59593-649-3/07/09. African god of fate and destiny 711 

2 . Day A B C Day A B C A −1 B −1 C −1 C 1 Day A−2 B −1 C1 5 36 24 17 5 36 24 17 −− −− −− 16 5 −− −− 16 6 12 46 16 6 12 46 16 36 24 17 17 6 −− 24 17 7 36 46 17 7 36 46 17 12 46 16 69 7 36 46 69 8 12 47 69 8 12 47 69 36 46 17 17 8 12 46 17 9 35 25 17 9 35 25 17 12 47 69 68 9 36 47 68 10 35 46 68 10 35 46 68 35 25 17 16 10 12 25 16 11 13 46 16 11 13 46 16 35 46 68 68 11 35 46 68 12 13 46 68 12 13 46 68 13 46 16 68 12 35 46 68 13 35 46 68 13 35 46 68 13 46 68 16 13 13 46 16 14 36 46 16 14 36 46 16 35 46 68 16 14 13 46 16 15 35 25 16 15 35 25 16 36 46 16 68 15 35 46 68 16 13 47 68 16 13 47 68 35 25 16 16 16 36 25 16 17 12 25 16 17 12 25 16 13 47 68 ? 17 35 47 ? Figure 1: Example datasets. (a) Usage; (b) and (c) are transformed versions of Usage The problem we address in this paper is how to process sions, particularly in high-speed streaming applications. forecasting queries automatically and efficiently in order to Furthermore, plans must adapt as old patterns disappear generate the most accurate answers possible based on pat- and new patterns emerge in time-varying streams. terns in the historic data; also giving accuracy estimates for forecasts. A forecasting query can be processed using an exe- 1.1 Our Contributions and Outline cution plan that builds and uses a statistical model from the One-time and Continuous Forecasting Queries: In historic data. The model captures the relationship between Section 2, we introduce the syntax and semantics of fore- the value we want to forecast and the recent data available casting queries, showing how these queries can be expressed to make the forecast. Before building the model, the plan through simple extensions to conventional declarative lan- may apply a series of transformations to the historic data. guages for querying time-series datasets and data streams. Let us consider a plan p to process our example query Q1 . Plan p first transforms the Usage dataset to generate the Plan Space: Section 3 describes a space of execution plans dataset shown in Figure 1(b). A tuple with timestamp τ (in for forecasting queries. As illustrated above, a plan for fore- days) in this transformed dataset contains the values of at- casting is a combination of (i) transformers that transform tributes A, B, and C for timestamps τ −1 and τ from Usage, the input data in desired ways, (ii) builders that generate as well as the value of C for timestamp τ + 1. These figures statistical models from the transformed data, and (iii) pre- use the notation Xδ to denote the attribute whose value at dictors that make forecasts using the models generated. time τ is the value of attribute X ∈ Usage at time τ + δ. Plan Selection: Sections 4 and 5 describe how to find a Using the tuples from Day 6 to Day 16 in the transformed plan efficiently whose accuracy of forecasting is close to that dataset as training samples, plan p builds a Multivariate of the best plan from the extremely large plan space for a Linear Regression (MLR) model [21] that can estimate the forecasting query. The technical challenge comes from the value of attribute C1 from the values of attributes A, B, C, fact that there are no known ways to estimate the accuracy A−1 , B−1 , and C−1 . The MLR model built is: of a plan without actually running the plan. Hence, conven- C1 = −0.7A−1.04B−0.43C−A−1 +1.05B−1 −0.32C−1 +114.4 tional optimization frameworks based on cost models (e.g., Once this model has been built, it can be used to compute [16]) are inapplicable here. Furthermore, running a plan is Q1 ’s result, which is the “?” in Figure 1(b) because C1 for costly since statistical models can take a long time to build. Day 17 is equal to C for Day 18 given our transformation. In effect, we need algorithms that converge to fairly-accurate By substituting A = 12, B = 25, C = 16, A−1 = 13, B−1 = plans by running as few plans as possible. 47, and C−1 = 68 from Day 17 (Figure 1(b)) into the MLR Adaptive Query Processing: Section 8 describes how we model, we get the forecast 87.78. process continuous forecasting queries over windowed data However, plan p has some severe shortcomings that illus- streams, where our plans need to adapt to the time-varying trate the challenges in accurate and efficient forecasting: nature of the streams. 1. It is nontrivial to pick the best set of transformations to Experimental Evaluation: Sections 6 and 8 report an ex- apply before building the model. For example, if plan tensive experimental evaluation based on synthetic datasets, p had performed the appropriate attribute creation and datasets collected on a testbed, and real operational datasets removal to generate the transformed dataset shown in collected from two production settings (a popular web-site Figure 1(c), then the MLR model built from this data and a departmental cluster). This evaluation gives inter- would forecast 64.10 which is more accurate than 87.78. esting insights on plans for forecasting queries, and demon- Notice from the Usage data that when A−2 and B−1 are strates the effectiveness and scalability of our algorithms. around 35 and 47 respectively, then C1 is around 68. 2. Linear regression may fail to capture complex data pat- terns needed for accurate forecasting. For example, by 2. FORECASTING QUERIES building and using a Bayesian Network model on the We consider multidimensional time-series datasets hav- dataset in Figure 1(c), the forecast can be improved to ing a relational schema Γ, X1 , X2 , . . . , Xn . Γ is a timestamp 68.5 (see Example 2 in Section 3). This observation attribute with values drawn from a discrete and ordered do- raises a challenging question: how can we pick the best main DOM(Γ). A dataset can contain at most one tuple for statistical model to use in a forecasting plan? any timestamp τ ∈ DOM(Γ). Each Xi is a time series. We 3. For high-dimensional datasets, most statistical models use Xi (τ ) to denote Xi ’s value at time τ . (including MLR) have very high model-building times, We defer the discussion of continuous forecasting queries and often their accuracy degrades as well. This fact is over windowed data streams to Section 8. A one-time fore- problematic when forecasts are needed for real-time deci- casting query over a fixed dataset has the general form: 712 

3 . Select AttrList positive (negative), then X is copy of Xj that is shifted From D backward (forward) in time. Forecast [absolute] L [, [absolute] L ] Example 1. The dataset in Figure 1(c) was computed from D(Γ, X1 , . . . , Xn ) is a time-series dataset, AttrList is a sub- the Usage(A, B, C) dataset in Figure 1(a) by applying the set of X1 , . . . , Xn , and L, L are intervals or timestamps from transformers Shift(A, −2), Shift(B, −1), Shift(C, 1), and the DOM(Γ). Terms enclosed within “[“ and “]” are optional. transformer πA−2 ,B−2 ,C1 in sequence. ✷ Before we consider the general case, we will first explain Multivariate Linear Regression (MLR): An MLR syn- the semantics of a simple forecasting query “Select Xi From opsis with input attributes Y1 , . . . , YN and output attribute D Forecast L,” which we denote as Forecast(D, Xi , L). Let Z estimates the value of Z as a linearPcombination of the D consist of m tuples with respective timestamps τ1 < τ2 < Yj values using the equation Z = c + N j=1 αj Yj [20]. The · · · < τm . Then, the result of Forecast(D, Xi , L) is the two- MLR-builder uses a dataset D(Γ, Y1 , . . . , YN , Z) to compute tuple Xi (τm +L), acc ; Xi (τm +L) is the forecast and acc is the regression coefficients αj and the constant c. Note that the estimated accuracy of this forecast. Intuitively, the re- this equation is actually a system of linear equations, one sult of Forecast(D, Xi , L) is the forecast of attribute Xi for equation for each tuple in D. The MLR-builder computes a timestamp that is L time units after the maximum times- the least-squares solution of this system of equations, namely, tamp in D; hence, L is called the lead-time of the forecast. the values of αj s and c that minimize the sum of (Z(τ ) − The extension to forecasting multiple attributes is straight- ˆ ))2 over all the tuples in D [21]. Here, Z(τ ) and Z(τ Z(τ ˆ ) are forward. For example, the result of “Select Xi , Xj From respectively the actual and estimated values of Z in the tuple D Forecast L,” is a four-tuple Xi (τm + L), acci , Xj (τm + with timestamp τ in D. Once all αj s and c have been com- L), accj , where acci and accj are the accuracy estimates of puted, the MLR-predictor can estimate Z in a tuple given the Xi (τm + L) and Xj (τm + L) forecasts. the values of attributes Y1 , . . . , YN . If the query specifies two lead-times L and L , then the query is called a range forecasting query, as opposed to a Bayesian Networks (BN): A BN synopsis is a summary point forecasting query that specifies a single lead-time. The structure that can represent the joint probability distribu- result of a range forecasting query contains a forecast and tion P rob(Y1 , . . ., YN , Z) of a set of random variables Y1 , accuracy estimate for each specified attribute for each times- . . ., YN , Z [20]. A BN for variables Y1 , . . . , YN , Z is a di- tamp in the [L, L ] range. If the keyword absolute is speci- rected acyclic graph (DAG) with N + 1 vertices correspond- fied before a lead-time L, then L is a treated as an absolute ing to the N + 1 variables. Vertex X in the BN is as- timestamp (e.g., March 1, 2007) rather than as an interval sociated with a conditional probability table that captures relative to the maximum timestamp in D. P rob(X|P arents(X)), namely, the conditional probability distribution of X given the values of X’s parents in the Problem Setting: In this paper we consider point forecast- DAG. The DAG structure and conditional probability ta- ing queries of the form Forecast(D, Xi , L). Range forecasting bles in the BN satisfy the following equation for all (Y1 = is not a straightforward extension of point forecasting, and y1 , . . . , YN = yN , Z = z) [20]: will be considered in future work. N Y 3. EXECUTION PLANS P rob(y1 , . . . , yN , z) = P rob(Yi = yi |P arents(Yi )) i=1 A plan for a forecasting query contains three types of log- ical operators—transformers, predictors, and builders—and ×P rob(Z = z|P arents(Z)) a summary data structure called synopsis. Given a dataset D(Γ, Y1 , . . . , YN , Z), the BN-builder finds • A transformer T (D) takes a dataset D as input, and the DAG structure and conditional probability tables that outputs a new dataset D that may have a different approximate the above equation most closely for the tuples schema from D. in D. Since this problem is NP-Hard, the BN-builder uses heuristic search over the space of DAG structures for Y1 , . . ., • A synopsis Syn({Y1 , . . . , YN }, Z) captures the relation- YN , Z [20]. ship between attribute Z and attributes Y1 , . . . , YN , The BN-predictor uses the synopsis generated by the BN- such that a predictor P (Syn, u) can use Syn to esti- builder from D(Γ, Y1 , . . . , YN , Z) to estimate the unknown mate the value of Z in a tuple u from the known values value of Z in a tuple u from the known values of u.Y1 , . . ., of Y1 , . . . , YN in u. Z is called Syn’s output attribute, u.YN . The BN-predictor first uses the synopsis to infer the and Y1 , . . . , YN are called Syn’s input attributes. distribution P rob(u.Z = z|u.Yj = yj , 1 ≤ j ≤ N ). The exact value of u.Z is then estimated from this distribution, • A builder B(D, Z) takes a dataset D(Γ, Y1 , . . . , YN , Z) e.g., by picking the expected value. as input and generates a synopsis Syn({Y1 , . . . , YN }, Z). Next, we give two example physical implementations each Example 2. Figure 2 shows the BN synopsis built by the for the logical entities defined above. BN-builder from the Usage(A−2 , B−1 , C1 ) dataset in Fig- Project transformer: A project transformer πlist retains ure 1(c). To compute example query Q1 ’s result, the BN- attributes in the input that are part of the attribute list list, predictor will use the synopsis to compute P rob(C1 ∈ [16 − and drops all other attributes in the input dataset; so it is 17]|A−2 = 35, B−1 = 47) and P rob(C1 ∈ [68 − 69]|A−2 = similar to a duplicate-preserving project in SQL. 35, B−1 = 47), which are 0 and 1 respectively; hence the forecast 68.5 will be output. ✷ Shift transformer: Shift(Xj ,δ), where 1 ≤ j ≤ n and δ is an interval from DOM(Γ), takes a dataset D(Γ, X1 , . . . , Xn ) 3.1 Initial Plan Space Considered (Φ) as input, and outputs dataset D (Γ, X1 , . . . , Xn , X ) where There is a wealth of possible synopses, builders, predic- the newly-added attribute X (τ ) = Xj (τ + δ). When δ is tors, and transformers from the statistical machine-learning 713 

4 . Prob( A −2 < 24) = 0.4 Prob( B−1 < 35) = 0.2 4. PLAN-SELECTION PRELIMINARIES A−2 B−1 In this section we describe the important characteristics of the problem of selecting a good plan from Φ for a Forecast(D, C1 Xi , L) query. We describe the structure of plans from Φ, estimate the total size of the plan space, and show the dif- Prob( C 1 = [16−17] |A −2 < 24, B−1 < 35) = 1 ficulty in estimating the forecasting accuracy of a plan. Prob( C 1 = [16−17] |A −2 < 24, B−1 > 35) = 1 Observation 1. (Plan structure) Let D(Γ, X1 , . . . , Xn ) Prob( C 1 = [16−17] |A −2 > 24, B−1 < 35) = 1 be a time-series dataset. A plan p ∈ Φ for a Forecast(D, Xi , L) Prob( C 1 = [68−69] |A −2 > 24, B−1 > 35) = 1 query can be represented as Y1 , . . ., YN , type, Z where: • type ∈ {MLR,BN,CART,SVM,RF} is p’s synopsis type. Figure 2: BN synopsis built from data in Fig. 1(c) The synopsis type uniquely determines both p’s builder literature [20]. For clarity of presentation, we begin by con- and p’s predictor. sidering a focused physical plan space Φ. Section 7 describes • Y1 , . . . , YN are attributes such that each Yi = Xj (τ + δ) how our algorithms can be applied to larger plan spaces. for some j and δ, 1 ≤ j ≤ n and δ ≤ 0. Y1 , . . . , YN are An execution plan p ∈ Φ for a Forecast(D, Xi , L) query the input attributes of p’s synopsis. first applies a sequence of transformers to D, then uses a • Attribute Z = Xi (τ + L) is the output attribute of p’s builder to generate a synopsis from the transformed dataset, synopsis. and finally uses a predictor to make a forecast based on the This observation can be justified formally based on our as- synopsis and the transformed dataset. For example, the sumptions about Φ and the definitions of synopses, builders, transformers in Example 1, followed by the BN synopsis predictors, and transformers. Because of space constraints, built by the BN-builder and used to make the forecast by we provide an intuitive explanation only. the BN-predictor in Example 2, is one complete plan in Φ. Recall that plan p for Forecast(D, Xi , L) will use a syn- Transformers: The transformers in a plan p ∈ Φ are lim- opsis to estimate the query result, namely, the value of ited to Shift and π which play a critical role in presenting Xi (τm + L), where τm is the maximum timestamp in D. p’s the input data in ways that a synopsis built from the data synopsis has access only to data in D up to timestamp τm can capture patterns useful for forecasting. Shift creates in order to estimate Xi (τm + L). Furthermore, Φ has only relevant new attributes—not present in the original input the Shift transformer to create new attributes apart from dataset—to include in a synopsis. π eliminates irrelevant attributes X1 , . . . , Xn . Given these restrictions, the input and redundant attributes that harm forecasting if included attributes in p’s synopsis can only be Xj (τ + δ), 1 ≤ j ≤ n in synopses: (i) irrelevant attributes can reduce forecasting and δ ≤ 0, and the output attribute is Xi (τ + L). accuracy by obscuring relevant patterns, and (ii) redundant Observation 2. (Size of plan space) Suppose we restrict attributes can increase the time required to build synopses. the choice of Shift transformers to derive input attributes for Synopses, Builders, and Predictors: A plan p ∈ Φ contains synopses in a plan to Shift(Xj , δ), 1 ≤ j ≤ n and −∆ ≤ δ ≤ one of five popular synopses—along with the builder and 0. Then, the number of unique plans in Φ, |Φ| = 5×2n(1+∆) . predictor for that synopsis—from the machine-learning lit- erature: Multivariate Linear Regression (MLR), Bayesian In one of our application domains, n = 252 and ∆ = 90, so Networks (BN), Classification and Regression Trees (CART), |Φ| = 5 × 222932 ! Support Vector Machines (SVM), and Random Forests (RF) 4.1 Estimating Forecasting Accuracy of a Plan [20]. The choice of which synopses to include in Φ was guided by some recent studies that compare various syn- The forecasting accuracy (accuracy) of a plan p = Y1 , . . ., opses; see Section 9 for details. MLR and BN are described YN , type, Z is the accuracy with which p’s synopsis can in Section 3. We give very brief descriptions of the other estimate the true value of Z given the values of Y1 , . . . , YN . synopses below; more details, including descriptions of re- The goal of plan selection for a Q =Forecast(D, Xi , L) query spective builders and predictors, are in the technical report is to find a plan that has accuracy close to the best among [8]. It is not necessary to understand the specific details of all plans for Q in Φ. To achieve this goal, we need a way to these synopses to understand our contributions. compute the accuracy of a given plan. The preferred technique in statistical machine-learning to • CART synopses capture attribute relationships as a estimate the accuracy of a synopsis is called K-fold cross- decision tree where the nonleaf nodes check conditions validation (K-CV) [20]. K-CV can estimate the accuracy of and the leaf nodes forecast values. a plan p that builds its synopsis from the dataset D(Γ, Y1 , . . ., YN , Z). K-CV partitions D into K (nonoverlapping) • SVM synopses map training data points into a high- partitions, denoted D1 , . . . , DK . (Typically, K = 10.) Let dimensional space and determine linear hyperplanes Di = D − Di . For i ∈ [1, K], K-CV builds a synopsis that best separate (classify) the data. Syni ({Y1 , . . . , YN }, Z) using the tuples in Di , and uses this • RF synopses learn many CARTs by choosing attributes synopsis to estimate the value of u.Z for each tuple u ∈ Di . randomly from a dataset, and combine forecasts from This computation will generate a pair aj , ej for each of the individual CARTs. RFs represent ensemble learning m tuples in D, where aj is the tuple’s actual value of Z and [20] that is used widely in machine-learning today. ej is the estimated value. Any desired accuracy metric can beq computed from these pairs, e.g., root mean squared error • Time-Series Methods: In conjunction with Shift = Pm (aj −ej )2 , giving an accuracy estimate for p. j=1 m transformers, MLR synopses can capture popular time- series forecasting methods like univariate autoregres- Observation 3. (Estimating accuracy) K-CV is a ro- sion [5] and multivariate Muscles [21]. bust technique to estimate the accuracy of a plan p = Y1 , 714 

5 . Original A B C dataset Algorithm Fa’s Plan Search (FPS) Input: Forecast(D(Γ, X1 , . . . , Xn ), Xi , L) query Dataset generated by Shift A B C A−1 B−1 C−1 A−2 B−2 C−2 C1 Output: Forecasts and accuracy estimates are output as FPS runs. FPS is terminated when a forecast with satisfactory transformers accuracy is obtained, or when lead-time runs out; Ranked list A−2 B−1 B−2 A−1 C B C−1 A C−2 C1 1. l = 0; /* current iteration number of outer loop */ BEGIN OUTER LOOP Traverse ranked 2. Attribute set Attrs = {}; /* initialize to an empty set */ list in chunks 3. l = l + 1; /* consider ∆ more shifts than in last iteration */ A−2 4. FOR j ∈ [1, n] and δ ∈ [−l∆, 0] Selected attributes A−2 B−1 Add to Attrs the attribute created by Shift(j, δ) on D; 5. Generate attribute Z = Xi (τ + L) using Shift(Xi , L) on D; A−2 B−1 A−2 B−1 6. Let the attributes in Attrs be Y1 , . . . , Yq . Rank Y1 , . . . , Yq in decreasing order of relevance to Z; /* Section 5.2 */ ( A−2,BN) /* Traverse the ranked list of attributes from start to end */ Chosen plan (A−2, B−1,BN) BEGIN INNER LOOP and accuracy (A−2, B−1,BN) (A−2, B−1,BN) 7. Pick next chunk of attributes from list; /* Section 5.3 */ 8. Decide whether a complete plan should be generated 95% 100% 100% 100% using the current chunk of attributes; /* Section 5.5 */ 9. IF Yes, find the best plan p that builds a synopsis using Best plan and accuracy (A−2, B−1,BN) 100% attributes in the chunk. If p has the best accuracy among all plans considered so far, output the value forecast Figure 4: Pictorial view of FPS processing Example by p, as well as p’s accuracy estimate; /* Section 5.4 */ END INNER LOOP query Q1 from Section 1 END OUTER LOOP vance to attribute Z. Techniques for ranking are described Figure 3: Plan selection and execution algorithm for in Section 5.2. In its inner loop, FPS traverses the ranked one-time forecasting queries list from highly relevant to less relevant attributes, and ex- tracts one chunk of attributes at a time. Techniques for traversing the ranked list are described in Section 5.3. . . ., YN , type, Z without knowing the actual query result. For each chunk C, FPS decides whether or not to derive However, K-CV builds a synopsis of type type K times, and a complete plan from C. Section 5.5 describes how this uses these synopses to estimate Z for each input tuple. decision is made, and the implications of making a wrong In effect, K-CV is computationally expensive. However, dis- decision. If the decision is to derive a plan, then FPS finds cussions with researchers in statistical machine-learning re- a highly-predictive subset of attributes Y1 , . . . , YN from C, vealed that there are no known techniques to estimate the and an appropriate synopsis type type, to produce the best accuracy of an MLR, BN, CART, SVM, or RF synopsis plan p = Y1 , . . . , YN , type, Z possible from C. These tech- fairly accurately on a dataset D without actually building niques are described in Section 5.4. Recall from Section 4.1 the synopsis on D. (In Section 6.6, we report experimental that FPS has to build p’s synopsis in order to estimate p’s results related to this point.) Therefore, K-CV is as good a accuracy. Once the synopsis is built, the extra cost to use technique as any to estimate the accuracy of a plan, and we the synopsis to compute the value forecast by p is small. will use it for that purpose. Whenever FPS finds a plan p whose accuracy estimate is better than the accuracy estimates of all plans produced so 5. PROCESSING ONE-TIME QUERIES far, FPS outputs the value forecast by p as well as p’s accu- The observations in Section 4 motivate our algorithm, racy estimate. Thus, FPS produces more and more accurate called Fa’s Plan Search (FPS), to process a one-time fore- forecasts in a progressive fashion, similar to online aggrega- casting query Forecast(D, Xi , L) query. tion techniques proposed for long-running SQL queries [11]. FPS runs until it is terminated by the application/user who 5.1 Overview of FPS issued the query, e.g., a user may terminate FPS when she Figures 3 and 4 give an overview of FPS which runs as a is satisfied with the current accuracy estimate. two-way nested for loop. For simplicity of presentation, Fig- We now present the options we considered to implement ure 3 does not show how computation can be shared within each step in FPS. These options are evaluated experimen- and across the loops of FPS; sharing and other scalability tally in Section 6, and a concrete instantiation of FPS is issues are discussed in Section 5.6. presented in Section 7. FPS’s outer loop enumerates a large number of attributes of the form Xj (τ + δ), 1 ≤ j ≤ n and −l∆ ≤ δ ≤ 0, where 5.2 Ranking Attributes ∆ ≥ 0 is a user-defined constant. The value of l is in- Line 6 in Figure 3 ranks the attributes enumerated by creased across iterations of the loop so that more and more FPS’s outer loop in decreasing order of relevance to the out- attributes will be enumerated progressively. FPS aims to put attribute Z. Intuitively, attributes more relevant to Z pick subsets of attributes from the enumerated set such that are more likely to give accurate forecasts when included in synopses built from these subsets give good accuracy. Intu- a synopsis to forecast Z. Such relevance can be computed itively, a combination of a highly-predictive attribute subset in one of two ways: (i) correlation-based, where attributes Y1 , . . . , YN and an appropriate synopsis type type gives a are ranked based on their correlation with Z; and (ii) time- plan p = Y1 , . . . , YN , type, Z for estimating Z = Xi (τ + L) based, where attributes whose values are more recent are with good accuracy. ranked higher. As illustrated in Figure 4 and Line 6 of Figure 3, FPS Correlation-based Ranking: There exist two general ap- ranks the enumerated attributes in decreasing order of rele- proaches to measure correlation between attributes Y and Z, 715 

6 .one based on linear-correlation theory and the other based should contain attributes Ω ⊆ C and a synopsis type type on information theory [22]. Linear correlation coefficient that together give the best accuracy in estimating the out- (LCC) is a popular measure of linear correlation [20]. put attribute Z among all choices for (Ω, type). We break P (yi − Y )(zi − Z) this problem into two subproblems: (i) finding an attribute LCC(Y, Z) = LCC(Z, Y ) = qP i qP subset Ω ⊆ C that is highly predictive of Z, and (ii) finding 2 2 a good synopsis type for Ω. i (yi − Y ) i (zi − Z) Each (yi , zi ) is a pair of (Y, Z) values in a tuple in the input dataset, and Y and Z denote the respective means. LCC 5.4.1 Selecting a Predictive Attribute Subset is efficient to compute, but it may not capture nonlinear The problem of selecting a predictive attribute subset correlation. Ω ⊆ C can be attacked as a search problem where each Information gain of Z given Y , denoted IG(Z, Y ), is an state in the search space represents a distinct subset of C information-theoretic measure of correlation between Y and [10]. Since the space is exponential in the number of at- Z computed as the amount by which the entropy of Z de- tributes, heuristic search techniques can be used. The search creases after observing the value of Y . IG(Z, Y ) = H(Z) − technique needs to be combined with an estimator that can H(Z|Y ) = H(Y ) − H(Y P |Z) = IG(Y, Z), where H denotes quantify the predictive ability of a subset of attributes. We entropy, e.g., H(Y ) = − i P rob(yi ) log2 (P rob(yi )). consider three methods for attribute selection: X 1. Wrapper [10] estimates the predictive ability of an at- IG(Z, Y ) = IG(Y, Z) = − P rob(zi ) log2 (P rob(zi )) + tribute subset Ω by actually building a synopsis with Ω as i X X the input attribute set, and using K-CV to estimate ac- P rob(yj ) P rob(zi |yj ) log2 (P rob(zi |yj )) curacy. Wrapper uses Best First Search (BFS) [20] as its j i heuristic search technique. BFS starts with an empty set of Information gain is biased towards attributes with many dis- attributes and enumerates all possible single attribute ex- tinct values, so a normalized variant called symmetrical un- pansions. The subset with the highest accuracy estimate is certainty (SU) is often used to measure ů correlation. ÿ chosen and expanded in the same manner by adding single IG(Y, Z) attributes. If no improvement results from expanding the SU (Y, Z) = SU (Z, Y ) = 2 (1) H(Y ) + H(Z) best subset, up to k (usually, k = 5) next best subsets are Time-based Ranking: Time-based ranking assumes that considered. The best subset found overall is returned when an attribute whose value was collected closer in time to τ the search terminates. Building synopses for all enumerated is likely to be more predictive of Z(τ ) than an attribute subsets makes Wrapper good at finding predictive subsets, whose value was collected earlier in time. For example, con- but computationally expensive. sider attributes Y1 and Y2 created from the input dataset D 2. Correlation-based Feature Selection (CFS) [10] by Shift(X1 , δ1 ) and Shift(X2 , δ2 ) transformers respectively. is based on the heuristic that a highly-predictive attribute Because of the shift, the value of Y1 (τ ) (Y2 (τ )) comes from a subset Ω is composed of attributes that are highly correlated tuple in D with timestamp τ + δ1 (τ + δ2 ). Let δ1 < δ2 ≤ 0. with the (output) attribute Z, yet the attributes in Ω are Then, Y2 (τ ) is more relevant to Z(τ ) than Y1 (τ ). uncorrelated with each other. This heuristic gives the fol- lowing estimator, called CFS Score, to evaluate the ability 5.3 Traversal of the Ranked List in Chunks of a subset Ω, containing k (input) attributes Y1 , . . . , Yk , to Single Vs. Multiple Chunks: FPS traverses the ranked predict the (output) attributePZ (Equation 1 defines SU): k list in multiple overlapping chunks C1 ⊂ C2 ⊂ · · · ⊂ Ck i=1 SU (Yi , Z) CFS Score(Ω) = q Pk Pk (2) that all start from the beginning of the list (see Figure 4). k + i=1 j=i,j=1 SU (Yi , Yj ) If all the attributes are considered as a single chunk (i.e., if The numerator in Equation 2 is proportional to the input- k = 1), then the time for attribute selection and synopsis output attribute correlation, so it captures how predictive Ω learning can be high because these algorithms are nonlinear is of Z. The denominator is proportional to the input-input in the number of attributes. Overlapping chunks enable FPS attribute correlation within Ω, so it captures the amount of to always include the highly relevant attributes that appear redundancy among attributes in Ω. CFS uses BFS to find at the beginning of the list. The potential disadvantage of the attribute subset Ω ⊆ C with the highest CFS Score. overlapping chunks is the inefficiency caused by repetition of 3. Fast Correlation-based Filter (FCBF) [22] is based computation when the same attributes are considered multi- on the same heuristic as CFS, but it uses an efficient de- ple times. However, as we will show in Section 5.6, FPS can terministic algorithm to eliminate attributes in C that are share computation across overlapping chunks, so efficiency either uncorrelated with the output attribute Z, or redun- is not compromised. dant when considered along with other attributes in C that Fixed-size Vs. Variable-size Increments: Successive have higher correlation with Z. While CFS’s processing- overlapping chunks C1 ⊂ C2 ⊂ · · · ⊂ Ck can be chosen with time is usually proportional to n2 for n attributes, FCBF’s fixed-size increments or variable-size increments. An exam- processing-time is proportional to n log n. ple of consecutive chunk sizes with fixed-size increments is |C1 | = 10, |C2 | = 20, |C3 | = 30, |C4 | = 40 and so on (arith- 5.4.2 Selecting a Synopsis Type metic progression), while an example with variable-size in- To complete a plan from an attribute subset Ω, we need crements is |C1 | = 10, |C2 | = 20, |C3 | = 40, |C4 | = 80 and so to pick the synopsis type that gives the maximum accuracy on (geometric progression). in estimating Z using Ω. Recall from Section 4.1 that there are no known techniques to compute the accuracy of a syn- 5.4 Generating a Plan from a Chunk opsis without actually building the synopsis. One simple, At Line 9 in Figure 3, we need to generate a complete but expensive, strategy in this setting is to build all five plan from a chunk of attributes C. This plan Ω, type, Z synopsis types, and to pick the best one. As an alternative, 716 

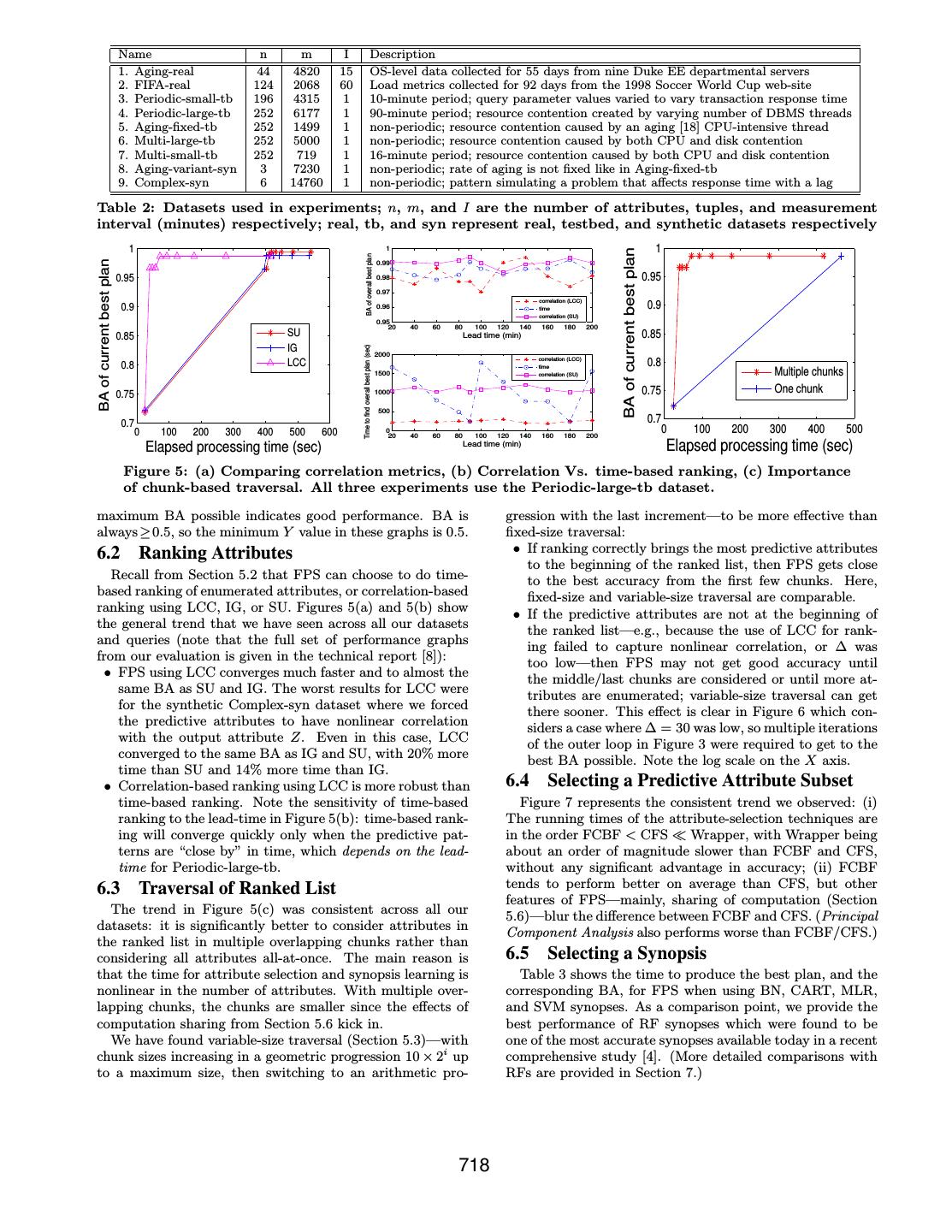
7 . Parameter/Option name Default management system being developed at Duke. Fa is tar- Forecast lead time (Sec. 2) 25 geted at managing the massive volumes of high-dimensional ∆ in FPS (Fig. 3) 90 Ranking attributes (Sec. 5.2) Correlation-based (LCC) data generated by system and database monitoring appli- Ranked-list traversal (Sec. 5.3) Variable-sized (10 × 2i ) cations. Fa’s implementation of all synopses is based on Attribute selection (Sec. 5.4) FCBF the open-source WEKA toolkit [20]. Table 1 indicates the Synopsis type (Sec. 5.4) BN experimental defaults. Generate plan or not? (Sec. 5.5) No pruning Sharing across chunks (Sec. 5.6) FPS-incr-cum 6.1 Datasets, Queries, and Balanced Accuracy Since Fa’s target domain is system and database monitor- Table 1: Defaults for experiments ing, the datasets, forecasting queries, and accuracy metrics we tried to determine experimentally whether one or more we present in this paper are drawn from this domain. The synopsis types in BN, CART, MLR, SVM, and RF compare complete details of our experimental evaluation—including well in general to the other types in terms of both the ac- results omitted due to lack of space and datasets from other curacy achieved and the time to build. The results are very application domains—are given in the technical report [8]. encouraging, and are reported in Section 6.5. We used real, testbed, and synthetic datasets; described next and in Table 2. 5.5 Decision to Generate a Plan or Not Real datasets: We consider two real datasets: Aging-real At Line 8 in Figure 3, we need to decide whether to gener- and FIFA-real. Aging-real is a record of OS-level data col- ate a complete plan using the current chunk of attributes C. lected over a continuous period of two months from nine pro- Generating a complete plan p from C involves an attribute duction servers in the Duke EE departmental cluster; [18] selection and building one or more synopses, so it is desir- gives a detailed analysis. The predictive patterns in this able to avoid or reduce this cost if p is unlikely to be better dataset include the effects of software aging—progressive than the current best plan. To make this decision efficiently, degradation in performance due to, e.g., memory leaks, un- we need an estimator that gives a reasonably-accurate and released file locks, and fragmented storage space—causing efficiently-computable estimate of the best accuracy possible transient system failures. We use Aging-real to process from chunk C. We can prune C if the estimated best accu- queries that forecast with lead-time L whether a server’s racy from C is not significantly higher than the accuracy of average response time will exceed a specified threshold. the current best plan. We considered two options: FIFA-real is derived from a 92-day log for the 1998 FIFA • No Pruning, where a plan is generated for all chunks. Soccer World Cup web-site; [2] gives a detailed analysis. We • Pruning(k), where chunk C is pruned if the best CFS use this dataset to process queries that forecast with lead- Score (Equation 2) among attribute subsets in C is worse time L whether the web-site load will exceed a specified than the k-th best CFS score among all chunks so far. threshold. The load on the FIFA web-site is characteris- tic of most popular web-sites—with periodic segments, high 5.6 Sharing Computation in FPS burstiness at small time scales, but more predictability at Recall from Section 5.3 that FPS traverses the ranked list larger time scales, and occasional traffic spikes. of attributes in overlapping chunks C1 ⊂ C2 ⊂ · · · ⊂ Ck Testbed datasets: These datasets contain OS, DBMS, starting from the beginning of the list. The version of FPS and transaction-level performance metrics collected from a described in Figure 3—which we call FPS-full—performs at- MySQL DBMS running an OLTP workload on a monitoring tribute selection and synopsis building from scratch for each testbed we have developed. Table 2 gives brief descriptions. chunk where a complete plan is generated. These datasets are used to process queries that forecast An incremental version of FPS, called FPS-incr, shares with lead-time L whether the average transaction response (or reuses) computation across chunks by generating a plan time will exceed a specified threshold. Our testbed datasets from the attributes Θ∪{Ci −Ci−1 } at the ith chunk, instead cover (i) periodic workloads—with different period lengths of generating the plan from Ci . Here, Ci − Ci−1 is the set of and complexity of pattern—(ii) aging behavior—both peri- attributes in Ci that are not in Ci−1 , and Θ ⊆ Ci−1 enables odic and non-periodic, fixed and varying rate of aging—and reuse of computation done for previous chunks. We consider (iii) multiple performance problems (e.g., CPU and I/O con- two options for choosing Θ: tention) happening in overlapping and nonoverlapping ways. ¡ Θi−1 (FPS-incr-cum) Synthetic datasets: We also generated synthetic time- Θ= series datasets to study the robustness of our algorithms; Θj , j = argmax1≤j≤i−1 accj (FPS-incr-best) see Table 2. Here, Θj ⊆ Cj is the attribute subset chosen in the plan Balanced Accuracy (BA): Notice that the queries we for chunk Cj (Section 5.4.1), with corresponding accuracy consider in our experimental evaluation forecast whether the accj . Intuitively, Θ in FPS-incr-cum tracks the cumulative system will experience a performance problem L time units attribute subset selected so far, while FPS-incr-best uses the from now. The accuracy metric preferred for such queries in best attribute subset among all chunks so far. the system management domain is called Balanced Accuracy Note that sharing can be done across chunks in a ranked (BA) [13]. BA is computed using K-CV (Section 4.1) as: BA list—like we described above—as well as across the much = 0.5(1 - FP) + 0.5(1 - FN). Here, FP is the ratio of false larger overlapping chunks of attributes considered by succes- positives (predicting a problem when there is none) in the sive iterations of FPS’s outer loop; our description applies actual value, estimated value pairs. Similarly, FN is the to this case as well. ratio of false negatives (failing to predict an actual problem). Graphs: The majority of our graphs track the progress of 6. EXPERIMENTAL EVALUATION FPS over time; the X axis shows the elapsed time since Our algorithms for processing one-time and continuous the query was submitted, and the Y axis shows the best forecasting queries have been implemented in the Fa data BA among plans generated so far. Fast convergence to the 717 

8 . Name n m I Description 1. Aging-real 44 4820 15 OS-level data collected for 55 days from nine Duke EE departmental servers 2. FIFA-real 124 2068 60 Load metrics collected for 92 days from the 1998 Soccer World Cup web-site 3. Periodic-small-tb 196 4315 1 10-minute period; query parameter values varied to vary transaction response time 4. Periodic-large-tb 252 6177 1 90-minute period; resource contention created by varying number of DBMS threads 5. Aging-fixed-tb 252 1499 1 non-periodic; resource contention caused by an aging [18] CPU-intensive thread 6. Multi-large-tb 252 5000 1 non-periodic; resource contention caused by both CPU and disk contention 7. Multi-small-tb 252 719 1 16-minute period; resource contention caused by both CPU and disk contention 8. Aging-variant-syn 3 7230 1 non-periodic; rate of aging is not fixed like in Aging-fixed-tb 9. Complex-syn 6 14760 1 non-periodic; pattern simulating a problem that affects response time with a lag Table 2: Datasets used in experiments; n, m, and I are the number of attributes, tuples, and measurement interval (minutes) respectively; real, tb, and syn represent real, testbed, and synthetic datasets respectively 1 1 1 BA of current best plan BA of overall best plan BA of current best plan 0.99 0.95 0.98 0.95 0.97 correlation (LCC) 0.9 0.96 time 0.9 correlation (SU) 0.95 20 40 60 80 100 120 140 160 180 200 0.85 SU Lead time (min) 0.85 IG Time to find overall best plan (sec) 2000 0.8 LCC correlation (LCC) time 0.8 1500 correlation (SU) Multiple chunks 0.75 1000 0.75 One chunk 500 0.7 0.7 0 100 200 300 400 500 600 0 20 40 60 80 100 120 140 160 180 200 0 100 200 300 400 500 Elapsed processing time (sec) Lead time (min) Elapsed processing time (sec) Figure 5: (a) Comparing correlation metrics, (b) Correlation Vs. time-based ranking, (c) Importance of chunk-based traversal. All three experiments use the Periodic-large-tb dataset. maximum BA possible indicates good performance. BA is gression with the last increment—to be more effective than always ≥ 0.5, so the minimum Y value in these graphs is 0.5. fixed-size traversal: 6.2 Ranking Attributes • If ranking correctly brings the most predictive attributes to the beginning of the ranked list, then FPS gets close Recall from Section 5.2 that FPS can choose to do time- to the best accuracy from the first few chunks. Here, based ranking of enumerated attributes, or correlation-based fixed-size and variable-size traversal are comparable. ranking using LCC, IG, or SU. Figures 5(a) and 5(b) show • If the predictive attributes are not at the beginning of the general trend that we have seen across all our datasets the ranked list—e.g., because the use of LCC for rank- and queries (note that the full set of performance graphs ing failed to capture nonlinear correlation, or ∆ was from our evaluation is given in the technical report [8]): too low—then FPS may not get good accuracy until • FPS using LCC converges much faster and to almost the the middle/last chunks are considered or until more at- same BA as SU and IG. The worst results for LCC were tributes are enumerated; variable-size traversal can get for the synthetic Complex-syn dataset where we forced there sooner. This effect is clear in Figure 6 which con- the predictive attributes to have nonlinear correlation siders a case where ∆ = 30 was low, so multiple iterations with the output attribute Z. Even in this case, LCC of the outer loop in Figure 3 were required to get to the converged to the same BA as IG and SU, with 20% more best BA possible. Note the log scale on the X axis. time than SU and 14% more time than IG. • Correlation-based ranking using LCC is more robust than 6.4 Selecting a Predictive Attribute Subset time-based ranking. Note the sensitivity of time-based Figure 7 represents the consistent trend we observed: (i) ranking to the lead-time in Figure 5(b): time-based rank- The running times of the attribute-selection techniques are ing will converge quickly only when the predictive pat- in the order FCBF < CFS Wrapper, with Wrapper being terns are “close by” in time, which depends on the lead- about an order of magnitude slower than FCBF and CFS, time for Periodic-large-tb. without any significant advantage in accuracy; (ii) FCBF 6.3 Traversal of Ranked List tends to perform better on average than CFS, but other features of FPS—mainly, sharing of computation (Section The trend in Figure 5(c) was consistent across all our 5.6)—blur the difference between FCBF and CFS. (Principal datasets: it is significantly better to consider attributes in Component Analysis also performs worse than FCBF/CFS.) the ranked list in multiple overlapping chunks rather than considering all attributes all-at-once. The main reason is 6.5 Selecting a Synopsis that the time for attribute selection and synopsis learning is Table 3 shows the time to produce the best plan, and the nonlinear in the number of attributes. With multiple over- corresponding BA, for FPS when using BN, CART, MLR, lapping chunks, the chunks are smaller since the effects of and SVM synopses. As a comparison point, we provide the computation sharing from Section 5.6 kick in. best performance of RF synopses which were found to be We have found variable-size traversal (Section 5.3)—with one of the most accurate synopses available today in a recent chunk sizes increasing in a geometric progression 10 × 2i up comprehensive study [4]. (More detailed comparisons with to a maximum size, then switching to an arithmetic pro- RFs are provided in Section 7.) 718 

9 . 1 0.73 0.7 CFS BA of current best plan BA of current best plan FCBF 0.95 0.72 Wrapper 0.65 0.9 0.71 0.6 BA 0.85 0.7 0.55 0.8 0.69 Variable−size increments Fixed−size increments 0.5 0.75 0.68 0.7 0.67 0.45 2 3 1 2 3 4 10 10 10 10 10 10 0 0.01 0.02 0.03 0.04 Elapsed processing time (sec, log scale) Elapsed processing time (sec, log scale) CFS score Figure 6: Choosing chunk sizes Figure 7: Comparing attribute- Figure 8: CFS-Score Vs. BA for (Periodic-large-tb, ∆=30 in Fig. 3) selection techniques (Aging-real) random subsets (Multi-large-tb) FPS (BN) FPS (CART) FPS (MLR) FPS (SVM) RF Dataset BA Time BA Time BA Time BA Time BA Time Aging-real 0.71 62.4 0.71 134.9 0.64 35.8 0.51 1948.7 FIFA-real 0.87 28.8 0.85 36.6 0.84 201.4 Periodic-small-tb 0.84 44.9 0.85 249.3 0.80 130.3 0.86 22339.7 Periodic-large-tb 0.98 71.98 0.98 167.7 0.97 92.6 Aging-fixed-tb 0.91 27.5 0.93 56.8 0.89 145.3 Multi-large-tb 0.72 99.7 0.73 197 0.71 100.8 Multi-small-tb 0.91 53.2 0.91 49.7 0.85 19.1 0.86 482.3 0.91 933.2 Aging-variant-syn 0.82 14.2 0.81 109.4 0.80 24.2 0.85 3200.1 Complex-syn 0.99 130.1 0.99 506.4 0.99 134.7 Table 3: Synopsis comparisons. The time in seconds to produce the best plan, and the corresponding BA, are shown. The missing data points are cases where Java ran out of heap space before convergence. • The running times for SVM and RF are consistently 7. MAKING FPS CONCRETE worse than for BN/CART/MLR. The missing data points The trends observed in our experimental evaluation point for SVM and RF are cases where Java runs out of heap to reasonable defaults for each step of FPS in Figure 3, to space on our machine before the algorithms converge; find a good plan quickly from Φ for a one-time Forecast(D, showing the high memory overhead of these algorithms. Xi , L) query: • BN and CART are competitive with other synopses in • Use LCC for ranking attributes. terms of both accuracy and running time; we attribute • Traverse the ranked list in multiple overlapping chunks, this performance to the fact that once the right transfor- with increasing increments in chunk size up to a point. mations are made, a reasonably-sophisticated synopsis • Generate a complete plan from each chunk considered. can attain close to the best accuracy possible. • Use FCBF or CFS for attribute selection. • Build BN or CART synopses. 6.6 Decision to Generate a Plan or Not • Use FPS-incr-cum for computation sharing. Our attempt to use the best CFS Score from a set of at- tributes Ω as an estimator of the best BA from Ω gave mixed A recent comprehensive study [4] found RFs to be one of the results. Figures 8 and 9 plot the CFS Score and correspond- most accurate synopses available today. Figure 12 compares ing BA for a large set of randomly chosen attribute subsets the above concrete instantiation of FPS with: from Multi-large-tb and Periodic-large-tb: CFS Score seems • RF-base, which builds an RF synopsis on the original to be a reasonable indicator of BA for Multi-large-tb (note input dataset. Intuitively, RF-base is similar to applying the almost linear relationship), but not so for Periodic-large- today’s most-recommended synopsis on the input data. tb (note the points where CFS Score is reasonably high, Note that RF-base does not consider transformations. but BA is far below the best). Figure 10 shows the per- • RF-shifts, which builds an RF synopsis on the input af- formance of CFS-Score-based pruning, for k=1 and k=5, ter applying all Shift(j, δ) transformers, 1 ≤ j ≤ n and for Periodic-large-tb. While pruning does sometimes reduce −∆ ≤ δ ≤ 0. the total processing-time considerably, it does not translate The results in Figure 12 demonstrate FPS’s superiority over into faster convergence; in fact, convergence can be delayed RF-base and RF-shifts in finding a good plan quickly for significantly as seen in Figure 10. one-time forecasting queries. In the technical report, we extend FPS to consider a much 6.7 Effect of Sharing larger space of transformers than Φ. This extension is based Figure 11 shows the consistent trend we observed across on two main observations: all datasets: computation sharing improves the speed of con- vergence of FPS significantly, without any adverse effect on • FPS handles a large space of shift transformations by accuracy. Note that sharing can be done across chunks in a first applying these transformations to create all cor- ranked list as well as across the much larger chunks of at- responding attributes, and then applying efficient at- tributes considered by successive iterations of FPS’s outer tribute traversal and selection techniques to find good loop. To show both effects, we set ∆ = 30 instead of the transformations quickly. The same technique can be default 90 in Figure 11, so multiple iterations of the outer used to consider more transformers, e.g., we consider loop are required to converge. log, wavelet, and difference in the technical report. 719 

10 . 1 1 1 BA of current best plan BA of current best plan 0.9 0.95 0.95 BA 0.8 0.9 0.9 0.7 0.85 No pruning 0.85 FPS−full Pruning (k5) 0.6 0.8 Pruning (k1) 0.8 FPS−incr−best FPS−incr−cum 0.5 0.75 0.75 0.4 0.7 0.7 0 0.02 0.04 0.06 0.08 0.1 0 100 200 300 400 500 600 0 500 1000 1500 CFS score Elapsed processing time (sec) Elapsed processing time (sec) Figure 9: CFS-Score Vs. BA for Figure 10: CFS-Score-based prun- Figure 11: Improvements with random subsets(Periodic-large-tb) ing (Periodic-large-tb) sharing (Periodic-large-tb) BA of current best plan BA of current best plan BA of current best plan BA of current best plan 0.66 0.75 FPS FPS RF−base 0.7 RF−base 0.8 0.64 0.95 FPS RF−shifts RF−shifts FPS RF−base 0.65 RF−base 0.62 RF−shifts 0.7 RF−shifts 0.9 0.6 0.6 0.6 0.55 0.58 0.85 0 1 2 3 0.5 0.5 0 1 2 3 0 1 2 3 4 0 1 2 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 Elapsed processing time (sec, log scale) Elapsed processing time (sec, log scale) Elapsed processing time (sec, log scale) Elapsed processing time (sec, log scale) Figure 12: FPS Vs. State-of-the-art synopsis (RF): (a)Aging-real, (b) Complex-syn, (c) Multi-large-tb, (d) Aging-variant-syn • FPS can first apply simple transformers (e.g., Shift, π) A good algorithm for processing a Forecast(S[W ], Xi , L) and synopses (e.g., BN) to identify the small subset Ω query should use the same plan that FPS would find for each of original and new attributes that contribute to good window of data, but incur minimal cost to maintain this plan plans. Then, more complex transformers and synopses as the window slides. FPS-A (FPS-Adaptive) is our attempt can be applied only on Ω. at such an algorithm. FPS-A exploits the structure (Figure 4) and defaults (Section 7) we established for FPS. FPS-A 8. CONTINUOUS FORECASTING QUERIES works as follows: So far we considered one-time forecasting of the form • The ranked list of all enumerated attributes is main- Forecast(D, Xi , L) where the dataset D is fixed for the dura- tained efficiently. Because FPS uses LCC for rank- tion of the query. We now extend our techniques to handle ing, FPS-A gets two useful properties. First, LCC can continuous queries of the form Forecast(S[W ], Xi , L) where be updated incrementally, and batched updates make S is a data stream of relational tuples, and W is a sliding this overhead very low. Second, recent work [23] shows window specification over this stream. how tens of thousands of LCCs can be maintained in Semantics: The semantics of a Forecast(S[W ], Xi , L) query real-time; we haven’t used this work yet since batched is a straightforward extension of the one-time semantics updates give us the desired performance. from Section 2. The result of a Forecast(S[W ], Xi , L) query at time τ is the same as the result of Forecast(D, Xi , L), • If there are significant changes to the ranked list, then where D is the time-series dataset containing the window the overall “plan structure” is updated efficiently (e.g., W of data in stream S at τ . As time advances, this window the best attribute subset for a chunk may have changed, of data shifts, and a continuous stream of forecasts will be giving a new best plan). produced in the result of Forecast(S[W ], Xi , L). At all points of time, FPS-A maintains a reference rank list Example 3. Consider the example continuous query Fore- Rr composed of k chunks C1r ⊂ C2r ⊂ · · · ⊂ Ckr , the best cast(Usage[Range 5 days],C,1 day) that treats the Usage plans pr1 , . . . , prk for these chunks, and the overall best plan data in Figure 1(a) as a stream. CQL syntax is used to prbest . The current prbest is used for producing forecasts and specify a sliding window containing tuples in the last 5 days. accuracy estimates at any point of time. The reference val- Thus, e.g., on Day 10, a forecast will be output for C for ues are initialized by running FPS on the initial window of Day 11, based on the data (window) for Days 6-10. ✷ tuples. Figure 13 shows how FPS-A maintains these values as the window slides over time. FPS-A uses two user-defined 8.1 FPS-Adaptive (FPS-A) thresholds: α for detecting significant changes in LCC val- We could process a Forecast(S[W ], Xi , L) query by run- ues, and β that determines the batch size for updating LCC ning FPS on the initial window of data to get the best plan values. The notation Level(Y )r is used to denote the num- p, and then keep producing new forecasts using p as the ber of the largest chunk to which attribute Y belongs in Rr . window of data changes. However, this technique will pro- That is, Level(Y )r = i if Y ∈ Cir and Y ∈ r / Ci+1 . duce inaccurate forecasts as the predictive patterns in the After updating LCC scores, FPS-A computes two sets data change over time. Another option is to rerun FPS from of attributes: Gainers (Losers) that moved up (down) one scratch to generate the current best plan whenever the win- or more levels in the ranked list, and whose LCC values dow changes; this option is inefficient. changed significantly. If there are no Gainers or Losers, 720 

11 . 1 1 Algorithm Fa’s Adaptive Plan Maintenance (FPS-A) FPS−A(batch=10) BA of current best plan BA of current best plan Strawman Input: A β-sized batch of tuples inserted/deleted from the 0.9 0.9 sliding window for a Forecast(S[W ], Xi , L) query. Rr , 0.8 0.8 C1r , . . . , Ckr , pr1 , . . . , prk , prbest are the current reference values; Output: The reference values will be updated if required; 0.7 0.7 1. Do batched update of all LCC values to get the new ranked 0.6 0.6 list R and its chunks C1 , . . . , Ck ; 2. For attribute Y , let LCC(Y, Z)r and LCC(Y, Z) be the 0.5 0.5 FPS−A(batch=10) Strawman reference and current LCC between Y and Z = Xi (τ + L); 0.4 3. For attribute Y , Level(Y )r = i if Y ∈ Cir and Y ∈ r ; / Ci+1 0.4 0 1000 2000 3000 4000 5000 0 500 1000 1500 2000 2500 4. For attribute Y , Level(Y ) = i if Y ∈ Ci and Y ∈ / Ci+1 ; Number of tuples processed so far Number of tuples processed so far // Attributes that gained LCC significantly and moved up levels Figure 14: Adaptivity and convergence properties 5. Gainers = Set of Y such that Level(Y )r > Level(Y ) AND |LCC(Y, Z)r − LCC(Y, Z)| > α); β Without property changes With property changes // Attributes that lost LCC significantly and moved down levels FPS-A Strawman % FPS-A Strawman % 6. Losers = Set of Y such that Level(Y )r < Level(Y ) 5 32.02 32.83 2.53 33.41 36.69 9.82 AND |LCC(Y, Z)r − LCC(Y, Z)| > α); 10 61.17 62.24 1.74 66.37 60.73 -8.5 7. IF (|Gainers| = 0 AND |Losers| = 0) 15 89.5 90.99 1.56 81.87 88.33 7.89 8. No changes are required for reference values. Exit; 20 116.27 118.17 1.64 95.50 112.82 18.13 9. FOR (i going from 1 to number of chunks k) { 25 129.34 132.10 2.13 108.54 126.24 16.30 10. IF (there exists a Y ∈ Losers such that Y ∈ pri ) { 11. Regenerate pri using the attribute subset in pri−1 and Table 4: Run-time overhead. Values for FPS-A and the attributes in Ci − Ci−1 , and using BN synopsis; Strawman are tuples processed per second. % is 12. } /* END IF */ FPS-A’s degradation relative to Strawman 13. ELSE { and (b) show FPS-A’s speed of adaptivity and convergence 14. N ewAttrs = Set of attributes Y ∈ Gainers such that properties for two input streams. The input stream used Y ∈ Ci and Y ∈ / pri ; 15. If |N ewAttrs| > 0, then regenerate pri using N ewAttrs in Figure 14(a) concatenates the Multi-large-tb and Aging- and current attribute subset in pri , and BN synopsis; fixed-tb datasets from Table 2 to create a scenario where 16. } /* END ELSE */ predictive patterns change because of a change in workload 17. } /* END FOR */ on the monitored system. The second stream is more ad- 18. Update the reference rank list, chunks, and best plan; versarial where we randomly permute the attributes in the Figure 13: FPS-Adaptive (FPS-A) Multi-small-tb dataset over time. We compare FPS-A’s performance with that of Strawman then the current reference values are fine as is. If one or which runs FPS on the initial window of data to choose the more attributes in the attribute subset of plan pri for the ith initial best plan. Like FPS-A, Strawman updates the BN chunk are in Losers, then pri may have become suboptimal. synopsis in the current best plan after every batch of tuples So, FPS-A regenerates pri using the best attribute subset have been processed. However, unlike FPS-A, Strawman for the previous chunk and the attributes at this level (re- never updates the set of attributes selected. The X-axis call Section 5.6). Similarly, if new attributes have moved in Figure 14 shows the number of tuples processed so far, into the ith chunk, then pri can be updated efficiently to and the Y axis shows the estimated accuracy of the current (possibly) include these attributes. FPS-A builds BN syn- best plan. Note that FPS-A adapts fairly quickly in Figure opses, and updates the synopsis in the current best plan after 14(a) when the stream properties change at X = 2000, but every batch of tuples are processed. While these synopses Strawman does not because the set of predictive attributes can be updated incrementally, we have got equally efficient has changed. Comparing the accuracies before and after the performance from simply rebuilding the synopsis on the few change in Figure 14(a) with the respective individual best (< 10) attributes chosen by attribute selection. accuracies for the Multi-large-tb and Aging-fixed-tb datasets Notice that FPS-A reacts to changes in the ranked list in Table 3, shows that FPS-A indeed finds plans comparable only when attributes transition across levels. (The thresh- to FPS. The behavior in Figure 14(b) is similar. old α filters out spurious transitions at chunk boundaries.) Table 4 shows the extra overhead for FPS-A over Straw- This feature makes FPS-A react aggressively to changes at man for the adversarial stream. When there are no changes the head of the ranked list—where attributes have a higher in stream properties, FPS-A’s extra overhead is limited to chance of contributing to the best plan—and be lukewarm LCC maintenance; which is around 2%. Even when stream to changes in the tail. FPS-A gets this feature from the fact properties change and FPS-A has to update attribute sub- that successive overlapping chunk sizes in FPS increase in a sets, the worst-case overhead is < 20%. Note that FPS-A’s geometric progression. overhead can be lower than that of Strawman if FPS-A finds We now report experiments where we evaluate FPS-A on a smaller attribute subset. the three metrics for adaptive query processing defined in [3]: (i) speed of adaptivity (how quickly can FPS-A adapt to 9. RELATED WORK changes in stream properties?), (ii) convergence properties Time-series forecasting has been a topic of extensive re- (when stream properties stabilize, can FPS-A produce the search for years because of its use in many domains like accuracy that FPS gives for the stable properties?), and (iii) weather and econometric forecasting. Reference [5] is a re- run-time overhead (how much extra overhead does FPS-A cent and comprehensive review of this research over the past incur in settings where stream properties are stable, and in 25 years. The motivation of making systems and DBMSs settings where properties change over time?). easier to manage (ideally self-tuning) has attracted recent We consider continuous queries with a 200-minute win- interest in forecasting (e.g., [13, 14]). Our work differs from dow on the input stream. α = 0.1 for FPS-A. Figures 14(a) previous work on forecasting in two fundamental ways: (i) 721 

12 .we consider declaratively-specified forecasting queries, and 11. REFERENCES develop automated algorithms for choosing plans composed [1] A. Arasu, S. Babu, and J. Widom. The CQL continuous query language: Semantic foundations and query execution. of transformation, prediction, and synopsis-building opera- VLDB Journal, 15(2):121–142, 2006. tors; (ii) our algorithms balance accuracy against the time [2] M. Arlitt and T. Jin. Workload Characterization of the to generate forecasts. 1998 World Cup E-Commerce Site. Technical report, Our goal in this paper is not to propose new synopses or HPL-1999-62, 1999. transformers for forecasting—plenty of such operators are [3] S. Babu. Adaptive Query Processing for Data Stream listed in [5]—but to develop algorithms that can compose Management Systems. PhD thesis, Stanford University, existing operators into a good plan for a given query and Sept. 2005. [4] R. Caruana and A. Niculescu-Mizil. An empirical dataset. While [13, 14] show how various synopses can fore- comparison of supervised learning algorithms. In Intl. cast performance problems and failures in real enterprise Conf. on Machine Learning, June 2006. environments, transformations are selected manually in [13, [5] J. G. De Gooijer and R. J. Hyndman. 25 Years of IIF Time 14]. Muscles [21] uses MLR synopses to process continuous Series Forecasting: A Selective Review. June 2005. forecasting queries over data streams. While Muscles up- Tinbergen Institute Discussion Papers No. TI 05-068/4. dates synopses incrementally as new tuples arrive, the set of [6] A. Deshpande, C. Guestrin, S. Madden, J. Hellerstein, and transformations is not updated. W. Hong. Model-driven data acquisition in sensor networks. In Intl. Conf. on Very Large Databases, Sept. 2004. The design of FPS has been influenced by recent com- [7] A. Deshpande and S. Madden. MauveDB: Supporting parison studies on synopses and transformations done by model-based user views in database systems. In ACM the machine-learning community [4, 10, 19]. Reference [4] SIGMOD Intl. Conf. on Management of Data, June 2006. reports a large-scale empirical comparison of the accuracy [8] S. Duan and S. Babu. Processing forecasting queries. (processing time is not considered) of ten synopses, including Technical report, Duke University, Mar. 2007. regression, BN, CART, SVM, and RF. This study found RF [9] Amazon’s EC2. aws.amazon.com/ec2. to be one of the most accurate synopses available. Reference [10] M. Hall and G. Holmes. Benchmarking attribute selection [19] is a similar study, but with a much smaller scope—only techniques for discrete class data mining. IEEE Trans. on Knowledge and Data Engineering, 15(3), Nov. 2003. BN and CART synopses are considered. However, [19] eval- [11] J. Hellerstein, P. Haas, and H. Wang. Online aggregation. uates processing time and considers some attribute-selection In ACM SIGMOD Intl. Conf. on Management of Data, algorithms. Reference [10] is a comprehensive evaluation of May 1997. attribute-selection algorithms, with findings similar to ours. [12] Data Mining Algorithms in SQL Server 2005. None of this work considers algorithms for determining a msdn2.microsoft.com/en-us/library/ms175595.aspx. good combination of synopses and transformations. [13] R. Powers, M. Goldszmidt, and I. Cohen. Short term Synopses have found many uses recently in database and performance forecasting in enterprise systems. In ACM data stream systems, e.g., in approximate query answer- SIGKDD Intl. Conf. on Knowledge Discovery and Data Mining, Aug. 2005. ing, query optimization, self-tuning, and acquisitional query [14] R. K. Sahoo et al. Critical event prediction for proactive processing [6, 12, 17]. While most of this work focuses on management in large-scale computer clusters. In ACM conventional SQL or XML queries, Fa can benefit from some SIGKDD Intl. Conf. on Knowledge Discovery and Data of it. For example, [23] develops techniques to maintain a Mining, Aug. 2003. large number of LCCs in real-time. Reference [5] urges the [15] S. Sarawagi, S. Thomas, and R. Agrawal. Integrating time-series forecasting community to develop multivariate Association Rule Mining with Relational Database synopses that are robust and easy to use as well as good Systems: Alternatives and Implications. Data Mining and Knowledge Discovery, 4(2-3), 2000. at multi-step-ahead forecasting. Commercial DBMSs have [16] P. Selinger et al. Access path selection in a relational made rapid strides towards becoming self-tuning (e.g., see database management system. In ACM SIGMOD Intl. [17]). However, these systems take a predominantly reac- Conf. on Management of Data, June 1979. tive approach to tuning and diagnosis, which can be made [17] Special issue on self-managing database systems. IEEE proactive with Fa’s accurate and automated forecasting. Data Engineering Bulletin, 29(3), Sept. 2006. Fa can leverage as well as extend work on integrating data- [18] K. Vaidyanathan and K. S. Trivedi. A comprehensive mining algorithms (e.g., [12, 15]) and synopses (e.g., [7]) into model for software rejuvenation. IEEE Transactions on Dependable and Secure Computing, 2(2), 2005. DBMSs. MauveDB [7] proposes a declarative language and [19] N. Williams et al. A Preliminary Performance Comparison efficient materialization and update strategies for synopsis- of Five Machine Learning Algorithms for Practical IP based views. None of this work addresses how to choose Traffic Flow Classification. Computer Communication the best algorithm or synopsis for a specific query or mining Review, 36(5), 2006. task automatically; where ideas from Fa apply. [20] I. H. Witten and E. Frank. Data Mining: Practical Machine Learning Tools and Techniques. Morgan 10. CONCLUSION Kaufmann, second edition, June 2005. In conclusion, the Fa system enables users and applica- [21] B. Yi, N. Sidiropoulos, T. Johnson, H. V. Jagadish, tions to pose declarative forecasting queries—both one-time C. Faloutsos, and A. Biliris. Online data mining for and continuous—and get forecasts in real-time along with co-evolving time sequences. In Intl. Conf. on Data accuracy estimates. We described the FPS algorithm to Engineering, Mar. 2000. process one-time forecasting queries using plans composed of [22] L. Yu and H. Liu. Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution. In Intl. operators for transforming data, building statistical models Conf. on Data Engineering, Aug. 2003. from data, and doing inference using these models. We also [23] Y. Zhu and D. Shasha. Statstream: Statistical monitoring described the FPS-A algorithm that adapts plans for con- of thousands of data streams in real time. In Intl. Conf. on tinuous forecasting queries based on the time-varying prop- Very Large Data Bases, Sept. 2002. erties of input data streams. Finally, we demonstrated the effectiveness and scalability of both algorithms empirically. 722