Macro Base: Analytic Monitoring for the Internet of Things

1 . MacroBase: Analytic Monitoring for the Internet of Things Peter Bailis, Edward Gan, Samuel Madden† , Deepak Narayanan, Kexin Rong, Sahaana Suri Stanford InfoLab and † MIT CSAIL ABSTRACT ample, production infrastructure at LinkedIn and Twitter generates arXiv:1603.00567v3 [cs.DB] 23 Jul 2016 An increasing proportion of data today is generated by automated over 12M events per second [10, 80]. In addition to posing a clear processes, sensors, and devices—collectively, the Internet of Things scalability challenge, these high data rates are also a challenge for in- (IoT). IoT applications’ rising data volume, demands for time- terpretability. We can identify interesting behaviors by applying one sensitive analysis, and heterogeneity exacerbate the challenge of of the many techniques for online outlier detection in the literature, identifying and highlighting important trends in IoT deployments. but the number of outlying points occurring in high-volume IoT In response, we present MacroBase, a data analytics engine that per- data streams may be immense; it is infeasible for users to manually forms statistically-informed analytic monitoring of IoT data streams inspect thousands or more anomalies per second. Consequently, by identifying deviations within streams and generating potential ex- analytic monitoring for IoT requires the use of data explanation planations for each. MacroBase is the first analytics engine to com- techniques that can group and categorize large numbers of outliers bine streaming outlier detection and streaming explanation operators, so users can diagnose their underlying causes. allowing cross-layer optimizations that deliver order-of-magnitude Second, IoT applications often require timely analyses. Analysts speedups over existing, primarily non-streaming alternatives. As frequently reported needs to identify and respond to errors (e.g., a result, MacroBase can deliver accurate results at speeds of up failing devices, resource oversubscription) in minutes or less. As to 2M events per second per query on a single core. MacroBase a result, almost all IoT deployments we encountered in production has delivered meaningful analytic monitoring results in production, used simple rule-based techniques that quickly fire in response to pre- including an IoT company monitoring hundreds of thousands of defined threshold violations. While these rules identify catastrophic vehicles. behavior, they often fail to detect systemic inefficiency and are difficult to adapt to scenarios where typical behavior may vary. In contrast, more sophisticated explanation techniques can overcome 1. INTRODUCTION these shortcomings but are overwhelmingly designed for lower An increasing proportion of data today is generated by automated volume and offline operation (Section 2.2). processes, sensors, and systems in a variety of domains including Third, IoT applications frequently exhibit heterogeneous behav- manufacturing, mobile computing, and transportation—collectively, ior. IoT data streams may contain sources with varying operating the Internet of Things (IoT). Inexpensive hardware, widespread characteristics. For example, the Android ecosystem contains over communication networks, and decreased storage costs have led to 24K distinct device types [65]: an Android application developer tens of billions of dollars in recent commercial investment [57] and must reason about her application’s behavior across each of these projected 40% year-over-year growth in overall data volume [49]. devices and their sensors, each version of the Android operating This increase in machine-generated data leads to a key data man- system, and each of her application releases. Manually identifying agement challenge: while data volumes rise, the capacity of human misbehaving or anomalous groups of software versions, devices, attention remains fixed. It is increasingly intractable to understand and users at scale and in a timely manner is highly challenging. IoT application behavior via manual data inspection. In a series of In response to these challenges, we present MacroBase, a new interviews, system operators and analysts in several IoT domains data analysis system that is specialized for high-performance ana- including datacenter operations, mobile applications, and industrial lytic monitoring of IoT streams.1 MacroBase’s goal is to provide a manufacturing highlighted a common desire for more sophisticated flexible framework for executing analytic monitoring queries in a analytic monitoring, or automated detection of unusual or interest- wide variety of current and future IoT domains while employing spe- ing behaviors in IoT data streams. However, this analytic monitoring cialized analytic monitoring operators for improved efficiency and of IoT streams is made particularly difficult given three key charac- accuracy. Consequently, our focus in this paper is two-fold. First, teristics of IoT applications: we propose a general architecture for combining streaming outlier First, IoT applications generate immense data volume. For ex- detection and streaming data explanation techniques and show how it can be used to enable analytic monitoring of a range of IoT ap- plications. Second, we investigate the design of high-performance analytic monitoring operators that can take advantage of the combi- nation of detection and explanation as well as the characteristics of IoT data streams in order to improve performance and result quality. Architecturally, MacroBase is designed for extensibility. Given the variety of IoT applications as well as the diversity of outlier de- 1 MacroBase is available as open source at http://macrobase.io/. 

2 .tection and data explanation techniques, MacroBase supports a range to reduce update time in risk ratio computation via a new counting of IoT workloads and operators. By default, MacroBase executes sketch, the Amortized Maintenance Counter (AMC). These opti- analytic monitoring queries using a pipeline of domain-independent, mizations improve performance while highlighting the small subset unsupervised streaming detection and explanation operators that of stream attributes that matter most. delivers results with limited end-user intervention. However, Mac- MacroBase’s flexible architecture and optimized operators have roBase users can tailor their queries by i.) adding domain-specific proven useful in production. The system has already identified pre- feature transformations (e.g., time-series operations such as auto- viously unknown behaviors in production, including a telematics correlation and Fourier transformation) to their pipelines—without company monitoring hundreds of thousands of vehicles. We report modification to the rest of the pipeline ii.) providing supervised de- on these experiences and quantitatively evaluate MacroBase’s per- tection rules (or labels) that can complement or replace unsupervised formance and accuracy on both production telematics data as well detectors and iii.) authoring custom streaming transformation, detec- as a range of publicly available real-world datasets. MacroBase’s tion, and explanation operators, whose interoperability is enforced optimized operators exhibit order-of-magnitude performance im- by MacroBase’s type system. provements over less specialized operators at rates of up to 2M E XAMPLE . MacroBase’s default operator pipeline may report that events per second per query while delivering accurate results in devices of type B264 running application version 2.26.3 are sixty controlled studies using both synthetic and real-world data. As we show, this ability to quickly process large data volumes can times more likely to experience abnormally high power drain read- ings than the rest of the stream, indicating a potential problem with also improve result quality by combating bias due to the multiple the interaction between B264 devices and version 2.26.3. If the user testing problem [72], thereby improving statistical significance of also wishes to find time-varying power spikes within the stream, she results. Finally, we demonstrate MacroBase’s extensibility via case can employ a time-series feature transformation to identify time pe- studies in mobile telematics, electricity metering, and video-based surveillance, and via integration with existing analysis frameworks. riods with abnormal time-varying patterns instead. She might later add a manual rule to capture all readings with power drain greater Our contributions in this paper are as follows: than 100W and a custom time-series explanation operator [56], all • MacroBase, an analytics engine and architecture for analytic without modifying the remainder of the operator pipeline. monitoring of IoT data streams that is the first to combine As this example illustrates, compared to conventional dataflow- streaming outlier detection and streaming data explanation. oriented analysis engines such as Heron [54] and Dryad [51], Mac- • The Adaptable Damped Reservoir, the first exponentially roBase provides users with a set of interfaces that are specialized damped reservoir sample to operate over arbitrary windows, for analytic monitoring. However, MacroBase’s analytic monitoring which MacroBase leverages to improve detector responsive- operators can be combined with relational operators, and, just as ness. relational operators can be executed via many dataflow implementa- • An optimization for improving the efficiency of combined tions, MacroBase’s operators preserve compatibility with existing detection and explanation by exploiting cardinality imbalance streaming dataflow engines. between outliers and inliers in streams. Using this flexible architecture, we subsequently develop a set of high-performance analytic monitoring operators that are special- • The Amortized Maintenance Counter, a new heavy-hitters ized for handling the volume, time-sensitivity, and heterogeneity sketch that allows fast updates by amortizing sketch pruning of IoT analyses as well as the combination of outlier detection and across multiple observations of the same item. explanation. Specifically: The remainder of this paper proceeds as follows. Section 2 de- To provide responsive analysis over IoT streams in which a chang- scribes our target environment by presenting motivating use cases ing set of devices may exhibit outlying behavior, MacroBase’s de- and discussing related work. Section 3 presents the MacroBase’s fault operators are designed to track shifts in data. MacroBase interaction model and core pipeline architecture. Section 4 de- leverages a novel sampler, called the Adaptable Damped Reser- scribes MacroBase’s default streaming outlier detection operators voir (ADR), which performs sampling over arbitrarily-sized, expo- and presents the ADR sampler. Section 5 describes MacroBase’s de- nentially damped stream windows. MacroBase uses the ADR to fault streaming explanation operator, including its cardinality-aware incrementally train outlier detectors based on robust statistical esti- optimization and the AMC sketch. We experimentally evaluate Mac- mation [45], which can reliably identify typical behavioral modes roBase’s accuracy and runtime, report on experiences in production, despite large numbers of extreme data points. MacroBase also and demonstrate extensibility via case studies in Section 6. Section 7 adopts exponentially weighted sketching and streaming data struc- concludes with a discussion of ongoing extensions. tures [26, 77] in explanation, which further improve responsiveness and accuracy. To provide interpretable explanations of often relatively rare be- 2. TARGET ENVIRONMENT haviors in IoT streams, MacroBase adopts a metric from statistical MacroBase provides IoT application writers and system analysts epidemiology called the relative risk ratio, which describes the rel- an end-to-end analytic monitoring engine capable of highlighting ative occurrence of key attributes (e.g., age, sex) among infected outlying data within IoT streams while explaining the properties of and healthy populations. MacroBase employs two IoT-specific op- the data that make it outlying. In this section, we describe our target timizations in computing this statistic. First, MacroBase exploits analytic monitoring environment via three motivating use cases and the cardinality imbalance between detected outliers and inliers to a comparison with related work. accelerate explanation generation, an optimization enabled by the combination detection and explanation. Instead of inspecting out- 2.1 Analytic Monitoring Scenarios liers and inliers separately, MacroBase first examines outliers, then As examples of the types of workloads we seek to support, we aggressively prunes its search over inliers. Second, because IoT draw on three use cases from industry. streams contain repeated measurements from devices with similar attributes (e.g., firmware version), MacroBase utilizes this property Mobile applications. Cambridge Mobile Telematics (CMT) is a five-year-old commercial IoT company whose mission is to make 

3 .roads safer by making drivers more aware of their driving habits. but dangerous temperature changes that were taking place much CMT provides drivers with a smartphone application and mobile (i.e. hours) earlier.” The auditor noted that “it should be possible to sensor for their vehicles, and collects and analyzes data from many design a more modern control system that could draw attention to hundreds of thousands of vehicles at rates of tens of Hz. CMT uses trends that are potentially hazardous” [47]. this IoT data to provide users with feedback about their driving. In this paper, we evaluate analytic monitoring’s potential to draw CMT’s engineers report that analytic monitoring has proven es- attention to behaviors within electrical utilities. pecially challenging. CMT’s operators, who include database and systems research veterans, report difficulty in answering several 2.2 Related Work questions: is the CMT application behaving as expected? Are all Performing analytic monitoring in IoT applications as in the users able to upload and view their trips? Are sensors operating at a preceding scenarios requires high-volume, streaming analytics tech- sufficiently granular rate and in a power-efficient manner? The most niques. In this section, we discuss related techniques and systems severe problems in the CMT application are caught by quality assur- from the literature. ance and customer service, but many behaviors are more pernicious. For example, Apple iOS 9.0 beta 1 introduced a buggy Bluetooth Streaming and Specialized Analytics. MacroBase is a stream- stack that prevented iOS devices from connecting to CMT’s sensors. ing data analysis system that is specialized for analytic monitor- Few devices ran these versions, so the overall failure rate was low; ing. In its architecture, MacroBase builds upon a series of systems as a result, CMT’s data volume and heterogeneous install base ob- for streaming data and specialized, advanced analytics tasks. A scured a potentially serious widespread issue in later releases of the range of systems from both academia [4, 20] and industry (e.g., application. Given low storage costs, CMT records all of the data Storm, StreamBase, IBM Oracle Streams) provide infrastructure required to perform analytic monitoring to detect such behaviors, for executing streaming queries. MacroBase adopts dataflow as its yet CMT’s engineers report they have lacked a solution for doing so execution substrate, but its goal is to provide a set of high-level in a timely and efficient manner. analytic monitoring operators; in MacroBase, dataflow is a means In this paper, we report on our experiences deploying MacroBase to an end rather than an end in itself. In designing a specialized en- at CMT, where the system has highlighted interesting behaviors gine, we were inspired by several past projects, including Gigascope such as those above, in production. (specialized for network monitoring) [27], WaveScope (special- ized for signal processing) [35], MCDB (specialized for Monte Datacenter operation. Datacenter and server operation represents Carlo-based operators) [52], and Bismarck (providing extensible ag- one of the highest-volume sources for machine-generated data. In gregation for gradient-based optimization) [32]. In addition, a range addition to the billion-plus events per minute volumes reported at of commercially-available analytics packages provide advanced an- Twitter and LinkedIn, engineers report a similar need to quickly alytics functionality—but, to the best of our knowledge, not the identify misbehaving servers, applications, and virtual machines. streaming explanation operations we seek here. MacroBase con- For example, Amazon AWS recently suffered a failure in its tinues this tradition by providing a specialized set of operators for DynamoDB service, resulting in outages at sites including Netflix analytic monitoring of IoT, which in turn allows new optimizations and Reddit. The Amazon engineers reported that “after we addressed within this design space. the key issue...we were left with a low overall error rate, hovering between 0.15-0.25%. We knew there would be some cleanup to do Outlier detection. Outlier detection dates to at least the 19th after the event,” and therefore the engineers deferred maintenance. century; the literature contains thousands of techniques from com- However, the engineers “did not realize soon enough that this low munities including statistics, machine learning, data mining, and overall error rate was giving some customers disproportionately information theory [7, 18, 43]. Outlier detection techniques have high error rates” due to a misbehaving server partition [3]. seen major success in several domains including network intrusion This public postmortem is representative of many scenarios de- detection [31, 63], fraud detection (leveraging a variety of classifiers scribed by system operators. At a major social network, engineers and techniques) [13, 66], and industrial automation and predictive report that the challenge of identifying transient slowdowns and fail- maintenance [8, 58]. A considerable subset of these techniques ures across hosts and containers is exacerbated by the heterogeneity operates over data streams [6, 17, 67, 76]. of workload tasks. Failure postmortems can take hours to days, At stream volumes in the hundreds of thousands or more events and, due to the labor-intensive nature of manual analysis, engineers per second, statistical outlier detection techniques will (by nature) report an inability to efficiently and reliably identify slowdowns, produce a large stream of outlying data points. As a result, while leading to suspected inefficiency. outlier detection forms a core component of an IoT analytic mon- Unlike the CMT use case, we do not directly present results over itoring solution, it must be coupled with streaming explanation production data from these scenarios. However, datacenter telemetry (below). In the design of MacroBase, we treat the array of outlier is an area of active research within the MacroBase project. detection techniques as inspiration for a modular architecture. In MacroBase’s default pipeline, we leverage detectors based on robust Industrial monitoring. IoT has spurred considerable interest in statistics [45, 59], adapted to the streaming context. However, in monitoring of industrial deployments. While many industrial sys- this paper, we also demonstrate compatibility with detectors from tems already rely on legacy monitoring systems, several industrial Elki [74], Weka [37], RapidMiner [44], and OpenGamma [2]. application operators reported a desire for analytics and alerting that can adapt to new sensors and analyses. These industrial scenarios Data explanation. Data explanation techniques assist in summa- can have particularly important consequences. For example, an rizing differences between datasets. The literature contains several explosion and fire in July 2010 killed two workers at Horsehead recent explanation techniques leveraging decision-tree [22] and Holding Corp.’s Monaca, PA, zinc manufacturing plant. Last year’s Apriori-like [38, 81] pruning, grid search [70, 83], data cubing [71], postmortem review by the US Chemical Safety board revealed that Bayesian statistics [79], visualization [16,64], causal reasoning [82], “the high rate-of-change alarm warned that the [plant] was in immi- and several others [30, 42, 50, 60]. While we are inspired by these nent danger 10 minutes before it exploded, but there appears to have results, none of these techniques executes over streaming data or at been no specific alarm to draw attention of the operator to the subtle the scale we seek. Several exhibit runtime exponential in the number of attributes (which can number in the hundreds of thousands to 

4 .millions in the IoT data we examine) [71, 79] and, when reported, measurements (e.g., trip time, battery drain), and attributes, corre- runtimes in the batch setting often vary from hundreds to approxi- sponding to metadata about the measurements (e.g., user ID and mately 10K points per second [70, 79, 81] (we also directly compare device ID). MacroBase uses metrics to detect abnormal or unusual throughput with several techniques [22, 71, 79, 81] in Appendix D). events, and attributes to explain behaviors. In this paper, we consider To address the demands of streaming operation and to scale to real-valued metrics and categorical attributes.2 millions of events per second, MacroBase’s explanation techniques As an example, to detect the OS version problem at CMT, Mac- draw on sketching and streaming data structures [21, 23, 24, 26, 28, roBase could have used failed or short trips as metrics and device 61, 73, 77] adapted to our use case of analytic monitoring for IoT. and OS type as attributes. To detect the outages at DynamoDB, We view existing explanation techniques as a useful second step in MacroBase could have used failed requests as a metric and server or analysis following the explanations generated by MacroBase, and IP address as an attribute. To detect the Horsehead pressure losses, we see promise in adapting these existing techniques to streaming MacroBase could have used the pressure gauge readings as met- execution at IoT volumes. Given our goal of providing a generic ar- rics and their locations as attributes along with an autocorrelation- chitecture for analytic monitoring, future improvements in streaming enabled time-series pipeline (Section 6.4). Today, selecting at- explanation should be complementary to our results here. tributes, metrics, and a pipeline is a user-initiated process; ongoing extensions (Section 7) seek to automate this. 3. MacroBase ARCHITECTURE AND APIS 2.) Feature Transformation. Following ingestion, MacroBase ex- As an analytic monitoring engine for IoT, MacroBase is tasked ecutes a series of optional domain-specific data transformations over with executing complex analytics over large stream volumes in the stream, allowing operations including time-series operations a number of IoT application domains. As a result, MacroBase’s (e.g., windowing, seasonality removal, autocorrelation, frequency architecture is designed to allow high-performance execution as analysis), statistical operations (e.g., normalization, dimensionality well as the flexibility to operate in a range of domains using an array reduction), and datatype-specific operations (e.g., hue extraction of detection and explanation operators. In this section, we describe for images, optical flow for video). For example, in Section 6.4, MacroBase’s query processing architecture approach to extensibility, execute a pipeline containing a grouped Fourier transform operator and interaction modes. that aggregates the stream into hour-long windows, then outputs a stream containing the twenty lowest Fourier coefficients for each Query pipelines. MacroBase performs analytic monitoring of IoT window as metrics and properties of the window time (hour of day, data by executing pipelines of specialized dataflow operators over month) as attributes. Placing this feature transformation functional- input data streams. Each MacroBase query specifies a set of input ity at the start of the pipeline allows users to encode domain-specific data sources as well as a logical query plan, or pipeline of streaming analyses without modifying later stages. The base type of the stream operators, that describes the analytic monitoring computation. is unchanged (Point → Point), allowing transform chaining. For spe- MacroBase’s pipeline design is guided by two principles. First, cialized data types like video frames, operators can subclass Point all operators operate over streams. Batch execution is supported by to further increase the specificity of types (e.g., VideoFramePoint). streaming over stored data. Second, MacroBase uses the compiler’s type system to enforce a particular pipeline structure. Each operator 3.) Outlier Detection. Following ingestion, MacroBase performs must implement one of several type signatures (depicted in Table 1). outlier detection, labeling each Point as an inlier or an outlier based In turn, the compiler enforces that all pipelines composed of these on its input metrics and producing a stream of labeled Point outputs operators will adhere to a common structure that we describe below. (Point → (bool, Point)); we discuss binary classification here). This architecture via typing strikes a balance between the ele- This stage is responsible for both training and evaluating outlier gance of more declarative but often less flexible interfaces, and detectors on the metrics in the incoming data stream. MacroBase the expressiveness of more imperative but often less composable supports a range of models, which we describe in Section 6. The interfaces. More precisely, this use of the type system facilitates simplest include rule-based models, which simply check specific three important kinds of interoperability. First, users can substitute metrics for particular values (e.g., whether the Point metric’s L2- streaming detection and explanation operators without concern for norm is greater than a fixed constant). In Section 4, we describe their interoperability. Early versions of the MacroBase prototype MacroBase’s default unsupervised models, which perform density- that lacked this pipeline modularity proved brittle to adapt. Second, based outlier classification. Users can also use operators that execute users can write a range of domain-specific feature transformation supervised and pre-trained models. operators (described in detail below) to perform advanced process- 4.) Explanation. Rather than returning all outlying data points, ing (e.g., time-series operations) to input streams without requiring given a stream of points classified as inliers and outliers, MacroBase expertise in outlier detection or explanation. Third, MacroBase’s performs summarization to generate explanations by finding at- operators preserve compatibility with dataflow operators found in tributes that are common among outliers and uncommon among traditional stream processing engines. For example, an MacroBase stream inliers ((bool, Point)→Explanation). As we describe in pipeline can contain standard selection, project, join, windowing, detail in Section 5, MacroBase’s default pipeline returns explana- aggregation, and group-by operators. tions in the form of attribute-value combinations (e.g., device ID As dictated by MacroBase’s type system, a MacroBase pipeline 5052) that are common among outlier points but uncommon among is structured as follows: inlier points. For example, at CMT, MacroBase could highlight 1.) Ingestion. MacroBase ingests data streams for analysis from a devices that were found in at least 0.1% of outlier trips and were number of external data sources. For example, MacroBase’s JDBC at least 3 times more common among outliers than inliers. Expla- interface allows users to specify columns of interest from a base view nation operators can subclass explanations to provide additional defined according to a SQL query. MacroBase subsequently reads information, such as statistics about the explanation or representa- the result-set from the JDBC connector in order to construct data tive sequences of points to contextualize time-series outliers. points to process, with one point per row in the view. MacroBase currently requires this initial operator perform any stream ordering. 2 It is straightforward to handle continuous attributes via discretization Each data point contains a set of metrics, corresponding to IoT (e.g., [82]). We provide two examples of discretization in Section 6.4. 

5 . 1. INGEST 2. TRANSFORM 3. DETECT 4. EXPLAIN 5. PRESENT ETL & conversion Optional domain- Identification of Discovery, ranking Export and to datum; pairs of specific data inliers, outliers of descriptive consumption: GUI, (metrics, attrs) transformations using metrics outlier attributes alerts, dashboards Figure 1: MacroBase’s default analytic monitoring pipeline: MacroBase ingests IoT data as a series of points, which are scored and classified by an outlier detector operator, summarized by a streaming explanation operator, then ranked and presented to end users. DATA T YPES retraining outlier summary data structures inlier + outlier streams res Point := (array<double> metrics, array<varchar> attributes) Threshold outlier summary AMC M-CPS-Tree sco Explanation := (array<varchar> attributes, stats statistics) ADR Model: retraining O PERATOR I NTERFACE MAD/MCD filter using OI-ratio Operator Type Signature ADR AMC M-CPS-Tree Ingestor external data source(s) → stream<Point> input sample score sample inlier summary data structures Transformer stream<Point> → stream<Point> OUTLIER DETECTION EXPLANATION Detector stream<Point> → stream<(bool, Point)> Explainer stream<(bool, Point)> → stream<Explanation> Figure 2: MDP: MacroBase’s default streaming outlier detec- Pipeline Ingestor → stream<Explanation> tion (Section 4) and streaming explanation (Section 5) opera- tors. Table 1: MacroBase’s core data and operator types. Each op- erator implements a strongly typed, stream-oriented dataflow author and test a new pipeline. interface specific to a given pipeline stage. A pipeline can uti- By providing a set of interfaces with which to extend pipelines lize multiple operators of each type via transformations, such (with varying expertise required), MacroBase places emphasis on as group-by and one-to-many stream replication, as long as the “pay as you go” deployment. MacroBase’s Default Operator Pipeline pipeline ultimately returns a single stream of explanations. (MDP, which we illustrate in Figure 2 and describe in the following two sections) is optimized for efficient, accurate execution over a Because MacroBase processes streaming data, explanation oper- variety of data types without relying on labeled data or rules. It fore- ators continuously summarize the stream. However, continuously goes domain-specific feature extraction and instead operates directly emitting explanations may be wasteful if users only need expla- over raw input metrics. However, as we illustrate in Section 6.4, this nations at the granularity of seconds, minutes, or longer. As a interface design also enable users to incorporate more sophisticated result, MacroBase’s explanation operators are designed to emit ex- features such as domain-specific feature transformation, time-series planations on demand, either in response to a user request, or in analysis, and supervised models. response to a periodic timer. In this way, explanation operators act In this paper, we have chosen to present MacroBase’s interfaces as streaming view maintainers whose output can be queried at any using an object-oriented interface, reflecting their current implemen- time. tation. However, each of MacroBase’s operator types is compatible 5.) Presentation. The number of output explanations may be large. with existing stream-to-relation semantics [9], theoretically allowing As a result, most pipelines rank explanations before presentation additional relational and stream-based processing between stages. according to statistics corresponding to each explanation. For ex- Realizing this mapping and the potential for even higher-level declar- ample, by default, MacroBase sorts explanations by their degree of ative interfaces above MacroBase’s analytic monitoring pipelines occurrence in the outliers and delivers this ranked list of explana- are promising areas for future work. tions to a range of downstream consumers. MacroBase’s default Operating modes. MacroBase supports three operating modes. presentation mode is a static report rendered via a REST API or First, MacroBase’s graphical front-end allows users to interactively via a GUI. In the former, programmatic consumers (e.g., reporting explore their data by configuring different inputs and selecting dif- tools such as PagerDuty) can automatically forward explanations to ferent combinations metrics and attributes. This is typically the first downstream reporting or operational systems. In the GUI, users can step in interacting with the engine. Second, MacroBase can execute interactively inspect the outlier explanations and iteratively define one-shot queires that can be run programmatically in a single pass their MacroBase queries. In practice, we have found that GUI- over data. Third, MacroBase can execute a streaming queries that based exploration is an important first step in formulating standing can be run programmatically over potentially infinite stream of data. MacroBase queries. In streaming mode, MacroBase continuously ingests a stream of Extensibility. As we discussed in Section 1 and demonstrate in Sec- data points and supports exponentially decayed damped-window tion 6.4, MacroBase’s pipeline architecture lends itself to three major streaming to give precedence to more recent points (e.g., decreasing means of extensibility. First, users can add new domain-specific the importance of points at a rate of 50% every hour). MacroBase feature transformations to the start of a pipeline without modifying continuously re-renders query results, and if desired, triggers auto- the other operators. Second, users can input rules and/or labels mated alerting for downstream consumers. to MacroBase to perform supervised classification. Third, users can write their own feature transformation, outlier detector, data 4. MDP OUTLIER DETECTION explanation operators, and pipelines. This third option is the most MacroBase’s outlier detection operators monitor the input for labor-intensive, but is also the interface with which MacroBase’s data points that exhibit deviant behavior. While MacroBase allows maintainers author new pipelines. These interfaces have also proven users to configure their own operators, in this section, we describe useful to non-experts: a master’s student at Stanford and a master’s the design of MacroBase’s default detection operators, which use student at MIT each implemented and tested a new outlier detector robust estimation procedures to fit a distribution to data streams and operator in less than a week of part-time work, and MacroBase’s identify the least likely points with the distribution using quantile core maintainers currently require less than an afternoon of work to estimation. To enable streaming execution, we introduce the ADR 

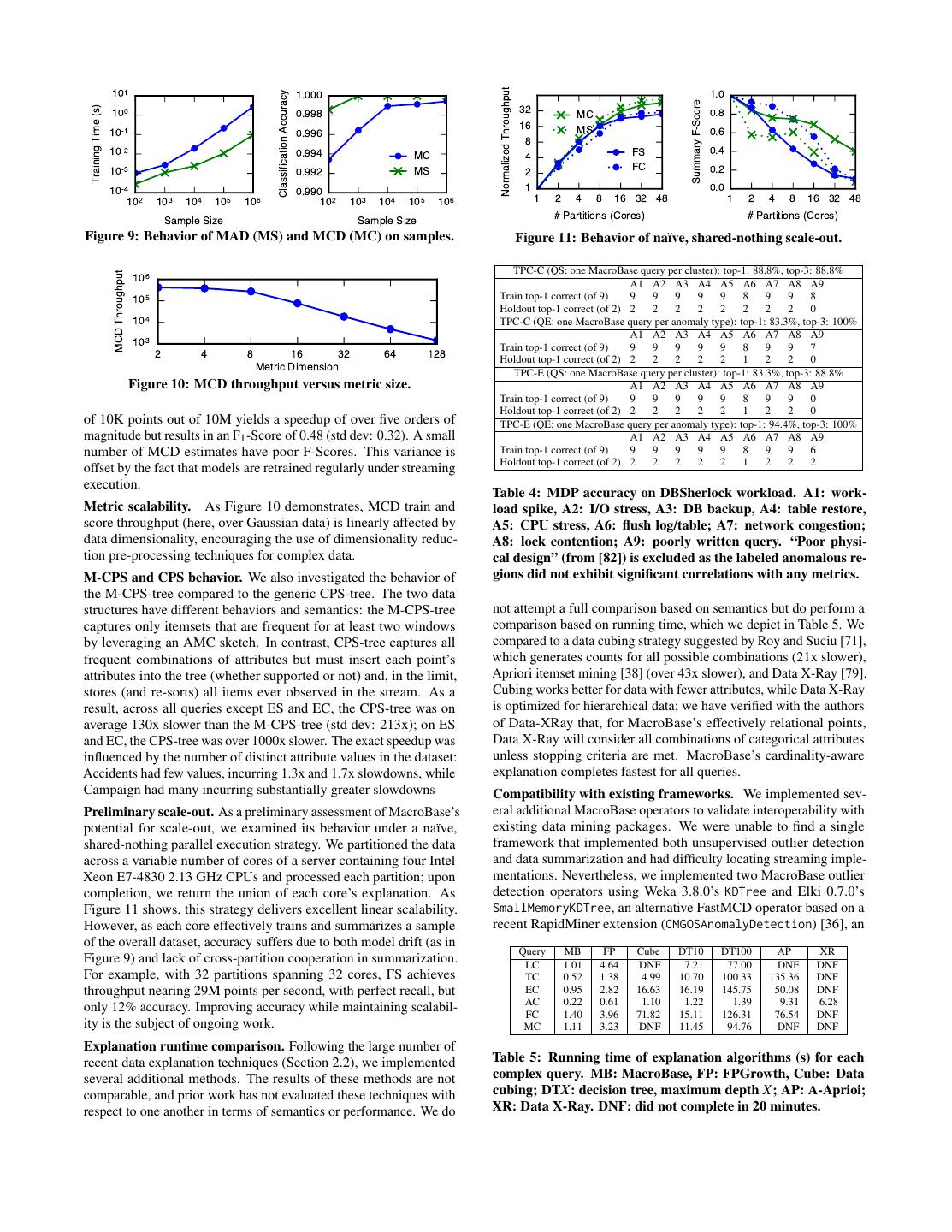
6 . MCD MAD Z-Score above the percentile-based cutoff are classified as outliers, reflecting 60 their distance from the body of the distribution. Mean Outlier Score 50 As a notable caveat, MAD and MCD are parametric estimators, 40 assigning scores based on an assumption that data is normally dis- 30 tributed. While extending these estimators to multi-modal behavior 20 10 is straightforward [40] and MacroBase allows substitution of more 0 sophisticated detectors (e.g., Appendix D), we do not consider them 0.0 0.1 0.2 0.3 0.4 0.5 here. Instead, we have found that looking for far away points using Proportion Outliers these parametric estimators yields useful results: as we empirically Figure 3: Discriminative power of estimators under contami- demonstrate, many interesting behaviors in IoT applications man- nation by outliers (high scores better). Robust methods (MCD, ifest as extreme deviations from the overall population. Robustly MAD) outperform the Z-score-based approach. locating the center of a population—while ignoring local, small- scale deviations in the body of the distribution—suffices to identify many important classes of outliers in the applications we study. The sampler, which MacroBase uses for model retraining and quantile robust statistics literature discusses this phenomena in the case of estimation. the MCD [41] and echoes Aggarwal’s observation that “even for arbitrary distributions, [extreme value analysis techniques] provide 4.1 Use of Robust Statistics a good heuristic idea of the outlier scores of data points, even when A small number of anomalous behaviors may have a large effect they cannot be interpreted statistically” [7]. on detector accuracy. As an example, consider the Z-Score of a point drawn from a univariate sample, which measures the number 4.2 MDP Streaming Execution of standard deviations that a point lies away from the sample mean. Despite their utility, we are not aware of an existing algorithm for This provides a normalized way to measure the “outlying”-ness of a training MAD or MCD in a streaming context.3 This is especially point (e.g., a Z-Score of three indicates the point lies three standard problematic because, as the distributions within data streams change deviations from the mean). However, the Z-Score is not robust to over time, MDP estimators should be updated to reflect the change. outliers: a single outlying value can skew the mean and standard deviation by an unbounded amount, limiting its usefulness. ADR: Adaptable Damped Reservoir. MDP’s solution to the re- To address this challenge, MacroBase’s MDP pipeline leverages training problem is a novel adaptation of reservoir sampling over robust statistical estimation [45], a branch of statistics that pertains to streams, which we call the Adaptable Damped Reservoir (ADR). finding statistical distributions for data that is mostly well-behaved The ADR maintains a sample of input data that is exponentially but may contain a number of ill-behaved data points. If we can find weighted towards more recent points; the key difference from tra- a distribution that reliably fits most of the data, we can measure each ditional reservoir sampling is that the ADR operates over arbitrary point’s distance from this distribution in order to find outliers [59]. window sizes, allowing greater flexibility than existing damped A robust replacement for the Z-Score is to use the median and samplers. As Figure 2 illustrates, MDP maintains an ADR sample the Median Absolute Deviation (MAD) as a measure of distance of the detector input to periodically recompute its estimator and a in place of mean and standard deviation. The MAD measures the second ADR sample of the outlier scores to periodically recompute median of the absolute distance from each point in the sample to the its classification threshold. sample median. Thus, each outlying data point has limited impact The classic reservoir sampling technique can be used to accumu- on the MAD score of all other points in the sample, since the median late a uniform sample over a set of data using finite space and one itself is resistant to outliers. pass [78]. The probability of insertion into the sample, or “reservoir,” The Minimum Covariance Determinant (MCD) provides robust is inversely proportional to the number of points observed thus far. estimates for multivariate data. The MCD estimator finds the tightest In the context of stream sampling, we can treat the stream as an group of points that best represents a sample, and summarizes the infinitely long set of points and the contents of the reservoir as a set of points according to its location and scatter (i.e., covariance) uniform sample over the data observed so far. in metric space [46]. Given an estimate of location µ and scatter C, In MacroBase, we wish to promptly reflect changes in the un- we can compute the distance between the distribution and a point derlying data stream, and therefore we adapt a weighted sampling x via the Mahalanobis distance (x − µ)T C−1 (x − µ); intuitively, approach, in which the probability of data retention decays over time. the Mahalanobis distance normalizes (or warps) the metric space The literature contains several existing algorithms for weighted reser- via the scatter and then measures the distance to the center of the voir sampling [5, 21, 28]. Most recently, Aggarwal described how to transformed space using the mean (see also Appendix A). perform exponentially weighted sampling on a per-record basis: that As Figure 3 demonstrates, MAD and MCD are empirically able is, the probability of insertion is an exponentially weighted function to reliably identify points in outlier clusters despite increasing out- of the number of points observed so far [5]. While this is useful, as lier contamination (experimental setup in Appendix A). Whereas we demonstrate in Section 6, under workloads with variable arrival MAD and MCD are resilient to contamination up to 50%, the Z- rates, we may wish to employ a decay policy that decays in time, Score is unable to distinguish inliers and outliers under even modest not number of tuples; tuple-at-a-time decay may skew the reservoir contamination. towards periods of high stream volume. To support more flexible reservoir behavior, MacroBase adapts an Classifying outliers. Given a query with a single, univariate metric, earlier variant of weighted reservoir sampling due to Chao [21,28] to MDP uses a MAD-based detector, and, given a query with multiple provide the first exponentially decayed reservoir sampler that works metrics, MacroBase computes the MCD via an iterative approxima- over arbitrary decay intervals. We call this variant the Adaptable tion called FastMCD [69]. By adopting these unsupervised models, MDP can score points without requiring labels or rules from users. 3 Specifically, MAD requires computing the median of median distances, Subsequently, MDP uses a percentile-based cutoff over scores to meaning streaming quantile estimation alone is insufficient. FastMCD is an identify the most extreme points in the sample. Points with scores inherently iterative algorithm that iteratively re-sorts data. 

7 .Algorithm 1 ADR: Adaptable Damped Reservoir Algorithm 2 MDP’s Outlier-Aware Explanation Strategy given: max_size ∈ N; r: decay rate ∈ (0, 1) Given: minimum OI-ratio r and minimum support s initialization: reservoir R ← {}; current weight cw ← 0 1: find attributes w/ support ≥ s in O and OI-ratio ≥ r in O, I function OBSERVE(x: point, w: weight) 2: mine FP-tree over O using only attributes from (1) cw ← cw + w 3: filter (2) by removing patterns w/ OI-ratio < r in I; return if |R| < max_size then R ← R ∪ {x} else with probability c1w 5.1 Semantics: Support and OI-Ratio remove random element from R and add x to R MacroBase’s outlier explanations describe attribute values that function DECAY( ) are common to the outliers but relatively uncommon to the inliers cw ← r · cw through two complementary metrics. First, to identify combinations of attribute values that are relatively uncommon in the inliers, MDP finds combinations with high outlier-inlier (OI-ratio), or the ratio Damped Reservoir, or ADR (Algorithm 1). In contrast with existing of its rate of occurrence (i.e., support) in the outliers to its rate of approaches that decay on a per-tuple basis, the ADR separates the occurrence in the inliers. This metric corresponds to a standard di- insertion process from the decay decision, allowing both time-based agnostic measure used in epidemiology called the relative risk ratio, and tuple-based decay policies. Specifically, the ADR maintains a which is used to determine potential causes for disease [62]. Second, running count cw of items inserted into the reservoir so far. Each to optionally eliminate explanations corresponding to rare but non- time an item is inserted, cw is incremented by one (or an arbitrary systemic combinations, MDP finds combinations with high support, weight, if desired). With probability c1w , the item is placed into the or occurrence (by count) in the outliers. MDP accepts a minimum reservoir and a random item is evicted from the reservoir. When OI-ratio and level of outlier support as input parameters. As an the ADR is decayed (e.g., via a periodic timer or tuple count), its example, MDP may find that 500 of 890 records flagged as outliers running count is multiplied by a decay factor (i.e., cw := (1 − α)cw ). correspond to iPhone 6 devices (outlier support of 56.2%), but, if MacroBase currently supports two decay policies: time-based 80191 of 90922 records flagged as inliers also correspond to iPhone decay, which decays the reservoir at a pre-specified rate measured 6 devices (inlier support of 88.2%), we are likely uninterested in according to real time, and batch-based decay, which decays the iPhone 6 as it has a low OI-ratio of 0.634. reservoir at a pre-specified rate measured by arbitrarily-sized batches of data points (Appendix A). The validity of this procedure follows 5.2 Basic Explanation Strategy from Chao’s algorithm, which requires the user to manually manage To efficiently compute support and OI-ratio, we draw upon a weights and decay. connection to two classic problems in data mining: frequent itemset MacroBase’s MDP uses the ADR to solve the model and per- mining and emerging pattern mining. A naïve solution is to run an centile retraining and problems: algorithm for frequent itemset mining twice, once on all inlier points Maintaining inputs for training. Either on a tuple-based periodic and once on all outlier points, and then look for differences between basis or using a real-time timer, MDP periodically retrains models the inlier and outlier sets. As we experimentally demonstrate in using an ADR that samples the input of the data stream. This Section 6, this can be inefficient because we waste time searching streaming robust estimator maintenance and evaluation strategy is over attributes in the inlier set that eventually get filtered due to the first of which we are aware. We discuss the statistical validity of insufficient support in the outlier set. In addition, the number of this procedure in Appendix D. outliers is much smaller than the inliers, so processing the two sets independently ignores possibilities for additional pruning. To Maintaining percentile thresholds. While streaming quantile reduce this wasted effort, MacroBase takes advantage of both the estimation is well studied, we were not able to find many computa- cardinality imbalance between inliers and outliers as well as the tionally inexpensive options in an exponentially damped model with joint explanation of each set. arbitrary window sizes. Thus, instead, MacroBase uses an ADR to sample the outlier scores produced by MAD and MCD. The ADR Optimization: Item ratios are cheap. While computing OI- maintains an exponentially damped sample of the scores, which it ratios for all attribute combinations is expensive, computing OI- uses to periodically compute the appropriate outlier score quantile.4 ratios for single attributes is inexpensive: we can compute support A sample of size O( ε12 log( δ1 )) yields an ε-approximation of an counts over both inliers and outliers via a single pass over the arbitrary quantile with probability 1 − δ [14], so a ADR of size 20K attributes. Accordingly, MDP first computes OI-ratios for single provides an ε = 1%, δ = 1% approximation. attribute values, then computes attribute combinations using only attribute values with sufficient OI-ratios. 5. MDP OUTLIER EXPLANATION Optimization: Exploit cardinality imbalance. The cardinality of the outlier input stream is by definition much smaller than that of Once MDP classifies the most outlying data points as outliers the input stream. Therefore, instead of mining the outlier supports according to their metrics, MDP produces explanations that differ- and the inlier supports separately, MDP first finds outlier attribute entiate the inliers and outliers according to their attributes. In this value sets with minimum support and subsequently mines the inlier section, we discuss how MacroBase explains outlying data using an attributes, while only searching for attributes that were supported in severity metric from epidemiology, the risk ratio. We again begin the outliers.5 This reduces the space of inlier attributes to explore. with a discussion of an efficient batch-oriented operation employing outlier-aware optimizations, then discuss how MacroBase executes End result. The result is a three-stage process (Algorithm 2). streaming explanation via the Amortized Maintenance Counter. MDP first calculates the attribute values with minimum OI-ratio 4 This enables a simple mechanism for detecting quantile drift: if the propor- (support counting, followed by a filtering pass based on OI-ratio). tion of outlier points significantly deviates from the target percentile (i.e., 5 In contrast with [55], this optimization for ratio computation is enabled by via application of a binomial proportion confidence interval), MDP should the fact that we wish to find supported itemsets to avoid overwhelming the recompute the quantile. user with explanations. 

8 .From the first stage’s outlier attribute values, MDP then computes Algorithm 3 AMC: Amortized Maintenance Counter supported outlier attribute combinations. Finally, MDP computes given: ε ∈ (0, 1); r: decay rate ∈ (0, 1) the OI-ratio for each attribute combination based on their support in initialization: (item → count) C ← {}; weight wi ← 0 the inliers (support counting, followed by a filtering pass to exclude function OBSERVE(i: item, c: count) any attribute sets with insufficient OI-ratio). C[i] ← wi + c if i ∈ / C else C[i] + c Significance. We discuss confidence intervals on MDP explana- function MAINTAIN( ) tions as well as quality improvements achievable by processing large remove all but the ε1 largest entries from C data volumes in Appendix B. wi ← the largest value just removed, or, if none removed, 0 Algorithms and Data Structures. In the one-pass setting, single function DECAY( ) attribute value counting is straightforward, requiring a single pass decay the value of all entries of C by r over the data; the streaming setting below is more interesting. We call MAINTAIN( ) experimented with several itemset mining techniques and ultimately decided on prefix-tree-based approaches inspired by FPGrowth [39]. AMC provides the same counting functionality as a traditional In brief, the FPGrowth algorithm maintains a frequency-descending heavy-hitters sketch but exposes a second method, maintain, that is prefix tree of attributes that can subsequently be mined by recur- called to periodically prune the sketch size. AMC allows the sketch sively generating a set of “conditional” trees. Corroborating recent size to increase between calls to maintain, and, during maintenance, benchmarks [33], the FPGrowth algorithm was fast and proved the sketch size is reduced to a desired stable size, which is specified extensible in our streaming implementation below. as an input parameter. Therefore, the maximum size of the sketch is controlled by the period between calls to maintain: as in SpaceSav- 5.3 Streaming Explanation ing, a stable size of ε1 yields an nε approximation of the count of As in MDP detection, streaming explanation mining proved more n points, but the size of the sketch may grow within a period. This challenging. We again turn to the sketching and streaming literature separation of insertion and maintenance has two implications. First, in order to provide theoretically justified but practical summarization. it allows constant-time insertion, which we describe below. Second, We present the MDP implementation of single-attribute streaming it allows a range of maintenance policies, including a sized-based explanation, then extend the approach to multi-attribute streaming policy, which performs maintenance once the sketch reaches a pre- explanation. specified upper bound, as well as a variable period policy, which Implementation: Single Attribute Summarization. In a stream- operates over real-time and tuple-based windows (similar to ADR). ing setting, we wish to find individual attributes with sufficient To implement this functionality, AMC maintains a set of approx- support and OI-ratio. We would like to do so in a way that both imate counts for all items that were among the most common in respects bias in the stream and limits the overall amount of memory the previous period along with approximate counts for all other required to store the counts. Fortunately, the problem of maintaining items that observed in the current period. During maintenance, a count of frequent items (i.e., heavy hitters, or attributes with top AMC prunes all but the ε1 items with highest counts and records k occurrence) in data streams is well studied [24]. Given a heavy- the maximum count that is discarded (wi ). Upon insertion, AMC hitters sketch over the inlier and outlier stream, we can compute an checks to see if the item is already stored. If so, the item’s count is approximate support and OI-ratio for each attribute by comparing incremented. If not, AMC stores the item count plus wi . If an item the contents of the sketches at any time. is not stored in the current window, the item must have had count Initially, we implemented the MDP item counter using the Space- less than or equal to wi at the end of the previous period. Saving algorithm [61], which has been demonstrated to provide AMC has three major differences compared to SpaceSaving. First, excellent performance [25], with extensions to the exponentially AMC updates are constant time (hash table insertion) compared decayed setting [26]. However, like many of the sketches in the to O(log( ε1 )) for SpaceSaving. Second, AMC has an additional literature, SpaceSaving was designed to strike a balance between maintenance step, which is amortized across all items seen in a sketch size and performance, with a strong emphasis on limited window. Using a min-heap, with I items in the sketch, maintenance size. For example, in its heap-based variant, SpaceSaving maintains requires O(I · log( ε1 )) time. If we observe even one item more 1 than once, this is faster than performing maintenance on every k -approximate counts for the top k item counts by maintaining a heap of the items. For a stream of size n, this requires O(n log(k)) observation. Third, AMC has higher space overhead; in the limit, it update time. (In the case of exponential decay, the linked-list-based must maintain all items it has seen between maintenance windows. variant can require O(n2 ) processing time.) Implementation: Streaming Combinations. While AMC tracks While logarithmic update time is modest for small sketches, given single items, MDP also needs to track combinations of attributes. As there are only two heavy-hitters sketches per MacroBase query, such, we sought a tree-based technique that would admit exponen- MDP can expend more memory on its sketches for better accuracy; tially damped arbitrary windows but eliminate the requirement that for example, 1M items require less than ten megabytes of memory each attribute be stored in the tree, as in recent proposals such as the for double-encoded counts, which is small given modern server CPS-tree [77]. As a result, MDP adapts a combination of two data memory sizes. As a result, we developed a heavy-hitters sketch, structures: AMC for the frequent attributes, and a novel adaptation called the Amortized Maintenance Counter (AMC, Algorithm 3), of the CPS-Tree data structure to store frequent attributes. that occupies the opposite end of the design spectrum: the AMC Given the set of recently frequent items, MDP monitors the at- uses a much greater amount of memory for a given accuracy level tribute stream for frequent attribute combinations by maintaining an but is in turn faster to update and still limits total space utilization. approximately frequency-descending prefix tree of attribute values. The key insight behind the AMC is that, if we observe even a single MDP adopts the basic CPS-tree data structure [77], with several item in the stream more than once, we can amortize the overhead modifications, which we call the M-CPS-tree. of maintaining the sketch across multiple observations. In contrast, Like the CPS-tree, the M-CPS-tree maintains both the basic FP- SpaceSaving maintains the sketch for every observation but in turn tree data structures as well as a set of leaf nodes in the tree. However, keeps the sketch size smaller. 

9 .in an exponentially damped model, the CPS-tree stores at least one # Devices: 6400 12800 25600 node for every item ever observed in the stream. This is infeasible 1.0 1.0 at scale. As a compromise, the M-CPS-tree only stores items that 0.8 0.8 were frequent in the previous window: at each window boundary, F1-Score F1-Score 0.6 0.6 MacroBase updates the frequent item counts in the M-CPS-tree 0.4 0.4 based on an AMC sketch. Any items that were frequent in the previous window but were not frequent in this window are removed 0.2 0.2 from the tree. MacroBase then decays all frequency counts in 0.0 0.0 0 10 20 30 40 50 0 10 20 30 40 50 the M-CPS-tree nodes and re-sorts the M-CPS-tree in frequency Label Noise (%) Measurement Noise (%) descending order (as in the CPS-tree, by traversing each path from leaf to root and re-inserting as needed). Subsequently, attribute Figure 4: Precision-recall of explanations. Without noise, MDP insertion can continue as in the FP-tree, with the caveat that the item exactly identifies misbehaving devices. MDP’s use of OI-ratio order is not maintained until query time. improves resiliency to both label and measurement noise. In summary, MDP’s streaming explanation operator consists of two primary parts: maintenance and querying. When a new data demonstrate adaptivity to changes in data streams, and report on point arrives at the MacroBase summarization operator, MacroBase experiences in production deployment. inserts each of the point’s attributes into an AMC sketch. Subse- quently, MacroBase inserts a subset of the point’s attributes into Synthetic dataset accuracy. We ran MDP over a synthetic dataset a prefix tree that maintains an approximate, frequency descending generated in line with those used to evaluate recent anomaly de- order. When a window has elapsed, MacroBase decays the counts tection systems [70, 81]. The generated dataset contains 1M data of the items as well as the counts in each node of the prefix tree. points across a number of synthetic devices, each of which maps MacroBase removes any items that are no longer supported and re- to a unique attribute ID and whose metrics are drawn from either arranges the prefix tree in frequency-descending order. To produce an inlier distribution (N (10, 10)) or outlier distribution (N (70, 10)). explanations, MacroBase runs FPGrowth on the prefix tree. We subsequently evaluated MacroBase’s ability to automatically determine the device IDs corresponding to the outlying distribution. · recall 6. EVALUATION We report the F1 -score 2 · precision precision+recall for the set of device In this section, we evaluate the accuracy, efficiency, and flexibility IDs identified as outliers as a proxy for reporting explanation quality. of MacroBase and the MDP pipeline operators. Our goals are to Since MDP’s statistical techniques are a natural match for this demonstrate that: experimental setup, we also perturbed the base experiment to un- derstand when MDP might underperform. We introduced two types • MacroBase’s MDP pipeline is accurate: on controlled, syn- of noise into the measurements to quantify their effects on MDP’s thetic data, under changes in stream behavior (via ADR), and performance. First, we introduced label noise by randomly assign- over real-world workloads from the literature and in produc- ing readings from the outlier distribution to inlying devices and tion (Section 6.1). vice-versa. Second, we introduced measurement noise by randomly • MacroBase can process up to 2M points per second per query assigning a proportion of both outlying and inlying points to a third, on a range of real-world datasets (Section 6.2). uniform distribution over the interval [0, 80]. • MacroBase’s cardinality-aware explanation strategy produces Figure 4 illustrates the results. In the the noiseless regions of meaningful speedups (average: 3.2× speedup; Section 6.3). Figure 4, MDP correctly identified 100% of the outlying devices. • MacroBase’s use of AMC is up to 500× faster than existing As the outlying devices are solely drawn from the outlier distri- sketches on production IoT data (Section 6.3). bution, constructing outlier explanations via the OI-ratio enables MacroBase to perfectly recover the outlying device IDs. In contrast, • MacroBase’s architecture is extensible, which we illustrate techniques that rely solely on individual outlier classification deliver via three case studies (Section 6.4). less accurate results on this workload [70, 81]. Under label noise, Experimental environment. We report results from deploying the MacroBase robustly identified the outlying devices until approx- MacroBase prototype on a server with four Intel Xeon E5-4657L imately 25% noise, which corresponds a 3 : 1 ratio of correct to 2.40GHz CPUs containing 12 cores per CPU and 1TB of RAM. incorrect labels. As our default OI-ratio is set to 3, exceeding this To isolate the effects of pipeline processing, we exclude loading threshold causes rapid performance degradation. Under measure- time from our results. By default, we issue MDP queries with a ment noise, accuracy degrades linearly with the amount of noise. minimum support of 0.1% and minimum OI-ratio of 3, a target MDP is more robust to this type of noise when fewer devices are outlier percentile of 1%, ADR and AMC sizes of 10K, a decay present. MDP accuracy suffers with a larger number of devices, as rate of 0.01 every 100K points, and report the average of at least each device type is subject to more noisy readings. three runs per experiment. We vary these parameters in subsequent In summary, for well-behaved data (e.g., < 10−20% noisy points), experiments in this section and the Appendix. MDP is able to accurately identify correlated causes of outlying data. The noise threshold is improved by both MDP’s use of robust Implementation. We describe MacroBase’s implementation, pro- methods as well as the use of OI-ratio to prune irrelevant summaries. cessing runtime, and approach to parallelism in Appendix C. Noise of this magnitude is likely rare in practice, and, if such noise Large-scale datasets. To compare the efficiency of MacroBase exists, is likely indicative of another interesting behavior in the data. and related techniques, we compiled a set of large-scale real-world Real world dataset accuracy. In addition to synthetic data, we datasets (Table 2) for evaluation (descriptions in Appendix D). also performed experiments to determine MacroBase’s ability to accurately identify systemic abnormalities in real-world data. We 6.1 Result Quality evaluated MacroBase’s ability to distinguish abnormally-behaving In this section, we focus on MacroBase’s statistical result qual- OLTP servers within a cluster, as defined according to data and man- ity. We evaluate precision/recall on synthetic and real-world data, 

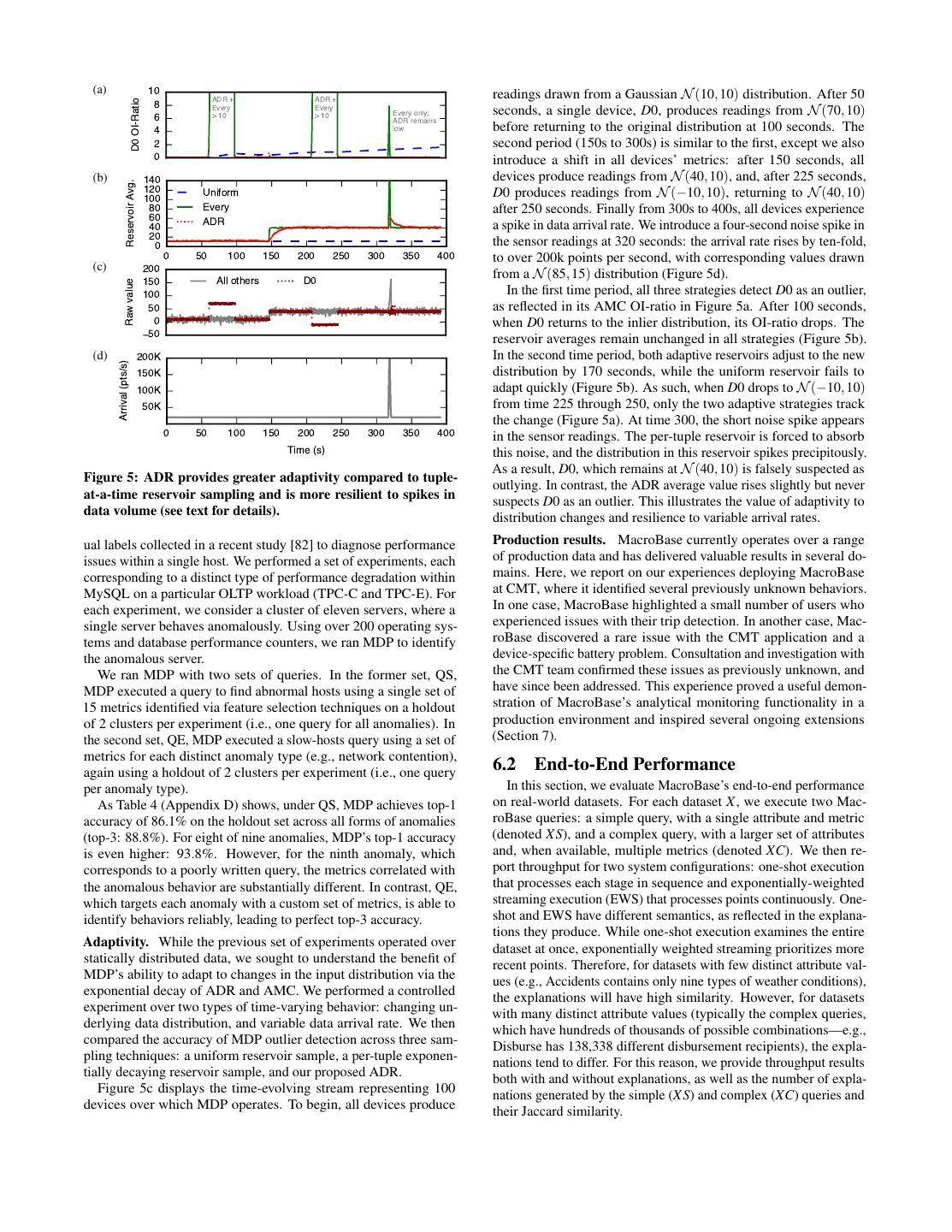
10 . (a) 10 readings drawn from a Gaussian N (10, 10) distribution. After 50 ADR + ADR + 8 D0 OI-Ratio Every Every seconds, a single device, D0, produces readings from N (70, 10) Every only; 6 > 10 > 10 ADR remains 4 low before returning to the original distribution at 100 seconds. The 2 second period (150s to 300s) is similar to the first, except we also 0 introduce a shift in all devices’ metrics: after 150 seconds, all (b) 140 devices produce readings from N (40, 10), and, after 225 seconds, Reservoir Avg. 120 Uniform D0 produces readings from N (−10, 10), returning to N (40, 10) 100 80 Every after 250 seconds. Finally from 300s to 400s, all devices experience 60 ADR 40 a spike in data arrival rate. We introduce a four-second noise spike in 20 the sensor readings at 320 seconds: the arrival rate rises by ten-fold, 0 0 50 100 150 200 250 300 350 400 to over 200k points per second, with corresponding values drawn (c) 200 from a N (85, 15) distribution (Figure 5d). 150 All others D0 Raw value 100 In the first time period, all three strategies detect D0 as an outlier, 50 as reflected in its AMC OI-ratio in Figure 5a. After 100 seconds, 0 when D0 returns to the inlier distribution, its OI-ratio drops. The 50 reservoir averages remain unchanged in all strategies (Figure 5b). (d) 200K In the second time period, both adaptive reservoirs adjust to the new Arrival (pts/s) 150K distribution by 170 seconds, while the uniform reservoir fails to 100K adapt quickly (Figure 5b). As such, when D0 drops to N (−10, 10) 50K from time 225 through 250, only the two adaptive strategies track the change (Figure 5a). At time 300, the short noise spike appears 0 50 100 150 200 250 300 350 400 in the sensor readings. The per-tuple reservoir is forced to absorb Time (s) this noise, and the distribution in this reservoir spikes precipitously. As a result, D0, which remains at N (40, 10) is falsely suspected as Figure 5: ADR provides greater adaptivity compared to tuple- outlying. In contrast, the ADR average value rises slightly but never at-a-time reservoir sampling and is more resilient to spikes in suspects D0 as an outlier. This illustrates the value of adaptivity to data volume (see text for details). distribution changes and resilience to variable arrival rates. ual labels collected in a recent study [82] to diagnose performance Production results. MacroBase currently operates over a range issues within a single host. We performed a set of experiments, each of production data and has delivered valuable results in several do- corresponding to a distinct type of performance degradation within mains. Here, we report on our experiences deploying MacroBase MySQL on a particular OLTP workload (TPC-C and TPC-E). For at CMT, where it identified several previously unknown behaviors. each experiment, we consider a cluster of eleven servers, where a In one case, MacroBase highlighted a small number of users who single server behaves anomalously. Using over 200 operating sys- experienced issues with their trip detection. In another case, Mac- tems and database performance counters, we ran MDP to identify roBase discovered a rare issue with the CMT application and a the anomalous server. device-specific battery problem. Consultation and investigation with We ran MDP with two sets of queries. In the former set, QS, the CMT team confirmed these issues as previously unknown, and MDP executed a query to find abnormal hosts using a single set of have since been addressed. This experience proved a useful demon- 15 metrics identified via feature selection techniques on a holdout stration of MacroBase’s analytical monitoring functionality in a of 2 clusters per experiment (i.e., one query for all anomalies). In production environment and inspired several ongoing extensions the second set, QE, MDP executed a slow-hosts query using a set of (Section 7). metrics for each distinct anomaly type (e.g., network contention), again using a holdout of 2 clusters per experiment (i.e., one query 6.2 End-to-End Performance per anomaly type). In this section, we evaluate MacroBase’s end-to-end performance As Table 4 (Appendix D) shows, under QS, MDP achieves top-1 on real-world datasets. For each dataset X, we execute two Mac- accuracy of 86.1% on the holdout set across all forms of anomalies roBase queries: a simple query, with a single attribute and metric (top-3: 88.8%). For eight of nine anomalies, MDP’s top-1 accuracy (denoted XS), and a complex query, with a larger set of attributes is even higher: 93.8%. However, for the ninth anomaly, which and, when available, multiple metrics (denoted XC). We then re- corresponds to a poorly written query, the metrics correlated with port throughput for two system configurations: one-shot execution the anomalous behavior are substantially different. In contrast, QE, that processes each stage in sequence and exponentially-weighted which targets each anomaly with a custom set of metrics, is able to streaming execution (EWS) that processes points continuously. One- identify behaviors reliably, leading to perfect top-3 accuracy. shot and EWS have different semantics, as reflected in the explana- tions they produce. While one-shot execution examines the entire Adaptivity. While the previous set of experiments operated over dataset at once, exponentially weighted streaming prioritizes more statically distributed data, we sought to understand the benefit of recent points. Therefore, for datasets with few distinct attribute val- MDP’s ability to adapt to changes in the input distribution via the ues (e.g., Accidents contains only nine types of weather conditions), exponential decay of ADR and AMC. We performed a controlled the explanations will have high similarity. However, for datasets experiment over two types of time-varying behavior: changing un- with many distinct attribute values (typically the complex queries, derlying data distribution, and variable data arrival rate. We then which have hundreds of thousands of possible combinations—e.g., compared the accuracy of MDP outlier detection across three sam- Disburse has 138,338 different disbursement recipients), the expla- pling techniques: a uniform reservoir sample, a per-tuple exponen- nations tend to differ. For this reason, we provide throughput results tially decaying reservoir sample, and our proposed ADR. both with and without explanations, as well as the number of expla- Figure 5c displays the time-evolving stream representing 100 nations generated by the simple (XS) and complex (XC) queries and devices over which MDP operates. To begin, all devices produce their Jaccard similarity. 

11 . Queries Thru w/o Explain (pts/s) Thru w/ Explain (pts/s) # Explanations Jaccard Dataset Name Metrics Attrs Points One-shot EWS One-shot EWS One-shot EWS Similarity LS 1 1 1549.7K 967.6K 1053.3K 966.5K 28 33 0.74 Liquor 3.05M LC 2 4 385.9K 504.5K 270.3K 500.9K 500 334 0.35 TS 1 1 2317.9K 698.5K 360.7K 698.0K 469 1 0.00 Telecom 10M TC 5 2 208.2K 380.9K 178.3K 380.8K 675 1 0.00 ES 1 1 2579.0K 778.8K 1784.6K 778.6K 2 2 0.67 Campaign 10M EC 1 5 2426.9K 252.5K 618.5K 252.1K 22 19 0.17 AS 1 1 998.1K 786.0K 729.8K 784.3K 2 2 1.00 Accidents 430K AC 3 3 349.9K 417.8K 259.0K 413.4K 25 20 0.55 FS 1 1 1879.6K 1209.9K 1325.8K 1207.8K 41 38 0.84 Disburse 3.48M FC 1 6 1843.4K 346.7K 565.3K 344.9K 1710 153 0.05 MS 1 1 1958.6K 564.7K 354.7K 562.6K 46 53 0.63 CMTD 10M MC 7 6 182.6K 278.3K 147.9K 278.1K 255 98 0.29 Table 2: Datasets and query names, throughput, and explanations produced under one-shot and exponentially weighted streaming (EWS) execution. MacroBase’s sustained throughput is up to three orders of magnitude higher than related systems. Table 2 displays results across all queries. Throughput varied AMC SSL SSH from 147K points per second (on MC with explanation) to over 15M 15M Updates per Second Updates per Second 2.5M points per second (on T S without explanation); the average throughput for one-shot execution was 1.39M points per second, 12M 12M and the average throughput for EWS was 599K points per second. 9M 9M The better-performing mode depended heavily on the particular data 6M 6M 3M TC 3M FC set and characteristics. In general, queries with multiple metrics were slower in one-shot than queries with single metrics (due to 0 0 101 102 103 104 105 106 101 102 103 104 105 106 increased training time, as streaming trains over samples). Mining Stable Size (Items) Stable Size (Items) for each explanation incurred an approximately 22% overhead. In all cases, these queries far exceed the current arrival rate of data for Figure 6: Streaming heavy hitters sketch comparison. AMC: each dataset. EWS typically returned fewer explanations (Telecom Amortized Maintenance Counter with maintenance every 10K provides an extreme example) due to its temporal bias. In prac- items; SSL: Space Saving List; SSH: Space Saving Hash. All tice, users tune their decay on a per-application basis (e.g., at CMT, share the same accuracy bound. Varying maintenance period streaming queries may prioritize trips from the last hour to catch produced similar results. errors arising from the most recent deployment). These throughputs exceed those of related techniques we have encountered in the lit- in FPGrowth is wasted. However, both MacroBase and FPGrowth erature (by up to three orders of magnitude); we examine specific must perform a linear pass over all of the inliers, which places a factors that contribute to this performance in the next section. lower bound on the running time. The exact benefit of this expla- Runtime profiling. To further understand how each pipeline oper- nation strategy depends on the OI-ratio (here, 3), which we vary in ator contributed to overall performance, we profiled MacroBase’s Appendix D. one-shot execution (EWS is more challenging to accurately instru- AMC Comparison. We also compare the performance of AMC ment due to its streaming execution). On MC, MacroBase spent with existing heavy-hitters sketches (Figure 6). AMC outperforms approximately 52% of its execution training MCD, 21% scoring both implementations of SpaceSaving in all configurations by a points, and 26% summarizing them. On MS, MacroBase spent margin of up to 500× except for SpaceSaving implemented using approximately 54% of its execution training MAD, 16% scoring a list with fewer than 100 items. This is because the overhead points, and 29% summarizing them. In contrast, on FC, which of heap maintenance on every operation is expensive with even returned over 1000 explanations, MacroBase spent 31% of its ex- modestly-sized sketches, while the list traversal is costly for de- ecution training MAD, 4% scoring points, and 65% summarizing cayed, non-integer counts. In contrast, with an update period of them. Thus, the overhead of each component is dependent on the 10K points, AMC sustains in excess of 10M updates per second. query. The primary cost of these performance improvements is additional space: for example, with a minimum sketch size of 10 items and 6.3 Microbenchmarks and Comparison update period of 10K points, AMC retains up to 10,010 items while each SpaceSaving sketch retains only 10. As a result, when memory In this section, we explore two key aspects of MacroBase’s design: sizes are especially constrained, SpaceSaving may be preferable, at cardinality-aware explanation and use of AMC sketches. a measurable cost to performance. Cardinality-aware explanation. We evaluated the efficiency of Additional results. In Appendix D, we provide additional results MacroBase’s OI-pruning compared to traditional FPGrowth. Mac- examining the distribution of outlier scores, the effect of varying roBase leverages a unique pruning strategy that exploits the low support and OI-ratio, the effect of training over samples and oper- cardinality of outliers, which delivers large speedups—on average, ating over varying metric dimensions, the behavior of the M-CPS over 3× compared to unoptimized FPGrowth. Specifically, Mac- tree, preliminary scale-out behavior, comparing the runtime of MDP roBase’s produces a summary of each datasets’s inliers and outliers explanation to both existing batch explanation procedures, and MDP in 0.22–1.4 seconds. In contrast, running FPGrowth separately detection and explanation to operators from frameworks including on inliers and outliers is, on average, 3.2× slower; compared to Weka, Elki, and RapidMiner. MacroBase’s joint explanation according to support and OI-ratio, much of the time spent mining inliers (with insufficient OI-ratio) 

12 .6.4 Case Studies and Extensibility Video Surveillance. We further highlight MacroBase’s ability to MacroBase is designed for extensibility, as we demonstrate via easily operate over a wide array of data sources and domains by three case studies in three separate IoT domains. We report on the searching for interesting patterns in the CAVIAR video surveillance pipeline structures, performance, and interesting explanations from dataset [1]. Using OpenCV 3.1.0, we compute two types of time- applying MacroBase over: hybrid supervised-unsupervised models, series video feature transformations: first, we compute the average time-series data, and video surveillance data. difference between pixels, and, second, we compute the average optical flow velocity. Each transformed frame is tagged with a Hybrid Supervision. We demonstrate MacroBase’s ability to eas- time interval attribute, which we use to identify interesting video ily synthesize supervised and unsupervised outlier detection models segments and, as depicted below, the remainder of the pipeline via a use case from CMT. Each trip in the CMTD dataset is accom- executes the standard MDP operators: panied by a supervised diagnostic score representing the trip quality. optical flow mean MDP’s unsupervised operators can use this score as an input, but video .. .. . MDP ingest . MAD %ile explain CMT also wishes to capture low-quality scores independent of their optical flow mean distribution in the population. Accordingly, we authored a new Mac- groupby(video) + CV xform roBase pipeline that feeds CMT metrics to the MDP MCD operator but also feeds the diagnostic metric to a special rule-based operator Using this pipeline, MacroBase detected periods of abnormal mo- that flags low quality scores as anomalies. The pipeline, which tion in the video dataset. Optical flow, which has been successfully we depict below, performs a logical or over the two classification applied in human action detection [29] produced particularly inter- results: esting results: for example, the MacroBase pipeline highlighted a three-second period in which two characters fought onscreen: MCD %ile logical MDP ingest or explain supervised classifier hybrid detection With this hybrid supervision strategy, MacroBase identified addi- tional behaviors within the CMTD dataset. Since the quality scores This result was particularly surprising given the lack of supervision were generated external to MacroBase and the supervision rule in in the pipeline. Like our STFT pipeline, feature transformation via MacroBase was lightweight, runtime was unaffected. This kind of optical flow dominated runtime (22s vs. 34ms for MDP); this is pipeline can easily be extended to more complex supervised models. unsurprising given our CPU-based implementation of a relatively Time-series. Many interesting behaviors in IoT data are time- expensive algorithm but nevertheless illustrates MDP’s ability to varying; MacroBase’s architecture can detect these via feature trans- process video streams. formation, which we demonstrate using a dataset of 16M points capturing a month of electricity usage from devices within a house- hold [11]. We augment MDP by adding a sequence of feature 7. CONCLUSIONS AND FUTURE WORK transforms that i.) partition the stream by device ID, ii.) window We have presented MacroBase, a new analytics engine designed the stream into hourly intervals, with attributes according to hour of to facilitate extensible, accurate, and fast analytic monitoring of IoT day, day of week, and date, then iii.) apply a Discrete-Time Short- data streams. MacroBase provides a flexible architecture that com- Term Fourier Transform (STFT) to each window, and truncate the bines streaming outlier detection and data explanation techniques transformed data to a fixed number of dimensions. As the diagram to deliver interpretable summaries of unusual behavior in streams. below shows, we feed the transformed stream into an unmodified MacroBase’s default analytic monitoring operators, which include MDP pipeline and search for outlying time periods and devices: new sampling and sketching procedures, take advantage of this com- bination of detection and explanation and are specifically optimized window STFT drop dim. ingest .. . .. . .. . MCD %ile MDP for high-volume, time-sensitive, and heterogeneous IoT scenarios, explain window STFT drop dim. resulting in improved performance and result quality. This empha- groupby(plug)+time-series transform sis on flexibility, accuracy, and speed has proven useful in several production deployments, where MacroBase has already identified With this time-series pipeline, MacroBase detected several systemic previously unknown behaviors at high volume. periods of abnormal device behavior. For example, the following MacroBase is available as open source and is under active devel- dataset of power usage by a household refrigerator spiked on an opment. In addition, the system serves as the vehicle for a number hourly basis (likely corresponding to compressor activity); instead of of ongoing research efforts, including decentralized, edge-based highlighting the hourly power spikes, MacroBase was able to detect analytic monitoring, temporally-aware explanation techniques, het- that the refrigerator consistently behaved abnormally compared to erogeneous sensor data fusion, online non-parametric density esti- other devices in the household and compared to other time periods mation, and contextual outlier detection. New production use cases between the hours of 12PM and 1PM—presumably, lunchtime—as continue to stimulate the development of new analytic monitoring highlighted in the excerpt below: functionality to expand the set of supported domains and leverage 200 the flexibility provided by MacroBase’s pipeline architecture. Power (W) 150 100 50 Acknowledgments 9AM 10AM 11AM 12PM 1PM 2PM 3PM The authors would like to thank the many members of the Stanford InfoLab as well as the early production users of MacroBase for feed- Without feature transformation, the entire MDP pipeline completed back and inspiration in the development of MacroBase; Ali Ghodsi, in 158ms. Feature transformation dominated the runtime, utilizing Joe Hellerstein, Mark Phillips, and Leif Walsh for useful feedback 516 seconds to transform the 16M points via unoptimized STFT. on this work; Xu Chu, Vivek Jain, Vayu Kishore, Ihab Ilyas, and Arsen Mamikonyan for ongoing contributions to the MacroBase 

13 .engine; and Pavlos S. Efraimidis for his lucid explanation and dis- management system. In ICDE, 2006. cussion of weighted reservoir sampling. This research is supported [36] M. Goldstein and S. Uchida. A comparative evaluation of unsupervised anomaly detection algorithms for multivariate data. PLoS ONE, 11(4):1–31, 04 2016. in part by Toyota Research, RWE AG, and Phillips Lighting. [37] M. Hall et al. The WEKA data mining software: an update. ACM SIGKDD explorations newsletter, 11(1):10–18, 2009. 8. REFERENCES [38] J. Han et al. Frequent pattern mining: current status and future directions. Data Mining and Knowledge Discovery, 15(1):55–86, 2007. [1] Caviar test case scenarios. http://homepages.inf.ed.ac.uk/rbf/CAVIAR/. [2] Opengamma, 2015. http://www.opengamma.com/. [39] J. Han, J. Pei, and Y. Yin. Mining frequent patterns without candidate generation. In SIGMOD, 2000. [3] Summary of the Amazon DynamoDB service disruption and related impacts in the US-East region, 2015. https://aws.amazon.com/message/5467D2/. [40] J. Hardin and D. M. Rocke. Outlier detection in the multiple cluster setting using the Minimum Covariance Determinant estimator. Computational [4] D. J. Abadi et al. The design of the borealis stream processing engine. In CIDR, Statistics & Data Analysis, 44(4):625–638, 2004. 2005. [41] J. Hardin and D. M. Rocke. The distribution of robust distances. Journal of [5] C. C. Aggarwal. On biased reservoir sampling in the presence of stream Computational and Graphical Statistics, 14(4):928–946, 2005. evolution. In VLDB, 2006. [42] J. M. Hellerstein. Quantitative data cleaning for large databases. United Nations [6] C. C. Aggarwal. Data streams: models and algorithms, volume 31. Springer Economic Commission for Europe (UNECE), 2008. Science & Business Media, 2007. [43] V. J. Hodge and J. Austin. A survey of outlier detection methodologies. [7] C. C. Aggarwal. Outlier Analysis. Springer, 2013. Artificial Intelligence Review, 22(2):85–126, 2004. [8] R. Ahmad and S. Kamaruddin. An overview of time-based and condition-based [44] M. Hofmann and R. Klinkenberg. RapidMiner: Data mining use cases and maintenance in industrial application. Computers & Industrial Engineering, business analytics applications. CRC Press, 2013. 63(1):135–149, 2012. [45] P. J. Huber. Robust statistics. Springer, 2011. [9] A. Arasu, S. Babu, and J. Widom. The cql continuous query language: semantic foundations and query execution. The VLDB Journal, 15(2):121–142, 2006. [46] M. Hubert and M. Debruyne. Minimum covariance determinant. Wiley interdisciplinary reviews: Computational statistics, 2(1):36–43, 2010. [10] A. Asta. Observability at Twitter: technical overview, part i, 2016. https://blog.twitter.com/2016/ [47] W. H. Hunter. US Chemical Safety Board: analysis of Horsehead Corporation observability-at-twitter-technical-overview-part-i. Monaca Refinery fatal explosion and fire, 2015. http://www.csb.gov/ horsehead-holding-company-fatal-explosion-and-fire/. [11] C. Beckel, W. Kleiminger, R. Cicchetti, T. Staake, and S. Santini. The ECO data set and the performance of non-intrusive load monitoring algorithms. In [48] J.-H. Hwang, M. Balazinska, et al. High-availability algorithms for distributed BuildSys. ACM, 2014. stream processing. In ICDE, 2005. [12] Y. Benjamini and D. Yekutieli. The control of the false discovery rate in [49] IDC. The digital universe of opportunities: Rich data and the increasing value multiple testing under dependency. Annals of statistics, pages 1165–1188, 2001. of the internet of things, 2014. http://www.emc.com/leadership/digital-universe/. [13] R. J. Bolton and D. J. Hand. Statistical fraud detection: A review. Statistical science, pages 235–249, 2002. [50] I. F. Ilyas and X. Chu. Trends in cleaning relational data: Consistency and deduplication. Foundatations and Trends in Databases, 2015. [14] C. Buragohain and S. Suri. Quantiles on streams. In Encyclopedia of Database Systems, pages 2235–2240. Springer, 2009. [51] M. Isard, M. Budiu, Y. Yu, A. Birrell, and D. Fetterly. Dryad: distributed data-parallel programs from sequential building blocks. In EuroSys, 2007. [15] R. Butler, P. Davies, and M. Jhun. Asymptotics for the minimum covariance determinant estimator. The Annals of Statistics, pages 1385–1400, 1993. [52] R. Jampani, F. Xu, M. Wu, L. L. Perez, C. Jermaine, and P. J. Haas. MCDB: a Monte Carlo approach to managing uncertain data. In SIGMOD, 2008. [16] L. Cao, Q. Wang, and E. A. Rundensteiner. Interactive outlier exploration in big data streams. Proceedings of the VLDB Endowment, 7(13):1621–1624, 2014. [53] Y. Klonatos, C. Koch, T. Rompf, and H. Chafi. Building efficient query engines in a high-level language. In VLDB, 2014. [17] L. Cao, D. Yang, Q. Wang, Y. Yu, J. Wang, and E. A. Rundensteiner. Scalable distance-based outlier detection over high-volume data streams. In ICDE, 2014. [54] S. Kulkarni, N. Bhagat, M. Fu, V. Kedigehalli, C. Kellogg, S. Mittal, J. M. Patel, K. Ramasamy, and S. Taneja. Twitter heron: Stream processing at scale. In [18] V. Chandola, A. Banerjee, and V. Kumar. Anomaly detection: A survey. ACM SIGMOD, 2015. computing surveys (CSUR), 41(3):15, 2009. [55] H. Li, J. Li, L. Wong, M. Feng, and Y.-P. Tan. Relative risk and odds ratio: A [19] B. Chandramouli, J. Goldstein, et al. Trill: A high-performance incremental data mining perspective. In PODC, 2005. query processor for diverse analytics. In VLDB, 2014. [56] J. Lin, E. Keogh, and S. Lonardi. Visualizing and discovering non-trivial [20] S. Chandrasekaran et al. TelegraphCQ: Continuous dataflow processing for an patterns in large time series databases. Information visualization, 4(2):61–82, uncertain world. In CIDR, 2003. 2005. [21] M. Chao. A general purpose unequal probability sampling plan. Biometrika, [57] J. Manyika. McKinsey Global Institute: The internet of things: mapping the 69(3):653–656, 1982. value beyond the hype. 2015. [22] M. Chen, A. X. Zheng, J. Lloyd, M. I. Jordan, and E. Brewer. Failure diagnosis [58] R. Manzini, A. Regattieri, H. Pham, and E. Ferrari. Maintenance for industrial using decision trees. In ICAC, 2004. systems. Springer Science & Business Media, 2009. [23] J. Cheng et al. A survey on algorithms for mining frequent itemsets over data [59] R. Maronna, D. Martin, and V. Yohai. Robust statistics. John Wiley & Sons, streams. Knowledge and Information Systems, 16(1):1–27, 2008. Chichester. ISBN, 2006. [24] G. Cormode, M. Garofalakis, P. J. Haas, and C. Jermaine. Synopses for massive [60] A. Meliou, S. Roy, and D. Suciu. Causality and explanations in databases. In data: Samples, histograms, wavelets, sketches. Foundations and Trends in VLDB, 2014. Databases, 4(1–3):1–294, 2012. [61] A. Metwally et al. Efficient computation of frequent and top-k elements in data [25] G. Cormode and M. Hadjieleftheriou. Methods for finding frequent items in streams. In ICDT. Springer, 2005. data streams. The VLDB Journal, 19(1):3–20, 2010. [62] J. A. Morris and M. J. Gardner. Statistics in medicine: Calculating confidence [26] G. Cormode, F. Korn, and S. Tirthapura. Exponentially decayed aggregates on intervals for relative risks (odds ratios) and standardised ratios and rates. British data streams. In ICDE. IEEE, 2008. medical journal (Clinical research ed.), 296(6632):1313, 1988. [27] C. Cranor, T. Johnson, O. Spataschek, and V. Shkapenyuk. Gigascope: a stream [63] B. Mukherjee, L. T. Heberlein, and K. N. Levitt. Network intrusion detection. database for network applications. In SIGMOD, 2003. Network, IEEE, 8(3):26–41, 1994. [28] P. S. Efraimidis. Weighted random sampling over data streams. In Algorithms, [64] V. Nair et al. Learning a hierarchical monitoring system for detecting and Probability, Networks, and Games, pages 183–195. Springer, 2015. diagnosing service issues. In KDD, 2015. [29] A. A. Efros, A. C. Berg, G. Mori, and J. Malik. Recognizing action at a [65] OpenSignal. Android fragmentation visualized (august 2015). distance. In ICCV, 2003. http://opensignal.com/reports/2015/08/android-fragmentation/. [30] K. El Gebaly, P. Agrawal, L. Golab, F. Korn, and D. Srivastava. Interpretable [66] C. Phua, V. Lee, K. Smith, and R. Gayler. A comprehensive survey of data and informative explanations of outcomes. In VLDB, 2014. mining-based fraud detection research. arXiv preprint arXiv:1009.6119, 2010. [31] T. Escamilla. Intrusion detection: network security beyond the firewall. John [67] D. Pokrajac, A. Lazarevic, and L. J. Latecki. Incremental local outlier detection Wiley & Sons, Inc., 1998. for data streams. In CIDM, 2007. [32] X. Feng, A. Kumar, B. Recht, and C. Ré. Towards a unified architecture for [68] B. Reiser. Confidence intervals for the Mahalanobis distance. Communications in-RDBMS analytics. In SIGMOD, 2012. in Statistics-Simulation and Computation, 30(1):37–45, 2001. [33] P. Fournier-Viger. SPMF: An Open-Source Data Mining Library – Performance, [69] P. J. Rousseeuw and K. V. Driessen. A fast algorithm for the minimum 2015. http://www.philippe-fournier-viger.com/spmf/. covariance determinant estimator. Technometrics, 41(3):212–223, 1999. [34] P. H. Garthwaite and I. Koch. Evaluating the contributions of individual [70] S. Roy, A. C. König, I. Dvorkin, and M. Kumar. Perfaugur: Robust diagnostics variables to a quadratic form. Australian & New Zealand Journal of Statistics, for performance anomalies in cloud services. In ICDE, 2015. 58(1):99–119, 2016. [71] S. Roy and D. Suciu. A formal approach to finding explanations for database [35] L. Girod, K. Jamieson, Y. Mei, R. Newton, S. Rost, A. Thiagarajan, queries. In SIGMOD, 2014. H. Balakrishnan, and S. Madden. Wavescope: a signal-oriented data stream 

14 .[72] G. Rupert Jr et al. Simultaneous statistical inference. Springer Science & evaluate the effect of outlier contamination on the Z-Score, MAD, Business Media, 2012. and MCD (using univariate points for Z-Score and MAD). [73] F. I. Rusu. Sketches for aggregate estimations over data streams. PhD thesis, University of Florida, 2009. [74] E. Schubert, A. Koos, T. Emrich, A. Züfle, K. A. Schmid, and A. Zimek. A B. EXPLANATION framework for clustering uncertain data. In VLDB, 2015. [75] W. Shi and B. Golam Kibria. On some confidence intervals for estimating the Confidence. To provide confidence intervals on its output expla- mean of a skewed population. International Journal of Mathematical Education nations, MDP leverages existing results from the epidemiology in Science and Technology, 38(3):412–421, 2007. [76] S. Subramaniam, T. Palpanas, D. Papadopoulos, V. Kalogeraki, and literature, applied to the MDP data structures. For a given attribute D. Gunopulos. Online outlier detection in sensor data using non-parametric combination appearing ao times in the outliers and ai times in the models. In VLDB, 2006. inliers, with an OI-ratio of o, no total outlier points, and ni total [77] S. K. Tanbeer et al. Sliding window-based frequent pattern mining over data inlier points, we can compute a 1 − p% confidence interval as: streams. Information sciences, 179(22):3843–3865, 2009. [78] J. S. Vitter. Random sampling with a reservoir. ACM Transactions on 1 1 1 1 Mathematical Software (TOMS), 11(1):37–57, 1985. exp ln(o) ± z p − + − [79] X. Wang, X. L. Dong, and A. Meliou. Data x-ray: A diagnostic tool for data ao no ai ni errors. In SIGMOD, 2015. where z p is the z-score corresponding to the 1 − 2p percentile [62]. [80] A. Woodie. Kafka tops 1 trillion messages per day at LinkedIn. Datanami, September 2015. http://www.datanami.com/2015/09/02/ For example, an attribute combination with OI-ratio of 5 appearing kafka-tops-1-trillion-messages-per-day-at-linkedin/. in 1% of the outlier tuples, with 1% outliers in a dataset of 10M [81] E. Wu and S. Madden. Scorpion: Explaining away outliers in aggregate queries. points has a 95th percentile confidence interval of (4.69, 5.33) (99th: In VLDB, 2013. (4.60, 5.43)). Given an OI-ratio threshold is 3, MacroBase can [82] D. Y. Yoon, N. Niu, and B. Mozafari. DBSherlock: A performance diagnostic tool for transactional databases. In SIGMOD, 2016. return this explanation with confidence. [83] Z. Zheng, Y. Li, and Z. Lan. Anomaly localization in large-scale clusters. In However, because MDP performs a repeated set of statistical tests ICCC, 2007. to find attribute combinations with sufficient OI-ratio, MDP subject to the multiple testing problem: large numbers of statistical tests are statistically likely to contain false positives. To address this APPENDIX problem, MDP applies a correction intervals. For example, under the Bonferroni correction [72], if a user seeks a confidence of 1 − p and MDP tests k attribute combinations, MDP should instead assess A. DETECTION the confidence at 1 − kp . We can compute k at explanation time by MCD. Computing the exact MCD requires examining all subsets recording the number of support computations. of points to find the subset whose covariance matrix exhibits the k is likely to be large as, in the limit, MDP may examine the minimum determinant. This is computationally intractable for even power set of all attribute values in the outliers. However, in our modestly-sized datasets. Instead, for the actual computation of IoT scenario, k is less problematic. First, the pruning power of the MCD covariance and mean, MacroBase adopts an iterative itemset mining eliminates many tests. Second, on production data, approximation called FastMCD [69]. In FastMCD, an initial subset many of MacroBase’s explanations have very high OI-ratio—often of points S0 is chosen from the input set of points P. FastMCD in the tens or hundreds. This is because many problematic IoT computes the covariance C0 and mean µ0 of S0 , then performs a behaviors are highly systemic. Third, and perhaps most interestingly, “C-step” by finding the set S1 of points in P that have the |S1 | closest MacroBase analyzes large streams. In the above example, even with Mahalanobis distances (to C0 and µ0 ). FastMCD subsequently k = 10M, the 95th percentile confidence interval is still (4.14, 6.04). repeats C-steps (i.e., computes the covariance C1 and mean µ1 Compared to, say, medical studies with study sizes in the range of S1 , selects a new subset S2 of points in P, and repeats) until of hundreds to thousands, the large volume of IoT data mitigates the change in the determinant of the sample covariance converges many of the problems associated with multiple testing. For example, (i.e., det(Si−1 ) − det(Si ) < ε, for small ε). To determine which given only 1000 points, k = 10M yields a 95th percentile confidence dimensions are most anomalous in MCD, MacroBase uses the corr- interval of (0, 776M), which is effectively meaningless. (This trend max transformation [34]. also applies to alternative corrective methods such as the Benjamini- Hochberg Procedure [12].) Thus, while the volumes of IoT data Handling variable ADR arrival rates. We consider two policies streams pose significant computational challenges, they can actually for collecting samples using an ADR over real-time periods with benefit the statistical quality of analytic monitoring results. variable tuple arrival rates. The first policy is to compute a uniform sample per decay period, with decay across periods. This can be C. IMPLEMENTATION achieved by maintaining an ADR for the stream contents from all In this section, we describe the MacroBase prototype implemen- prior periods and a regular, uniform reservoir sample for the current tation and runtime. As of June 2016, MacroBase’s core comprises period. At the end of the period, the period sample can be inserted approximately 9,105 lines of Java, over 7,000 of which are devoted into the ADR. The second policy is to compute a uniform sample to operator implementation, along with an additional 1,000 lines of over time, with decay according to time. In this setting, we can Javascript and HTML for the front-end and 7,600 lines of Java for choose a sampling period for the stream (e.g., 1 second), and, for diagnostics and prototype pipelines. each period, insert the average of all points within the sampling We chose Java due to its high productivity, support for higher- period into the ADR. order functions, and popularity in open source. However, there is considerable performance overhead associated with the Java virtual Contamination plot details. In Figure 3, we configured a synthetic machine (JVM). Despite interest in bytecode generation from high- dataset of 10M points with a combination of two distributions: a level languages such as Scala and .NET [19, 53], we are unaware uniform inlier distribution Di , with radius 50 centered at the origin, of any generally-available, production-strength operator generation and a uniform outlier distribution Do , with radius 50 centered at tools for the JVM. As a result, MacroBase leaves performance on (1000, 1000). We varied the proportion of points in Di and Do to the table in exchange for programmer productivity. To understand 

15 . LS TS ES AS FS MS Throughput (points/sec) 7.86M 8.70M 9.35M 12.31M 7.05M 6.22M 1.0 1.000 Speedup over Java 7.46× 24.11× 5.24× 16.87× 5.32× 17.54× 0.8 0.998 . 0.6 0.996 CDF CDF Table 3: Speedups of hand-optimized C++ over Java Mac- 0.4 0.994 roBase prototype for simple queries (queries described in Sec- 0.2 0.992 tion 6). 0.0 0.990 10-2 10 100 10 102 103 -1 1 101 102 103 104 105 the performance gap, we rewrote a simplified MDP pipeline in Outlier Score Outlier Score hand-optimized C++. As Table 3 shows, we measure an average Figure 7: CDF of outlier scores for all datasets, with average in throughput gap of 12.76× for simple queries. Future advances in red; the datasets exhibit a long tail with extreme outlier scores JVM code generation should only improve this gap. at the 99th percentile and higher. MacroBase executes operator pipelines via a single-core data- flow execution engine. MacroBase’s streaming dataflow decouples 104 104 producers and consumers: each operator writes (i.e,. pushes) to an # Summaries # Summaries 103 MC 103 output stream but consumes tuples as they are pushed to the operator EC by the runtime (i.e., implements a consume(OrderedList<Point>) 102 102 interface). This facilitates a range scheduling policies: operator 101 101 execution can proceed sequentially, or by passing batches of tu- 100 100 ples between operators. MacroBase supports several styles of 10-4 10-3 10-2 10-1 100 10-2 10-1 100 101 pipeline construction, including a fluent, chained operator API Minimum Support Minimum OI-Ratio (i.e., ingester .then(transformer) .then(classifier)). By 14 default, MacroBase amortizes calls to consume across several thou- 10 12 sand points, reducing function call overhead. This API also allows 8 10 Time (s) Time (s) 6 8 stream multiplexing and is compatible with a variety of existing 6 4 4 dataflow execution engines, including Storm, Heron, and Amazon 2 2 Streams, which could also form the basis of an execution substrate 0 0 for MacroBase operators in the future. We demonstrate interoper- 10-4 10-3 10-2 10-1 100 10-2 10-1 100 101 ability with several existing data mining frameworks in Appendix D. Minimum Support Minimum OI-Ratio The MacroBase prototype does not currently implement fault Figure 8: Number of summaries produced and summarization tolerance, although classic techniques such as state-based check- time under varying support (percentage) and OI-Ratio. pointing are applicable here [48], especially as MDP’s operators contain modest state. The MacroBase prototype is also oriented Score distribution. We plot the CDF of scores in each of our real- towards single-core deployment. For parallelism, users currently run world dataset queries in Figure 7. While many points have high one query per core; for example, in the event of larger deployments, anomaly scores, the tail of the distribution (at the 99th percentile) we run multiple MacroBase queries on different partitions of data is extreme: a very small proportion of points have outlier scores (e.g., one query pipeline per application cluster in a datacenter). over over 150. Thus, by focusing on this small upper percentile, However, we report on preliminary multi-core scale-out results in MacroBase highlights the most extreme behaviors. Appendix D. The MacroBase prototype and all code evaluated in this paper are Varying support and OI-Ratio. To understand the effect of sup- available online under a permissive open source license. port and OI-ratio on explanation, we varied each and measured the resulting runtime and the number of summaries produced on the EC and MC datasets, which we plot in Figure 8. Each dataset has few D. EXPERIMENTAL RESULTS attributes with outlier support greater than 10%, but each had over Dataset descriptions. CMTD contains user drives at CMT, includ- 1700 with support greater than 0.001%. Past 0.01%, support had ing anonymized metadata such as phone model, drive length, and limited impact on runtime; most time in explanation is spent in sim- battery drain; Telecom contains aggregate internet, SMS, and tele- ply iterating over the inliers rather than maintaining tree structures. phone activity for a Milanese telecom; Accidents contains statistics This effect is further visible when varying the OI-Ratio, which has about United Kingdom road accidents between 2012 and 2014, in- less than 40% impact on runtime yet leads to an order of magnitude cluding road conditions, accident severity, and number of fatalities; change in number of summaries. We find that our default setting of Campaign contains all US Presidential campaign expenditures in support and OI-Ratio yields a reasonable trade-off between number election years between 2008 and 2016, including contributor name, of summaries and runtime. occupation, and amount; Disburse contains all US House and Senate Operating on samples. MDP periodically trains models using candidate disbursements in election years from 2010 through 2016, samples from the input distribution. The statistics literature of- including candidate name, amount, and recipient name; and Liquor fers confidence intervals on the MAD [75] and the Mahalanobis contains sales at liquor stores across the state of Iowa. distance [68] (e.g., for a sample of size n, the confidence interval Several of these datasets, such as Disburse, are not explicitly IoT of MAD shrinks with n1/2 ), while MCD converges at a rate of datasets. However, all but CMT are i.) publicly accessible, allowing n−1/2 [15]. To empirically evaluate their performance, we measured reproducibility, and ii.) representative of many challenges we have the accuracy and efficiency of training models on samples. In Fig- encountered in analyzing production data beyond CMT in scale and ure 9, we plot the outlier classification F1 -Score versus sample size general trends. While none of these datasets contain ground-truth for the CMT queries. MAD precision and recall are unaffected by labels, we have verified several of the explanations from our queries sampling, allowing a four order-of-magnitude speedup without loss over CMT and plan to make all non-CMT explanation outputs pub- in accuracy. In contrast, MCD accuracy is more sensitive due to licly available. variance in the sample selection: for example, training on a sample 

16 . 101 Normalized Throughput 1.000 1.0 Classification Accuracy Summary F-Score 32 Training Time (s) 100 0.998 MC 0.8 10-1 16 MS 0.6 0.996 8 10-2 0.994 MC 4 FS 0.4 10-3 0.992 MS 2 FC 0.2 10-4 0.990 1 0.0 102 103 104 105 106 102 103 104 105 106 1 2 4 8 16 32 48 1 2 4 8 16 32 48 Sample Size Sample Size # Partitions (Cores) # Partitions (Cores) Figure 9: Behavior of MAD (MS) and MCD (MC) on samples. Figure 11: Behavior of naïve, shared-nothing scale-out. TPC-C (QS: one MacroBase query per cluster): top-1: 88.8%, top-3: 88.8% MCD Throughput 106 A1 A2 A3 A4 A5 A6 A7 A8 A9 105 Train top-1 correct (of 9) 9 9 9 9 9 8 9 9 8 Holdout top-1 correct (of 2) 2 2 2 2 2 2 2 2 0 104 TPC-C (QE: one MacroBase query per anomaly type): top-1: 83.3%, top-3: 100% A1 A2 A3 A4 A5 A6 A7 A8 A9 103 Train top-1 correct (of 9) 9 9 9 9 9 8 9 9 7 2 4 8 16 32 64 128 Holdout top-1 correct (of 2) 2 2 2 2 2 1 2 2 0 Metric Dimension TPC-E (QS: one MacroBase query per cluster): top-1: 83.3%, top-3: 88.8% Figure 10: MCD throughput versus metric size. A1 A2 A3 A4 A5 A6 A7 A8 A9 Train top-1 correct (of 9) 9 9 9 9 9 8 9 9 0 Holdout top-1 correct (of 2) 2 2 2 2 2 1 2 2 0 of 10K points out of 10M yields a speedup of over five orders of TPC-E (QE: one MacroBase query per anomaly type): top-1: 94.4%, top-3: 100% magnitude but results in an F1 -Score of 0.48 (std dev: 0.32). A small A1 A2 A3 A4 A5 A6 A7 A8 A9 number of MCD estimates have poor F-Scores. This variance is Train top-1 correct (of 9) 9 9 9 9 9 8 9 9 6 Holdout top-1 correct (of 2) 2 2 2 2 2 1 2 2 2 offset by the fact that models are retrained regularly under streaming execution. Table 4: MDP accuracy on DBSherlock workload. A1: work- Metric scalability. As Figure 10 demonstrates, MCD train and load spike, A2: I/O stress, A3: DB backup, A4: table restore, score throughput (here, over Gaussian data) is linearly affected by A5: CPU stress, A6: flush log/table; A7: network congestion; data dimensionality, encouraging the use of dimensionality reduc- A8: lock contention; A9: poorly written query. “Poor physi- tion pre-processing techniques for complex data. cal design” (from [82]) is excluded as the labeled anomalous re- M-CPS and CPS behavior. We also investigated the behavior of gions did not exhibit significant correlations with any metrics. the M-CPS-tree compared to the generic CPS-tree. The two data structures have different behaviors and semantics: the M-CPS-tree not attempt a full comparison based on semantics but do perform a captures only itemsets that are frequent for at least two windows comparison based on running time, which we depict in Table 5. We by leveraging an AMC sketch. In contrast, CPS-tree captures all compared to a data cubing strategy suggested by Roy and Suciu [71], frequent combinations of attributes but must insert each point’s which generates counts for all possible combinations (21x slower), attributes into the tree (whether supported or not) and, in the limit, Apriori itemset mining [38] (over 43x slower), and Data X-Ray [79]. stores (and re-sorts) all items ever observed in the stream. As a Cubing works better for data with fewer attributes, while Data X-Ray result, across all queries except ES and EC, the CPS-tree was on is optimized for hierarchical data; we have verified with the authors average 130x slower than the M-CPS-tree (std dev: 213x); on ES of Data-XRay that, for MacroBase’s effectively relational points, and EC, the CPS-tree was over 1000x slower. The exact speedup was Data X-Ray will consider all combinations of categorical attributes influenced by the number of distinct attribute values in the dataset: unless stopping criteria are met. MacroBase’s cardinality-aware Accidents had few values, incurring 1.3x and 1.7x slowdowns, while explanation completes fastest for all queries. Campaign had many incurring substantially greater slowdowns Compatibility with existing frameworks. We implemented sev- Preliminary scale-out. As a preliminary assessment of MacroBase’s eral additional MacroBase operators to validate interoperability with potential for scale-out, we examined its behavior under a naïve, existing data mining packages. We were unable to find a single shared-nothing parallel execution strategy. We partitioned the data framework that implemented both unsupervised outlier detection across a variable number of cores of a server containing four Intel and data summarization and had difficulty locating streaming imple- Xeon E7-4830 2.13 GHz CPUs and processed each partition; upon mentations. Nevertheless, we implemented two MacroBase outlier completion, we return the union of each core’s explanation. As detection operators using Weka 3.8.0’s KDTree and Elki 0.7.0’s Figure 11 shows, this strategy delivers excellent linear scalability. SmallMemoryKDTree, an alternative FastMCD operator based on a However, as each core effectively trains and summarizes a sample recent RapidMiner extension (CMGOSAnomalyDetection) [36], an of the overall dataset, accuracy suffers due to both model drift (as in Query MB FP Cube DT10 DT100 AP XR Figure 9) and lack of cross-partition cooperation in summarization. LC 1.01 4.64 DNF 7.21 77.00 DNF DNF For example, with 32 partitions spanning 32 cores, FS achieves TC 0.52 1.38 4.99 10.70 100.33 135.36 DNF throughput nearing 29M points per second, with perfect recall, but EC 0.95 2.82 16.63 16.19 145.75 50.08 DNF AC 0.22 0.61 1.10 1.22 1.39 9.31 6.28 only 12% accuracy. Improving accuracy while maintaining scalabil- FC 1.40 3.96 71.82 15.11 126.31 76.54 DNF ity is the subject of ongoing work. MC 1.11 3.23 DNF 11.45 94.76 DNF DNF Explanation runtime comparison. Following the large number of recent data explanation techniques (Section 2.2), we implemented Table 5: Running time of explanation algorithms (s) for each several additional methods. The results of these methods are not complex query. MB: MacroBase, FP: FPGrowth, Cube: Data comparable, and prior work has not evaluated these techniques with cubing; DTX: decision tree, maximum depth X; AP: A-Aprioi; respect to one another in terms of semantics or performance. We do XR: Data X-Ray. DNF: did not complete in 20 minutes. 

17 .alternative MAD operator from the OpenGamma 2.31.0, and an alter- implementation, SPMF was still 2.8× slower than MacroBase due native FPGrowth-based summarizer based on SPMF version v.0.99i. to MDP’s cardinality-aware optimizations. The primary engineering As none of these packages allowed streaming operation (e.g., Weka overheads came from adapting to each framework’s data formats; allows adding points to a KDTree but does not allow removals, while however, with a small number of utility classes, we were able to Elki’s SmallMemoryKDTree does not allow modification), we imple- easily compose operators from different frameworks and also from mented batch versions. We do not perform accuracy comparisons MacroBase, without modification. Should these frameworks begin here but note that the kNN performance was substantially slower to prioritize streaming execution and/or explanation, this interoper- (>100x) than MDP’s operators (in line with recent findings [36]) ability will prove especially fruitful in the future. and, while SPMF’s operators were faster than our generic FPGrowth