Event Regularity and Irregularity in a Time Unity

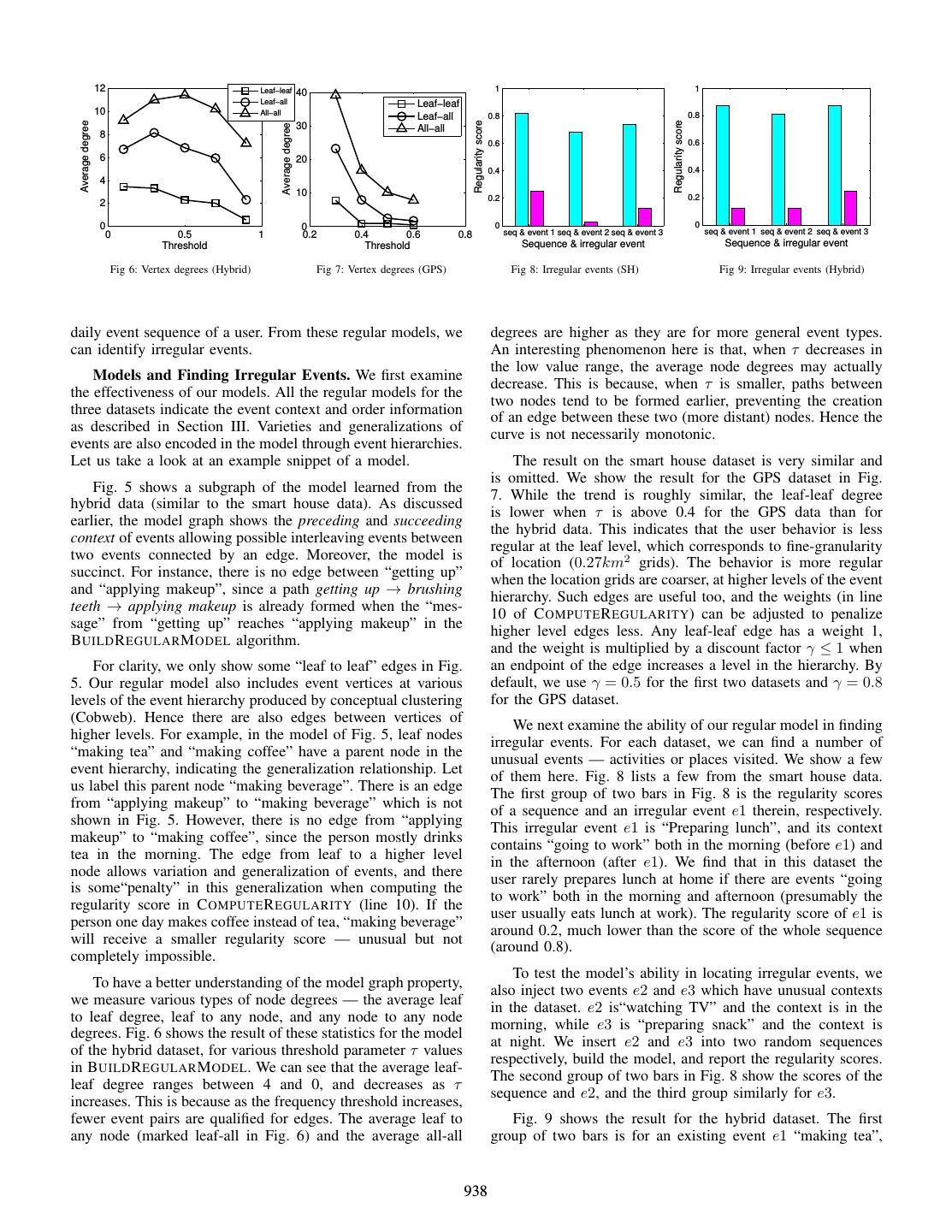
1 . Event Regularity and Irregularity in a Time Unit Lijian Wan Tingjian Ge University of Massachusetts, Lowell University of Massachusetts, Lowell lwan@cs.uml.edu ge@cs.uml.edu Abstract—In this paper, we study the problem of learning going up and down with the selected altitude) would have been a regular model from a number of sequences, each of which automatically detected, and the tragedy in the subsequent flight contains events in a time unit. Assuming some regularity in such could have been prevented. sequences, we determine what events should be deemed irregular in their contexts. We perform an in-depth analysis of the model Example 2: Elderly people (or persons with autism) who we build, and propose two optimization techniques, one of which live alone often lead a dangerous life. If they fall down on is also of independent interest in solving a new problem named the floor, or pass out in the bathroom, no one may notice it the Group Counting problem. Our comprehensive experiments for a long time. It would be useful to continuously sense the on real and hybrid datasets show that the model we build is very location, movement, and other signals from the person, and effective in characterizing regularities and identifying irregular have a software program automatically monitor the situation. events. One of our optimizations improves model building speed by more than an order of magnitude, and the other significantly These people’s normal daily activities are usually simple, upon saves space consumption. which a regular model may be built (the time unit here is one day) and abnormal events may be detected as soon as they happen. Many lives could be saved from such continuous I. I NTRODUCTION automatic monitoring. We live in “interesting times”. For computing, this is true Example 3: Consider a person who lives a normal life in that we are inundated with data, and computing power is with established and habitual daily activities, such as going to ever increasing. Much of this data has to do with ubiquitous office for work, having meetings with some group of people, computing — data given by sensors that detect various at- dining in a certain set of restaurants, entertaining at a number tributes of the state of the world, e.g., GPS (for locations), of places, and so on. Variations are possible, say, between temperature and light sensors, accelerometers and gyroscopes workdays and weekends. Automatic recognizing and logging (for movements and orientations), among many others that “irregular” events are often of interest. For instance, if a even come with smartphones today. Continuous sensing creates meeting takes place with someone who I do not usually interact relational sequence data where one of the attributes is time, with or at a place I do not typically visit, it may be useful to along with any number of other attributes. Each tuple in the have this logged. Or if anything significant happens, I may look sequence describes the state at an instant of time, which often back to see if any recent irregular events might have caused implies the event, activity, or action that is occurring. Certain this outcome. events and activities often have some patterns within a time unit (typically a day or the duration of a process), and the Event detection and activity recognition have been well- same pattern is repeated periodically over many time units. studied in the ubiquitous computing and artificial intelligence It is useful to find out the model of such regularity, and to communities (e.g., [2]). In the above motivating applications, identify irregular or unusual events when they happen. Let us each tuple at a time instant may have an event/activity label look at some examples. indicating the event or action that is happening. Each time unit — e.g., a flight in the pilot example or a day in the latter Example 1: On March 24, 2015, the copilot Lubitz crashed two examples — has a sequence of tuples, and we may have Germanwings Flight 4U9525 in the French Alps, killing all a number of such sequences, from which a regular model is 150 people on board. Data shows that in the flight into to be learned. Using this regular model, irregular events are Barcelona prior to the doomed flight, Lubitz practiced a further identified. Outlier/anomaly detection has been studied controlled descent, where he toyed with the plane’s settings, for sequence data (cf. a survey [3]), temporal data (cf. a survey programming it for sharp descent multiple times [1]. The [4]), and in more general contexts (cf. a survey [5]). However, “selected altitude” of the flight changed repeatedly, including previous work is designed for different problems and is very several times being set as low as 100 feet above the ground. different from ours. We discuss it in detail in Sec. VIII (related Lubitz also put the engines on idle, which gives the plane the work) and Sec. VII (experiments). ability to quickly descend. It is highly unusual for a pilot to do these. The airline company technically could have known about Our Contributions. We begin with formally stating the Lubitz’ apparent rehearsal on this previous flight, but only if it problem, and proposing to cluster events into an event hi- had looked at the flight data in the short period while the plane erarchy tree. This abstracts events into higher level com- was unloading and loading passengers in Barcelona. There monalities, which we call generalized events, to build into are various sensors in a modern airplane to record operations the regular model. In this way, even though specific events and settings of the pilot. Suppose a “regular” model for a may differ, variations can be permitted, and the higher level single flight (which is the time unit mentioned above) had common characteristics of the events are recognized in the been built, irregular and unusual events during this flight (i.e., model. Then we first study how to build a regular model. 978-1-5090-2020-1/16/$31.00 © 2016 IEEE 930 ICDE 2016 Conference 

2 .Our algorithm performs message passing progressively and builds the regular model at the same time. This framework is easily parallelizable. The resulting model characterizes events and their contexts. Next we devise a method that returns the regularity score of each event in a sequence, based on the model. Our experiments show that our model is very effective in identifying irregular events. We further perform an in-depth analysis of property of the model graph. We adaptively estimate the probability of creating a new edge into the model graph during the model building Fig. 1: Illustrating the event hierarchy tree created by Cobweb. process, based on a novel two function recursive approach, also incorporating runtime information obtained from actual data. This results in an optimization that we can stop the model building algorithm early when the new edge probability Given S, the first aspect of our problem is to obtain a is very small. Our experiments show that this optimization model M that characterizes the regularity of the sequences in is very effective. The performance improvement is dramatic, S. Most, if not all, sequences in S share this same model. often over an order of magnitude. Moreover, there is virtually We call it a regular model. The second aspect of our problem no loss in accuracy. The precision is 1, and the recall is 0.99 is to return a function R, such that given the regular model or higher for edges in the model graph. M and any sequence s (regardless of whether s ∈ S), one Another optimization is to reduce memory consumption. can obtain the regularity score of any event in s, denoted as We first abstract out a general problem called the Group R(s, j, M) for the jth event in s. Moreover, one can obtain the Counting Problem, which is of independent interest. It is a regularity score of the sequence s, denoted as R(s, M). Such generalization of the commonly known set membership prob- regularity scores are between 0 and 1, with 1 being the most lem in computer science. We devise a low memory footprint regular and 0 the least. Note that, in the problem statement, approximate solution named blended bitmap set (BBS). Our we intentionally do not restrict the form of the regular model experiments show that with BBS our regular model building or the score function, in order to make the possible solutions uses significantly less memory (e.g., one eighth) without losing flexible. much accuracy and model power. Finally, we carry out a comprehensive experimental study to examine our regular B. Preprocessing Events model properties, effectiveness in finding irregular events, and For building a regular model, we propose to preprocess the efficiency of our algorithms. Our contributions can be the events in the data into an event hierarchy tree T. The summarized as follows: idea is that a (new) generalized higher-level event incorporates • We identify and formulate an interesting problem with multiple more specific events, hence allowing us to model practical significance (Sec. II). variations of the same general event. For example, the events • We propose an algorithmic framework based on mes- “drinking coffee” and “drinking tea” can be generalized to a sage passing and event hierarchies to build a regular higher level event “drinking beverage”, even though “drinking model, which can be easily parallelized (Sec. III). beverage” is not an event in the original sequence set S (while • We propose a method that returns the regularity of “drinking coffee” and “drinking tea” are). Similarly, suppose all events in a sequence, which is shown to be very a person sometimes has lunch at restaurant A, sometimes at effective in experiments (Sec. IV). restaurant B. Then the events “lunch at restaurant A” and • We perform two optimizations: one is to estimate “lunch at restaurant B” can be generalized into a higher level a statistic dynamically at runtime and can stop the event “lunch at a restaurant”, or even further, just “having execution early, while the other is a new compact ap- lunch”. All original events in S appear as leaves of the event proximate data structure to significantly save memory tree T, while internal nodes of T are higher-level events. Thus, consumption (Sec. V, VI). if different sequences in S show variations of a general event, • We perform a systematic experimental study to eval- their commonality can still be modeled, knowing the event uate our approaches (Sec. VII). hierarchy T. An event in that context that does not belong to the more general event can be an irregular event. II. P ROBLEM S TATEMENT AND P REPROCESSING We merely propose the general strategy of clustering events into an event hierarchy T. There can be multiple ways to A. Problem Statement implement this strategy. In fact, if nothing is done, all the We are given a set of event sequences S = {s1 , s2 , . . . , sm } original events in S can be deemed a “flat” tree, as leaves under as input, where each sequence si (1 ≤ i ≤ m) consists of a a single root node. Hence, our subsequent algorithm framework list of events within the duration of a time unit. Thus, the time is always applicable to any event data. Such clustering is units are repeated, and each time unit is a time interval, such as based on the attributes in an event. We use a technique called a day or the duration of a flight. The whole set S spans m time conceptual clustering [6] in machine learning. Given a set units. The events in si are denoted as si [1],si [2], . . . Note that of events (or object descriptions in general), it produces a si ’s may be of different lengths. Each event si [j] is a tuple classification scheme over the events based on their attributes. with a number of attributes including a timestamp attribute, Specifically, we use the Cobweb algorithm provided as part which is monotonically increasing within each sequence si . of the commonly used Weka machine learning tools [7]. Fig. 931 

3 .1 shows a snippet of the event tree produced by Cobweb on Algorithm 1: B UILD R EGULAR M ODEL (S, T) one of our test datasets. After this conceptual clustering, each Input: S: a set of m event sequences, sequence si in S corresponds to a sequence of leaf nodes of T: an event hierarchy tree T. Each of these leaf nodes e belongs to more general event Output: a regular model M types that are e’s ancestors in T. 1 G ←(V, E) where V is nodes of T and E is to be determined 2 set of agents A ← leaves of T 3 for each s ∈ S in parallel do III. B UILDING A R EGULAR M ODEL 4 for each event s[i] ∈ s in parallel do 5 agent a[i] initiates a message and sends to a[i + 1] In this section, we propose an approach to solve the first aspect of the problem stated in Section II-A, namely to build 6 R(u, v) ← 0, ∀u, v ∈ V, u = v a regular model. This takes as input a set of event sequences 7 R(v, v) ← 1, ∀v ∈ V S and the event hierarchy tree T discussed in Section II-B. 8 for each time step t do Intuitively, the general idea is that an event e is “regular” if it 9 for each agent a in parallel do “fits in” its “context”, in terms of what other events are before 10 if a receives a message msg then and after it. If this context is common for e to be in, then e is 11 a0 ← msg’s initiator regular. However, one has to keep in mind that the relevant 12 for each v1 ∈ ancestors (a0 ), v2 ∈ ancestors(a) do surrounding events in the context may not be immediately 13 if R(v1 , v2 ) = 1 then preceding or succeeding e, as some random events could occur 14 continue in between. 15 set the bit in bm(v1 , v2 ) for a’s sequence Our algorithm is based on “message passing”. Each event 16 if |bm(v1 , v2 )| > τ · m then (in each sequence of S) initiates a message to its right neighbor 17 E ← E (v1 , v2 ) event. These messages propagate one step at a time to the 18 l ← max(l(v1 ), l(v2 )) receiver’s right neighbor. During this progressive propagation, 19 for each x ∈ V do 20 for each y ∈ V do each event pair (message initiator, receiver) is added to a 21 if max(l(x), l(y)) ≥ l and counter maintained for each event pair. When the counter for 22 R(x, v1 ) = R(v2 , y) = 1 then an event pair is above a threshold, this event pair is added 23 R(x, y) ← 1 as an edge in a graph, which we will eventually return as the regular model. The event pairs we keep track of include general event types as well, i.e., the internal nodes of T. Thus, the model tolerates variations of events belonging to a general 24 for each s ∈ S in parallel do type, although an edge over a more general event type carries 25 for each event s[i] ∈ s in parallel do 26 agent a[i] propagates its message to a[i + 1] less weight when we compute the “regularity score” in Section IV. 27 return G as regular model M Another point is that the regular model that we return is concise. During the message propagation, we do not add an edge from event e1 to event e2 to the model graph if there already exists a path from e1 to e2 in the model graph (which In lines 6-7, the binary matrix R(u, v) is to keep track of means each edge in this path takes fewer message passing “reachability” from vertex u to vertex v in the model graph G steps). Thus, if there is a common event sequence a → b → so far. More precisely, R(u, v) = 1 if there exists a path from u c, then we only have two edges a → b and b → c in the to v where every vertex on this path has a level no greater than model graph, but not a → c. Besides efficiency, another reason max(l(u), l(v)). This is exactly the condition under which we for doing this is that, in considering an event e’s “context”, do not create a new edge from u to v. Note that if there is a we would prefer events closer to e, even though we do allow vertex on this path with a level greater than those of both u interleaving irrelevant events. and v, it is still beneficial to add a direct edge from u to v, since it does not go through a more general event (which is a For a node v in T , we define the level of v, denoted as stronger relationship). Lines 6-7 are to initialize R such that a l(v), to be the maximum number of edges to traverse from vertex is only reachable to itself. v to a leaf that is a descendant of v (i.e., in v’s subtree). Thus, all leaves have a level of 0. We show the algorithm At each time step (line 8), the receiver agent receives in B UILD R EGULAR M ODEL. the message from the sender agent. We call it a time step here, which simply means the propagation of one hop of the In line 1, we initialize a model graph, where the vertices messages. Line 11 gets the original initiator of the message are just the nodes of T, and the edges are to be determined in (the event/agent) who creates the message in the beginning this algorithm. In line 2, we start an “agent” for each distinct (i.e., line 5). In line 12, we iterate through each ancestor of leaf event. These agents will be responsible for sending and a0 and each ancestor of a in the input event tree T, where a0 receiving messages. In lines 3-4, we use the keyword “in and a correspond to leaves of the tree. If there is a path from parallel” to emphasize the fact that each loop can be executed v1 to v2 (lines 13-14), then we do not bother to create a new independently in parallel. Indeed, our message passing algo- edge. Otherwise, in line 15, we “increment the counter” for rithmic framework is highly parallelizable. For event s[i] in this event pair v1 , v2 . However, this is not a simple counter, sequence s, we denote its agent as a[i]. In line 5, a[i + 1] is as each sequence in S can only be counted once. That is, we the agent for the event’s right neighbor. keep track of, out of the m sequences in total, how many have 932 

4 .encountered the event pair (v1 , v2 ) in the message passing so hierarchy of T, if not the most specific event type (i.e., leaf far. Therefore, we use a bitmap bm(v1 , v2 ) of m bits (one bit level of T). However, different penalty weights may be inflicted for each sequence) as the “counter” for this event pair. In line depending on the application. For example, variations on the 16, |bm(v1 , v2 )| denotes the number of 1’s in this bitmap. If duration of an event may be significant for some applications, it is above a threshold (fraction τ ), we add this event pair as such as in the living-alone elder people example (Example 2), an edge into E of the model graph. where a long stay in the bathroom is irregular and must be alerted. Edge weights in the model graph will be discussed in Lines 18-23 are to maintain the reachability matrix R. Section IV when we compute regularity scores. Since we have just added an edge (v1 , v2 ) into the graph, we want to find all vertex pairs (x, y) that are changed in R. Clearly, if there is already a path (x, v1 ) and a path (v2 , y) IV. R EGULARITY S CORE AND I RREGULAR E VENTS indicated in R (line 22), there now exists a path (x, y) due to Given a regular model M found in Section III, we now the addition of edge (v1 , v2 ). There is an additional condition address the second aspect of the problem, i.e., to give a that x and y must not both be at levels lower than l in T (line function/procedure that returns a regularity score R(s, j, M) 21); this is required by the definition of R(x, y) being 1, as for event s[j], as well as the regularity R(s, M) of the whole discussed earlier. sequence s. The procedure we give is a novel “ping” message Lines 24-26 simply propagate each message to the right, based algorithm that computes the regularity scores of all preparing for the next time step (back to the loop in line 8). events in a sequence (at the same time), as well as the The loop in line 8 ends when there are no more messages to regularity score of the whole sequence. process, i.e., all messages have propagated through the right ends of the sequences. When that happens, the graph G is The basic idea is that we let each event agent a[i] in s returned as the regular model M (line 27). initiate a ping message and send it to its right neighbor a[i+1], which in turn propagates the message to its right neighbor, and Example 4: Let us look at a simple example to have a so on. Then we see if we can match such an (initiator,receiver) more concrete idea of how the algorithm proceeds. Suppose pair to an edge e in M. Intuitively, a match to an edge with S has three sequences s1 , s2 , and s3 all being “abc”. That endpoints lower in T is a better match, as the events are more is, there are three leaf events a, b, and c. For simplicity, let specific. Thus, there is a multiplicative discount factor γ(0 < us assume the tree T is flat and we do not consider internal γ ≤ 1) for each level increment of one of the endpoins of e nodes for now. Let the threshold parameter τ = 2/3 (line in T (γ may further be customized for particular nodes in T, 16). We show how we obtain the final model, in which there but we omit such details). are two edges (a, b) and (b, c). In line 5, each sequence will have two messages a → b and b → c. In lines 6-7, R is a Informally, an irregular event is an event whose ping 3-by-3 matrix where only the diagonal entries are 1. In line receives no response (in terms of matching an edge in M), 10, agent for event b receives a message from the agent for or who does not respond to anyone else’ pings. This means event a. The bitmap bm(a, b) in line 15 has three bits, one for that the event is “strange” in its context in the sequence. each sequence. All three bits of bm(a, b) are set to 1 since Line 3 initializes two arrays pre[i] and post[i] that indicate all three sequences encounter this event pair message. In line the regularity of s[i] with respect to the events before and after 16, it is above the threshold 2; hence the edge (a, b) is added s[i], respectively. As in B UILD R EGULAR M ODEL, we iterate to the edge set E of the model graph (line 17). Lines 18-23 through each pair of event (message initiator and receiver, lines will set the entry (a, b) in R to be 1. In the same manner, the 5-7), and check if this event pair is an edge in the regular model other message b → c in this round will create an edge (b, c) (line 10). If it is, we get the weight of this edge (line 11). As in the model graph, and set the reachability entry R(b, c) to discussed earlier, the weight w is based on a discount factor be 1. Since both R(a, b) and R(b, c) are 1, lines 19-23 will γ(0 < γ ≤ 1) that signifies the importance of an upper level set R(a, c) to be 1 as well. Now lines 24-26 propagate the edge. If both v0 and v are leaves (i.e., level 0), then w is 1. If message initiated by a and received by b to its right neighbor a model has fewer leaf level edges but more edges on higher c, for all three sequences. Then in the next time step (loop level events, γ can be set higher to give more weight to such at line 8), c receives this message originally initiated by a. edges. We will get to this issue in the experiment section. Thus, we are considering the event pair (a, c). However, line 13 finds that R(a, c) = 1; therefore (a, c) will not be added as Lines 12-15 update the pre[·] value of the receiver and an edge in the model graph. At this point, all messages have the post[·] value of the message initiator if we get a higher propagated to the right end of the sequences, and the graph G weight. In lines 16-17, the messages are passed on to the right containing two edges (a, b) and (b, c) is returned as the model. neighbors. In the end, the regularity score r[i] of each event s[i] is the product of its pre[·] score and post[·] score (line 19), We can see that the message passing framework in B UIL - and the regularity score of the whole sequence is the average D R EGULAR M ODEL can be easily parallelized. Except for the of the individual events’ scores (line 20). serial time steps in line 8, all the execution steps within each time step are highly parallelizable. A few comments are in Since w, pre[·], and post[·] values are all between 0 place. First, we have to understand the complexity that the and 1, the regularity scores are between 0 and 1 too. The “preceding” and “succeeding” relevant events in the context lower the score, the more irregular the event (or sequence) might not immediately precede or follow the event in question. is. This algorithm essentially does what we can do given the There can be irrelevant or irregular events in between. This information of a set of sequences S: checking if the event is one source of “noise”. Second, we allow another type of in question has a context that is common in S (through its variation that events may agree on a more general type in the model M). We find in the experiments (Section VII) that this 933 

5 . Algorithm 2: C OMPUTE R EGULARITY (s, M) Input: s: an event sequence, M: regular event model Output: regularity r[i] of each event s[i], and regularity r of s 1 for each event s[i] ∈ s in parallel do 2 agent a[i] initiates a message and sends to a[i + 1] 3 initialize pre[i] and post[i] to 0 4 for each time step t do Fig. 2: Illustrating the impact of a missing event “e” from a 5 for each agent a[i] in parallel do sequence. (a) A regular model where missing e will only make events d and f irregular. (b) A regular model where missing e 6 if a[i] receives a message msg then will not have a significant impact on the regularity scores of 7 a[j] ← msg’s initiator other events in the sequence. 8 for each v0 ∈ ancestors (a[j]), 9 v ∈ ancestors(a[i]) do 10 if (v0 , v) ∈ M then 11 w ← γ l(v0 )+l(v) 12 if w > pre[i] then probability that there exists an edge to an event n time steps 13 pre[i] ← w later (i.e., an edge that spans n hops), and let qn denote the 14 if w > post[j] then probability that there exists a path to an event n time steps 15 post[j] ← w later. We devise a novel two function (pn and qn ) recursive approach to solve pn and qn simultaneously. 16 for each letter s[i] ∈ s in parallel do We further define fn as the probability that an event s[i] in 17 agent a[i] propagates its message to a[i + 1] S and an event s[i + n] is a frequent pair in S, i.e., the event order s[i] followed by s[i+n] appears in more than τ sequences 18 for each event s[i] ∈ s in parallel do in S. fn can be estimated as the empirical probability as 19 r ← pre[i] · post[i] B UILD R EGULAR M ODEL is run and messages are propagated |s| r[i] incrementally. 20 r← i=1 |s| We then have: n−1 metric is very effective in identifying irregular events within pn = fn · (1 − pi qn−i ) (1) a sequence, even though the sequence itself is overall regular i=1 (having a high regularity score). Note that an event at the very n beginning (or very end, resp.) of a sequence may have the qn = pi qn−i (2) pre[·] score (or post[·] score, resp.) being 0, which gives a i=1 low regularity score. However, we can quickly find such an event at the border of a sequence and only look at its post[·] In Equation (1), there is an edge to a vertex n hops away score (or pre[·] score, resp.) that truly indicates its regularity. (pn ) if and only if the pair is frequent (fn ) and there is no path n−1 with multiple edges between the two nodes (1− i=1 pi qn−i ). As another remark, consider the scenario that an event e The case of multiple-edge path is subdivided according to the is missing from a sequence. What impact does it have on the number of hops of the first edge in the path (i.e., pi ), and regularity scores of other events in this sequence? Informally, the remaining path (qn−i ). Similarly, in Equation (2), the case it depends on how “important” this event e is to other events of existing a path of n hops is subdivided according to the (with respect to the regular model M). If M is “linear” around number of hops of the first edge in the path (i.e., pi ). The e, like the one shown in Fig. 2(a), missing e would only affect boundary conditions are q0 = 1 and p1 = f1 . d’s post[·] score and f ’s pre[·] score — hence only d and f ’s regularity scores. If, on the other hand, M is like in Fig. 2(b), It is not hard to see that, by applying Equations (2) and where e’s incoming neighbor d has multiple outgoing edges, (1) alternately, we can iteratively obtain all qi ’s and pi ’s up to and e’s outgoing neighbor f has multiple incoming edges, qn and pn (i.e., in the order q1 , p2 , q2 , p3 , and so on). We can then the regularity scores of these other events would not be stop the process, as well as the algorithm, when pn is small significantly changed by the absence of e. enough (i.e., when n is big enough). A few remarks are in place. The above analysis serves V. A NALYSIS AND O PTIMIZATION both as understanding of the model graph property (i.e., how Intuitively, during the B UILD R EGULAR M ODEL algorithm, likely an edge crosses over n events in the sequence), and as as a message propagates a long way, the chance that it will a performance optimization in that we can stop the algorithm form new edges in G becomes very small. This is because it early when pn is small enough (i.e., the model is stable). is more likely to have a “path” between two farther nodes as Secondly, we choose to empirically measure fn and an- the number of possible paths increases. Hence, when the edge alytically derive pn because fn is much easier (in terms of probability becomes low enough, we may stop the lengthy accuracy) to be measured empirically (as a single frequency message propagation process. We now rigorously analyze this number for the whole set of sequences S). This is because idea. typically pn fn when n is large, as evidenced by Equation From an agent that initiates a message, let pn denote the (1) showing pn < fn and shown empirically. It is well 934 

6 .known that a very small probability number pn (when n is large) is extremely difficult to estimate empirically (requiring a very large sample size) [8]. Furthermore, the frequency measurement fn is increasingly more accurate as time step progresses (n increases) since more event pairs have been seen so far as the basis for determining if the frequency threshold τ · m is reached. Our experiments in Section VII show that (1) pn converges quickly to close to 0 (Fig. 14), (2) the performance improve- ment with early stop is dramatic, often more than an order of magnitude (Fig. 15), and (3) there is hardly any loss on Fig. 3: Illustrating a BBS structure where k = 3, w = 5, and accuracy, with precision 1 and recall 0.99 or higher (Fig. 16). m = 4. That is, there are 3 hash functions (one for each row), The details are in Section VII. Thus, this optimization should each hash function have 5 possible values (thus 5 columns), always be performed. and there is a bitmap of 4 bits at each cell (for 4 groups). An empty cell indicates its bitmap is all 0’s now. The final remark is that this is a dynamic analysis and estimation on the fly based on statistics collected at execution time. It is impossible to do this statically, as the result depends on the actual data. each of the k hash functions hi to e and get the hash value be hi (e). We take log w bits from hi (e), which corresponds to a VI. F URTHER E NHANCEMENT column (say, column j) in the ith row. Then we set the group information (group g) in the bitmap of cell (i, j), denoted as Recall that, in the B UILD R EGULAR M ODEL algorithm, we bm[i, j]. However, we do not directly set bit g of bm[i, j]. need to maintain a bitmap for each ordered pair (u, v) in Instead, we apply a random permutation permi over the m bits, S, which may be very space consuming when the number where permi is also determined by hi (e) (by taking a few bits of events is large. Consider this general problem that is of from it). Suppose bit g maps to bit g with this permutation. independent interest: Then we set bit g of bm[i, j]. This is done for each of the k Group Counting Problem: There are a large num- hash functions (k rows). ber of elements, and a set of m groups. There The query/lookup function on a BBS also first applies each are continuous, possibly duplicate input pairs of of the k hash functions and locates cell (i, j) and bm[i, j] in (element, group) information. Use a succinct data the same way. Then it applies the reverse of the permutation structure to store this information. A query is of the perm−1i on bm[i, j] (for each 1 ≤ i ≤ k). This gets the following form: given an element, return an estimate original bitmaps back. Then we do a bitwise AND over the of how many groups this element belongs to, and k recovered bitmaps to estimate the group membership and possibly which groups. group count. The bit permutations in BBS operations are for balancing the collision probabilities at each bit position (robust When m = 1, this problem is exactly the commonly known set to group size skewness) to accurately estimate group counts, membership problem, and can be approximately solved by a which is detailed later. We show these two algorithms below. hash table, or in particular, a Bloom filter [9]. Thus, the Group Counting problem is a generalization of the set membership problem. Algorithm 3: BBS-S ET E LEMENT G ROUP(bbs, e, g) The Group Counting problem is part of B UILD R EGULAR - Input: bbs: a blended bitmap set, e : element, M ODEL for counting the frequency of event pairs (lines 15-16 g : group id of B UILD R EGULAR M ODEL). Specifically, each distinct event Output: updated bbs, group size sum sum0 pair (v1 , v2 ) is an element, and each sequence in S is a group 1 for each i ← 1 . . . k do (hence there are m groups). Given an event pair element, we 2 ri ← hi (e) need to query how many groups (sequences) it is in (and 3 use bits from ri to determine column id j ∈ 1 . . . w compare this number with τ · m). Therefore, we discuss our 4 use bits from ri to determine a random permutation space-efficient approximate solution to the Group Counting permi problem. 5 g ← permi (g) 6 if bit g of the bitmap bm[i, j] in cell c[i, j] = 0 then We devise a novel approximation technique, which we 7 set that bit to 1 call a blended bitmap set (BBS), to solve this problem. A BBS consists of k rows and w columns of bitmaps, while 8 if line 7 is performed at least once then each bitmap has m bits. The choice of k and w is based on 9 sum0 ← sum0 + 1 memory constraint and will be discussed shortly. We choose k hash functions hi (1 ≤ i ≤ k) randomly from a universal hash function family [10]. Each hi corresponds to a row of w BBS-S ET E LEMENT G ROUP is exactly as discussed above. bitmaps. Fig. 3 shows an example BBS structure. The ri in line 2 is the (random) hash value from the ith hash function. One detail we have not discussed is the permutation The basic idea is as follows. Whenever an element-group permi in line 4. A fully uniformly random permutation over pair (e, g) arrives (meaning element e is in group g), we apply m bits requires log m! bits to describe. This is too many bits to 935 

7 .take from ri . Moreover, doing permi and perm−1 i would be 0.14 rather costly. As mentioned earlier, the goal of permutation is 0.12 to have an accurate estimation of group count (detailed later). 0.1 We must balance between feasibility and accuracy. Thus, we 0.08 partition a bitmap into a constant number b of blocks, and pi 0.06 permute the blocks uniformly at random. This only requires 0.04 log b! bits from ri , and is much more efficient. There are standard algorithms to do the random permutation of b blocks, 0.02 such as the Knuth shuffle [11] with a cost O(b). 0 0 5 10 15 20 i Line 5 is to apply this permutation function to bit position g, and g is the position it is permuted to (along with its Fig. 4: The convergence of the pi series block). We set that bit (line 7). Lines 8-9 are to maintain a counter sum0 , which is the total (estimated) number of distinct elements currently in the BBS — it can be an under- Proof: Element e maps to k cells in BBS (one in each estimate due to collisions. This will be used in BBS-L OOK U P row) due to the hash functions. For this bit in gm (let it be for adjusting the group count estimate. bit x) to be a false positive, it must have been set to 1 in the bitmaps of all these k cells. Let us consider these k cells one at Algorithm 4: BBS-L OOK U P(bbs, e, sum0 ) a time, say cell (i, j). In order for bit x of bm[i, j] to be 1, there are two conditions: (1) with a random permutation determined Input: bbs: a blended bitmap set, e : element, by its hash value, another elements group ID landed on bit sum0 : current group size sum x; and (2) that element’s hi hash value happens to go to j. Output: bitmap of groups e is in, and estimated group count The probability of (2) is w1 , and due to random permutation, 1 gm ← bitmap of all 1’s // group membership of e in expectation, c distinct elements satisfy (1), where c is the 2 for each i ← 1 . . . k do average group size stated in the theorem, i.e., the average 3 ri ← hi (e) number of distinct elements in each group. Therefore, the 4 use bits from ri to determine column id j ∈ 1 . . . w probability that at least one of such collisions happens in cell 5 use bits from ri to determine a random permutation (i, j) is 1 − (1 − w1 )c . For bit x to be a false positive, this permi needs to be true for all k cells, giving the probability stated in 6 bm ← perm−1 i (bm[i, j]) the theorem. 7 gm ← gm&bm 8 c0 ← sum0 /m In line 8 of BBS-L OOK U P, c0 is an under-estimate of the 9 if c0 has changed significantly from previous call then average group size c due to collisions (false positives). 10 i ← 0; p0 ← 0 Theorem 2: The pi series in the loop at lines 10-14 will 11 repeat c0 converge. Moreover, the converged value p is an unbiased 12 pi+1 ← [1 − (1 − w1 ) 1−pi ]k estimate of the bit false positive probability in gm, and x−mp 1−p 13 i←i+1 is an unbiased estimate of the number of groups that e is in. 14 until pi converges; let the converged value be p 15 x ← number of 1’s in gm Proof: First, we claim that the pi series in line 12 16 return gm and x−mp monotonically increases. We prove this by induction on i. 1−p In the base case, when i = 0, clearly pi+1 > pi since p1 = [1−(1− w1 )c0 ]k > 0 = p0 . For the induction step, suppose Line 1 of BBS-L OOK U P initializes a bitmap gm to be all pi > pi−1 is true. Thenc we show that pi+1 > pi . This is true 0 1’s for its m bits. Lines 2-4 are as before to apply each of the k because [1 − (1 − w1 ) 1−x ]k increases when x increases from hash functions and get to cell (i, j) of BBS. Then line 6 applies pi−1 to pi . Since the pi series monotonically increases, and the reverse permutation to bm[i, j], i.e., the reverse operations since it has an upper bound 1, from the Monotone Convergence of the b block permutation for BBS-S ET E LEMENT G ROUP. Let c0 Theorem [12], it must converge. Furthermore, since 1−p is an the recovered bitmap be bm (line 6). Note that only the same unbiased estimate of c, the converged value p must also be element e will use the same permi as it is determined by bits an unbiased estimate of the bit false positive probability from of hi (e). Line 7 is the bitwise AND operation. Thus, after the Theorem 1. Finally, if the true total number of groups that e loop, gm ends up being the bitwise AND of the k original is in is y, then x = y + (m − y)p in expectation, which gives bitmaps (before permutation) corresponding to e. Clearly, the y = x−mp 1−p as an unbiased estimation. bits corresponding to all the groups that element e is in must be 1 in gm. Fig. 4 plots the convergence of the pi series with (arbitrary) parameters k = 3, w = 500, and c0 = 300. Finally, let us At this point, although gm contains the estimated group discuss the optimal choice of parameters k and w. Suppose membership of element e, the total group count can be an we are given a space budget. Since each cell of BBS contains overestimate due to collisions on other bits. a bitmap of the same size, it is equivalent to having an upper bound on k · w. Let this limit be k · w = M . Theorem 1: After the loop in lines 2-7 of BBS-L OOK U P, any bit in gm that should be 0 (for a group that e is not in) Theorem 3: Given the constraint k · w = M , the choice has an estimated false positive probability of [1 − (1 − w1 )c ]k , of k and w that minimizes the bit false positive probability in where c is the average group size. Theorem 1 is k = M c c ln 2 and w = ln 2 . 936 

8 . Smart house data. This dataset originates from the work of Tapia et al. [14], downloaded from [15]. Between 77 and 84 sensor data collection boards equipped with reed switch sen- sors were installed in two single-person apartments collecting data about human activity for two weeks. The sensors were installed in everyday objects such as drawers, refrigerators, containers, etc. to record opening-closing events (activation de- activation events) as the subject carried out everyday activities. Activities associated with the sensor signals are labeled in the data. Fig. 5: A snippet (subgraph) of the regular model learned. Hybrid data. This is based on the research work on human activity recognition [16]. The dataset is called hybrid in that it is designed to combine user input data on daily activities and sensor signals with simulation tools for flexibility. We use it Proof: From Theorem 1, the false positive probability is to test our algorithms on data with various parameters. [1−(1− w1 )c ]k ∼ c = (1−e− w )k . To minimize it, we use Lagrange GPS data. This GPS trajectory dataset was collected in multipliers [13] and define a function Microsoft Research’s Geolife project over five years [17], [18]. c A GPS trajectory is represented by a sequence of timestamped Λ(k, w, λ) = (1 − e− w )k + λ(kw − M ) points, each of which contains the information of latitude, where we use the constraint that kw = M . We then solve the longitude, height, speed and heading direction. This dataset equation system ∂Λ ∂Λ ∂Λ contains 17,621 trajectories with a total distance of 1,292,951 ∂k = 0, ∂w = 0, and ∂λ = 0, which gives M c k = c ln 2 and w = ln 2 as in the theorem. kilometers and a total duration of 50,176 hours. These trajecto- ries were recorded by different GPS loggers and GPS-phones. Note that c is variant as new (element, group) pairs are This dataset is 1.6 GB. inserted. Thus, there is no optimal fixed choice throughout the process. In our problem, we estimate the maximum number of We implement all the algorithms in the paper — both a event pairs separately for each sequence (e.g., by sampling), serial version and a multi-threaded version — in Oracle Java and make the parameter choice optimal for the time when BBS 1.8.0 45. In addition, we download the Machine Learning nearly reaches its maximum element count. software Weka [7] to use its Cobweb conceptual clustering im- plementation for obtaining event hierarchies. All experiments are performed on a machine with an Intel Core i7 2860QM VII. E XPERIMENTS (Quad-Core) 2.50 GHz processor and an 8GB memory. In this section, we perform a systematic evaluation of In an excellent survey on anomaly detection for sequences our work using two real world datasets and a hybrid dataset [3], Chandola et al. categorize all previous work into solving (combining user input data with simulation tools). We study the three problems. Even though it is not specifically designed for effectiveness and efficiency of our framework and approach. event sequences as in our solution, potentially applicable to our Specifically, we answer the following questions: problem is their Category 2, i.e., detecting short subsequences • How effective is our regular model? In particular, what in a long sequence T that are anomalous w.r.t. the rest of are some properties of the model graphs such as vertex T (the other two categories are finding whole sequences that degrees? Do the models make sense? are anomalous w.r.t. a sequence database, and determining • What irregular events can we find? If we “inject” some if a given query pattern in a sequence is anomalous w.r.t. irregular events, can they be found using the model? its expected frequency, resp.). To apply it to our problem, How does it compare with previous work? a concatenation of the sequences over all time units is T , • The model building algorithm based on message and the detected short subsequences are irregular events. We passing is easily parallelizable. Can we verify this implement the t-STIDE based algorithm described in [3] for observation even in the most commonplace comput- Category 2 problems, which is also an overall best algorithm ing environment — multicore computers as for most as found in the experimental study by Chandola et al. [19]. laptops and desktops today? We compare with this work on the effectiveness in finding • Recall that we estimate the new-edge probability in irregular events. a model graph by an analysis based on a dynamic measurement on the fly. What does this probability B. Experimental Results series look like in practice? Is it effective in early stopping w.r.t. performance improvement and model We build a regular model for each dataset. The regular accuracy? models of the smart house data and the hybrid data indicate • How effective is the BBS optimization in the tradeoff the inherent regularity in daily activity sequences. For GPS between memory consumption and model accuracy? data, there is a concentration area at latitude range [39.90725, 40.05447] and longitude range [116.31632, 116.51534] (an A. Datasets and Setup area in Beijing near Microsoft Research Asia). We divide this rectangle into a 32 × 32 grid, where each of the 1024 areas is We use the following real-world and hybrid datasets to about 0.27km2 , and is treated as a discrete location. Thus, our perform the empirical study: model signifies the regularity in the location and movement 937 

9 . 12 Leaf−leaf 40 1 1 Leaf−all Leaf−leaf 10 All−all Leaf−all 0.8 0.8 Regularity score Regularity score Average degree 30 Average degree All−all 8 0.6 0.6 6 20 0.4 0.4 4 10 0.2 0.2 2 0 0 0 0 0 0.5 1 0.2 0.4 0.6 0.8 seq & event 1 seq & event 2 seq & event 3 seq & event 1 seq & event 2 seq & event 3 Threshold Threshold Sequence & irregular event Sequence & irregular event Fig 6: Vertex degrees (Hybrid) Fig 7: Vertex degrees (GPS) Fig 8: Irregular events (SH) Fig 9: Irregular events (Hybrid) daily event sequence of a user. From these regular models, we degrees are higher as they are for more general event types. can identify irregular events. An interesting phenomenon here is that, when τ decreases in the low value range, the average node degrees may actually Models and Finding Irregular Events. We first examine decrease. This is because, when τ is smaller, paths between the effectiveness of our models. All the regular models for the two nodes tend to be formed earlier, preventing the creation three datasets indicate the event context and order information of an edge between these two (more distant) nodes. Hence the as described in Section III. Varieties and generalizations of curve is not necessarily monotonic. events are also encoded in the model through event hierarchies. Let us take a look at an example snippet of a model. The result on the smart house dataset is very similar and is omitted. We show the result for the GPS dataset in Fig. Fig. 5 shows a subgraph of the model learned from the 7. While the trend is roughly similar, the leaf-leaf degree hybrid data (similar to the smart house data). As discussed is lower when τ is above 0.4 for the GPS data than for earlier, the model graph shows the preceding and succeeding the hybrid data. This indicates that the user behavior is less context of events allowing possible interleaving events between regular at the leaf level, which corresponds to fine-granularity two events connected by an edge. Moreover, the model is of location (0.27km2 grids). The behavior is more regular succinct. For instance, there is no edge between “getting up” when the location grids are coarser, at higher levels of the event and “applying makeup”, since a path getting up → brushing hierarchy. Such edges are useful too, and the weights (in line teeth → applying makeup is already formed when the “mes- 10 of C OMPUTE R EGULARITY) can be adjusted to penalize sage” from “getting up” reaches “applying makeup” in the higher level edges less. Any leaf-leaf edge has a weight 1, B UILD R EGULAR M ODEL algorithm. and the weight is multiplied by a discount factor γ ≤ 1 when For clarity, we only show some “leaf to leaf” edges in Fig. an endpoint of the edge increases a level in the hierarchy. By 5. Our regular model also includes event vertices at various default, we use γ = 0.5 for the first two datasets and γ = 0.8 levels of the event hierarchy produced by conceptual clustering for the GPS dataset. (Cobweb). Hence there are also edges between vertices of We next examine the ability of our regular model in finding higher levels. For example, in the model of Fig. 5, leaf nodes irregular events. For each dataset, we can find a number of “making tea” and “making coffee” have a parent node in the unusual events — activities or places visited. We show a few event hierarchy, indicating the generalization relationship. Let of them here. Fig. 8 lists a few from the smart house data. us label this parent node “making beverage”. There is an edge The first group of two bars in Fig. 8 is the regularity scores from “applying makeup” to “making beverage” which is not of a sequence and an irregular event e1 therein, respectively. shown in Fig. 5. However, there is no edge from “applying This irregular event e1 is “Preparing lunch”, and its context makeup” to “making coffee”, since the person mostly drinks contains “going to work” both in the morning (before e1) and tea in the morning. The edge from leaf to a higher level in the afternoon (after e1). We find that in this dataset the node allows variation and generalization of events, and there user rarely prepares lunch at home if there are events “going is some“penalty” in this generalization when computing the to work” both in the morning and afternoon (presumably the regularity score in C OMPUTE R EGULARITY (line 10). If the user usually eats lunch at work). The regularity score of e1 is person one day makes coffee instead of tea, “making beverage” around 0.2, much lower than the score of the whole sequence will receive a smaller regularity score — unusual but not (around 0.8). completely impossible. To test the model’s ability in locating irregular events, we To have a better understanding of the model graph property, also inject two events e2 and e3 which have unusual contexts we measure various types of node degrees — the average leaf in the dataset. e2 is“watching TV” and the context is in the to leaf degree, leaf to any node, and any node to any node morning, while e3 is “preparing snack” and the context is degrees. Fig. 6 shows the result of these statistics for the model at night. We insert e2 and e3 into two random sequences of the hybrid dataset, for various threshold parameter τ values respectively, build the model, and report the regularity scores. in B UILD R EGULAR M ODEL. We can see that the average leaf- The second group of two bars in Fig. 8 show the scores of the leaf degree ranges between 4 and 0, and decreases as τ sequence and e2, and the third group similarly for e3. increases. This is because as the frequency threshold increases, fewer event pairs are qualified for edges. The average leaf to Fig. 9 shows the result for the hybrid dataset. The first any node (marked leaf-all in Fig. 6) and the average all-all group of two bars is for an existing event e1 “making tea”, 938 

10 . 1 1 with the smarthouse data). This causes a serious problem 0.8 0.8 for previous work. Our approach based on message passing Anomaly score Anomaly score 0.6 0.6 and graph edges is much more robust to such noisy event sequences, since messages will be able to reach the relevant 0.4 0.4 context events. 0.2 0.2 Performance and Optimizations. In the next set of ex- All seq avg 0 One seq avg 0 periments, we examine the efficiency of the algorithm for event 1 event 2 event 3 event 1 event 2 event 3 Irregular event Event Irregular event building regular models. We have observed that our message passing algorithmic framework in B UILD R EGULAR M ODEL Fig 10: Previous work (SH data) Fig 11: Previous work (Hybrid) can be easily parallelized. This is indeed the case in our implementation. We can easily write a multi-threaded program that runs on the most commonplace hardware — multicore and the context does not have “heating water” anywhere processors. Our experimental machine has four cores. We show before it (but the sequence is merely “shower”, “applying the execution time results on the GPS dataset over various makeup”, “making tea”, followed by“making breakfast”). In threshold τ values in Fig. 12. As τ increases, execution time the dataset, however, making tea almost always has heating decreases. This is because a greater τ implies that fewer water somewhere in front of it. The second group of two bars event pairs are qualified as edges in the model graph, and is for another existing event e2 “having breakfast”, but there hence the bookkeeping work as well as “reachability” check is no “making breakfast” prior to it, which gives e2 a low in B UILD R EGULAR M ODEL is reduced. Furthermore, we can regularity score. The third group of two bars is for an injected see that the multi-threaded version achieves nearly four times event, where we change an existing event “making tea” to speedup over the serial version under the quad-core machine, a new event e3 “making coffee”. As discussed earlier, this verifying the parallelizability of the algorithm. user rarely makes coffee in the morning, but both leaf nodes In Fig. 13, likewise, we show the execution time result for generalize to the parent event node “making beverage”. The the hybrid dataset, varying the period over which a regular regularity score of the original “making tea” is 1, while the model is learned. The period ranges from 45 days to 730 new e3 “making coffee” only has a score of 0.25, which is days (typically it is not desirable to learn a model over too slightly higher than e1 and e2 due to the match of edges over long a period, as model changes over time, and should be the parent node “making beverage”. re-learned). There is a very interesting phenomenon here: as Then we examine the effectiveness of using the t-STIDE period increases, the speedup achieved by the multi-threaded algorithm in previous work for Category 2 problem [3], as version is much more than 4 times (its execution time still discussed at the end of Sec. VII-A. We set the window-size increases with the period, but much slower). This is because, parameter k to be 8, as found optimal in [19]. Fig. 10 shows as the number of events to be processed is large, the multi- the result with the smarthouse data for the same three irregular threaded version starts from many positions in the sequences, events as in Fig. 8, and Fig. 11 with the hybrid data for the and finds edges and paths in the model graph much earlier than same events in Fig. 9. Unlike our approach, this line of work the serial version. This has positive feedback (“the rich gets shows the anomaly score—the higher the score is (closer to richer”), in that such edges and paths will prune much work 1), the more anomalous it is. For each irregular event, we on those event pairs immediately. Certainly in principle a more show three bars, with the first being the average anomaly careful implementation of the serial version may improve its score over all sequences, the second being the average of the performance to be only 4 times worse than the multi-threaded sequence where the event is in, and the third being the anomaly version; the point is that such an implementation may involve score of the event itself. We can see that this algorithm is heavy tuning and is hard to do. completely ineffective in locating the three irregular events We next empirically verify our analysis in Section V of the in smarthouse data; all bars show anomaly scores close to 1. probability of a new edge as message passing progresses over For hybrid data (Fig. 11), it is better with event 1, but the time. The optimization here is that the algorithm can stop early sequence average is still close to e1’s score, indicating a great when this estimated probability on the fly is small enough. number of false positives inside the sequence. The detection The only statistics we need to collect during B UILD R EGU - result is completely wrong with e2, as its anomaly score is LAR M ODEL is fn for time step n, the empirical probability even lower than the sequence average. The result for e3 is fine that an event pair encountered at this time step is frequent after changing “making tea” to “making coffee”; however, we (above threshold τ ). Then our algorithm in Section V will find that before the change, when e3 is “making tea”, its score estimate the probability of a new edge at this time step. We plot is still close to 1, which is erroneous as it should not be an this probability series over time steps in Fig. 14, for all three anomaly. When we change the parameter k to smaller values, datasets. After a short initial instability, the probability of new all scores decrease, but it is still very ineffective in isolating edge quickly converges to almost 0 within 5 to 8 time steps the target irregular events. for all three datasets. The initial instability is due to inaccurate The reason is that the previous approaches are mostly estimate of fn in the beginning, as the number of total event designed for time series data with its discretized version [3]. pairs encountered is still small. Since fn is more accurate over They do not work well for our problem because relevant time, the confidence of our estimation of the probability of new context events, which mostly depend on time, can be rather far edge also increases over time. Fig. 14 informs us that the early away in terms of the number of other events in between. The stop optimization should be very effective, as the model should other events in between may also be in any order (especially usually be very stable within a limited number of time steps. 939 

11 . 10 4 x 10 0.8 40 Multi−threaded 12 Smart house Early stop Execution time (seconds) Execution time (seconds) Probability of new edge 8 Serial Multi−threaded Hybrid Hanging on 10 30 Execution time (ms) Serial 0.6 GPS 6 8 0.4 20 6 4 4 10 0.2 2 2 0 0 0 0 0 2 4 6 8 0 0.2 0.4 0.6 0.8 0 200 400 600 800 0 2 4 6 8 10 Threshold Period Time step Sequence length x 10 4 Fig 12: Execution time (GPS) Fig 13: Execution time (Hybrid) Fig 14: New edge probability Fig 15: Early stop optimization 1 0.4 12 1 1 Memory consumption (MB) Execution time (sec) 0.8 10 0.8 0.8 Precision & recall Precision & recall Precision & recall 0.3 8 0.6 0.6 0.6 0.2 6 0.4 0.4 0.4 4 0.1 0.2 0.2 0.2 2 0 0 0 0 0 Smart houseHybrid GPS BBS no BBS BBS no BBS Smart house Hybrid GPS SH,p SH,r Hy,p Hy,r GPS,p GPS,r Dataset Method Method Dataset Dataset, measure Fig 16: Accuracy of early stop Fig 17: BBS optimization Fig 18: Accuracy of BBS optim. Fig 19: Group count adjustment This is indeed verified in our next two figures, on performance optimization is the slight increase of execution time, as shown and accuracy (of the resulting model), respectively. in the left plot. In both plots, the left bar is with BBS optimization and the right bar is without. The slight increase Using the 90 days hybrid dataset, varying the average daily in execution time is due to applying a constant number of sequence length, in Fig. 15, we show the execution times with universal hashing and block random permutation during BBS and without the early stop optimization (i.e., stop when the operations. probability of new edge is below 0.01), marked as “early stop” and “hanging on” in the figure, respectively. We can see that In Fig. 18, we show the accuracy of the resulting model the performance improves tremendously (easily more than an in terms of precision and recall (defined in the same way as order of magnitude), especially for longer sequences, since for the early stop optimization). We can see that the precision stopping after a small number of time steps saves more work. and recall are typically around 0.9 or more, indicating that the obtained model is quite accurate. We verify that they can still We then examine the accuracy of the resulting model after be used to find the irregular events discussed earlier. this optimization, shown in Fig. 16 for all three datasets. We show the precision and recall of the edges in the model Finally, we evaluate and verify the necessity of the group graph with the optimization, compared to the one without count adjustment in lines 8-16 of BBS-L OOK U P, rather than optimization. Precision is defined as the fraction of edges in simply returning line 15 as the count estimate. In Fig. 19, we the model under optimization that are also in the one without show the precision and recall changes without this adjustment optimization, while recall is the other way around. We can for all three datasets, where SH (smart house), Hy (hybrid), and see that in all three datasets, the model under optimization is GPS stands for the three datasets, while “p” and “r” stands for almost identical to the original one. In particular, the precisions precision and recall, respectively. In each group of two bars, are all 1.0, and the recalls are 0.99 or higher. Precision is the left one is the original BBS, and the right one is without the always 1.0 is exactly expected, because the execution with count adjustment. This experiment shows that the adjustment early stop optimization is identical to the original one before is needed for better accuracy. Overall, BBS optimization is stopping, and hence all the edges it gets in the model are also useful in computing environments where memory is more of in the original model. In summary, this set of experiments a concern. (Figures 14-16) gives us more confidence that the early stop optimization should always be used. Summary of Results. The empirical study in this sec- tion is enlightening. The experiments give us more concrete In the final set of experiments, we examine the BBS opti- understanding of the regular models we find, as well as mization. We first show the performance result in Fig. 17 for their graph properties (node degrees). The regularity scores the hybrid dataset over a period of 365 days, measuring both combined with the models are very effective and informative execution times (left plot) and memory consumption (right in finding irregular events and sequences. The model building plot), where we explicitly set the memory constraint of the algorithm using message passing framework is efficient and BBS version to be about 1/8 of the original execution (which can be easily parallelized. Our analysis and dynamic estimation accordingly determines the optimal parameters of BBS). While of probability of new edge on the fly are very effective — significantly saving memory space, one tradeoff of the BBS the resulting early stop optimization should always be used. 940 

12 .Finally, the BBS optimization is effective and useful when IX. C ONCLUSIONS reducing memory consumption is a concern. In this paper, we study a novel problem with practical significance. We propose an algorithmic method based on VIII. R ELATED W ORK easily parallelizable message passing framework to build a Outlier/anomaly detection has been studied for sequence regular model graph, as well as a method to compute regularity data (cf. a survey [3]), temporal data (cf. a survey [4]), and in scores. One of our optimizations is to dynamically estimate more general contexts (cf. a survey [5]). Most related to our new edge probability based on runtime statistics and speeds up work is the one for sequence data [3], in which Chandola et model building often by over an order of magnitude, while the al. categorize all previous work into solving three problems. other significantly saves space consumption. Our systematic Closest to our work in the second category, i.e., detecting short experimental study verifies the effectiveness and efficiency of subsequences in a long sequence T that are anomalous w.r.t. our approaches. the rest of T , while the other two categories are finding whole ACKNOWLEDGMENT sequences that are anomalous w.r.t. a sequence database, and determining if a given known query pattern in a sequence is This work was supported in part by the NSF, under the anomalous w.r.t. its expected frequency. Since our main goal is grants IIS-1239176 and IIS-1319600. to find irregular events and we can concatenate the sequences across all time units into one (huge) sequence, previous work R EFERENCES in this category (detecting anomalous subsequences) could [1] http://www.chicagotribune.com/news/nationworld/ct-germanwings- potentially be used in the problem we study. However, as pilot-controlled-descent-20150506-story.html. shown in Section VII, it does not work well because relevant [2] T. Pl¨otz, N. Y. Hammerla, and P. Olivier, “Feature learning for activity context events, which mostly depend on time, can be rather far recognition in ubiquitous computing,” in IJCAI, 2011. away in terms of the number of other events in between. The [3] V. Chandola, A. Banerjee, and V. Kumar, “Anomaly detection for other events in between may also be in any order. This causes discrete sequences: A survey,” TKDE, 2012. a serious problem for previous work. Our approach based on [4] M. Gupta, J. Gao, C. Aggarwal, and J. Han, “Outlier detection for message passing and graph edges is much more robust to such temporal data,” TKDE, 2014. noisy event sequences, since messages will be able to reach [5] V. J. Hodge and J. Austin, “A survey of outlier detection methodolo- the relevant context events. gies,” Artificial Intelligence Review, 2004. [6] D. H. Fisher, “Knowledge acquisition via incremental conceptual clus- Matsubara et al. [20] study the problem of segmentation tering,” Machine learning, 1987. and regime detection in correlated time series occurring at the [7] http://sourceforge.net/projects/weka/files/weka-3-7-windows-x64/. same time. One example they give is to detect the dancing steps [8] A. Mood, F. Graybill, and D. Boes, “Introduction to the theory of from multiple signals of a dance. We are not concerned with statistics. 3rd mcgraw-hill,” 1974. segmentation and regime detection, as we only have known [9] B. H. Bloom, “Space/time trade-offs in hash coding with allowable time units in our problem (and applications). Event detection errors,” CACM, 1970. and activity recognition in general has been studied in the [10] J. L. Carter and M. N. Wegman, “Universal classes of hash functions,” ubiquitous computing and artificial intelligence communities in STOC, 1977. (e.g., [2]). This line of work, however, is not concerned with [11] D. E. Knuth, “Seminumerical algorithms, the art of computer program- building a regular model over activities/events from multiple ming, vol. 2,” 1981. time units and identifying irregular events. Our work is built [12] W. A. Sutherland, Introduction to metric and topological spaces. Oxford University Press, 1975. on top of such event detection work, as we build our regular [13] G. B. Arfken, Mathematical methods for physicists. Academic press, model (as well as event hierarchy) on top of discrete events. 2013. Complex event processing has been extensively studied [14] E. M. Tapia, S. S. Intille, and K. Larson, Activity recognition in the in the data management literature (e.g., [21] as a survey). It home using simple and ubiquitous sensors. Springer, 2004. focuses on detecting the occurrence of a particular complex [15] http://courses.media.mit.edu/2004fall/mas622j/04.projects/home/. event pattern, but not about finding a regular model or irregular [16] G. Azkune, A. Almeida, D. L´opez-de Ipi˜na, and L. Chen, “Combining users’ activity survey and simulators to evaluate human activity recog- events. Previous work on Bloom filters [9] and count min nition systems,” Sensors, vol. 15, no. 4, pp. 8192–8213, 2015. sketches [22] bear some similarity with our blended bitmap [17] Y. Zheng, L. Liu, L. Wang, and X. Xie, “Learning transportation mode set (BBS) technique. However, BBS is a non-trivial extension from raw gps data for geographic applications on the web,” in WWW, to solve the Group Counting problem that we identify. For 2008. example, a count min sketch only has counters at each cell of [18] http://research.microsoft.com/apps/pubs/?id=141896. the hash table, while we need to use bitmaps to represent a [19] V. Chandola, V. Mithal, and V. Kumar, “Comparative evaluation of potentially large number of groups. Moreover, we use random anomaly detection techniques for sequence data,” in ICDM, 2008. permutations to overcome the skewness of group sizes, and dy- [20] Y. Matsubara, Y. Sakurai, and C. Faloutsos, “Autoplait: Automatic namically estimate the average group size and collision prob- mining of co-evolving time sequences,” in SIGMOD, 2014. ability to adjust group counts. Finally, Beedkar and Gemulla [21] G. Cugola and A. Margara, “Processing flows of information: From [23] study frequent sequence mining under item hierarchies. data stream to complex event processing,” ACM Computing Surveys, 2012. This is related to our event hierarchy concept. However, they [22] G. Cormode, M. Garofalakis, P. J. Haas, and C. Jermaine, “Synopses study the classic frequent itemset mining problem under item for massive data: Samples, histograms, wavelets, sketches,” Foundations hierarchies. Thus, it is a different problem and they have no and Trends in Databases, vol. 4, no. 1–3, pp. 1–294, 2012. intention to learn a regular model from sequences over many [23] K. Beedkar and R. Gemulla, “Lash: Large-scale sequence mining with time units or to find irregular events. hierarchies,” in SIGMOD, 2015. 941