A Comparison of DFT and DWT Based Similarity Search in Timeserie

1 . A Comparison of DFT and DWT Based Similarity Search in Time-Series Databases Yi-Leh Wu Divyakant Agrawal Amr El Abbadi Department of Computer Science University of California, Santa Barbara fywu, agraw al, amrg@cs.ucsb.edu ABSTRACT the time-period during which two commodities have similar Similarity searc h in time-series databases has received sig- price patterns. ni cant attention lately .P opular tec hniques for e cien t re- There have been several e orts to develop e cient similar- trieval of time sequences in time-series databases has been ity searc h mechanisms in time-series databases. In 2], Dis- to use Discrete Fourier Transform (DFT). Recently, the Dis- crete F ourier Transform (DFT) was employed to map time- crete Wavelet T ransform (DWT) has gained popular interest series data from the time domain to the frequency domain. in database domain and several proposals have been made to After dropping all but the rst few frequency coe cients, replace DFT by DWT for similarity search over time-series the remaining ones are indexed through a multidimensional databases. In this paper, we explore the feasibility of replac- index structure such as R -T ree. Ho w ev er, in 2], one of ing DFT by DWT with a comprehensive analysis of the DFT the main constraints of this approach is that is it assumed and DWT as matching functions in time-series databases. that the data sequence and the query sequence have the Our results show that although the DWT based technique same length. This problem was tackled in 3] which allowed has several adv an tages,e.g., the D WThas complexity of subsequence matching by using a sliding window over the O(N ) whereas DFT is O(N log N ), D WT does not reduce data sequence, map each window to the frequency domain relativ e matching error and does not increase query precision using DFT and keep only the rst few coe cients. A data in similarity searc h as suggested by previous works 1]. We sequence is thus mapped into a trail in the feature space conclude that, by exploring the conjugate property of DFT and the trail is further divided into sub-trails that can be in real domain, the DFT-based and DWT-based techniques represen ted b y their minimum bounding rectangles (MBR) yield comparable results on similarity searc h in time-series and stored in a R -T reefor indexing. Ra ei and Mendel- databases. zon 4] extend previous w orksto handle time scaling, i.e., Key words. time-series analysis, fourier transform, wavelet stretching or shrinking the time axis. In 5], they proposed transform, time-series database, smoothing, time-series match- an improvement of DFT-based indexing techniques for time- ing series data b y using the last few Fourier coe cients in the distance computation to speed up similarity search without storing them. 1. INTRODUCTION All the abo veapproaches assume Euclidean distance as Time-series data constitute a large portion of the data the measurement of similarity. Agrawal et al. 6] propose a stored in computers. A time-series is a sequence of real new distance measure to capture the notions that tw ose- numbers, each number represents a data value at a point quences should be considered similar if they ha veenough in time. Examples of time-series data include stock prices, non-o verlapping ordered similar subsequences.In 7], Yi et w eather data, exchange rates, history of product sales, med- al. introduce "time warping" distance as the similarity mea- ical information, etc. Many applications with temporal data surement and tec hniquesto speed up the similarity query require the capability of searc hing, especially based on sim- processing. Park et al. 8] use time warping distance with a ilarity, over the data. F or example, w e may wan t to nd disk-based su x tree indexing method for retrieval similar the stocks that ha ve correlation with Microsoft stock, or subsequences without false dismissals. Perng et al. 9] pro- pose the L andmark Similarity measurement that is invarian t This research w as partially supported by the NSF under under six transformations (e.g., shifting, uniform amplitude grant numbers EIA98-18320, IIS98-17432 and IIS99-70700. scaling, etc.), where the landmarks are ltered local maxima and minima in the time sequences. Permission to make digital or hard copies of part or all of this work or Most of the previous works employ DFT to map time- personal or classroom use is granted without fee provided that copies are series data from the time domain to the frequency domain. not made or distributed for profit or commercial advantage and that copies By takingonly the rst few F ourier coe cients for index- bear this notice and the full citation on the first page. To copy otherwise, to ing they e ectiv ely reduce the search space and speed-up republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a fee. the similarity query .Chan and Fu 1] rst proposed to use the Discrete Wavelet T ransform (DWT) to replace the well- CIKM 2000, McLean, VA USA accepted DFT for various reasons e.g., the computation of © ACM 2000 1-58113-320-0/00/11 . . .$5.00 D WT is more e cient than DFT in general. They state that 488 

2 .the DWT as a matching function has more discrimination which is the aggregation of the point to point distance of power than DFT. two sequences. In this paper, we present a comprehensive comparison One way to solve this problem is as follows. Given a query between DFT and DWT as matching functions in time- sequence Q, we compare all sequences stored in the database series databases. Our experiment results show that there with Q using the distance function in Equation 1 and put all is marginal di erence for discrimination power with DWT sequences within distance d into the result set R. Although or DFT if we consider the conjugate property of DFT as this approach is correct, it is not practical for two reasons. proposed in 5]. First, the number of sequences in the database may be large The rest of the paper is organized as follows. In Section and a sequential scan of all such sequence for every query will 2, we gives an overview of the Discrete Fourier Transform result in severe performance penalty. Second, the number of (DFT) and Discrete Wavelet Transform (DWT). In Section data points in a query may need to be matched against each 3, we exam the hypothesis proposed by Chan and Fu 1], sequence not once but N (the database size) times so that and analyze DFT and DWT based matching for time-series all possible subsequences of that sequence are evaluated. datasets. In Section 4, we compare the relative matching Another approach is to use mathematical transforms to error and query precision by using the DFT and DWT in capture the essence of time-series sequences. One such trans- real-world time-series database. We conclude in Section 5. form is the discrete Fourier transform (DFT). The DFT takes the original signals in time/space domain and trans- 2. BACKGROUND forms them into the frequency domain. The signi cance of In this section, we start by giving a brief introduction the DFT is that there exists a fast algorithm that can com- of how to process similarity search in time-series database pute the DFT coe cients in O(n log n) time. followed by a brief description of DFT and DWT. Many previous proposals 2, 4, 5, 3] in time-series databases use the notion of DFT and separate the query processing 2.1 Query Processing in Time-series Databases phase from the indexing phase. The indexing phase will usually take the following steps, 180 real stock data 1. Take the original sequence data and chop it into xed sized subsequence samples using a sliding window. 2. Normalize all the subsequence samples so that all the 160 stock closing price in UD$ 140 sample data fall into a certain range. 3. Use the DFT to transform the subsequence samples into the frequency domain. 120 4. Use only the rst few DFT coe cients to represent the 100 80 0 50 100 150 200 250 300 350 original subsequence. time in days 5. Use any multidimensional index structure such as R- Figure 1: Real Stock Data for 360 days trees to index the resulting few coe cients. A time-series chart of the stock closing prices of IBM By using an appropriate transformation we can capture for 360 consecutive transaction days is shown in Figure 1. the approximate shape of a given long sequence and hence A time-series database consists of thousands of such time- use fewer data points to describe the overall shape. Note series sequences. A common operation/query against such that, the underlying shape of a sequence/signal, which is a database would be: Given a query sequence, e.g., Mi- the slow changing part, is the low frequency part of the crosoft stock closing prices for the past 3 months, nd the sequence/signal. Hence, in step 4, by keeping only the rst stocks in the database that have a close correlation with its few DFT coe cients, the approximate shape of the original behavior. Although the data-sequences used in this paper subsequence can be captured. are from nancial applications, such data-sequences arise In the querying phase, given a query sequence Q with the in a variety of applications. For example, observations of same number of data samples as all the subsequences in the physical phenomena (temperature, rainfall, etc.), for sci- database, nd the most similar ones to Q within a distance enti c applications over a period of time, seismic activity threshold, in southern California, EKG observations/samples of pa- tients in the last few years. etc. In the above applica- 1. Normalize and DFT Q as in indexing steps 2 and 3. tions, correlation or similarity based queries play an im- 2. Take the same number of coe cients as in indexing portant role. More formally, a time-series database is a step 4 from the resulting DFT coe cients or Q0 . set denoted DB = fX1 X2 ::: Xi ::: XN g, where Xi = xi0 xi1 :::: xin ] and a query sequence is a sequence of data 3. Search the index structure(e.g., R-tree) with the re- points Q = q0 q1 :::: qn ]. Given a query Q, the result set maining coe cients. Find all sequences in the indexing R from the database is R = fX1 X2 ::: Xj ::: Xm g, such structure that are within distance d to Q0. The result- that D(Xj Q) < d. The distance function D(X Y ) is the ing R0 contains all sequences with estimated distance Euclidean distance between X and Y , that is within d to Q0 . X D(X Y ) = ( jxj ; yj j2 )1=2 (1) 4. For each sequence in R0 , if the true distance to Q is j within d, put it in the nal result set R. 489 

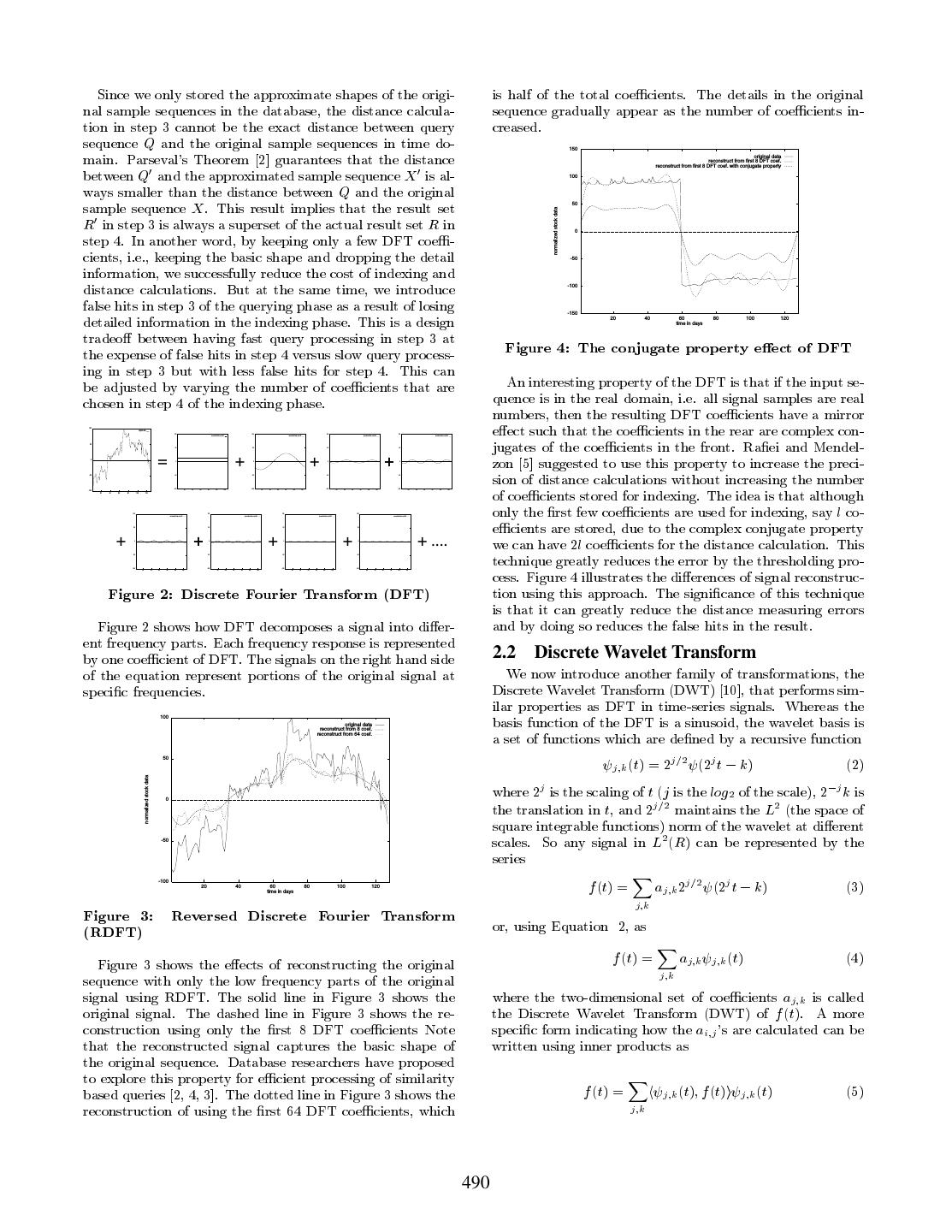
3 . Since we only stored the approximate shapes of the origi- is half of the total coe cients. The details in the original nal sample sequences in the database, the distance calcula- sequence gradually appear as the number of coe cients in- tion in step 3 cannot be the exact distance between query creased. sequence Q and the original sample sequences in time do- main. Parseval's Theorem 2] guarantees that the distance 150 original data between Q0 and the approximated sample sequence X 0 is al- reconstruct from first 8 DFT coef. reconstruct from first 8 DFT coef. with conjugate property 100 ways smaller than the distance between Q and the original sample sequence X . This result implies that the result set 50 R0 in step 3 is always a superset of the actual result set R in normalized stock data step 4. In another word, by keeping only a few DFT coe - 0 cients, i.e., keeping the basic shape and dropping the detail -50 information, we successfully reduce the cost of indexing and distance calculations. But at the same time, we introduce -100 false hits in step 3 of the querying phase as a result of losing detailed information in the indexing phase. This is a design -150 20 40 60 80 100 120 time in days tradeo between having fast query processing in step 3 at Figure 4: The conjugate property e ect of DFT the expense of false hits in step 4 versus slow query process- ing in step 3 but with less false hits for step 4. This can be adjusted by varying the number of coe cients that are An interesting property of the DFT is that if the input se- chosen in step 4 of the indexing phase. quence is in the real domain, i.e. all signal samples are real numbers, then the resulting DFT coe cients have a mirror 100 original data e ect such that the coe cients in the rear are complex con- jugates of the coe cients in the front. Ra ei and Mendel- 100 100 100 100 reconstruct from coef. #1 reconstruct from coef. #2 reconstruct from coef. #3 reconstruct from coef. #4 50 50 50 50 50 0 = 0 + 0 + 0 + 0 zon 5] suggested to use this property to increase the preci- -50 -50 -50 -50 -50 sion of distance calculations without increasing the number of coe cients stored for indexing. The idea is that although -100 -100 -100 -100 20 40 60 80 100 120 20 40 60 80 100 120 20 40 60 80 100 120 20 40 60 80 100 120 -100 20 40 60 80 100 120 100 100 100 100 only the rst few coe cients are used for indexing, say l co- e cients are stored, due to the complex conjugate property reconstruct from coef. #5 reconstruct from coef. #6 reconstruct from coef. #7 reconstruct from coef. #8 50 50 50 50 + 0 + 0 + 0 + 0 + .... we can have 2l coe cients for the distance calculation. This -50 -50 -50 -50 technique greatly reduces the error by the thresholding pro- cess. Figure 4 illustrates the di erences of signal reconstruc- -100 -100 -100 -100 20 40 60 80 100 120 20 40 60 80 100 120 20 40 60 80 100 120 20 40 60 80 100 120 Figure 2: Discrete Fourier Transform (DFT) tion using this approach. The signi cance of this technique is that it can greatly reduce the distance measuring errors Figure 2 shows how DFT decomposes a signal into di er- and by doing so reduces the false hits in the result. ent frequency parts. Each frequency response is represented by one coe cient of DFT. The signals on the right hand side 2.2 Discrete Wavelet Transform of the equation represent portions of the original signal at We now introduce another family of transformations, the speci c frequencies. Discrete Wavelet Transform (DWT) 10], that performs sim- ilar properties as DFT in time-series signals. Whereas the 100 original data basis function of the DFT is a sinusoid, the wavelet basis is a set of functions which are de ned by a recursive function reconstruct from 8 coef. reconstruct from 64 coef. j=2 (2j t ; k) j k (t) = 2 (2) 50 where 2j is the scaling of t (j is the log2 of the scale), 2;j k is normalized stock data the translation in t, and 2j=2 maintains the L2 (the space of 0 square integrable functions) norm of the wavelet at di erent -50 scales. So any signal in L2 (R) can be represented by the series -100 20 40 60 time in days 80 100 120 X f (t) = aj k 2j=2 (2j t ; k) (3) jk Figure 3: Reversed Discrete Fourier Transform or, using Equation 2, as (RDFT) f (t) = X aj k j k (t) (4) Figure 3 shows the e ects of reconstructing the original jk sequence with only the low frequency parts of the original signal using RDFT. The solid line in Figure 3 shows the where the two-dimensional set of coe cients aj k is called original signal. The dashed line in Figure 3 shows the re- the Discrete Wavelet Transform (DWT) of f (t). A more construction using only the rst 8 DFT coe cients Note speci c form indicating how the ai j 's are calculated can be that the reconstructed signal captures the basic shape of written using inner products as the original sequence. Database researchers have proposed to explore this property for e cient processing of similarity f (t) = Xh j k (t) f (t)i j k (t) (5) based queries 2, 4, 3]. The dotted line in Figure 3 shows the reconstruction of using the rst 64 DFT coe cients, which jk 490 

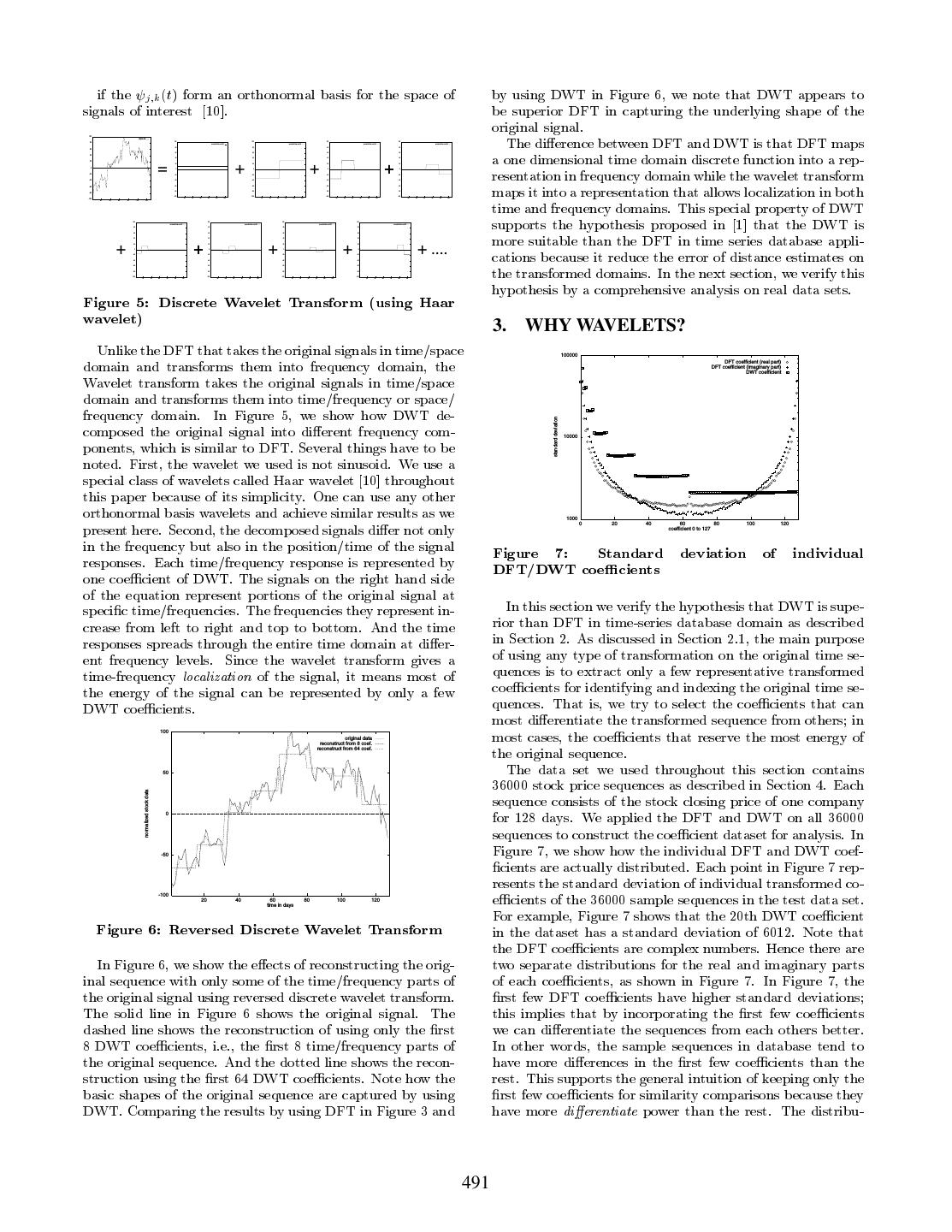
4 . if the j k (t) form an orthonormal basis for the space of by using DWT in Figure 6, we note that DWT appears to signals of interest 10]. be superior DFT in capturing the underlying shape of the original signal. The di erence between DFT and DWT is that DFT maps 100 original data 100 100 100 100 80 reconstruct from coef. #1 reconstruct from coef. #2 reconstruct from coef. #3 reconstruct from coef. #4 a one dimensional time domain discrete function into a rep- 80 80 80 80 60 60 60 60 60 40 40 40 40 40 20 = + + + resentation in frequency domain while the wavelet transform 20 20 20 20 0 0 0 0 0 -20 -20 -20 -20 -20 maps it into a representation that allows localization in both -40 -40 -40 -40 -40 -60 -60 -60 -60 -60 -80 -80 -80 -80 -80 time and frequency domains. This special property of DWT -100 -100 -100 -100 20 40 60 80 100 120 20 40 60 80 100 120 20 40 60 80 100 120 20 40 60 80 100 120 -100 20 40 60 80 100 120 100 reconstruct from coef. #5 100 reconstruct from coef. #6 100 reconstruct from coef. #7 100 reconstruct from coef. #8 supports the hypothesis proposed in 1] that the DWT is more suitable than the DFT in time series database appli- 80 80 80 80 60 60 60 60 40 40 40 40 + + + + + .... cations because it reduce the error of distance estimates on 20 20 20 20 0 0 0 0 -20 -20 -20 -20 the transformed domains. In the next section, we verify this -40 -40 -40 -40 -60 -60 -60 -60 -80 -80 -80 -80 hypothesis by a comprehensive analysis on real data sets. -100 -100 -100 -100 20 40 60 80 100 120 20 40 60 80 100 120 20 40 60 80 100 120 20 40 60 80 100 120 Figure 5: Discrete Wavelet Transform (using Haar wavelet) 3. WHY WAVELETS? Unlike the DFT that takes the original signals in time/space domain and transforms them into frequency domain, the 100000 DFT coefficient (real part) DFT coefficient (imaginary part) Wavelet transform takes the original signals in time/space DWT coefficient domain and transforms them into time/frequency or space/ frequency domain. In Figure 5, we show how DWT de- standard deviation composed the original signal into di erent frequency com- ponents, which is similar to DFT. Several things have to be 10000 noted. First, the wavelet we used is not sinusoid. We use a special class of wavelets called Haar wavelet 10] throughout this paper because of its simplicity. One can use any other orthonormal basis wavelets and achieve similar results as we present here. Second, the decomposed signals di er not only 1000 0 20 40 60 80 100 120 coefficient 0 to 127 in the frequency but also in the position/time of the signal Figure 7: Standard deviation of individual responses. Each time/frequency response is represented by DFT/DWT coe cients one coe cient of DWT. The signals on the right hand side of the equation represent portions of the original signal at speci c time/frequencies. The frequencies they represent in- In this section we verify the hypothesis that DWT is supe- crease from left to right and top to bottom. And the time rior than DFT in time-series database domain as described responses spreads through the entire time domain at di er- in Section 2. As discussed in Section 2.1, the main purpose ent frequency levels. Since the wavelet transform gives a of using any type of transformation on the original time se- time-frequency localization of the signal, it means most of quences is to extract only a few representative transformed the energy of the signal can be represented by only a few coe cients for identifying and indexing the original time se- DWT coe cients. quences. That is, we try to select the coe cients that can most di erentiate the transformed sequence from others in 100 original data most cases, the coe cients that reserve the most energy of the original sequence. reconstruct from 8 coef. reconstruct from 64 coef. 50 The data set we used throughout this section contains 36000 stock price sequences as described in Section 4. Each sequence consists of the stock closing price of one company normalized stock data 0 for 128 days. We applied the DFT and DWT on all 36000 sequences to construct the coe cient dataset for analysis. In Figure 7, we show how the individual DFT and DWT coef- cients are actually distributed. Each point in Figure 7 rep- -50 resents the standard deviation of individual transformed co- -100 20 40 60 80 100 120 e cients of the 36000 sample sequences in the test data set. For example, Figure 7 shows that the 20th DWT coe cient time in days Figure 6: Reversed Discrete Wavelet Transform in the dataset has a standard deviation of 6012. Note that the DFT coe cients are complex numbers. Hence there are In Figure 6, we show the e ects of reconstructing the orig- two separate distributions for the real and imaginary parts inal sequence with only some of the time/frequency parts of of each coe cients, as shown in Figure 7. In Figure 7, the the original signal using reversed discrete wavelet transform. rst few DFT coe cients have higher standard deviations The solid line in Figure 6 shows the original signal. The this implies that by incorporating the rst few coe cients dashed line shows the reconstruction of using only the rst we can di erentiate the sequences from each others better. 8 DWT coe cients, i.e., the rst 8 time/frequency parts of In other words, the sample sequences in database tend to the original sequence. And the dotted line shows the recon- have more di erences in the rst few coe cients than the struction using the rst 64 DWT coe cients. Note how the rest. This supports the general intuition of keeping only the basic shapes of the original sequence are captured by using rst few coe cients for similarity comparisons because they DWT. Comparing the results by using DFT in Figure 3 and have more di erentiate power than the rest. The distribu- 491 

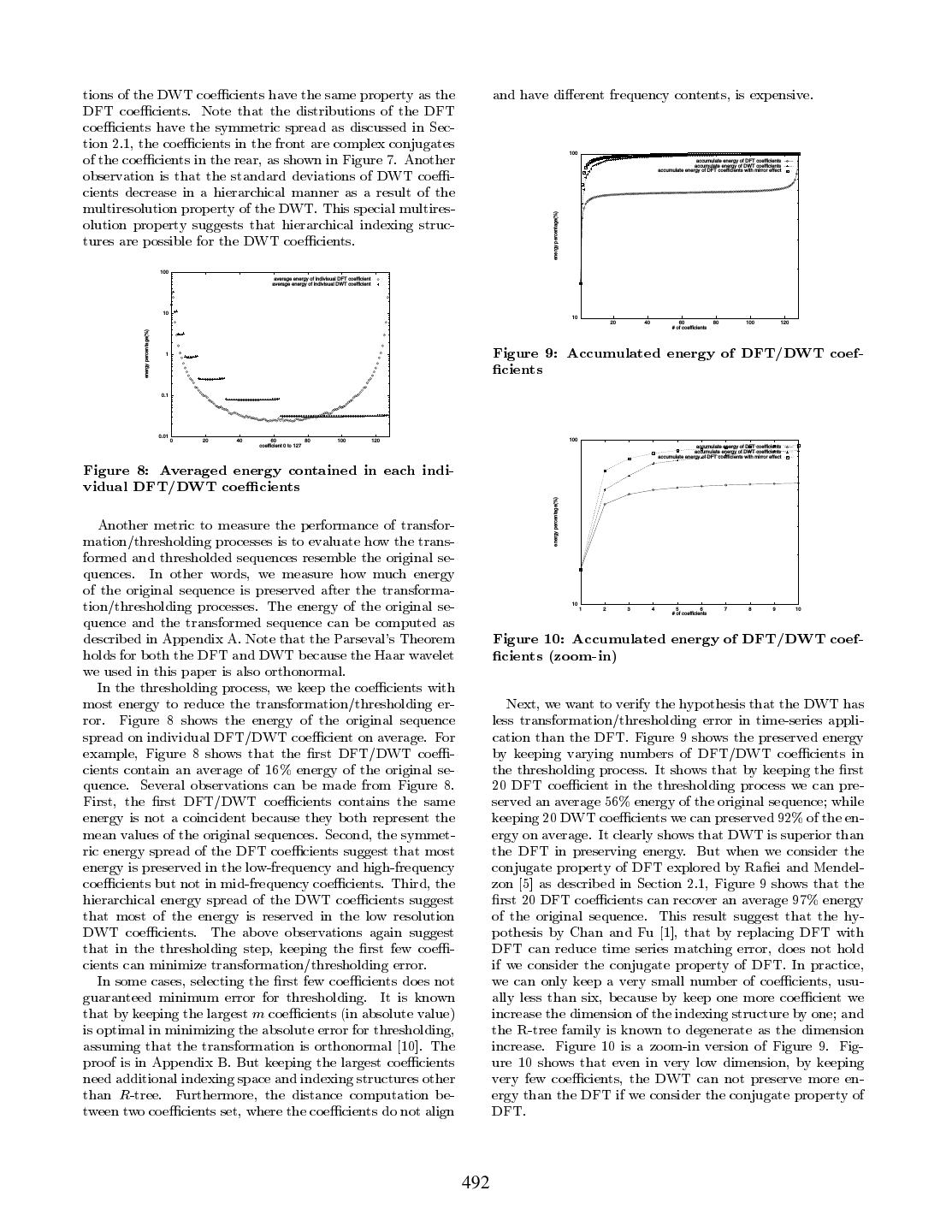
5 .tions of the DWT coe cients have the same property as the and have di erent frequency contents, is expensive. DFT coe cients. Note that the distributions of the DFT coe cients have the symmetric spread as discussed in Sec- tion 2.1, the coe cients in the front are complex conjugates of the coe cients in the rear, as shown in Figure 7. Another 100 accumulate energy of DFT coefficients observation is that the standard deviations of DWT coe - accumulate energy of DWT coefficients accumulate energy of DFT coefficients with mirror effect cients decrease in a hierarchical manner as a result of the multiresolution property of the DWT. This special multires- olution property suggests that hierarchical indexing struc- energy percentage(%) tures are possible for the DWT coe cients. 100 average energy of indivisual DFT coefficient average energy of indivisual DWT coefficient 10 10 20 40 60 80 100 120 # of coefficients energy percentage(%) Figure 9: Accumulated energy of DFT/DWT coef- cients 1 0.1 0.01 0 20 40 60 80 100 120 100 coefficient 0 to 127 accumulate energy of DFT coefficients accumulate energy of DWT coefficients Figure 8: Averaged energy contained in each indi- accumulate energy of DFT coefficients with mirror effect vidual DFT/DWT coe cients energy percentage(%) Another metric to measure the performance of transfor- mation/thresholding processes is to evaluate how the trans- formed and thresholded sequences resemble the original se- quences. In other words, we measure how much energy of the original sequence is preserved after the transforma- tion/thresholding processes. The energy of the original se- 10 1 2 3 4 5 6 7 8 9 10 quence and the transformed sequence can be computed as # of coefficients described in Appendix A. Note that the Parseval's Theorem Figure 10: Accumulated energy of DFT/DWT coef- holds for both the DFT and DWT because the Haar wavelet cients (zoom-in) we used in this paper is also orthonormal. In the thresholding process, we keep the coe cients with most energy to reduce the transformation/thresholding er- Next, we want to verify the hypothesis that the DWT has ror. Figure 8 shows the energy of the original sequence less transformation/thresholding error in time-series appli- spread on individual DFT/DWT coe cient on average. For cation than the DFT. Figure 9 shows the preserved energy example, Figure 8 shows that the rst DFT/DWT coe - by keeping varying numbers of DFT/DWT coe cients in cients contain an average of 16% energy of the original se- the thresholding process. It shows that by keeping the rst quence. Several observations can be made from Figure 8. 20 DFT coe cient in the thresholding process we can pre- First, the rst DFT/DWT coe cients contains the same served an average 56% energy of the original sequence while energy is not a coincident because they both represent the keeping 20 DWT coe cients we can preserved 92% of the en- mean values of the original sequences. Second, the symmet- ergy on average. It clearly shows that DWT is superior than ric energy spread of the DFT coe cients suggest that most the DFT in preserving energy. But when we consider the energy is preserved in the low-frequency and high-frequency conjugate property of DFT explored by Ra ei and Mendel- coe cients but not in mid-frequency coe cients. Third, the zon 5] as described in Section 2.1, Figure 9 shows that the hierarchical energy spread of the DWT coe cients suggest rst 20 DFT coe cients can recover an average 97% energy that most of the energy is reserved in the low resolution of the original sequence. This result suggest that the hy- DWT coe cients. The above observations again suggest pothesis by Chan and Fu 1], that by replacing DFT with that in the thresholding step, keeping the rst few coe - DFT can reduce time series matching error, does not hold cients can minimize transformation/thresholding error. if we consider the conjugate property of DFT. In practice, In some cases, selecting the rst few coe cients does not we can only keep a very small number of coe cients, usu- guaranteed minimum error for thresholding. It is known ally less than six, because by keep one more coe cient we that by keeping the largest m coe cients (in absolute value) increase the dimension of the indexing structure by one and is optimal in minimizing the absolute error for thresholding, the R-tree family is known to degenerate as the dimension assuming that the transformation is orthonormal 10]. The increase. Figure 10 is a zoom-in version of Figure 9. Fig- proof is in Appendix B. But keeping the largest coe cients ure 10 shows that even in very low dimension, by keeping need additional indexing space and indexing structures other very few coe cients, the DWT can not preserve more en- than R-tree. Furthermore, the distance computation be- ergy than the DFT if we consider the conjugate property of tween two coe cients set, where the coe cients do not align DFT. 492 

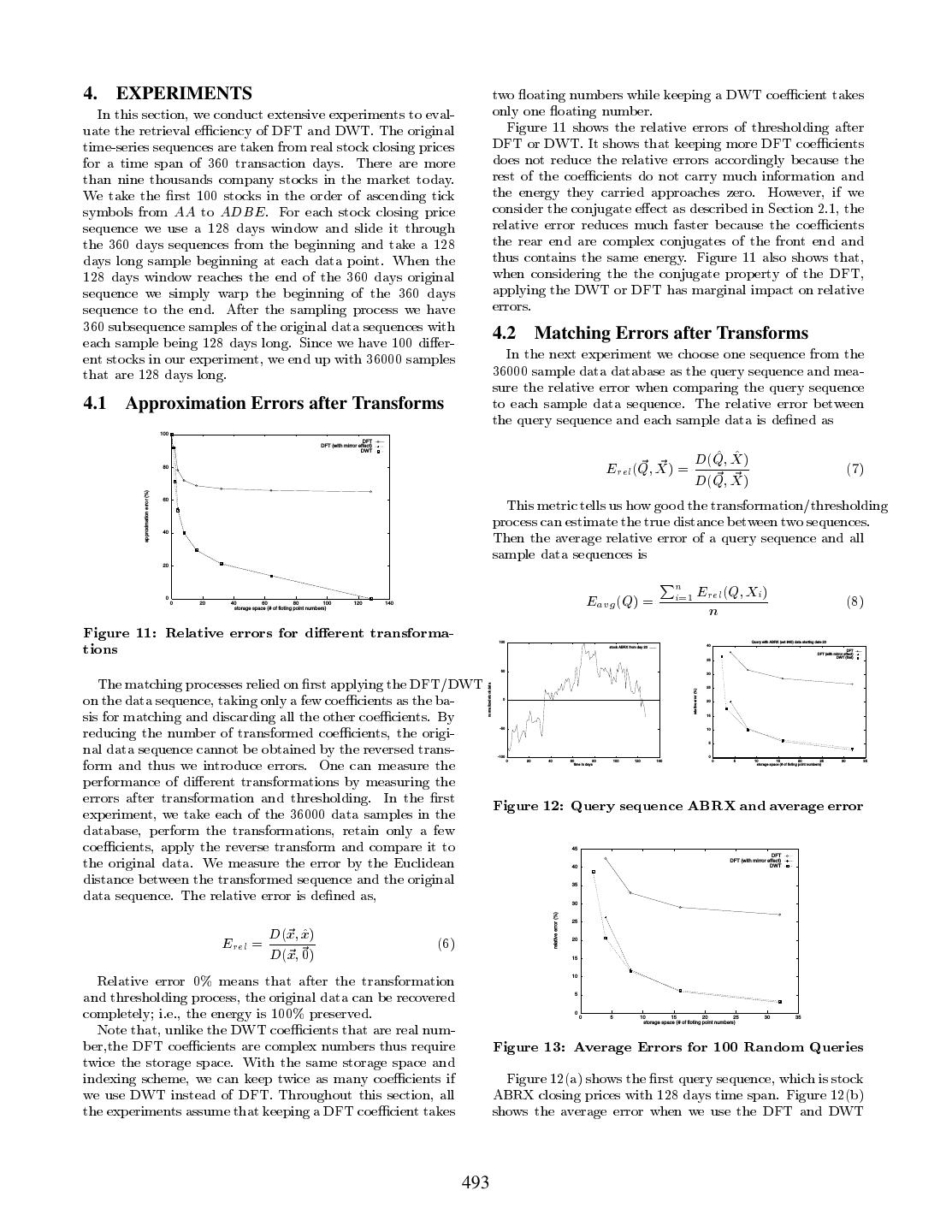
6 .4. EXPERIMENTS two oating numbers while keeping a DWT coe cient takes In this section, we conduct extensive experiments to eval- only one oating number. uate the retrieval e ciency of DFT and DWT. The original Figure 11 shows the relative errors of thresholding after time-series sequences are taken from real stock closing prices DFT or DWT. It shows that keeping more DFT coe cients for a time span of 360 transaction days. There are more does not reduce the relative errors accordingly because the than nine thousands company stocks in the market today. rest of the coe cients do not carry much information and We take the rst 100 stocks in the order of ascending tick the energy they carried approaches zero. However, if we symbols from AA to ADBE . For each stock closing price consider the conjugate e ect as described in Section 2.1, the sequence we use a 128 days window and slide it through relative error reduces much faster because the coe cients the 360 days sequences from the beginning and take a 128 the rear end are complex conjugates of the front end and days long sample beginning at each data point. When the thus contains the same energy. Figure 11 also shows that, 128 days window reaches the end of the 360 days original when considering the the conjugate property of the DFT, sequence we simply warp the beginning of the 360 days applying the DWT or DFT has marginal impact on relative sequence to the end. After the sampling process we have errors. 360 subsequence samples of the original data sequences with 4.2 Matching Errors after Transforms each sample being 128 days long. Since we have 100 di er- ent stocks in our experiment, we end up with 36000 samples In the next experiment we choose one sequence from the that are 128 days long. 36000 sample data database as the query sequence and mea- sure the relative error when comparing the query sequence 4.1 Approximation Errors after Transforms to each sample data sequence. The relative error between the query sequence and each sample data is de ned as 100 DFT ^ ^ Erel(Q~ X~ ) = D(Q~ X~ ) DFT (with mirror effect) DWT 80 (7) D(Q X ) approximation error (%) 60 This metric tells us how good the transformation/thresholding process can estimate the true distance between two sequences. 40 Then the average relative error of a query sequence and all sample data sequences is Pni 20 Eavg (Q) = =1 Erel(Q Xi ) (8) n 0 0 20 40 60 80 100 120 140 storage space (# of floting point numbers) Figure 11: Relative errors for di erent transforma- tions 100 stock ABRX from day 20 40 35 Query with ABRX (set #45) data starting date 20 DFT DFT (with mirror effect) DWT (first) The matching processes relied on rst applying the DFT/DWT 50 30 normalized stock data on the data sequence, taking only a few coe cients as the ba- 25 relative error (%) 0 20 sis for matching and discarding all the other coe cients. By 15 reducing the number of transformed coe cients, the origi- -50 10 nal data sequence cannot be obtained by the reversed trans- 5 form and thus we introduce errors. One can measure the -100 0 0 20 40 60 80 100 120 140 0 5 10 15 20 25 30 35 time in days storage space (# of floting point numbers) performance of di erent transformations by measuring the errors after transformation and thresholding. In the rst Figure 12: Query sequence ABRX and average error experiment, we take each of the 36000 data samples in the database, perform the transformations, retain only a few coe cients, apply the reverse transform and compare it to 45 the original data. We measure the error by the Euclidean DFT DFT (with mirror effect) DWT distance between the transformed sequence and the original 40 data sequence. The relative error is de ned as, 35 30 relative error (%) Erel = D(~x ~x^) 25 (6) 20 D(~x 0) 15 Relative error 0% means that after the transformation 10 and thresholding process, the original data can be recovered 5 completely i.e., the energy is 100% preserved. 0 Note that, unlike the DWT coe cients that are real num- 0 5 10 15 20 25 30 35 storage space (# of floting point numbers) ber,the DFT coe cients are complex numbers thus require Figure 13: Average Errors for 100 Random Queries twice the storage space. With the same storage space and indexing scheme, we can keep twice as many coe cients if Figure 12(a) shows the rst query sequence, which is stock we use DWT instead of DFT. Throughout this section, all ABRX closing prices with 128 days time span. Figure 12(b) the experiments assume that keeping a DFT coe cient takes shows the average error when we use the DFT and DWT 493 

7 .and keep di erent number of coe cients in the thresholding can be treated as a 1-dimension signal and DFT is a proven process. It shows that by using DFT and keeping only the technique that has been widely used in signal processing do- rst few coe cients as a distance measurement produces main. In this paper, we explore the feasibility of replacing large average error, no matter how many coe cients are the DFT by DWT with a comprehensive analysis of the DFT kept. By using the DWT and keeping that same number of and DWT as matching functions in time-series databases. coe cients we can achieve much smaller relative error than Our results show that although the DWT based technique using the DFT. But with the conjugate property, the average has several advantages, e.g., the DWT has complexity of relative error of the DFT is greatly reduced and comparable O(N ) whereas DFT is O(N log N ), DWT does not reduce to the DWT. Figure 13 shows the average relative errors of relative matching error and does not increase query pre- 100 random queries. It suggests similar result. cision in similarity search. We conclude that, by exploiting the conjugate property of DFT in the real domain, the DFT- 4.3 Precision of Epsilon Query with Trans- based and DWT-based techniques yield not much di erent forms behavior in the context of similarity search in time-series databases. Our suggestions for future work are to explore the unique 0.4 DFT (first 4 coef.) properties of DWT which the DFT does not have e.g, mul- DFT (first 4 coef. with mirror effect) DWT (first 8 coef.) 0.35 0.3 tiresolutional property. For example, since DWT is inher- ently multiresolutional, it is possible to match time-series data at di erent resolutions concurrently. More e cient hi- 0.25 precision 0.2 erarchical searching structures other than the R-tree fami- 0.15 lies can be derived by exploring this unique multiresolution 0.1 property of the DWT. 0.05 0 100 150 200 250 300 350 400 450 500 6. REFERENCES 1] Kin pong Chan and Ada Wai-Chee Fu. E cient time epsilon distance Figure 14: Average Precisions for 100 Random series matching by wavelets. In Proceedings of the 15th Queries International Conference on Data Engineering, 23-26 March 1999, Sydney, Austrialia, pages 126{133. IEEE One of the most important categories of query in time- Computer Society, 1999. series database is epsilon distance query: Given a query se- 2] R. Agrawal, C. Faloutsos, and A. Swami. E cient quence Q, nd all the data sequence Xi in the database such Similarity Search in Sequence Databases. In that the distance between Q and Xi is below a threshold d, Proceedings of the 4th Int'l Conference on Foundations i.e., D(Q Xi) <= d. In other words, nd all similar time of Data Organization and Algorithms, pages 69{84, sequences in the database to a query sequence Q with simi- Chicago, Oct 1993. larity threshold d. For example, when the similarity thresh- 3] C. Faloutsos, M. Ranganathan, and Y. Manolopoulos. old is 200, there are 3 data sequences in the data base which Fast Subsequence MAtching in Time-Series are under that range. As described in Section 2.1, accord- Databases. In Proceedings of the 1994 ACM SIGMOD ing to Parseval's theorem, the transformation/thresholding International Conference on Management of Data, processed will always result in underestimating the distance pages 419{429, Minneapolis, May 1994. in the transformed domains i.e., no false dismissal but false 4] Davood Ra ei and Alberto Mendelzon. hits. We want to reduce the size of the estimated result Similarity-Based Queries for Time Series Data. In set to be as close to the actual result set as possible, such Proceedings of the 1997 ACM SIGMOD International that we can save more real distances computations in the Conference on Management of Data, pages 13{24, post processing stage i.e., increase precision to reduce false Tucson, Arizona, May 1997. admissal. 5] Davood Ra ei and Alberto Mendelzon. E cient The precision of an epsilon query is de ned as Retrieval of Similar Time Sequences Using DFT. In Proceedings of the International Conference on jActualResultSet(Q)j PrecisionOfEpsilonQuery(Q) = jEstimatedResultSet Foundations of Data Organizations and Algorithms - (Q)j FODO 98, Kobe, Japan, November 1998. (9) 6] Rakesh Agrawal, King-Ip Lin, Harpreet S. Sawhney, and Kyuseok Shim. Fast Similarity Search in the Figure 14 shows the epsilon distance query precision result Presence of Noise, Scaling, and Translation in of 100 random queries. We can see that the precisions of Time-Series Databases. In Proceedings of the 21th epsilon distance queries using the DWT are similar to the VLDB Conference, pages 490{501, Zurich, DFT. The result suggests that the DWT is not likely to Switzerland, 1995. produce a smaller estimated epsilon distance query result 7] Byoung-Kee Yi, H.V. Jagadish, and Christos set than the DFT if we consider the conjugate property of Faloutsos. E cient Retrieval of Similar Time DFT. Sequences under Time Warping. In Proceedings of the International Conference on Data Engineering - ICDE 5. CONCLUSION 98, pages 201{208, Orlando, Florida, Feburary 1998. The DFT has been traditionally used as the de facto pro- 8] Sanghyun Park, Wesley W. Chu, Jeehee Yoon, and cessing function for time-series data because time-series data Chihcheng Hsu. E cient searches for similar 494 

8 . subsequences of di erent lengths in sequence where m^ < m. Then the L2 error between the original databases. In Proceedings of the 16th International function and the thresholded one is given by Conference on Data Engineering, 28 February - 3 March, 2000, San Diego, California, pages 23{32. kf (x) ; f^(^x)k2 = hf (x) ; f^(^x)jf (x) ; f^(^x)i IEEE Computer Society, 2000. = X m X m c (i) c hu i ju j i 9] Chang-Shing Perng, Haixun Wang, Sylvia R. Zhang, j ( ) ( ) ( ) and D. Stott Parker. Landmarks: a new model for i=m^ +1 j =m^ +1 similarity-based pattern querying in time series = Xm (c (i) )2 (17) databases. In Proceedings of the 16th International Conference on Data Engineering, 28 February - 3 i=m^ +1 March, 2000, San Diego, California, pages 33{42. if the basis is orthonormal. In order to minimize this error IEEE Computer Society, 2000. for any give m^ , (i) satis es jc (1) j ::: jc (m) j. The 10] C. Sidney Burrus, Remesh A. Gopinath, and Haitao complete proof can be found in 11]. Guo. Introduction to Wavelets and Wavelet Transforms: A Primer. Prentice-Hall, Inc., 1998. 11] Eric J. Stollnitz, Tony D. Derose, and David H. Salesin. Wavelets for Computer Graphics: Theory and Applications. Morgan Kaufmann Publishers, Inc., 1996. Appendix A: Mathematics for Discrete Fourier Transform (DFT) The n-point DFT of a signal x = xt ] t = 0 ::: n ; 1 is de ned to be a sequence X of n complex numbers Xf f = 0 ::: n ; i, given by p nX Xf = 1= n ; 1 xt e;j 2 ft=n f = 0 1 ::: n ; 1 (10) t=0 p where j is the imaginary unit j = ;1. The signal x can be recovered by the inverse transform: p nX xt = 1= n ; 1 Xf ej 2 ft=n t = 0 1 ::: n ; 1 (11) f =0 Xf is a complex number. If the signal is real, then X0 is real. The energy of Signal x is de ned as the sum of energies at every point of the sequence: E (x) kxk2 X jxj n;1 2 (12) t=0 The Parseval's Theorem X jxij = nX; jXj j n;1 2 1 2 (13) i=0 j =0 we have kx ; yk = kX ; Y k 2 2 (14) Appendix B: Minimizing Thresholding Error Let the original function be f (x) = X m ci ui (x) (15) i=1 and let (i) be a permutation of 1 ::: m and the function after thresholding is X m^ f^(x) = c (i) u (i) (x) (16) i=1 495