热门城市
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
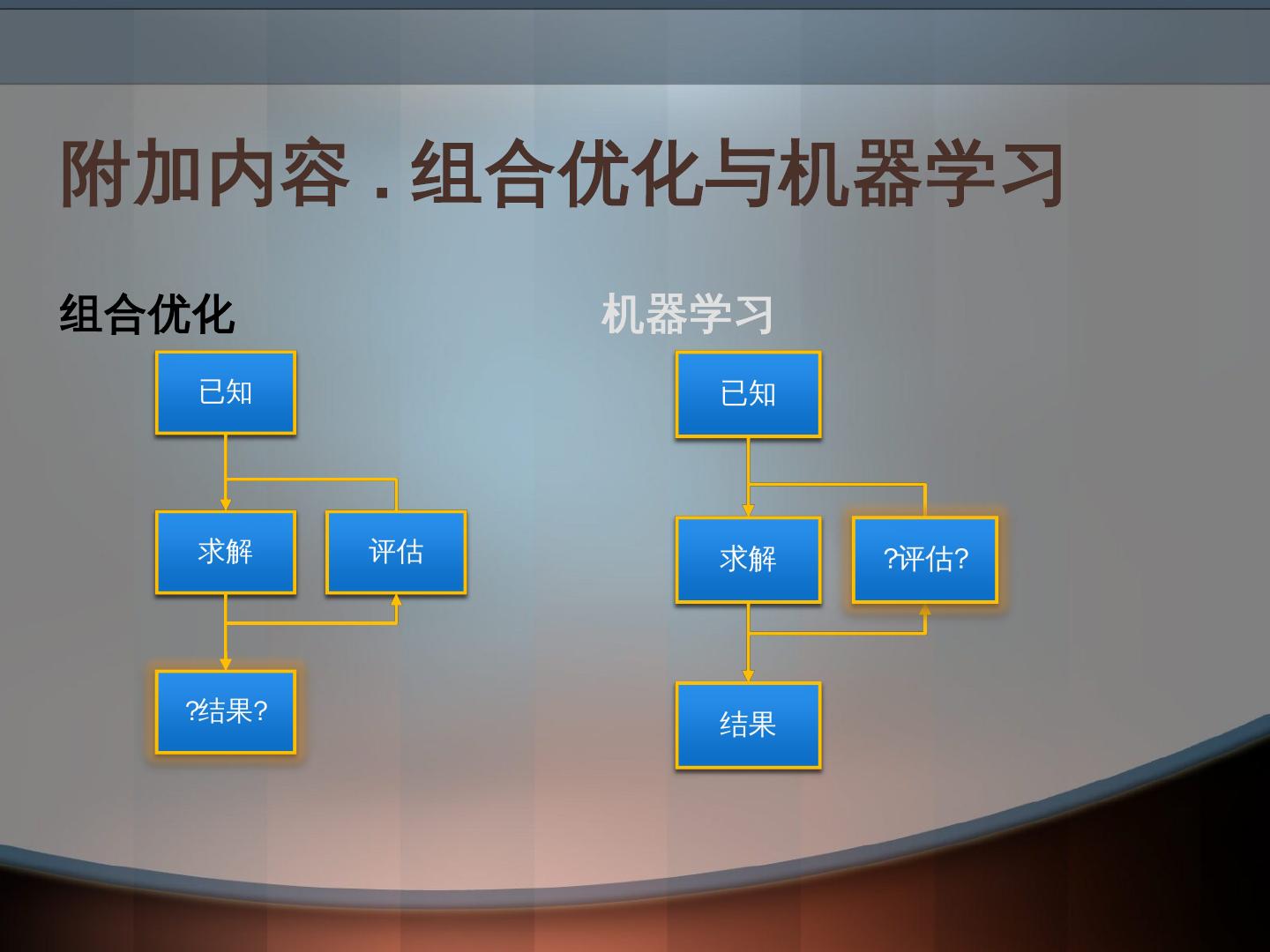
组合优化问题的数学建模
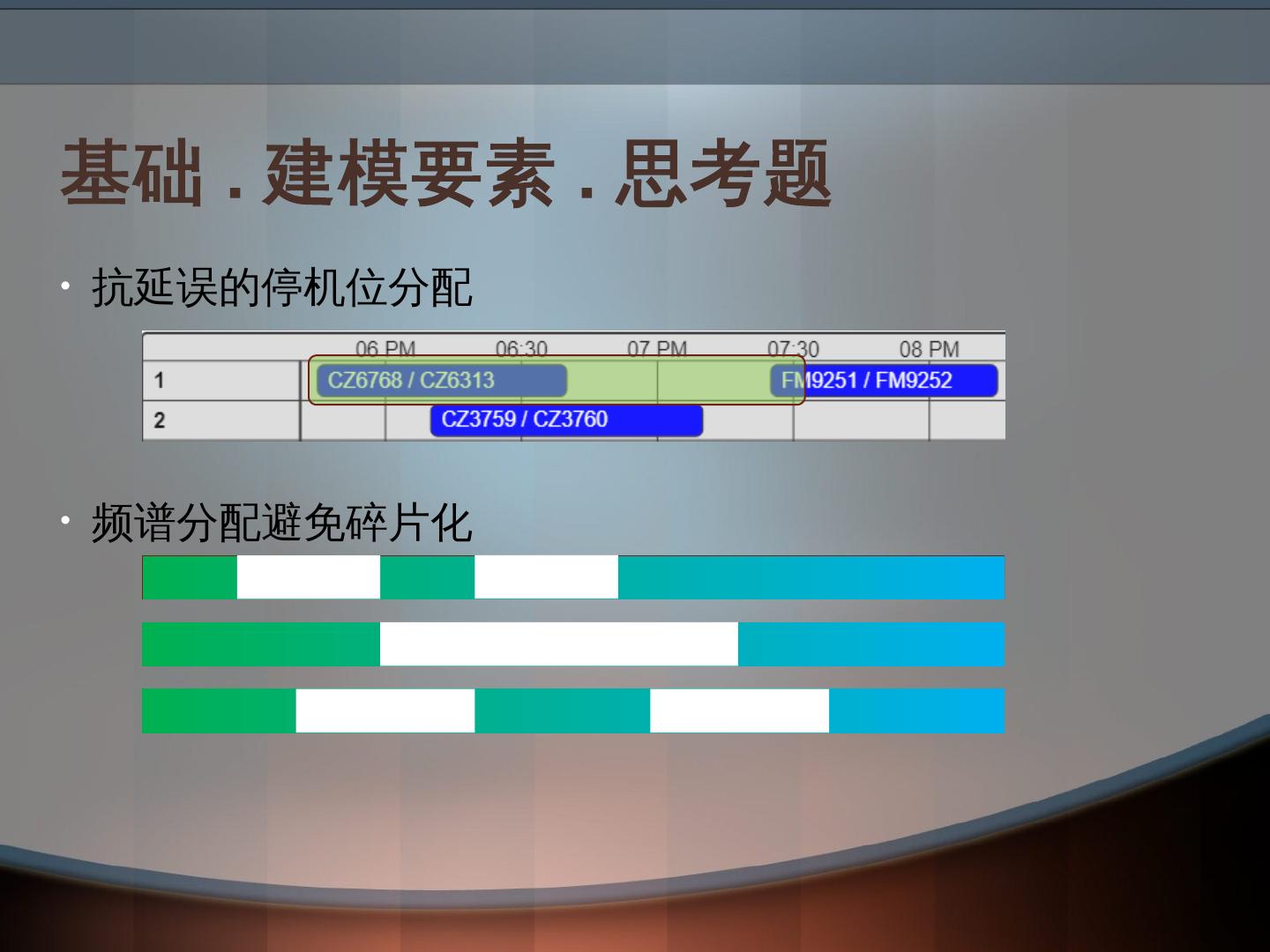
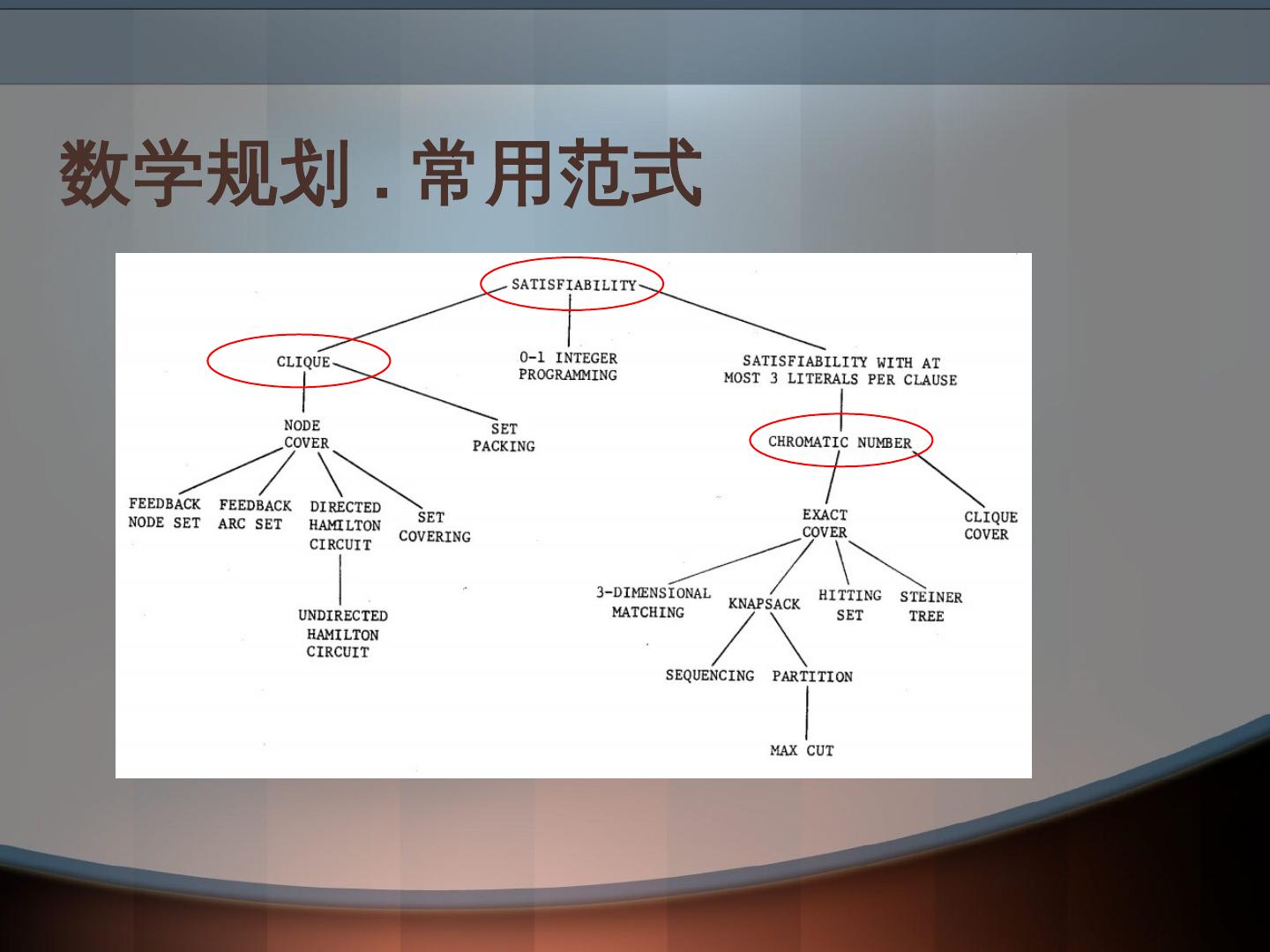
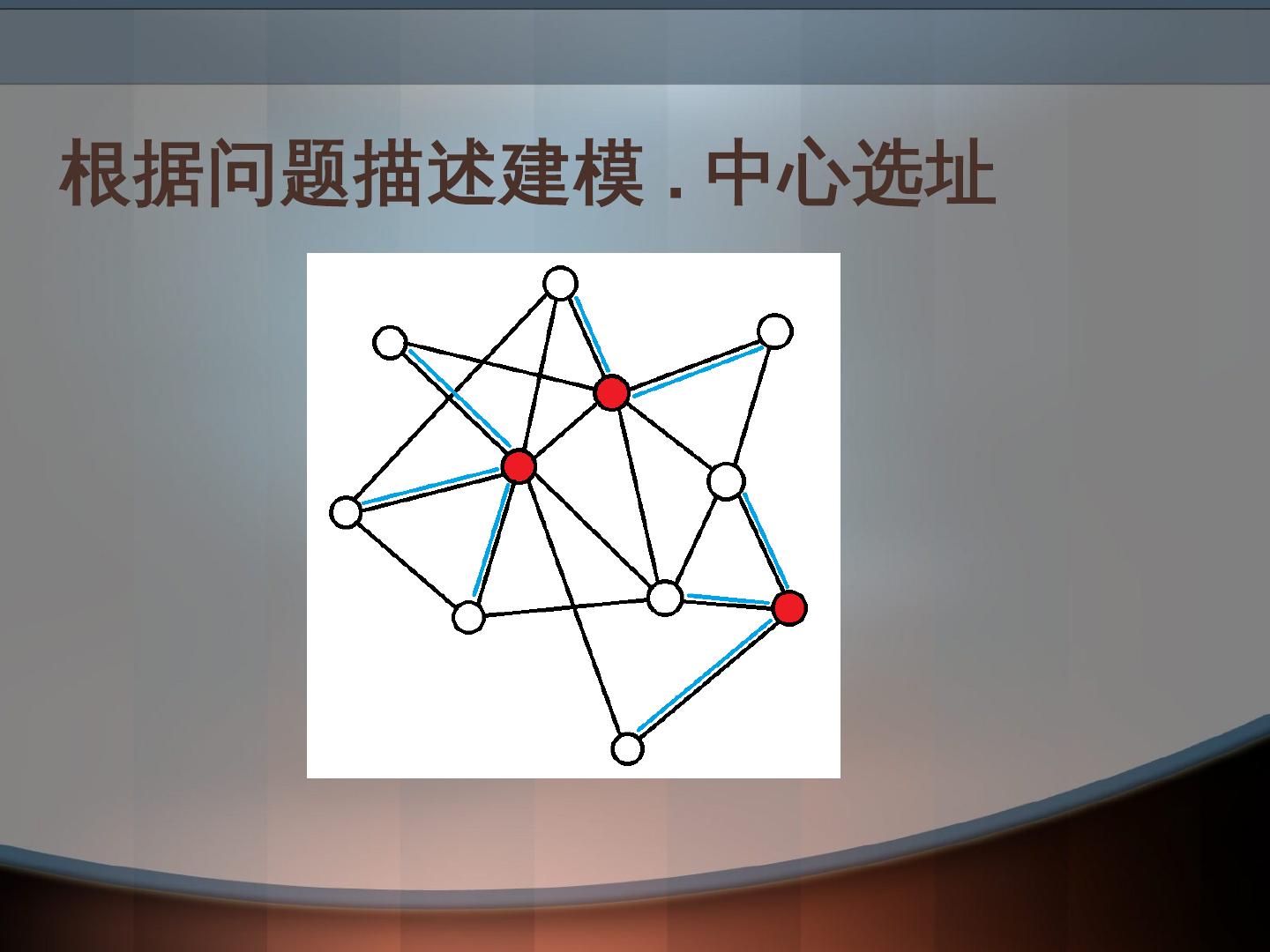
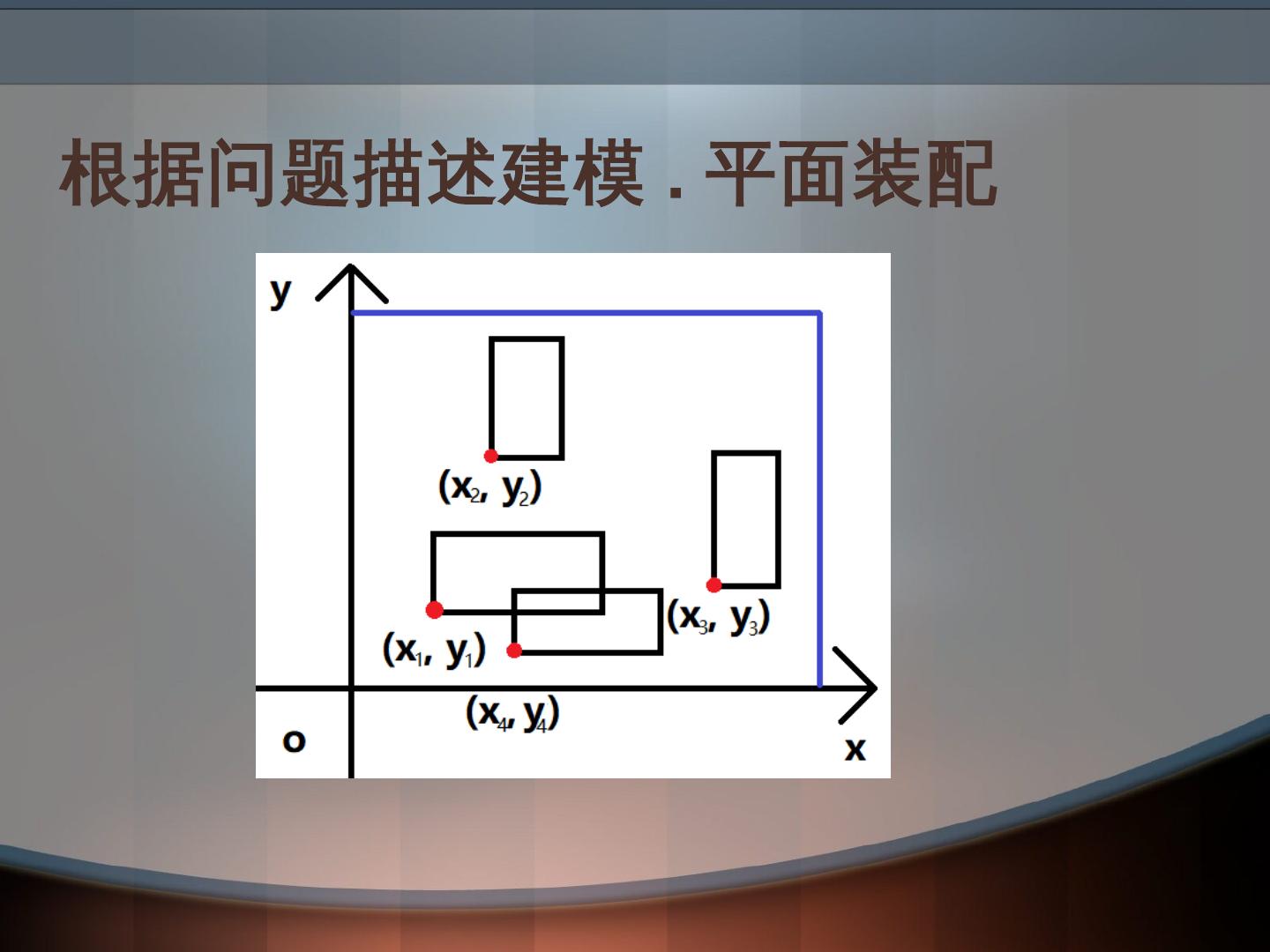
什么是数学建模？其基础是什么？它的意义是屏蔽技术细节，抽象出问题本质，规约成经典问题以及适配成熟的解决方案。数学建模规划的常用范式包括：凸优化（Convex Optimization），非凸优化（Nonconvex Optimization）；建模技巧包括：观察角度，多目标，非线性表达式，改进模型；一些常见根据问题描述建模方法举例：图着色，中心选址，TSP，平面装配，还有比如元启发式算法等。
3秒后跳转登录页面
去登陆
