- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
12 计算机视觉--图像的频域变换
展开查看详情
1 .成果展示 第十二章 图像的频域变换 巫义锐 河海大学 计算机与信息学院
2 .典型试题 1 :开运算 腐蚀 膨胀
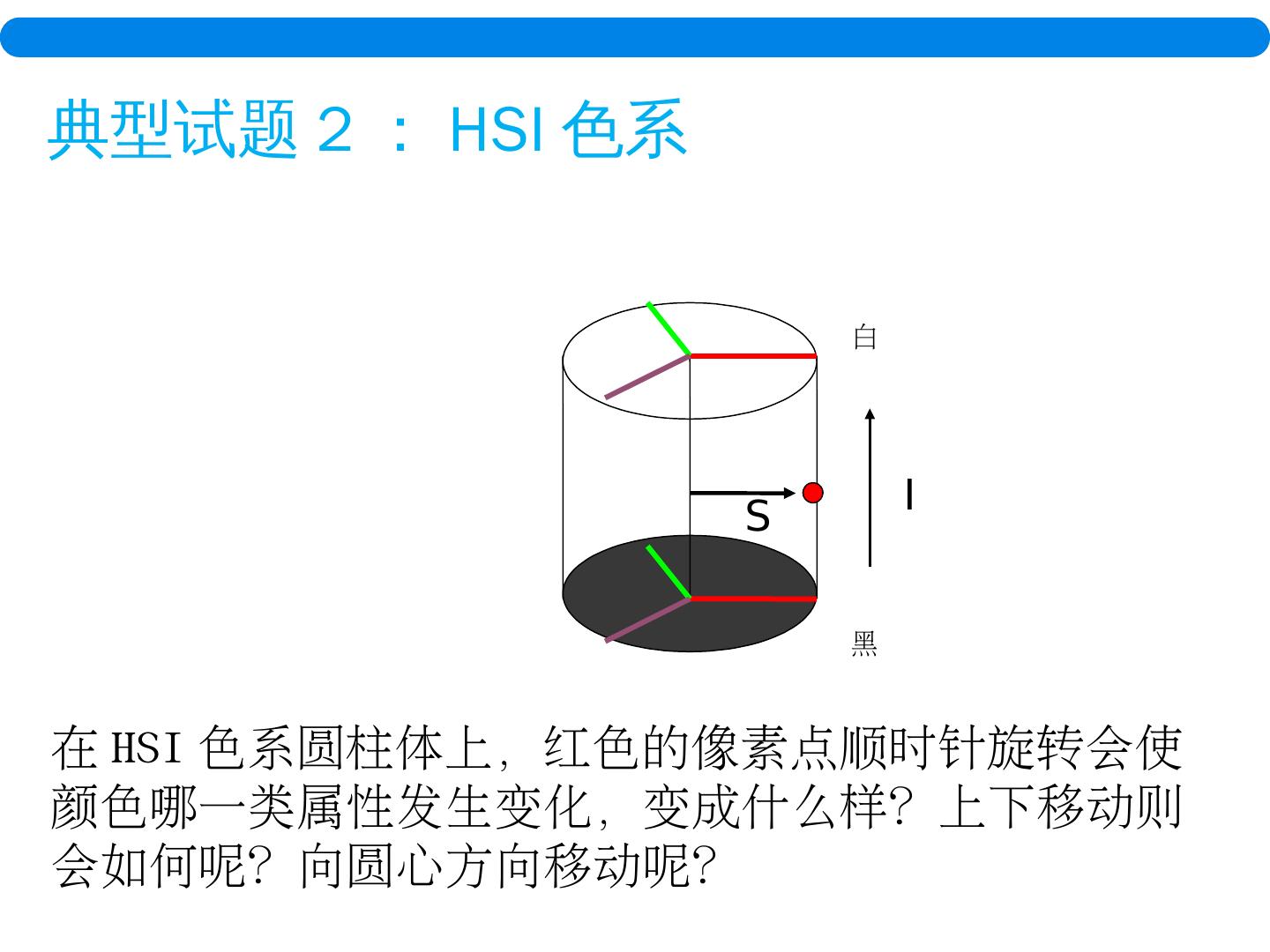
3 . 典型试题 2 : HSI 色系 黑 白 I S 在 HSI 色系圆柱体 上,红色 的像素点顺时针 旋转 会使颜色哪一类属性发生变化,变成 什么样?上下 移动则会如何呢 ?向圆心方向移动呢?
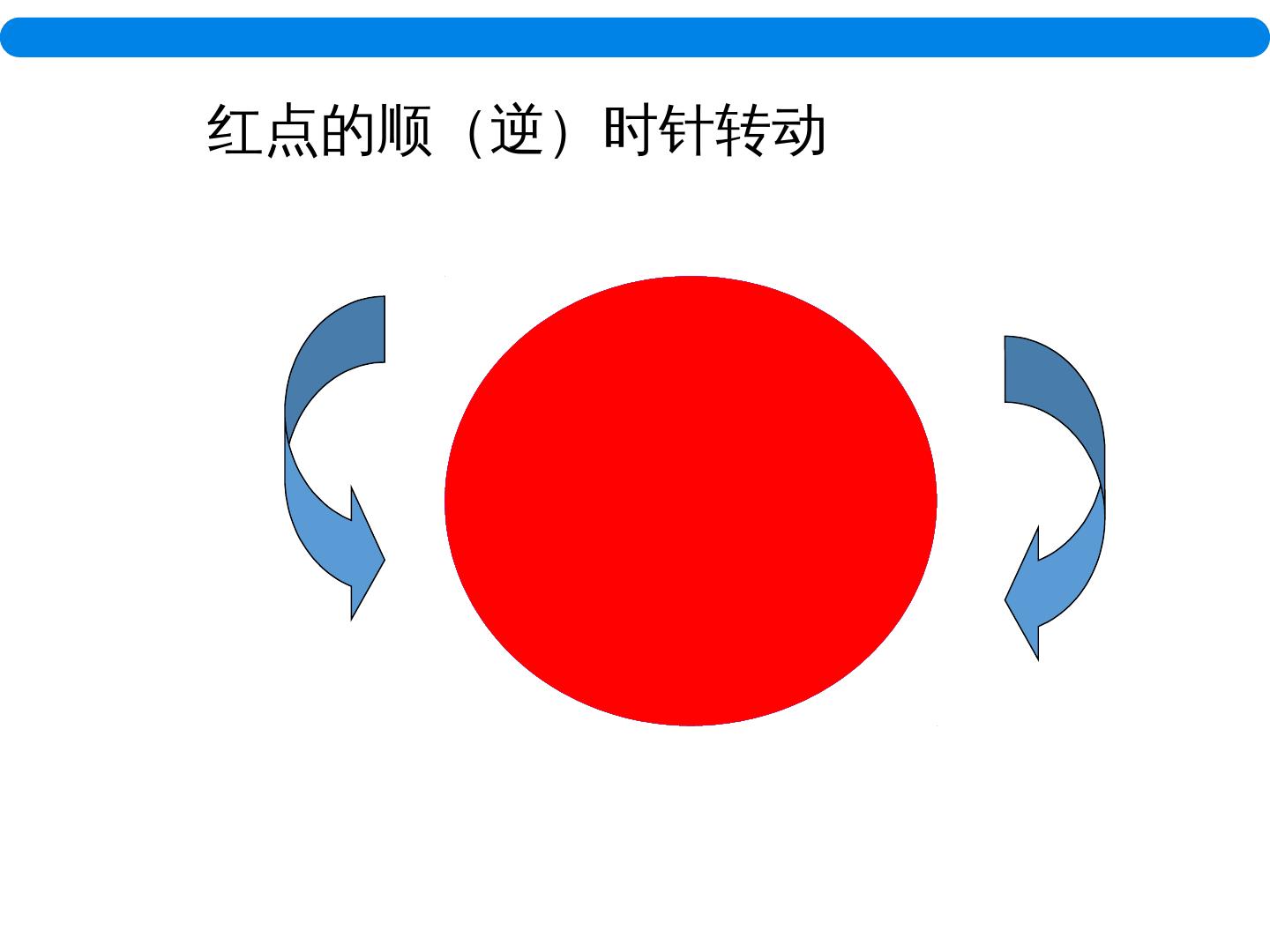
4 .红点的顺(逆)时针转动
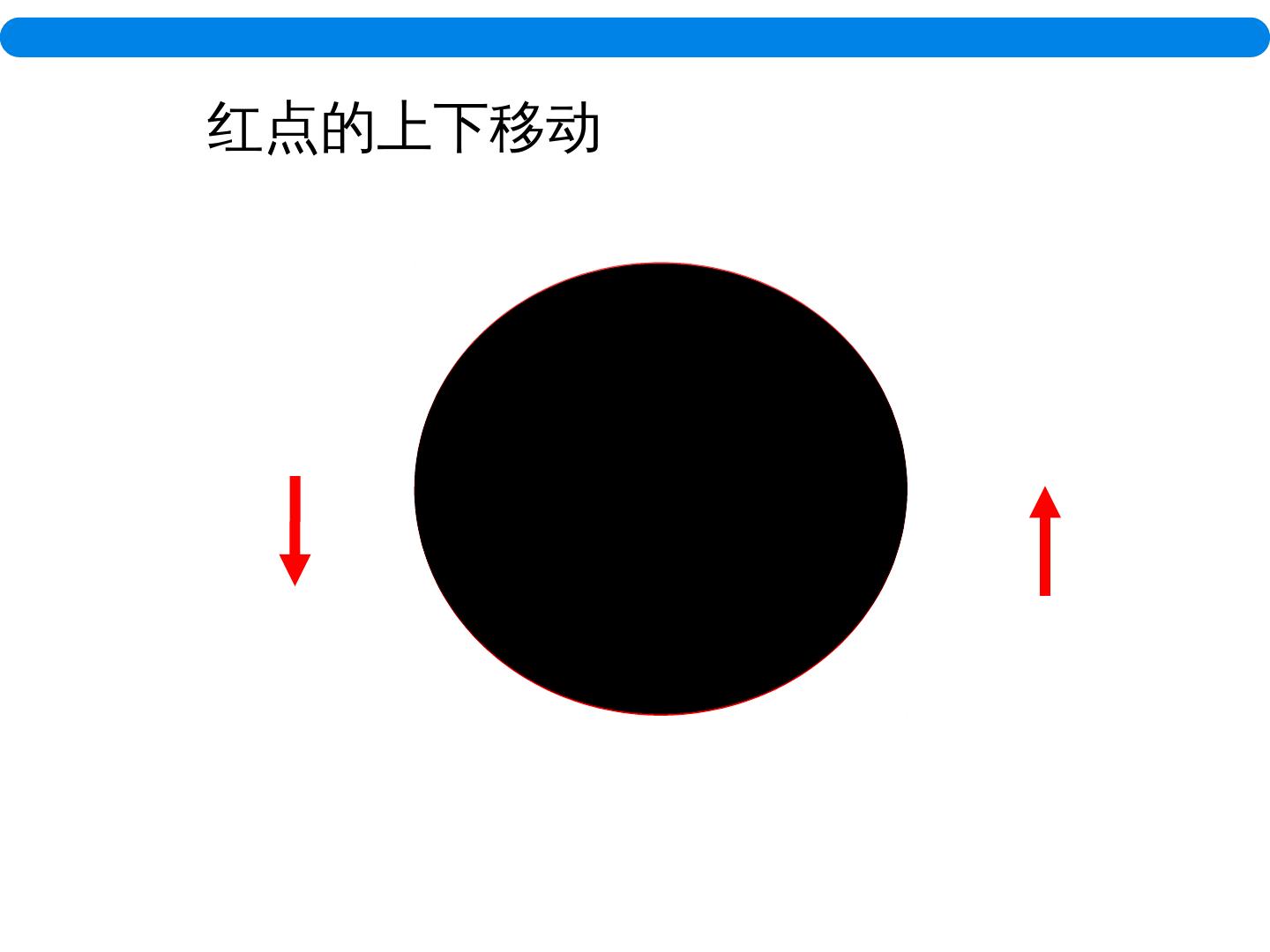
5 .红点的上下移动
6 .红点向圆心方向移动
7 . 本章提纲 频域的理解 傅立叶变换理解 二维离散傅立叶 变换 离散余弦变换及快速傅立叶变换
8 . 人类视觉所感受到的是在 空间域 和 时间域 的信号。 但是,往往许多问题在频域中讨论时,有其非常方便分析的一面。例如,空间位置上的变化不改变信号的 频域特性 。 问题的提出 如何理解空间域、时间域与频域?
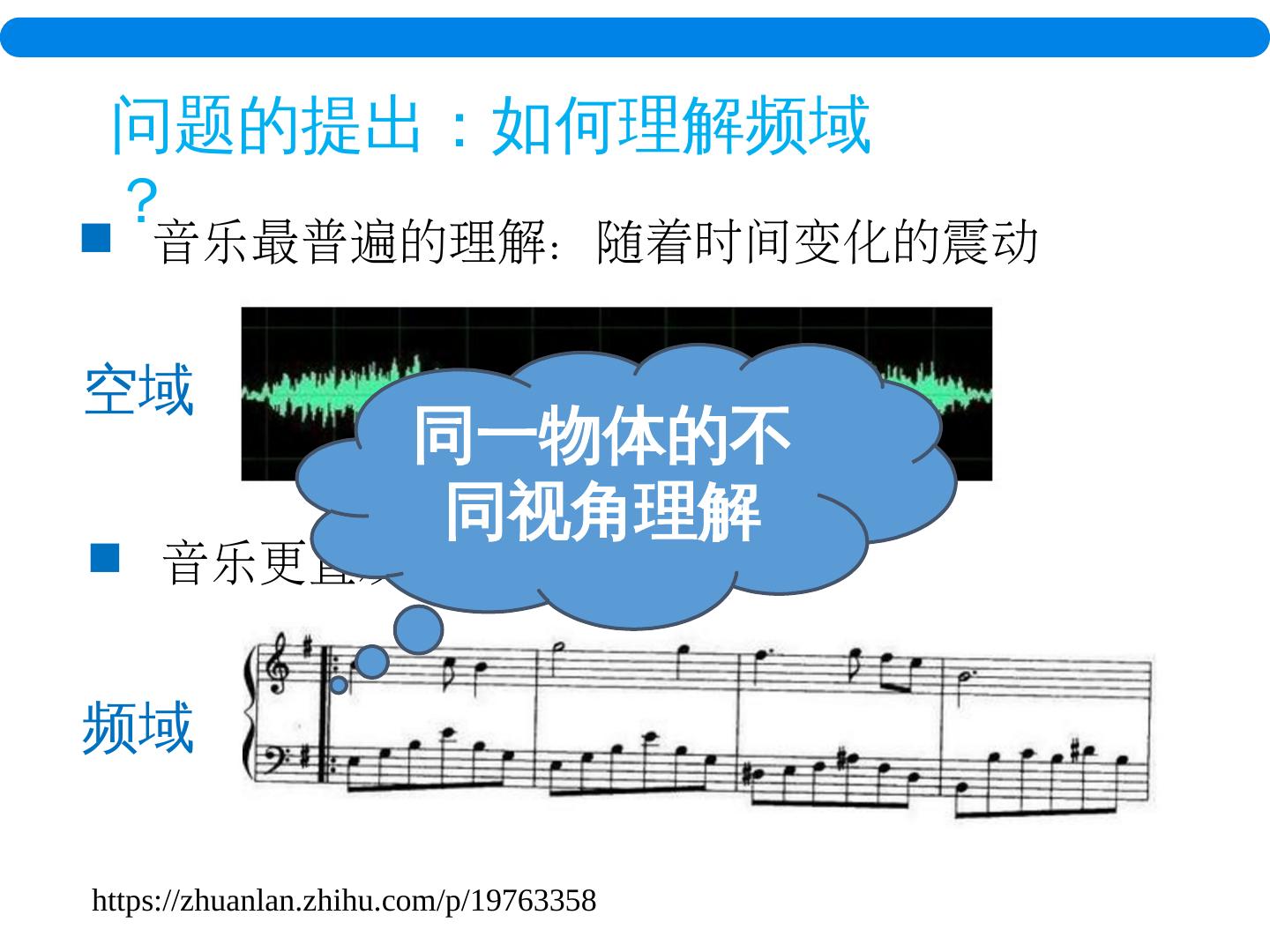
9 .问题的提出:如何理解频域? 音乐最普遍的理解:随着时间变化的震动 音乐更直观的理解 空域 频域 https://zhuanlan.zhihu.com/p/19763358 同一物体的不同视角理解
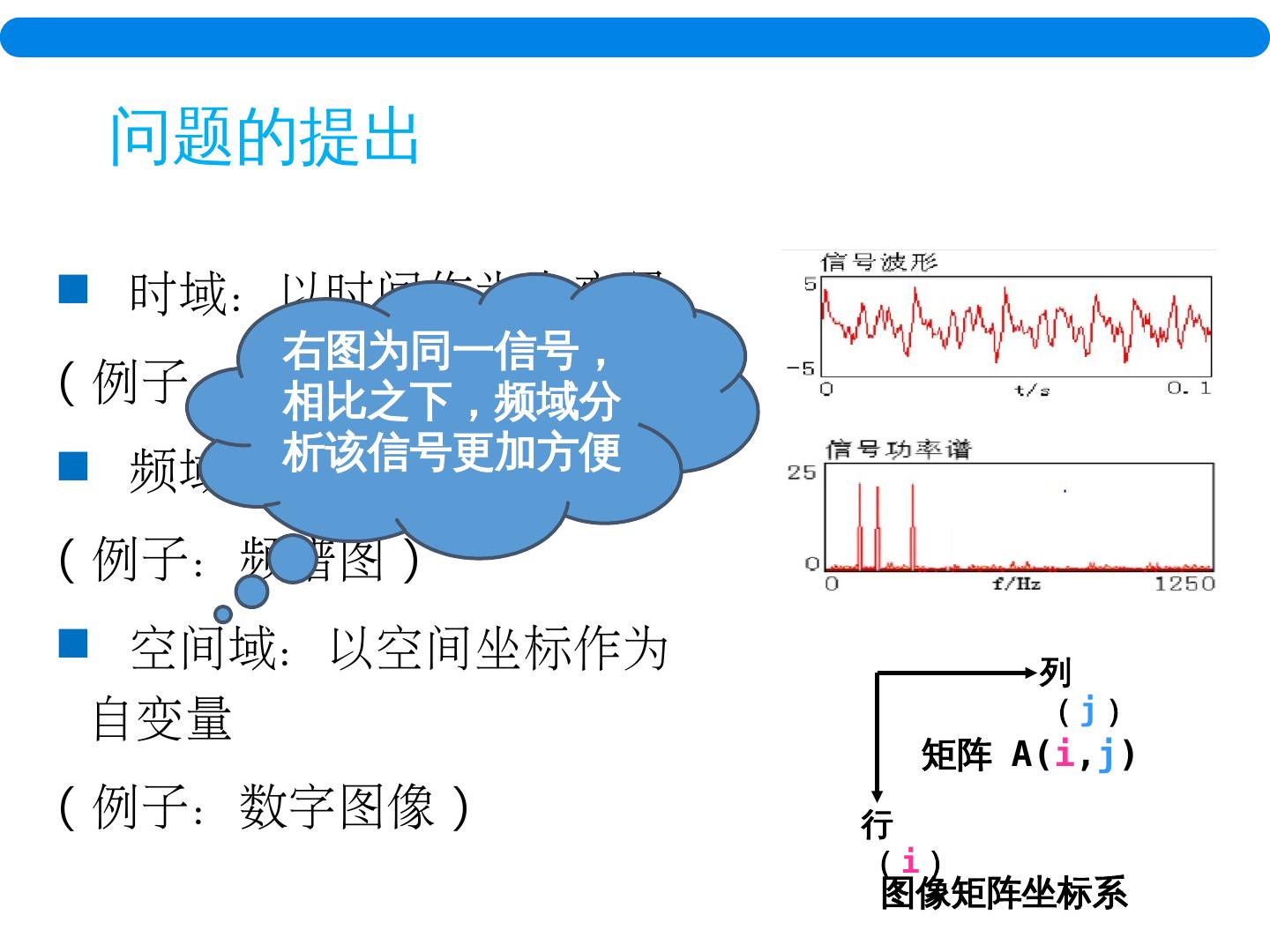
10 . 时域:以时间作为自变量 ( 例子:波形图 ) 频域:以频率作为自变量 ( 例子:频谱图 ) 空间域:以空间坐标作为自变量 ( 例子:数字图像 ) 问题的提出 行( i ) 列( j ) 矩阵 A( i , j ) 图像矩阵 坐标系 右图为同一信号,相比之下,频域分析该信号更加方便
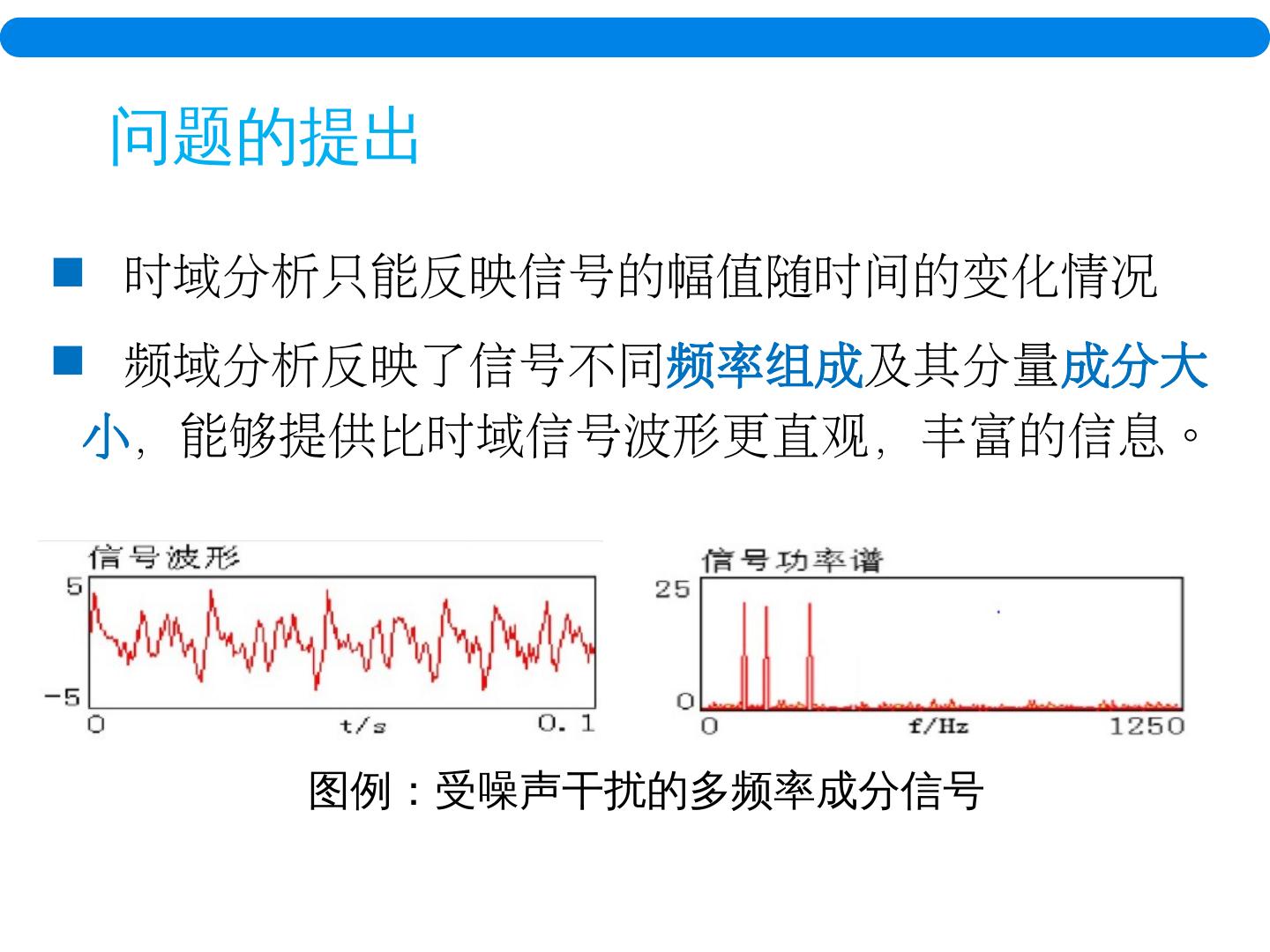
11 . 时域分析只能反映信号的幅值随时间的变化情况 频域分析反映了信号不同 频率组成 及其分量 成分大小 ,能够提供比时域信号波形更直观,丰富的信息。 问题的提出 图例:受噪声干扰的多频率成分信号
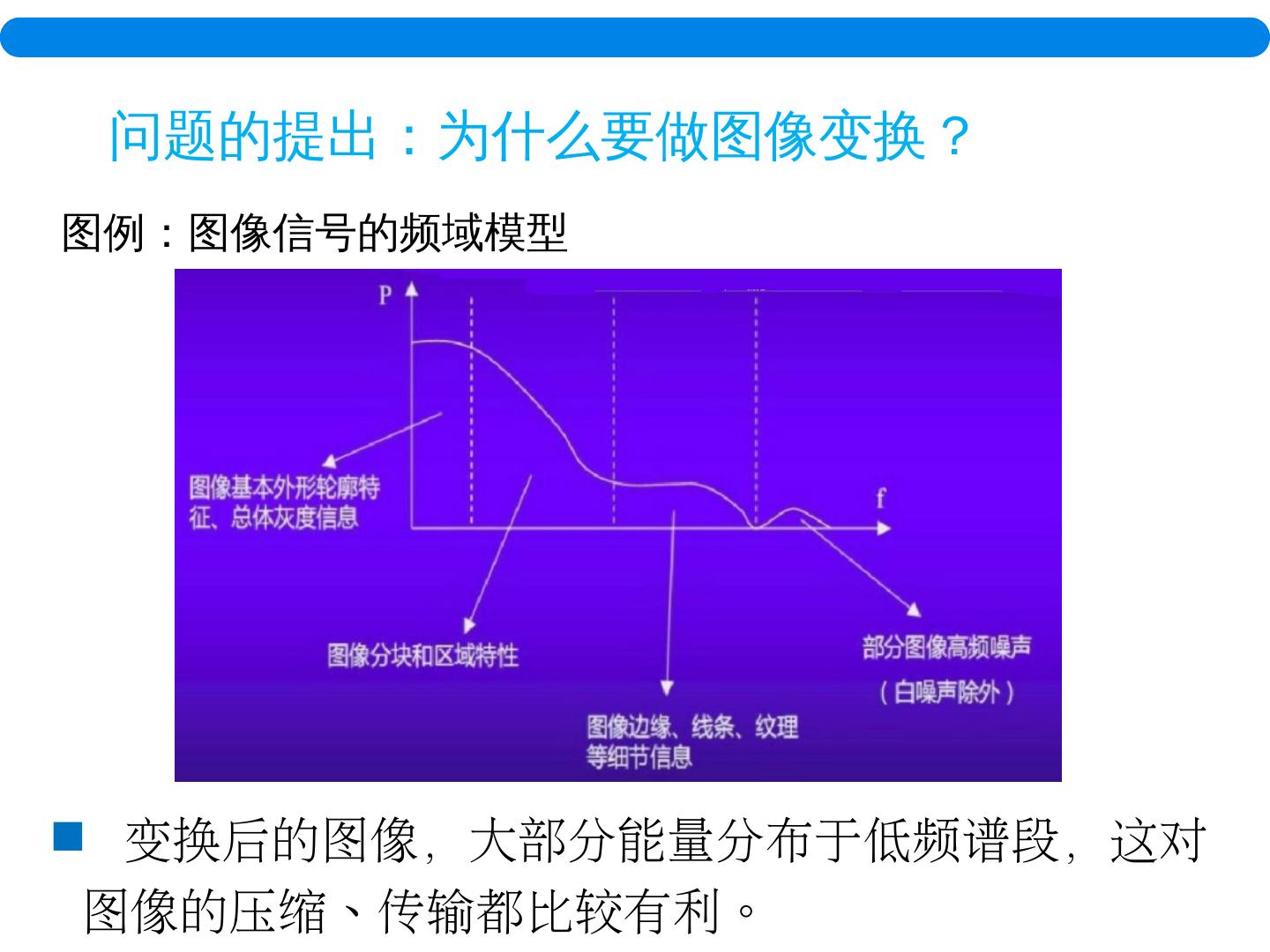
12 .问题的提出:为什么要做图像变换? 图例:图像信号的频域模型 变换后的图像,大部分能量分布于低频谱段,这对图像的压缩、传输都比较有利。
13 . 首先,提出的变换必须是有好处的,换句话说,可以解决时域中解决不了的问题。 其次,变换必须是 可逆的 ,可以通过逆变换还原回原时域中。 图像变换的前提条件 处理流程:时域 => 频域处理 => 时域
14 . 本章提纲 频域的理解 傅立叶变换理解 二维离散傅立叶 变换 离散余弦变换 及快速傅立叶变换
15 .图一:正弦波 cos ( x ) 图二: 2 个正弦波的叠加 cos (x)+a.cos(3x) 图三: 4 个正弦波的叠加 图四: 10 个正弦波的叠加 傅立叶变换理解 随着正弦波数量逐渐的增长,他们最终会叠加成一个标准的矩形
16 . 傅立叶变换理解: 傅立叶级数 傅立叶级数定义:任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示 选择正弦函数与余弦函数作为基函数是因为它们是正交的
17 . 傅立叶变换理解: 傅立叶的故事 1807 年,傅立叶向科学院呈交了题为“ 热的传播 ”的论文,内容是关于不连结的物质和特殊形状的连续体中的热扩散问题 在论文的审阅人中,拉普拉斯 、蒙日和拉克鲁瓦都是赞成接受这篇论文的,但是拉格朗日提出了强烈的反对 傅里叶在论文中运用正弦曲线来描述温度分布,并提出一个很有争议性的结论:任何连续周期信号可以由一组适当的正弦曲线组合而成 拉格朗日坚持认为傅里叶的方法无法表示带有棱角的信号,如在方波中出现非连续变化斜率 我们可以用正弦曲线来逼近地表示它,逼近到两种表示方法不存在能量差别,基于此,傅里叶是对的 这个小插曲导致傅立叶级数直到 1822 年才得以发表
18 . 黑色的线就是所有正弦波叠加而成的总和。 后面依不同颜色排列而成的 正弦波 就是组合为矩形波的各个 分量 。 这些正弦波按照 频率 从低到高从前向后排列开来。 傅立叶变换理解 正弦波分量如何表示?
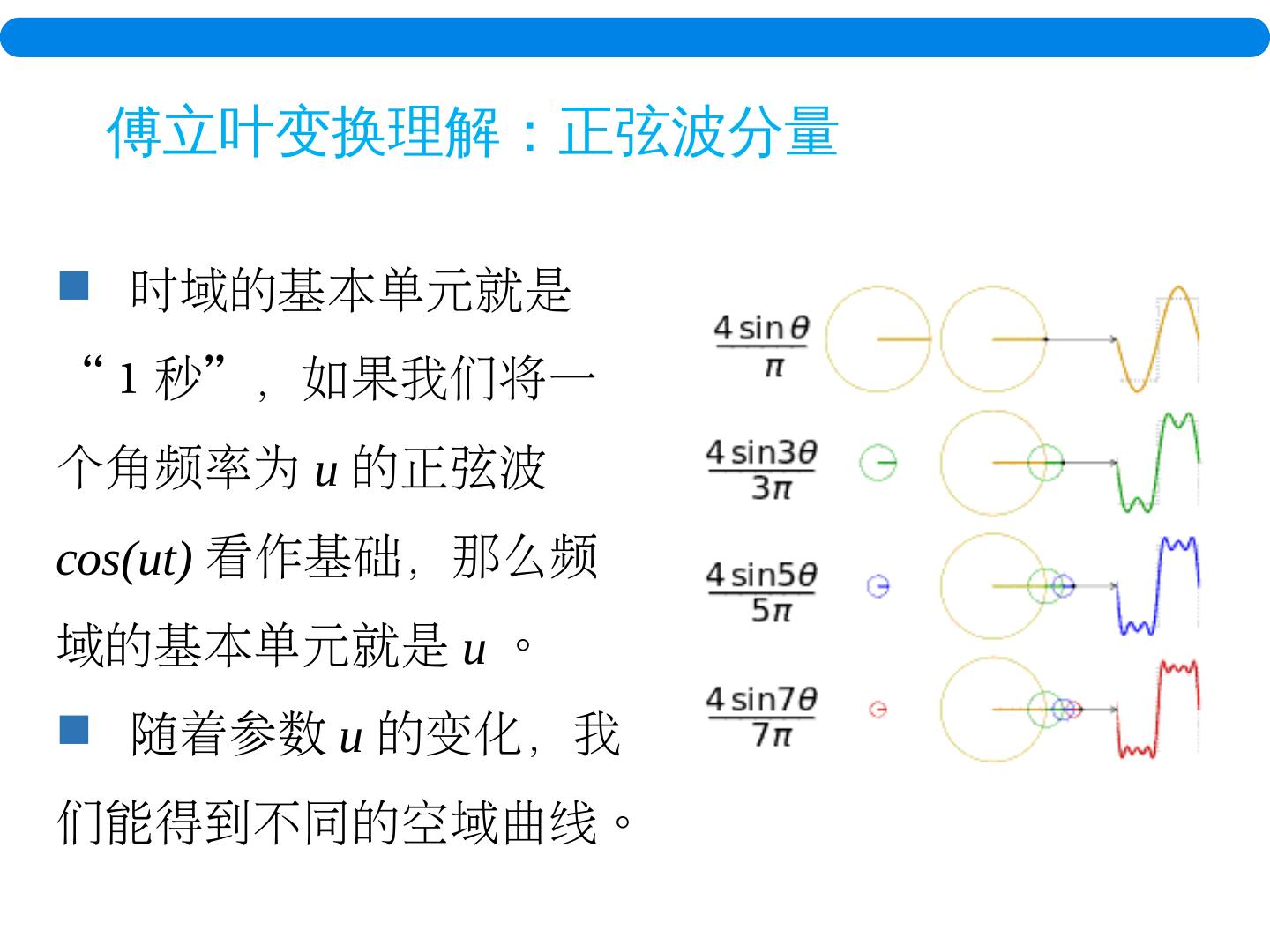
19 . 时域的基本单元就是“ 1 秒”,如果我们将一个角频率为 u 的正弦波 cos ( ut ) 看作基础,那么频域的基本单元就是 u 。 随着参数 u 的变化,我们能得到不同的空域曲线。 傅立叶变换理解:正 弦 波分量
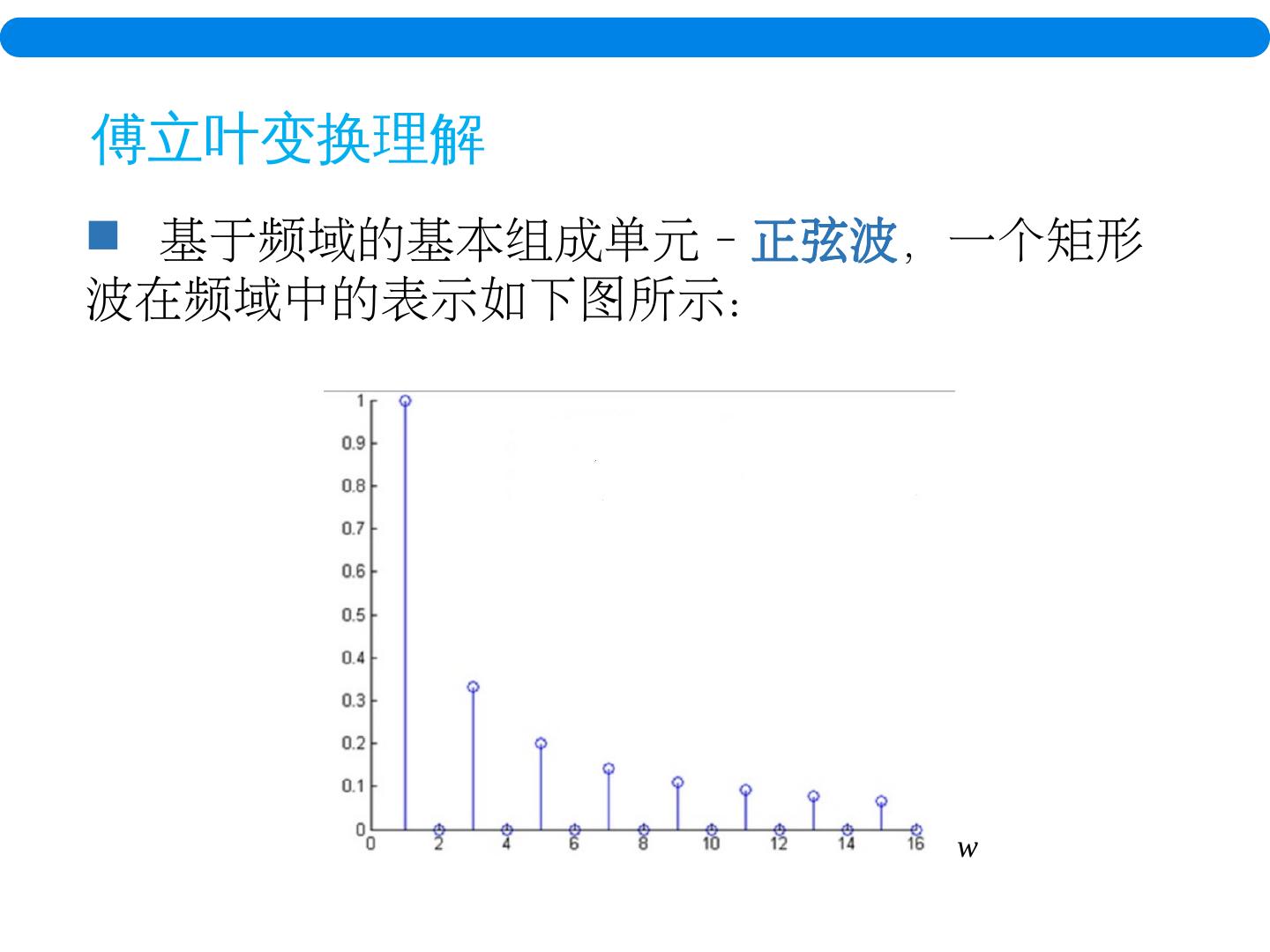
20 . 基于频域的基本组成单元 - 正弦波 ,一个矩形波在频域中的表示如下图所示: 傅立叶变换理解 w
21 . 傅立叶变换理解:全景理解图
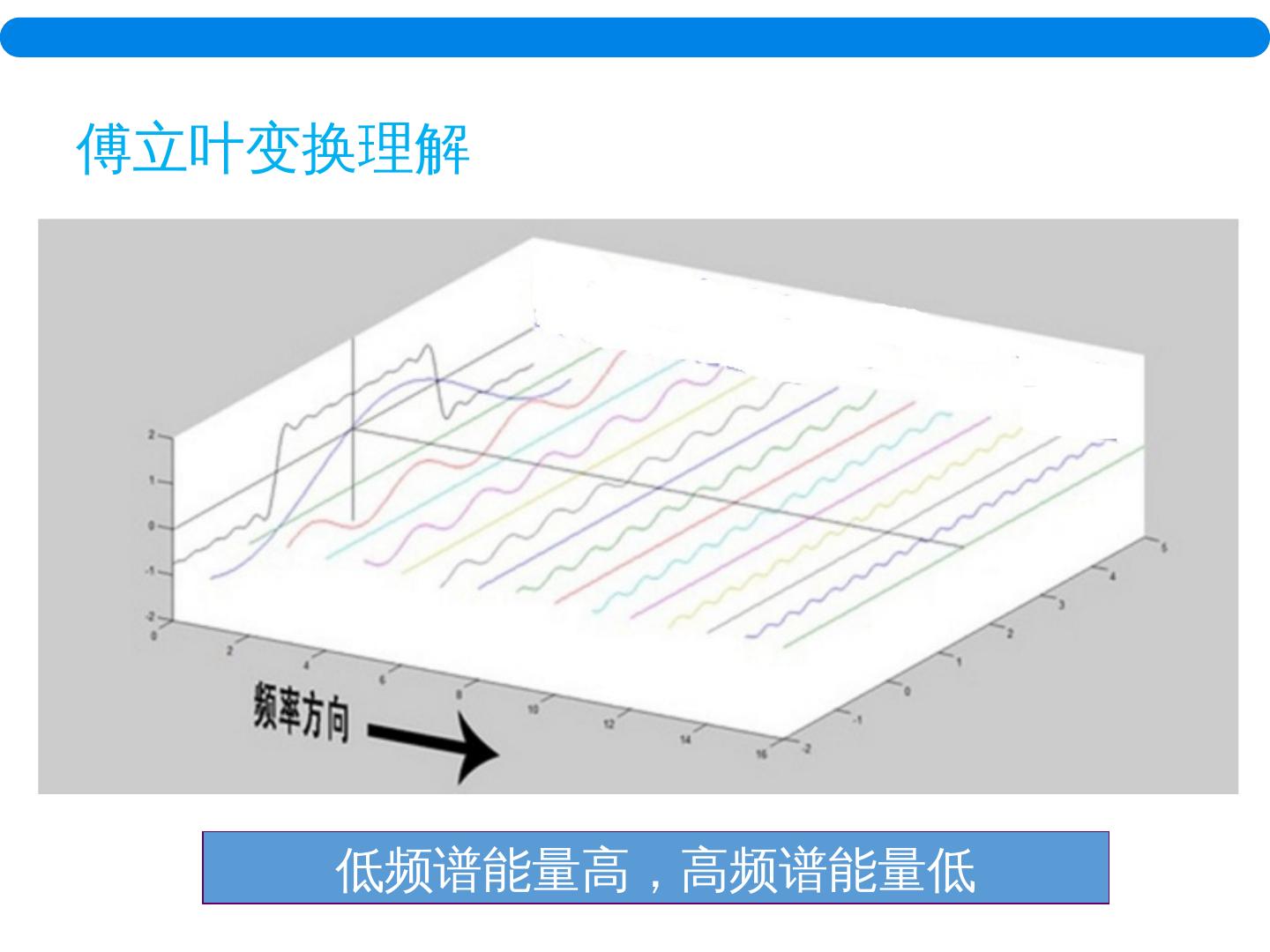
22 . 傅立叶变换理解 低频谱能量高,高频谱能量低
23 .傅立叶变换理解:欧拉公式 欧拉公式关键作用:将正弦波统一成了简单的指数形式 问题:正弦波形式复杂,周期函数,不易数学与计算机处理 解决方法:欧拉公式
24 .傅立叶变换理解:一维 FT 及其反变换 连续函数 f(x) 的傅立叶变换 F(u): 傅立叶变换 F(u) 的反变换: 将欧拉公式 带入可得离散傅立叶公式:
25 .傅立叶变换理解:一维 FT 及其反变换 F(u) 由 f(x) 与对应频率的正弦和余弦乘积和组成 u 值决定了变换的 频率成份 ,因此, F(u) 覆盖的域称为 频率域 ,其中每一项都被称为 FT 的 频率分量 频率域及频率分量与 f(x) 的 时间域 和 时间成分 相对应
26 .傅立叶变换理解:作用 傅立叶变换将信号分成不同频率成份。类似光学中的分色棱镜把白光按波长 ( 频率 ) 分成不同颜色,称 数学棱镜 信号变化的快慢与频率域的频率有关。噪声、边缘、跳跃部分代表图像的 高频分量 ;背景区域和慢变部分代表图像的 低频分量 。 因此,去噪滤波器应该是低通滤波器
27 .傅立叶变换理解:作用 傅立叶变换将信号分成不同频率成份。类似光学中的分色棱镜把白光按波长 ( 频率 ) 分成不同颜色,称 数学棱镜 信号变化的快慢与频率域的频率有关。噪声、边缘、跳跃部分代表图像的 高频分量 ;背景区域和慢变部分代表图像的 低频分量 。 因此,去噪滤波器应该是低通滤波器
28 .傅立叶变换理解:作用 傅立叶变换将信号分成不同频率成份。类似光学中的分色棱镜把白光按波长 ( 频率 ) 分成不同颜色,称 数学棱镜 信号变化的快慢与频率域的频率有关。噪声、边缘、跳跃部分代表图像的 高频分量 ;背景区域和慢变部分代表图像的 低频分量 。 因此,去噪滤波器应该是低通滤波器
29 .虚数的应用 红色的线段,它的长度是 1 。当它乘以 3 的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以 -1 的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了 180 度。 我们知道乘 -1 其实就是乘了两次 i 使线段旋转了 180 度,那么乘一次 i 被定义为旋转了 90 度。