展开查看详情
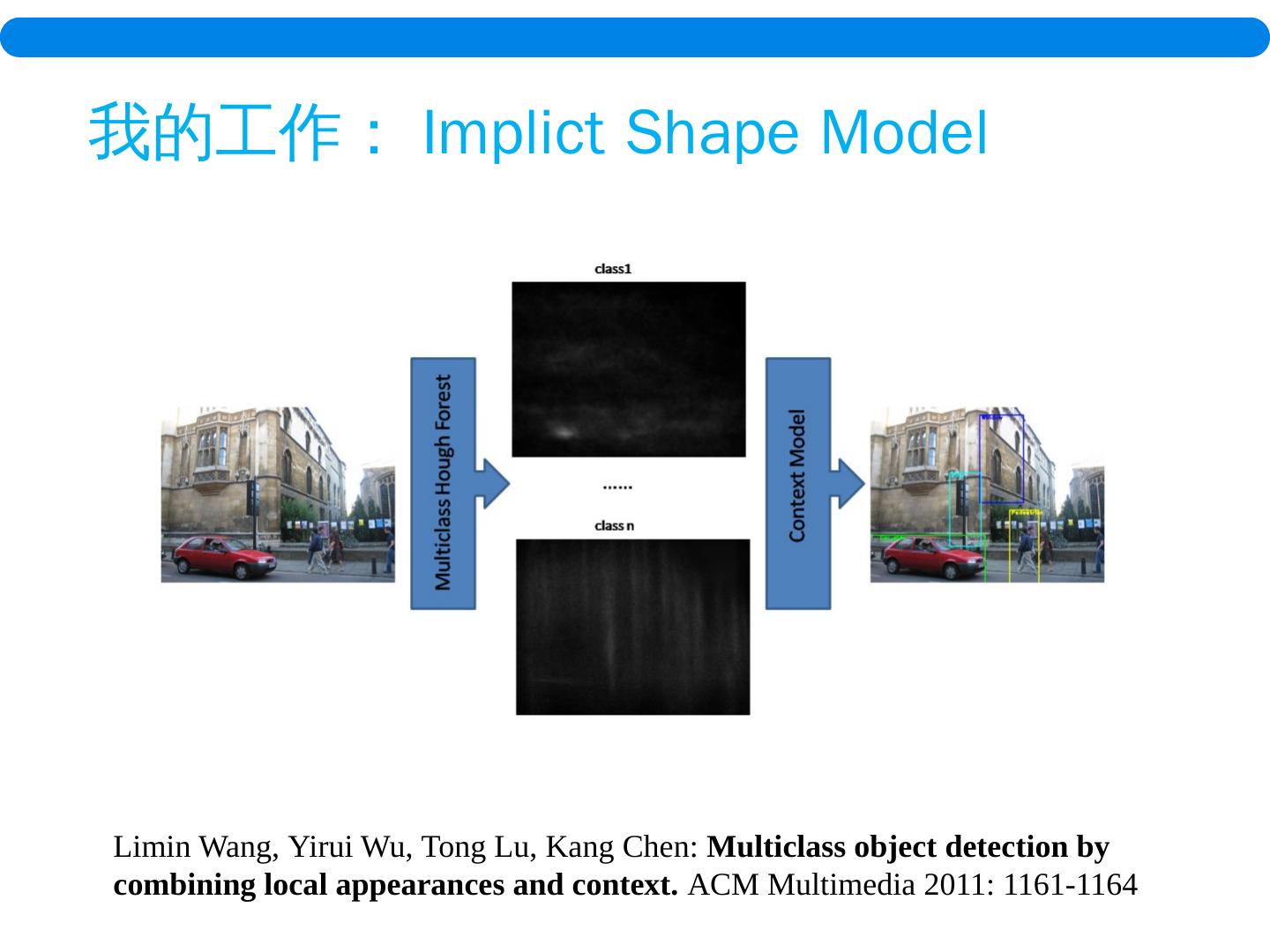
1 .成果展示 第九章 图像分割 巫义锐 河海大学 计算机与信息学院
2 . 典型试题 依据有无数据监督学习建模过程， Kmeans 聚类算法可分为哪一类机器学习算法？ A. 有监督学习 B. 无监督学习 C. 半监督学习 D. 以上三个均不是
3 . 典型试题 依据有无数据监督学习建模过程， Kmeans 聚类算法可分为哪一类机器学习算法？ A. 有监督学习 B. 无监督学习 C. 半监督学习 D. 以上三个均不是
4 . 本章提纲 图像分割定义 阈值法 边缘法 聚类法 区域法 边界法 图论法
5 .图像分割 (Image Segmentation ) 形式化定义： 已知一幅图像的像素集合 I 和一个 一致性谓词 ，求图像 I 表示成区域集合 R i 的一种划分： 一致性谓词和图像划分具有如下特性，即任何区域满足如下谓词： 任何两个相邻区域不能合并成单一区域，必满足谓词： 一致性谓词 定义了在区域 R i 上的所有点与区域模型的相似程度。
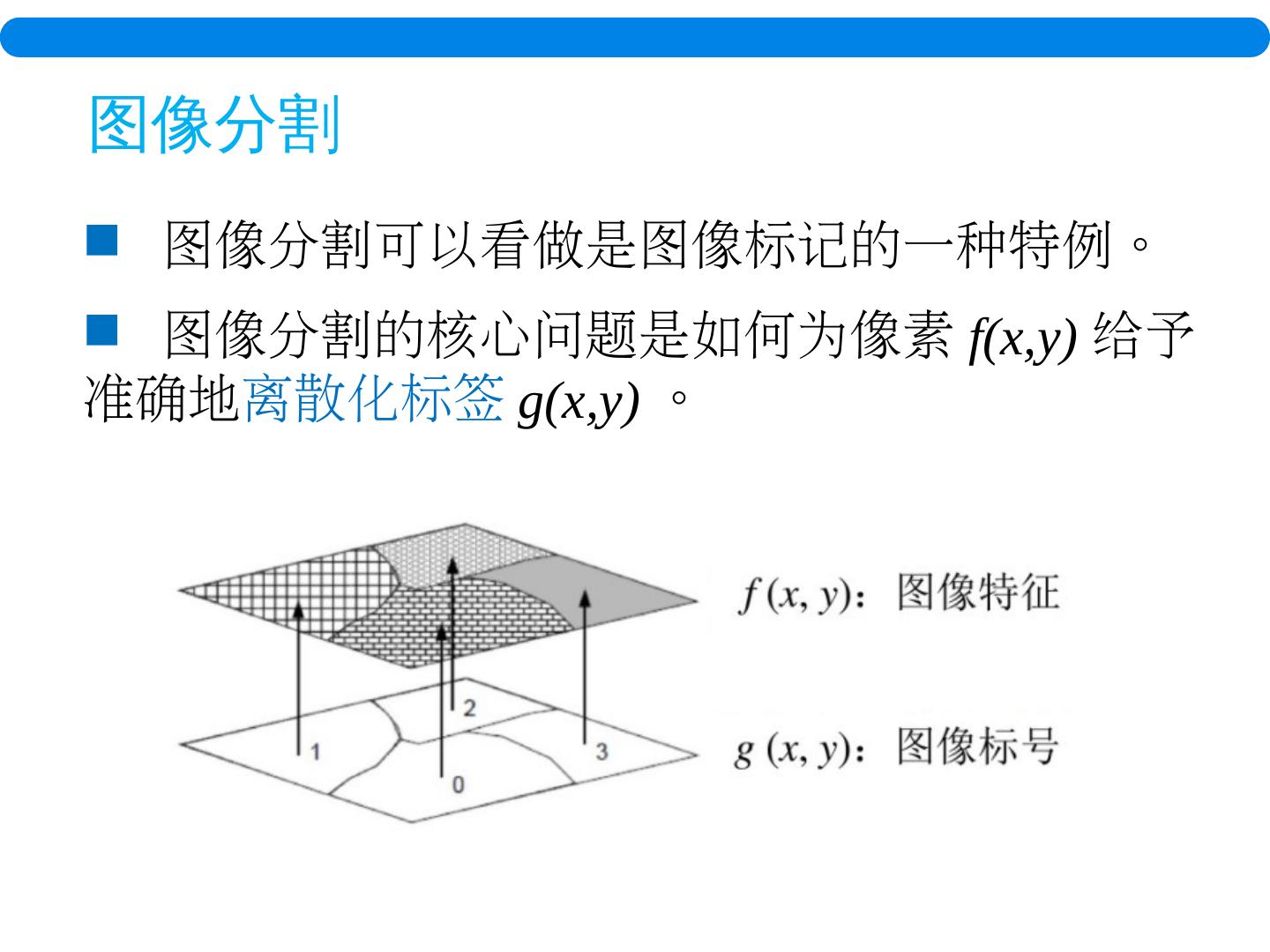
6 .图像 分割 图像分割可以看做是图像标记的一种特例。 图像分割的核心问题是如何为像素 f( x,y ) 给予准确地 离散化标签 g( x,y ) 。
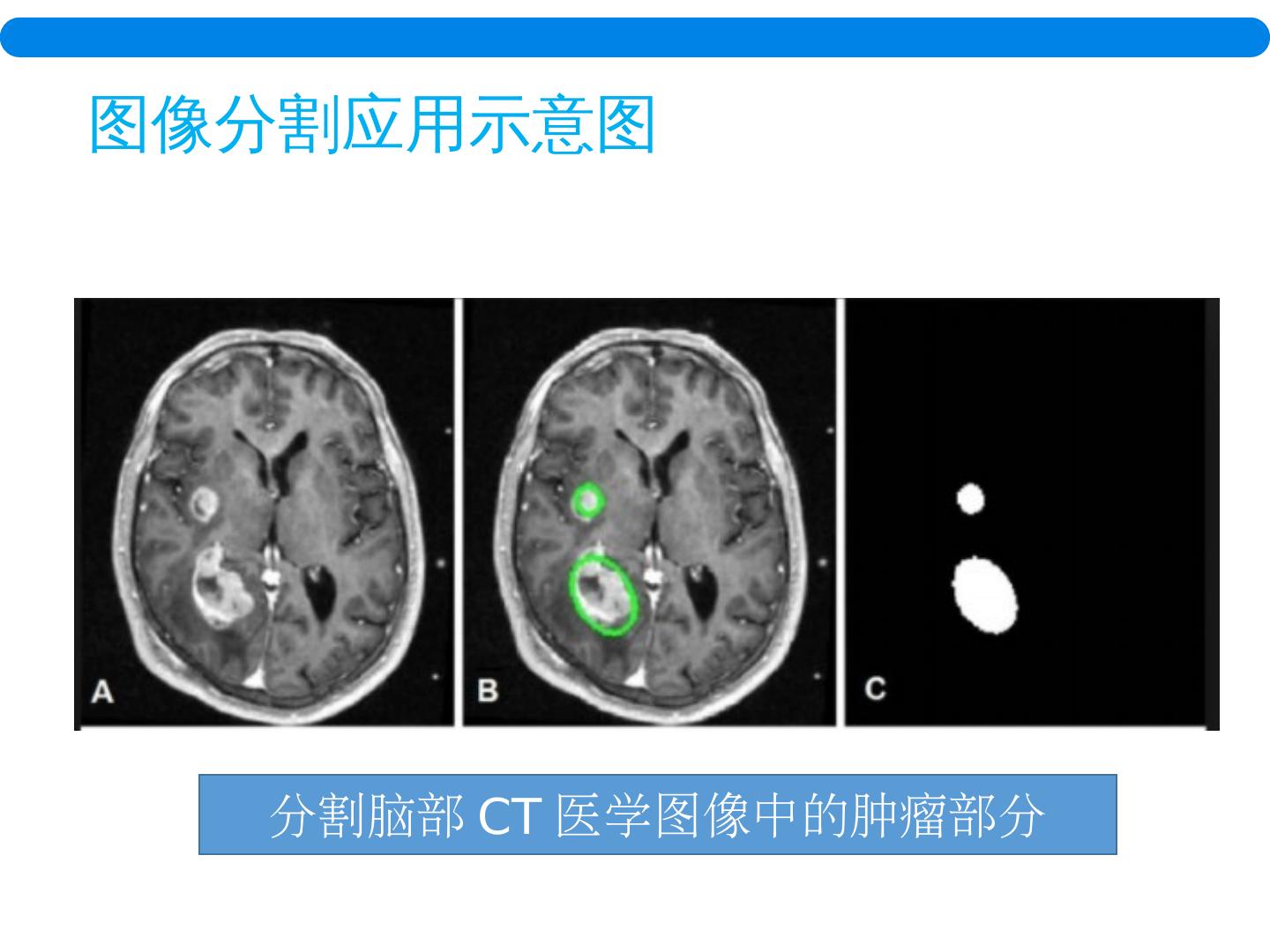
7 .图像 分割应用示意图 分割脑部 CT 医学图像中的肿瘤部分
9 . 本章提纲 图像分割定义 阈值法 边界法 聚类法 区域法 图论法
10 .阈值法的基本原理 阈值法的计算公式如下： 其中 f( i,j ) 为原始图像， g( i,j ) 为结果图像（二值）， Th 为阈值。
11 .类间类内最大方差比阈值法：算法关键步骤 选择 最佳阈值 Th=Th* ，使得下式成立： 类间离散度的数学定义： 类内方差定义： 分割需要使类内方差最小， 类间离散度最大：
12 . 本章提纲 图像分割定义 阈值法 聚类法 边界法 区域法 图论法
13 .聚类法 1 选择 K 个点作为初始质心 2 repeat 3 将每个点指派到最近的质心，形成 K 个簇 4 重新计算每个簇的质心 5 until 簇不发生变化 或 达到最大迭代次数
15 . 本章提纲 图像分割定义 阈值法 聚类法 边界法 区域法 图论法
16 .边界法原理 原理： 将待分割的区域看做由一个闭合边界包围的像 素集合，因此边界法实现分割的前提是边界的提取 关键技术： 边缘检测 霍夫变换 ……
17 .边界法：边缘检测 基于边缘检测的车牌区域分割 Sobel 边缘检测结果示意图
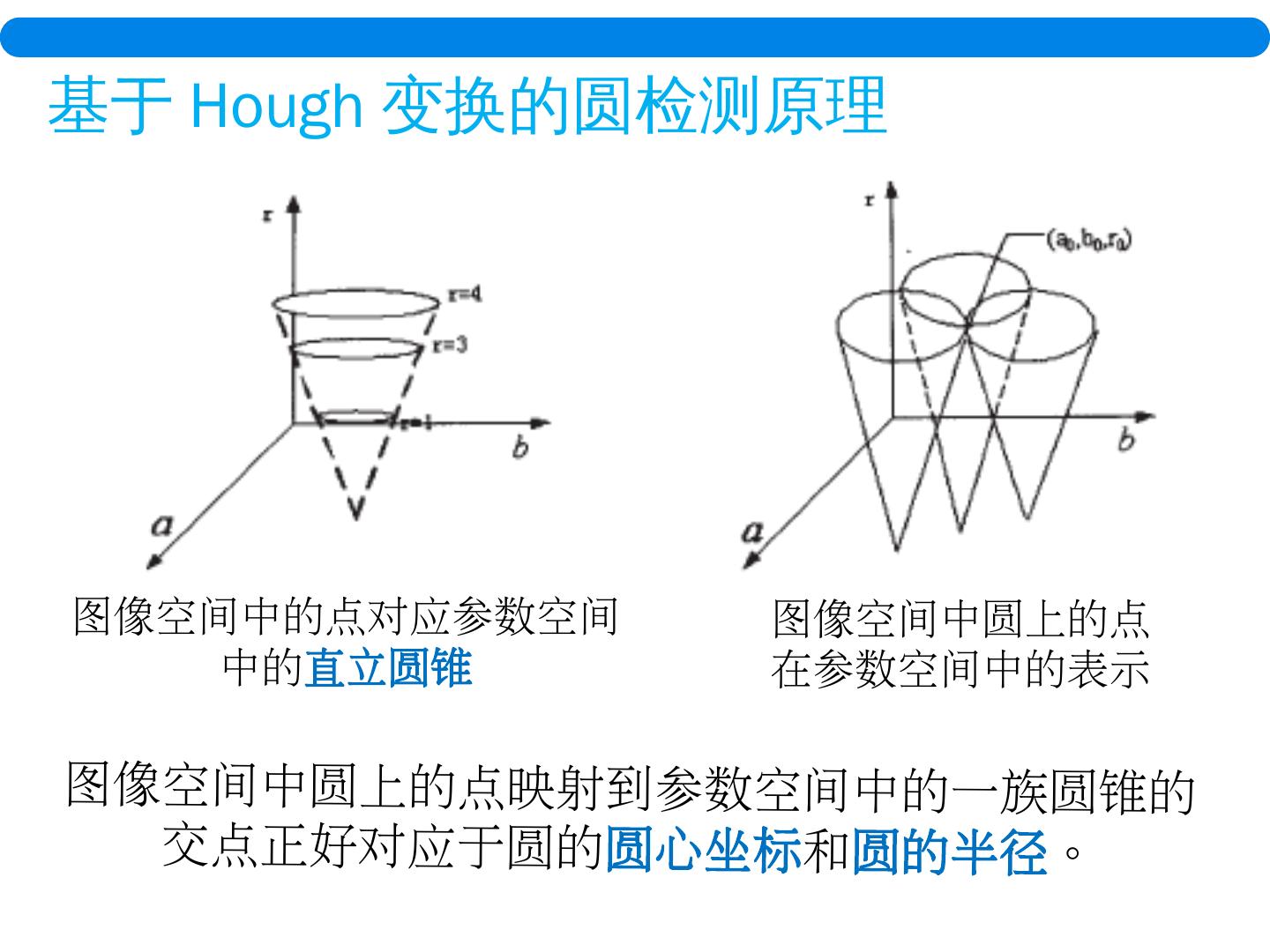
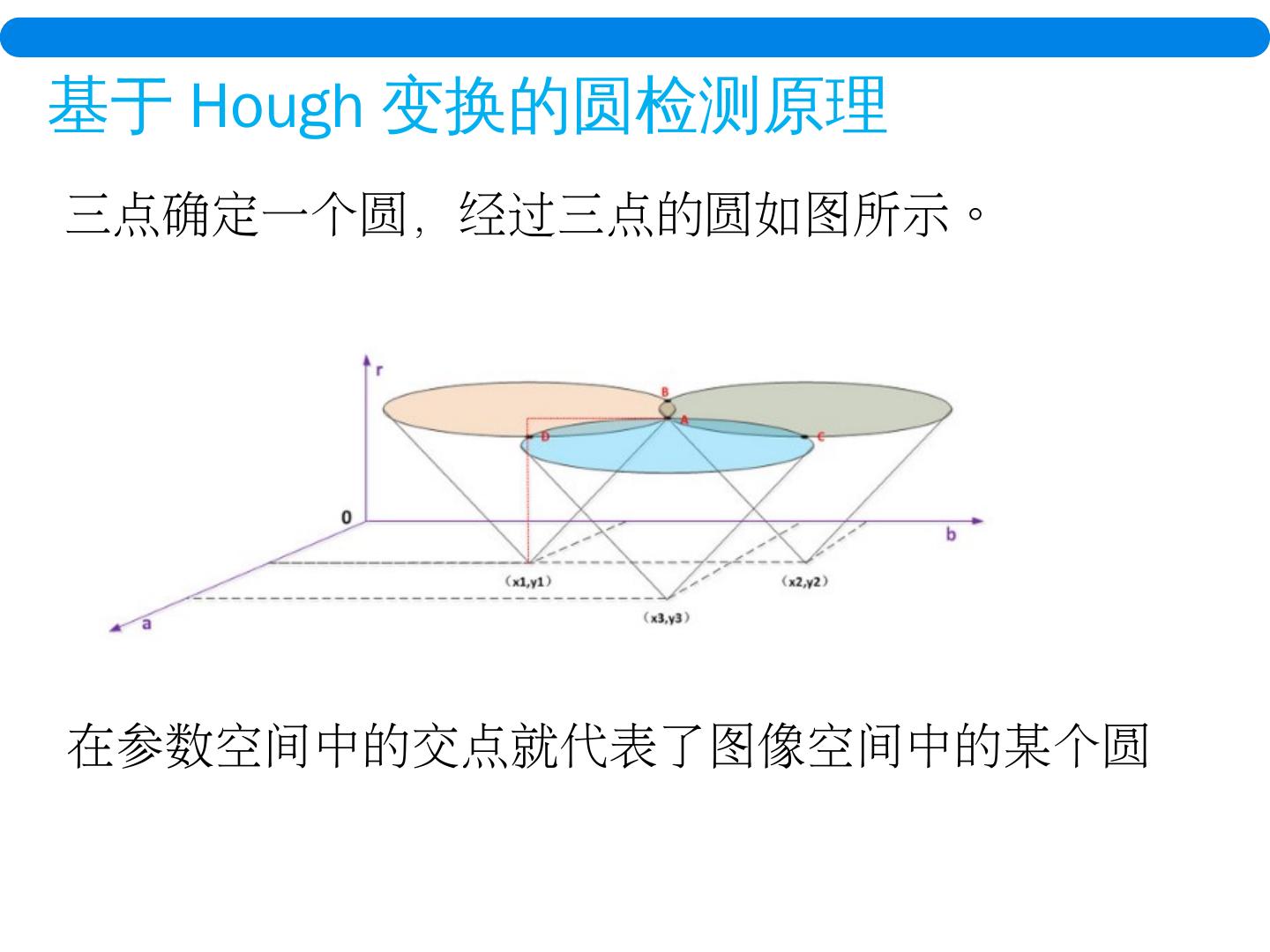
19 .基于 Hough 变换的分割方法 原理： 已知分割 目标 区域由直线 、曲线、圆等形状构成 。分割 问题转化 为对直线、曲线、圆的 检测问题。 Hough 变换： 将图像由图像空间变换为 参数空间
20 .Hough 变换 x y m b m 0 b 0 I mage space Hough space 图像空间中的 一条线 对应 Hough 空间中的 一个 点
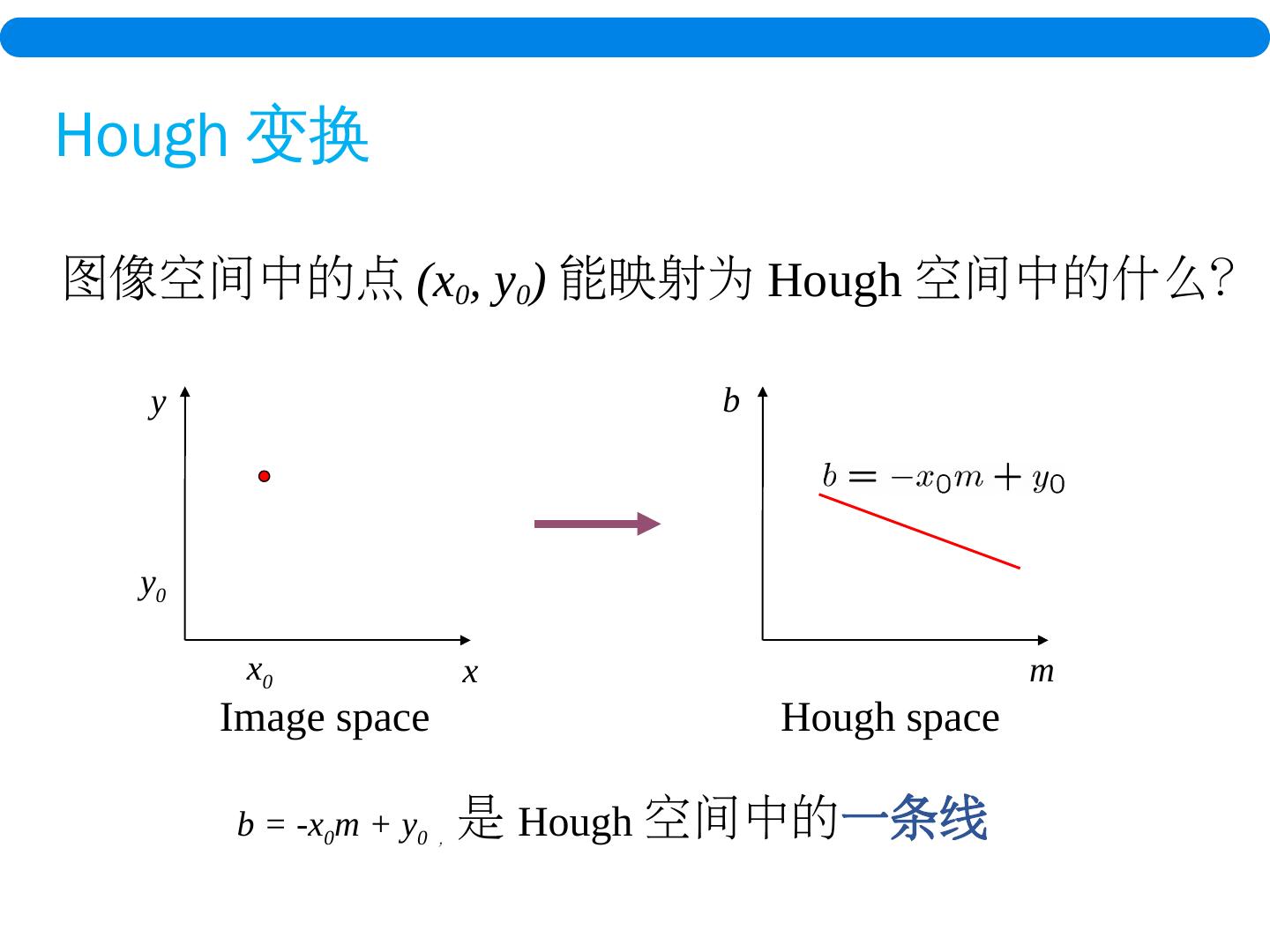
21 .x y m b I mage space Hough space b = -x 0 m + y 0 ， 是 Hough 空间中的 一条线 x 0 y 0 Hough 变换 图像空间中的点 (x 0 , y 0 ) 能映射为 Hough 空间中的什么？
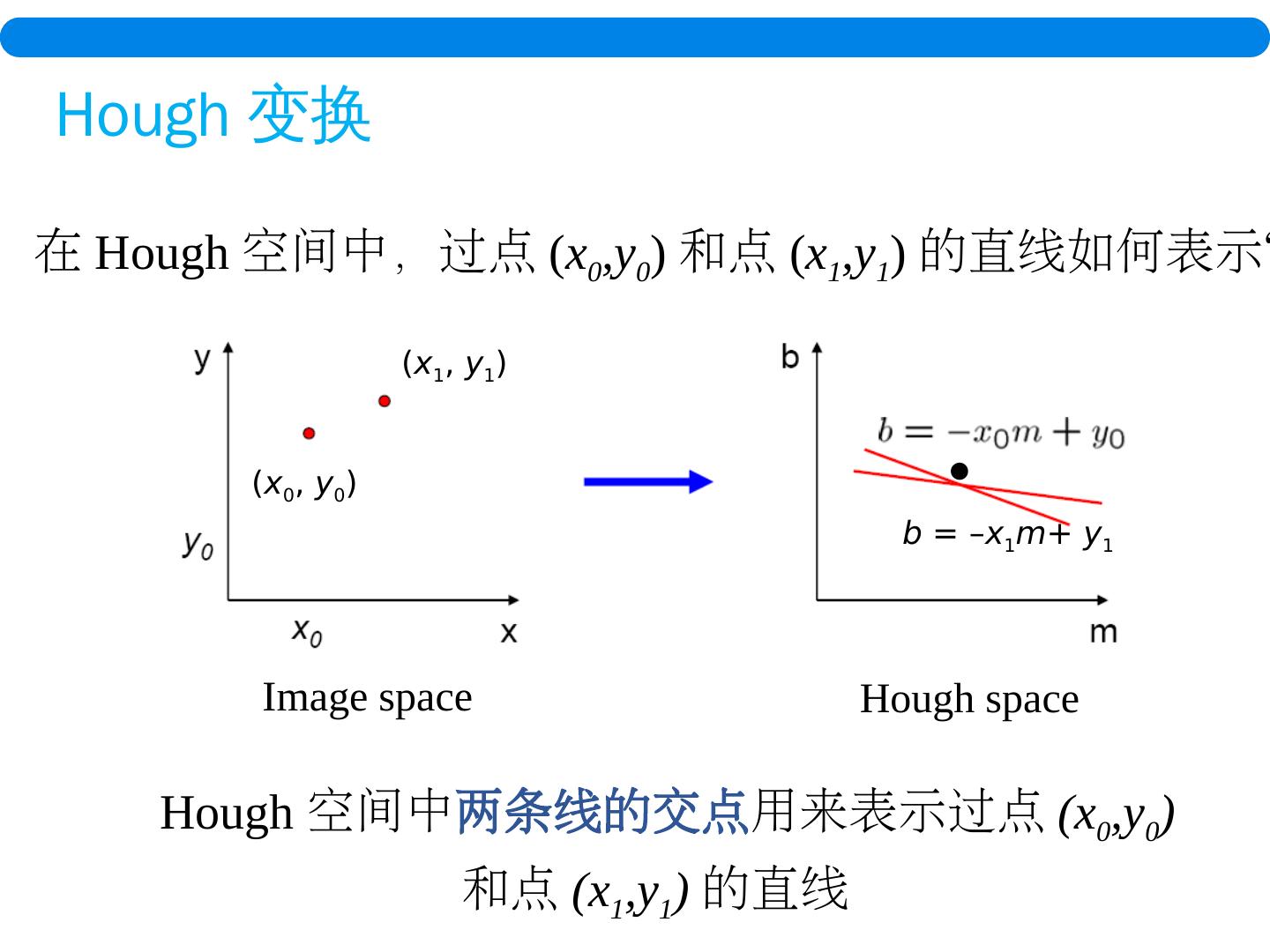
22 .I mage space Hough space b = – x 1 m + y 1 ( x 0 , y 0 ) ( x 1 , y 1 ) Hough 空间中 两条线的交点 用来表示过点 (x 0 ,y 0 ) 和点 (x 1 ,y 1 ) 的直线 Hough 变换 在 H ough 空间中，过点 ( x 0 ,y 0 ) 和点 ( x 1 ,y 1 ) 的直线如何表示？
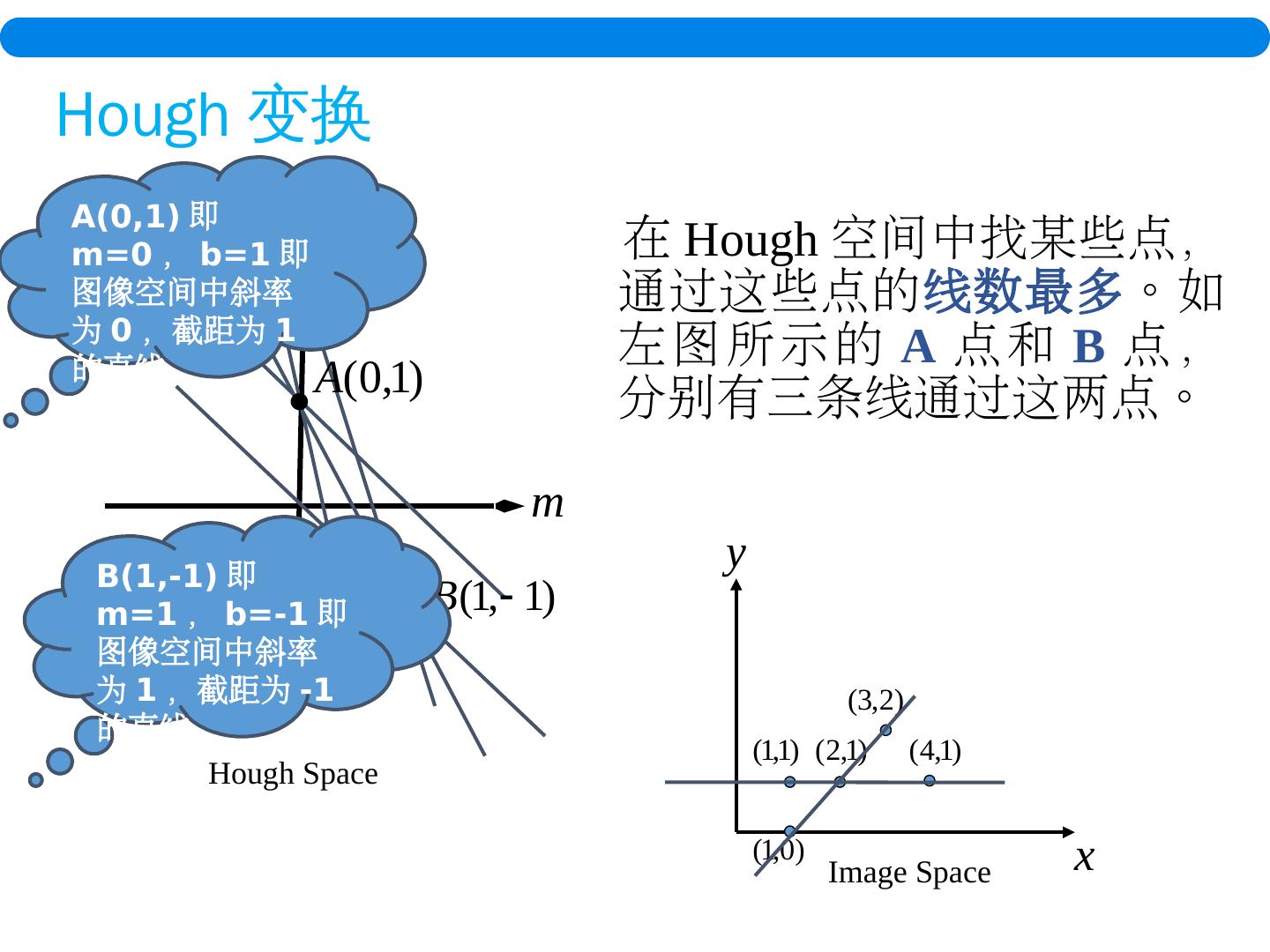
24 . 在 Hough 空间中找某些点 ，通过 这些点的 线数 最多 。如左 图所示的 A 点和 B 点，分别 有三 条线通过这两点。 Hough Space Image Space A(0,1) 即 m=0 ， b=1 即图像空间中斜率为 0 ，截距为 1 的直线 B(1,-1) 即 m=1 ， b=-1 即图像空间中斜率为 1 ，截距为 -1 的直线 Hough 变换
25 . 问题 ： Hough 变换的 这 种 实现 方式（ y=mx+b ) 不能表示 垂直线 ，因为 垂直线 的斜率为无穷大。 能否用别的直线的参数化方式呢？ Hough 变换
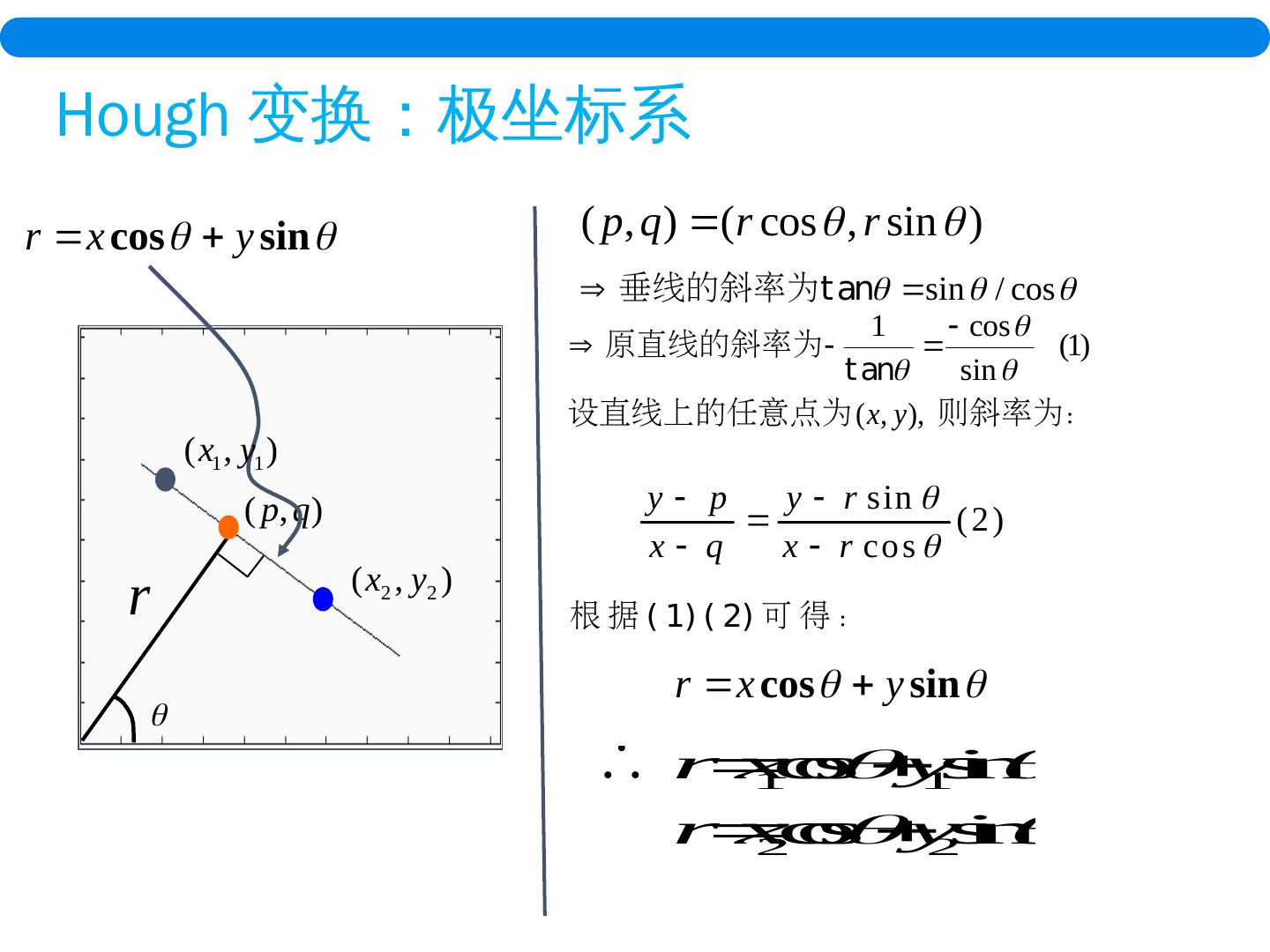
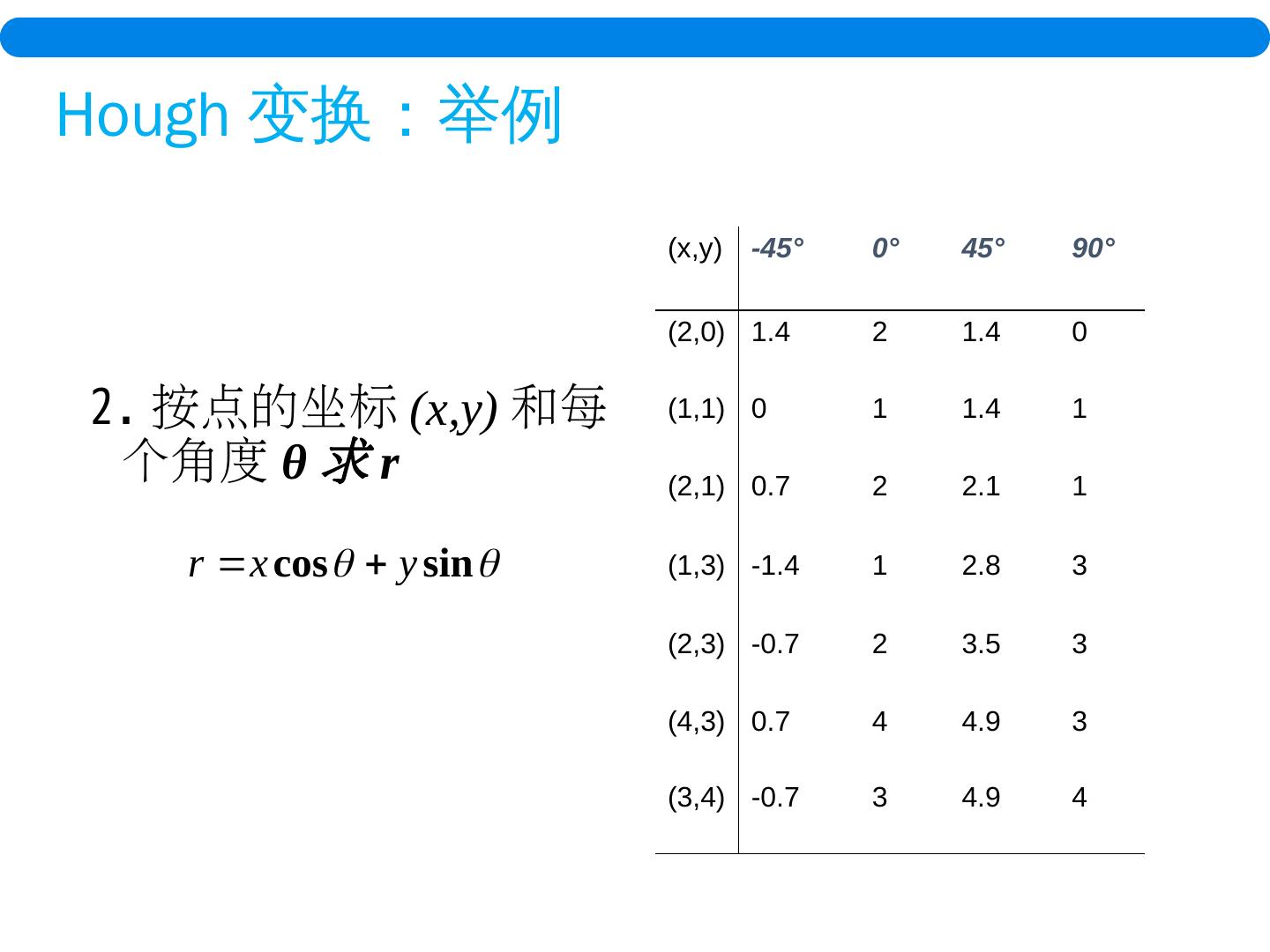
26 .设直线上的任意点为 则斜率为： Hough 变换 ：极坐标系
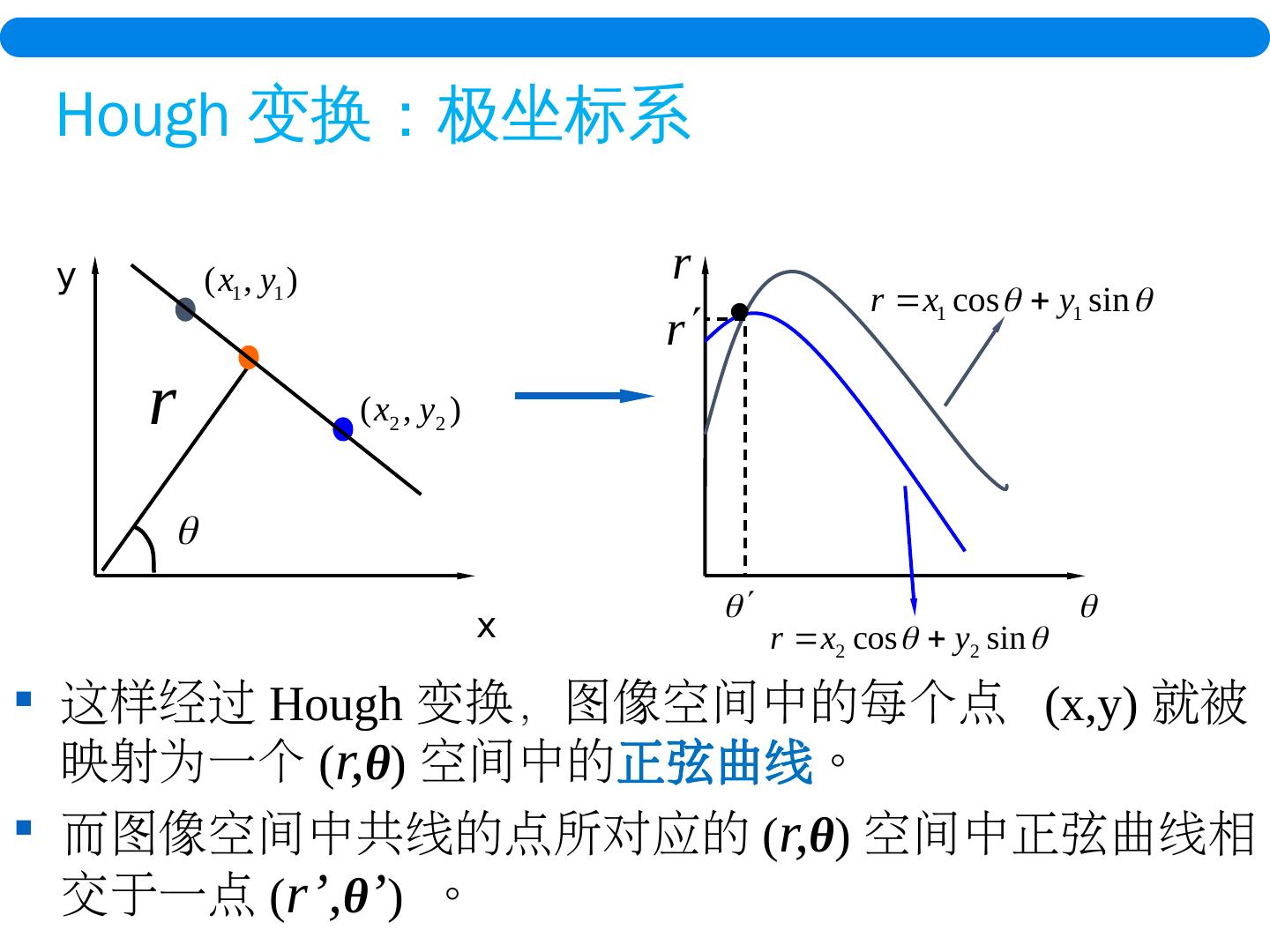
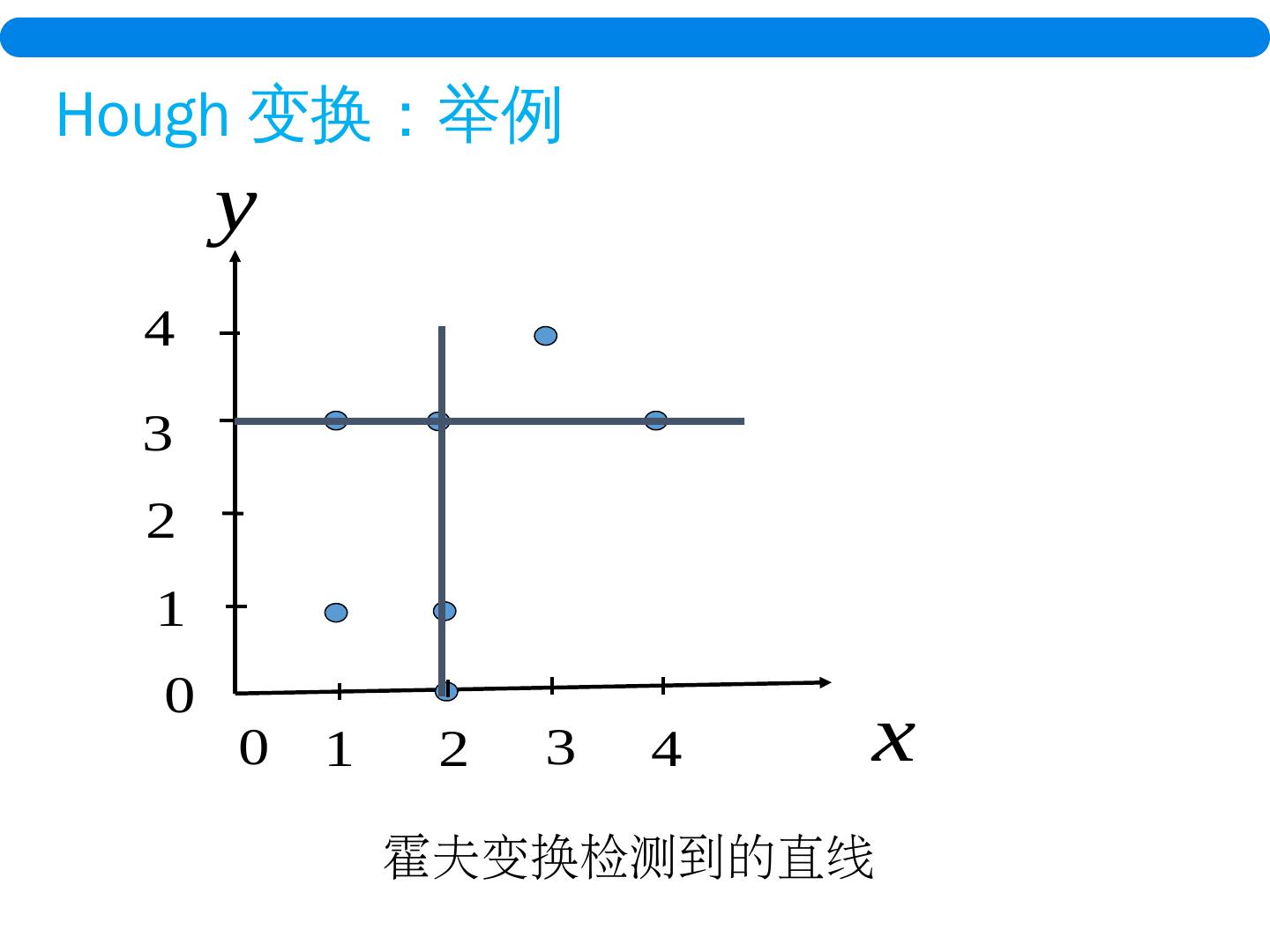
28 .x y 这样经过 Hough 变换，图像空间中的每个点 (x,y) 就被映射为一个 ( r, θ ) 空间中的 正弦曲线 。 而图像空间中共线的点所对应的 ( r, θ ) 空间中正弦曲线相交于一点 ( r ’ , θ ’ ) 。 Hough 变换 ：极坐标系
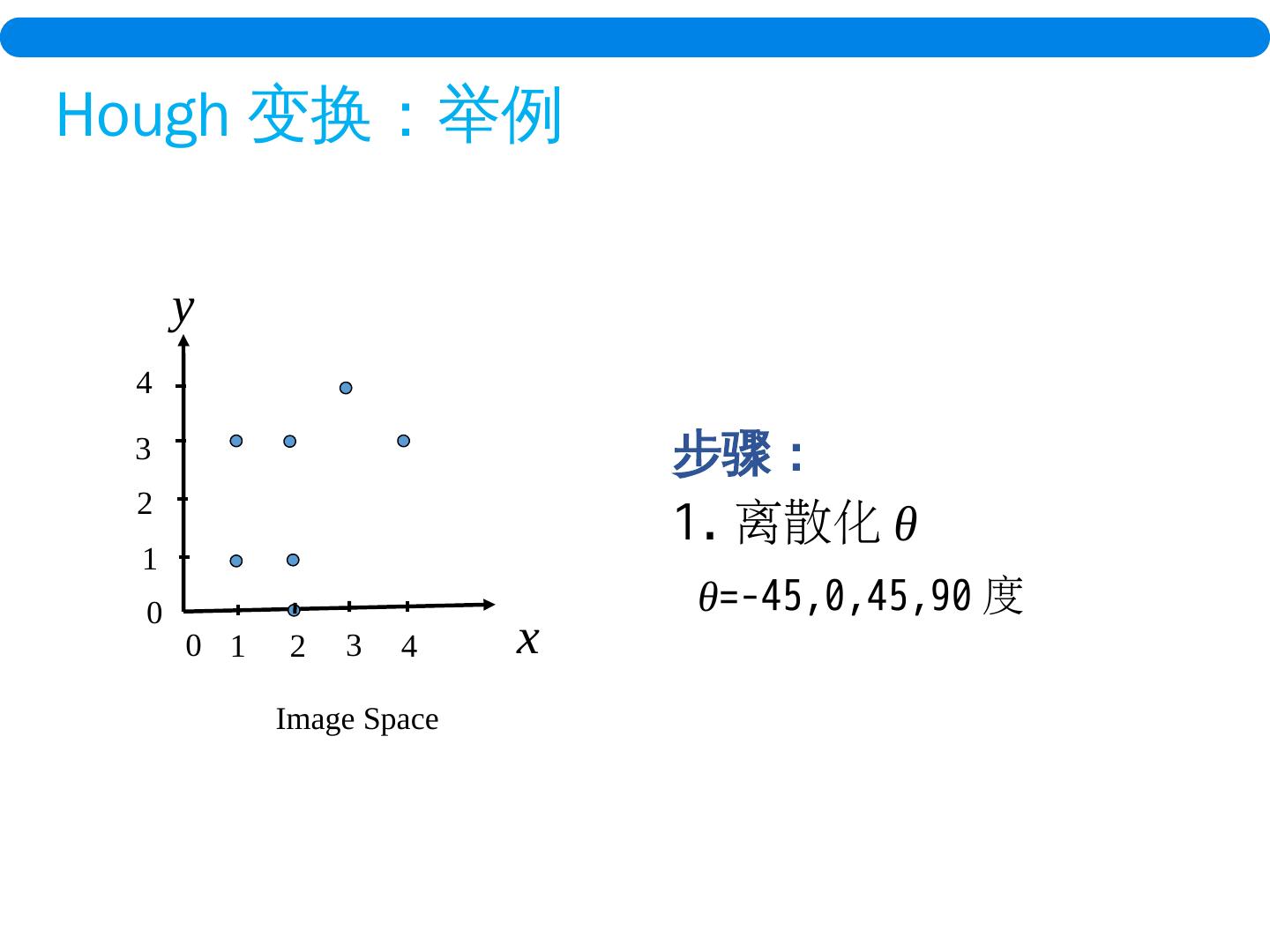
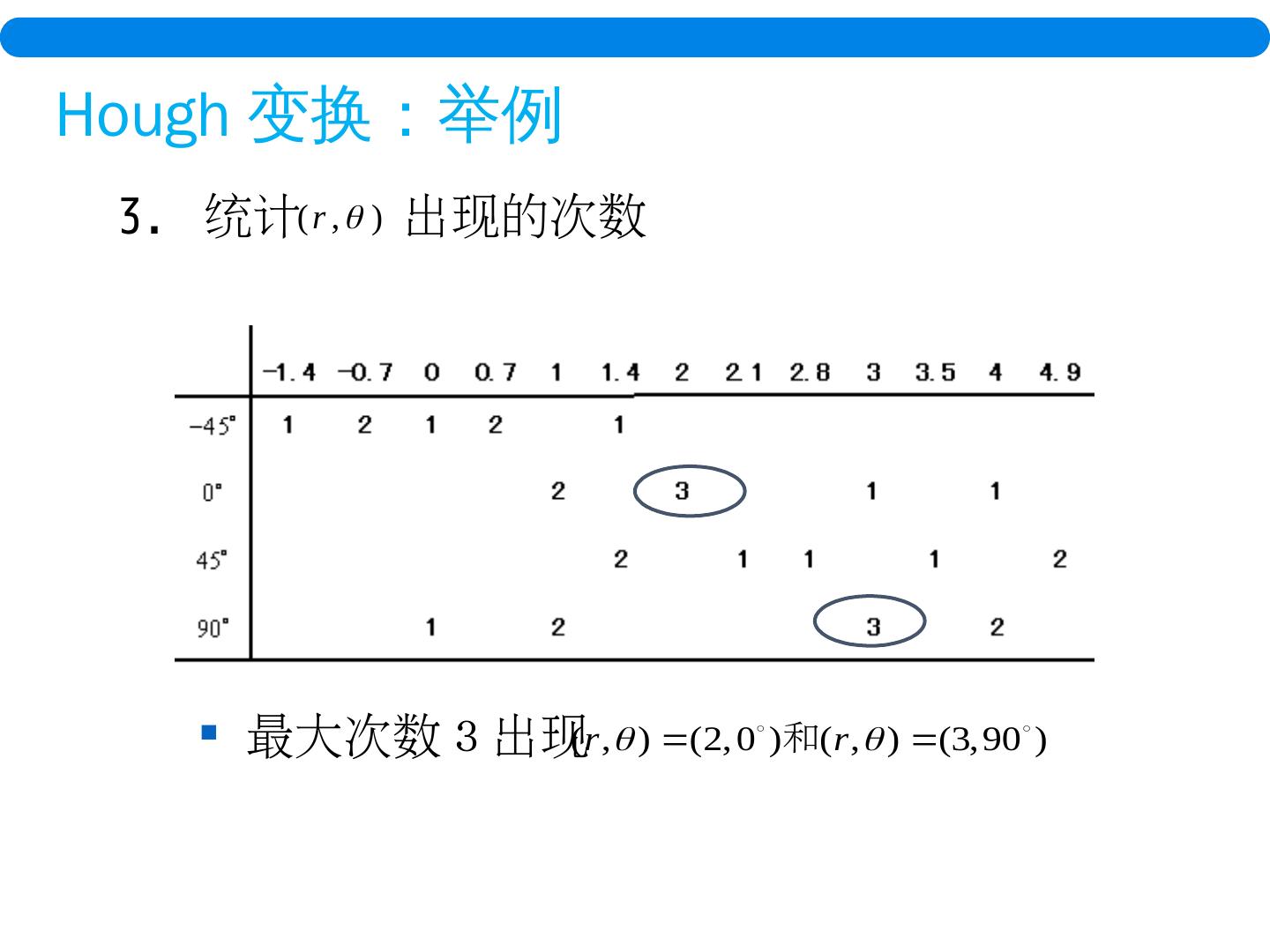
29 . 把 在图像空间中检测直线的问题转化为在极坐标参数空间中找通过点 ( r, θ ) 的 最多正弦曲线数 的问题。 如何检测参数空间中这样的点？ Hough 变换 ：极坐标系
热门城市
