展开查看详情
1 .成果展示 第六章 边缘检测 巫义锐 河海大学 计算机与信息学院
2 . 典型试题 下列属于二阶微分锐化算子的是？ A. Sobel 算子 B. Prewitt 算子 C. Laplacian 算子 D. 以上三个均是
3 . 典型试题 下列属于二阶微分锐化算子的是？ A. Sobel 算子 B. Prewitt 算子 C. Laplacian 算子 D. 以上三个均是
4 . 本章提纲 边缘检测概念 一阶 边缘检测算子 二阶边缘检测算子 Canny 算子
5 . 边缘( edge ) 是指图像 局部强度变化 最显著的部分； 边缘主要存在于目标与目标、目标与背景、区域与区域(包括不同色彩)之间； 边缘检测是图像分割、纹理特征和形状特征等图像分析的重要基础． 边缘检测定义
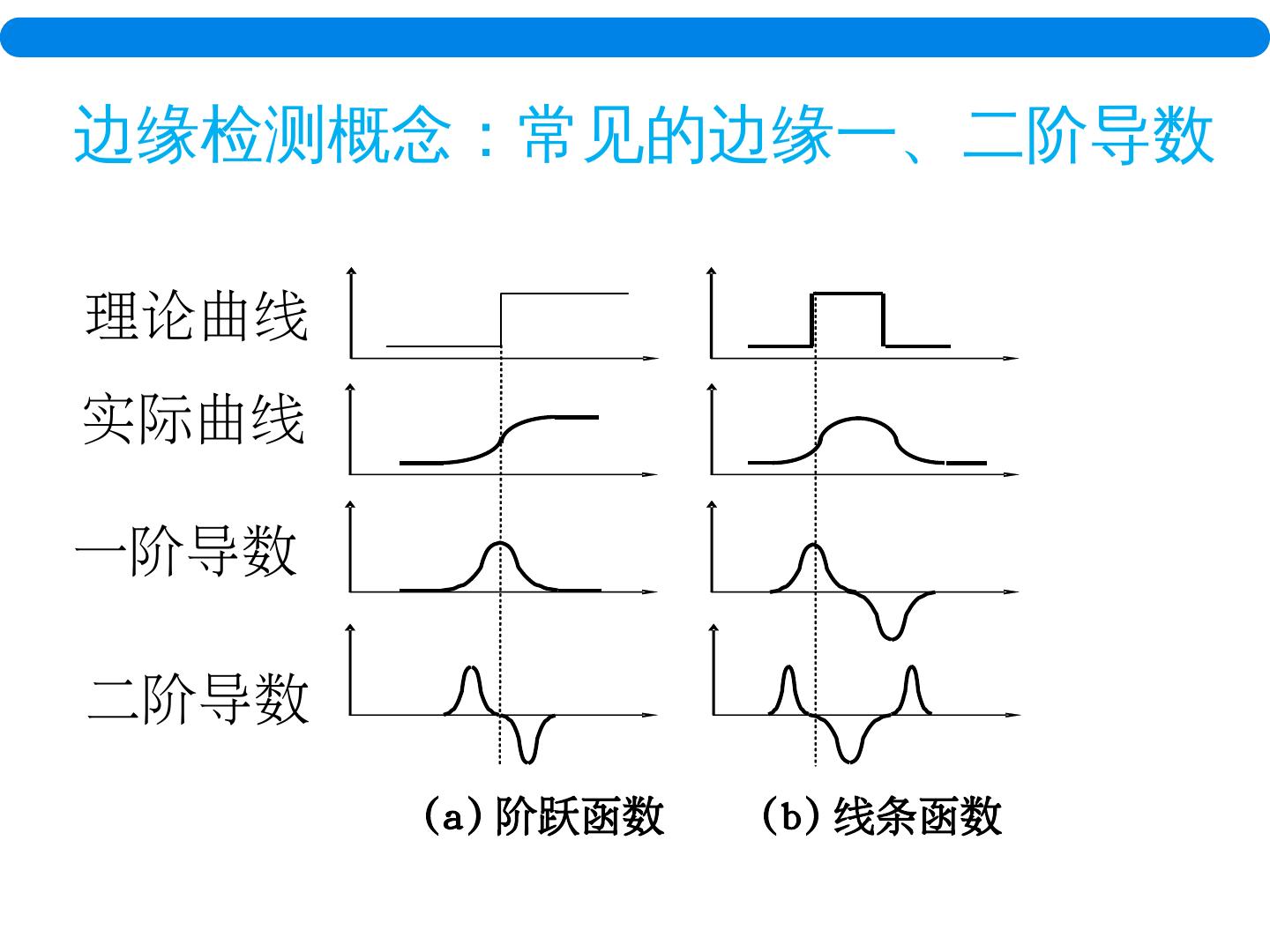
6 .局部强度变化（ 边缘 ）分类 ： 阶跃不连续，即图像强度在不连续处的像素灰度值有着 显著 的差异； 线条不连续，即图像强度突然从一个值变化到另一个值，保持一较小行程后又回到原来的值． 边缘检测概念 左图中那些部分属于阶跃不连续，哪些部分属于线条不连续？
7 . ( a) 阶跃函数 ( b) 线条函数 理论曲线 实际曲线 边缘检测概念：常见的边缘一、二阶导数 一阶导数 二阶导数
8 . 边缘检测器 ( Edge detector) ： 从图像中抽取边缘集合的算法 ; 轮廓 ( Boundary ) ： 一条表示边缘列表 的拟合曲线 ; 边缘连接 ( Edge linking ) ： 从无序边缘表形成 有序边缘表 的过程 ; 边缘检测概念：术语
9 . 边缘检测概念：边缘检测与锐化的关系 锐化 加强 图像 边缘， 使得图像 看起来轮廓更加明显。 边缘检测 是检测图像中的 边缘（ 定位 ）， 可以用于分割等多项应用。 二者紧密相关，因此边缘检测的一 阶、二 阶 算法的基础是锐化的一、二阶算法。
10 .基本步骤： 滤波： 改善噪声影响；一般滤波器 ( 均值滤波器 ) 导致边缘的损失；增强边缘和降低噪声之间需要折衷． 增强 ( 锐化 ) ： 将邻域强度值有 显著变化 的点突显出来． 检测： 最简单的边缘检测判据是 梯度幅值阈值 ； 定位： 估计边缘的位置和方位。 边缘检测的概念：边缘检测算法 检测怎么用数学化的公式进行表达呢 ？
11 .边缘检测判据公式 边缘检测判据的计算公式如下： 其中 f( i,j ) 为原始图像， g( i,j ) 为结果图像（二值 ）， Th 为阈值。 阈值 的选取决定 了边缘检测效果 的 好坏
12 . 本章提纲 边缘检测定义 一阶 边缘检测算子 二阶边缘检测算子 Canny 算子
13 .Roberts 算子 用 卷积模板表示： 用数学公式表示 ：
14 .Sobel 算子 梯度 幅值: 用 卷积模板来 实现：
15 .Prewitt 算子 与 Sobel 算子的方程完全一样，但 c=1,
16 .一阶算子边缘算子提取 结果 (a) 原图 (b) Roberts 算子 阈值 =142 (c) Sobel 算子 阈值 =142 (d) Prewitt 算子 阈值 =142
17 .梯度定义 梯度 是一阶导数的二维等效式，定义为矢量 性质： 1. 向量 的方向就是函数增大时的最大变化率方向； 2. 梯度 的幅值和方向: G x 与 G y 怎么计算？
18 . 用 差分来近似梯度 ： 用简单卷积模板表示: （ j 对应于 x 轴方向， i 对应于 y 负轴 方向） 梯度计算
19 . 用 差分来近似梯度 ： 用简单卷积模板表示: （ j 对应于 x 轴方向， i 对应于 y 负轴 方向） 梯度计算
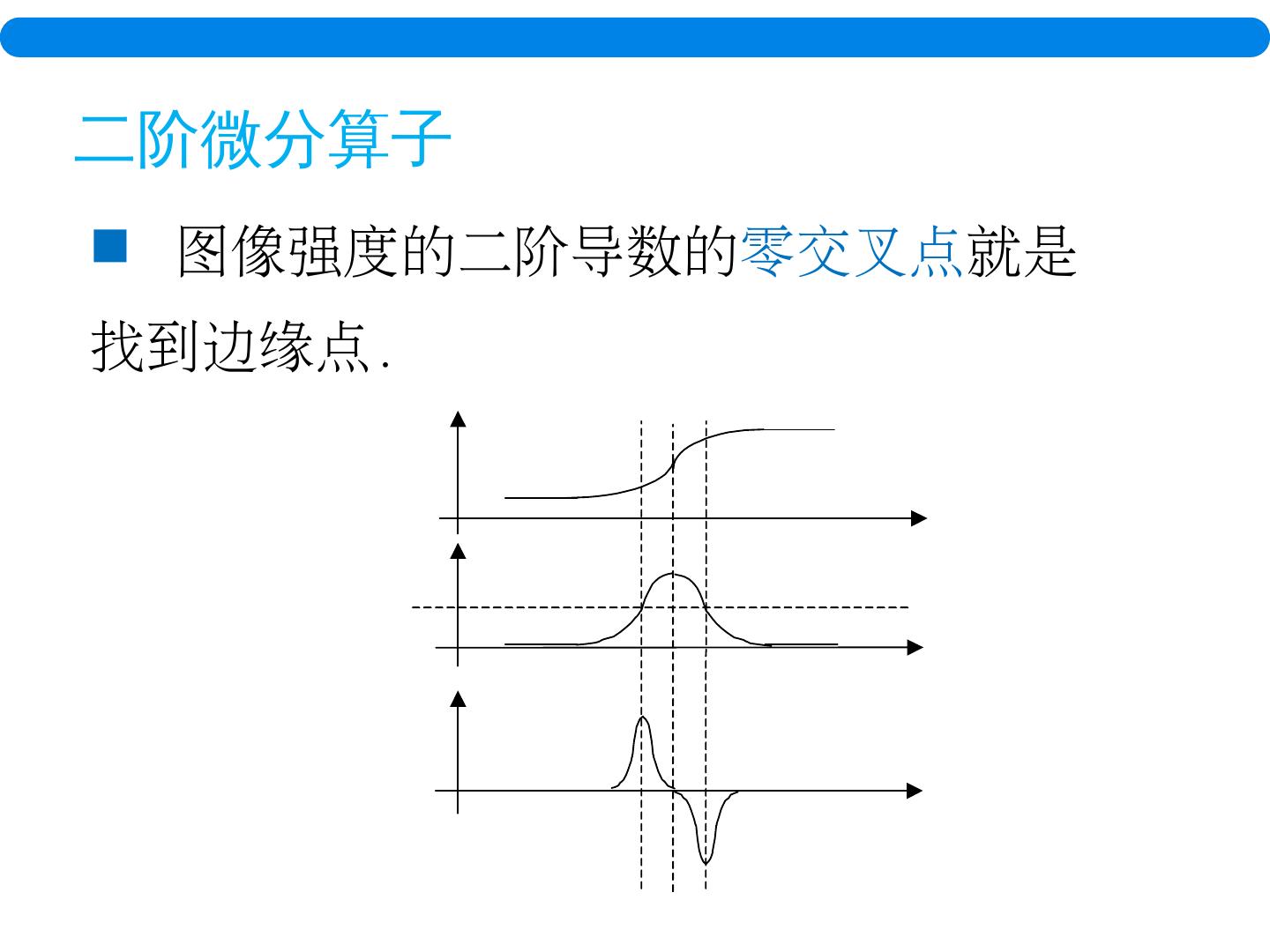
20 .二 阶微分算子 图像 强度的二阶导数的 零 交叉点 就是 找到 边缘点．
21 .拉普拉斯算子 拉普拉斯算子 是二阶导数的二维等效式 : 这一近似式是以点 [ i,j+1 ] 为中心的．用 j-1 替换: 对一阶导 结果 求偏导
22 . 用模板表示 ： 希望 邻域中心点具有更大的权值 拉普拉斯算子
23 .LoG 算法 基本 特征： 平滑滤波器是高斯滤波器． 增强步骤采用二阶导数(二维拉普拉斯函数 )． 边缘检测判据是二阶导数 零 交叉点 ． 将 高斯滤波和拉普拉斯边缘检测结合在一起，形成 LoG（Laplacian of Gaussian） 算法 ，称之为 拉普拉斯高斯算法 ．
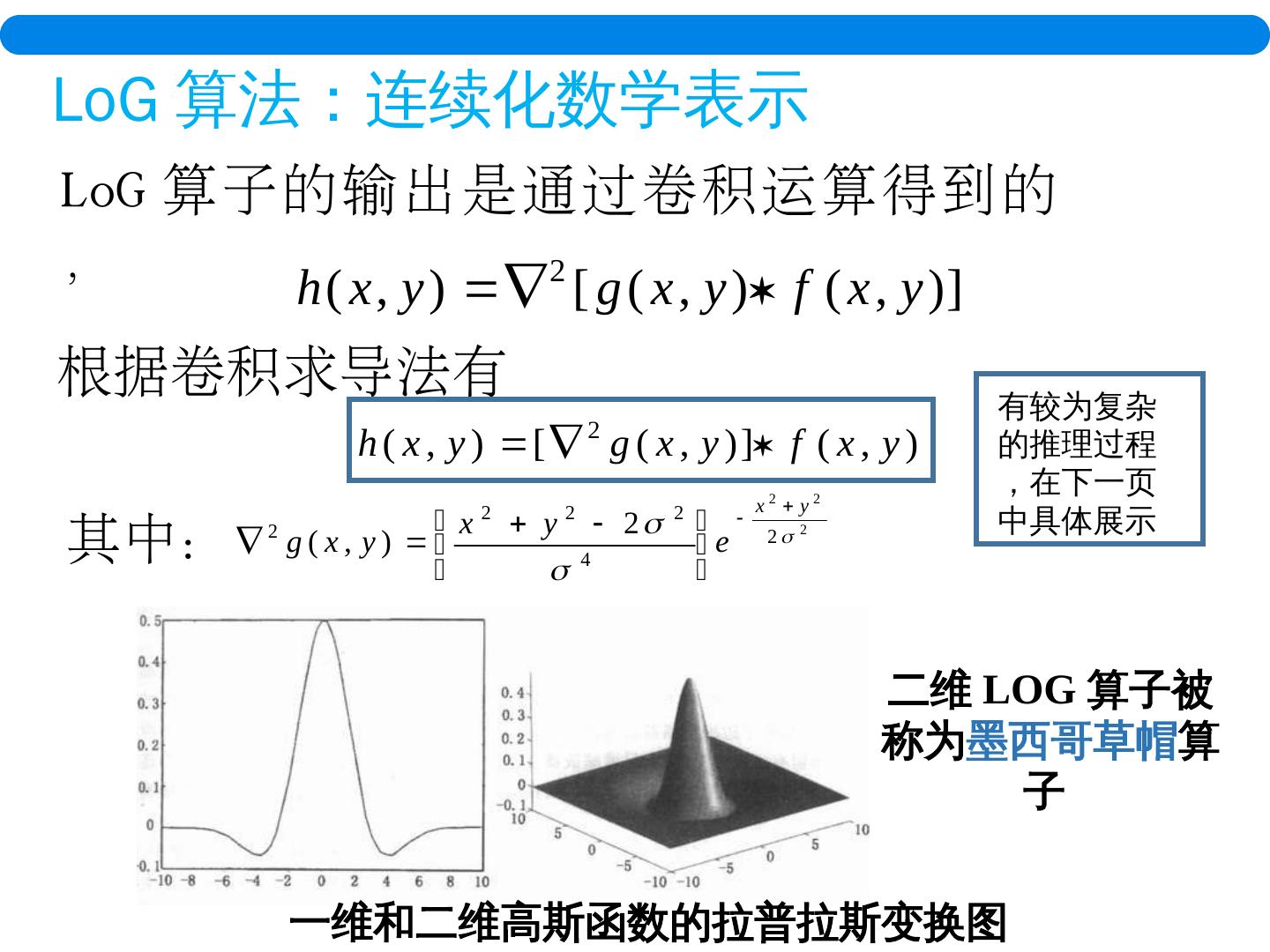
24 .LoG 算子的输出是通过卷积运算得到的， 根据卷积求导法有 其中： 二维 LOG 算子被称为 墨西哥 草帽 算子 一维和二维高斯函数的拉普拉斯变换 图 有较为复杂的推理过程，在下一页中具体展示 LoG 算法：连续化数学表示
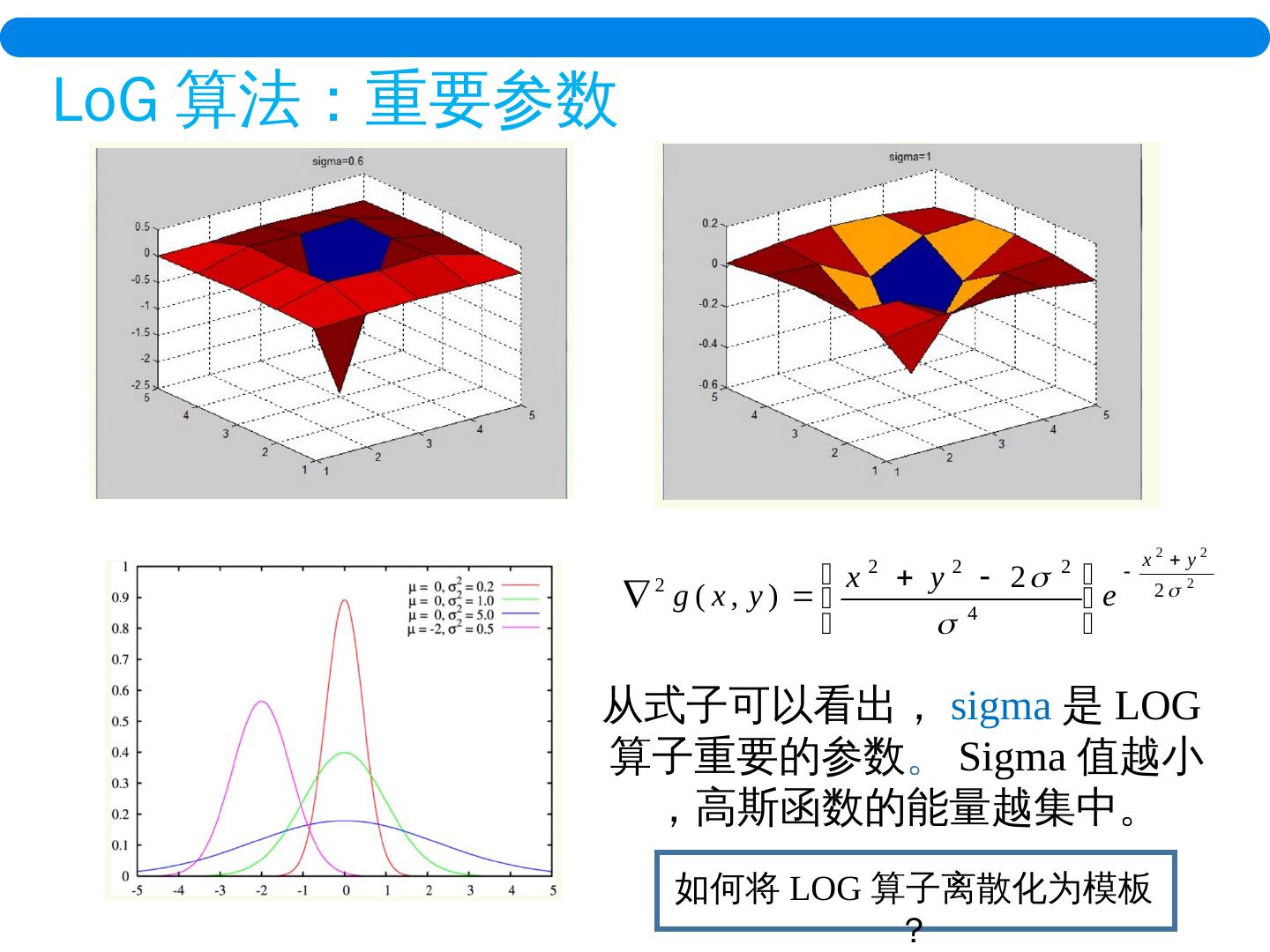
26 .从 式子 可以 看出， sigma 是 LOG 算子重要的参数 。 Sigma 值 越 小，高斯函数的能量越集中。 如何将 LOG 算子离散化为模板？ LoG 算法：重要参数
27 . 窗口 大小 根据 sigma 的值 确定 ( 提前定义的公式 ) ： 当 ，则 模板权值 ，根据 将 p=(0,0),(0,1) 等位置带入、 化 简 ， 可以得到 5 X5 拉普拉斯高斯模板 LoG 算法：离散化过程
28 . LoG 算法结果示意图 (a) 原图 ( b ) Roberts 算子 (c) Sobel 算子 (d) LOG 算子
热门城市
