- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
05 计算机视觉—图像锐化
展开查看详情
1 .成果展示 第六章 图像锐化 巫义锐 河海大学 计算机与信息学院
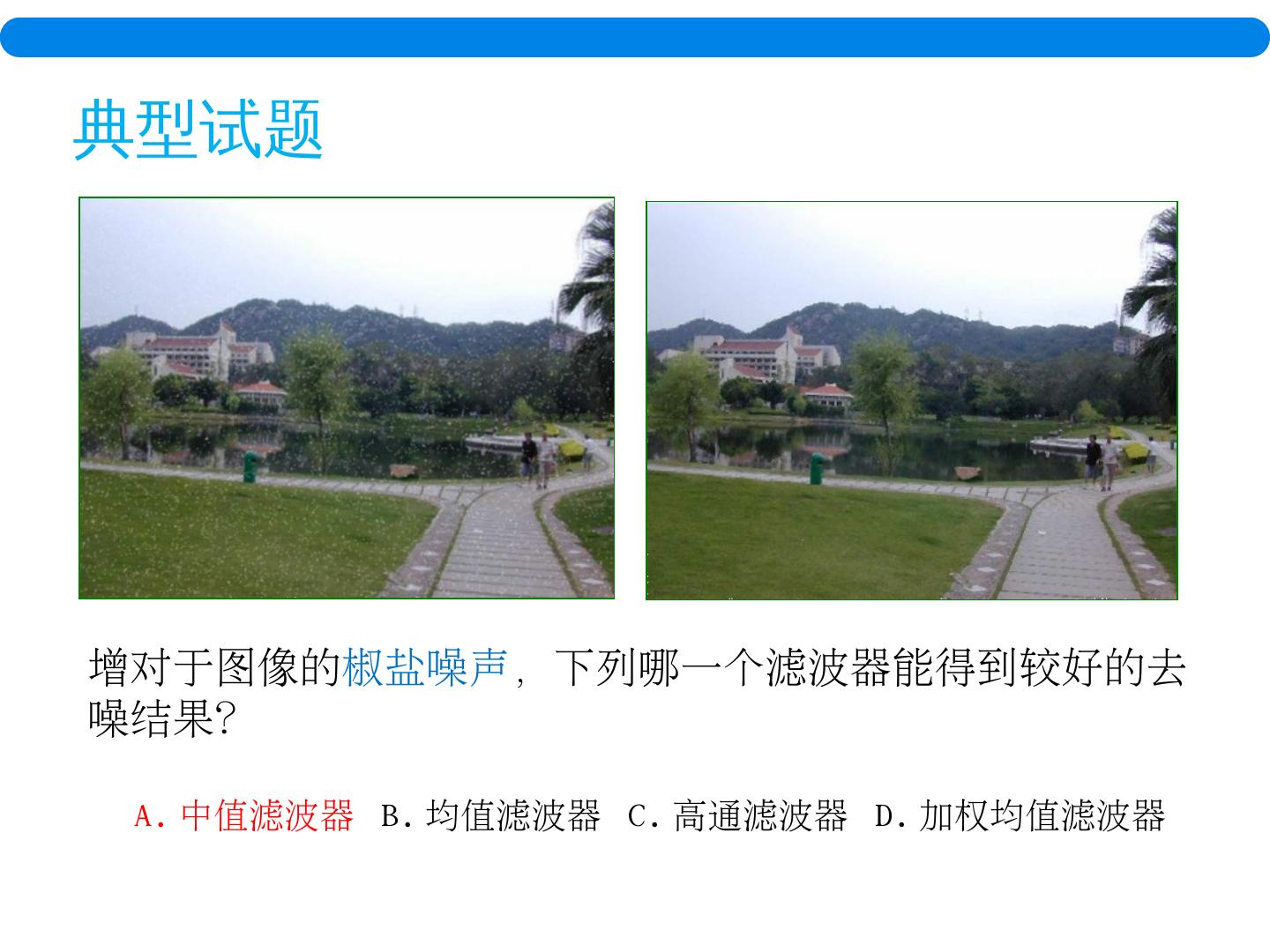
2 . 典型试题 增对于图像的 椒盐噪声 , 下列 哪一个滤波器能得到较好的去噪结果? A . 中值滤波器 B . 均值 滤波器 C . 高通滤波器 D . 加权均值滤波器
3 . 典型试题 增对于图像的 椒盐噪声 , 下列 哪一个滤波器能得到较好的去噪结果? A . 中值滤波器 B . 均值 滤波器 C . 高通滤波器 D . 加权均值滤波器
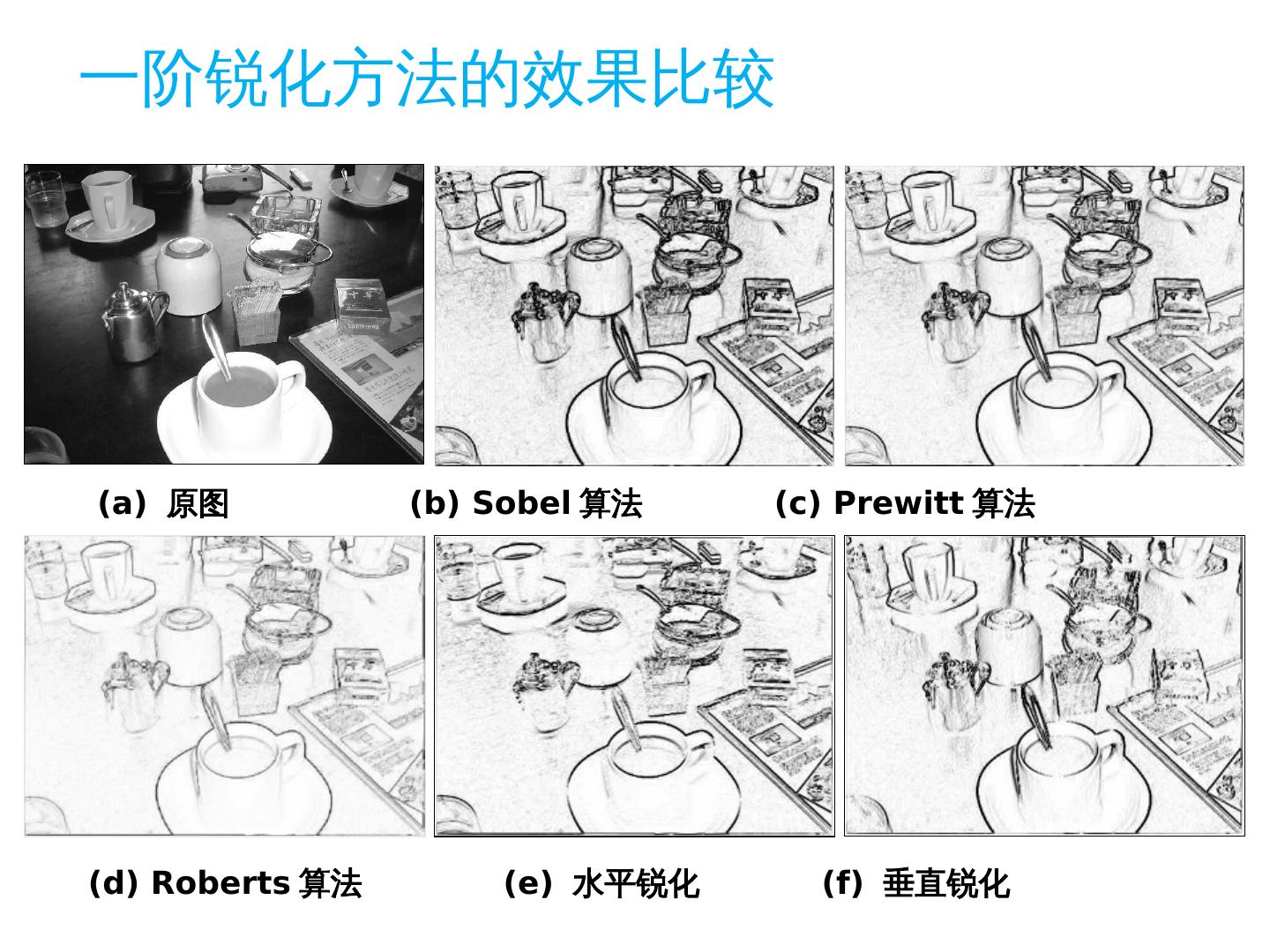
4 . 本章提纲 图像的景物细节特征 一阶微分锐化方法 二阶微分锐化方法 一阶、二阶微分锐化方法效果比较
5 . 目的:使灰度反差 增强 ,加强图像中景物的细节边缘和轮廓。 因为边缘和轮廓都位于 灰度突变 的地方,所以锐化算法的实现基于 微分 作用。 图像锐化的概念
6 .图像细节的灰度变化特性 扫描线 灰度渐变 孤立点 细线 灰度跃变 图像细节的灰度分布特性 平坦段
7 .图像细节的灰度变化微分特性 一阶微分曲线 灰度渐变 孤立点 细线 灰度跃变 图像细节的灰度分布特性 平坦段
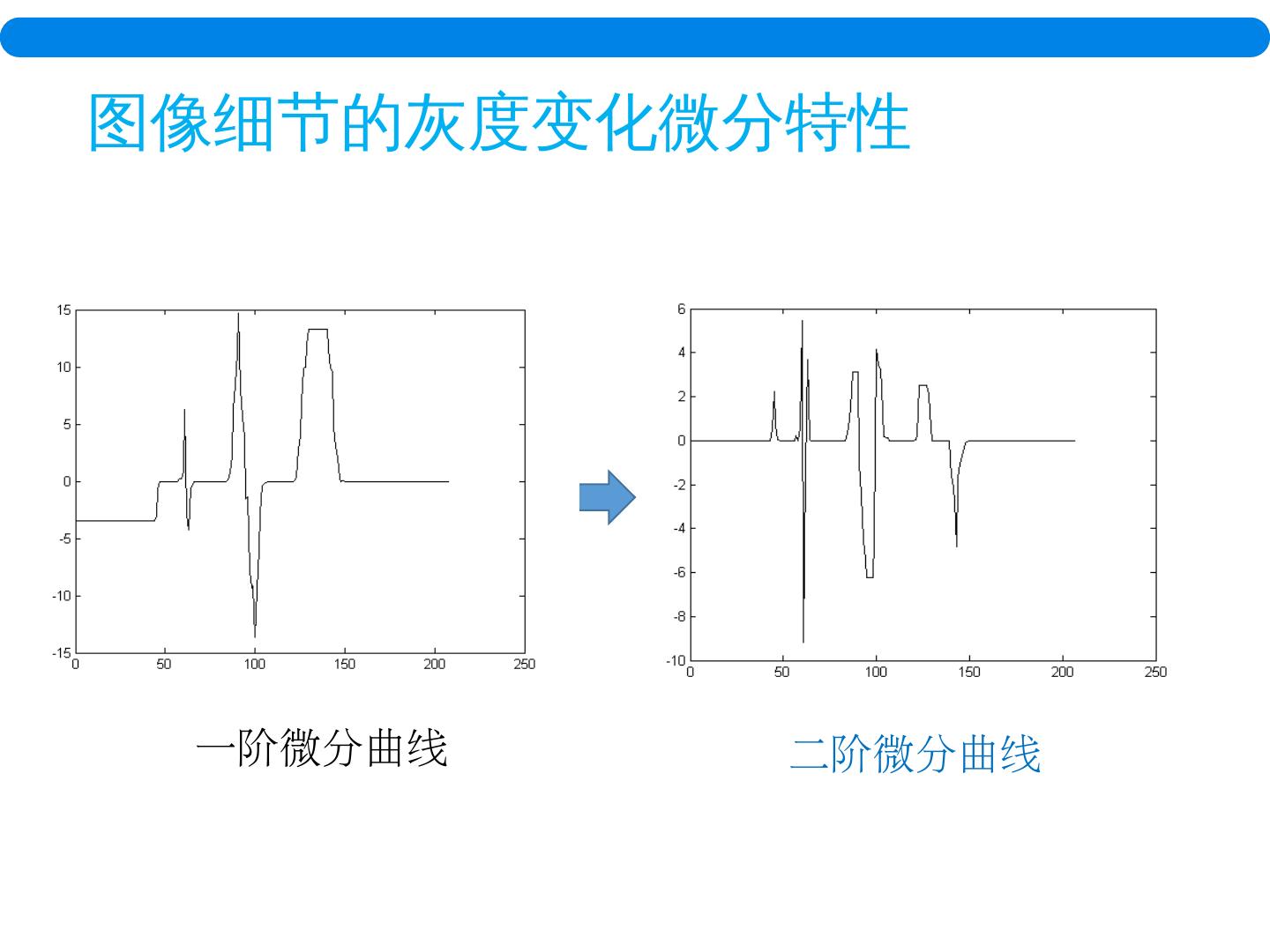
8 .图像细节的灰度变化微分特性 二阶微分曲线 一阶微分曲线
9 .图像细节的灰度变化微分特性 二阶微分曲线 一阶微分曲线
10 .一阶微分锐化:基本原理 一阶微分的计算公式非常简单: 离散化之后的差分方程: 考虑到图像的拓扑结构性,大量连续公式都需经 离散化 使用。
11 .一阶微分锐化算子 单方向一阶微分锐化 无方向一阶微分锐化 • 交叉微分锐化 • Sobel 锐化 • Prewitt 锐化
12 .单方向的一阶锐化:基本原理 定义:对某个特定方向上的边缘信息进行增强。 单方向锐化实际上是包括 水平方向 与 垂直方向 上的锐化。
13 .水平方向的一阶锐化:基本方法 水平方向的锐化,通过可以检测出水平方向上像素值变化的 模板 来实现。
14 .水平方向的一阶锐化:例题 1 2 3 2 1 2 1 2 6 2 3 0 8 7 6 1 2 7 8 6 2 3 2 6 9 0 0 0 0 0 0 -3 -13 -20 0 0 -6 -13 -13 0 0 1 12 5 0 0 0 0 0 0 1*1+2*2+1*3-1*3-2*0-1*8=-3
15 .垂直方向的一阶锐化:基本方法 垂直锐化算法的设计思想与水平锐化算法相同。
16 .垂直方向的一阶锐化:例题 1 2 3 2 1 2 1 2 6 2 3 0 8 7 6 1 2 7 8 6 2 3 2 6 9 0 0 0 0 0 0 -7 -17 4 0 0 -16 -25 5 0 0 -17 -22 -3 0 0 0 0 0 0 1*1+2*2+1*3-1*3-2*2-1*8=-7
17 .单方向锐化的后处理 此类锐化算法需进行后处理,以解决像素值为负的问题。 后处理的方法不同,则所得到的效果也就不同。
18 .单方向锐化的后处理:方法 1 方法 1 : 整体加一个正整数 ,以保证所有的像素值均为正。可以获得类似 浮雕 的效果。 20 20 20 20 20 20 17 7 0 20 20 14 7 7 20 20 21 32 25 20 20 20 20 20 20 0 0 0 0 0 0 -3 -13 -20 0 0 -6 -13 -13 0 0 1 12 5 0 0 0 0 0 0
19 .水平浮雕效果
20 .垂直浮雕效果
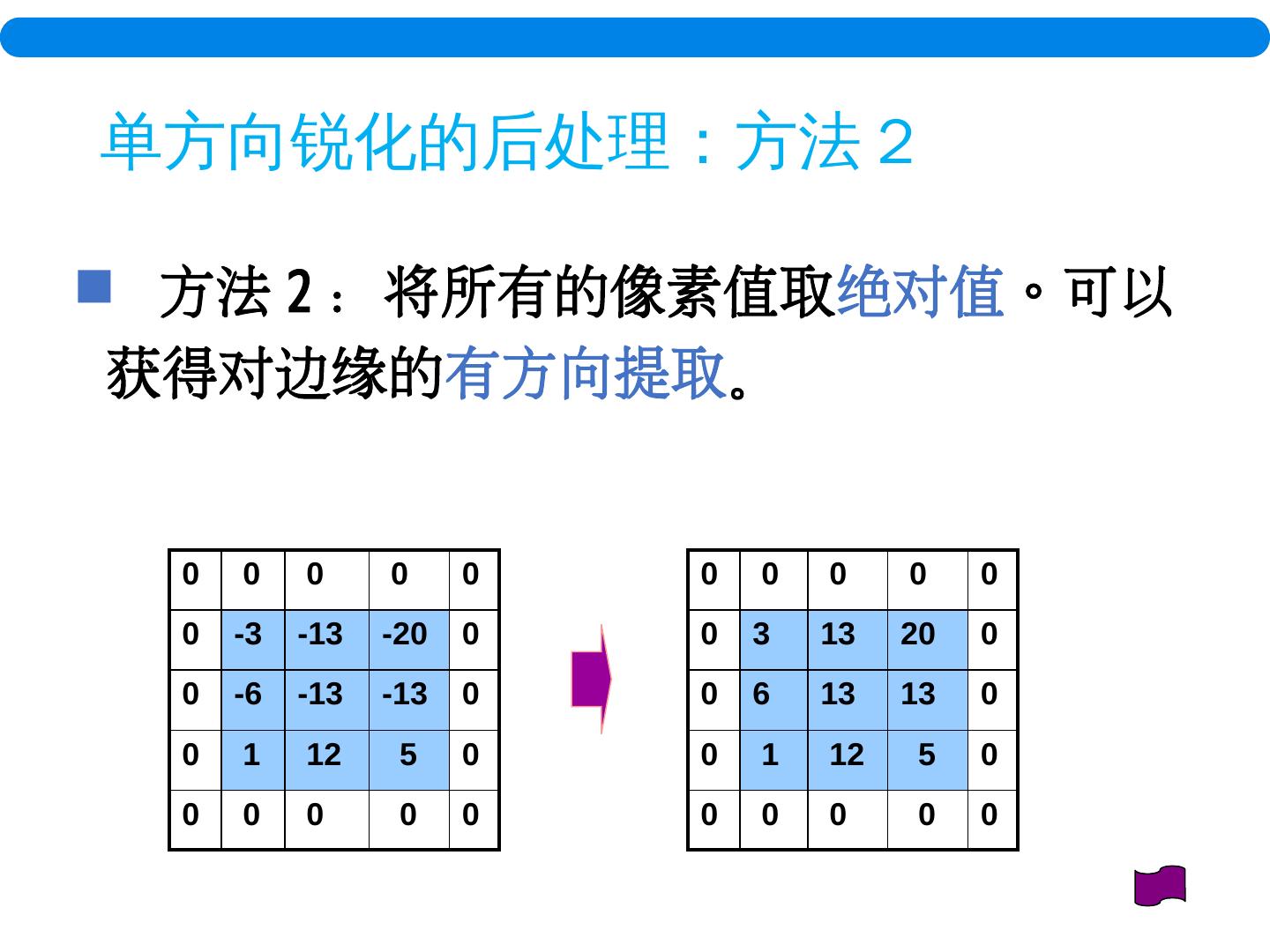
21 .单方向锐化的后处理:方法 2 方法 2 :将所有的像素值取 绝对值 。可以获得对边缘的 有方向提取 。 0 0 0 0 0 0 3 13 20 0 0 6 13 13 0 0 1 12 5 0 0 0 0 0 0 0 0 0 0 0 0 -3 -13 -20 0 0 -6 -13 -13 0 0 1 12 5 0 0 0 0 0 0
22 .水平边缘的提取效果
23 .垂直边缘的提取效果
24 .无方向一阶锐化:问题的提出 有方向一阶锐化对于人工设计制造的具有 矩形 特征物体(例如:楼房、汉字等)的边缘的提取很有效。 对于 不规则形状 (如:人物)的边缘提取,则存在信息的缺损。
25 .非矩形目标物的单方向锐化
26 .无方向一阶锐化:设计思想 为了解决上述问题,希望提出对任何方向边缘信息均 敏感 的锐化算法,即无方向的锐化算法。
27 .无方向一阶锐化:设计思想 为了解决上述问题,希望提出对任何方向边缘信息均 敏感 的锐化算法,即无方向的锐化算法。
28 .无方向一阶锐化:交叉微分 交叉微分算法( Roberts 算法)计算公式如下:
29 .交叉锐化效果图例 1