10 跳跃表和跳跃图

1 . SKIP LIST & SKIP GRAPH James Aspnes Gauri Shah Many slides have been taken from the original presentation by the authors 

2 . 2 Definition of Skip List A skip list for a set L of distinct (key, element) items is a series of linked lists L0, L1 , … , Lh such that Each list Li contains the special keys +∞ and -∞ List L0 contains the keys of L in non-decreasing order Each list is a subsequence of the previous one, i.e., L0 ⊃ L1 ⊃ … ⊃ Lh List Lh contains only the two special keys +∞ and -∞ 

3 . 3 Skip List (Idea due to Pugh ’90, CACM paper) Dictionary based on a probabilistic data structure. Allows efficient search, insert, and delete operations. Each element in the dictionary typically stores additional useful information beside its search key. Example: <student id. Transcripts> [for University of Iowa] <date, news> [for Daily Iowan] Probabilistic alternative to a balanced tree. 

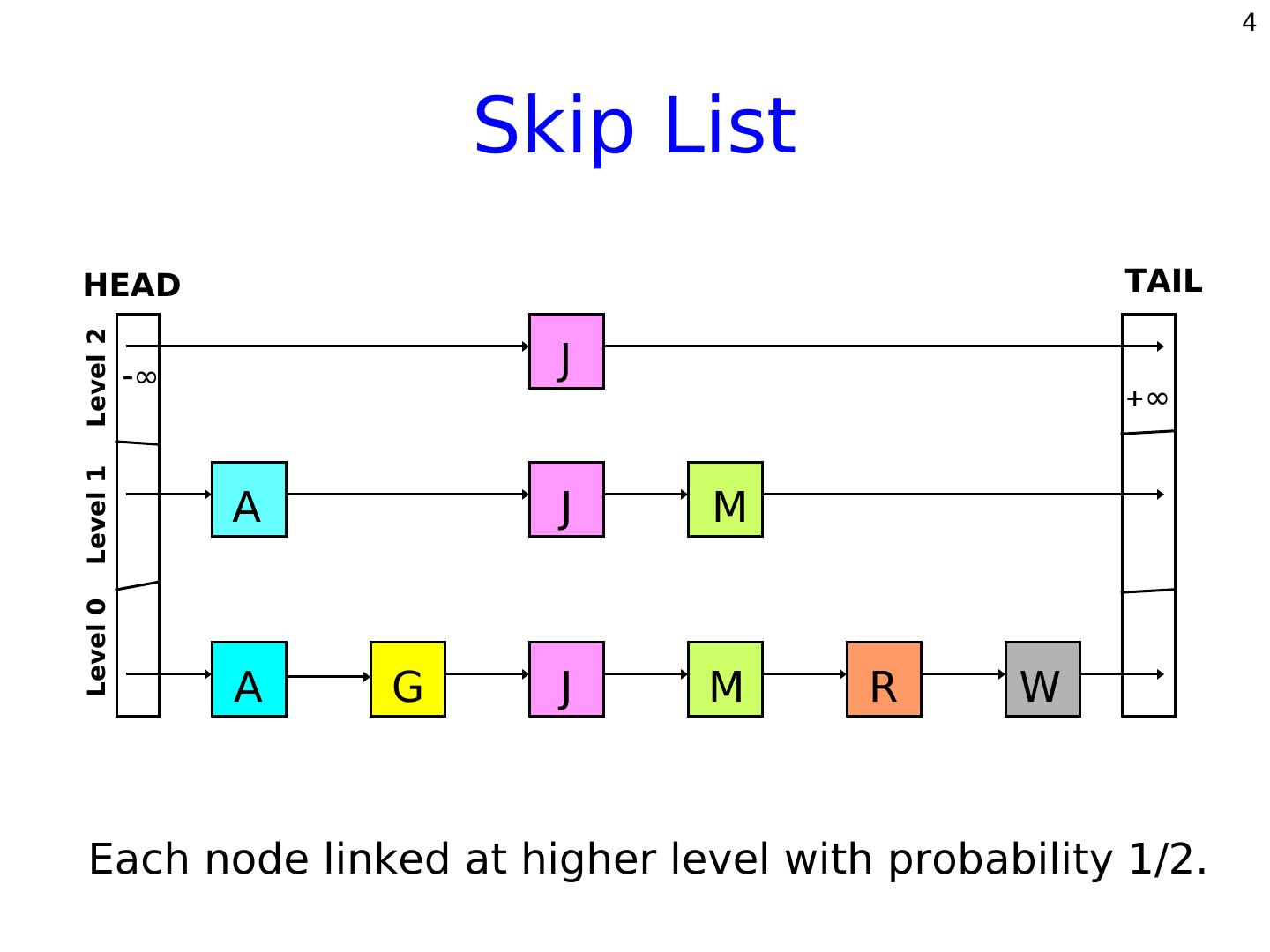
4 . 4 Skip List HEAD TAIL Level 2 ∞ J ∞ Level 1 A J M Level 0 A G J M R W Each node linked at higher level with probability 1/2. 

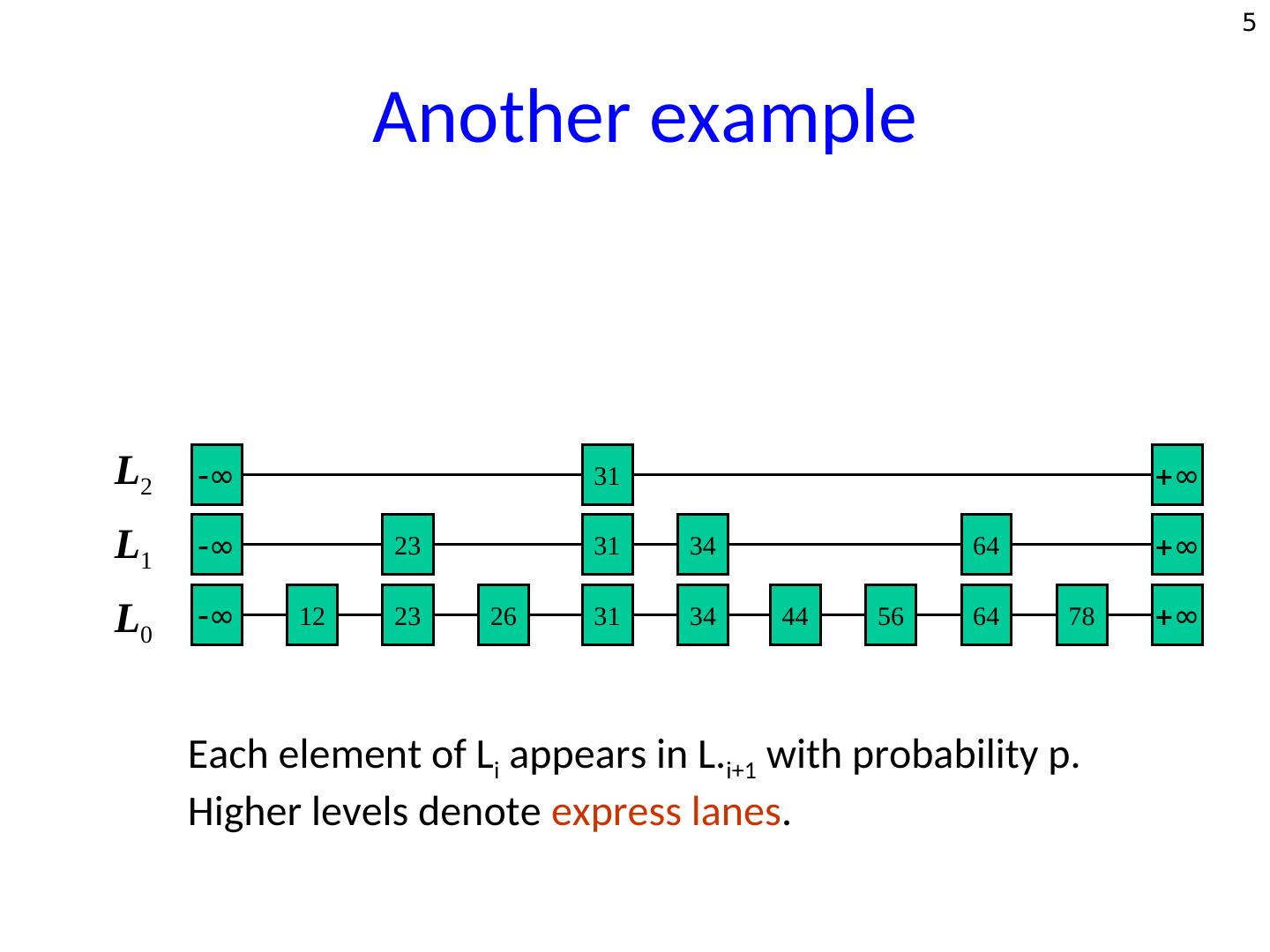
5 . 5 Another example L2 ∞ 31 ∞ L1 ∞ 23 31 34 64 ∞ L0 ∞ 12 23 26 31 34 44 56 64 78 ∞ Each element of Li appears in L.i+1 with probability p. Higher levels denote express lanes. 

6 . 6 Searching in Skip List Search for a key x in a skip: Start at the first position of the top list At the current position P, compare x with y ≥ key after P x = y -> return element (after (P)) x > y -> “scan forward” x < y -> “drop down” – If we move past the bottom list, then no such key exists 

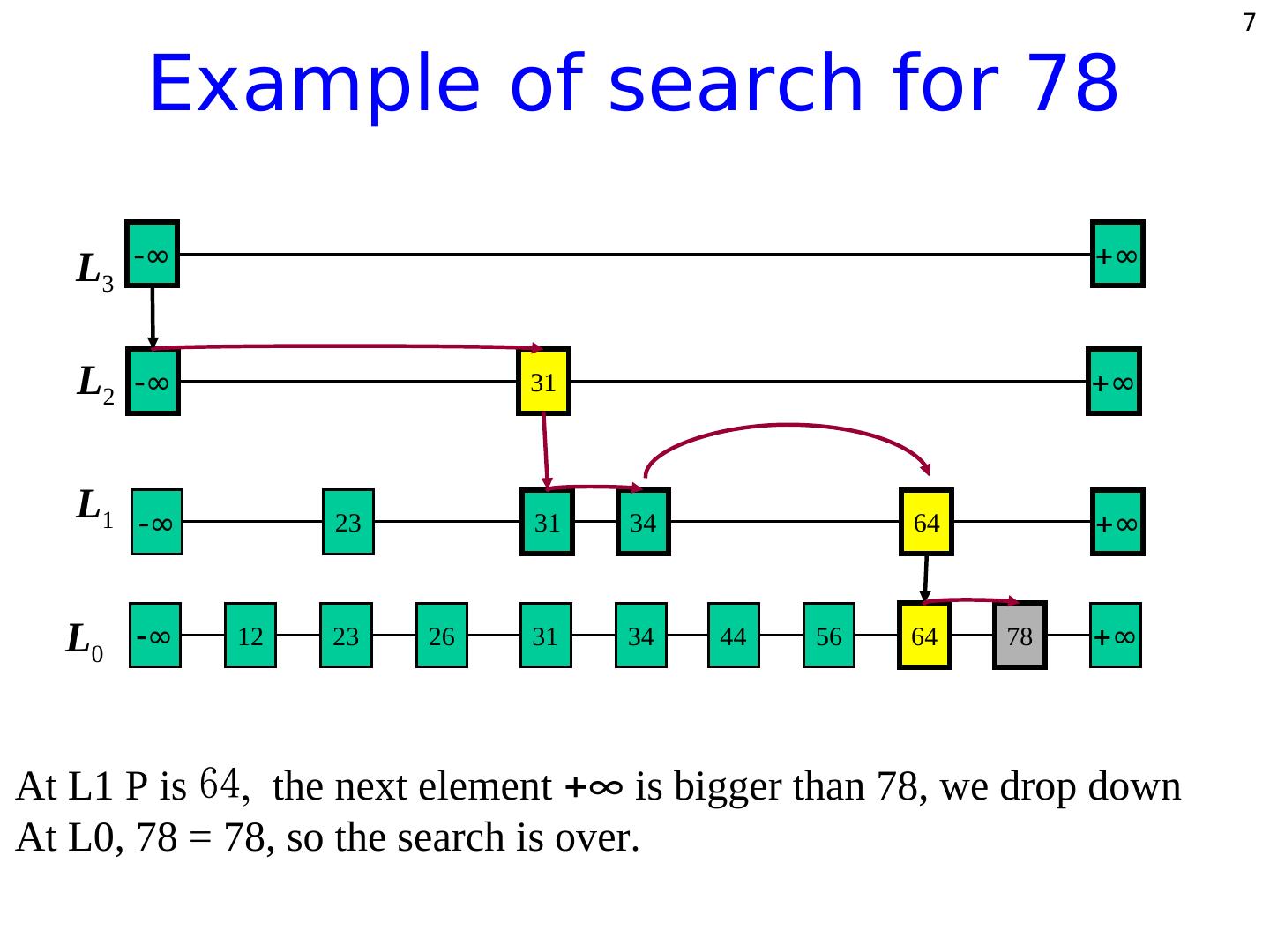
7 . 7 Example of search for 78 L3 ∞ ∞ L2 ∞ 31 ∞ L1 ∞ 23 31 34 64 ∞ L0 ∞ 12 23 26 31 34 44 56 64 78 ∞ At L1 P is the next element ∞ is bigger than 78, we drop down At L0, 78 = 78, so the search is over. 

8 . 8 Insertion • The insert algorithm uses randomization to decide in how many levels the new item <k> should be added to the skip list. • After inserting the new item at the bottom level flip a coin. • If it returns tail, insertion is complete. Otherwise, move to next higher level and insert <k> in this level at the appropriate position, and repeat the coin flip. 

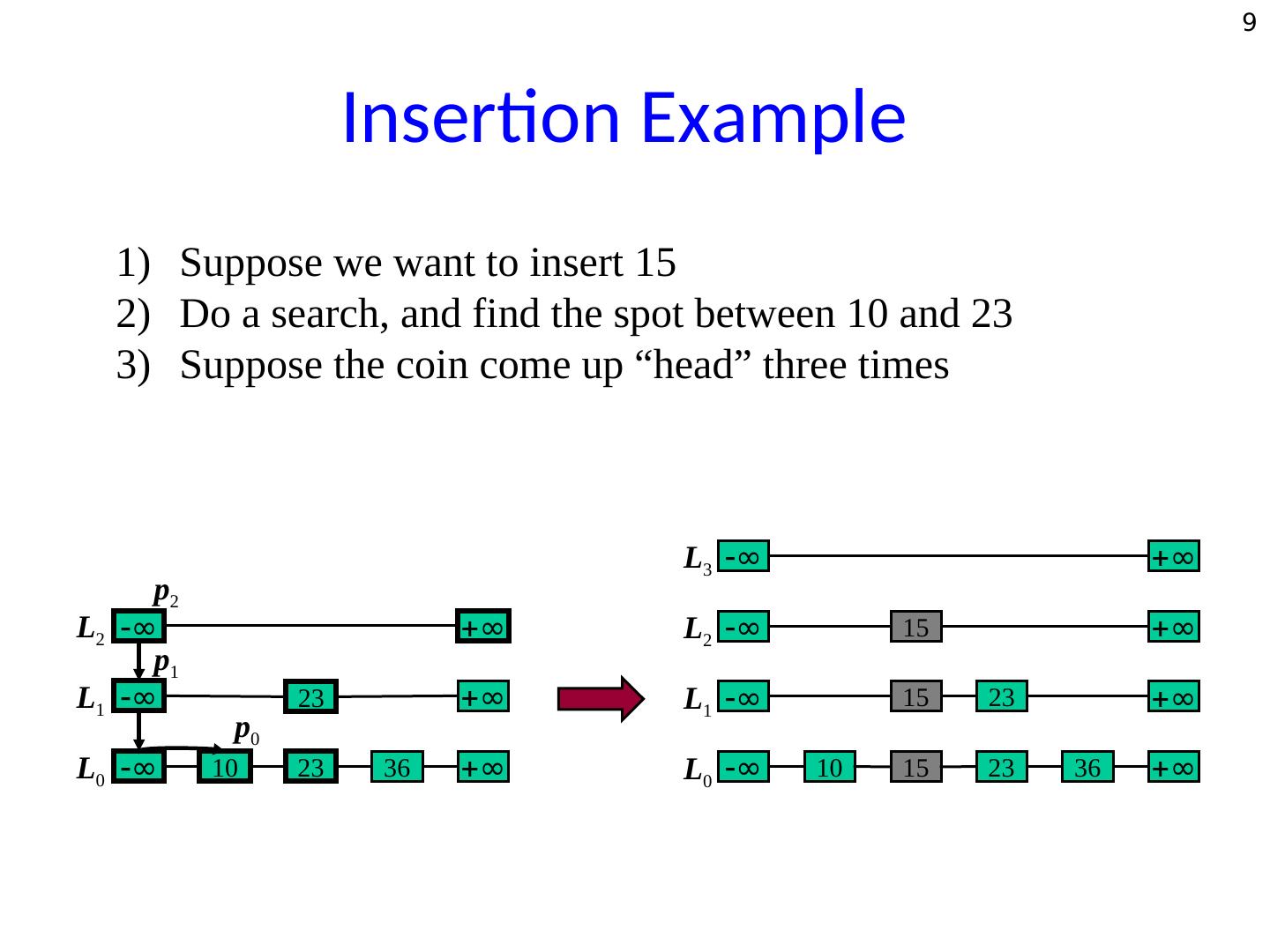
9 . 9 Insertion Example 1) Suppose we want to insert 15 2) Do a search, and find the spot between 10 and 23 3) Suppose the coin come up “head” three times L3 ∞ ∞ p2 L2 ∞ ∞ L2 ∞ 15 ∞ p1 L1 ∞ 23 ∞ L1 ∞ 15 23 ∞ p0 L0 ∞ 10 23 36 ∞ L0 ∞ 10 15 23 36 ∞ 

10 . 10 Deletion • Search for the given key <k>. If a position with key <k> is not found, then no such key exists. • Otherwise, if a position with key <k> is found (it will be definitely found on the bottom level), then we remove all occurrences of <k> from every level. • If the uppermost level is empty, remove it. 

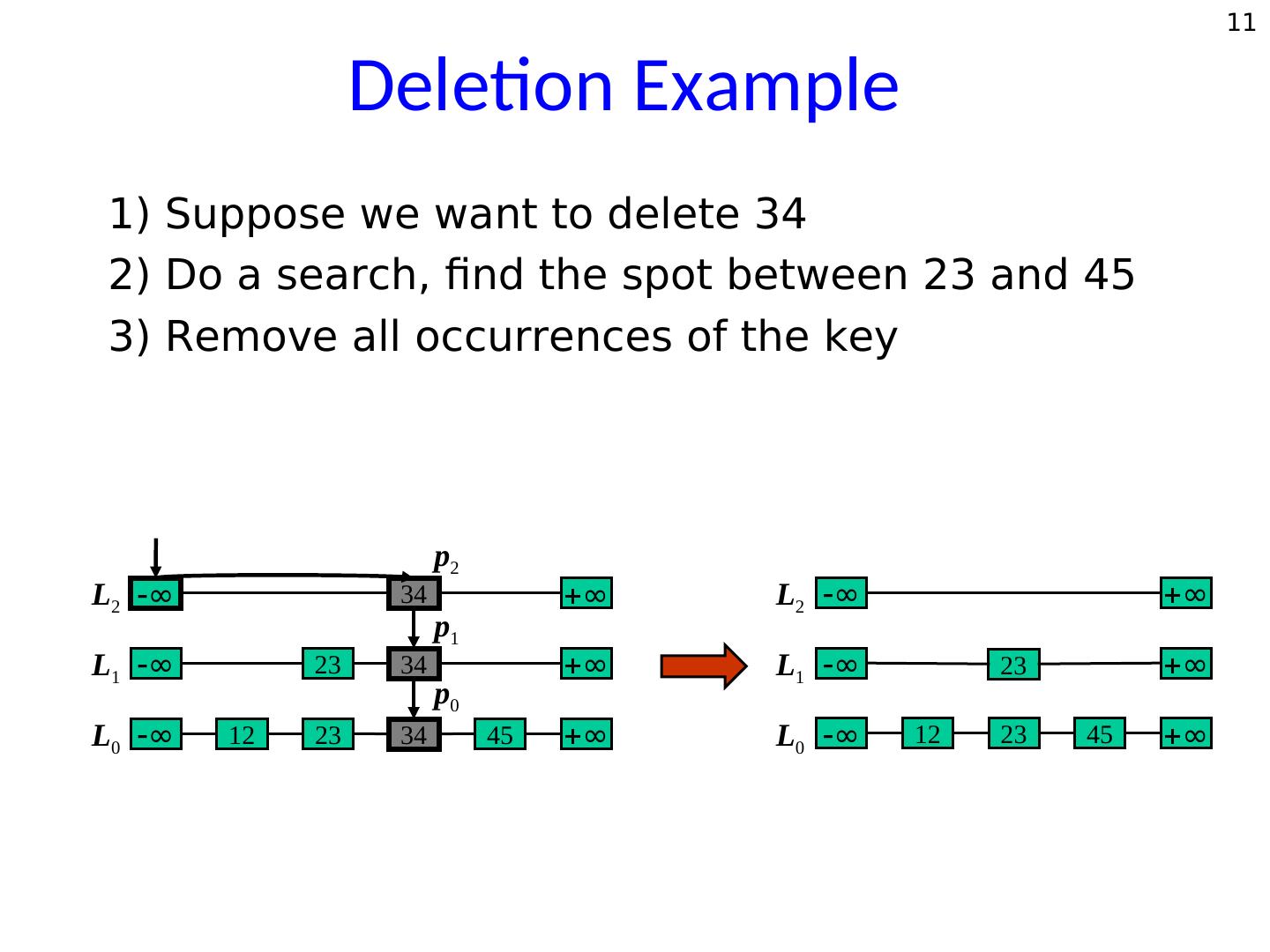
11 . 11 Deletion Example 1) Suppose we want to delete 34 2) Do a search, find the spot between 23 and 45 3) Remove all occurrences of the key p2 L2 ∞ 34 ∞ L2 ∞ ∞ p1 L1 ∞ 23 34 ∞ L1 ∞ 23 ∞ p0 L0 ∞ 12 23 34 45 ∞ L0 ∞ 12 23 45 ∞ 

12 . 12 O(1) pointers per node Average number of pointers per node = O(1) Total number of pointers = 2.n + 2. n/2 + 2. n/4 + 2. n/8 + … = 4.n So, the average number of pointers per node = 4 

13 . 13 Number of levels The number of levels = O(log n) w.h.p Pr[a given element x is above level c log n] = 1/2c log n = 1/nc Pr[any element is above level c log n] = n. 1/nc = 1/nc-1 So the number of levels = O(log n) with high probability 

14 . 14 Search time Consider a skiplist with two levels L0 and L1. To search a key, first search L1 and then search L0. Cost (i.e. search time) = length (L1) + n / length (L1) Minimum when length (L1) = n / length (L1). Thus length(L1) = (n) 1/2, and cost = 2. (n) 1/2 (Three lists) minimum cost = 3. (n)1/3 (Log n lists) minimum cost = log n. (n) 1/log n = 2.log n 

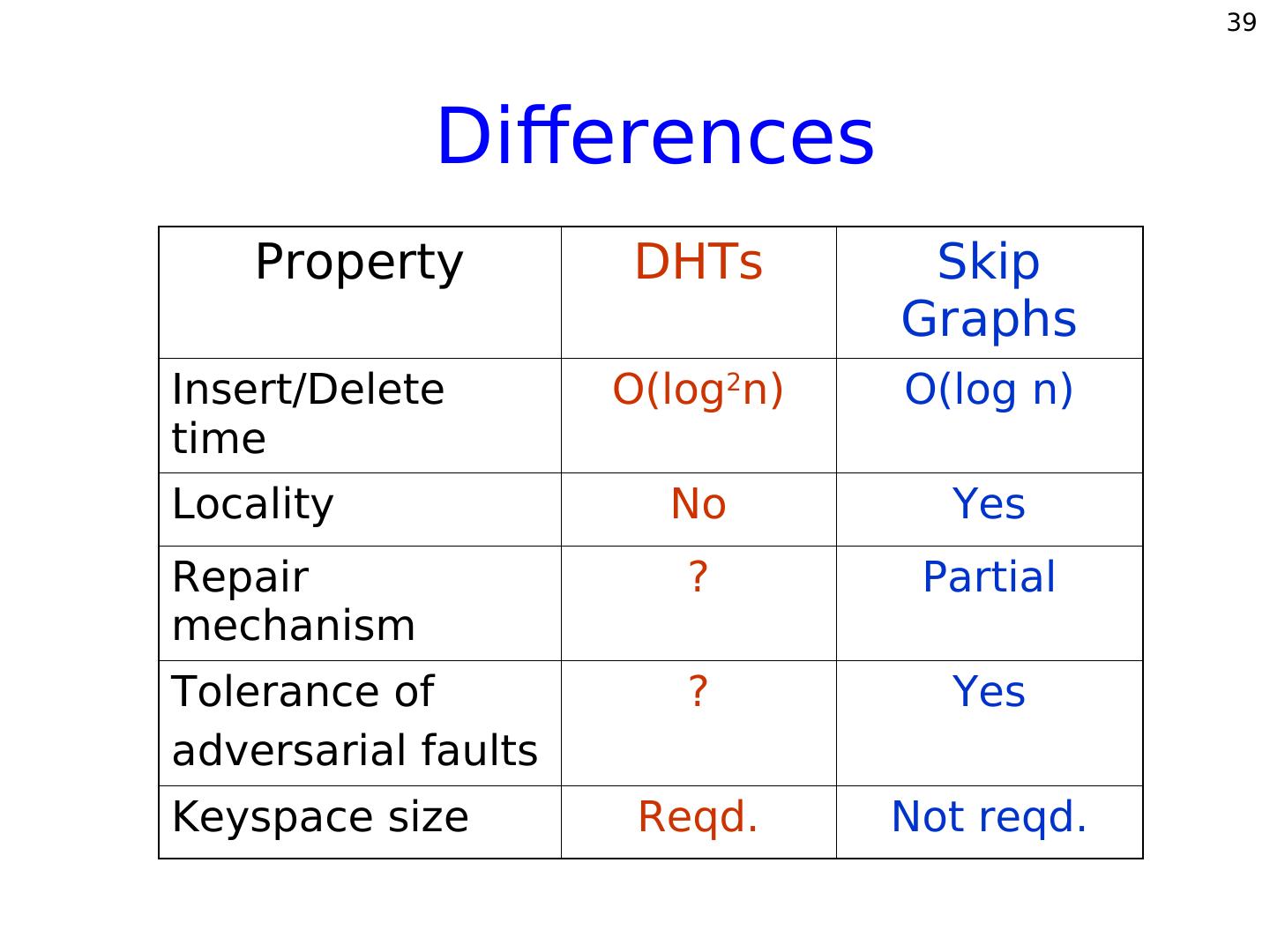
15 . 15 Skip lists for P2P? Advantages • O(log n) expected search time. • Retains locality. • Dynamic node additions/deletions. Disadvantages • Heavily loaded top-level nodes. • Easily susceptible to failures. • Lacks redundancy. 

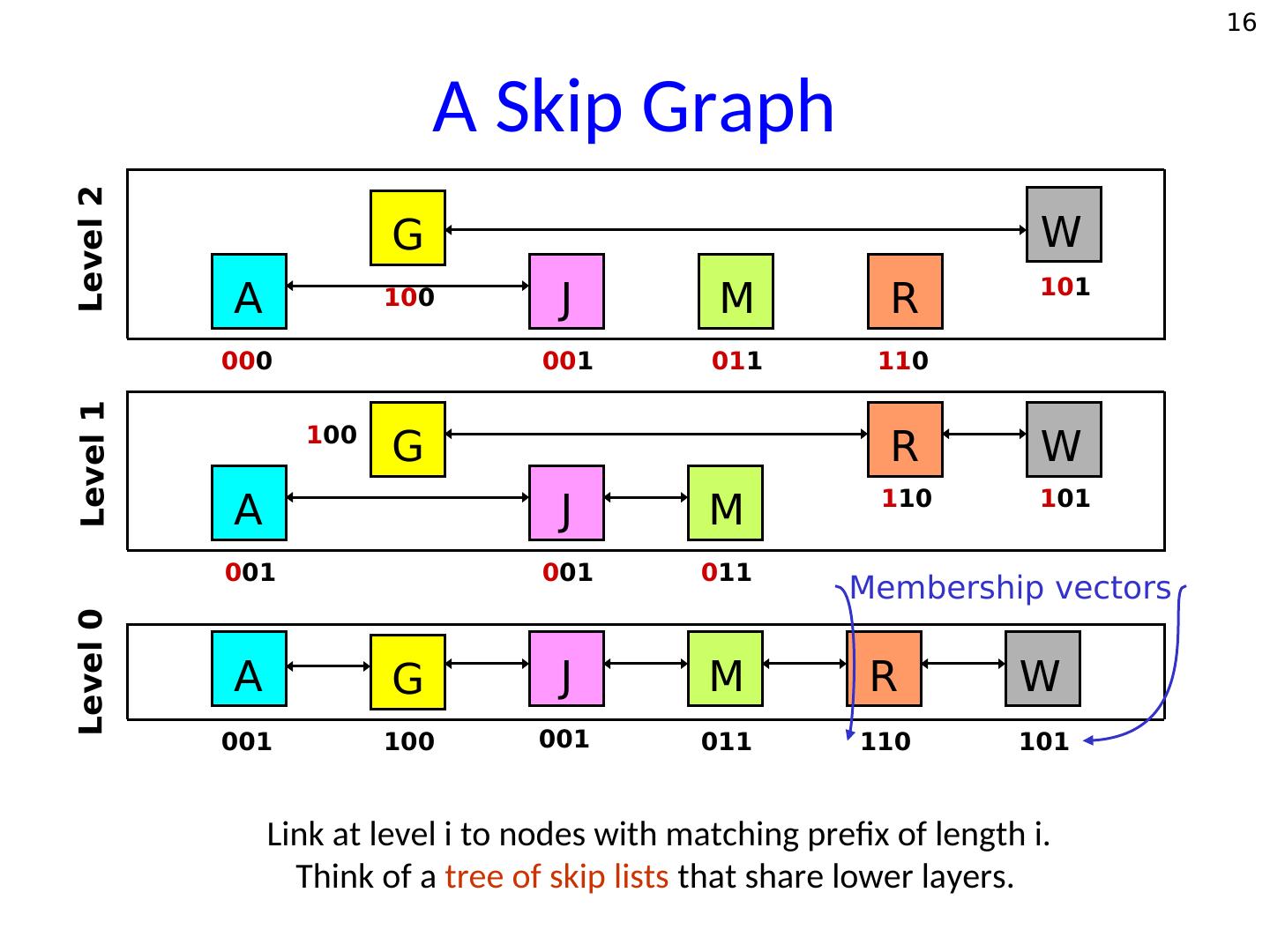
16 . 16 Level 2 A Skip Graph G W 101 A 100 J M R 000 001 011 110 Level 1 100 G R W 110 101 A J M 001 001 011 Membership vectors Level 0 A G J M R W 001 100 001 011 110 101 Link at level i to nodes with matching prefix of length i. Think of a tree of skip lists that share lower layers. 

17 . 17 Properties of skip graphs 1. Efficient Searching. 2. Efficient node insertions & deletions. 3. Independence from system size. 4. Locality and range queries. 

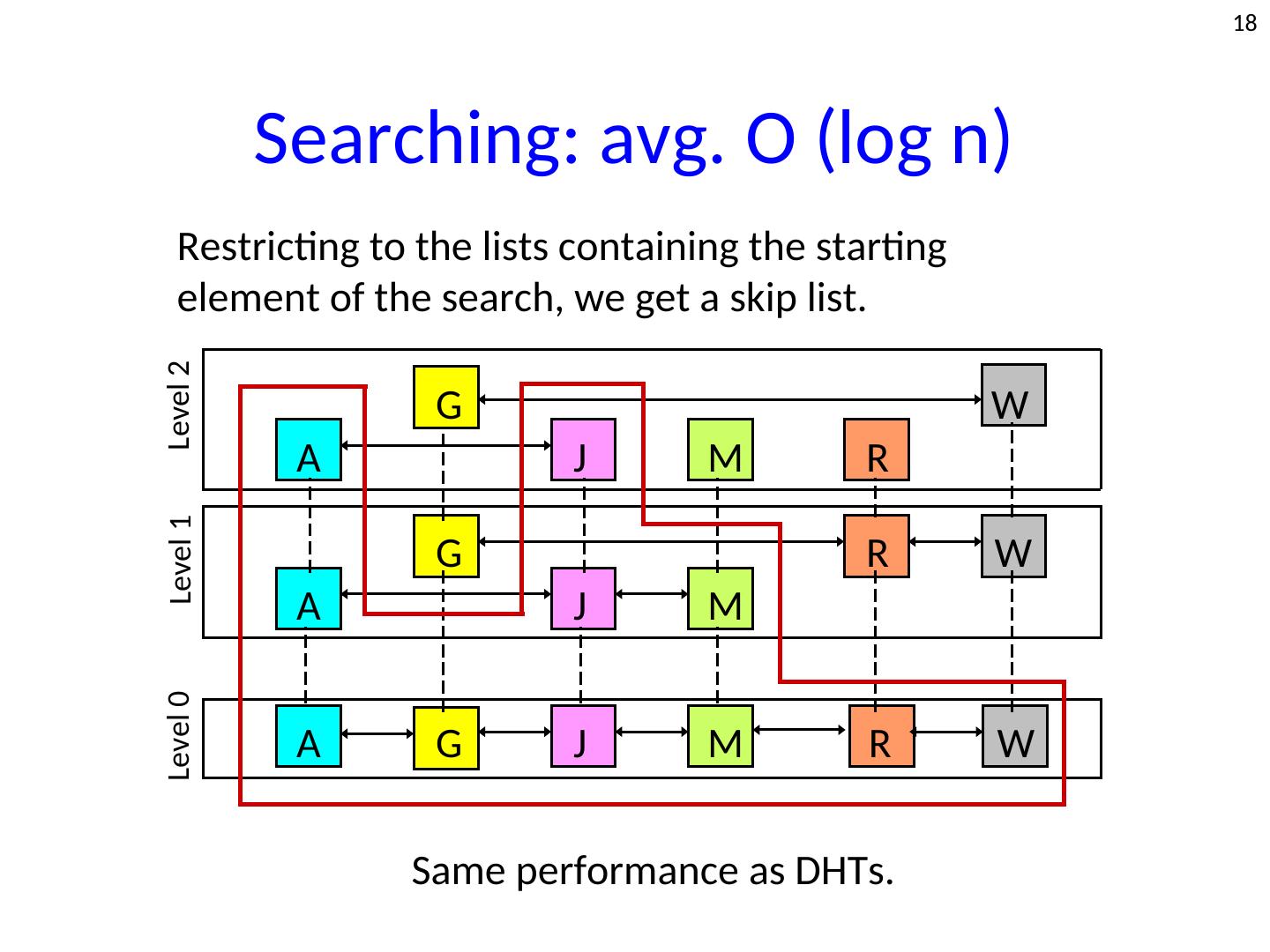
18 . 18 Searching: avg. O (log n) Restricting to the lists containing the starting element of the search, we get a skip list. Level 2 G W A J M R Level 1 G R W A J M Level 0 A G J M R W Same performance as DHTs. 

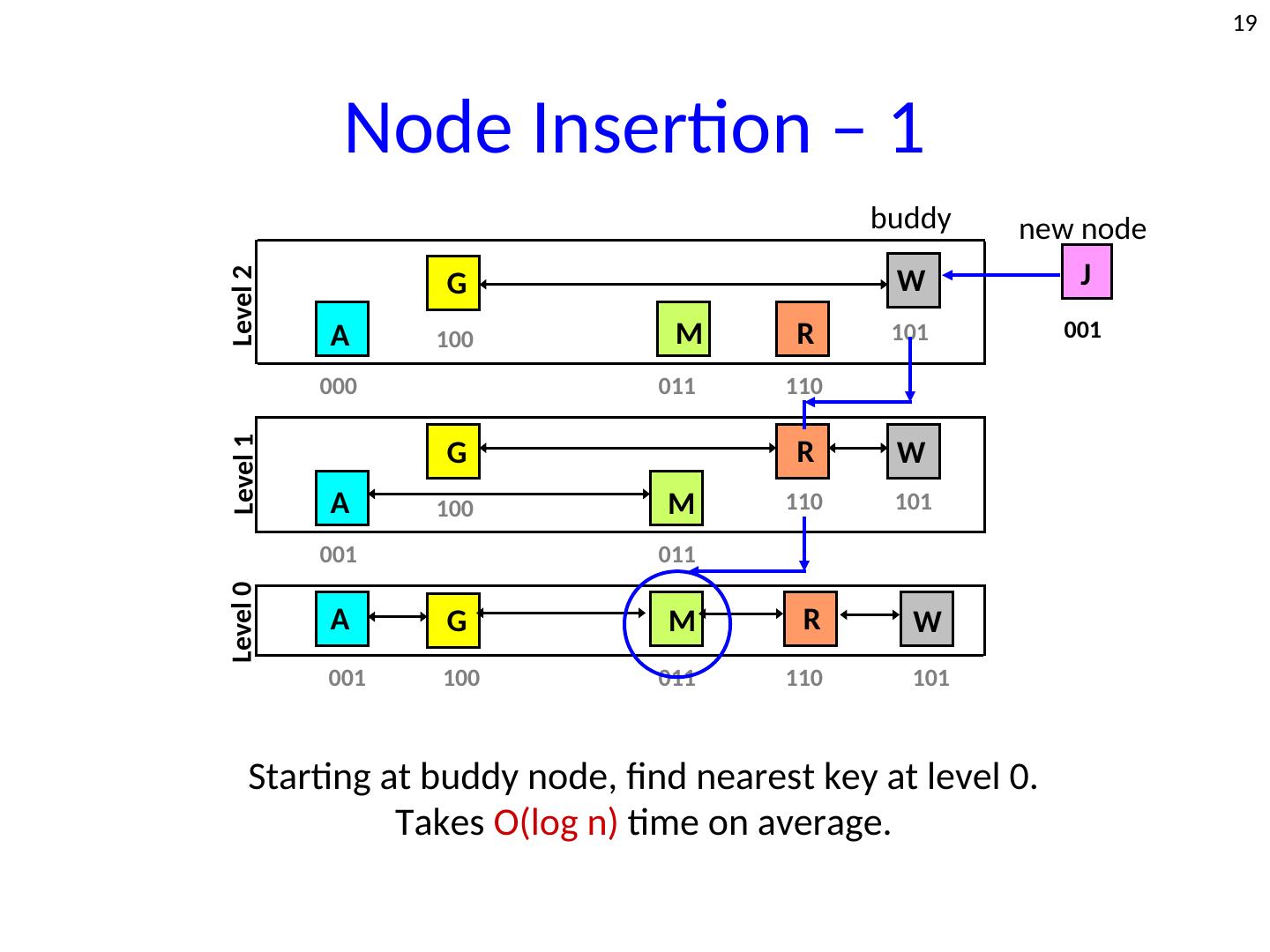
19 . 19 Node Insertion – 1 buddy new node J Level 2 G W A 100 M R 101 001 000 011 110 Level 1 G R W A 100 M 110 101 001 011 Level 0 A G M R W 001 100 011 110 101 Starting at buddy node, find nearest key at level 0. Takes O(log n) time on average. 

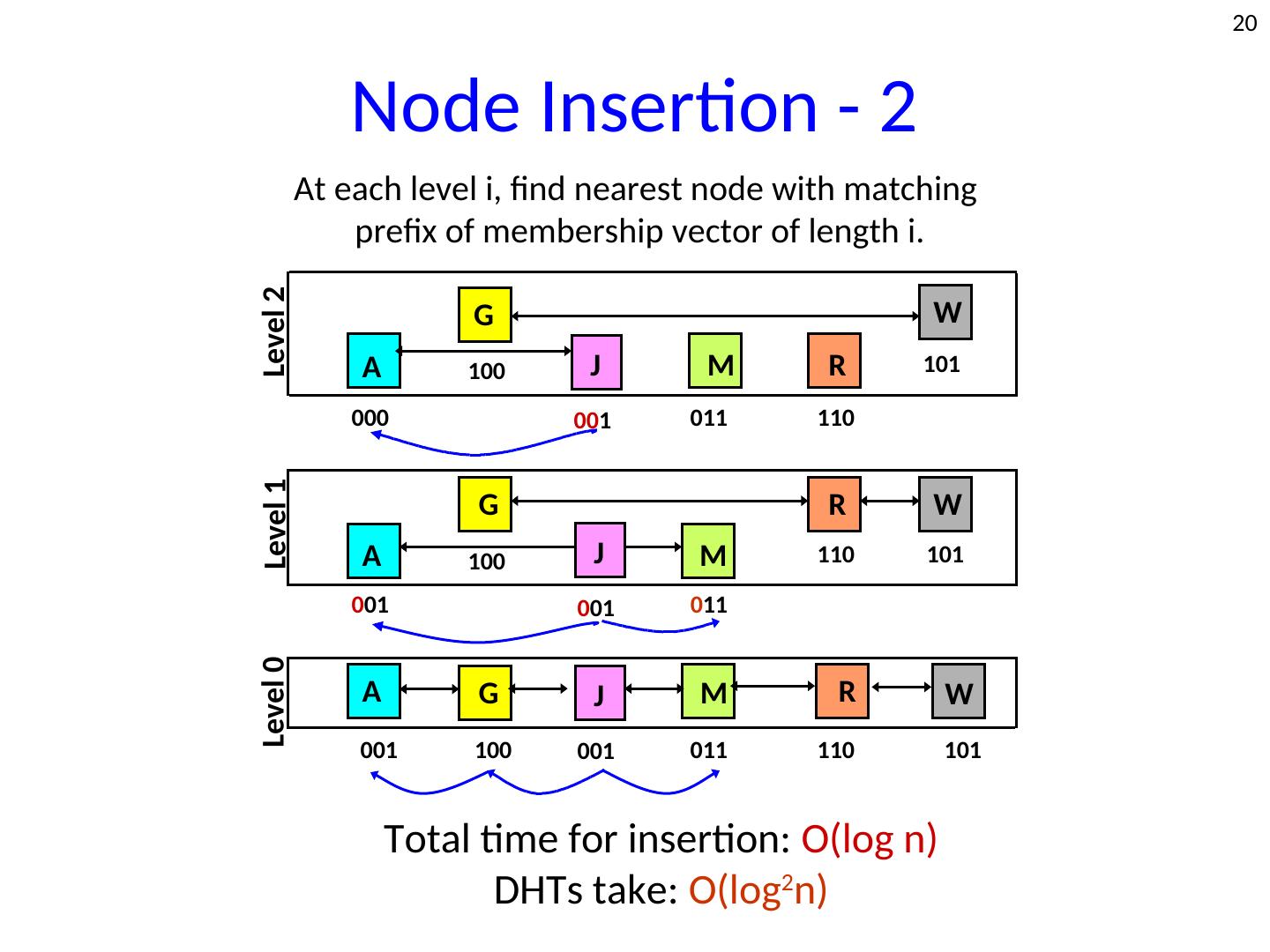
20 . 20 Node Insertion - 2 At each level i, find nearest node with matching prefix of membership vector of length i. Level 2 G W A 100 J M R 101 000 001 011 110 Level 1 G R W A 100 J M 110 101 001 001 011 Level 0 A G J M R W 001 100 001 011 110 101 Total time for insertion: O(log n) DHTs take: O(log2n) 

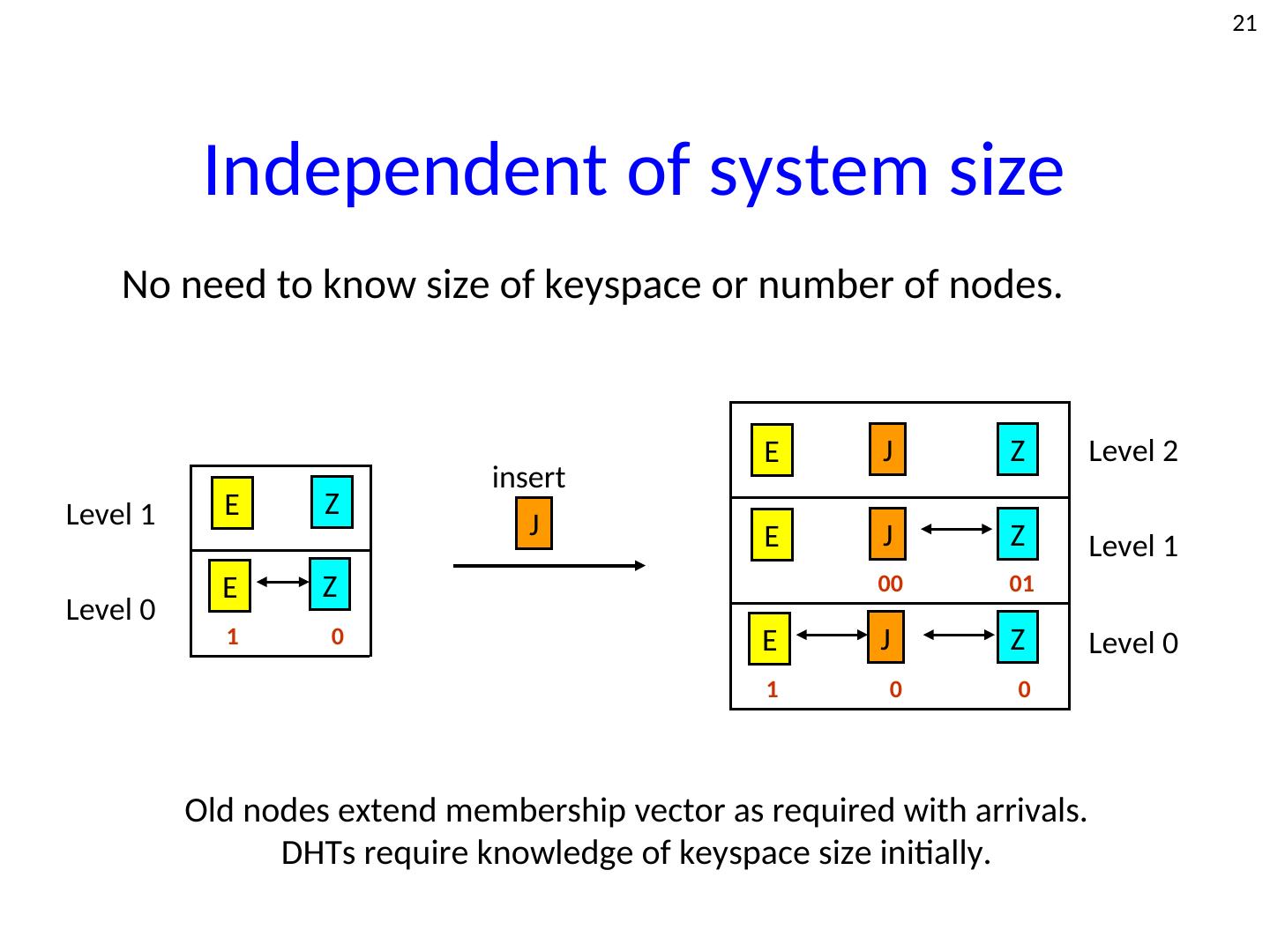
21 . 21 Independent of system size No need to know size of keyspace or number of nodes. E J Z Level 2 insert Level 1 E Z J E J Z Level 1 E Z 00 01 Level 0 1 0 E J Z Level 0 1 0 0 Old nodes extend membership vector as required with arrivals. DHTs require knowledge of keyspace size initially. 

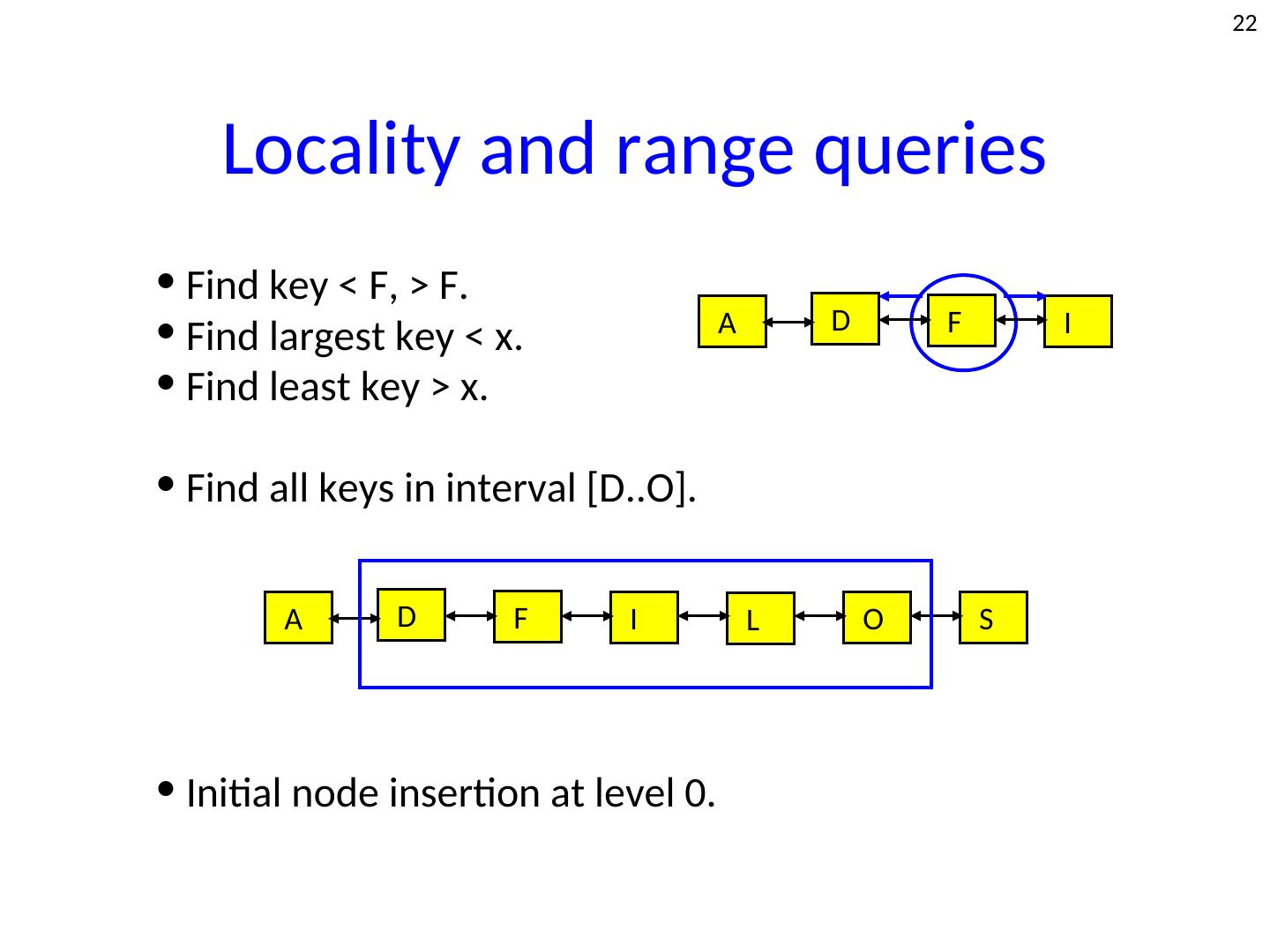
22 . 22 Locality and range queries • Find key < F, > F. • Find largest key < x. A D F I • Find least key > x. • Find all keys in interval [D..O]. A D F I L O S • Initial node insertion at level 0. 

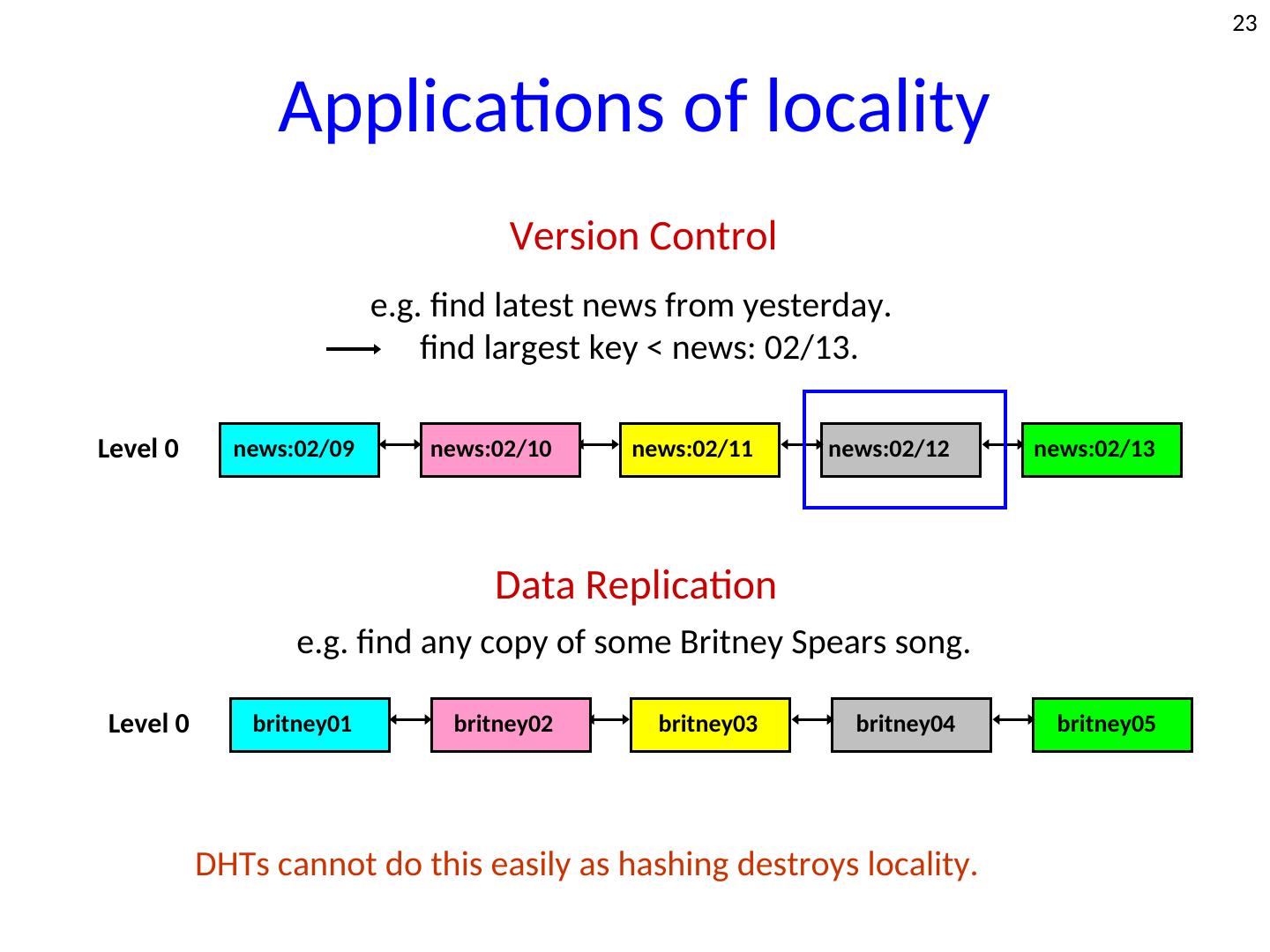
23 . 23 Applications of locality Version Control e.g. find latest news from yesterday. find largest key < news: 02/13. Level 0 news:02/09 news:02/10 news:02/11 news:02/12 news:02/13 Data Replication e.g. find any copy of some Britney Spears song. Level 0 britney01 britney02 britney03 britney04 britney05 DHTs cannot do this easily as hashing destroys locality. 

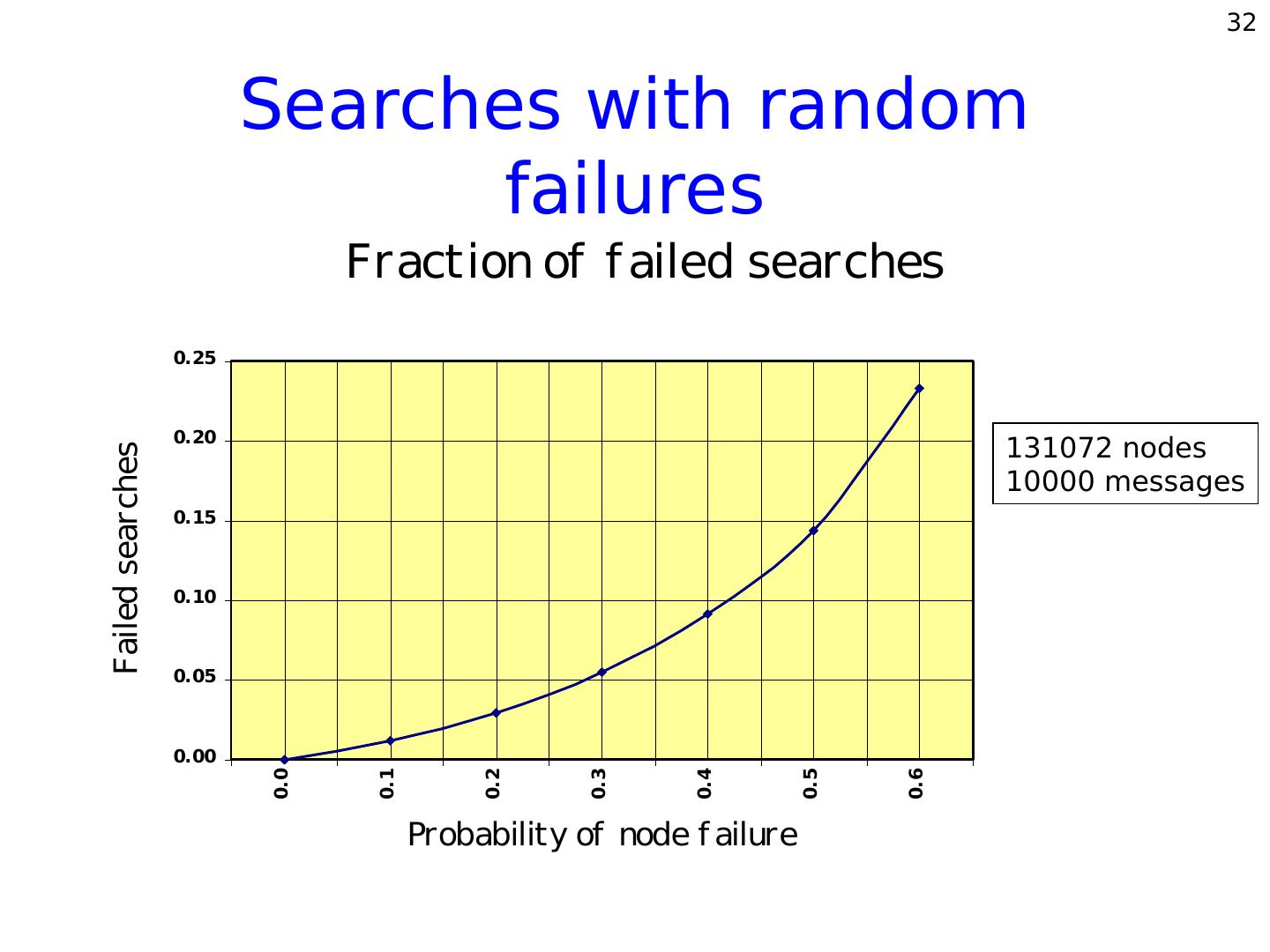
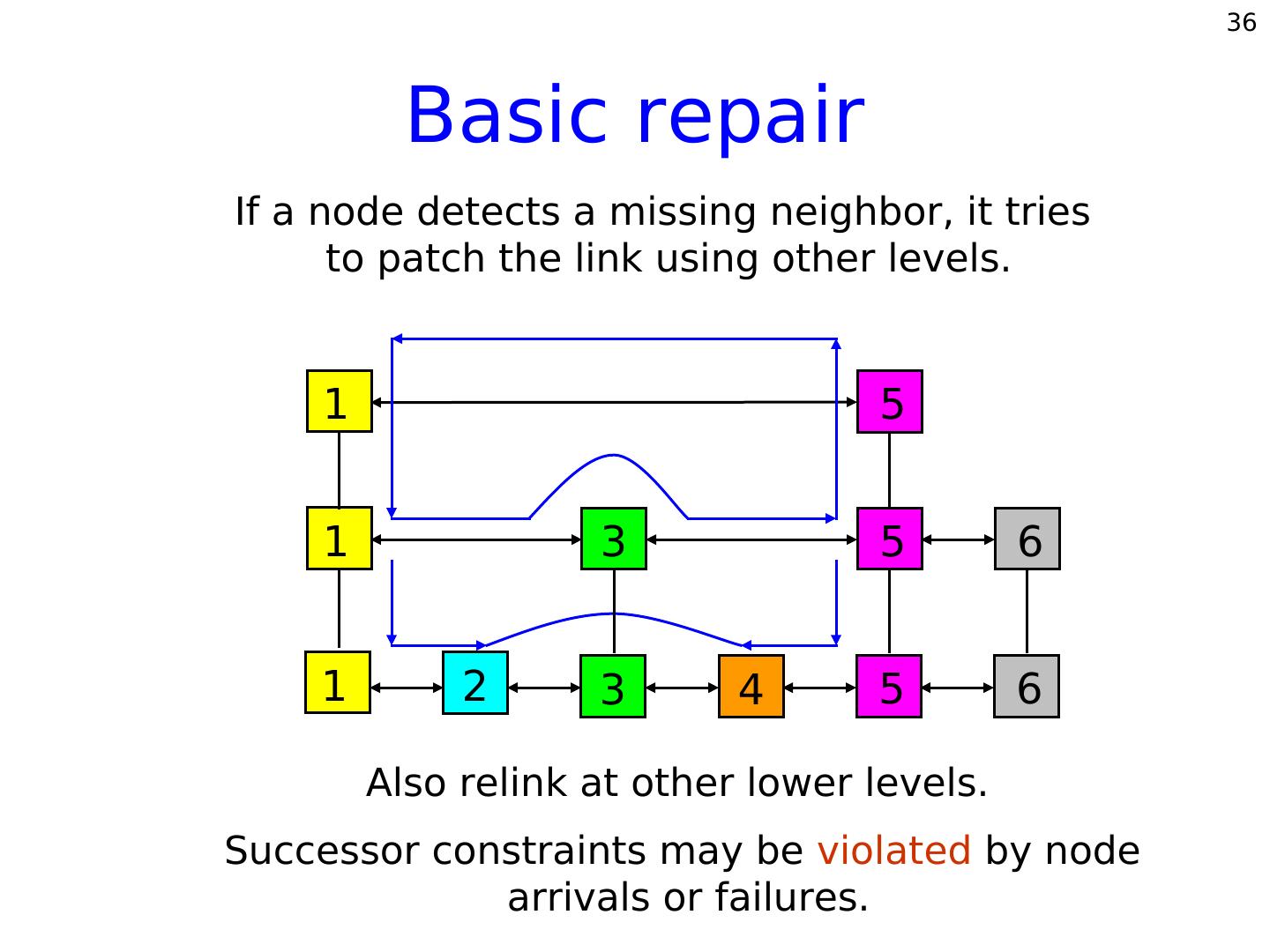
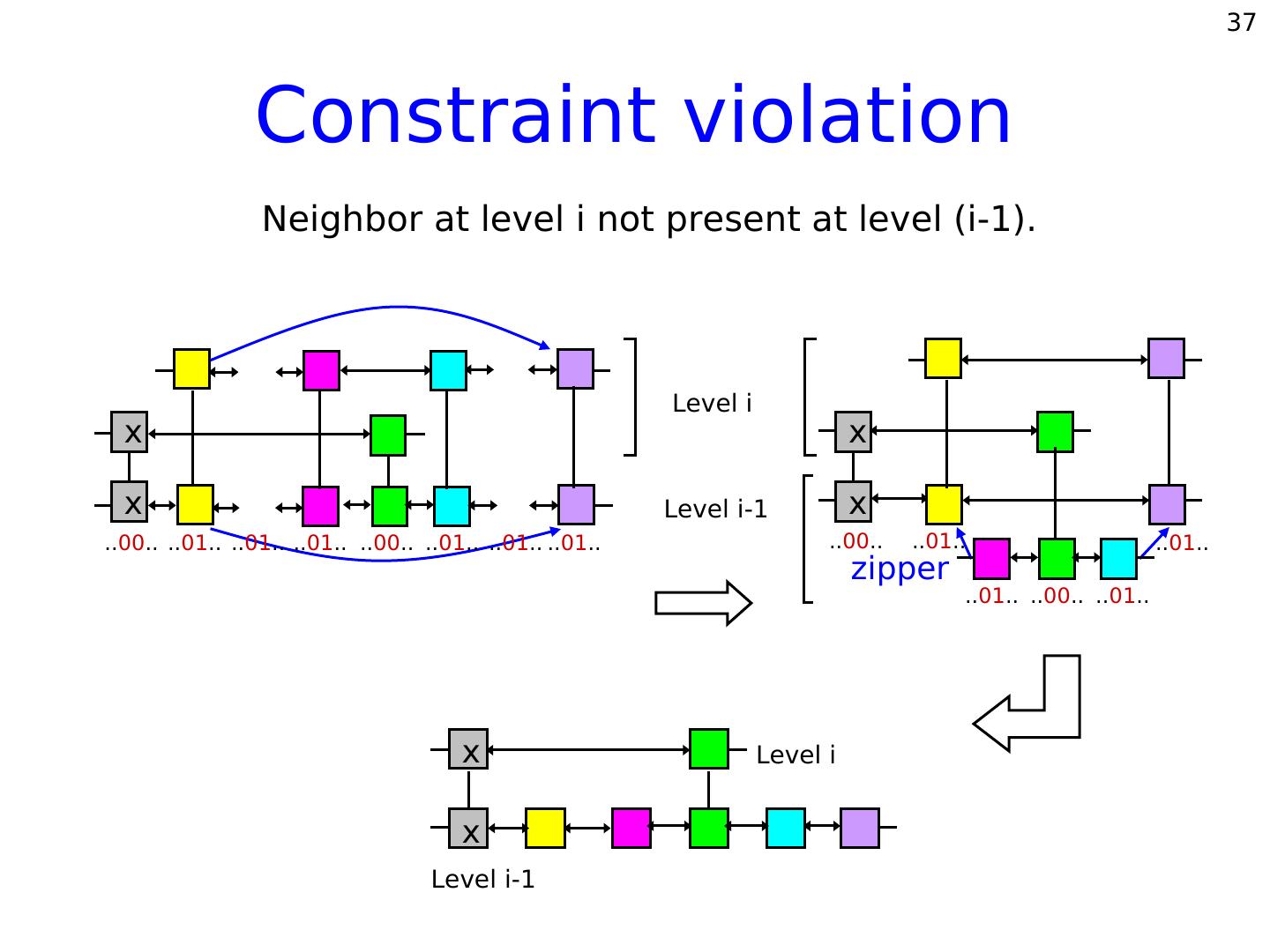
24 . 24 So far... Coming up... Decentralization. • Load balancing. •Tolerance to faults. Locality properties. O(log n) space per node.  • Random faults. O(log n) search, insert, • Adversarial faults.  and delete time. • Self-stabilization. Independent of system size. 

25 . 25 Load balancing Interested in average load on a node u. i.e. the number of searches from source s to destination t that use node u. Theorem: Let dist (u, t) = d. Then the probability that a search from s to t passes through u is < 2/(d+1). where V = {nodes v: u <= v <= t} and |V| = d+1. 

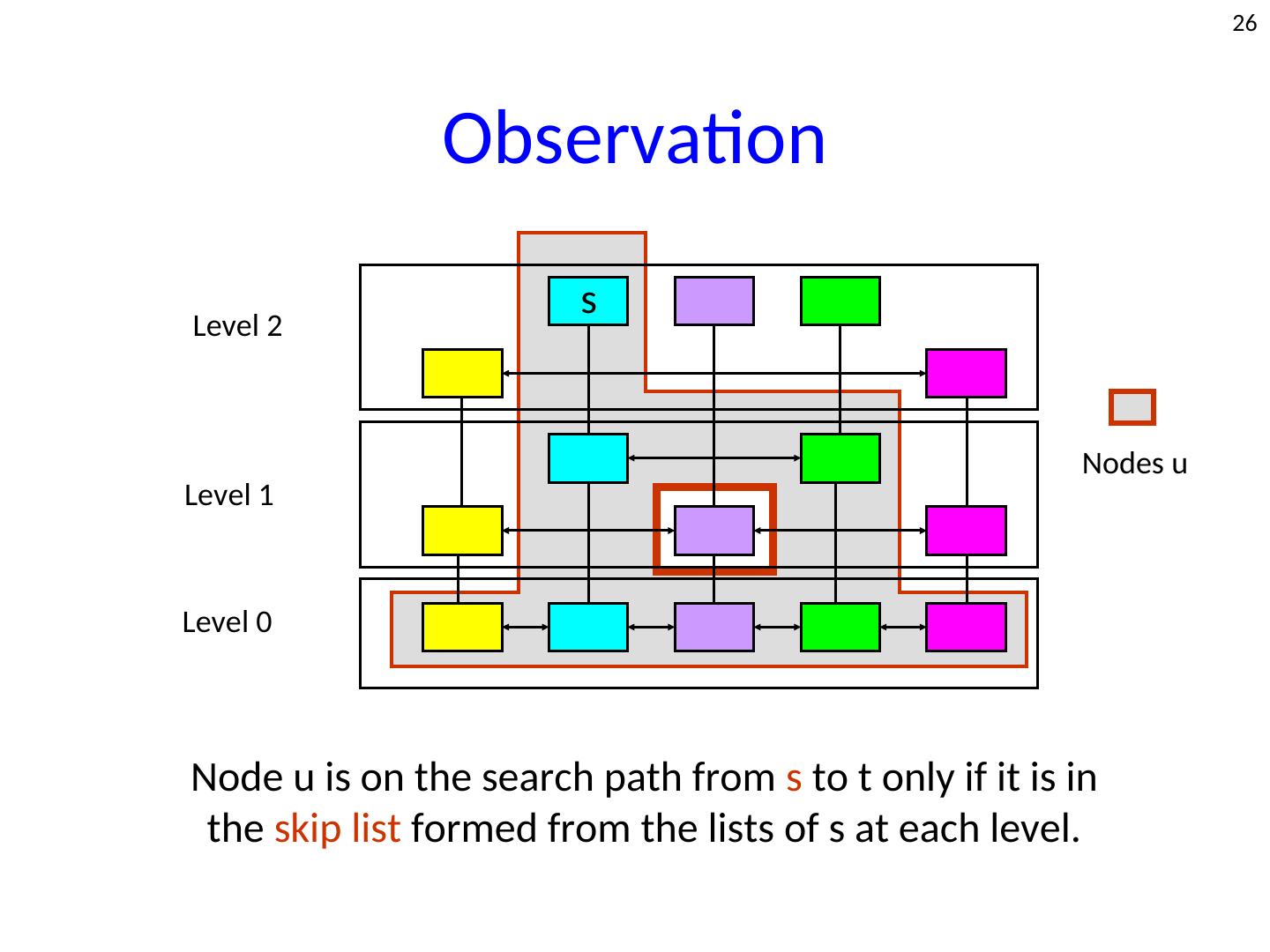
26 . 26 Observation s Level 2 Nodes u Level 1 Level 0 Node u is on the search path from s to t only if it is in the skip list formed from the lists of s at each level. 

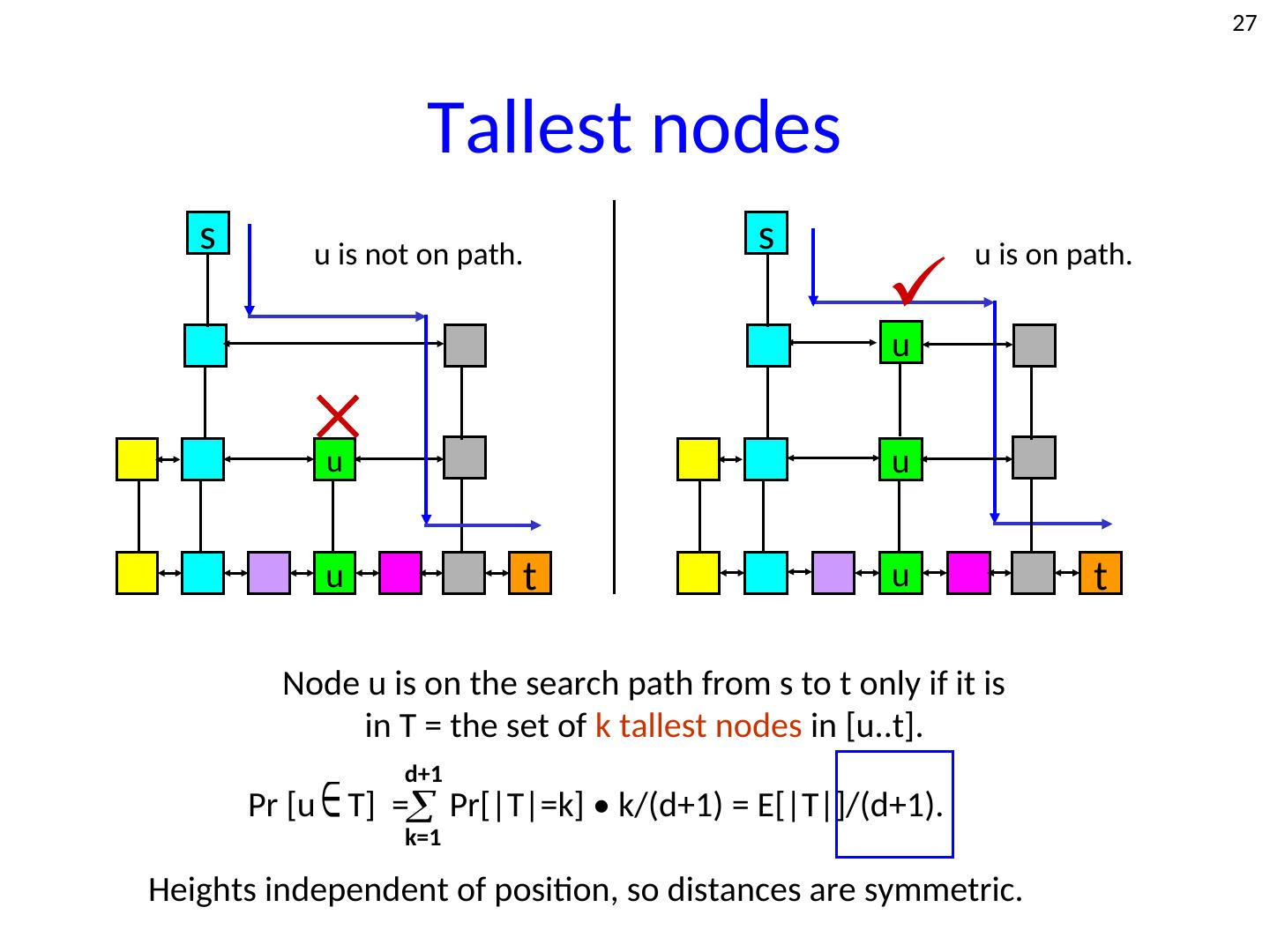
27 . 27 Tallest nodes s u is not on path. s u is on path.  u u u u t u t Node u is on the search path from s to t only if it is in T = the set of k tallest nodes in [u..t]. d+1 Pr [u ∈ T] = Pr[|T|=k] • k/(d+1) = E[|T|]/(d+1). k=1 Heights independent of position, so distances are symmetric. 

28 . 28 Load on node u Start with n nodes. Each node goes to next set with prob. 1/2. We want expected size of T = last non-empty set. We show that: E[|T|] < 2. =T Asymptotically: E[|T|] = 1/(ln 2) ± 2x10-5 ≃ 1.4427… [Trie analysis] Average load on a node is inversely proportional to the distance from the destination. 

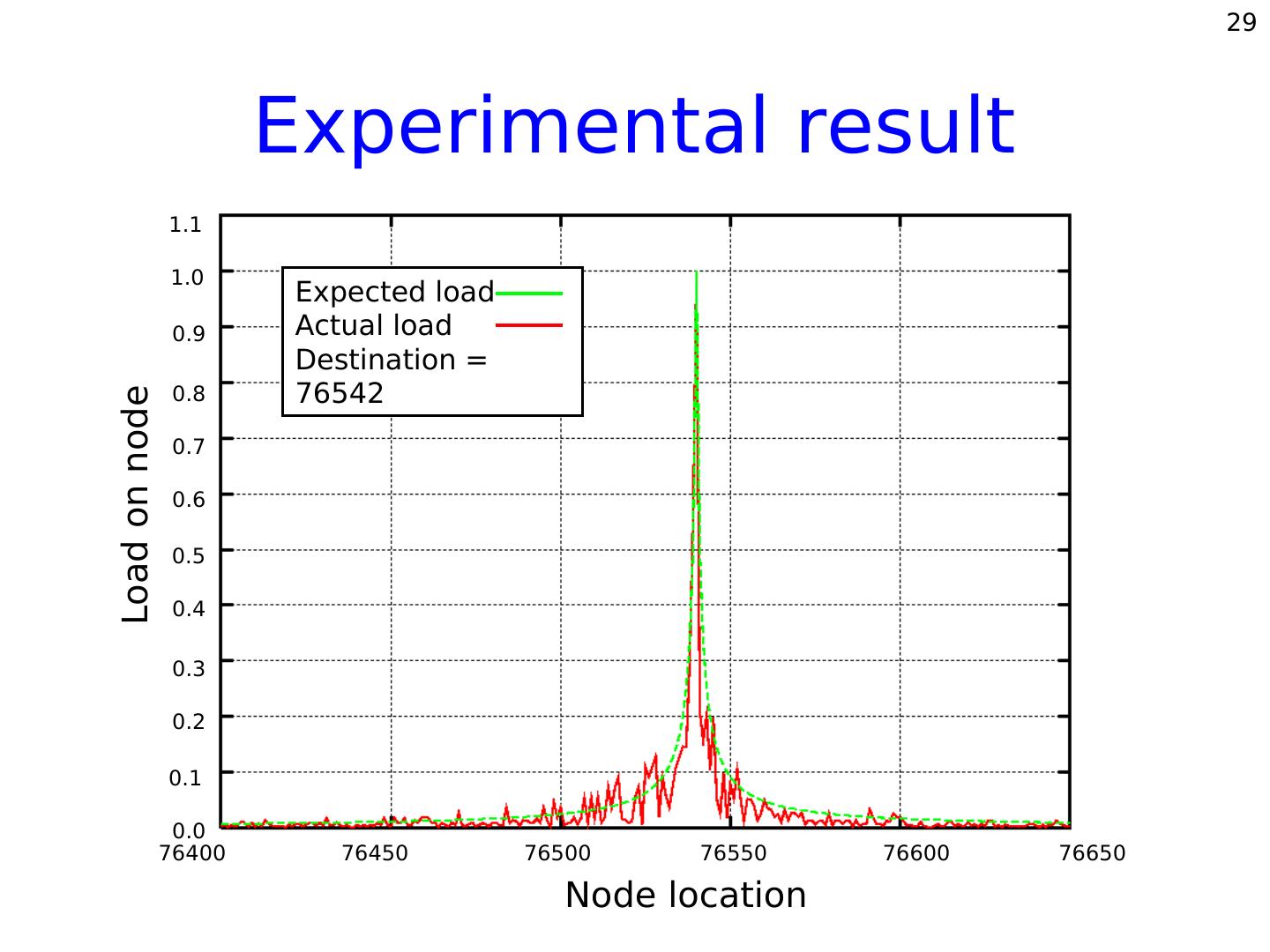
29 . 29 Experimental result 1.1 1.0 Expected load 0.9 Actual load Destination = 0.8 76542 Load on node 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.0 76400 76450 76500 76550 76600 76650 Node location