08 访问复制对象

1 .Accessing nearby copies of replicated objects Greg Plaxton, Rajmohan Rajaraman, Andrea Richa SPAA 1997 1 

2 . Goal A set A of m shared objects resides in a network G. Design an algorithm of so that processes can access a nearby copy of it. Supported operations are insert, delete, read (but not write) on shared objects. 2 

3 . Challenge What is the challenge here? Think about this: 1. if every node maintains a copy, then read is fast, but insert or delete are very expensive. Also, storage overhead grows. 2. If the object is stored in an arbitrary node, then the access may take a long time. The algorithm must be efficient w.r.t. both time and space 3 

4 . Plaxton Routing Plaxton routing provides an answer: it has been used in several important P2P networks like Microsoft’s Pastry and UC Berkeley’s Tapestry (Zhao, Kubiatowicz, Joseph et al.) that is also the backbone of Oceanstore, a persistent global-scale storage system 4 

5 . Object and Node names Objects and nodes acquire names independent of their location and semantic properties, in the form of random fixed-length bit-sequences (160 bits) using a hashing algorithm such as SHA-1 . This leads to roughly even distribution of objects in the name space) 5 

6 . The Main Idea For every object, form a rooted tree. The root node stores a pointer to the server that stores the object. The root does not hold a copy of the object itself. Once you access the root, you can navigate to the server storing that object. How to choose a root for a given object? 6 

7 . The Main idea continued Embed an n-node virtual height-balanced tree T into the network. Each node u maintains information about copies of the object in the subtree of T rooted at u. 7 

8 . Choosing the root An object’s root is a node whose name matches the object’s name in the largest number of trailing bit positions. In case there are multiple such nodes, choose the node with the largest such id. [Life of Pi]: 010 010110101000 Node X: 110 010110101000 Node Y: 011 010110101000 “Life of Pi” will be mapped to Node X 8 

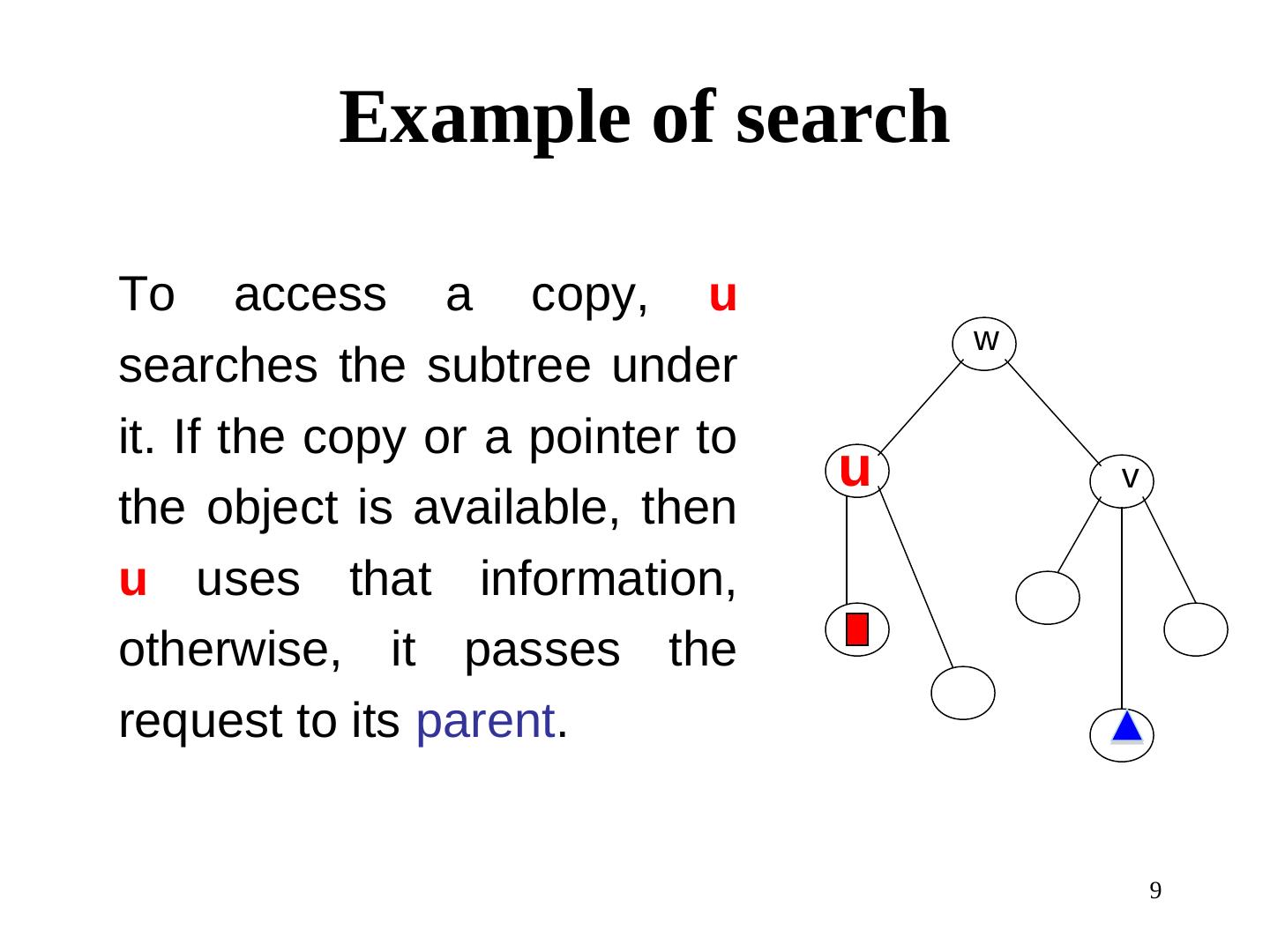
9 . Example of search To access a copy, u w searches the subtree under it. If the copy or a pointer to u v the object is available, then u uses that information, otherwise, it passes the request to its parent. 9 

10 . Plaxton tree Plaxton tree (some call it Plaxton mesh) is a data structure that allows peers to efficiently locate objects, and route to them across an arbitrarily- sized network, using a small routing map at each hop. Each node serves as a client, server and a router. 10 

11 . Examples of Object names Represent node ids and object names as strings of digits using base = 2b, where b is a fixed positive integer. Let b=2. Thus, the name of object B = 1032 (base 4 = 2b), name of object C = 3011, name of a node u = 3122 and so on. 11 

12 . Neighbor map L3 L2 L1 L0 Consider an example with b=3, i.e. the id base 2b = 8. Level i entries match i suffix entries. Number of entries per level = ID base = 8 Each entry is the suffix of a matching node with least cost. If no such entry exists, then pick the one that has highest id & largest suffix match y2 y2’ These are all primary entries Neighbor map of node 5642 12 

13 . More on neighbor map In addition to primary entries (lowest access cost), each level contains secondary entries. -- A node u is a secondary entry of node x at a level i, if (1) it is not the primary neighbor, and (2) the cost c(x,u) ≤ c(x,w) for all non-primary neighbor w with a matching suffix of size i. -- Each node also stores reverse neighbors for each level. A node y is a reverse neighbor of x if and only if x is a primary neighbor of y. -- Each node stores a pointer list (O,y,k) for each object in its subtree, where O is the object, y is the node holding a copy of A and k is the upper bound of the cost to access A All entries are statically chosen, and this needs global knowledge (-) 13 

14 .Neighbor map: another example x First hop for 0123 First hop for Destination=3623 Destination =4307 3187 A027 y1’ 9623 y1 Reverse L0 L2 pointer c(x,y1’) > c(x.y1) Secondary b=4,so node 2A53 1553 L1 neighbor names are in c(x,y2’) > c(x.y2) y2 y2’ Hex (base 24) Destination = 7353 Size of the routing table: base * log base (n) 14 

15 . Routing Algorithm To route to root of an object – Let shared suffix (between root id and node id) have length s – If s = log base (n) (i.e. this node is the root) then done, else look at level s+1 – Match the next digit of the destination id – Send the message to that node Eventually the message gets relayed to the destination This is called suffix routing (one could also use prefix routing). 15 

16 . Example of suffix routing Consider routing a message from 005712  627510 (base = 8) 005712 0 1 2 3 4 5 6 7 005712 340330 0 1 2 3 4 5 6 7 340330 743210 743210 0 1 2 3 4 5 6 7 134510 134510 0 1 2 3 4 5 6 7 307510 307510 0 1 2 3 4 5 6 7 How many hops? 727510 0 1 2 3 4 5 6 7 727510 627510 0 1 2 3 4 5 6 7 627510 16 

17 . Pointer list Root of O Each node x has a pointer list P(x): (O,S,5) P(x) is a list of triples (O, S, k), - where O is the object, (O,S,4) (O,S,3) - Node S holds a copy of O, - and k is the max cost of the access. (O,S,2) The pointer list is updated by insert (O,S,1) and delete operations. (O,S) Server S 17 

18 . Inserting a copy Root of O (O,S’,3) Intermediate nodes maintain the minimum cost of access. While (O,S’,2) (O,S’,1) inserting a duplicate copy, the pointers are modified, so that they Server S’ (O,S,2) direct to the closest copy (O,S,1) (O,S) Server S 18 

19 . Deleting a copy Root of O (O,S,5) Removes all pointers to that copy (O,S’,3) of the object in the pointer list on (O,S,3) the nodes leading to the root (O,S’,2) (O,S,4) (O,S’,1) Otherwise, it uses the reverse Server S’ pointers to update the entry. (O,S,2) (O,S,1) (O,S) Server S 19 

20 . Results Let C= (max{c(u,v): u,v in V} Cost of reading a file A of length L(A) from node v by node u =f(L(A)).c(u,v) Cost of inserting a new object = O(C) Cost of deleting an existing object = O(C log n) 20 

21 . Benefits and Limitations + Scalable solution Small routing table. All routing done using locally available data + Existing objects are guaranteed to be found + Simple fault handling 1234 1238  1278  1678  5678 3128  3178  3678 + Optimal routing distance 21 

22 . Benefits and limitations - Needs global knowledge to form the neighbor tables. How can we solve it? - The root node for each object may be a possible bottleneck. 22