- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
04 小世界模型--米尔格拉姆未能解答的问题
展开查看详情
1 .Peer-to-Peer and Social Networks Small World Graphs
2 .The small-world model [ Watts and Strogatz (1998)] They followed up on Milgram’s work and reason about why there is a small degree of separation between individuals in a social network. Research originally inspired by Watt’s efforts to understand the synchronization of cricket chirps , which show a high degree of coordination over long ranges, as though the insects are being guided by an invisible conductor. Disease spreads faster over a small-world network .
3 .Questions not answered by Milgram Why six degrees of separation? Any scientific reason? What properties do these social graphs have? Is clustering the only missing link? (Human beings prefer clustered environments). But the diameter must also be low! Time to reverse engineer this.
4 .What are small-world graphs Completely regular Small-world graphs ( ) Completely random n = number of nodes, k = number of neighbors of each node
5 .Completely regular A ring lattice If then The clustering coefficient is OK, but Diameter is too large!
6 .Completely random Diameter is small, but the Clustering coefficient is too small!
7 .Small-world graphs Start with the regular graph, and with probability p rewire each link to a randomly selected node. It results in a graph that has high clustering coefficient but low diameter …
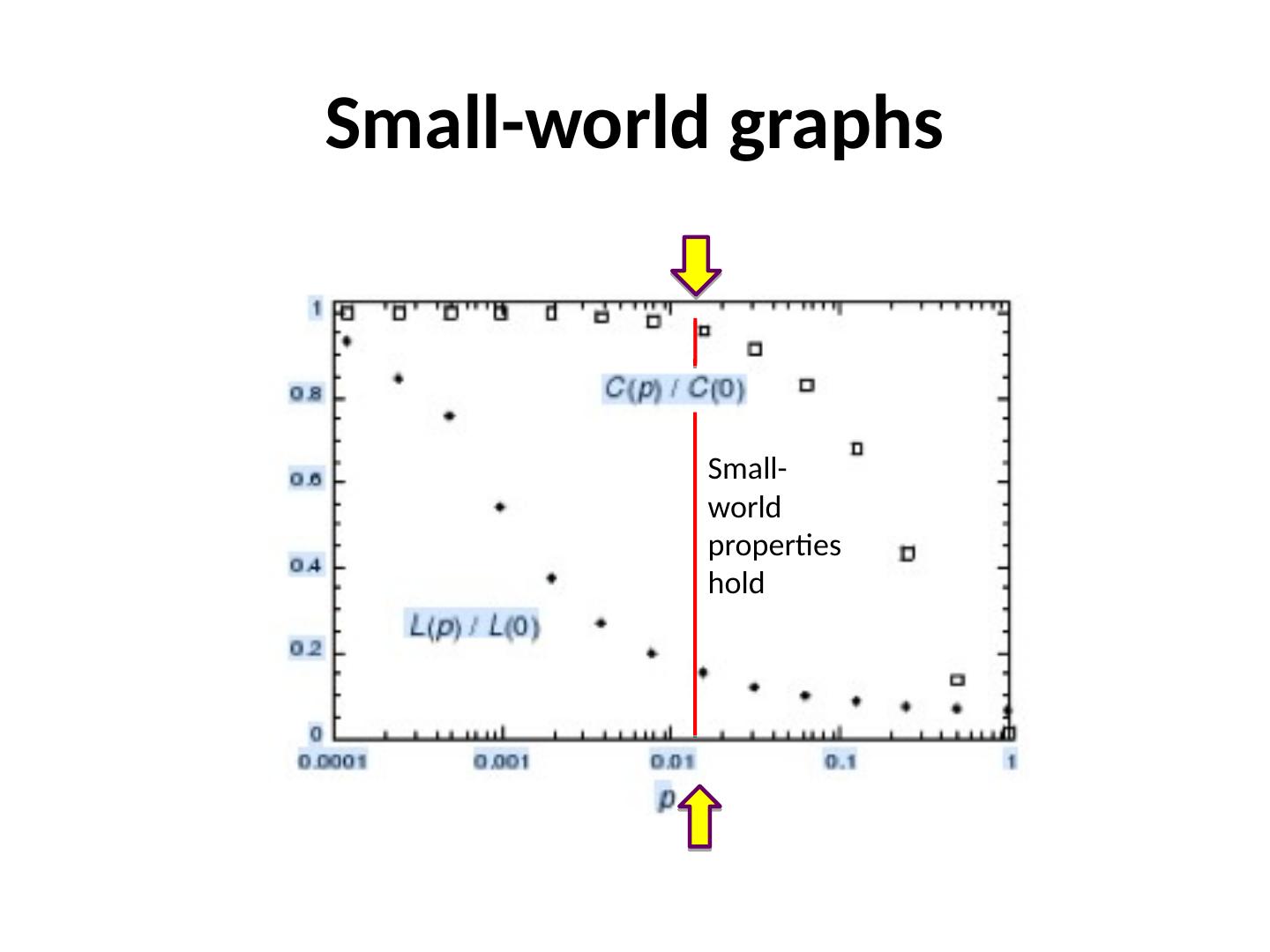
8 .Small-world graphs Small-world properties hold
9 .Limitation of Watts- Strogatz model Jon Kleinberg argues … Watts- Strogatz small-world model illustrates the existence of short paths between pairs of nodes. But it does not give any clue about how those short paths will be discovered . A greedy search for the destination will not lead to the discovery of these short paths.
10 .Kleinberg’s Small-World Model Consider an grid . Each node has a link to every node at lattice distance ( short range neighbors) & long range links. Choose long-range links at lattice distance with a probability proportional to (**See note below) r = 2 p = 1, q = 2 n n **Here r denotes the dimension of the space. Since we are considering a 2D grid, r=2
11 .Results Theorem 1. There is a constant ( depending on and but independent of ) , so that when , the expected delivery time of any decentralized algorithm is at least ** The above result is valid for a 2D grid only. For a 1D space like a Linear topology of a ring, the expected time will be different
12 .Proof of theorem 1 Probability to reach within a lattice distance from the target is So, it will take an expected steps to reach the target.
13 .More results Theorem 2 . There is a decentralized algorithm A and a constant (dependent on and ) but independent of n, such that when r=2 and , the expected delivery time of A is at most For a one-dimensional search space , the same result will hold for i.e the expected delivery time is O(log 2 n) when long-range links at distance d are chosen with probability proportional to d -1
14 .Variation of search time with r E x ponent r Log T This is for a 2D topology
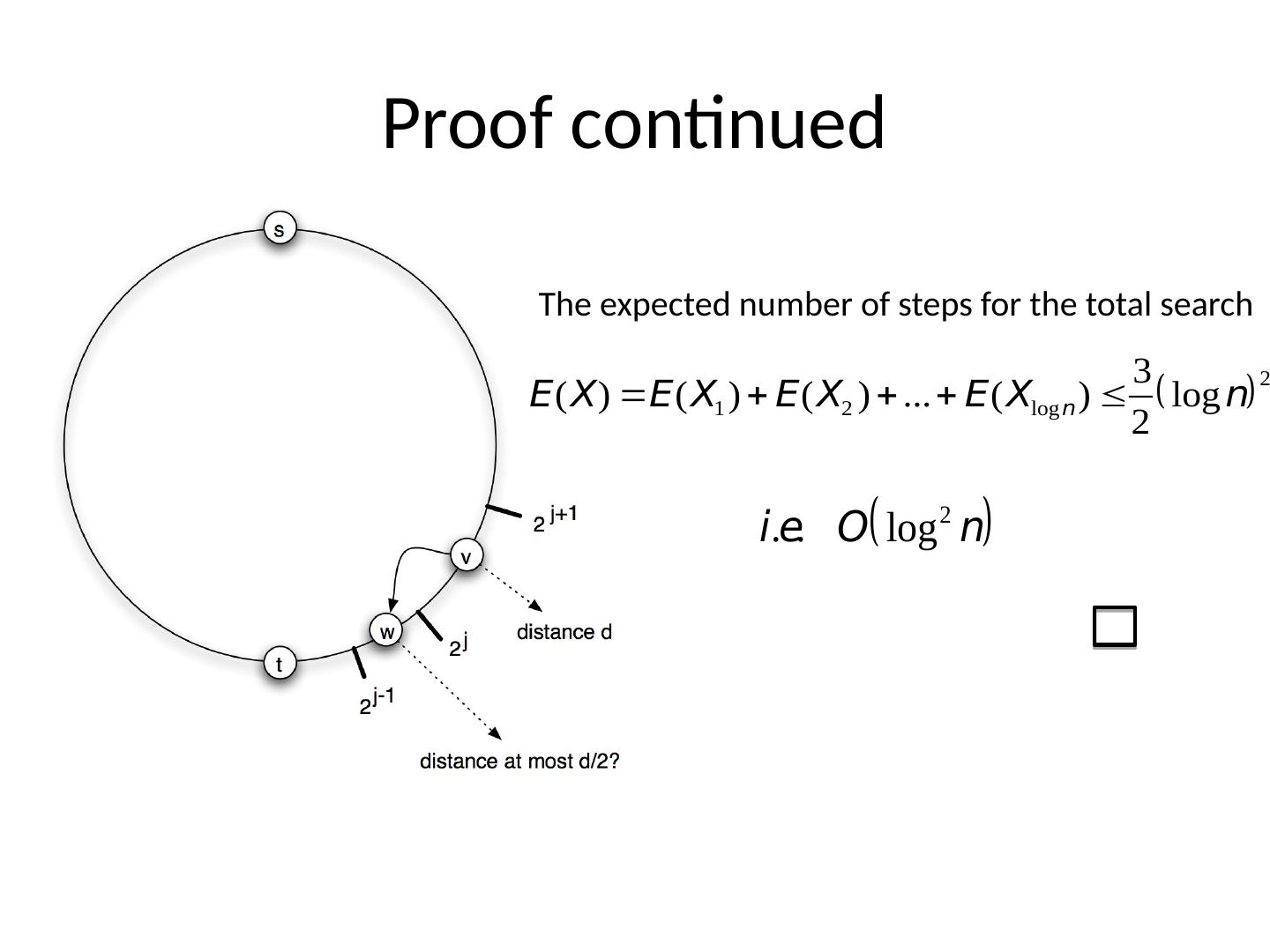
15 .Proof of Theorem 2 Main idea. We show that in phase j , the expected time before the current message holder has a long-range contact within lattice distance 2 j from t is O( log n ) ; at this point, phase j will come to an end. As there are at most log n phases , a bound proportional to log 2 n follows.
16 .Proof of Kleinberg’s theorem Probability (u linking to v) = Since For simplicity we prove it for a one dimensional ring topology, so r =1
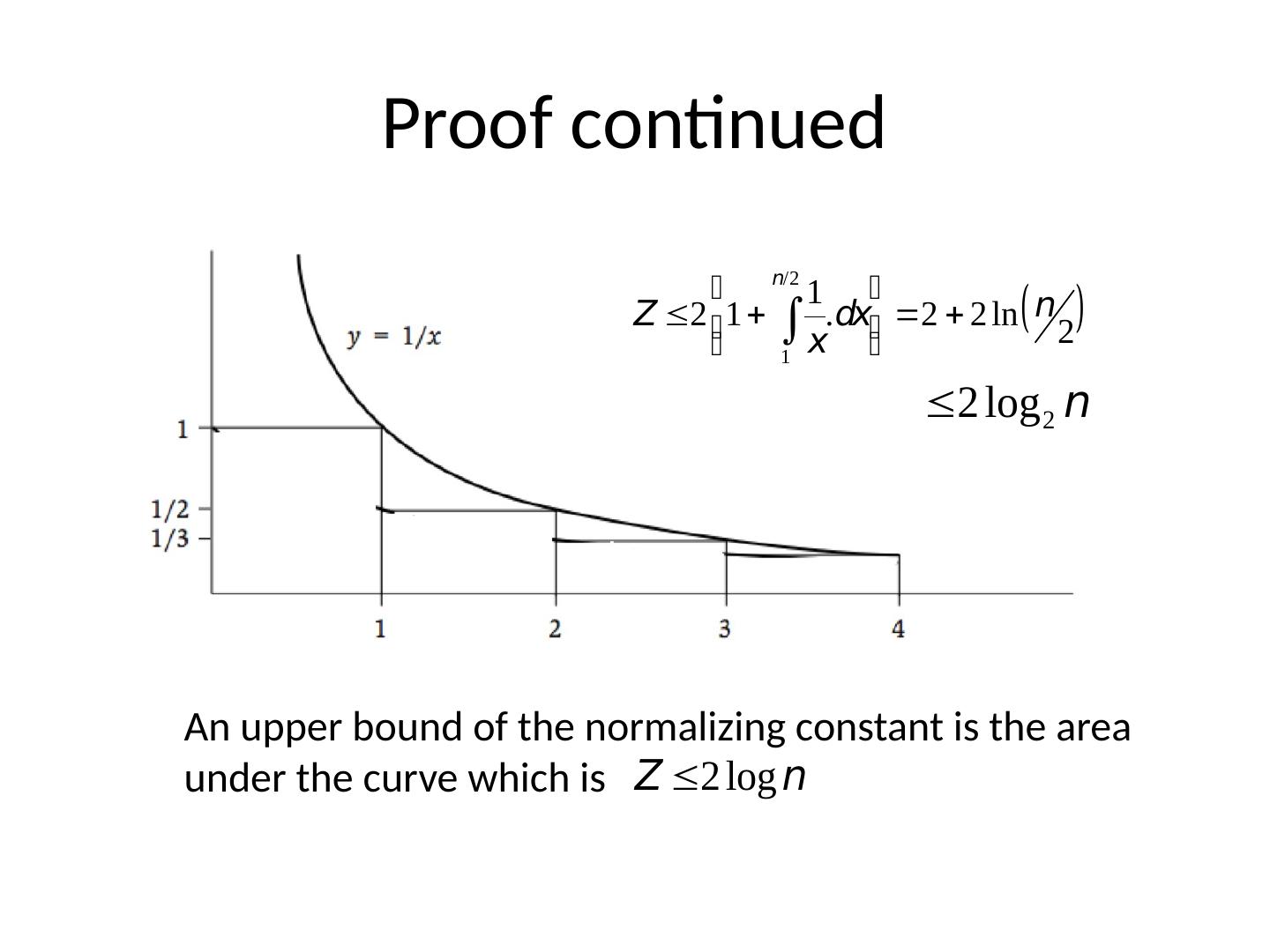
17 .Proof continued An upper bound of the normalizing constant is the area under the curve which is
18 .Proof continued Thus, probability that a link ( v,w ) exists is = We now calculate the time taken in one phase (implies that the distance to the target becomes less than d/2 . Probability in one step the search reaches a given node in the target zone ≥ Why? Probability that in one step the search reaches some node within distance d/ 2 ≥
19 .Proof continued How can this continue? Let be the number of steps in phase The probability that this phase continues for at least i steps ≤ The expected number of steps to complete phase j is = So, This leads to
20 .Proof continued The expected number of steps for the total search