- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
02 有向图和无向图
展开查看详情
1 .Peer-to-Peer and Social Networks Fall 2017 Random Graphs
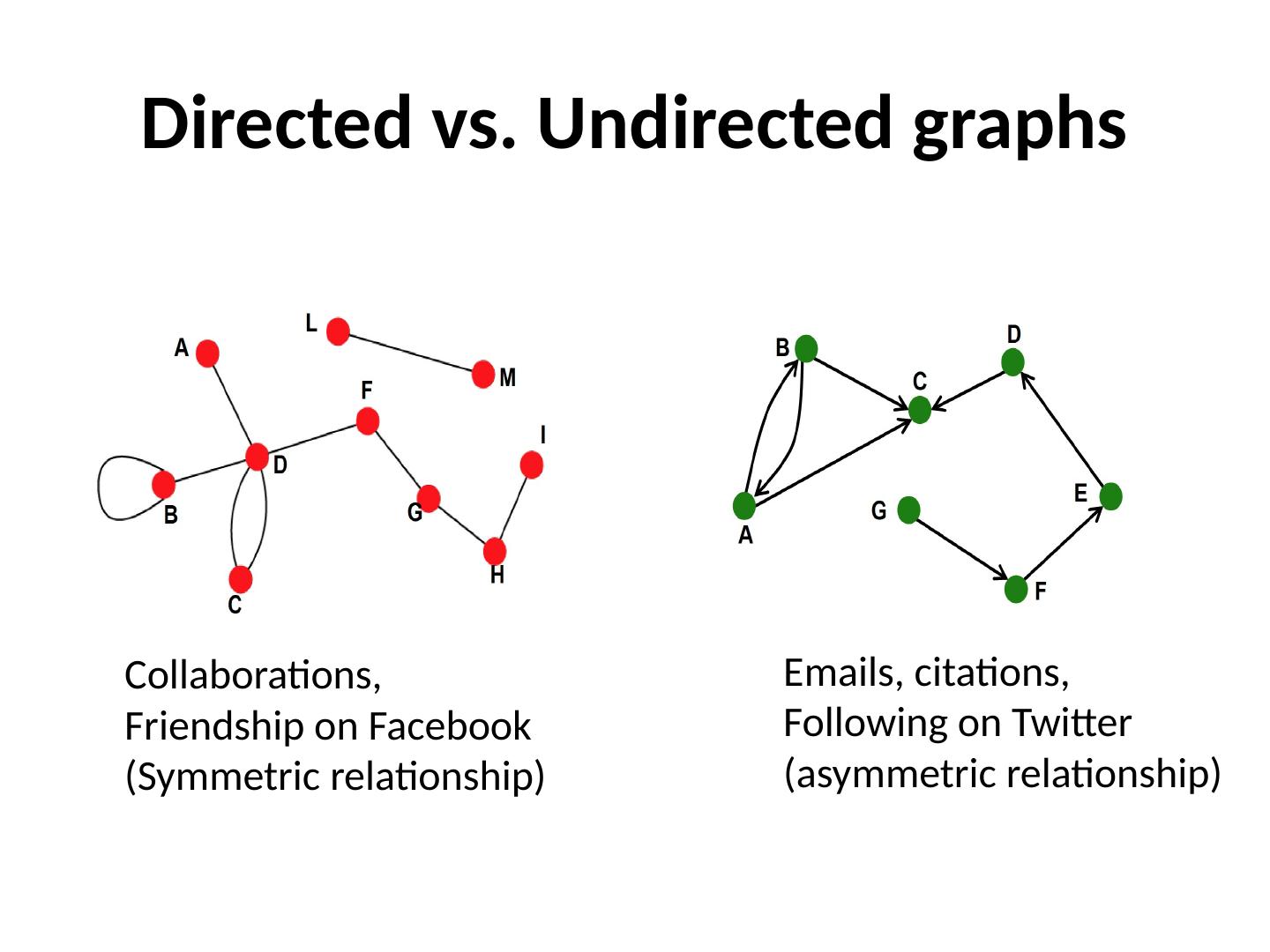
2 .Directed vs. Undirected graphs Collaborations, Friendship on Facebook (Symmetric relationship) Emails, citations, Following on Twitter (asymmetric relationship)
3 .Directed vs. Undirected graphs Degree of A = 4 In directed graphs, we have to define in-degree and out-degree of nodes. What is the average in-degree of the directed graph to the right? Degree of a node = number of edges incident on it . The average degree of nodes in an n-node graph G = (V, E) is
4 .Sparse and dense graphs In a clique with n nodes, the degree of each node is ( n-1) . In dense graphs, the average node degree is O(n ) . In sparse graphs, the average degree is much smaller. Are most real world social networks dense or sparse? A clique
5 .Real-world graphs Most real world graphs are sparse , i.e. the average degree is much less than n-1 for an n-node graph. Some examples are LinkedIn N = 6,946,668 Average degree = 8.87 Co-authorship (DBLP) = 317,080 Average degree = 6.62 Graphs can be weighted or un-weighted . Is the co-authorship network weighted or un-weighted ?
6 .Random graphs Erdös-Renyi model One of several models of real world networks Presents a theory of how social webs are formed. Start with a set of isolated nodes Connect each pair of nodes with a probability The resulting graph is known as
7 .Random graphs ER model is different from the model The model randomly selects one from the entire family of graphs with nodes and edges.
8 .Properties of ER graphs Property 1 . The expected number of edges is Property 2 . The expected degree per node is Property 3 . The expected diameter of is [deg = expected degree of a node] [Note the word expected ] Why?
9 .Degree distribution in random graphs Probability that a node connects with a given set of nodes (and not to the remaining remaining nodes) is One can choose out of the remaining nodes in ways. So the probability distribution is ( For large and small it is equivalent to Poisson distribution ) ( binomial distribution )
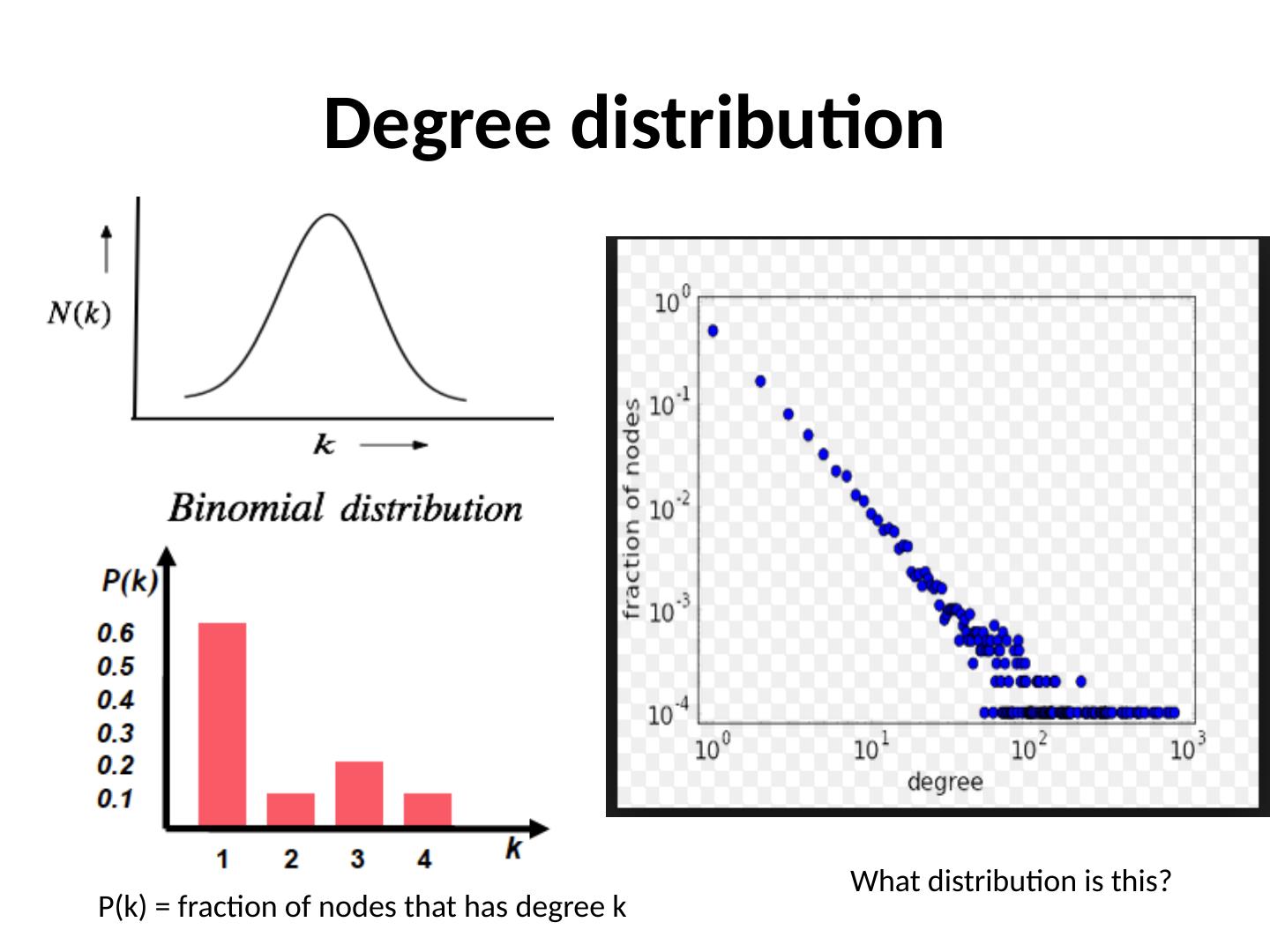
10 .Degree distribution P(k ) = fraction of nodes that has degree k What distribution is this?
11 .Important network properties Here path length means average path length between pairs of nodes
12 .Clustering coefficient For a given node, its local clustering coefficient (CC) measures what fraction of its various pairs of neighbors are neighbors of each other. CC(B) = 3/6 = ½ CC(D) = 2/3 = CC(E) The global CC is the average of the local CC values. B’s neighbors are {A,C,D,E}. Only (A,D), (D,E), (E,C) are connected CC of a graph is the mean of the CC of its various nodes
13 .Properties of ER graphs -- When , an ER graph is a collection of disjoint trees. -- When suddenly one giant (connected) component emerges. Other components have a much smaller size [ Phase change ]
14 .Properties of ER graphs When the graph is almost always connected why? (i.e. connected with high probability ) Hints. The probability that a single node remains disconnected is (1-p)^(n-1). Substitute p = c.logn /n The clustering coefficient of an ER graph = p ( why ?} But a social network is not necessarily an ER graph! Human society is a “clustered” society, but ER graphs have poor (i.e. very low) clustering coefficient.
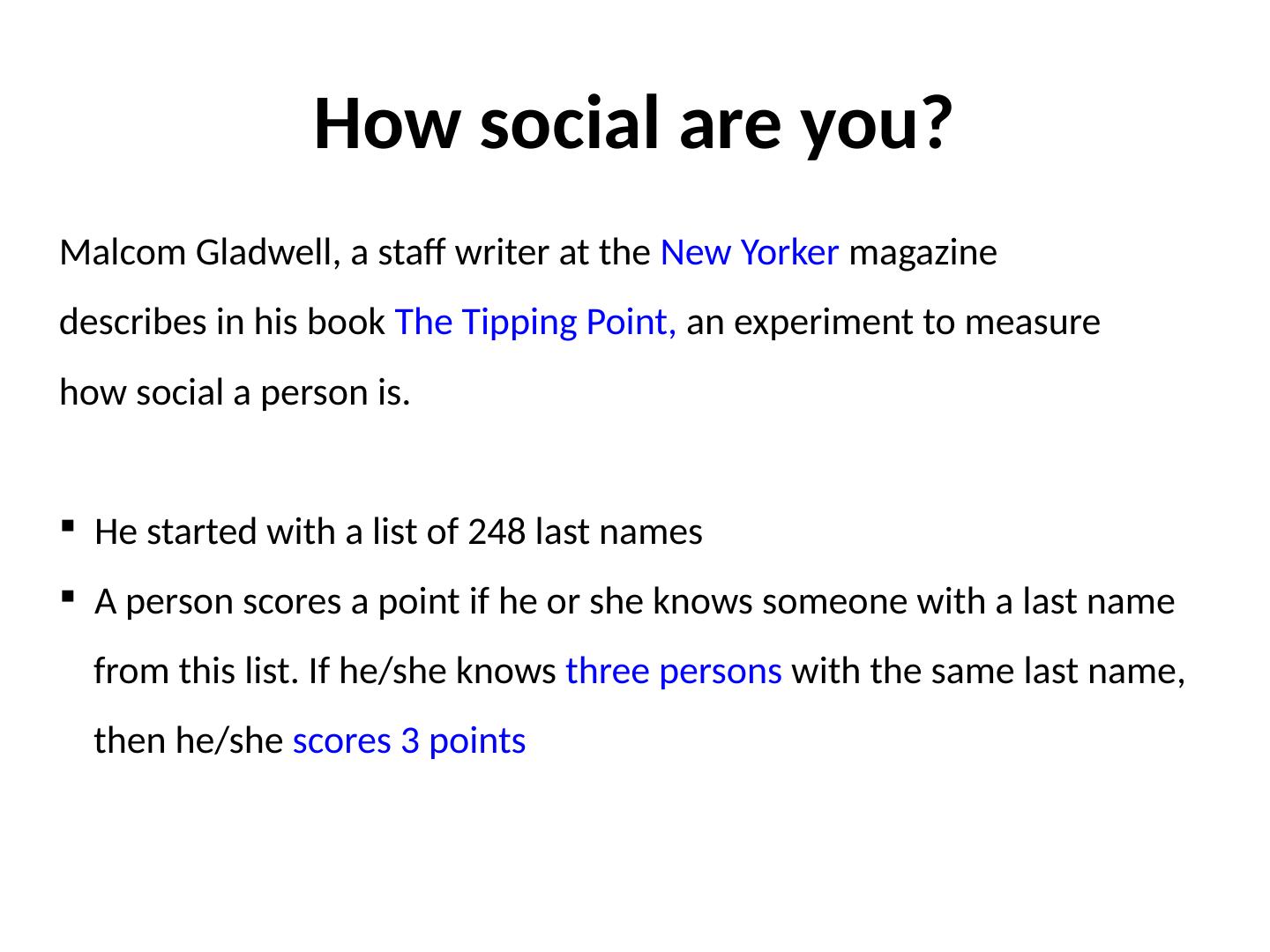
15 .How social are you? Malcom Gladwell , a staff writer at the New Yorker magazine describes in his book The Tipping Point, an experiment to measure how social a person is. He started with a list of 248 last names A person scores a point if he or she knows someone with a last name from this list. If he/she knows three persons with the same last name, then he/she scores 3 points
16 .How social are you? (Outcome of the Tipping Point experiment) Altogether 400 people from different groups were tested. (min) 9, (max) 118 {from a random sample} (min) 16, (max) 108 {from a highly homogeneous group} (min) 2, (max) 95 {from a college class} [Conclusion: Some people are very social, even in small or homogeneous samples. They are connectors ]
17 .Connectors Barabási observed that connectors are not unique to human society only, but true for many complex networks ranging from biology to computer science , where there are some nodes with an anomalously large number of links . Certainly these types of clustering cannot be expected in ER graphs. The world wide web, the ultimate forum of democracy , is not a random network, as Barabási’s web-mapping project revealed.
18 .Anatomy of the web Barabási first experimented with the Univ. of Notre Dame’s web. 325,000 pages 270,000 pages (i.e. 82%) had three or fewer links 42 had 1000+ incoming links each. The entire WWW exhibited even more disparity . 90% had ≤ 10 links , whereas a few (4-5) like Yahoo were referenced by close to a million pages! These are the hubs of the web . They help create short paths between nodes ( mean distance = 19 for WWW obtained via extrapolation ). ( Some dispute this figure now)
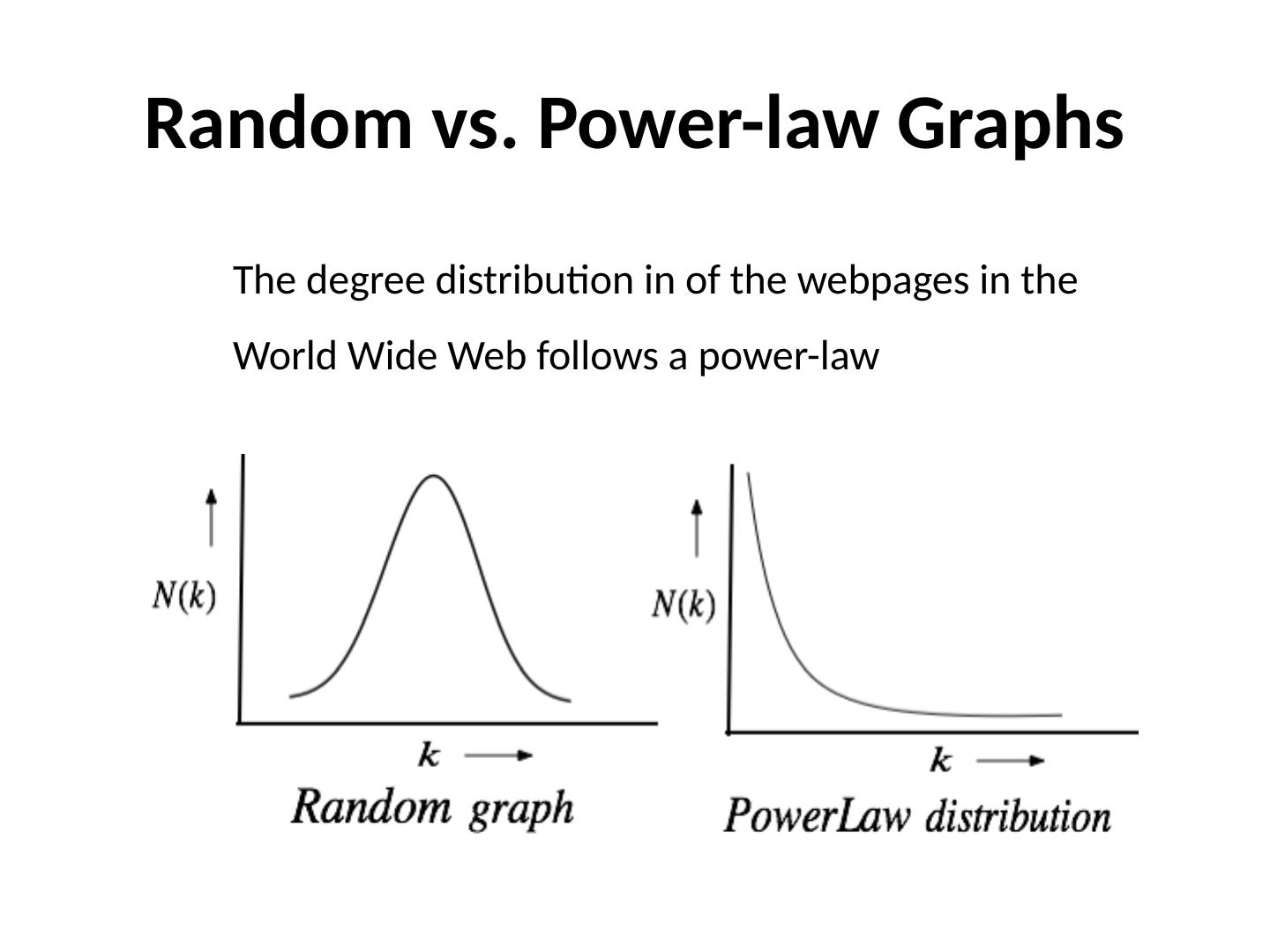
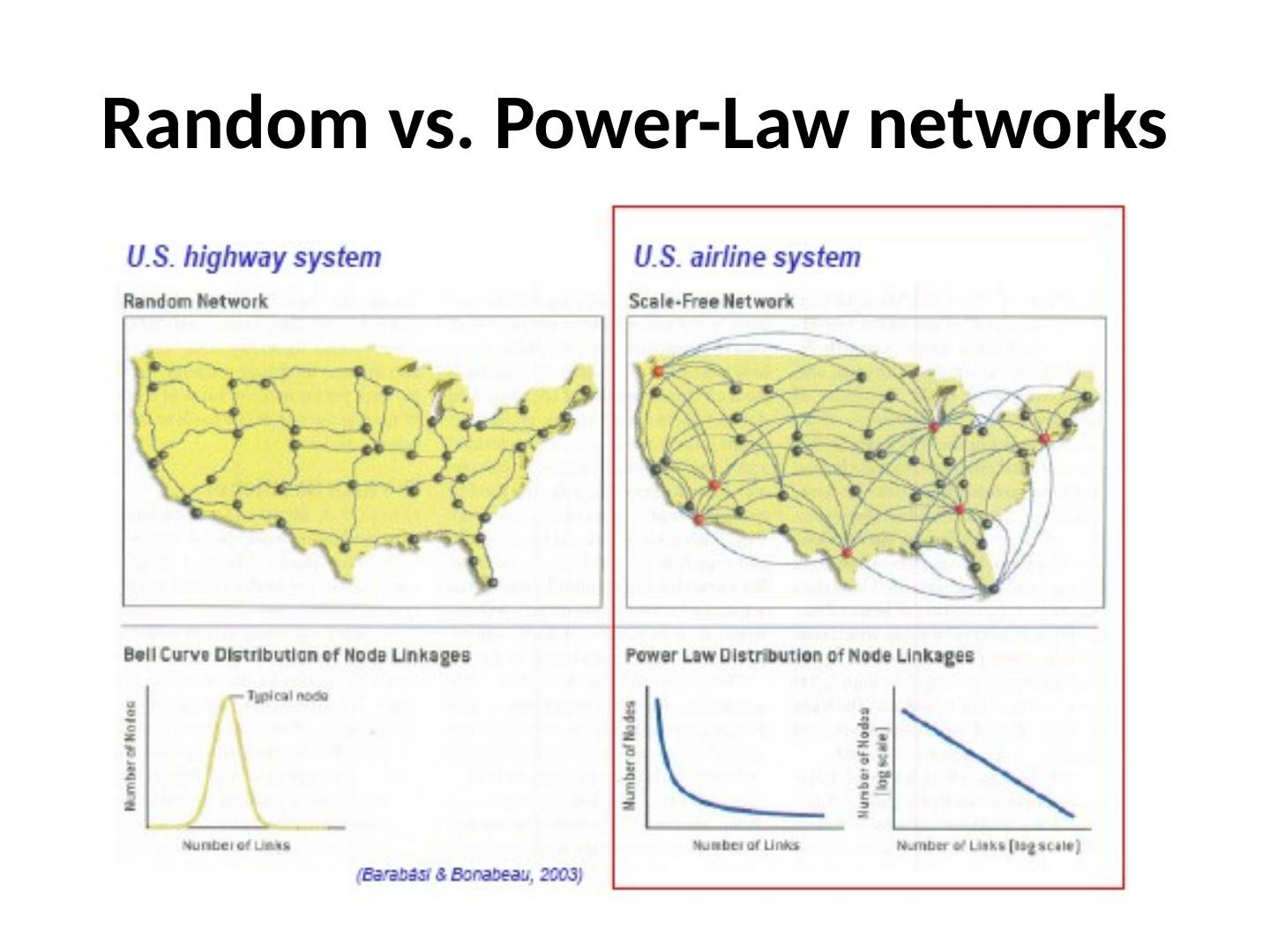
19 .Random vs. Power-law Graphs The degree distribution in of the webpages in the World Wide Web follows a power-law
20 .Random vs. Power-law Graphs
21 .Random vs. Power-Law networks
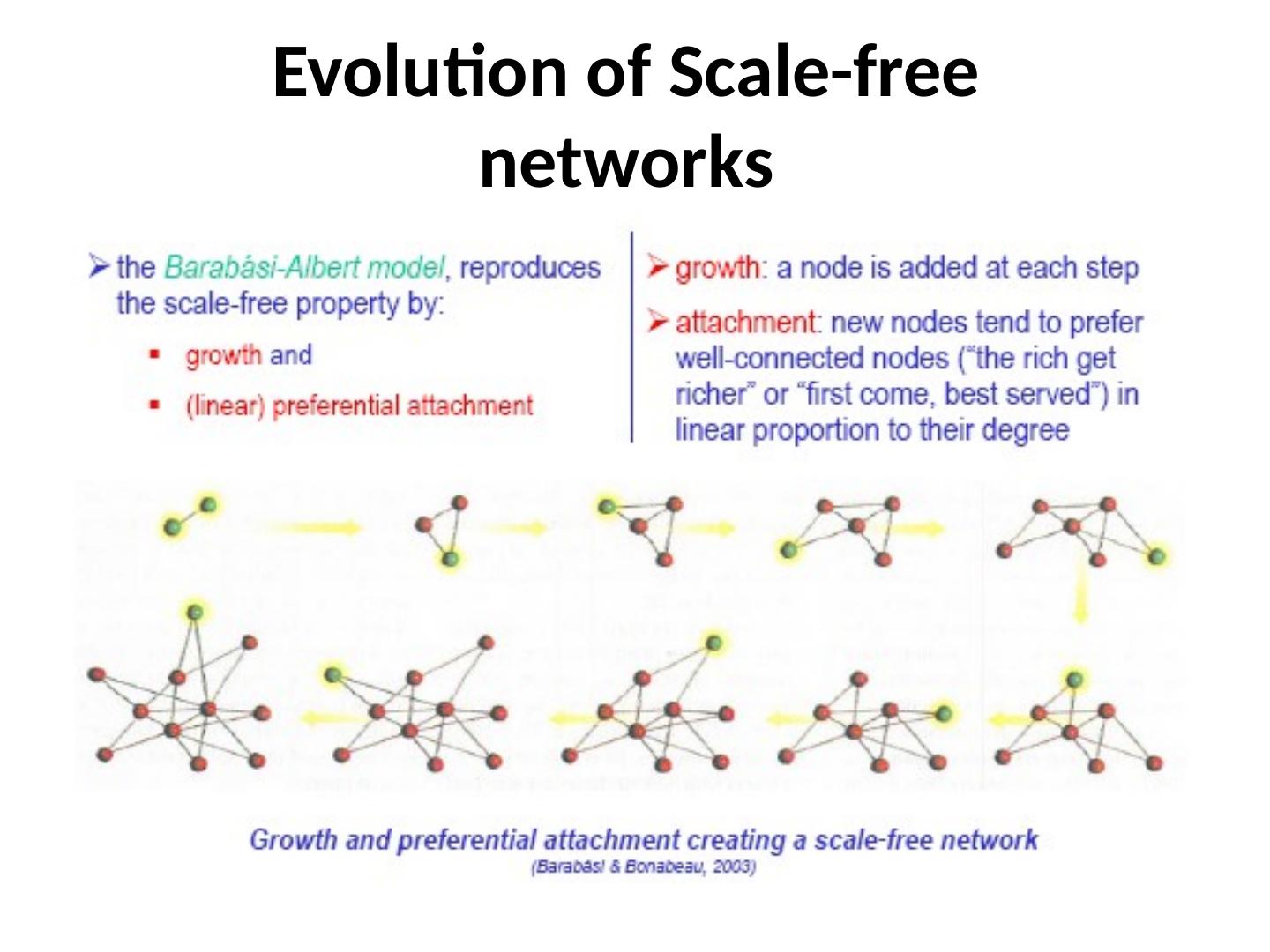
22 .Evolution of Scale -free networks
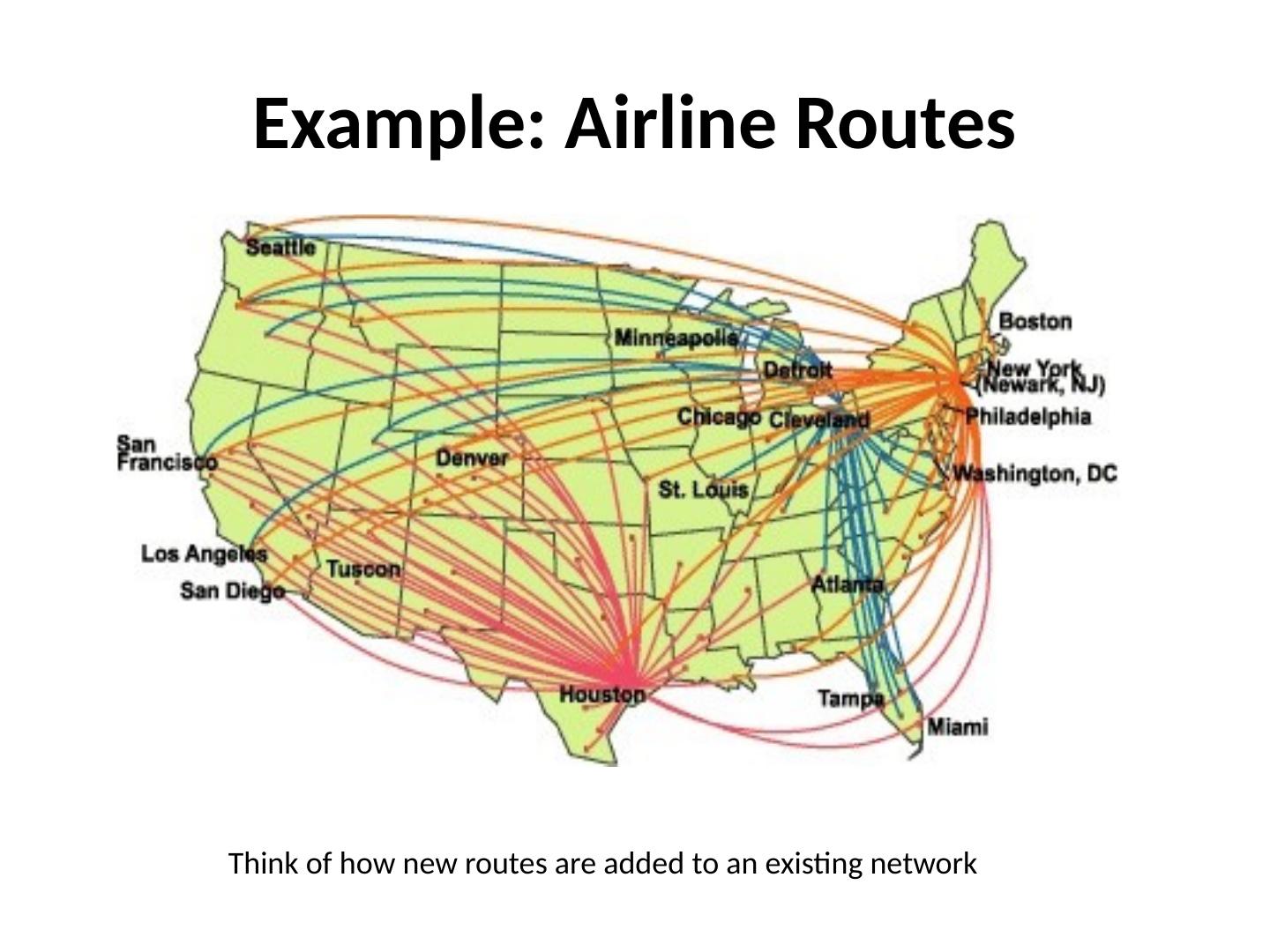
23 .Example: Airline Routes Think of how new routes are added to an existing network
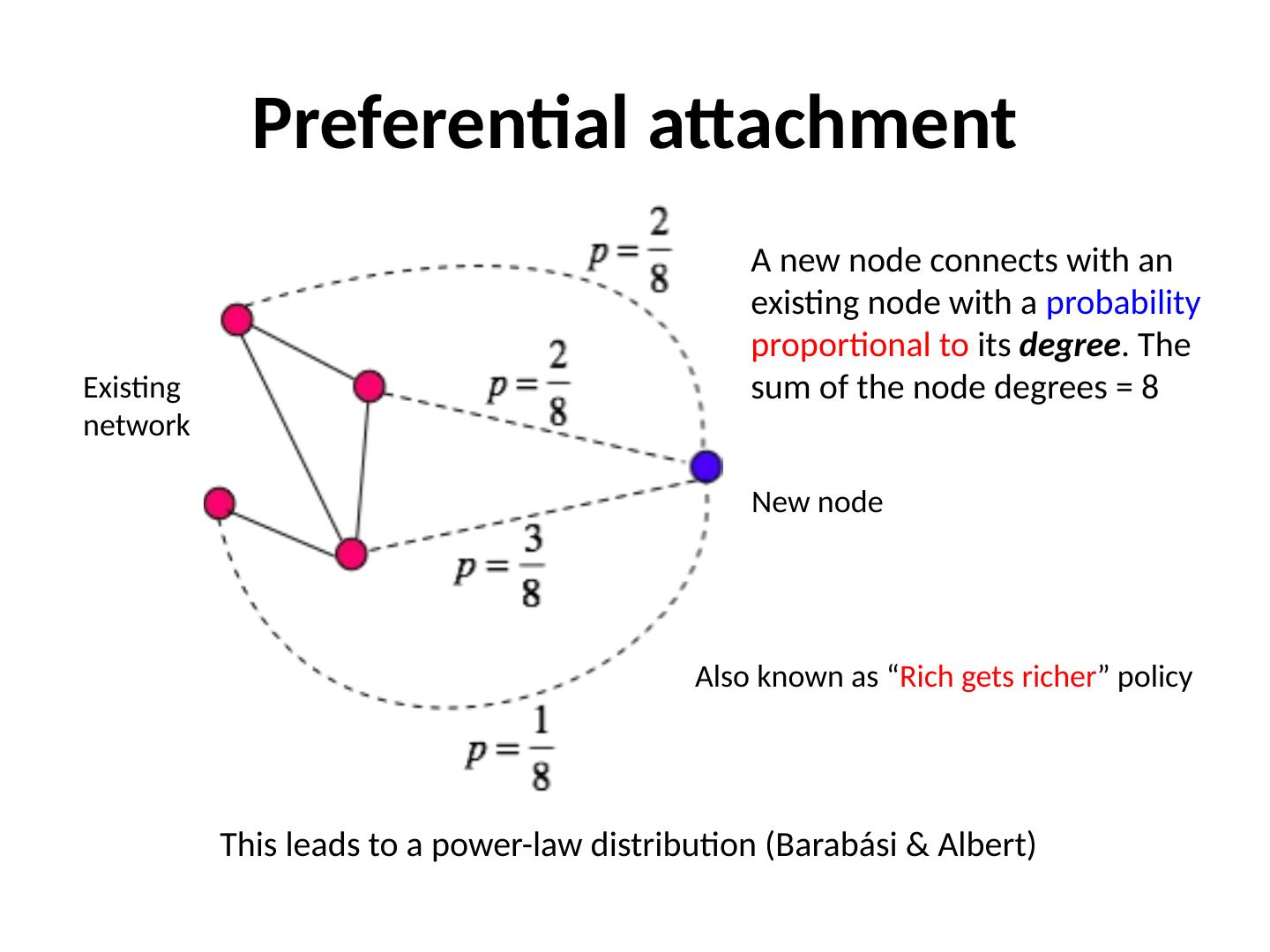
24 .Preferential attachment New node Existing network A new node connects with an existing node with a probability proportional to its degree . The sum of the node degrees = 8 This leads to a power-law distribution ( Barabási & Albert) Also known as “ Rich gets richer ” policy
25 .Anatomy of the web Albert, Jeong , B arabasi : Diameter of the World Wide Web. (Brief Communication). Nature 401, 9 Sep 1999
26 .The web is a bow tie Reference: Nature 405, 113(11 May 2000)
27 .Power law graph The degree distribution in of the webpages in the World Wide Web follow a power-law . In a power-law graph , the number of nodes with degree satisfies the condition Also known as scale-free graph . Other examples are -- Income and number of people with that income -- Magnitude and number of earthquakes of that magnitude -- Population and number of cities with that population