10 计算机组成--布尔代数

1 .Boolean Algebra A+0=A A + A’ = 1 A.1=A A. A’ = 0 1+A=1 A+B=B+A 0. A = 0 A.B=B.A A + (B + C) = (A + B) + C A. (B. C) = (A. B). C A+A=A A.A =A A. (B + C) = A.B + A.C Distributive Law A + B.C = (A+B). (A+C) A.B=A+B De Morgan’s theorem A+B=A.B 

2 .De Morgan’s theorem A.B=A+B A+B=A.B Thus, is equivalent to Verify it using truth tables. Similarly, is equivalent to These can be generalized to more than two variables: to A. B. C = A+B+C A+B+C= A.B.C 

3 .Synthesis of logic circuits Many problems of logic design can be specified using a truth table. Give such a table, can you design the logic circuit? Design a logic circuit with three inputs A, B, C and one output F such that F=1 only when a majority of the inputs is equal to 1. A B C F Sum of product form 0 0 0 0 F = A.B.C + A.B.C + A.B.C + A.B.C 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 Draw a logic circuit to generate F 

4 .Simplification of Boolean functions Using the theorems of Boolean Algebra, the algebraic forms of functions can often be simplified, which leads to simpler (and cheaper) implementations. Example 1 F = A.B + A.B + B.C = A. (B + B) + B.C How many gates do you save = A.1 + B.C from this simplification? = A + B.C A A F B B C F C 

5 .Example 2 F = A.B.C + A.B.C + A.B.C + A.B.C = A.B.C + A.B.C + A.B.C + A.B.C + A.B.C + A.B.C = (A.B.C + A.B.C) + (A.B.C + A.B.C) + (A.B.C + A.B.C) = (A + A). B.C + (B + B). C.A + (C + C). A.B = B.C + C.A + A.B Example 3 Show that A + A.B = A A + AB = A.1 + A.B = A. (1 + B) = A. 1 = A 

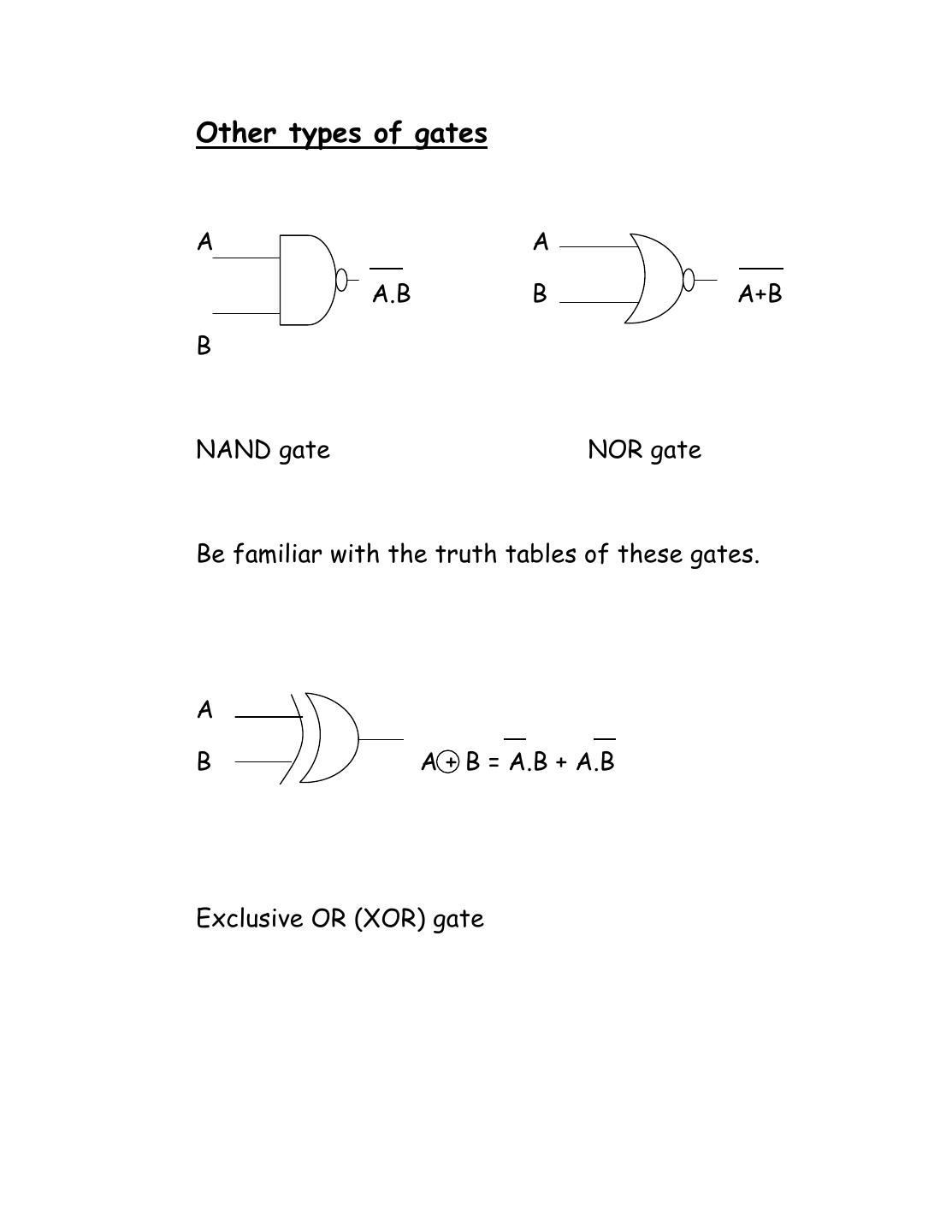
6 .Other types of gates A A A.B B A+B B NAND gate NOR gate Be familiar with the truth tables of these gates. A B A + B = A.B + A.B Exclusive OR (XOR) gate 

7 .NAND and NOR are universal gates Any function can be implemented using only NAND or only NOR gates. How can we prove this? (Proof for NAND gates) Any boolean function can be implemented using AND, OR and NOT gates. So if AND, OR and NOT gates can be implemented using NAND gates only, then we prove our point. 1. Implement NOT using NAND A A 

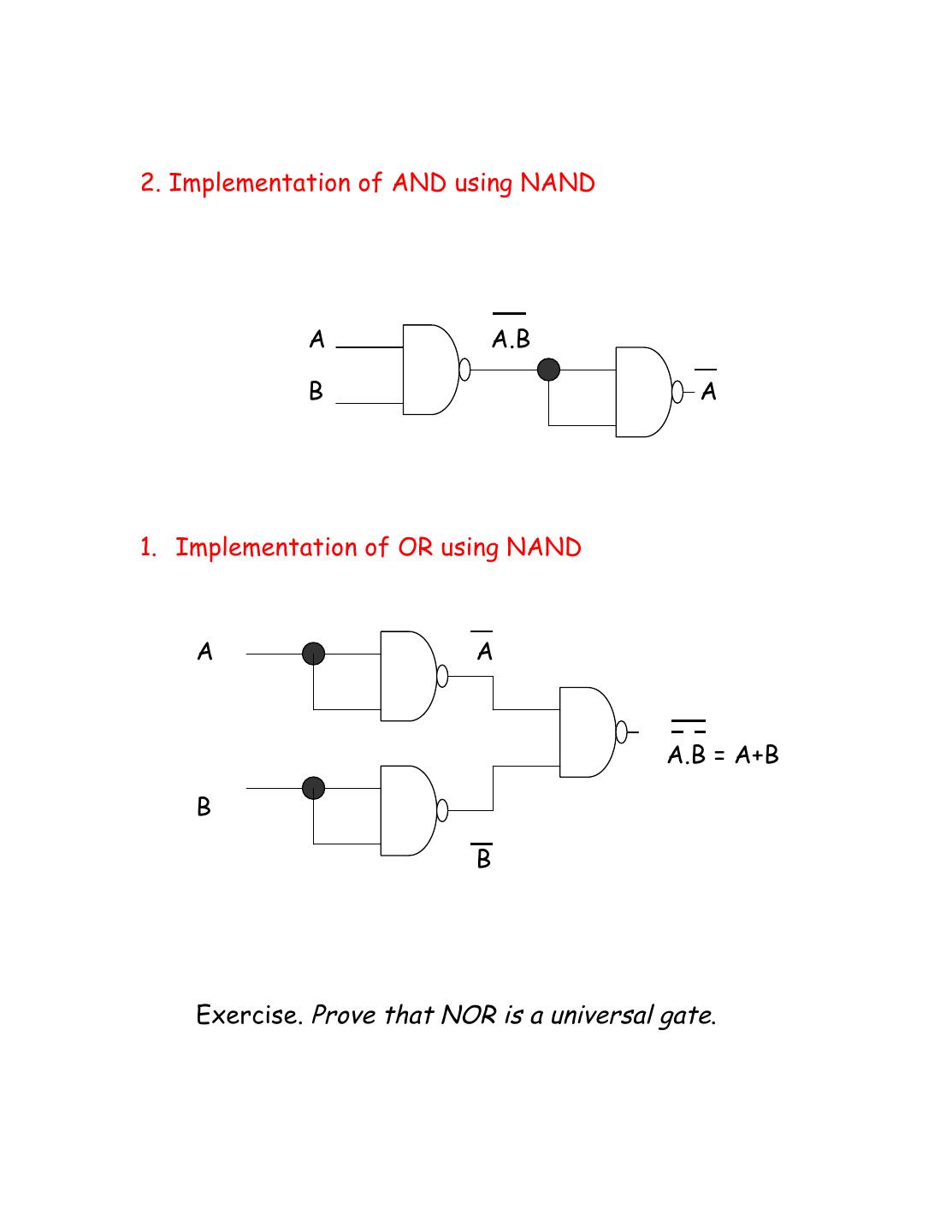
8 .2. Implementation of AND using NAND A A.B B A 1. Implementation of OR using NAND A A A.B = A+B B B Exercise. Prove that NOR is a universal gate.