分布式系统和算法：复制

1 . Replication • Improves reliability • Improves availability (What good is a reliable system if it is not available?) • Replication must be transparent and create the illusion of a single copy. 

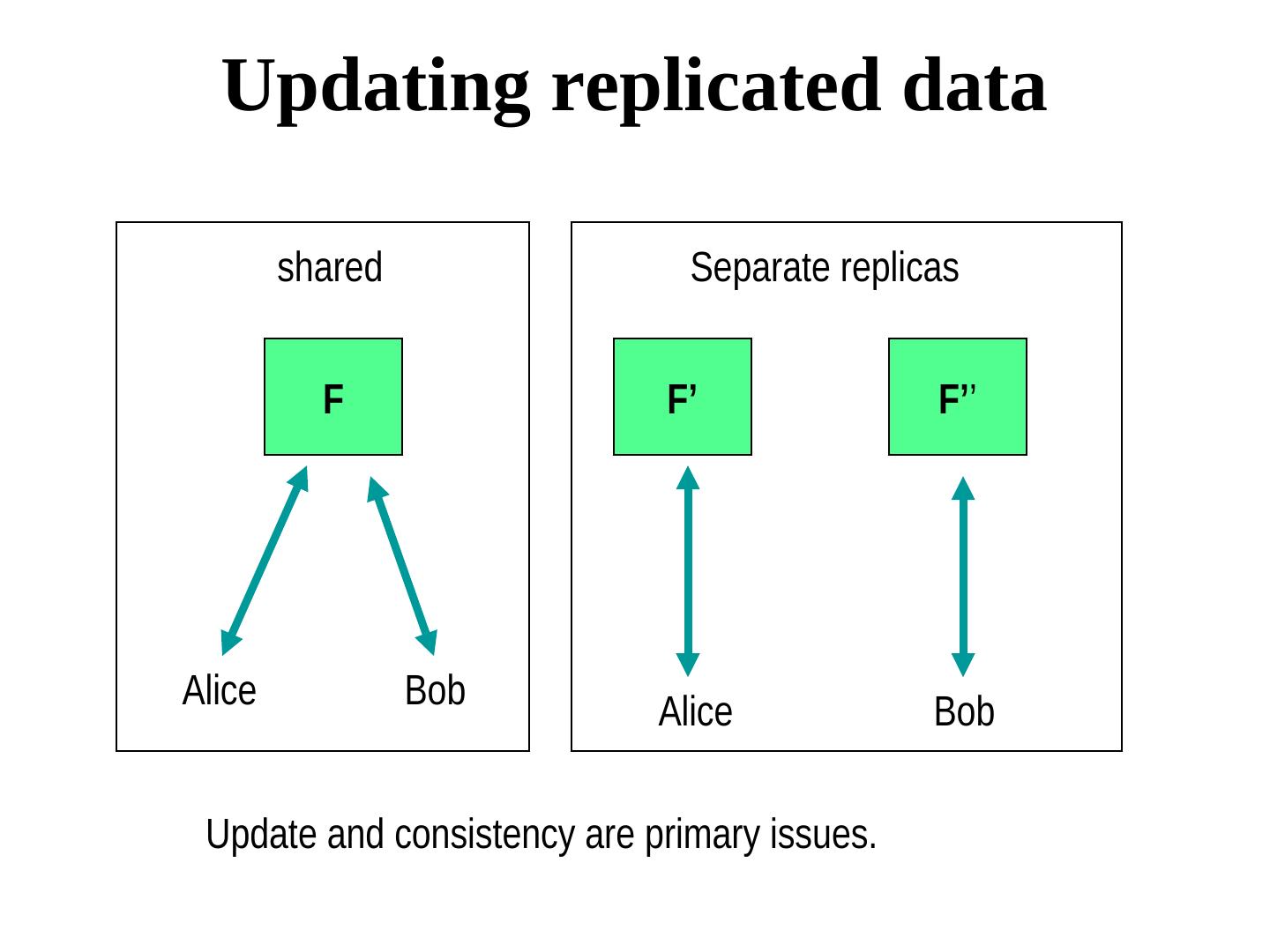
2 . Updating replicated data shared Separate replicas F F’ F’’ Alice Bob Alice Bob Update and consistency are primary issues. 

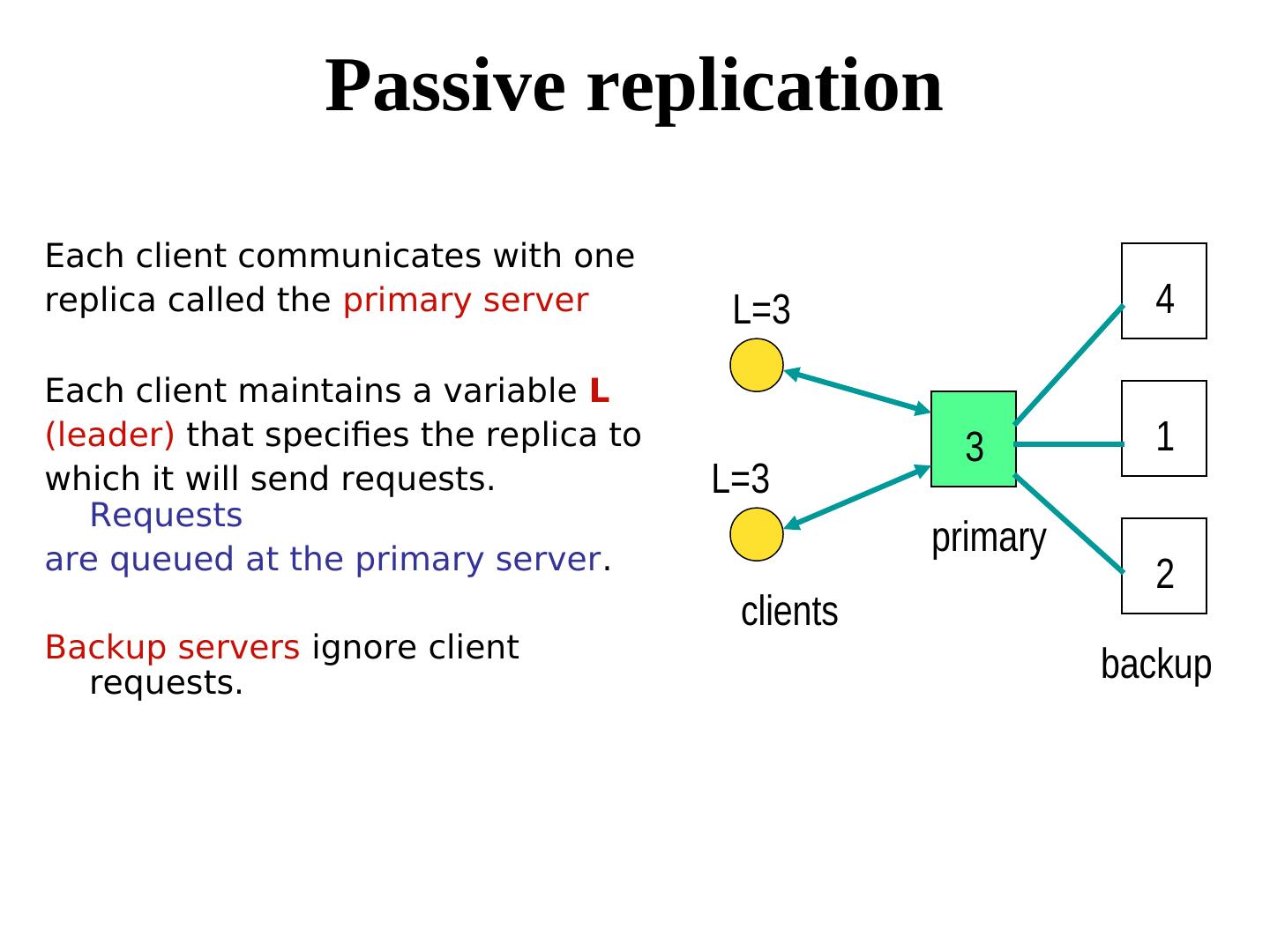
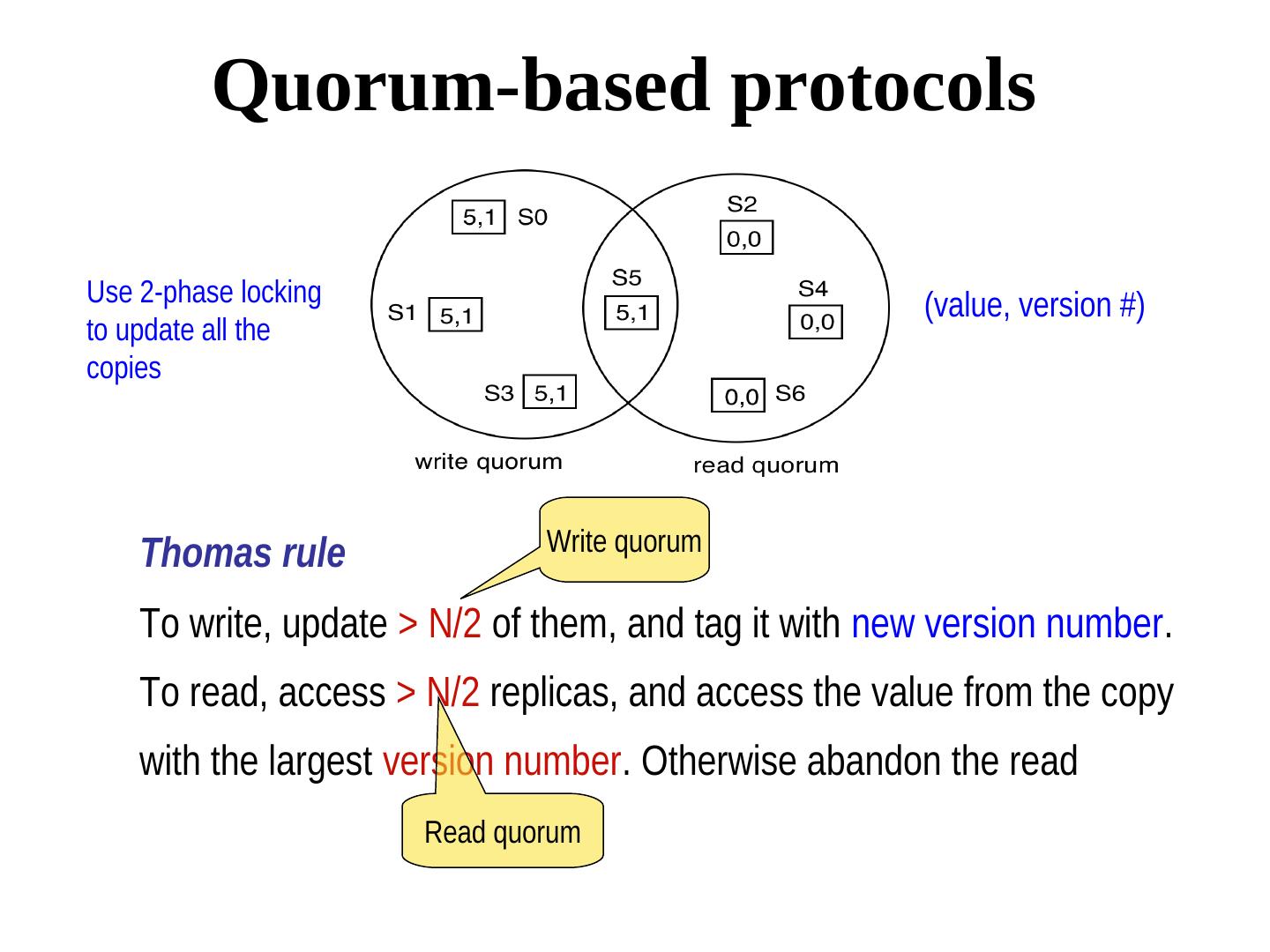
3 . Passive replication Each client communicates with one replica called the primary server L=3 4 Each client maintains a variable L (leader) that specifies the replica to 3 1 which it will send requests. L=3 Requests are queued at the primary server. primary 2 clients Backup servers ignore client requests. backup 

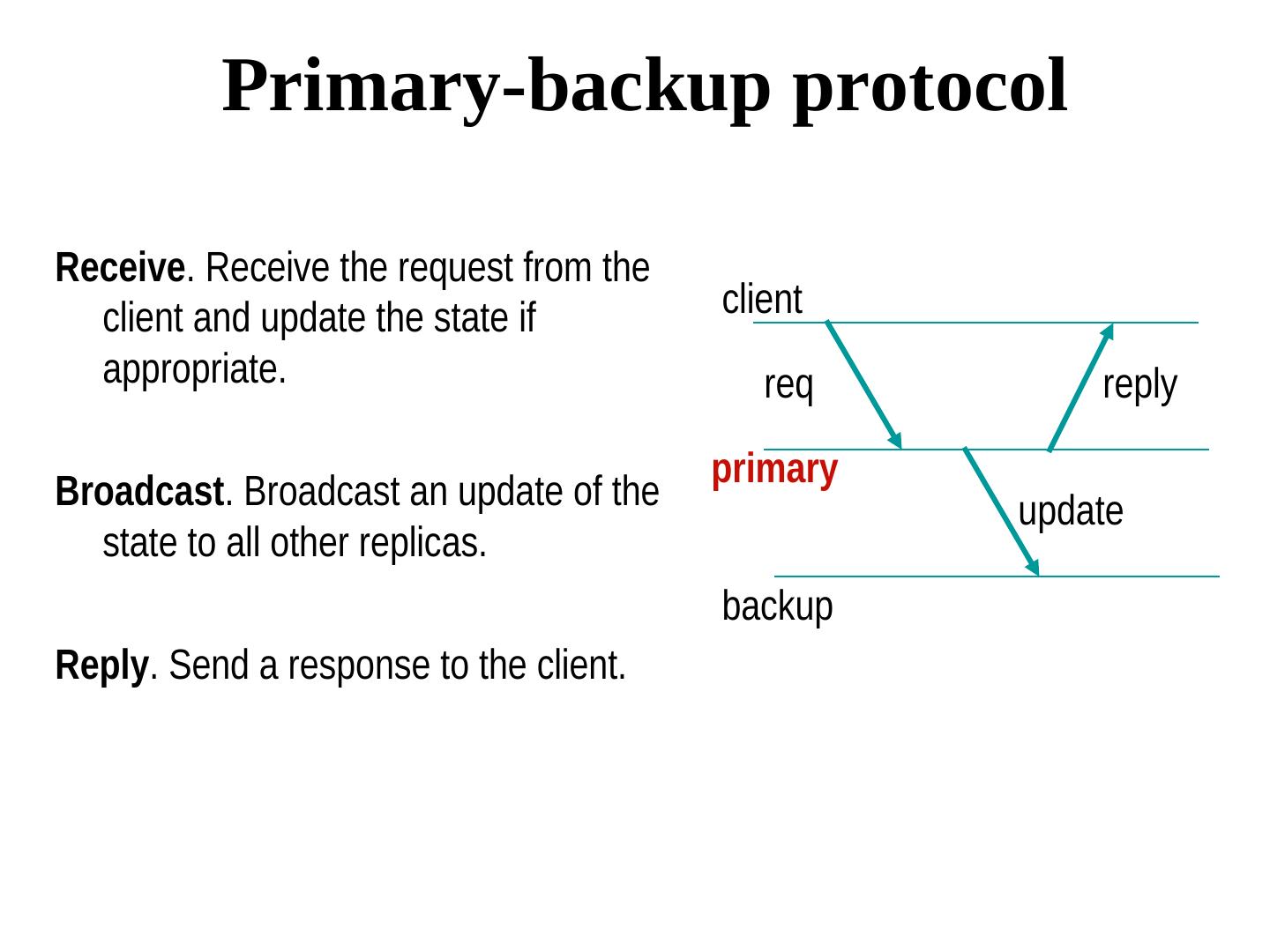
4 . Primary-backup protocol Receive. Receive the request from the client and update the state if client appropriate. req reply primary Broadcast. Broadcast an update of the update state to all other replicas. backup Reply. Send a response to the client. 

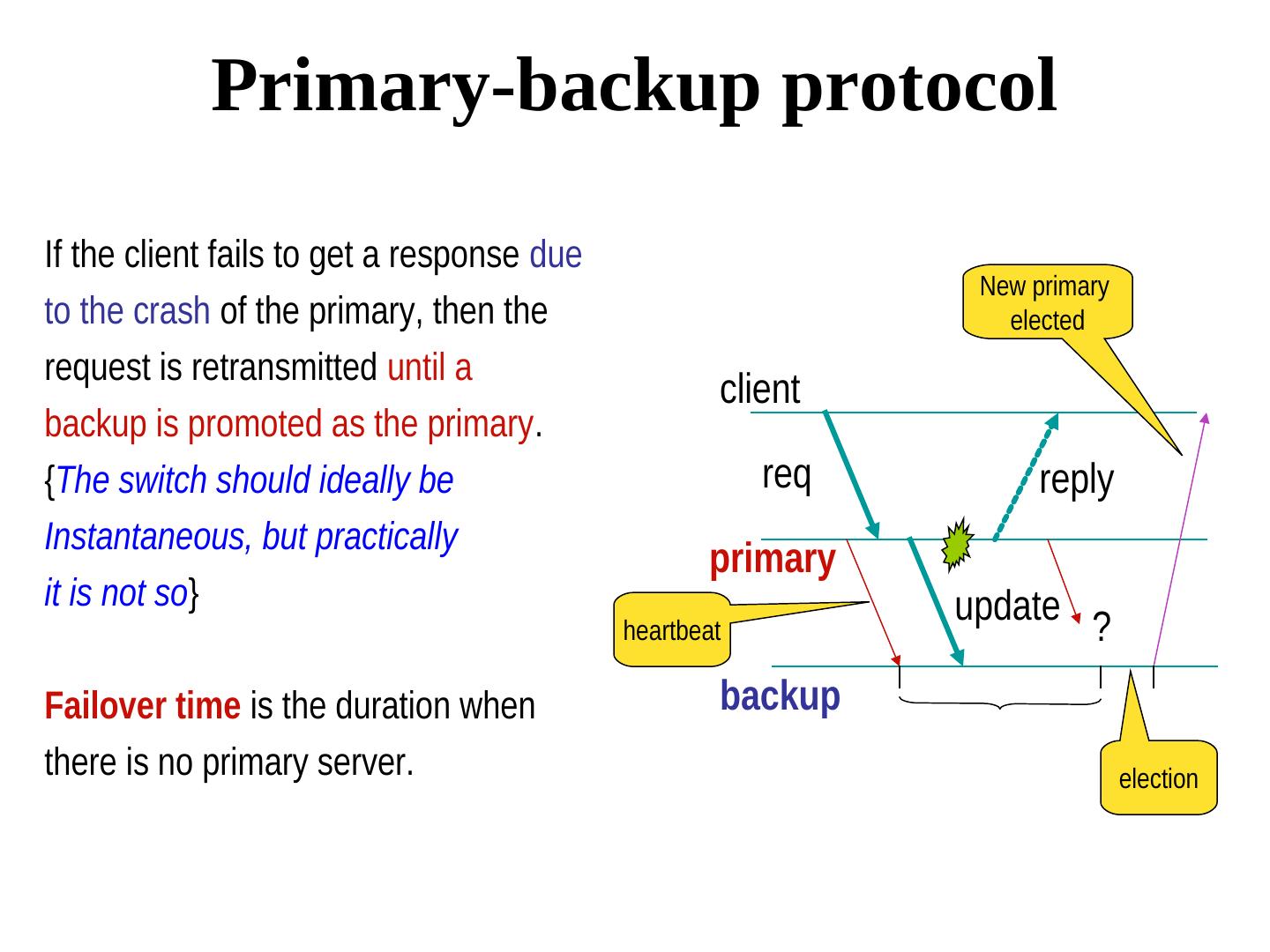
5 . Primary-backup protocol If the client fails to get a response due New primary to the crash of the primary, then the elected request is retransmitted until a client backup is promoted as the primary. {The switch should ideally be req reply Instantaneous, but practically primary it is not so} update ? heartbeat Failover time is the duration when backup there is no primary server. election 

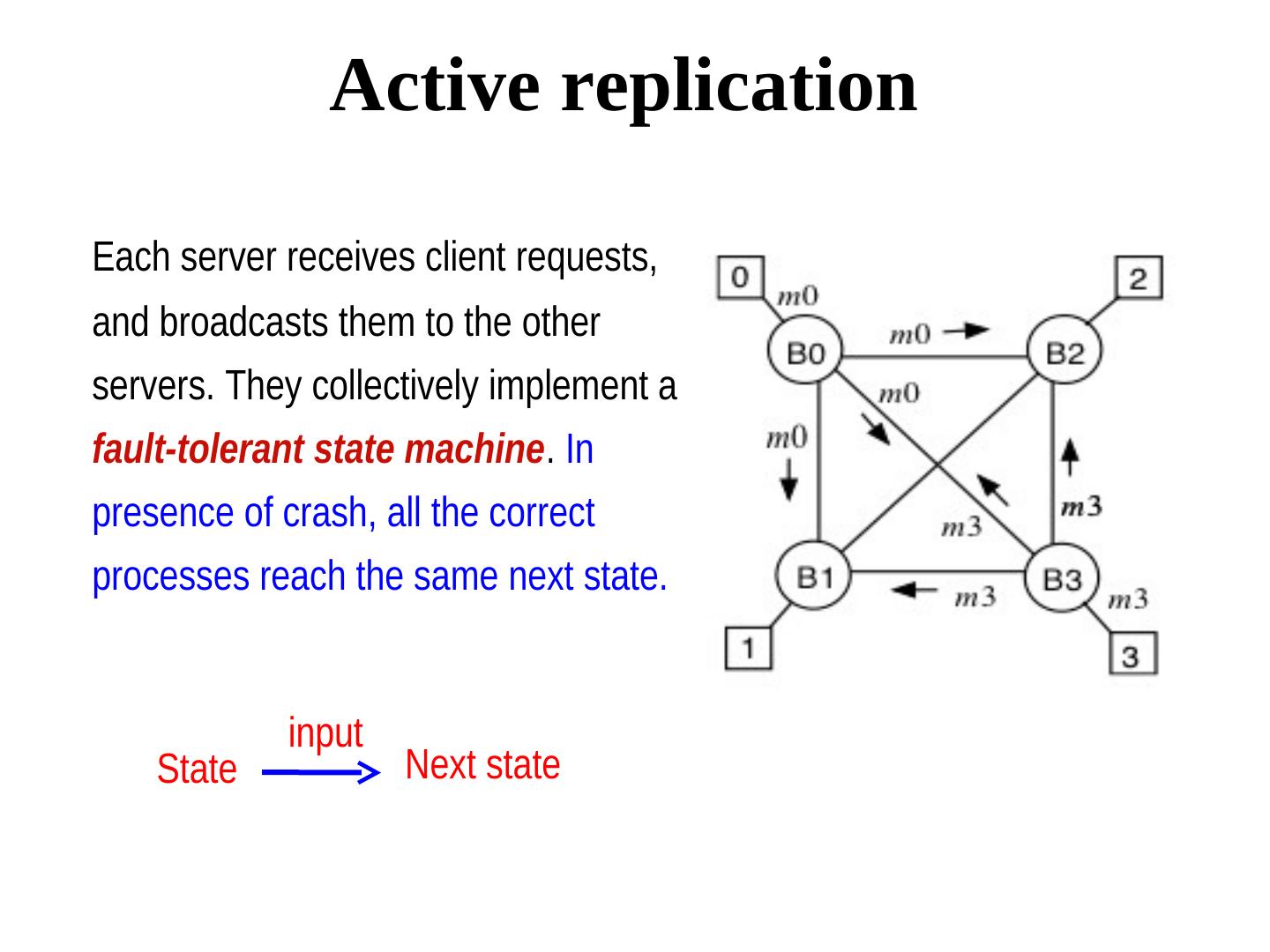
6 . Active replication Each server receives client requests, and broadcasts them to the other servers. They collectively implement a fault-tolerant state machine. In presence of crash, all the correct processes reach the same next state. input State Next state 

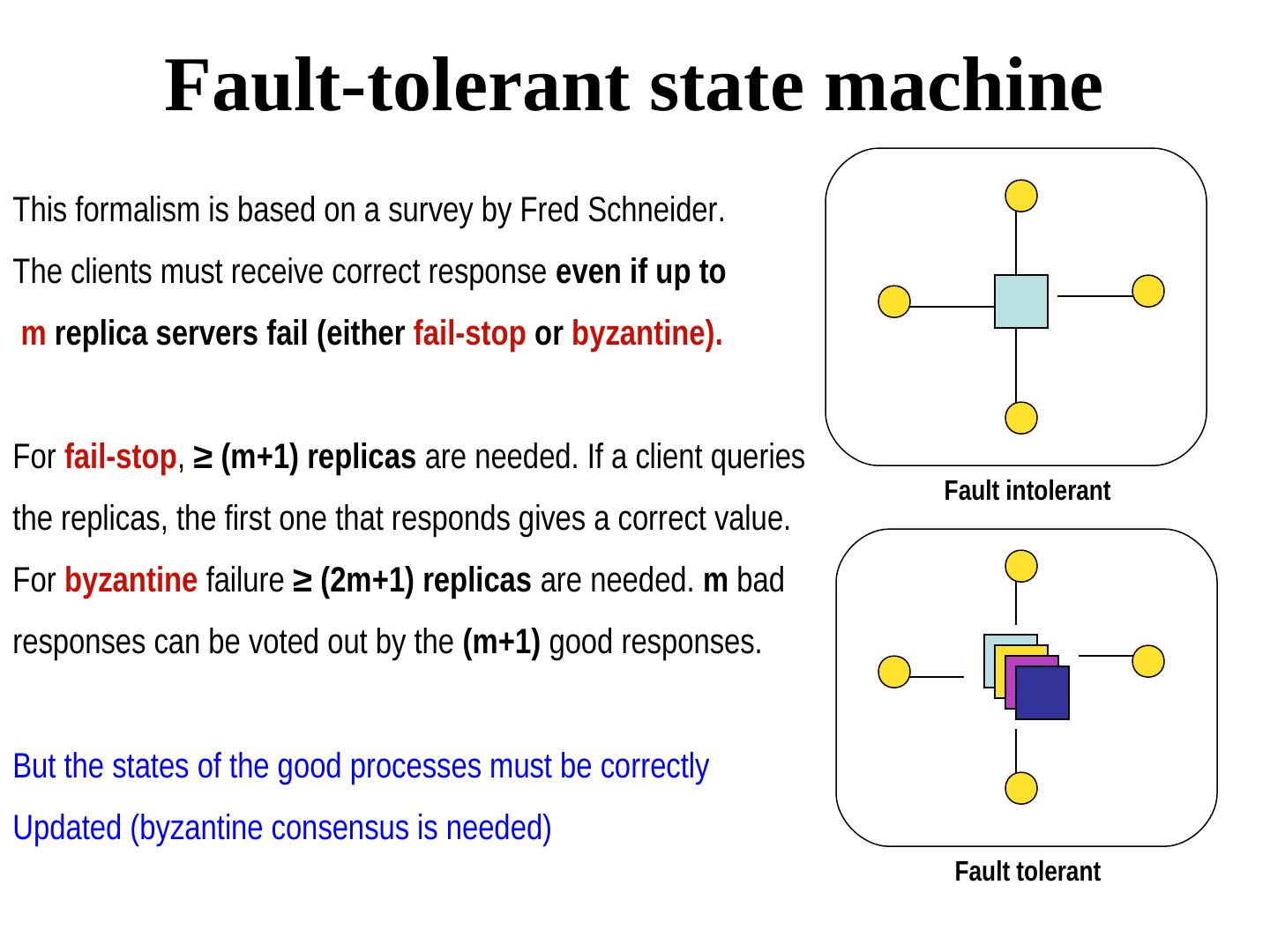
7 . Fault-tolerant state machine This formalism is based on a survey by Fred Schneider. The clients must receive correct response even if up to m replica servers fail (either fail-stop or byzantine). For fail-stop, ≥ (m+1) replicas are needed. If a client queries Fault intolerant the replicas, the first one that responds gives a correct value. For byzantine failure ≥ (2m+1) replicas are needed. m bad responses can be voted out by the (m+1) good responses. But the states of the good processes must be correctly Updated (byzantine consensus is needed) Fault tolerant 

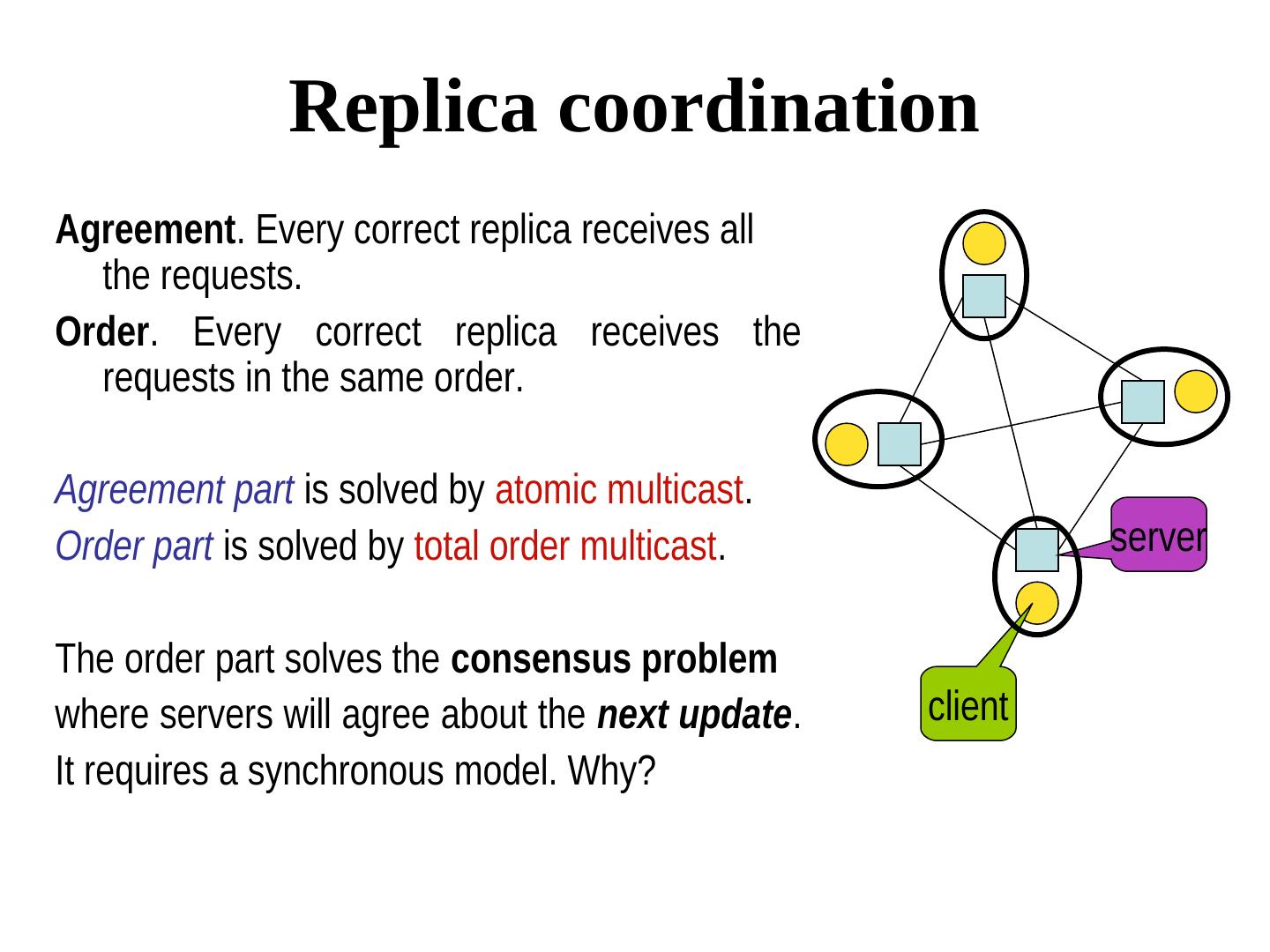
8 . Replica coordination Agreement. Every correct replica receives all the requests. Order. Every correct replica receives the requests in the same order. Agreement part is solved by atomic multicast. Order part is solved by total order multicast. server The order part solves the consensus problem where servers will agree about the next update. client It requires a synchronous model. Why? 

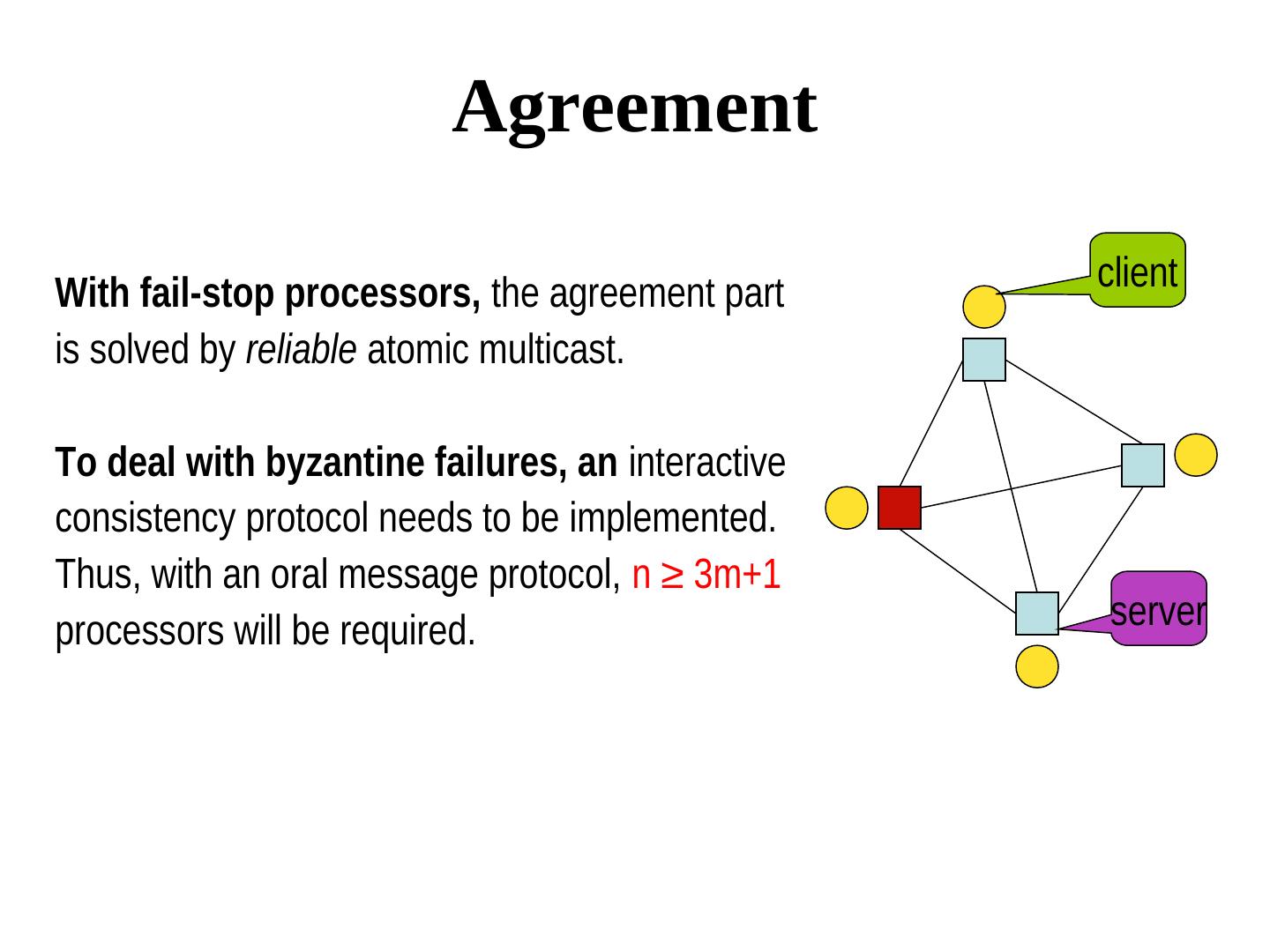
9 . Agreement With fail-stop processors, the agreement part client is solved by reliable atomic multicast. To deal with byzantine failures, an interactive consistency protocol needs to be implemented. Thus, with an oral message protocol, n ≥ 3m+1 processors will be required. server 

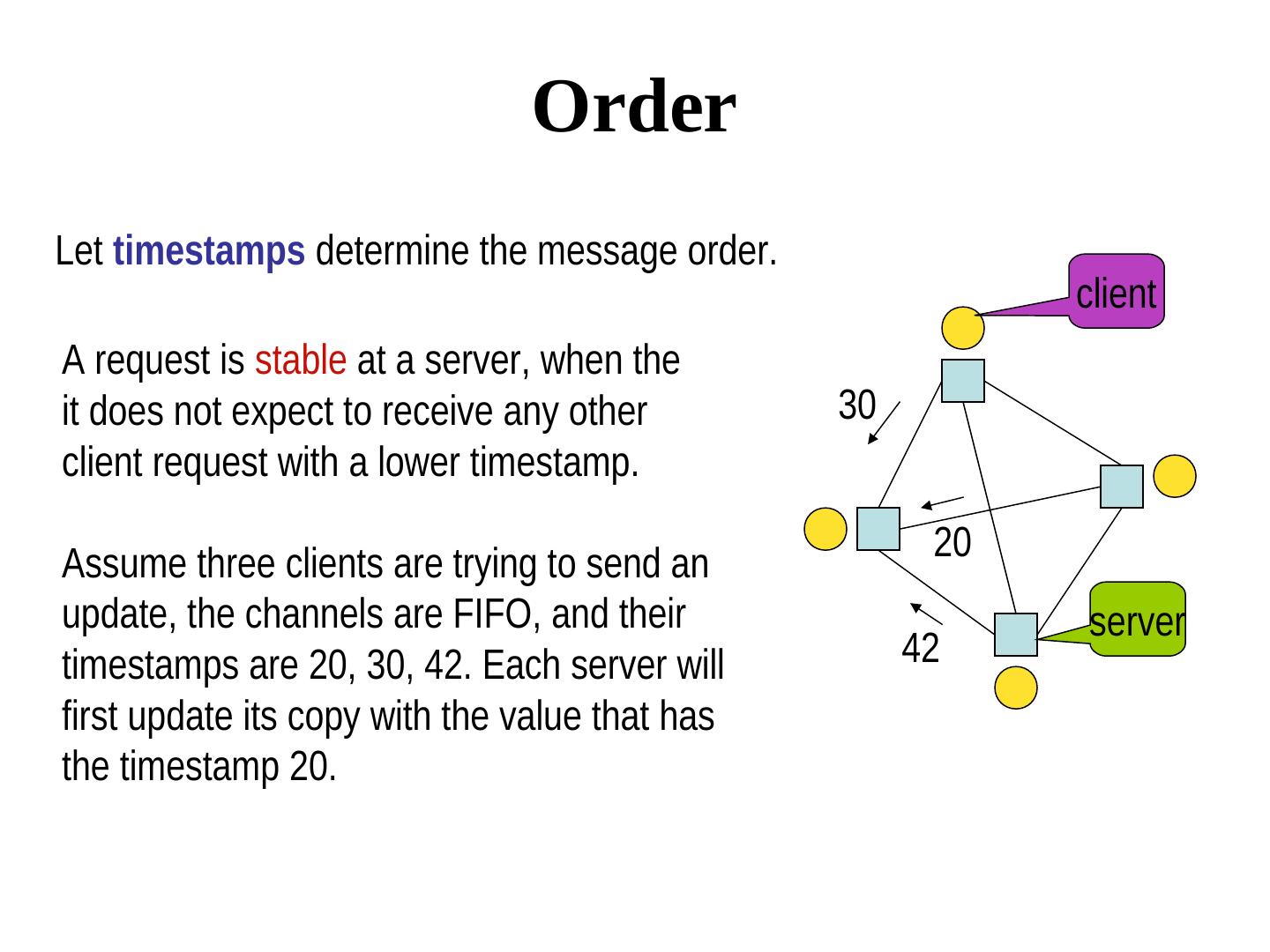
10 . Order Let timestamps determine the message order. client A request is stable at a server, when the it does not expect to receive any other 30 client request with a lower timestamp. Assume three clients are trying to send an 20 update, the channels are FIFO, and their server timestamps are 20, 30, 42. Each server will 42 first update its copy with the value that has the timestamp 20. 

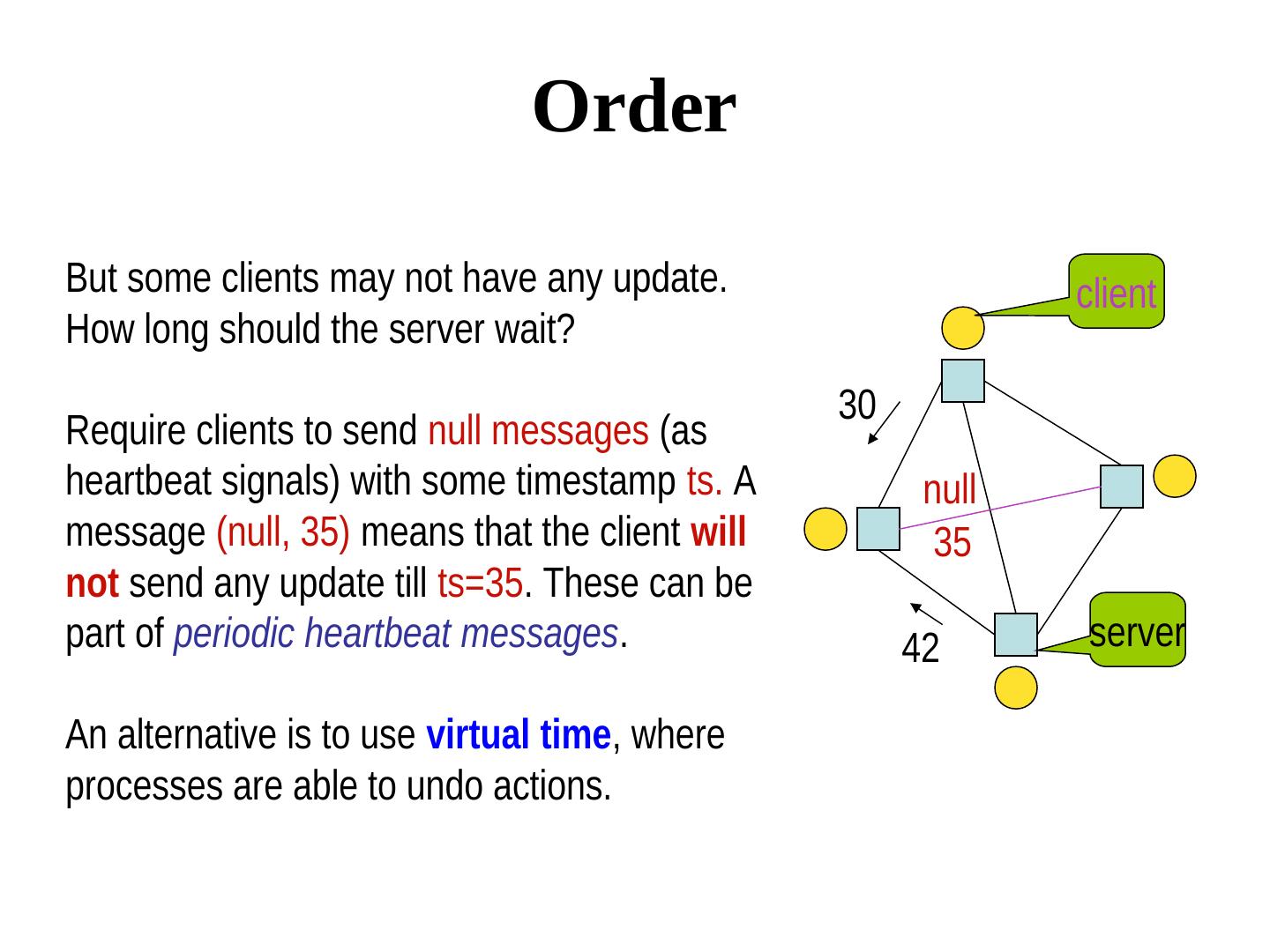
11 . Order But some clients may not have any update. client How long should the server wait? 30 Require clients to send null messages (as heartbeat signals) with some timestamp ts. A null message (null, 35) means that the client will 35 not send any update till ts=35. These can be part of periodic heartbeat messages. 42 server An alternative is to use virtual time, where processes are able to undo actions. 

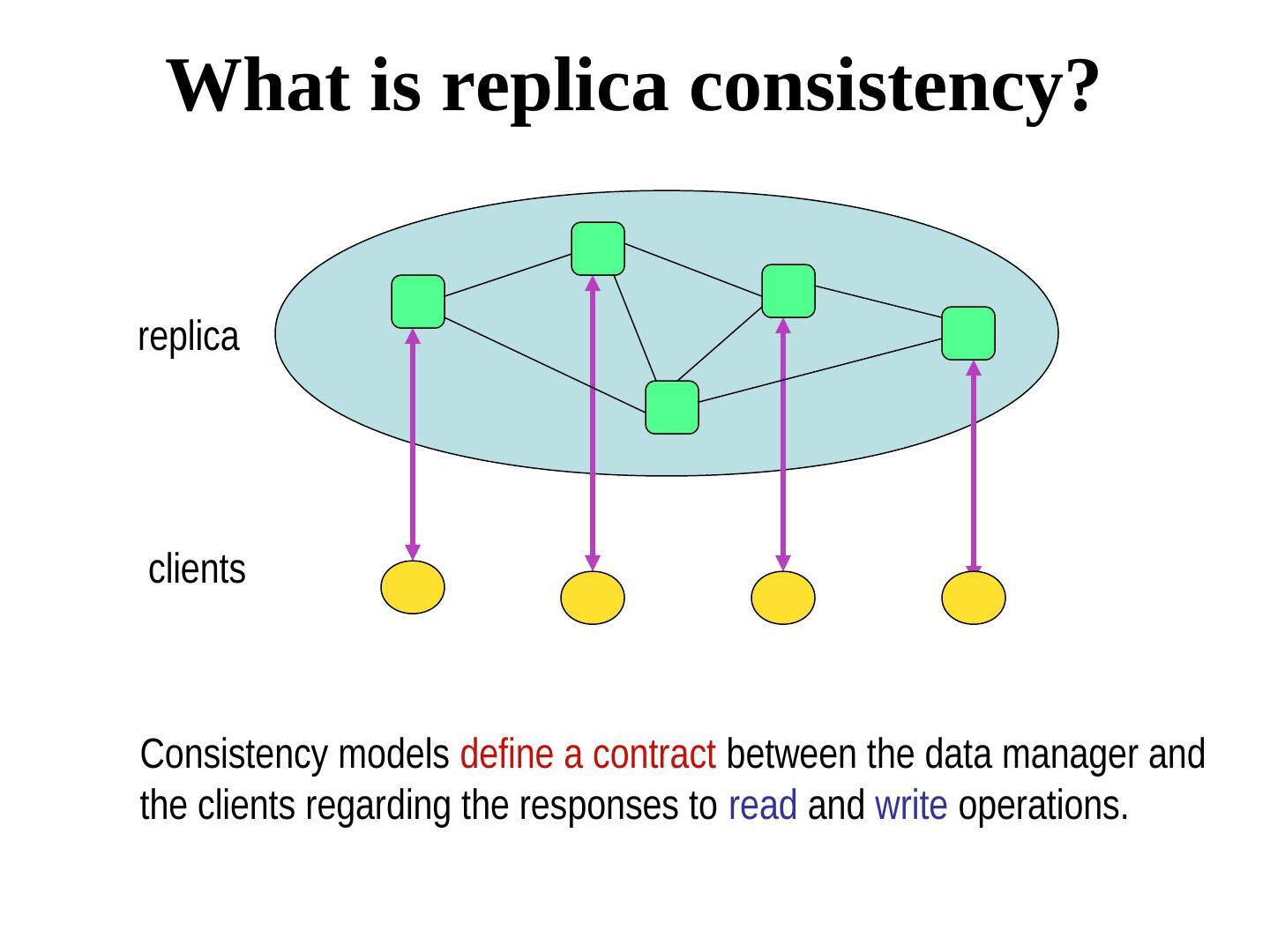
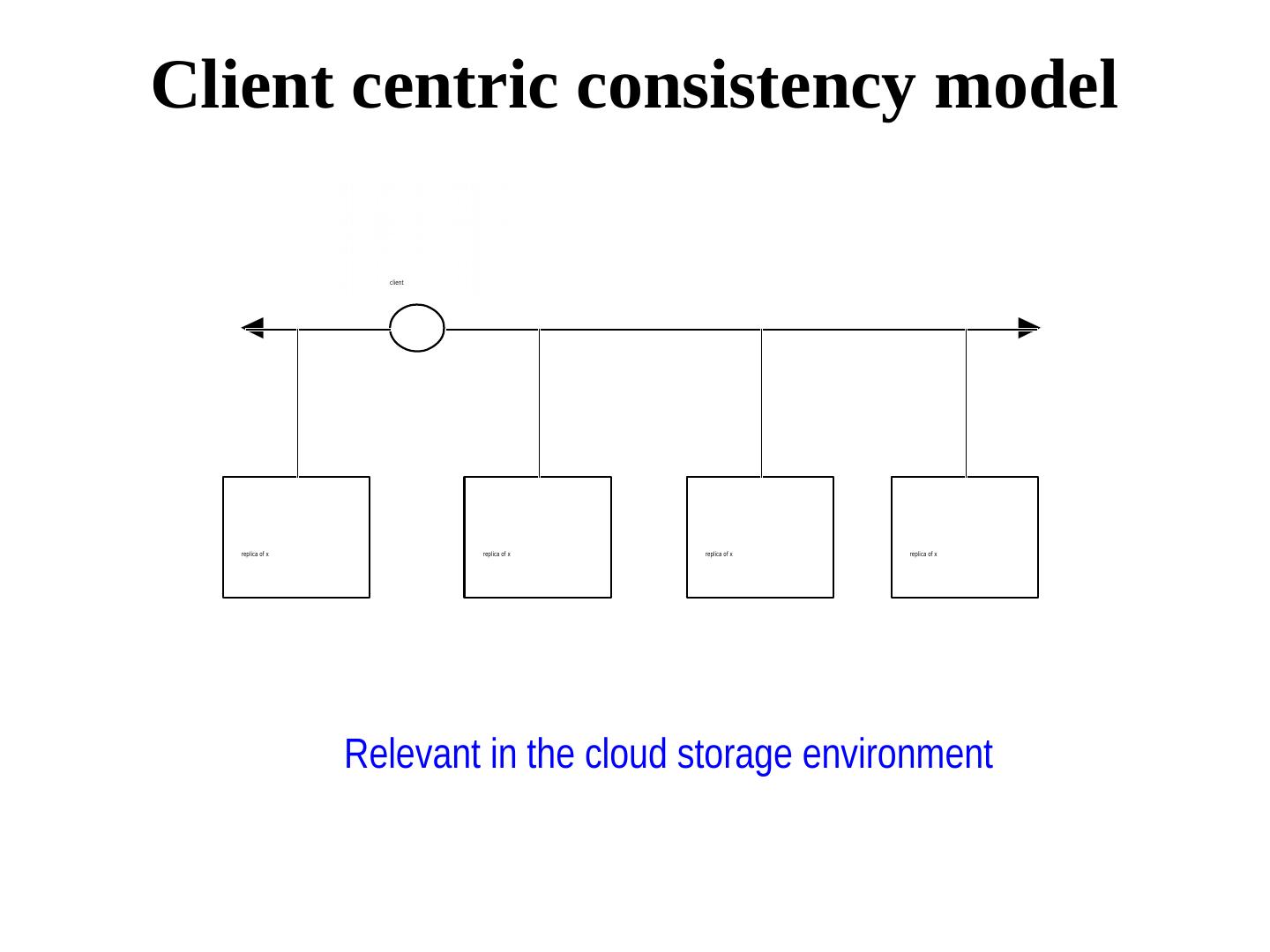
12 . What is replica consistency? replica clients Consistency models define a contract between the data manager and the clients regarding the responses to read and write operations. 

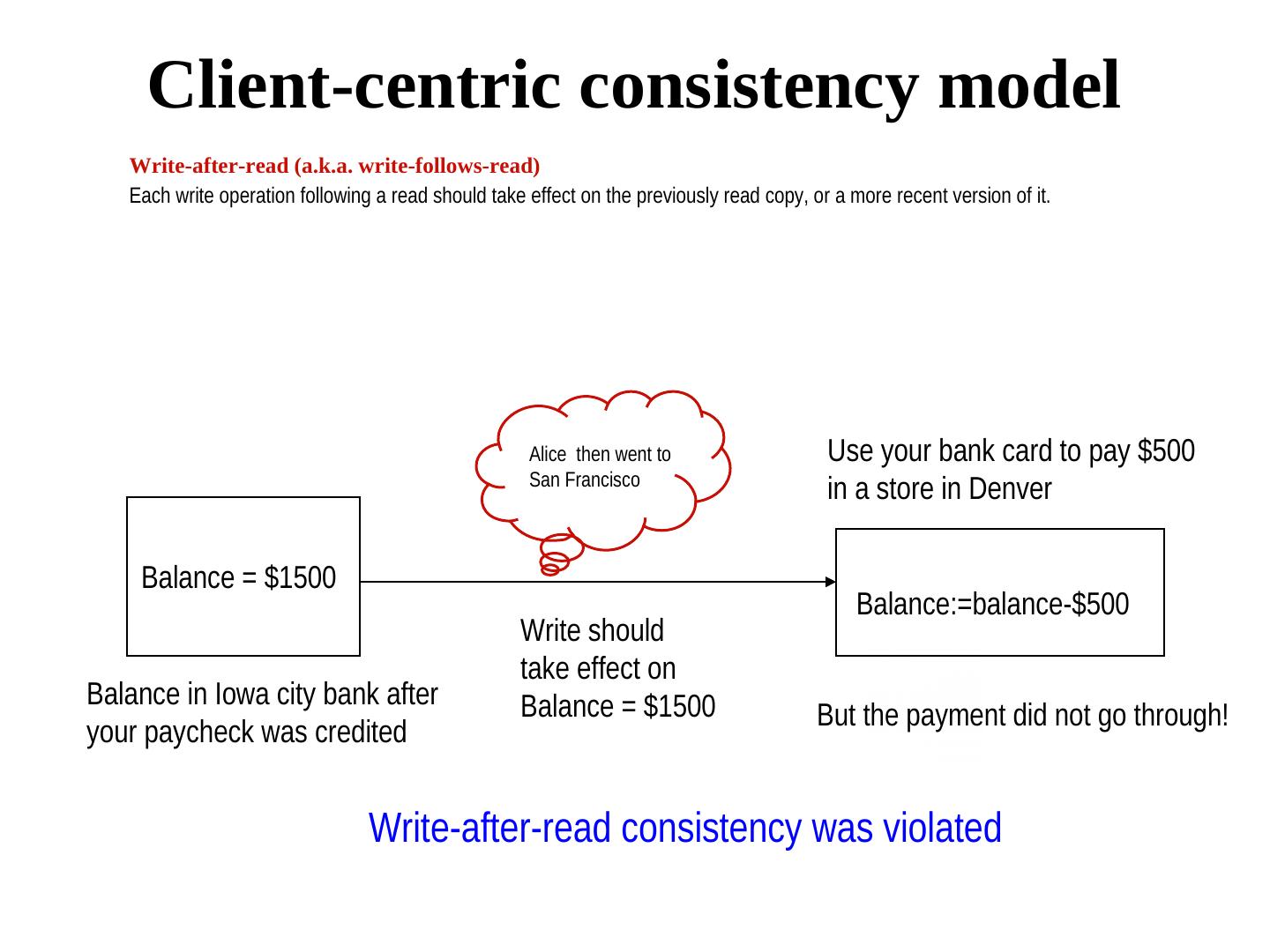
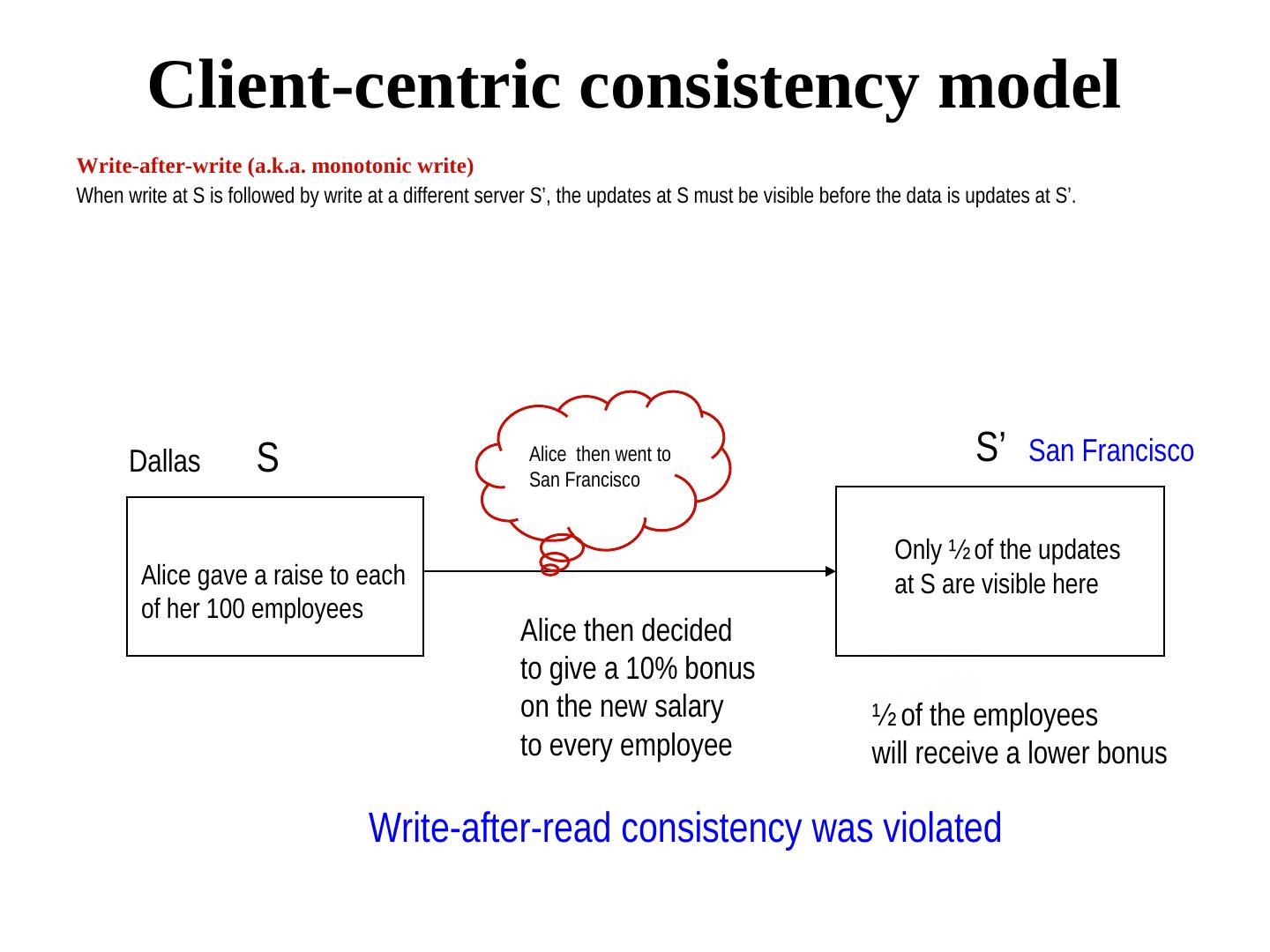
13 . Replica Consistency • Data Centric Client communicates with the same replica • Client centric Client communicates with different replica at different times. This may be the case with mobile clients. 

14 .Data-centric Consistency Models 1. Strict consistency 2. Linearizability 3. Sequential consistency 4. Causal consistency 5. Eventual consistency (as in DNS) 6. Weak consistency There are many other models 

15 . Strict consistency Strict consistency corresponds to true replication transparency. If one of the processes executes x:= 5 at real time t and this is the latest write operation, then at a real time t’ > t, every process trying to read x will receive the value 5. Too strict! Why? W(x:=5) p1 R(x=5) p2 t t’ {Assume the read or write operations are non-blocking} 

16 . Sequential consistency Some interleaving of the local temporal order of events at the different replicas is a consistent trace. W(x:=100) W(x:=99] R(x=100) R(x=99) 

17 . Sequential consistency Is sequential consistency satisfied here? Initially x = y = 0 W(x:=10) W(x:=8] R(x:=10) W(x=20) R(x=20) R(x=10) 

18 . Causal consistency All writes that are causally related must be seen by every process in the same order. W(x:=10) W(x:=20) R(x=10) R(x=20) R(x=20) R(x=10) 

19 . Linearizability Linearizability is a correctness criterion for concurrent object (Herlihy & Wing ACM TOPLAS 1990). It provides the illusion that each operation on the object takes effect in zero time, and the results are “equivalent to” some legal sequential computation. 

20 . Linearizability A trace is in a read-write system is consistent, when every read returns the latest value written into the shared variable preceding that read operation. A trace is linearizable, when (1) it is consistent, and (2) the temporal ordering among the reads and writes is respected (may be based on real time or logical time). W (x:=0) R (x=1) W (x:=0) ts=10 ts=21 ts=27 W (x:=1) R(x=1) (Initially x=y=0) ts=19 ts=38 Linearizability is stronger than Is it a linearizable trace? sequential consistency, i.e. every linearizable object is also sequentially consistent. 

21 . Exercise What consistency model is satisfied by the above? 

22 . Implementing consistency models Why are there so many consistency models? Each model has a use in some type of application. The cost of implementation (as measured by message complexity) decreases as the models become “weaker”. 

23 . Implementing linearizability W (x:=20) Read x Read x W(x:=10) Needs total order multicast of all reads and writes 

24 . Implementing linearizability • The total order multicast forces every process to accept and handle all reads and writes in the same temporal order. • The peers update their copies in response to a write, but only send acknowledgments for reads. After all updates and acknowledgments are received, the local copy is returned to the client. 

25 . Implementing sequential consistency Use total order broadcast all writes only, but for reads, immediately return local copies. 

26 . Eventual consistency Only guarantees that all replicas eventually receive all updates, regardless of the order. The system does not provide replication transparency but large scale systems like Bayou allows this. Conflicting updates are resolved using occasional anti-entropy sessions that incrementally steer the system towards a consistent configuration. 

27 . Implementing eventual consistency Updates are propagated via epidemic protocols. Server S1 randomly picks a neighboring server S2, and passes on the update. Case 1. S2 did not receive the update before. In this case, S2 accepts the update, and both S1 and S2 continue the process. Case 2. S2 already received the update from someone else. In that case, S1 loses interest in sending updates to S2 (reduces the probability of transmission to S2 to 1/p (p is a tunable parameter) There is always a finite probability that some servers do not receive all updates. The number can be controlled by changing p. 

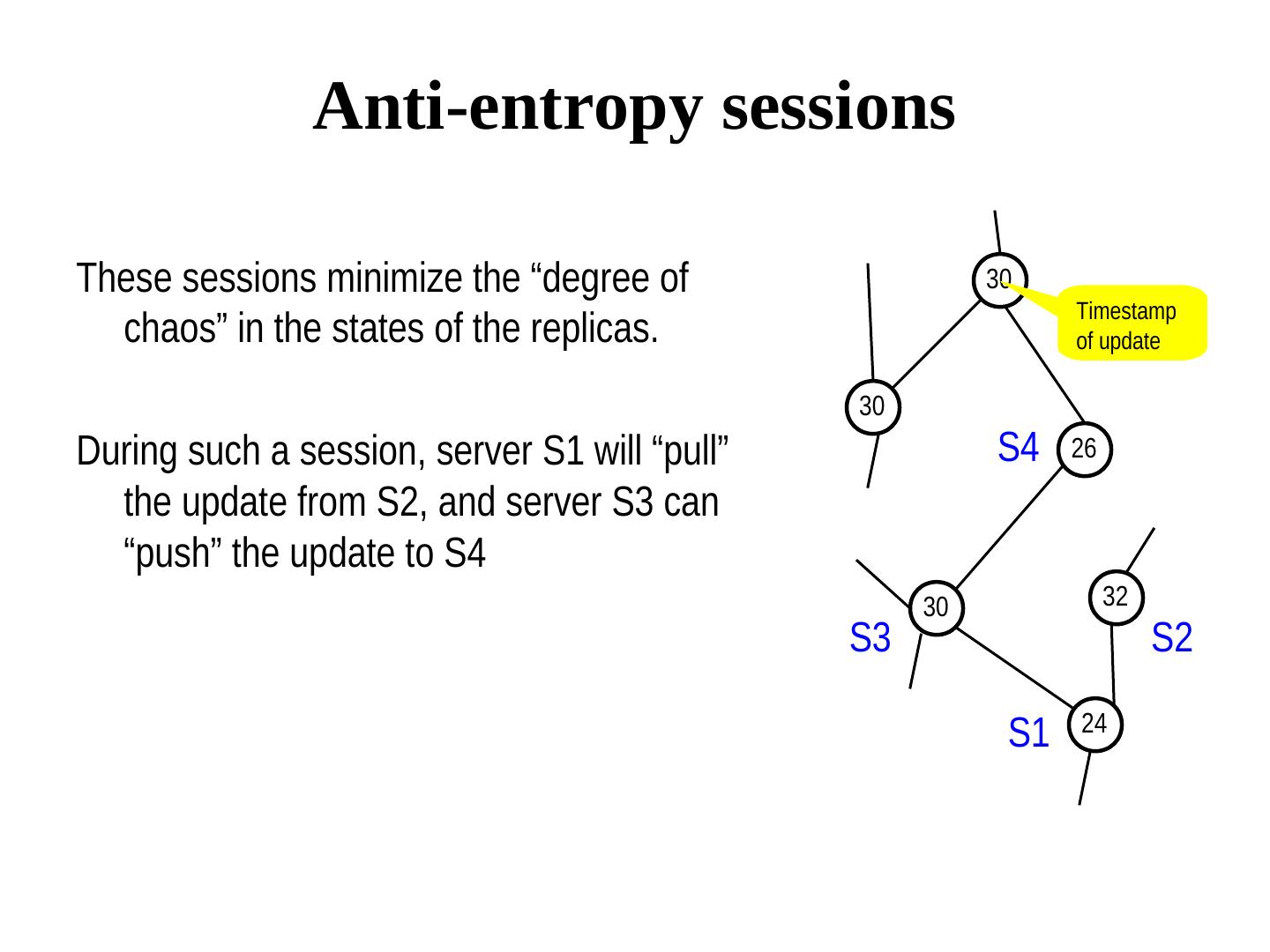
28 . Anti-entropy sessions These sessions minimize the “degree of 30 Timestamp chaos” in the states of the replicas. of update 30 During such a session, server S1 will “pull” S4 26 the update from S2, and server S3 can “push” the update to S4 30 32 S3 S2 24 S1 

29 . Exercise Let x, y be two shared variables Process P Process Q {initially x=0} {initially y=0} x :=1; y:=1; if y=0  x:=2 fi; if x=0  y:=2 fi; Print x Print y If sequential consistency is preserved, then what are the possible values of the printouts? List all of them.