分布式系统和算法：故障检测

1 .Distributed Consensus (continued) 

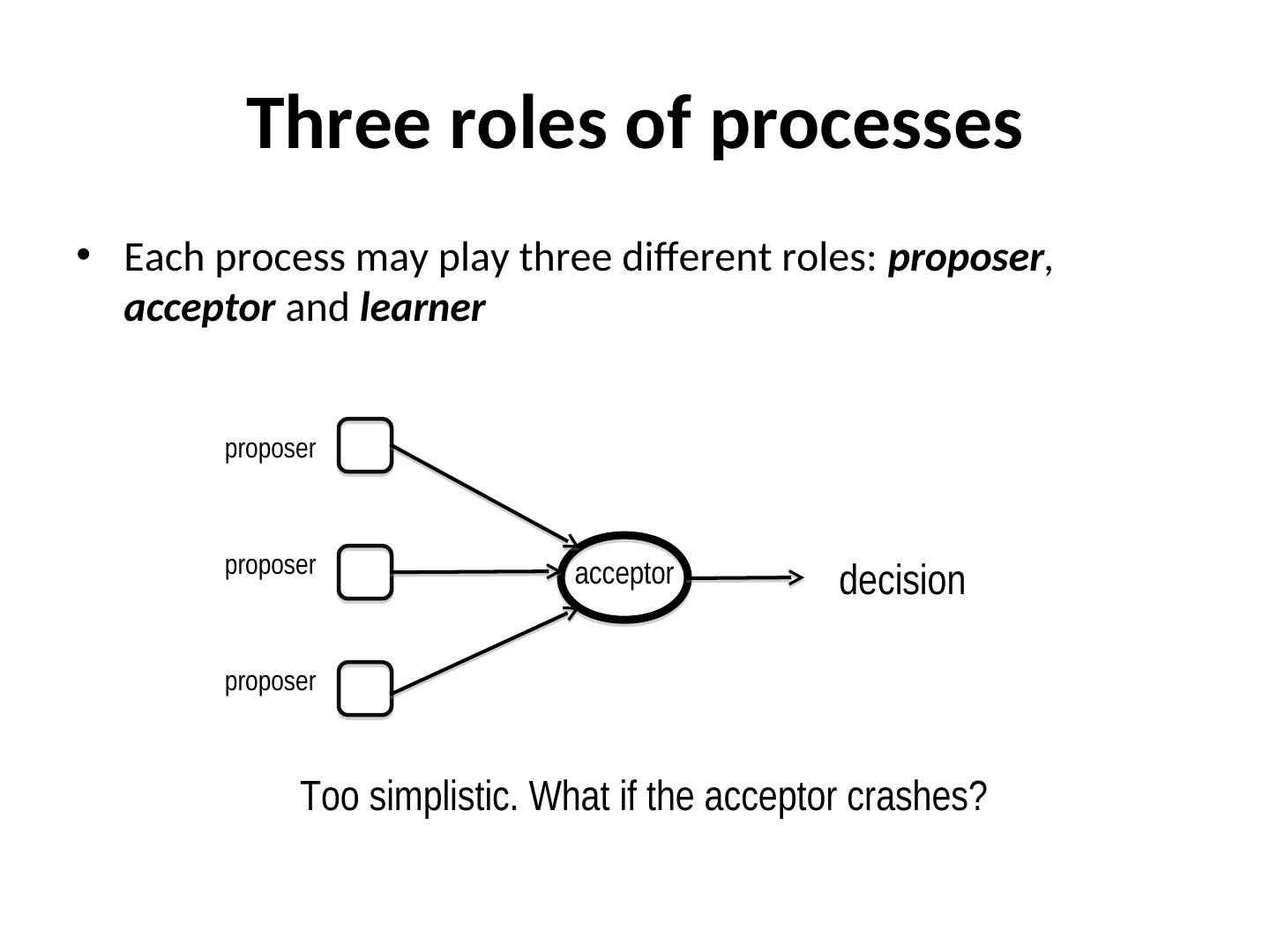
2 . Byzantine Generals Problem Solution with signed message A signed message satisfies all the conditions of oral message, plus two extra conditions • Signature cannot be forged. Forged message are detected and discarded by loyal generals. • Anyone can verify its authenticity of a signature. Signed messages improve resilience. 

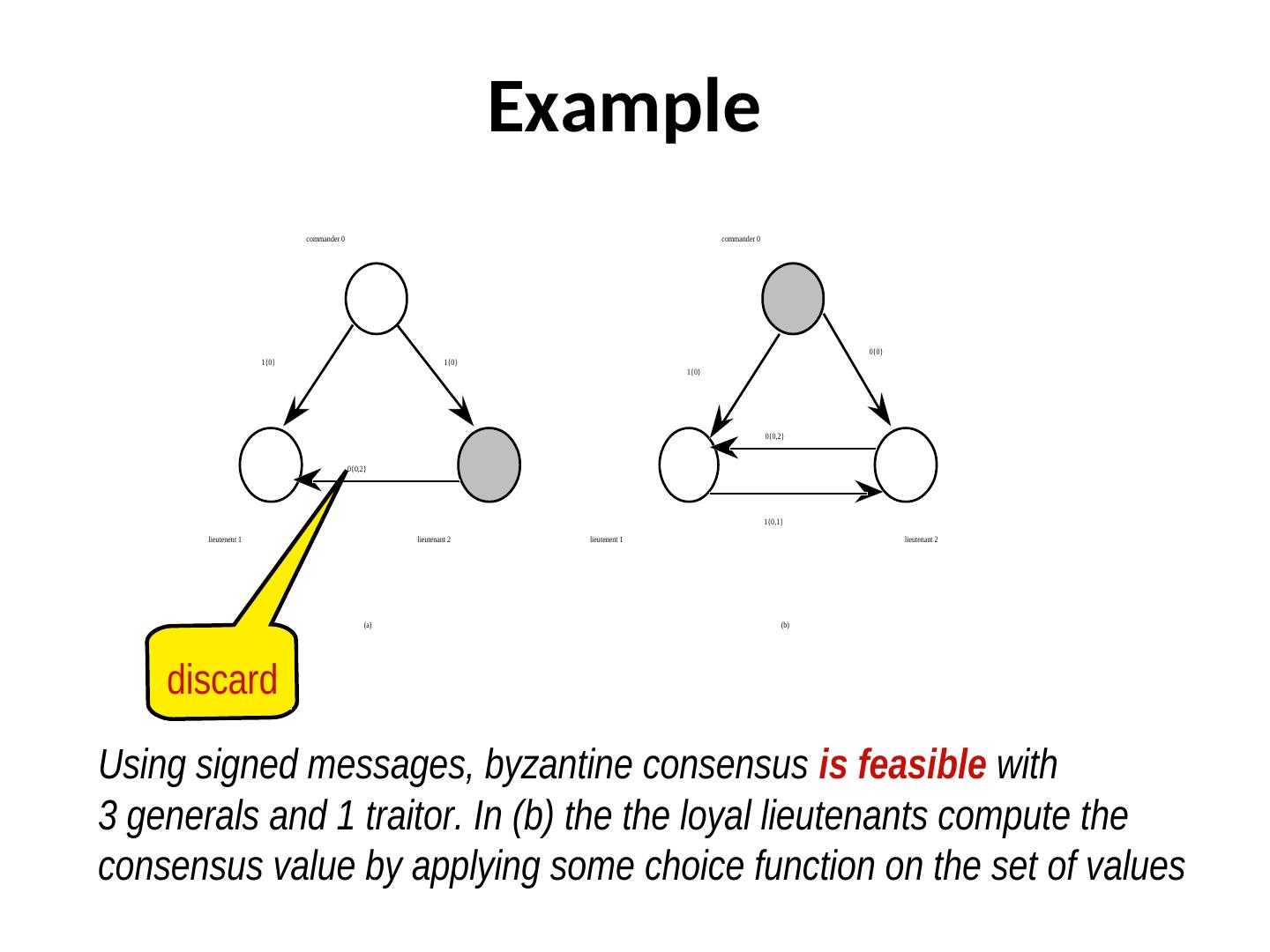
3 . Example commander 0 commander 0 0{0} 1{0} 1{0} 1{0} 0{0,2} 0{0,2} 1{0,1} lieutenent 1 lieutenant 2 lieutenent 1 lieutenant 2 (a) (b) discard Using signed messages, byzantine consensus is feasible with 3 generals and 1 traitor. In (b) the the loyal lieutenants compute the consensus value by applying some choice function on the set of values 

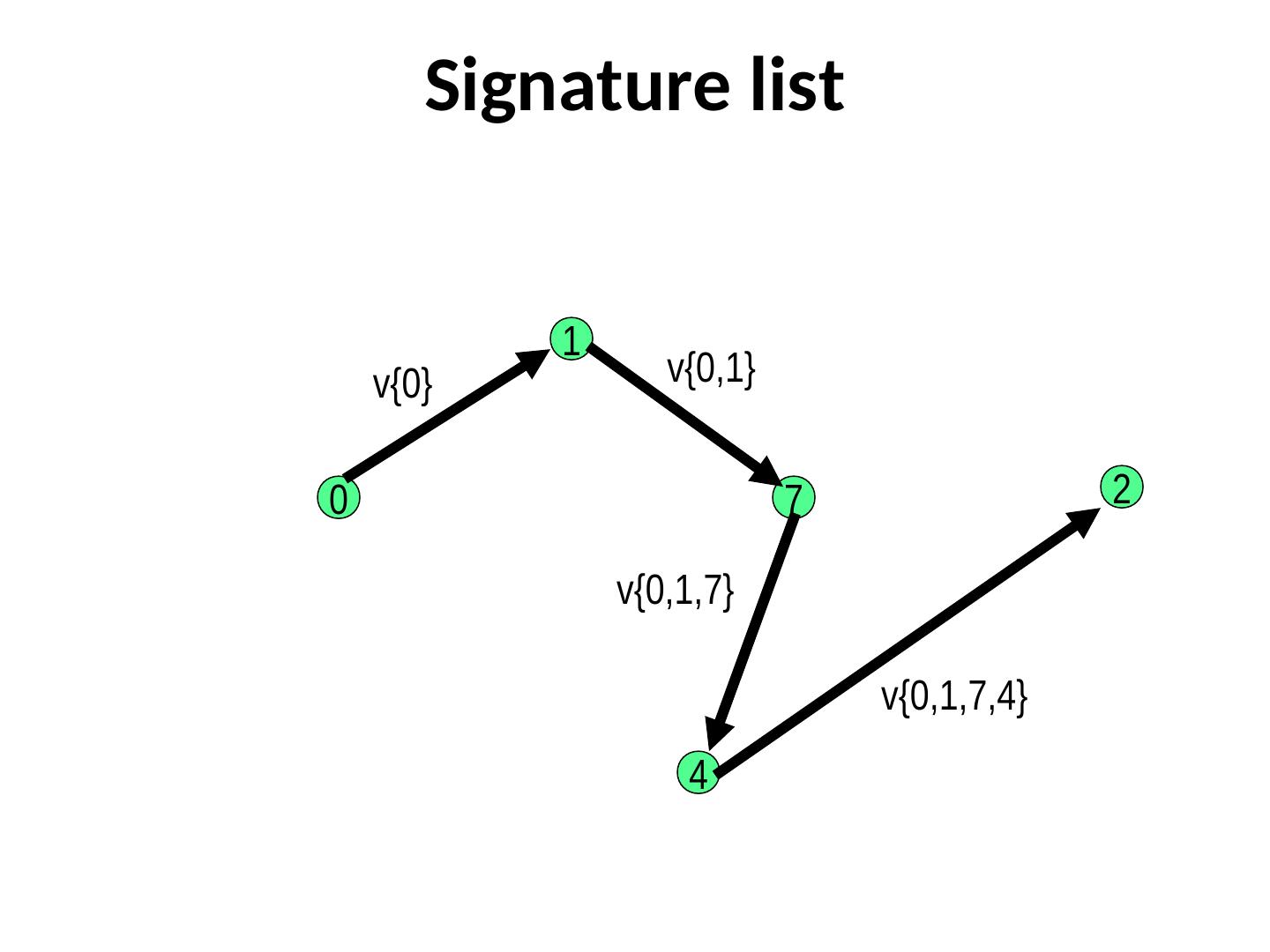
4 . Signature list 1 v{0} v{0,1} 0 7 2 v{0,1,7} v{0,1,7,4} 4 

5 . Byzantine consensus: The signed message algorithms SM(m) Commander i sends out a signed message v{i} to each lieutenant j ≠ i Lieutenant j, after receiving a message v{S}, appends it to a set V.j, only if (i) it is not forged, and (ii) it has not been received before. If the length of S is less than m+1, then lieutenant j (i) appends his own signature to S, and (ii) sends out the signed message to every other lieutenant whose signature does not appear in S. Lieutenant j applies a choice function on V.j to make the final decision. 

6 . Theorem of signed messages If n ≥ m + 2, where m is the maximum number of traitors, then SM(m) satisfies both IC1 and IC2. Proof. Case 1. Commander is loyal. The bag of each process will contain exactly one message, that was sent by the commander. (Try to visualize this) 

7 . Proof of signed message theorem Case 2. Commander is traitor. • The signature list has a size (m+1), and there are m traitors, so at least one lieutenant signing the message must be loyal. • Every loyal lieutenant i will receive every other loyal lieutenant’s message. So, every message accepted by j is also accepted by i and vice versa. So V.i = V.j. 

8 . Example 0 a c b {a, b, c} 3 1 c a f b 2 3 accepts c, but 2 rejects f {a, b,-} With m=2 and a signature list of length 2, the loyal generals may not receive the same order from the commander who is a traitor. When the length of the signature list grows to 3, the problem is resolved 

9 . Concluding remarks • The signed message version tolerates a larger number (n-2) of faults. • Message complexity however is the same in both cases. Message complexity = (n-1)(n-2) … (n-m+1) 

10 .Failure detectors 

11 . Failure detector for crash failures • The design of fault-tolerant algorithms will be simple if processes can detect (crash) failures. • In synchronous systems with bounded delay channels, crash failures can definitely be detected using timeouts. 

12 . Failure detectors for asynchronous systems In asynchronous distributed systems, the detection of crash failures is imperfect. There will be false positives and false negatives. Two properties are relevant: Completeness. Every crashed process is eventually suspected. Accuracy. No correct process is ever suspected. 

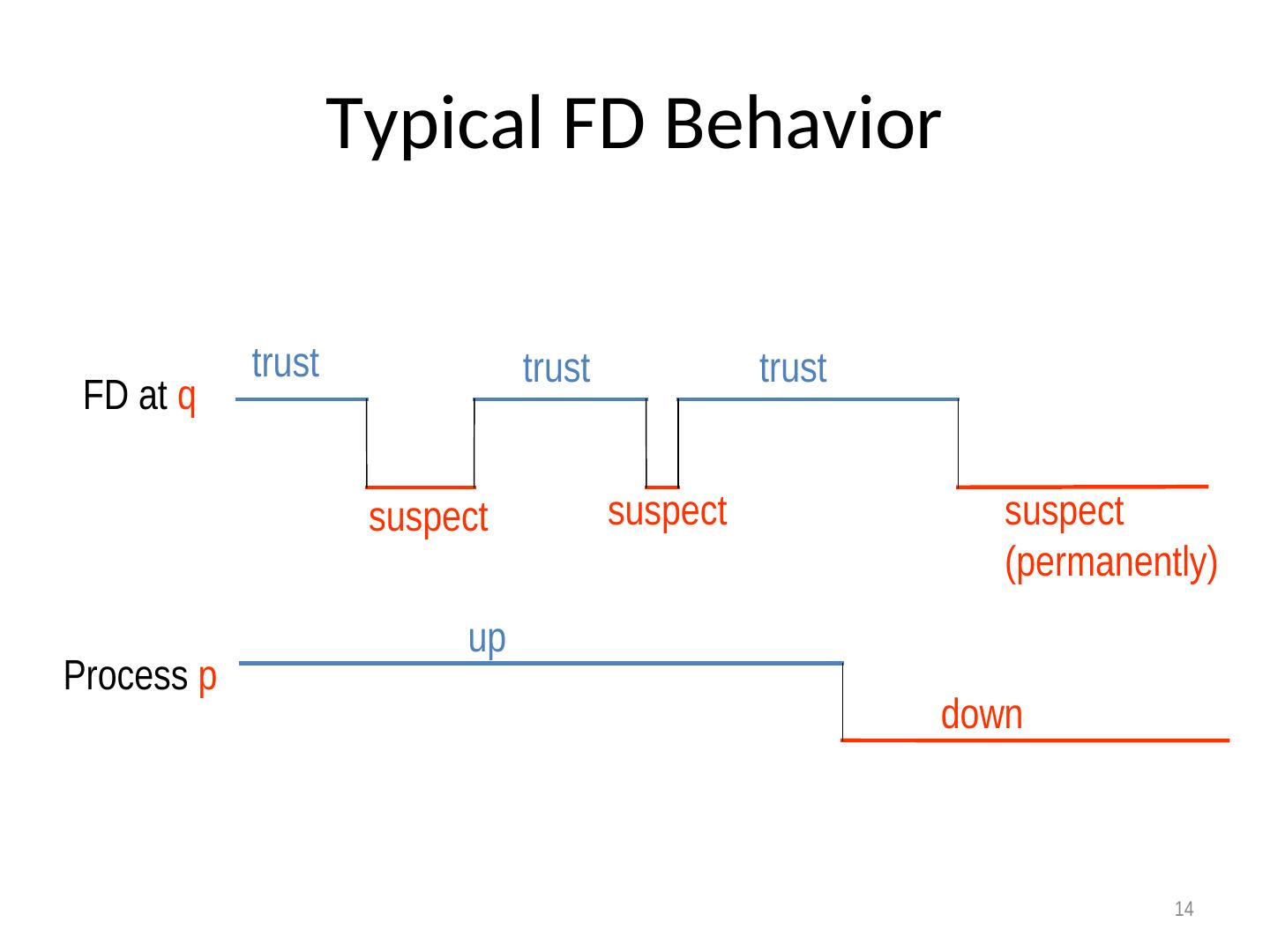
13 . Failure Detectors An FD is a distributed oracle that provides hints about the operational status of processes. However: • Hints may be incorrect • FD may give different hints to different processes • FD may change its mind (over & over) about the operational status of a process 13 

14 . Typical FD Behavior trust trust trust FD at q suspect suspect suspect (permanently) up Process p down 14 

15 .Revisit the Consensus problem input output 1 2 Agreed value 3 4 

16 . Example 1 3 0 6 5 7 4 2 0 suspects {1,2,3,7} to have failed. Does this satisfy completeness? Does this satisfy accuracy? 

17 . Classification of completeness • Strong completeness. Every crashed process is eventually suspected by every correct process, and remains a suspect thereafter. • Weak completeness. Every crashed process is eventually suspected by at least one correct process, and remains a suspect thereafter. Note that we don’t care what mechanism is used for suspecting a process. 

18 . Classification of accuracy • Strong accuracy. No correct process is ever suspected. • Weak accuracy. There is at least one correct process that is never suspected. 

19 . Transforming completeness Weak completeness can be transformed into strong completeness Program strong completeness (program for process i}; define D: set of process ids (representing the suspects); initially D is generated by the weakly complete failure detector of i; {program for process i} do true  send D(i) to every process j ≠ i; receive D(j) from every process j ≠ i; D(i) := D(i) ∪ D(j); D(j); if j ∈ D(i) D(i)  D(i) := D(i) \ j fi od 

20 . Eventual accuracy A failure detector is eventually strongly accurate, if there exists a time T after which no correct process is suspected. (Before that time, a correct process be added to and removed from the list of suspects any number of times) A failure detector is eventually weakly accurate, if there exists a time T after which at least one process is no more suspected. 

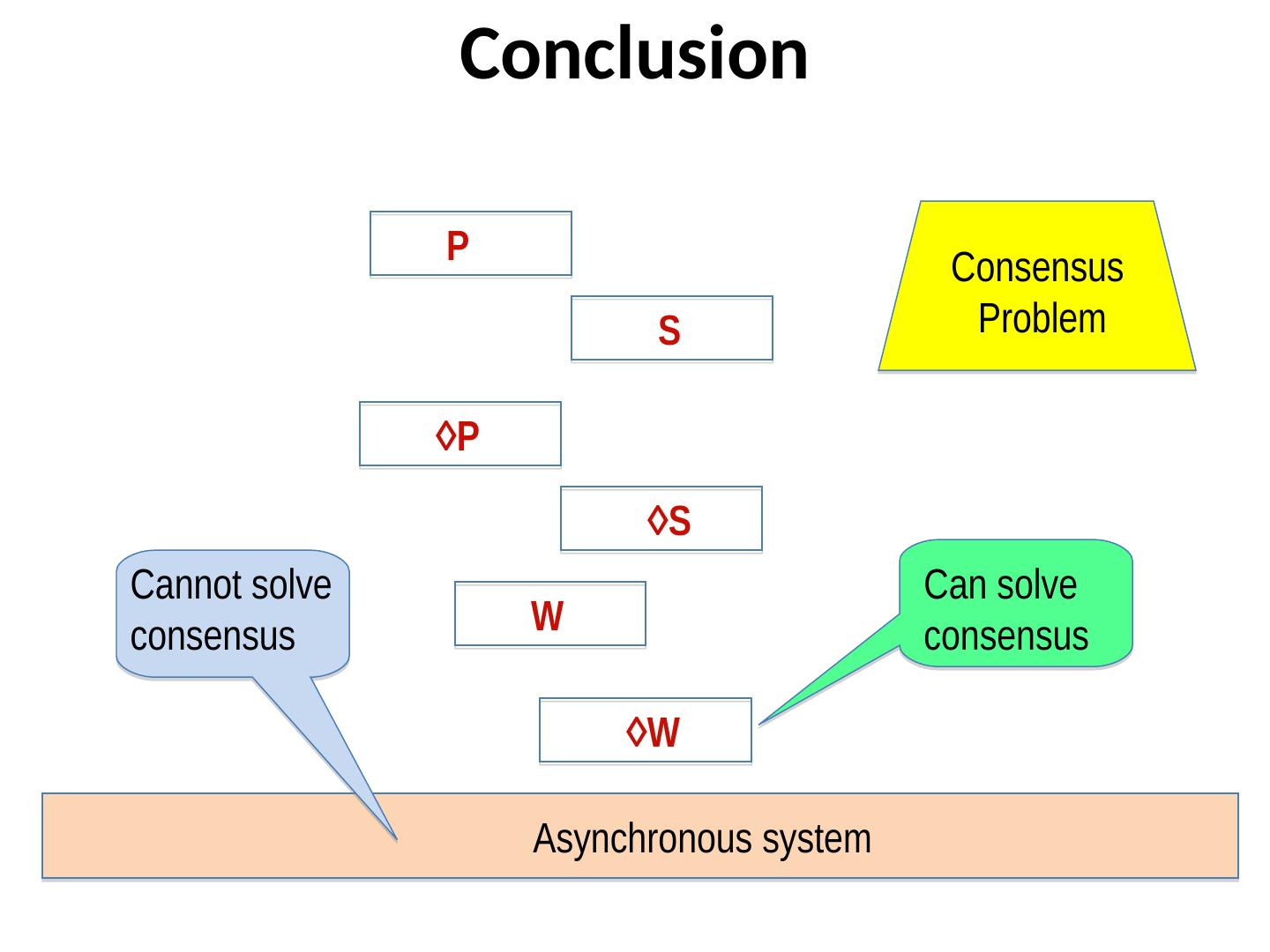
21 . Classifying failure detectors Perfect P. (Strongly) Complete and strongly accurate Strong S. (Strongly) Complete and weakly accurate Eventually perfect ◊P. (Strongly) Complete and eventually strongly accurate Eventually strong ◊S (Strongly) Complete and eventually weakly accurate Other classes are feasible: W (weak completeness) and weak accuracy) and ◊W 

22 . Motivation Question 1. Given a failure detector of a certain type, how can we solve the consensus problem? Question 2. How can we implement these classes of failure detectors in asynchronous distributed systems? Question 3. What is the weakest class of failure detectors that can solve the consensus problem? (Weakest class of failure detectors is closest to reality) 

23 . Application of Failure Detectors Applications often need to determine which processes are up (operational) and which are down (crashed). This service is provided by Failure Detector. FDs are at the core of many fault-tolerant algorithms and applications, like • Group Membership • Atomic Commitment • Group Communication • Consensus • Atomic Broadcast • Leader Election • Primary/Backup systems • ….. 23 

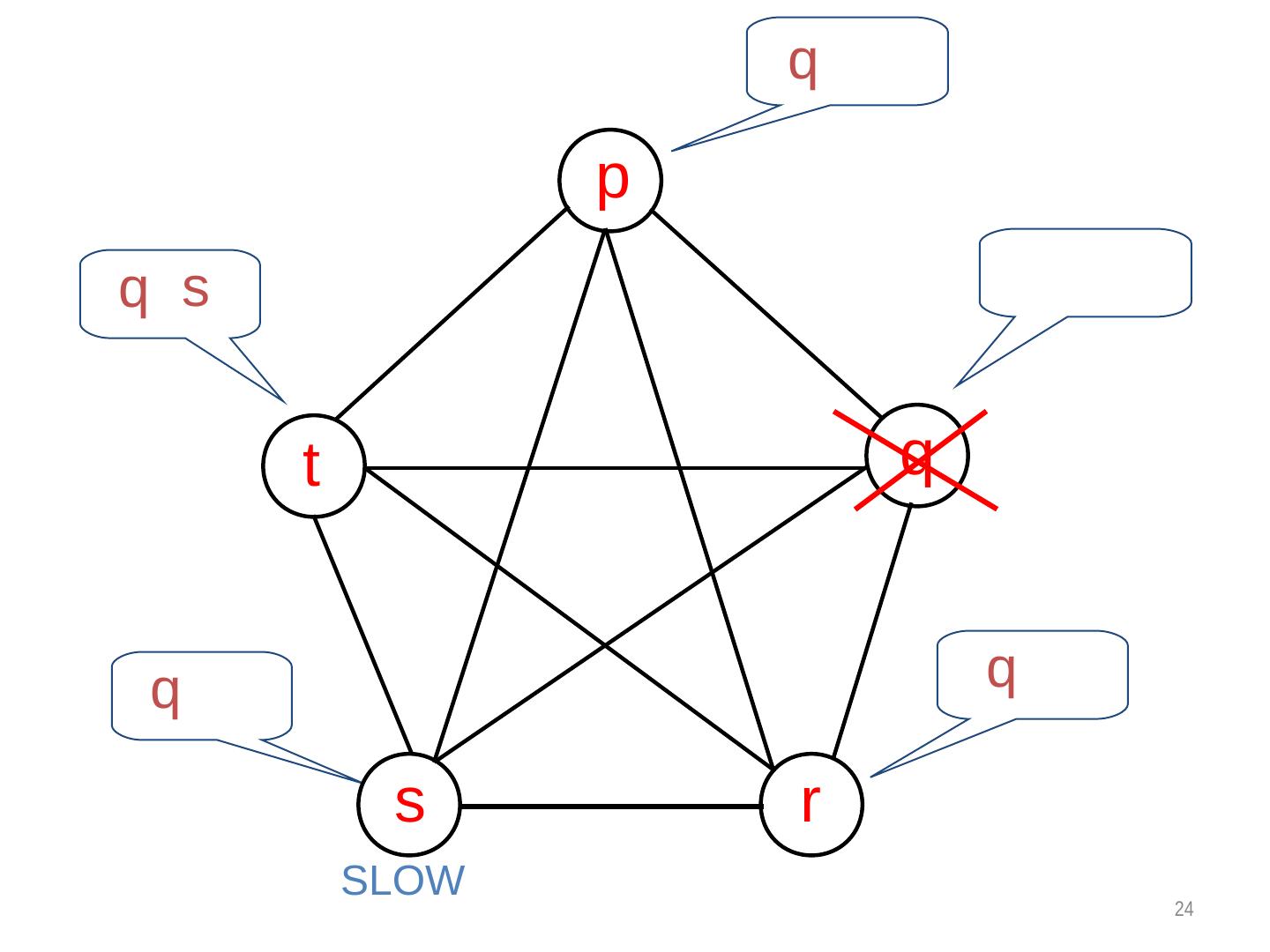
24 . q s p q s t q q q s r SLOW 24 

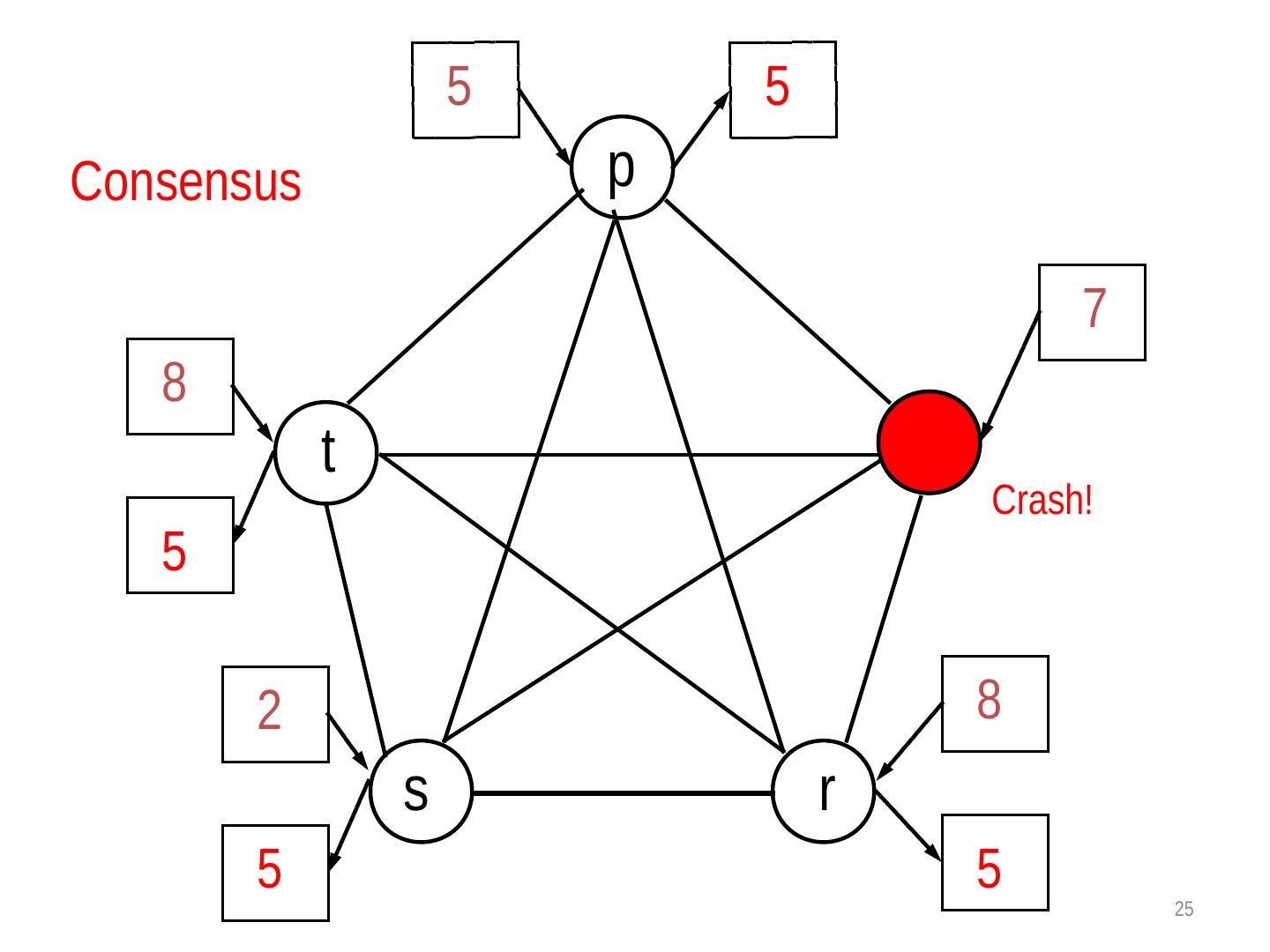
25 . 5 5 Consensus p 7 8 t q Crash! 5 2 8 s r 5 5 25 

26 . Solving Consensus • In synchronous systems: Possible • In asynchronous systems: Impossible [FLP83] even if: • at most one process may crash, and • all links are reliable 26 

27 . A more complete classification of failure detectors strong accuracy weak accuracy ◊ strong accuracy ◊ weak accuracy strong completeness Perfect P Strong S ◊P ◊S weak completeness Weak W ◊W 

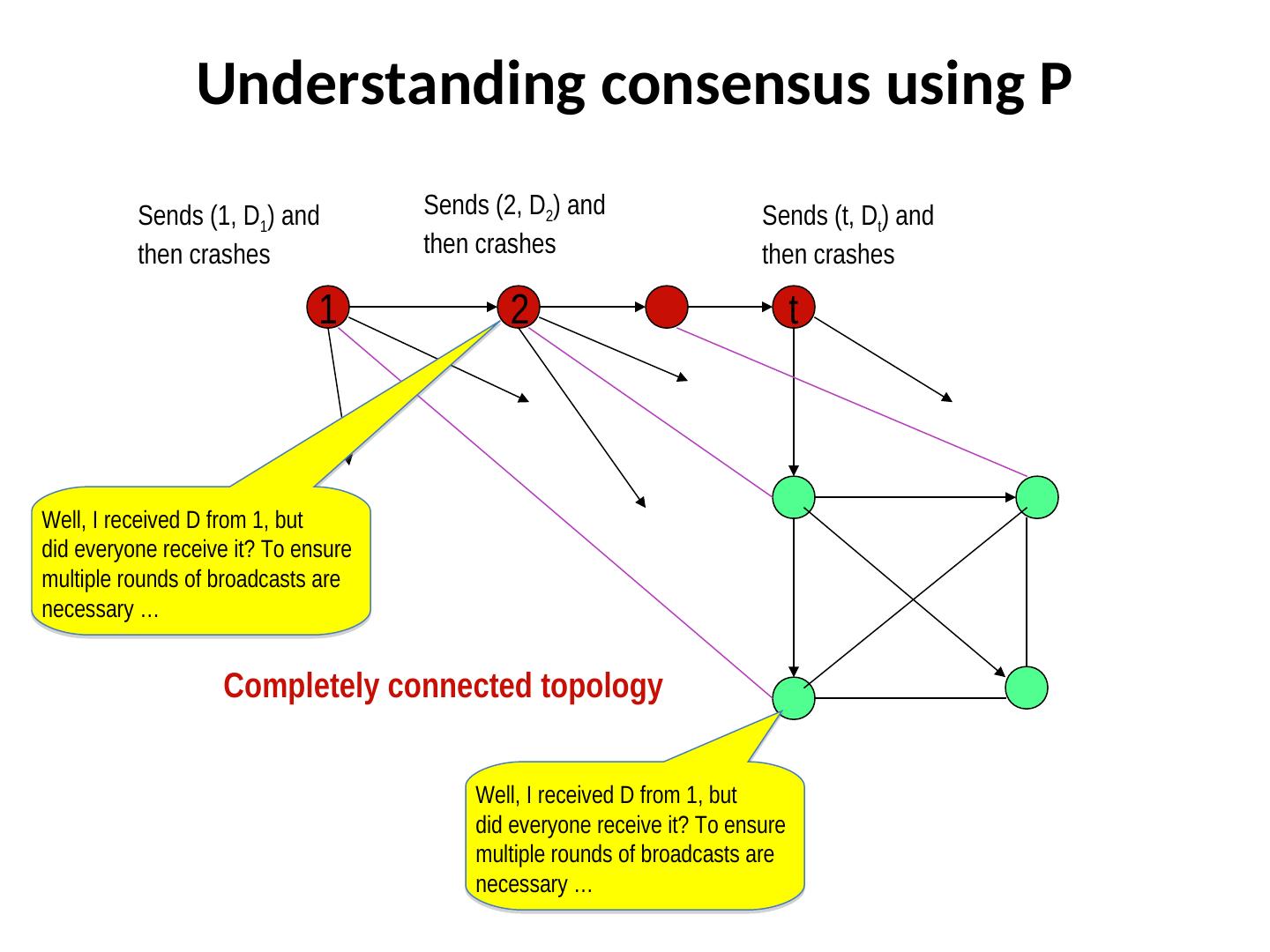
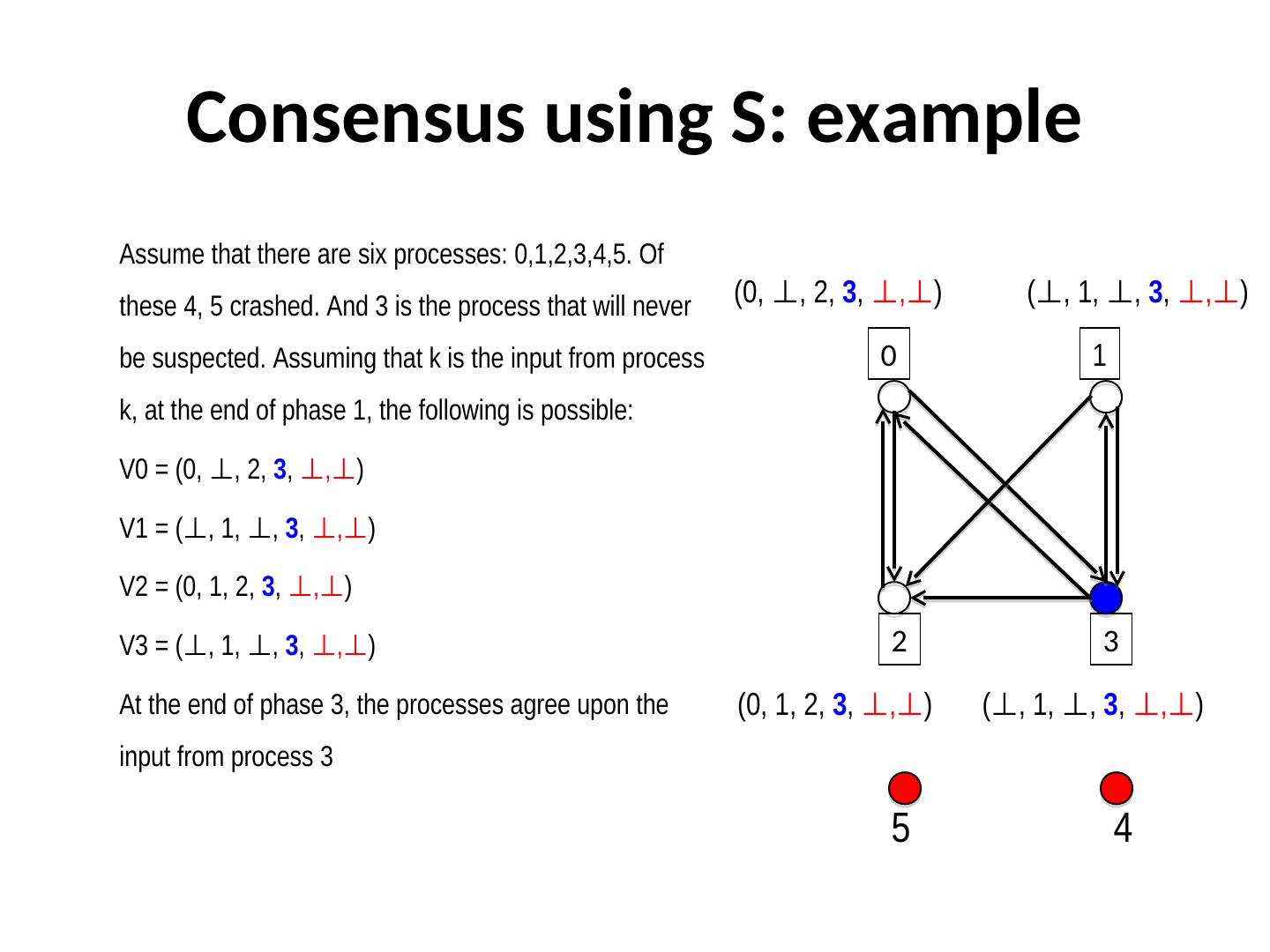
28 . Consensus using P {program for process p, t = max number of faulty processes} initially Vp := (⊥, ⊥, ⊥, …, ⊥); {array of size n}, ⊥, ⊥, ⊥, …, ⊥); {array of size n}, ⊥, ⊥, ⊥, …, ⊥); {array of size n}, …, ⊥, ⊥, ⊥, …, ⊥); {array of size n}); {array of size n} Vp[p] = input of p; Dp := Vp; rp :=1 {Vp[q] = ⊥, ⊥, ⊥, …, ⊥); {array of size n} means, process p thinks q is a suspect. Initially everyone is a suspect} {Phase 1} for round rp= 1 to t +1 send (rp, Dp, p) to all; wait to receive (rp, Dq, q) from all q, {or else q becomes a suspect}; for k = 1 to n Vp[k] = ⊥, ⊥, ⊥, …, ⊥); {array of size n} ∧ ∃ (r ∃ (r (rp, Dq, q): Dq[k] ≠ ⊥, ⊥, ⊥, …, ⊥); {array of size n}  Vp[k] := Dq[k] end for end for {at the end of Phase 1, Vp for each correct process is identical} {Phase 2} Final decision value is the input from the first element Vp[j]: Vp[j] ≠ ⊥, ⊥, ⊥, …, ⊥); {array of size n} 

29 .Understanding consensus using P Why continue (t+1) rounds? It is possible that a process p sends out the first message to q and then crashes. If there are n processes and t of them crashed, then after at most (t +1) asynchronous rounds, Vp for each correct process p becomes identical, and contains all inputs from processes that may have transmitted at least once.