分布式系统和算法：最小生成树

1 .Minimum Spanning Tree 

2 . Minimum Spanning Tree Given a weighted graph G = (V, E), generate a spanning tree T = (V, E’) such that the sum of the weights of all the edges is minimum. A few applications Minimum cost vehicle routing. A cable TV company will use this to lay cables in a new neighborhood. On Euclidean plane, approximate solutions to the traveling salesman problem, We are interested in distributed algorithms only The traveling salesman problem asks for the shortest route to visit a collection of cities and return to the starting point. It is a well-known NP-hard problem 

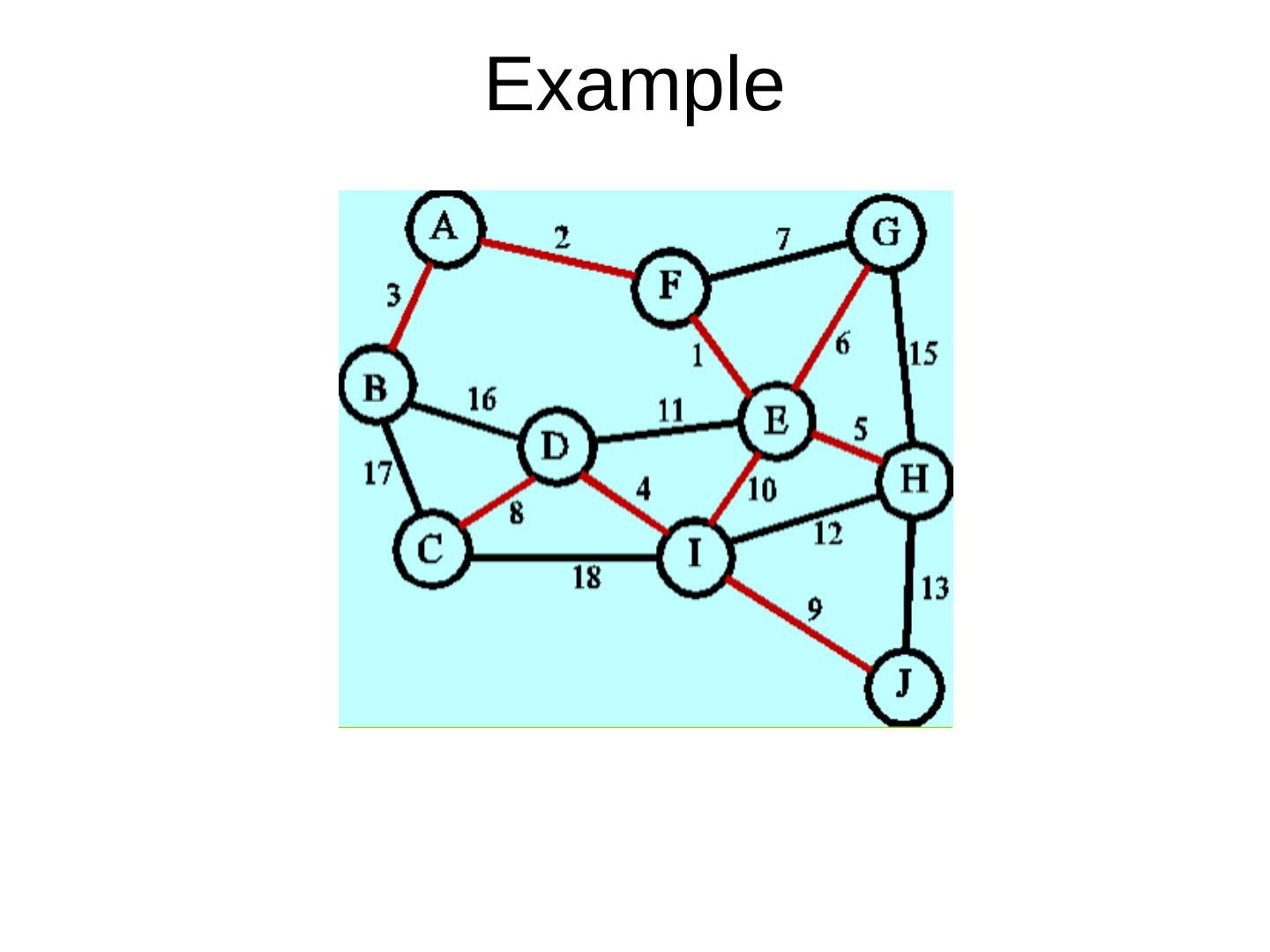
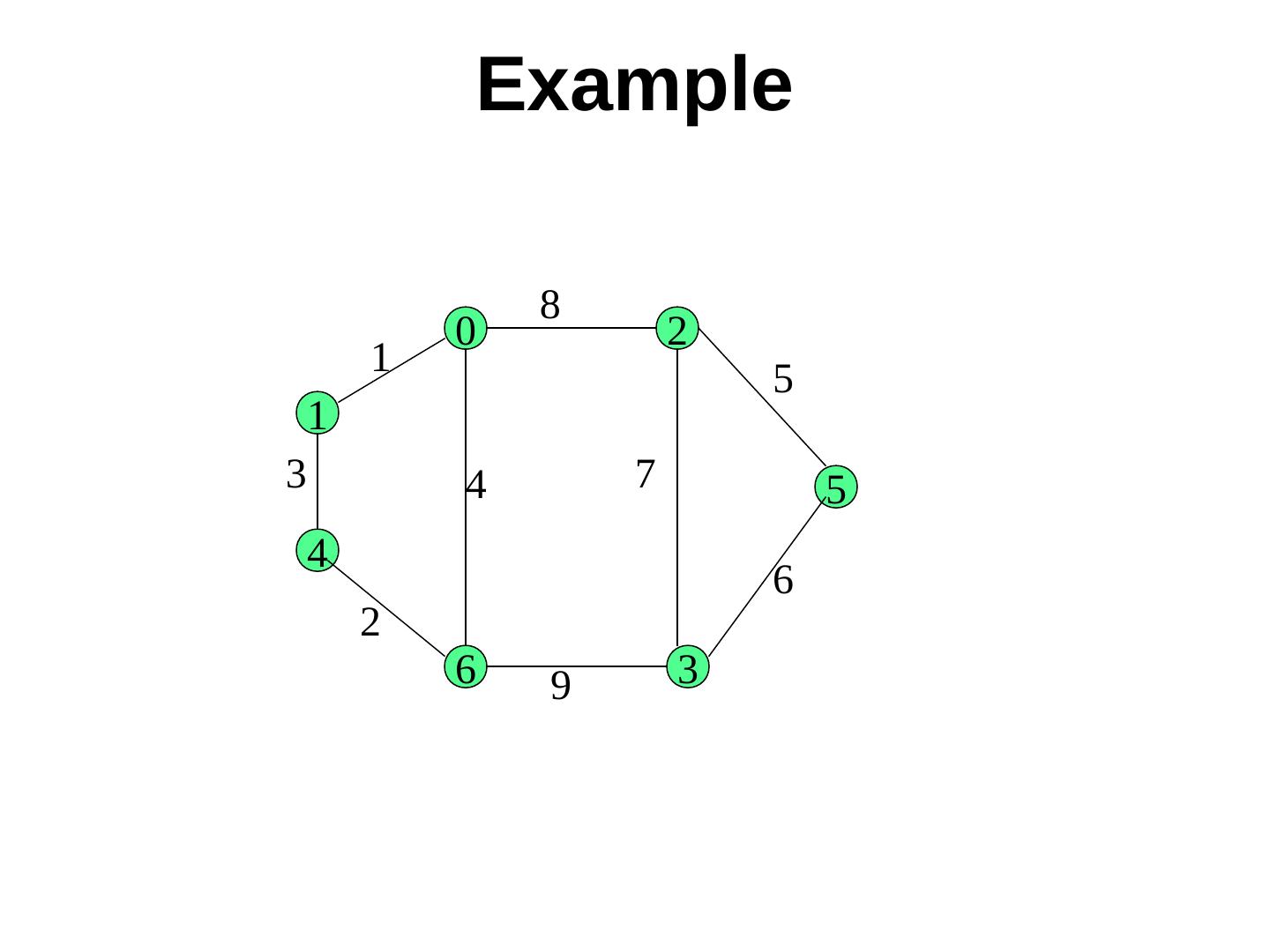
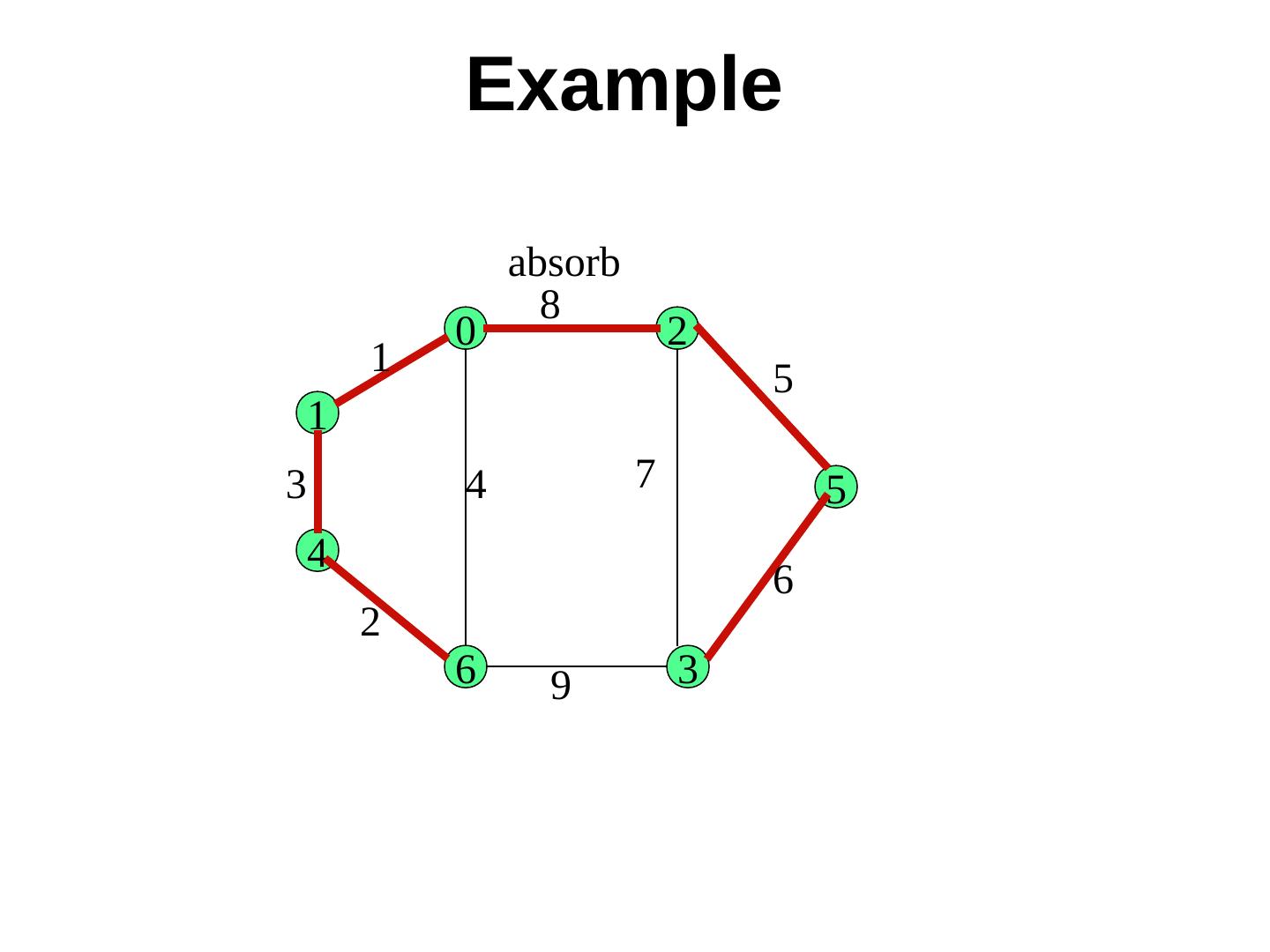
3 .Example 

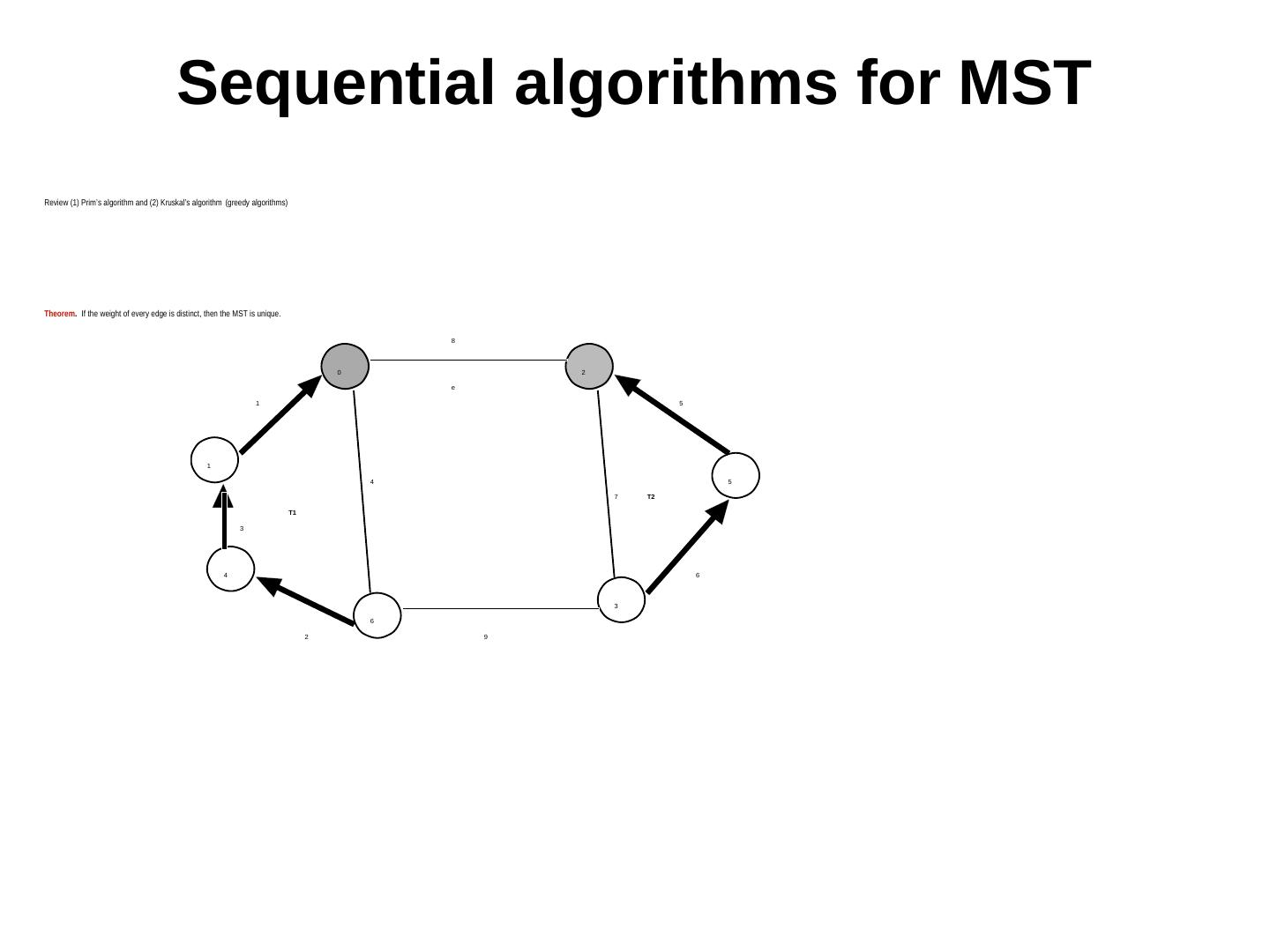
4 . Sequential algorithms for MST Review (1) Prim’s algorithm and (2) Kruskal’s algorithm (greedy algorithms) Theorem. If the weight of every edge is distinct, then the MST is unique. 8 0 2 e 1 5 1 4 5 7 T2 T1 3 4 6 3 6 2 9 

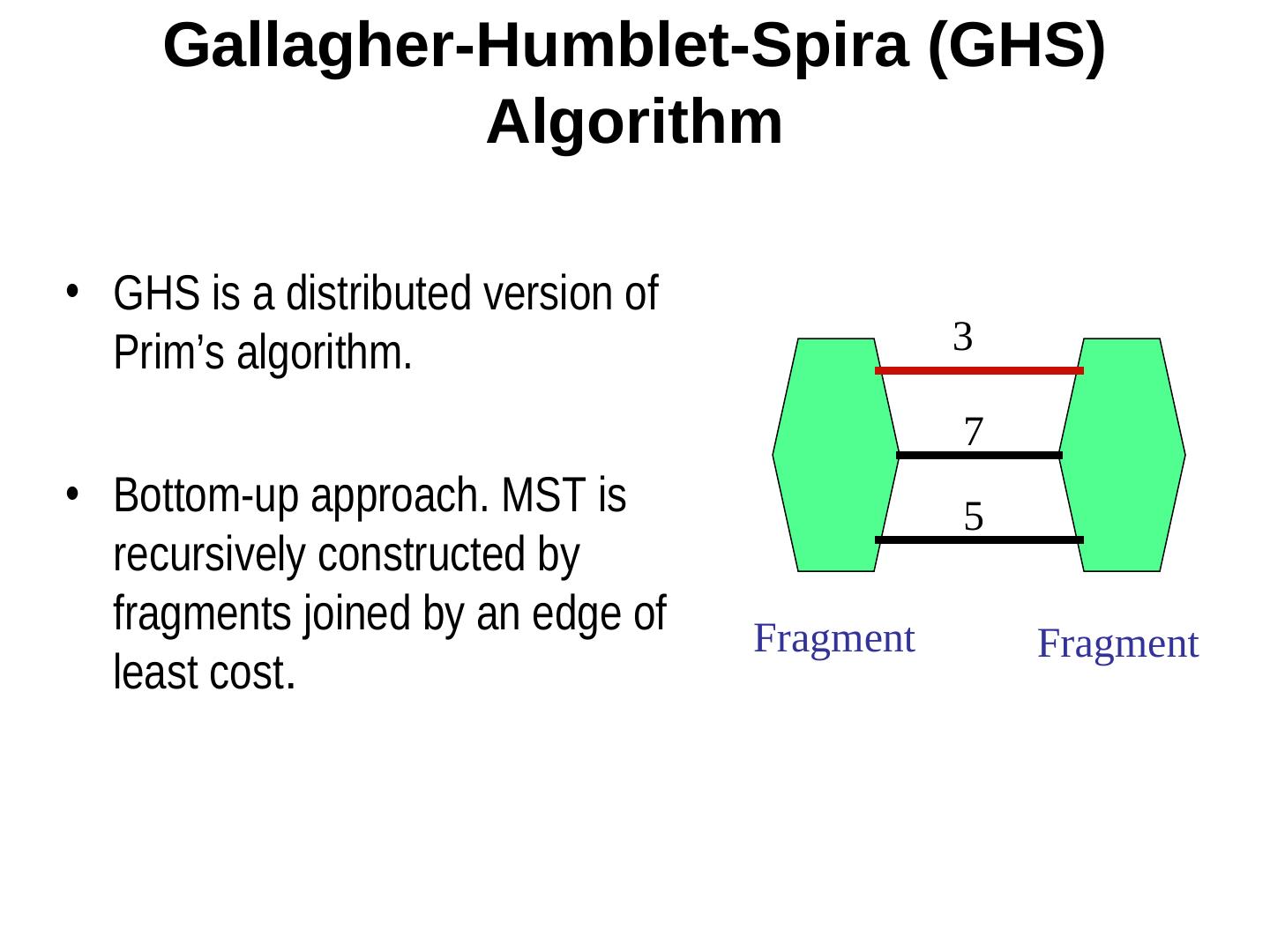
5 . Gallagher-Humblet-Spira (GHS) Algorithm • GHS is a distributed version of Prim’s algorithm. 3 7 • Bottom-up approach. MST is 5 recursively constructed by fragments joined by an edge of Fragment Fragment least cost. 

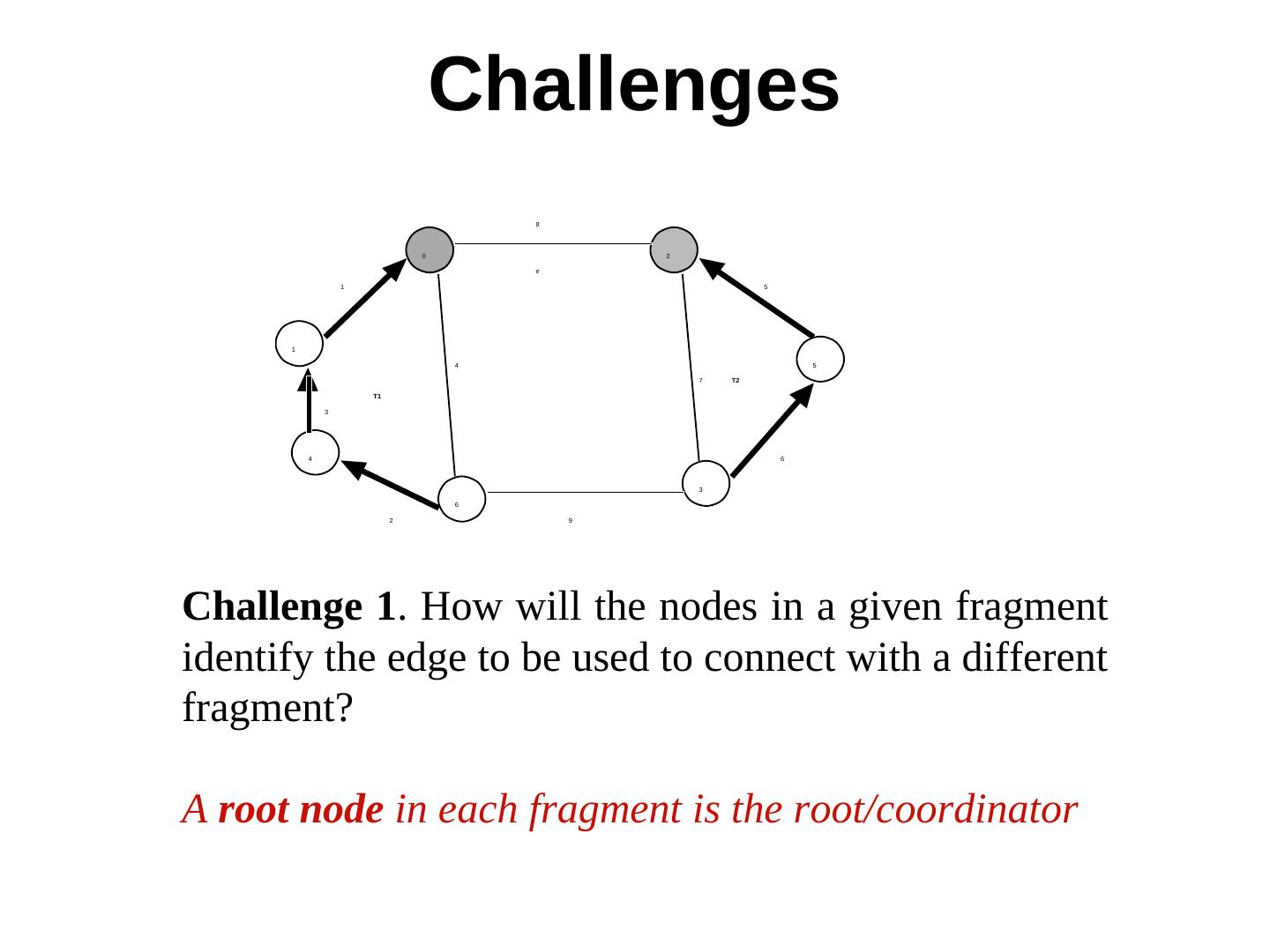
6 . Challenges 8 0 2 e 1 5 1 4 5 7 T2 T1 3 4 6 3 6 2 9 Challenge 1. How will the nodes in a given fragment identify the edge to be used to connect with a different fragment? A root node in each fragment is the root/coordinator 

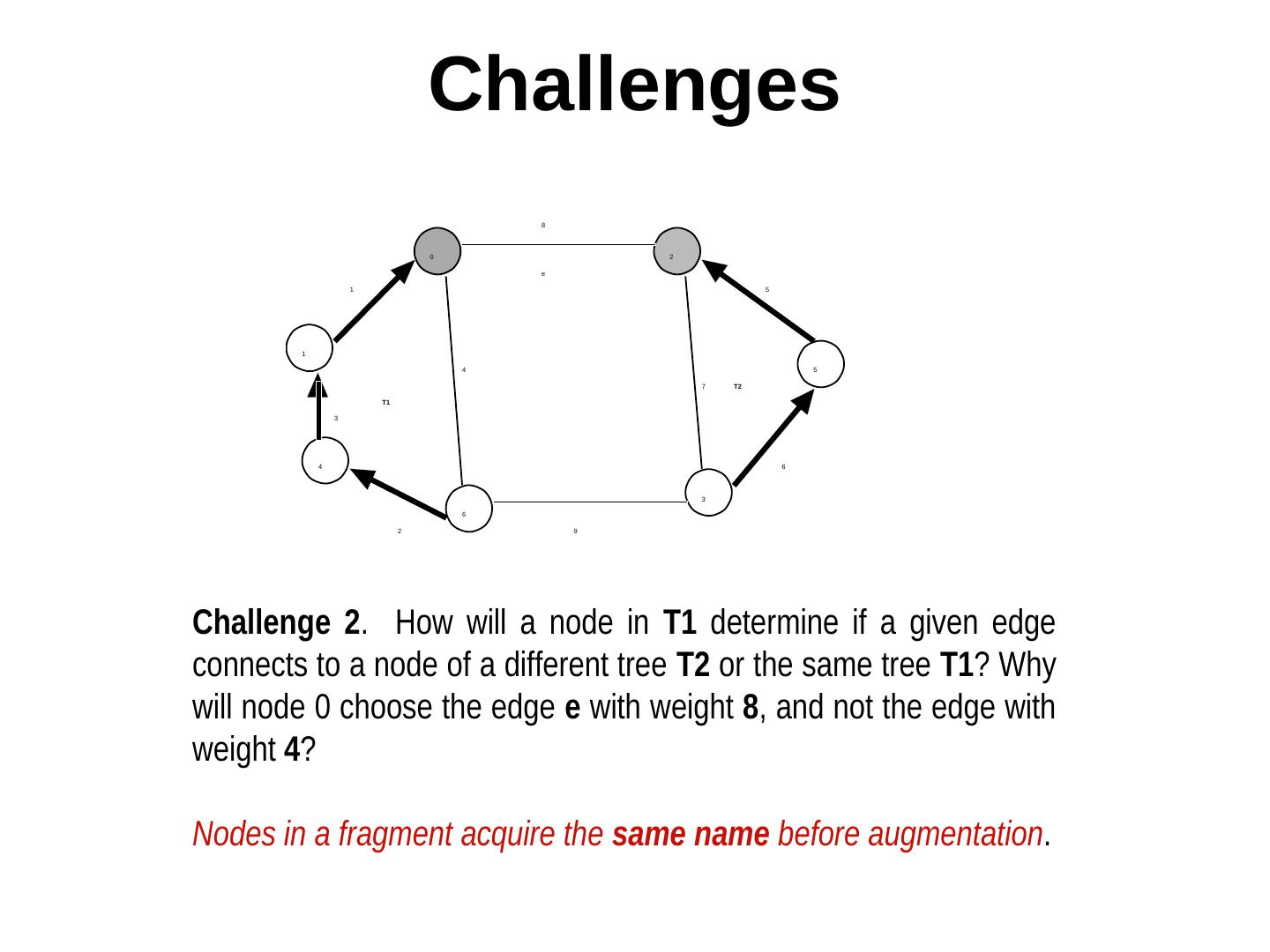
7 . Challenges 8 0 2 e 1 5 1 4 5 7 T2 T1 3 4 6 3 6 2 9 Challenge 2. How will a node in T1 determine if a given edge connects to a node of a different tree T2 or the same tree T1? Why will node 0 choose the edge e with weight 8, and not the edge with weight 4? Nodes in a fragment acquire the same name before augmentation. 

8 . Two main steps • Each fragment has a level. Initially each node is a fragment at level 0. • (MERGE) Two fragments at the same level L combine to form a fragment of level L+1 • (ABSORB) A fragment at level L is absorbed by another fragment at level L’ (L < L’). The new fragment has a level L’. (Each fragment in level L has at least 2L nodes) 

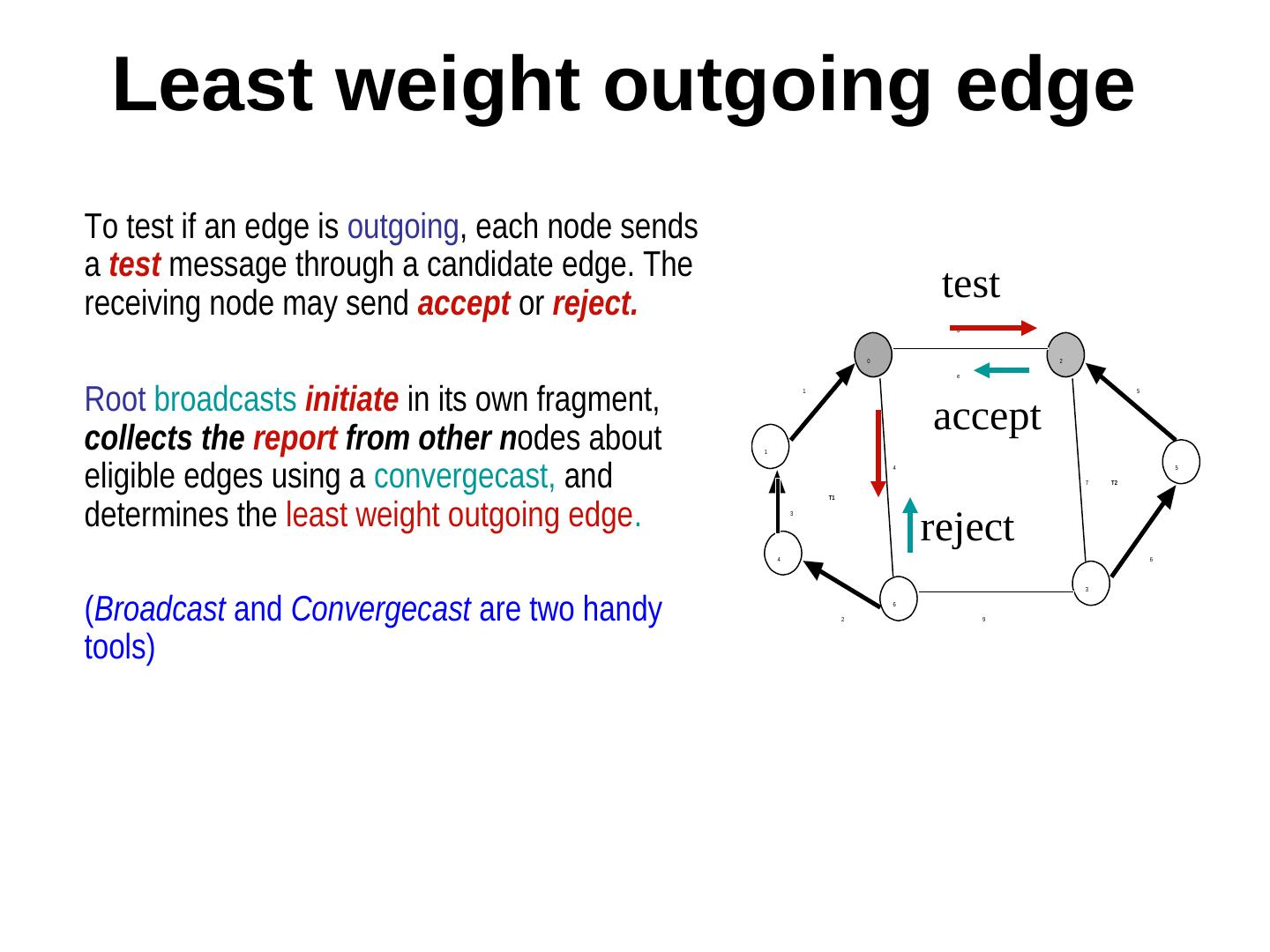
9 . Least weight outgoing edge To test if an edge is outgoing, each node sends a test message through a candidate edge. The receiving node may send accept or reject. test 8 0 2 e Root broadcasts initiate in its own fragment, 1 5 collects the report from other nodes about accept 1 eligible edges using a convergecast, and 4 5 7 T2 determines the least weight outgoing edge. T1 reject 3 4 6 3 (Broadcast and Convergecast are two handy 2 6 9 tools) 

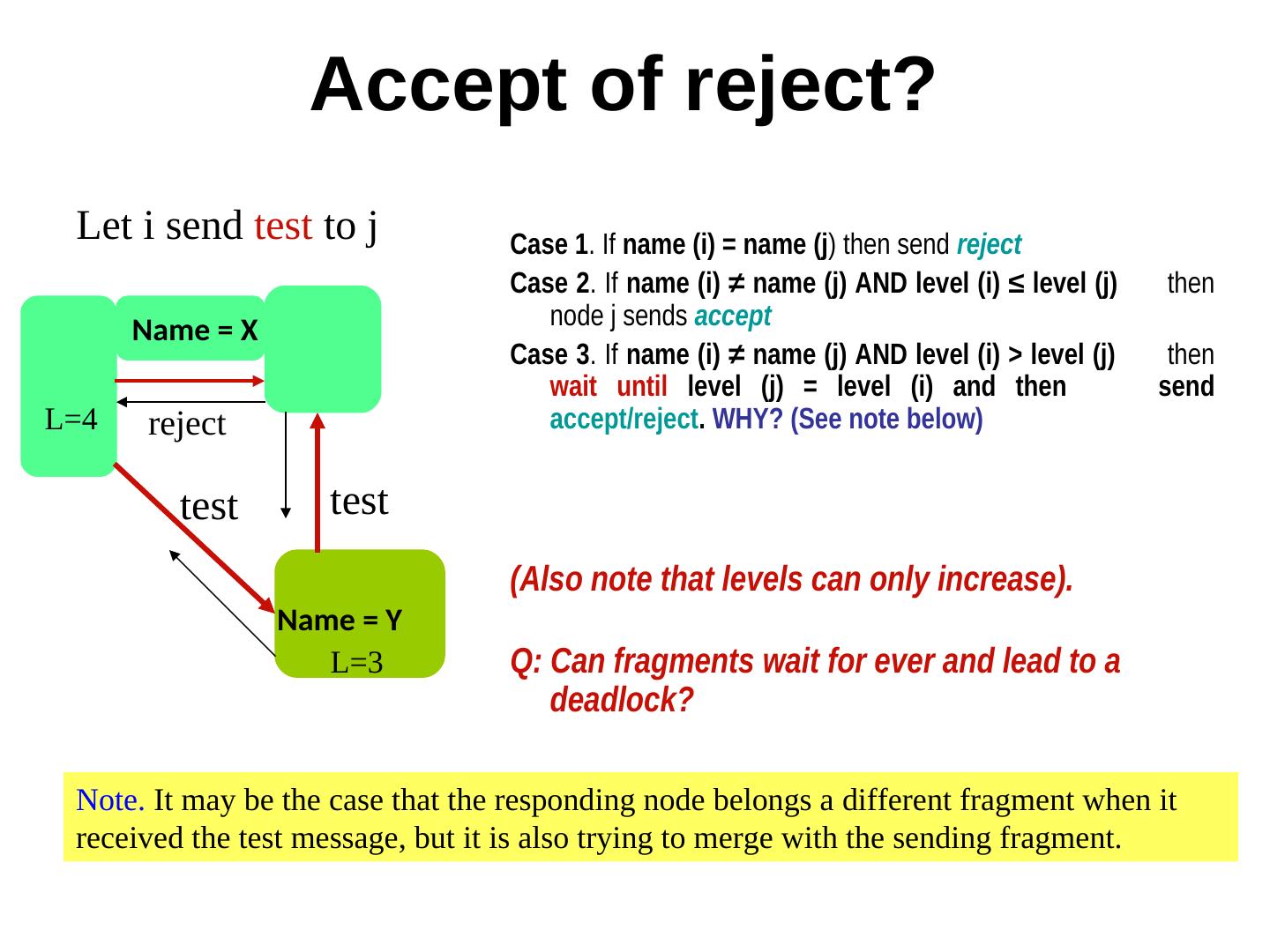
10 . Accept of reject? Let i send test to j Case 1. If name (i) = name (j) then send reject Case 2. If name (i) ≠ name (j) AND level (i) ≤ level (j) then node j sends accept Name = X Case 3. If name (i) ≠ name (j) AND level (i) > level (j) then wait until level (j) = level (i) and then send L=4 reject accept/reject. WHY? (See note below) test test (Also note that levels can only increase). Name = Y L=3 Q: Can fragments wait for ever and lead to a deadlock? Note. It may be the case that the responding node belongs a different fragment when it received the test message, but it is also trying to merge with the sending fragment. 

11 . The major steps repeat 1 Test edges as outgoing or not 2 Determine least weight outgoing edge - it becomes a tree edge 3 Send join (or respond to join) 4 Update level & name & identify new coordinator/root until there are no outgoing edges 

12 . Types of messages (Initiate) Root initiates the “lwoe” search (report) Nodes respond to the root with info about outgoing edges (test) nodes test if an edge is outgoing (accept) the recipient of the test message certifies the edge as “outgoing” (reject) the recipient of the test message certifies the edge as “not outgoing” (join) An edge node send join to the fragment at the other end (changeroot) nodes broadcast the id of the new root in the fragment 

13 . Classification of edges • Basic (initially all branches are basic) • Branch (all tree edges) • Rejected (not a tree edge) Branch and rejected are stable attributes (once tagged as rejected, it remains so for ever. The same thing holds for tree edges too.) 

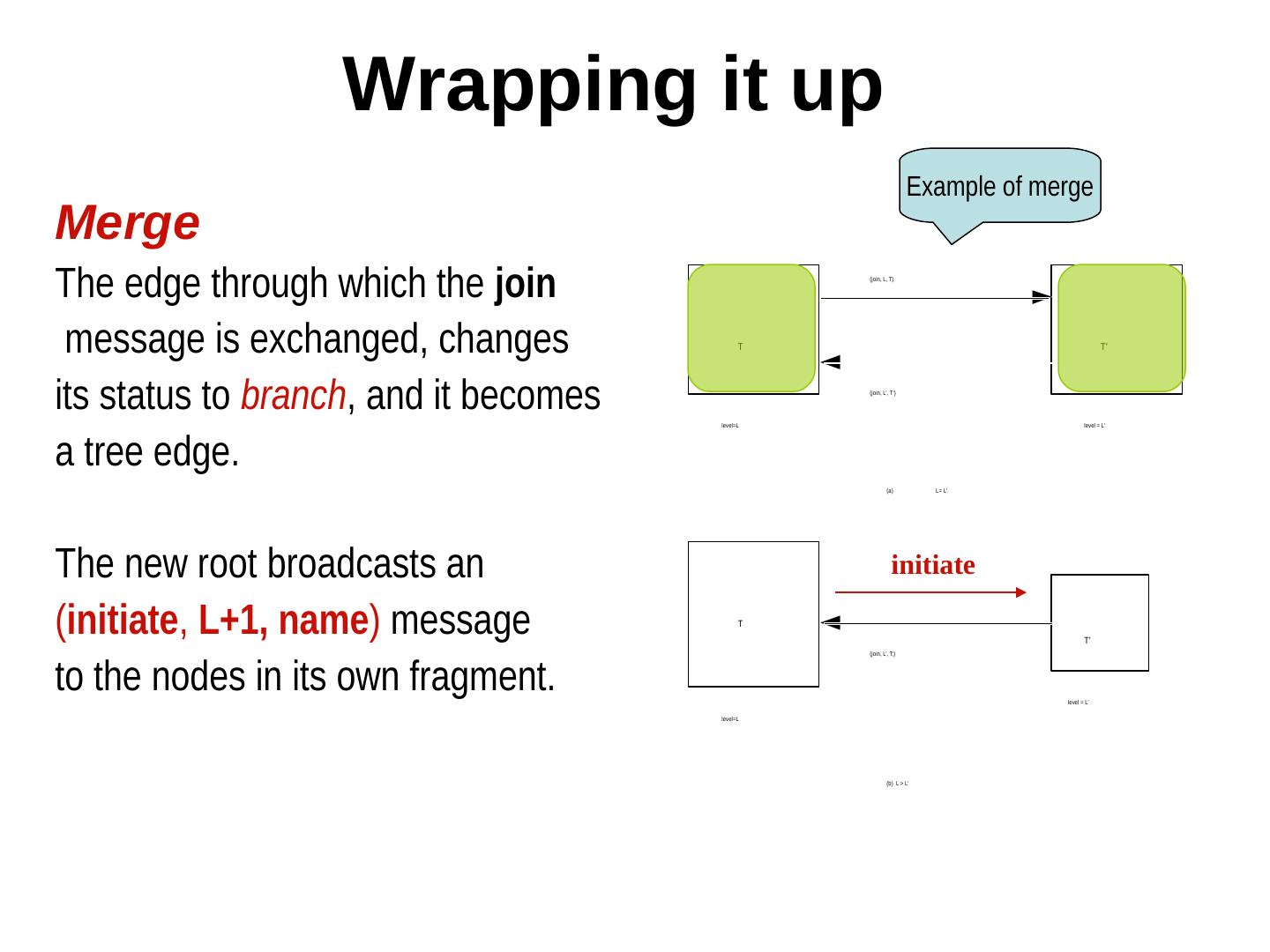
14 . Wrapping it up Example of merge Merge The edge through which the join (join, L, T) message is exchanged, changes T T’ its status to branch, and it becomes level=L (join, L’, T’) level = L’ a tree edge. (a) L= L’ The new root broadcasts an initiate (initiate, L+1, name) message T T’ (join, L’, T;) to the nodes in its own fragment. level = L’ level=L (b) L > L’ 

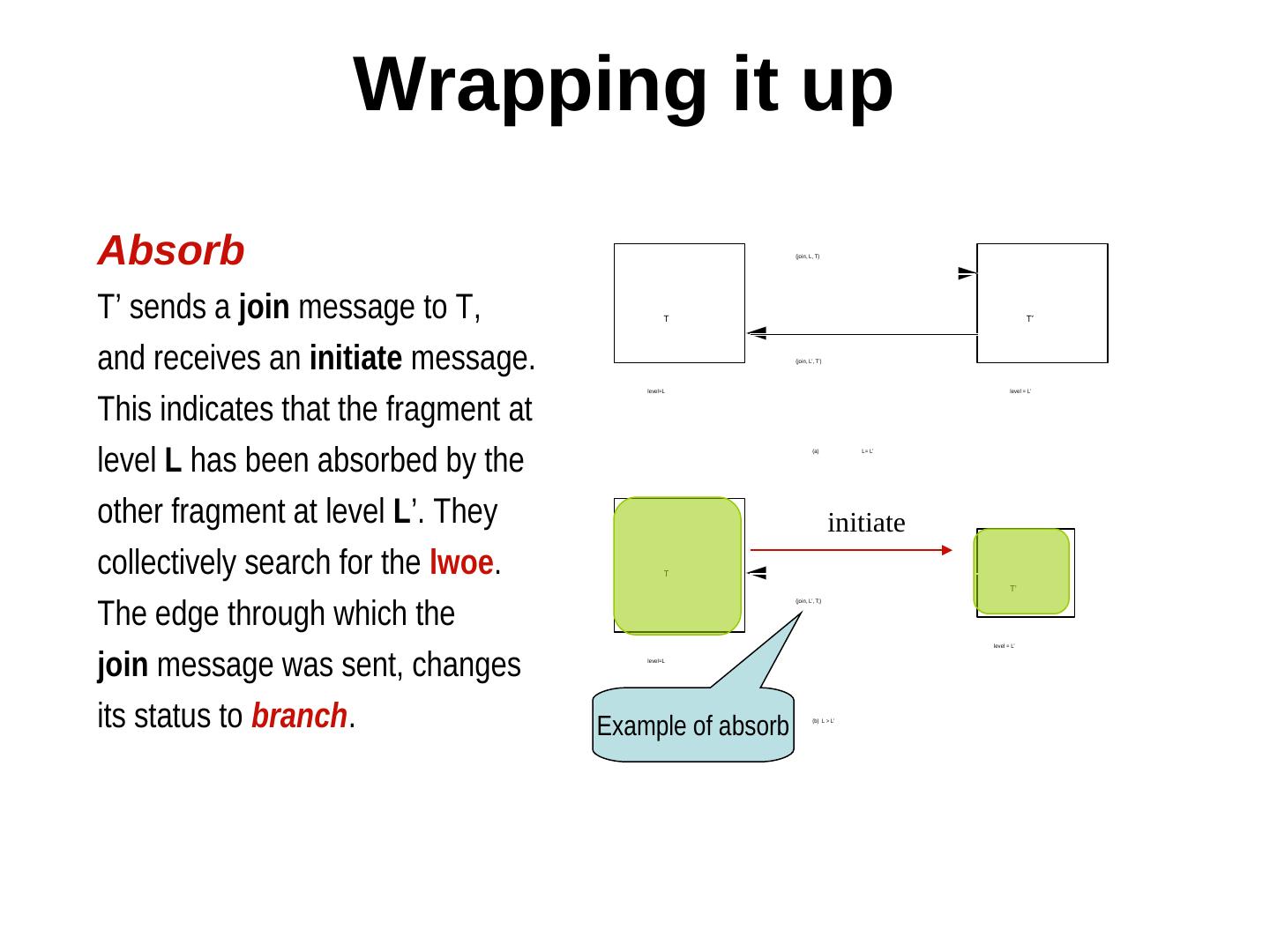
15 . Wrapping it up Absorb (join, L, T) T’ sends a join message to T, T T’ and receives an initiate message. (join, L’, T’) This indicates that the fragment at level=L level = L’ level L has been absorbed by the (a) L= L’ other fragment at level L’. They initiate collectively search for the lwoe. T T’ The edge through which the (join, L’, T;) level = L’ join message was sent, changes level=L its status to branch. Example of absorb (b) L > L’ 

16 . Example 8 0 2 1 5 1 3 4 7 5 4 6 2 6 9 3 

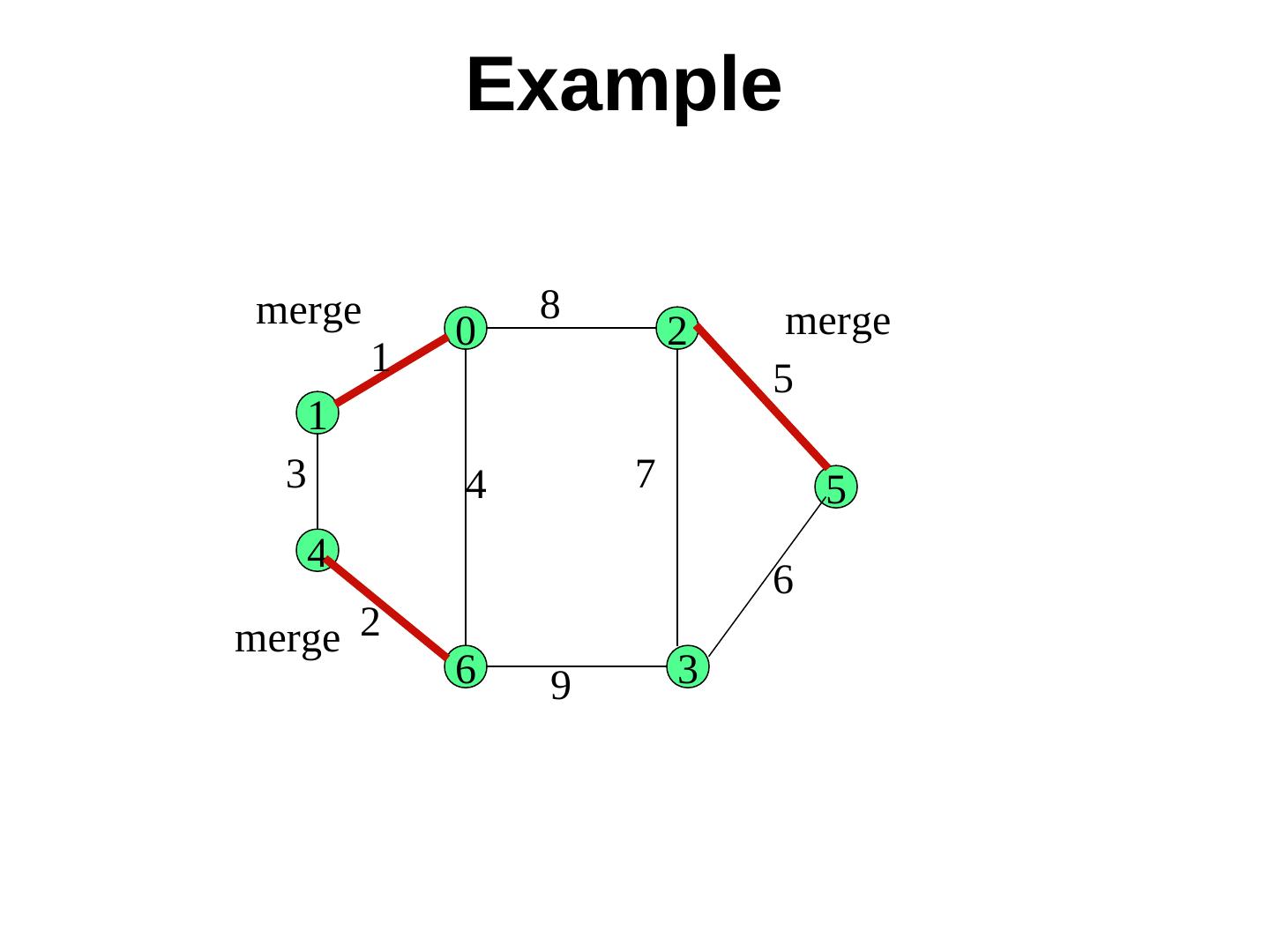
17 . Example merge 8 merge 0 2 1 5 1 3 4 7 5 4 6 merge 2 6 9 3 

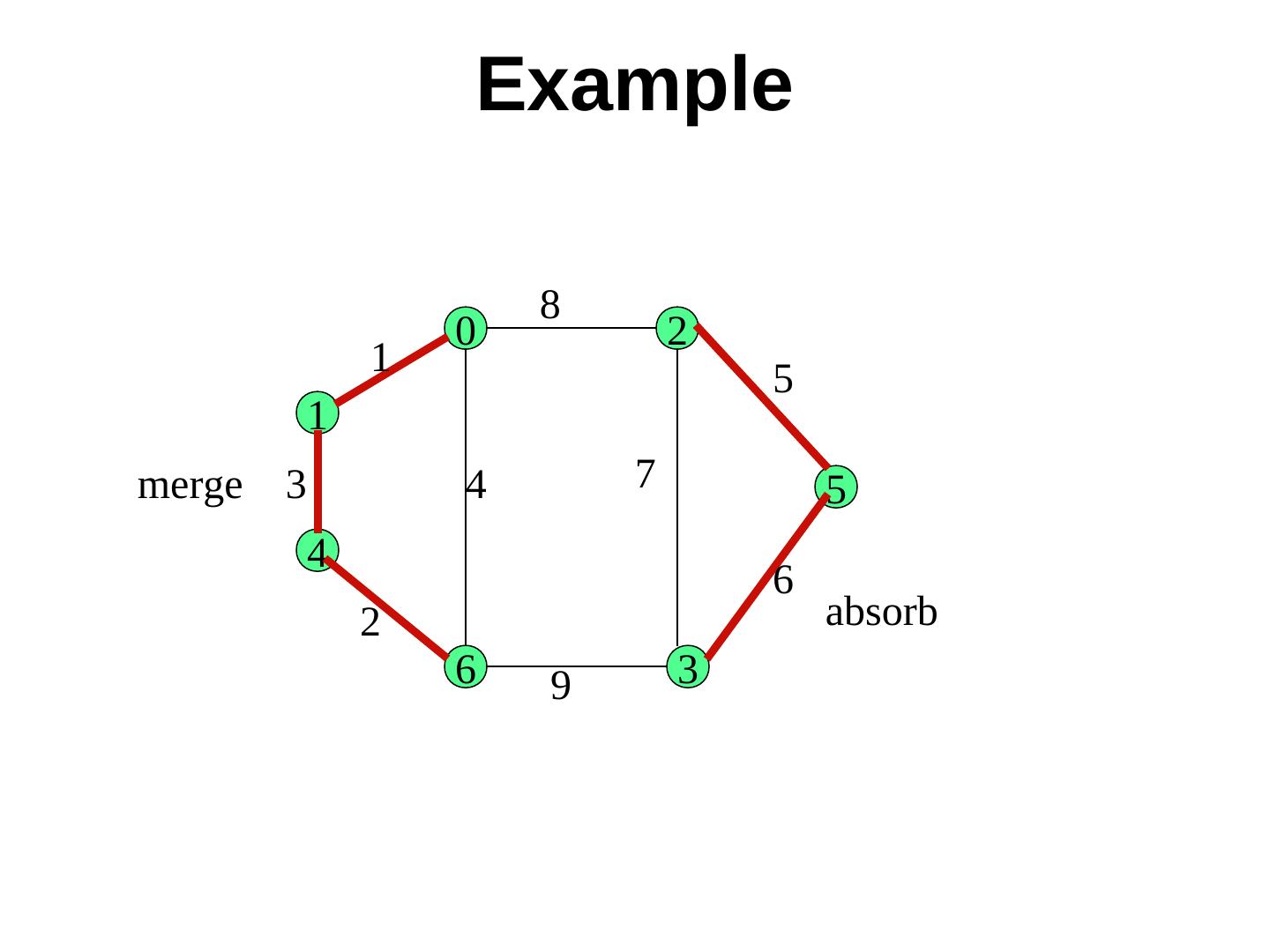
18 . Example 8 0 2 1 5 1 merge 3 4 7 5 4 6 2 absorb 6 9 3 

19 . Example absorb 8 0 2 1 5 1 3 4 7 5 4 6 2 6 9 3 

20 . Message complexity Each edge may be rejected at most once. It requires two messages (test + reject). The upper bound is 2|E| messages. At each of the (max) log N levels, a node RECEIVES at most (1) one initiate message and (2) one accept message and SENDS (3) one report message (4) one test message not leading to a rejection, and (5) one changeroot or join message. So, the total number of messages has an upper bound of 2|E| + 5N log N 

21 .Coordination Algorithms: Leader Election 

22 . Leader Election Let G = (V,E) define the network topology. Each process i has a variable L(i) that defines the leader. The goal is to reach a configuration, where ∀ i,j ∈ V V  i,j are non-faulty :: (1) L(i) ∈ V V and (2) L(i) = L(j) and (3) L(i) is non-faulty Often reduces to maxima (or minima) finding problem. (if we ignore the failure detection part) 

23 . Leader Election Difference between mutual exclusion & leader election The similarity is in the phrase “at most one process.” But, Failure is not an issue in mutual exclusion, a new leader is elected only after the current leader fails. No fairness is necessary - it is not necessary that every aspiring process has to become a leader. 

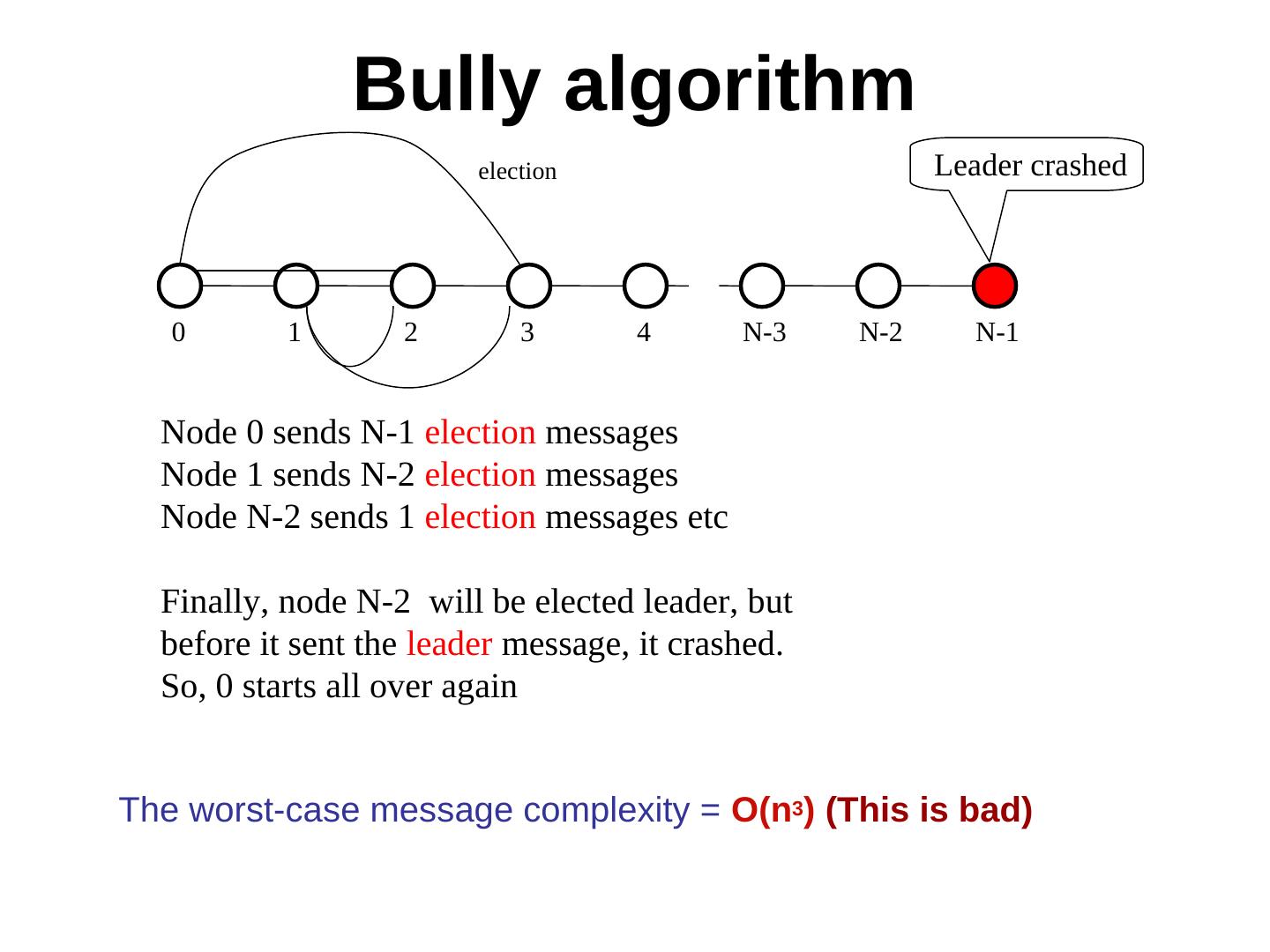
24 . Bully algorithm (Assumes that the topology is completely connected) 1. Send election message (I want to be the leader) to processes with larger id 2. Give up your bid if a process with larger id sends a reply message (means no, you cannot be the leader). In that case, wait for the leader message (I am the leader). Otherwise elect yourself the leader and send a leader message 3. If no reply is received, then elect yourself the leader, and broadcast a leader message. 4. If you receive a reply to the election message, but later don’t receive a leader message from a process of larger id (i.e. the leader-elect has crashed), then re-initiate election by sending election message. 

25 . Bully algorithm election Leader crashed 0 1 2 3 4 N-3 N-2 N-1 Node 0 sends N-1 election messages Node 1 sends N-2 election messages Node N-2 sends 1 election messages etc Finally, node N-2 will be elected leader, but before it sent the leader message, it crashed. So, 0 starts all over again The worst-case message complexity = O(n3) (This is bad) 

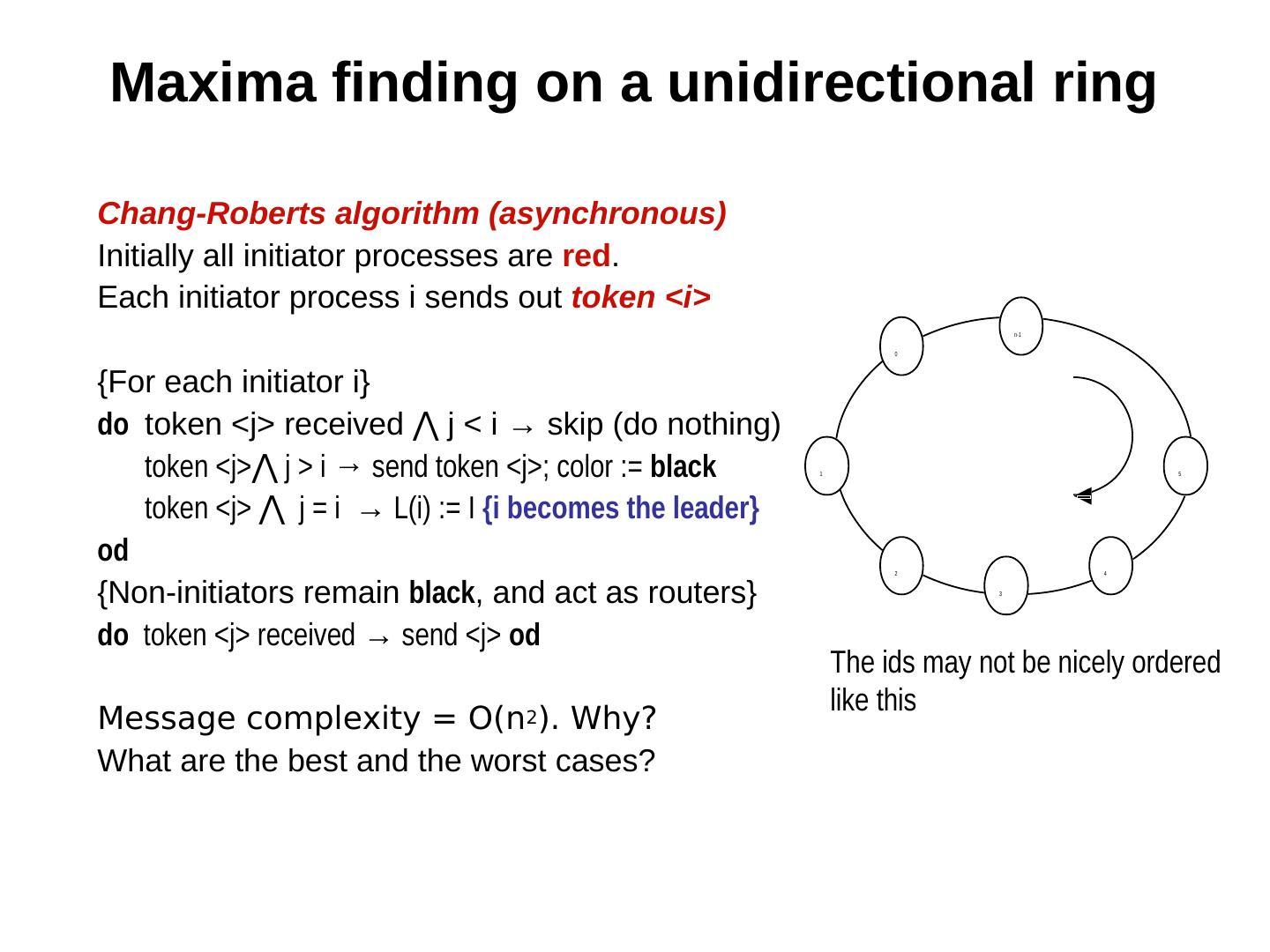
26 . Maxima finding on a unidirectional ring Chang-Roberts algorithm (asynchronous) Initially all initiator processes are red. Each initiator process i sends out token <i> n-1 0 {For each initiator i} do token <j> received ⋀ j < i → skip (do nothing) j < i → skip (do nothing) token <j>⋀ j < i → skip (do nothing) j > i → send token <j>; color := black 1 5 token <j> ⋀ j < i → skip (do nothing) j = i → L(i) := I {i becomes the leader} od 2 4 {Non-initiators remain black, and act as routers} 3 do token <j> received → send <j> od The ids may not be nicely ordered like this Message complexity = O(n2). Why? What are the best and the worst cases? 

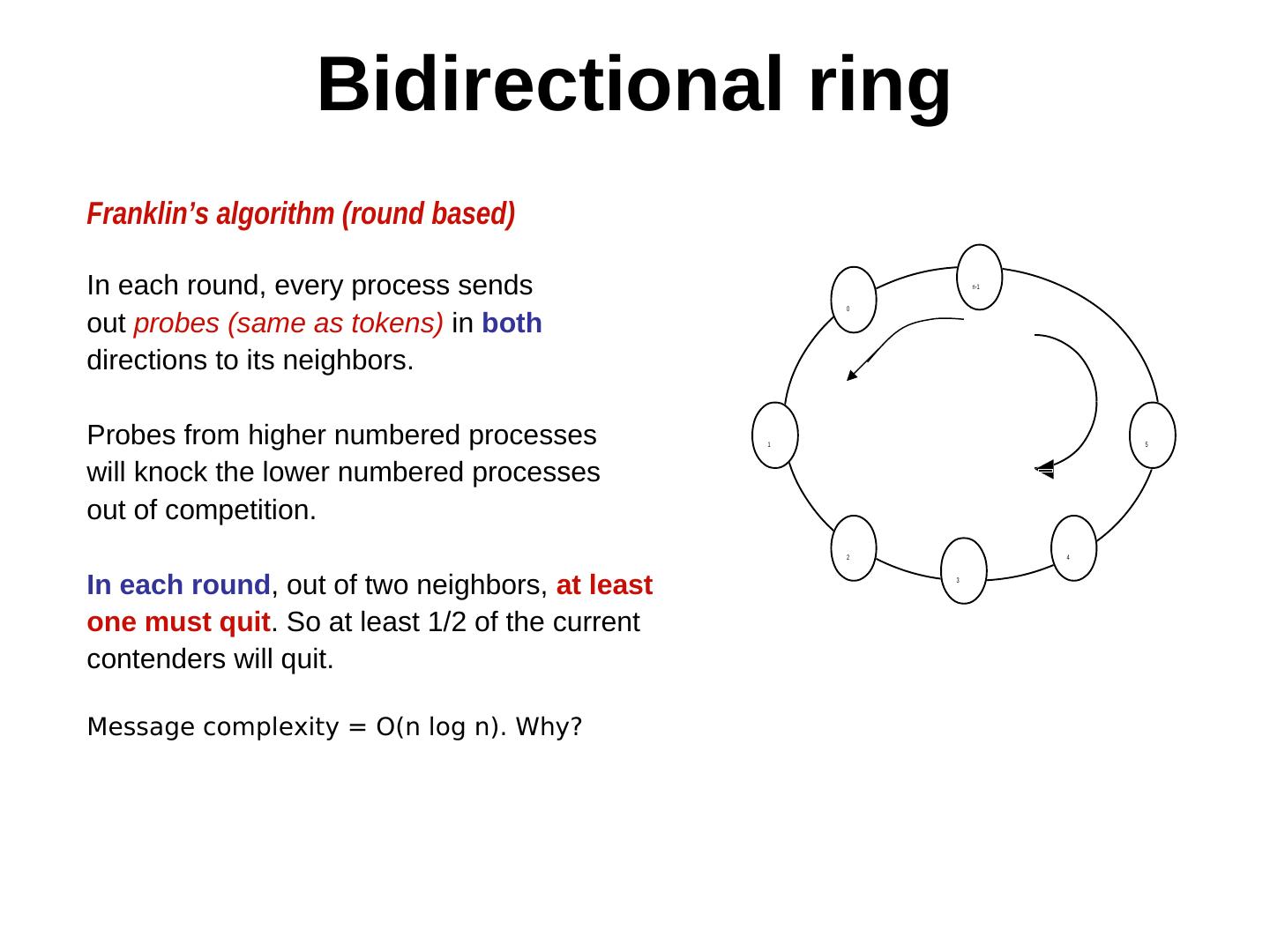
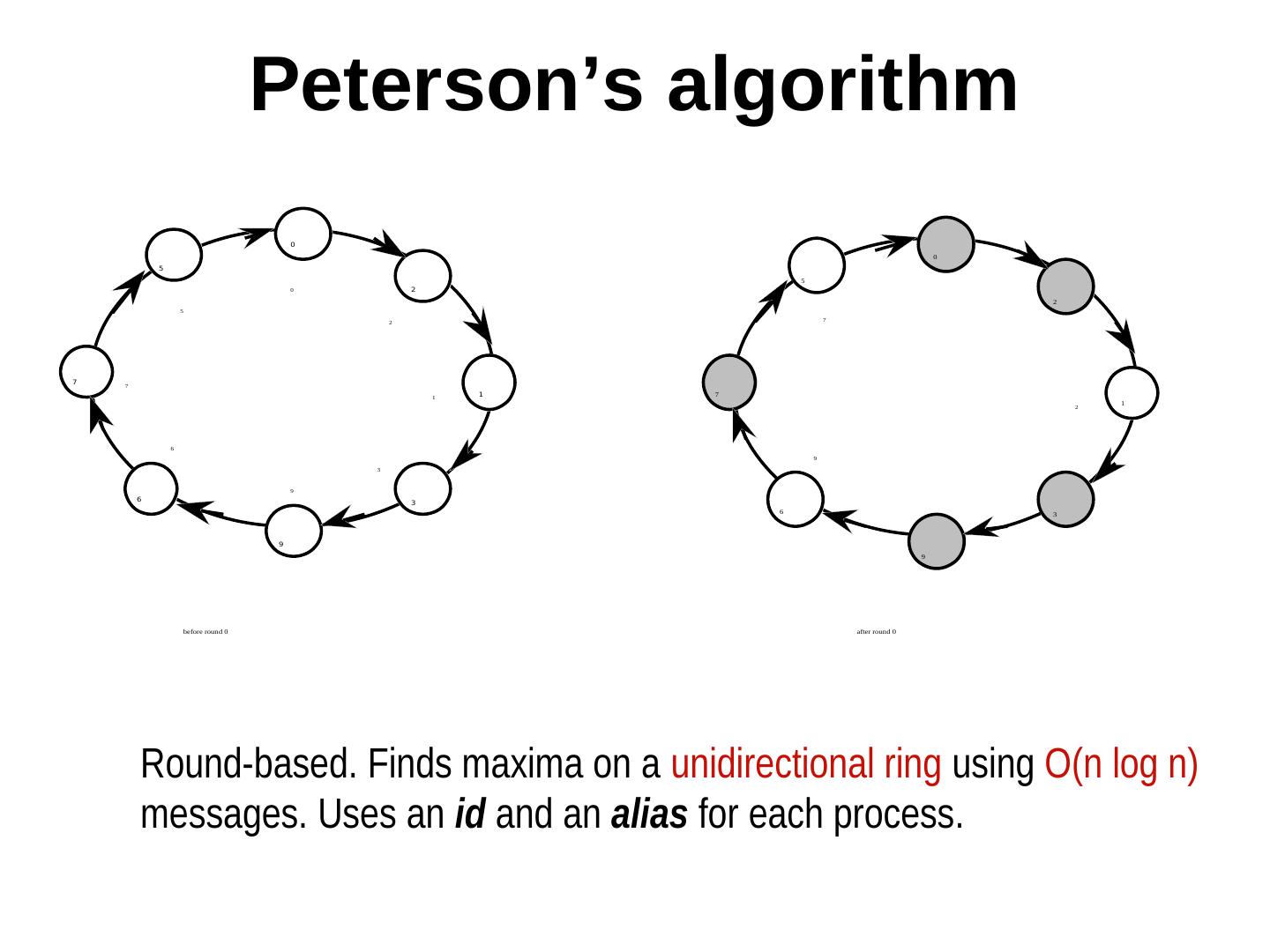
27 . Bidirectional ring Franklin’s algorithm (round based) In each round, every process sends n-1 0 out probes (same as tokens) in both directions to its neighbors. Probes from higher numbered processes 1 5 will knock the lower numbered processes out of competition. 2 4 In each round, out of two neighbors, at least 3 one must quit. So at least 1/2 of the current contenders will quit. Message complexity = O(n log n). Why? 

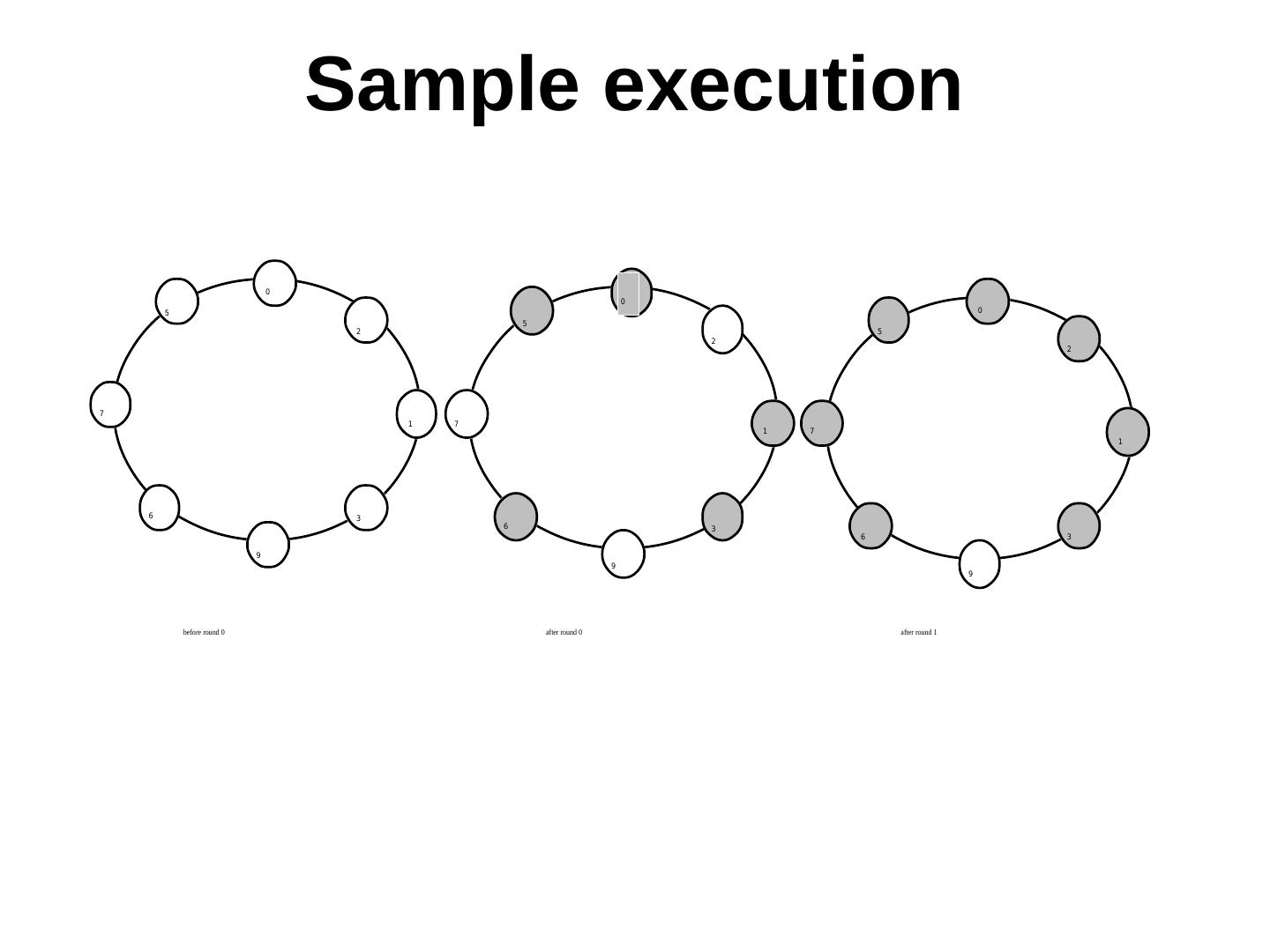
28 . Sample execution 0 0 5 0 5 2 5 2 2 7 1 7 1 7 1 6 3 6 3 6 3 9 9 9 before round 0 after round 0 after round 1 

29 . Peterson’s algorithm initially ∀ii : color(i) = red, alias(i) = i {program for each round and for each red process} send alias; receive alias (N); if alias = alias (N)  I am the leader alias ≠ alias (N)  send alias(N); receive alias(NN); if alias(N) > max (alias, alias (NN))  alias:= alias (N) alias(N) < max (alias, alias (NN))  color := black fi fi {N(i) and NN(i) denote neighbor and neighbor’s neighbor of i}