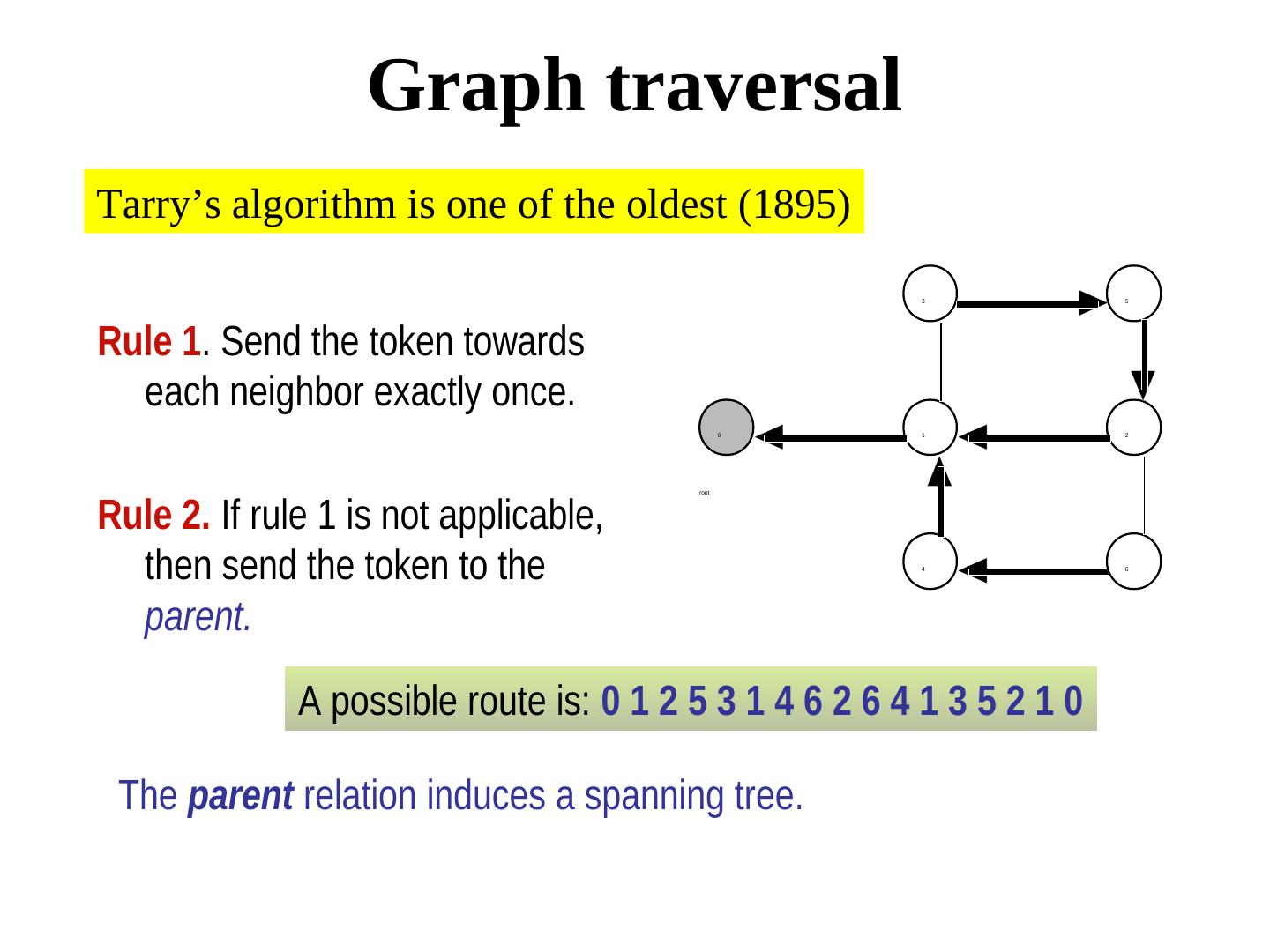
分布式系统和算法：图论

1 .Graph Algorithms 

2 . Graph Algorithms Many problems in networks can be modeled as graph problems. - The topology of a distributed system is a graph. - Routing table computation uses the shortest path algorithm - Efficient broadcasting uses a spanning tree of a graph - maxflow algorithm determines the maximum flow between a pair of nodes in a graph, etc etc. - graph coloring, maximal independent set etc have many applications 

3 . Routing • Shortest path routing • Distance vector routing • Link state routing • Routing in sensor networks • Routing in peer-to-peer networks 

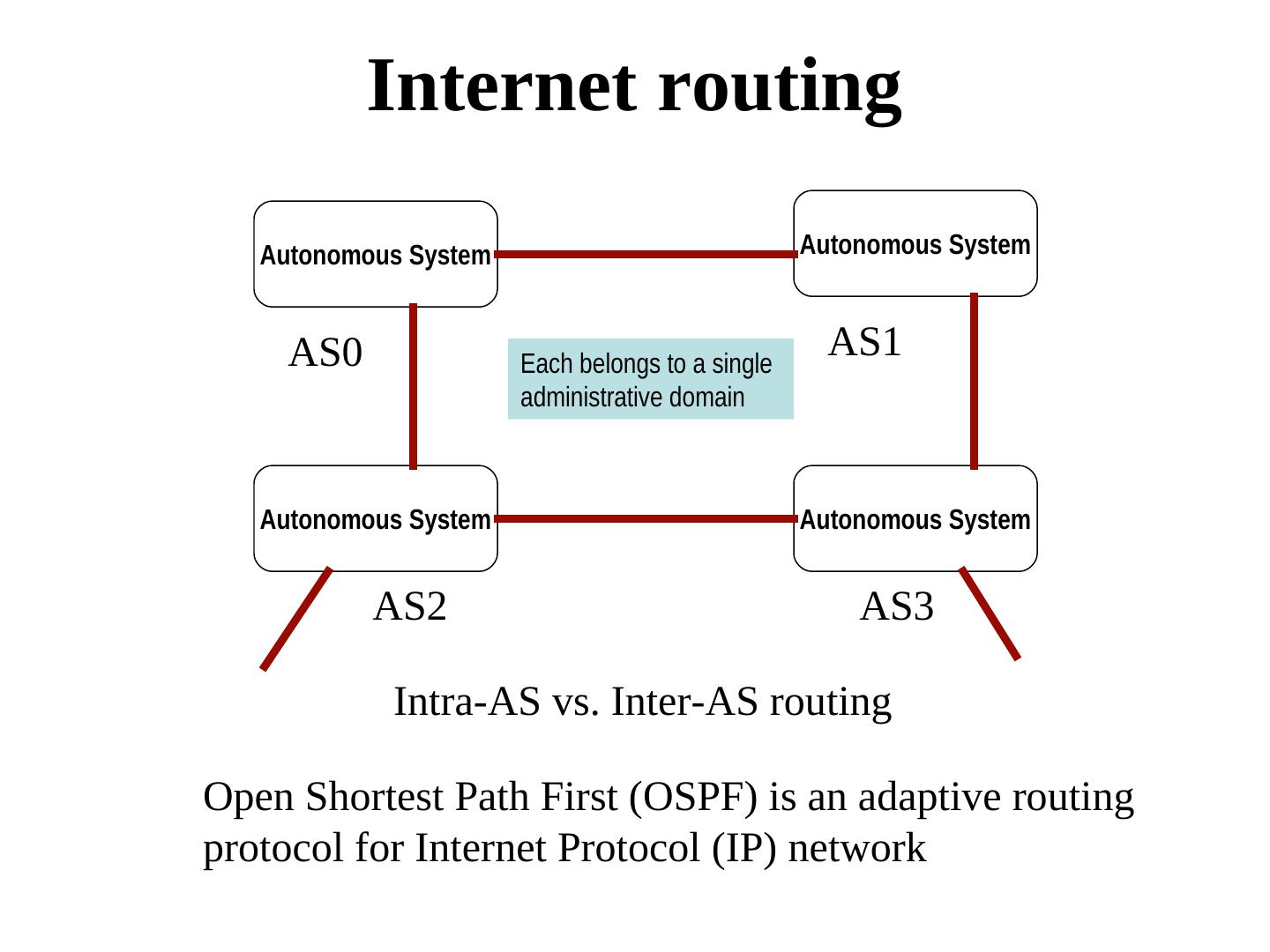
4 . Internet routing Autonomous System Autonomous System AS0 Each belongs to a single AS1 administrative domain Autonomous System Autonomous System AS2 AS3 Intra-AS vs. Inter-AS routing Open Shortest Path First (OSPF) is an adaptive routing protocol for Internet Protocol (IP) network 

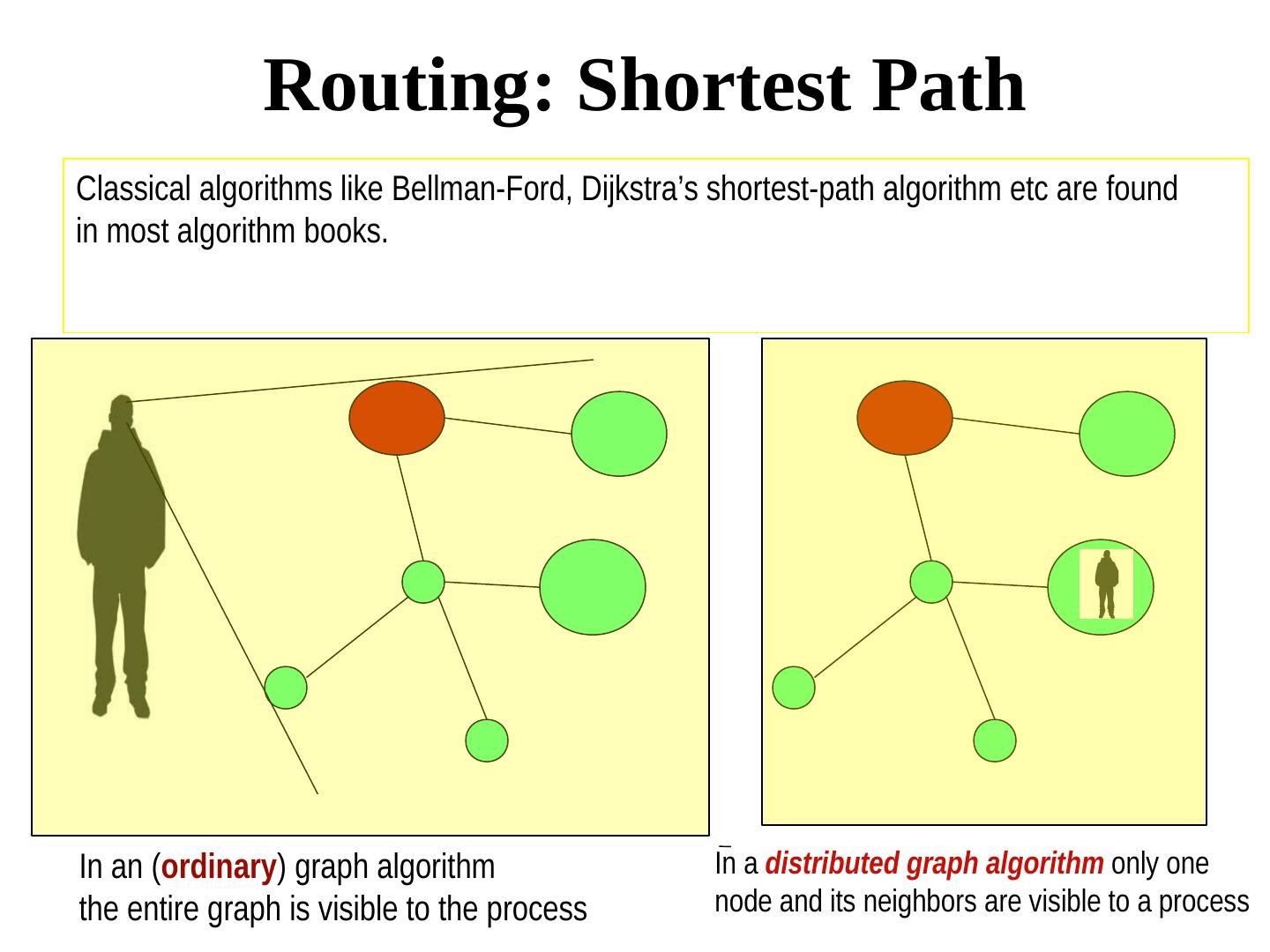
5 . Routing: Shortest Path Classical algorithms like Bellman-Ford, Dijkstra’s shortest-path algorithm etc are found in most algorithm books. In an (ordinary) graph algorithm In a distributed graph algorithm only one the entire graph is visible to the process node and its neighbors are visible to a process 

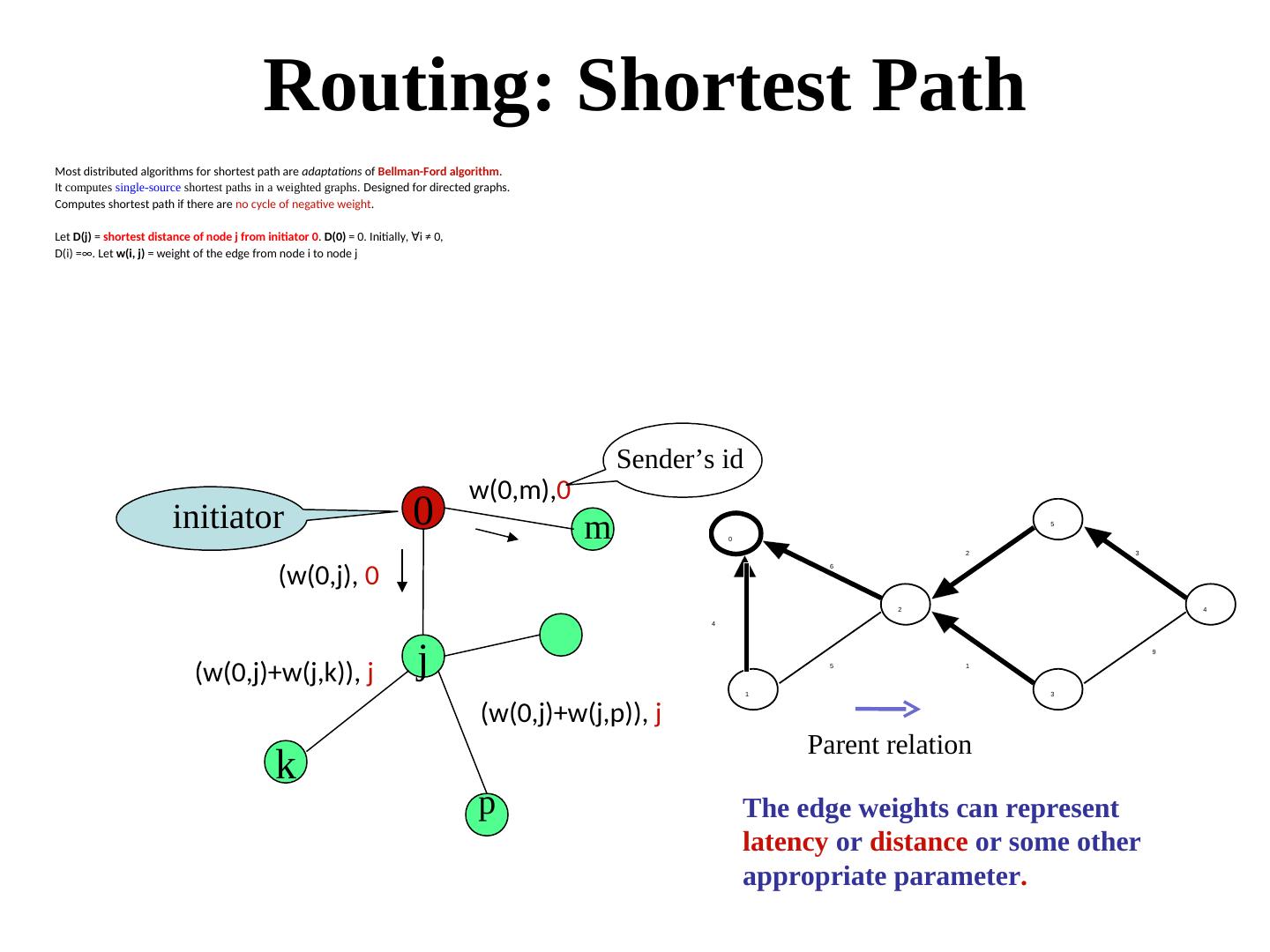
6 . Routing: Shortest Path Most distributed algorithms for shortest path are adaptations of Bellman-Ford algorithm. It computes single-source shortest paths in a weighted graphs. Designed for directed graphs. Computes shortest path if there are no cycle of negative weight. Let D(j) = shortest distance of node j from initiator 0. D(0) = 0. Initially, ∀i ≠ 0, i ≠ 0, D(i) =∞. Let w(i, j) = weight of the edge from node i to node j Sender’s id w(0,m),0 initiator 0 m 0 5 2 3 6 (w(0,j), 0 2 4 4 (w(0,j)+w(j,k)), j j 5 1 9 1 3 (w(0,j)+w(j,p)), j Parent relation k p The edge weights can represent latency or distance or some other appropriate parameter. 

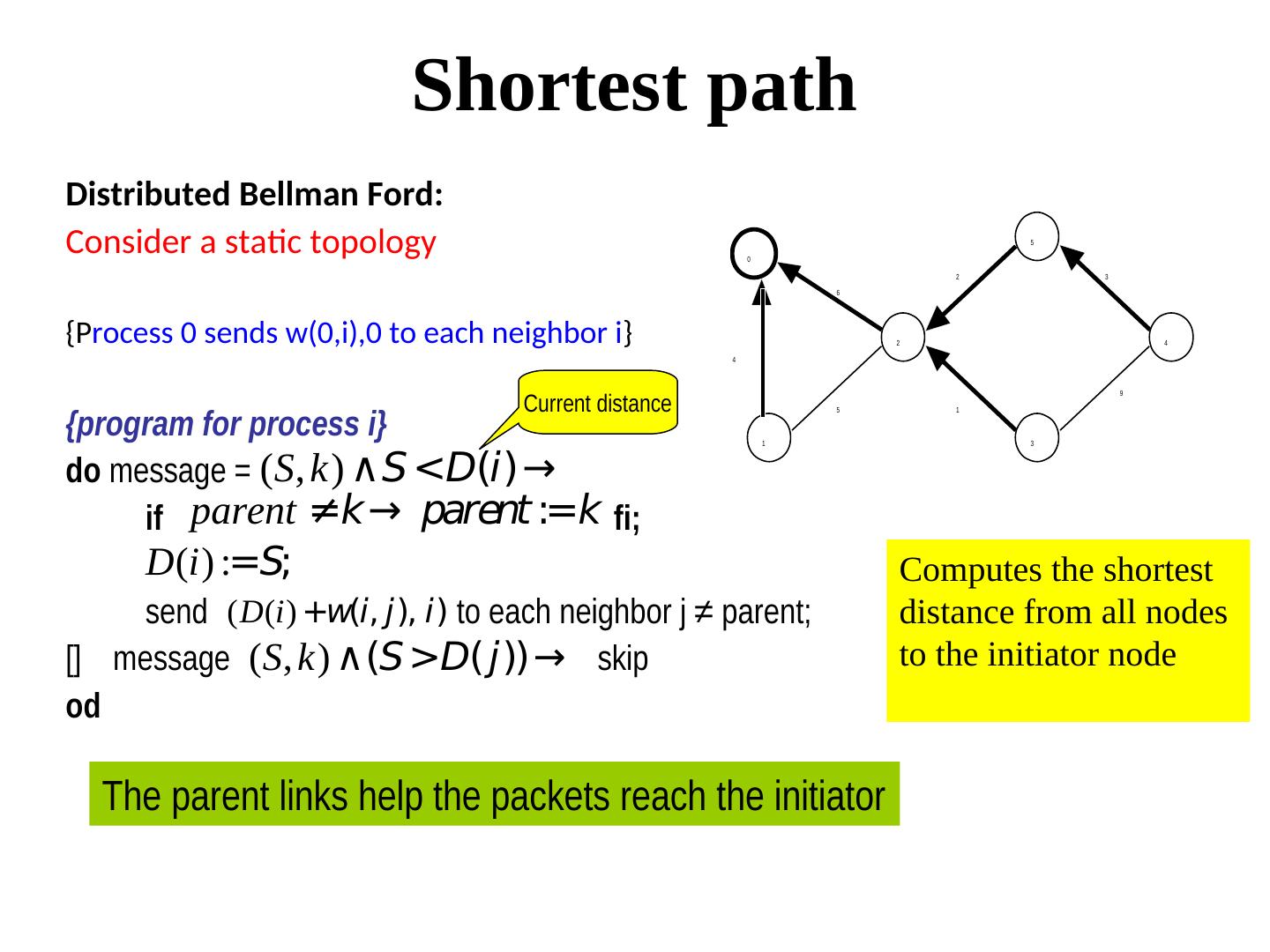
7 . Shortest path Distributed Bellman Ford: Consider a static topology 0 5 2 3 6 {Process 0 sends w(0,i),0 to each neighbor i} 2 4 4 Current distance 9 {program for process i} 5 1 1 3 do message = (S, k) ∧S <D(i)→ if parent ≠k→ parent :=k fi; D(i) :=S; Computes the shortest send (D(i) +w(i, j), i) to each neighbor j ≠ parent; distance from all nodes [] message (S, k) ∧(S >D( j))→ skip to the initiator node od The parent links help the packets reach the initiator 

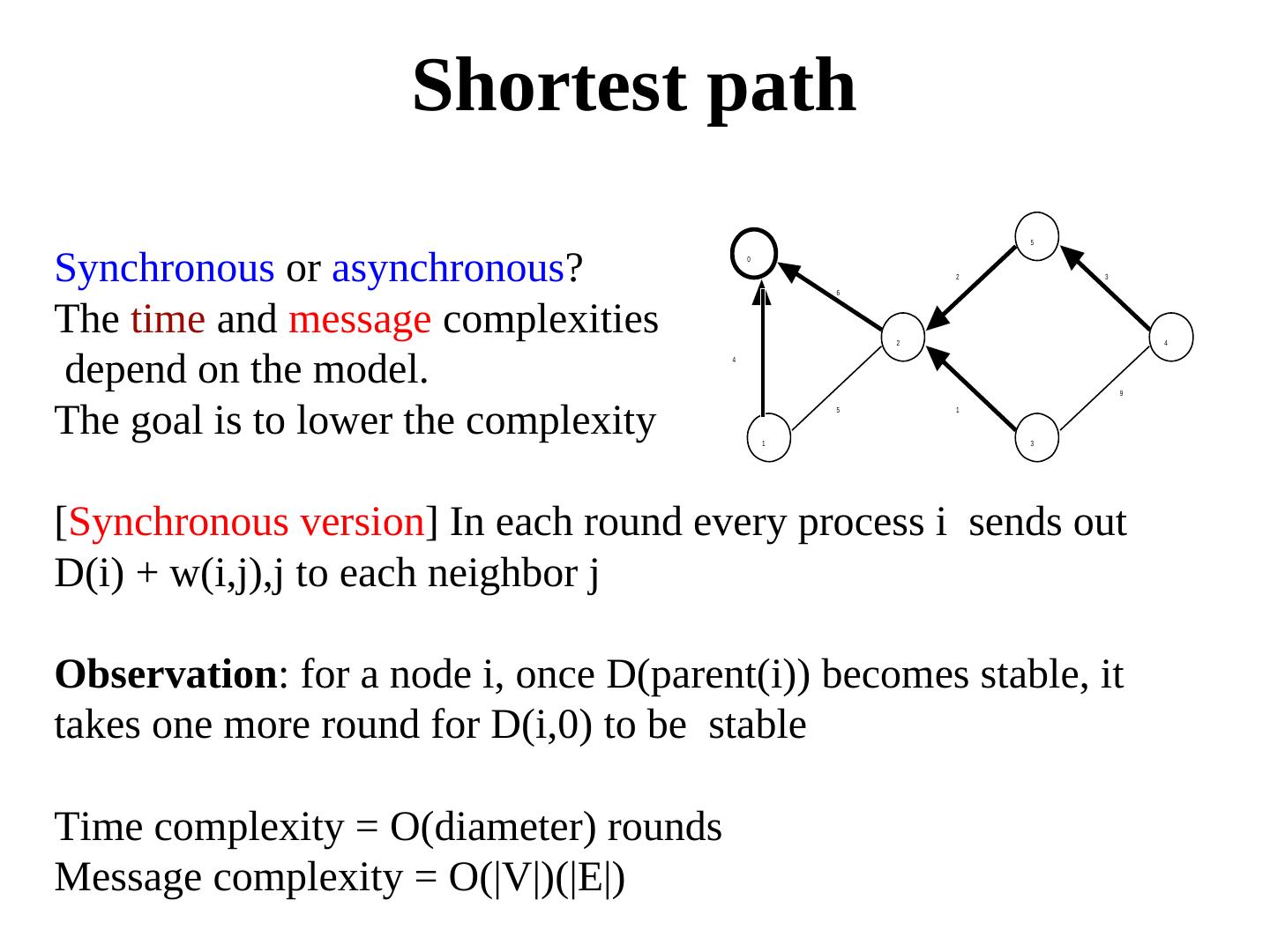
8 . Shortest path 5 Synchronous or asynchronous? 0 6 2 3 The time and message complexities 2 4 depend on the model. 4 9 The goal is to lower the complexity 1 5 1 3 [Synchronous version] In each round every process i sends out D(i) + w(i,j),j to each neighbor j Observation: for a node i, once D(parent(i)) becomes stable, it takes one more round for D(i,0) to be stable Time complexity = O(diameter) rounds Message complexity = O(|V|)(|E|) 

9 .Complexity of Bellman-Ford Theorem. The message complexity of asynchronous Bellman-Ford algorithm is exponential. Proof outline. Consider a topology with an odd number nodes 0 through n-1 (the unmarked edges have weight 0) n-4 n-2 1 3 5 2k 2k-1 22 21 20 0 4 n-5 n-3 n-1 2 An adversary can regulate the speed of the messages D(n-1) reduces from (2k+1- 1) to 0 in steps of 1. Since k = (n-3)/2, it will need 2(n-1)/2-1 messages to reach the goal. So, the message complexity is exponential. 

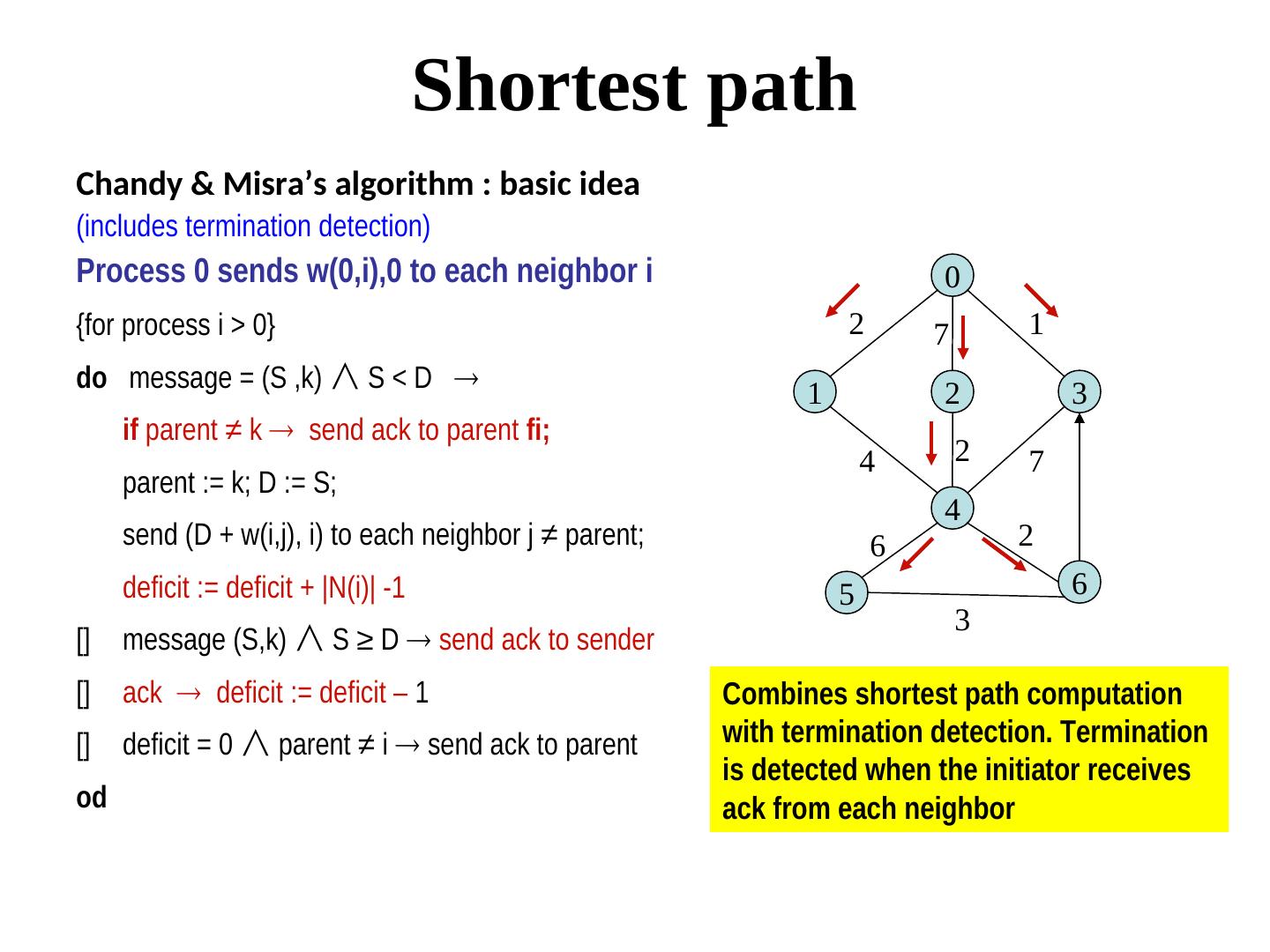
10 . Shortest path Chandy & Misra’s algorithm : basic idea (includes termination detection) Process 0 sends w(0,i),0 to each neighbor i 0 {for process i > 0} 2 7 1 do message = (S ,k) ∧ S < D  1 2 3 if parent ≠ k  send ack to parent fi; 4 2 7 parent := k; D := S; 4 send (D + w(i,j), i) to each neighbor j ≠ parent; 6 2 deficit := deficit + |N(i)| -1 5 6 3 [] message (S,k) ∧ S ≥ D  send ack to sender [] ack  deficit := deficit – 1 Combines shortest path computation [] deficit = 0 ∧ parent ≠ i  send ack to parent with termination detection. Termination is detected when the initiator receives od ack from each neighbor 

11 . Shortest path An important issue is: how well do such algorithms perform when the topology changes? No real network is static! Let us examine distance vector routing that is adaptation of the shortest path algorithm 

12 . Distance Vector Routing Distance Vector D for each node i contains N elements D[i,0], D[i,1], … D[i, N-1]. Here, D[i,j] denotes the distance from node i to node j. - Initially ∀i ≠ 0, i, D[i,j] =0 when j=i D(i,j) = 1 when j ∈N(i). and N(i). and D[i,j] = ∞ when j ∉ N(i) ∪{i} N(i) ∪{i}{i} - Each node j periodically sends its distance vector to its immediate neighbors. - Every neighbor i of j, after receiving the broadcasts from its neighbors, updates its distance vector as follows: ∀i ≠ 0, k ≠ i: D[i,k] = minj(w[i,j] + D[j,k] ) Used in RIP, IGRP etc 

13 .Distance Vector Routing 

14 . What if the topology changes? Assume that each edge has weight = 1. Currently, 1 Node 1: d(1,0) = 1, d(1, 2) = 1, d(1,2) = 2 Node 2: d(2,0) = 1, d(2,1) =1, d(2,3) = 1 Node 3: d(3,0) = 2, d(3,1) = 2, d(3,2) = 1 0 2 3 

15 . Counting to infinity Observe what can happen when the link (2,3) fails. D[j,k]=3 means j thinks k is 3 Node 1 thinks d(1,3) = 2 (old value) hops away Node 2 thinks d(2,3) = d(1,3) +1 = 3 1 Node 1 thinks d(1,3) = d(2,3) +1 = 4 and so on. So it will take forever for the distances to 0 2 3 stabilize. A partial remedy is the split horizon method that prevents node 1 from sending the advertisement about d(1,3) to 2 since its first hop (to 3) is node 2 ∀i ≠ 0, k≠ i: D[i,k] = minj(w[i,j] + D[j,k] ) Suitable for smaller networks. Larger volume of data is disseminated, but to its immediate neighbors only. Poor convergence property. 

16 . Link State Routing Each node i periodically broadcasts the weights of all edges (i,j) incident on it (this is the link state) to all its neighbors. Each link state packet (LSP) has a sequence number seq. The mechanism for dissemination is flooding. This helps each node eventually compute the topology of the network, and independently determine the shortest path to any destination node using some standard graph algorithm like Dijkstra’s. Smaller volume data disseminated over the entire network Used in OSPF of IP 

17 . Link State Routing: the challenges (Termination of the reliable flooding) How to guarantee that LSPs don’t circulate forever? A node forwards a given LSP at most once. It remembers the last LSP that it forwarded for each node. (Dealing with node crash) When a node crashes, all packets stored in it may be lost. After it is repaired, new packets are sent with seq = 0. So these new packets may be discarded in favor of the old packets! Problem resolved using TTL See: http://www.ciscopress.com/articles/article.asp?p=24090&seqNum=4 

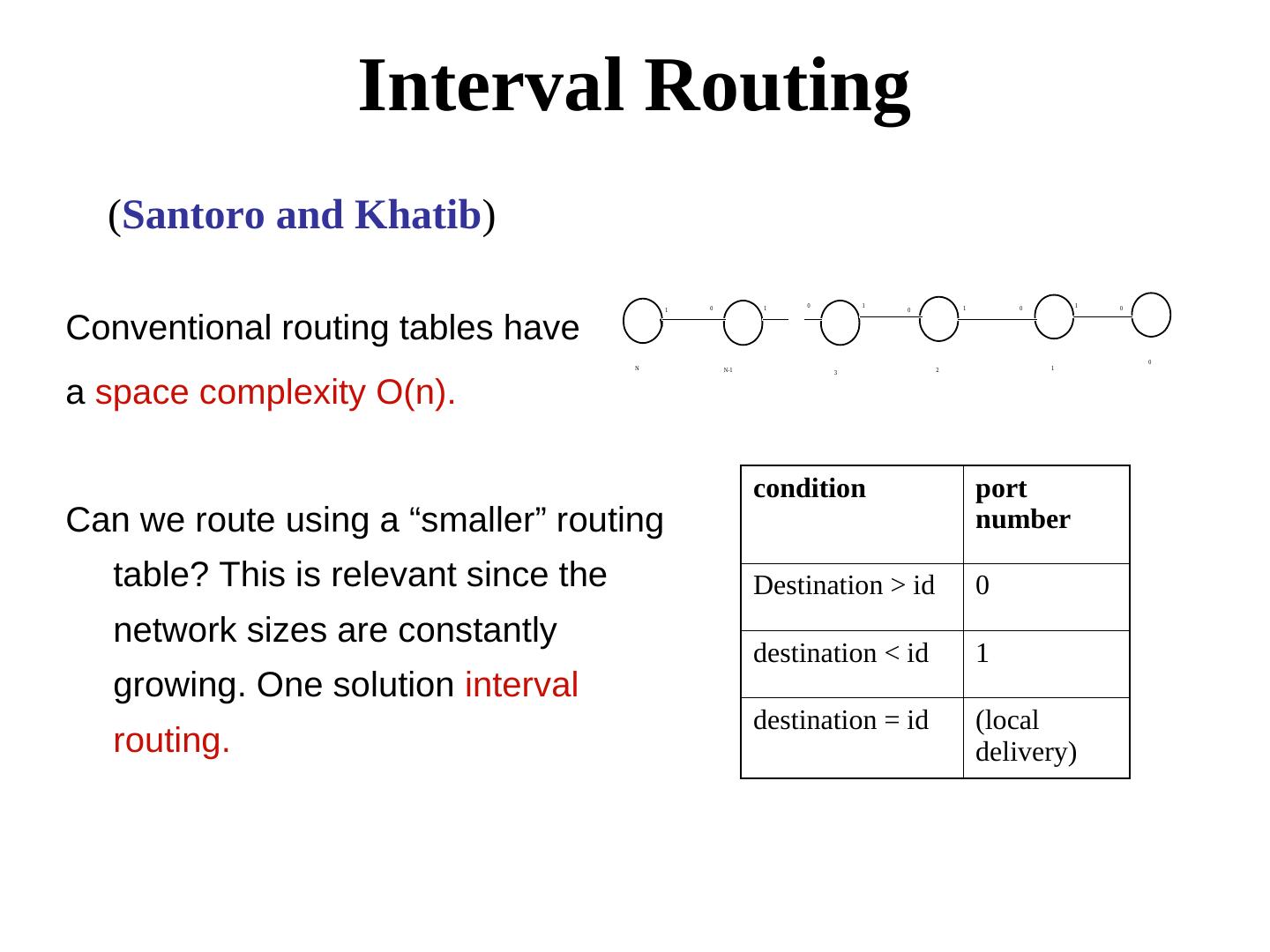
18 . Interval Routing (Santoro and Khatib) 0 1 0 1 1 0 1 0 1 0 Conventional routing tables have 0 N N-1 2 1 3 a space complexity O(n). condition port Can we route using a “smaller” routing number table? This is relevant since the Destination > id 0 network sizes are constantly destination < id 1 growing. One solution interval destination = id (local routing. delivery) 

19 . Interval Routing: Main idea • Determine the interval to which the destination belongs. • For a set of N nodes 0 . . N-1, the interval [p,q) between p and q (p, q < N) is defined as follows: • if p < q then [p,q) = p, p+1, p+2, .... q-2, q-1 • if p ≥ q then [p,q) = p, p+1, p+2, ..., N-1, N, 0, 1, ..., q-2, q-1 [5,1) destinations 5, 6. 7, 0 5 [1,3) [3,5) 1 3 destinations 3,4 destination 1,2 

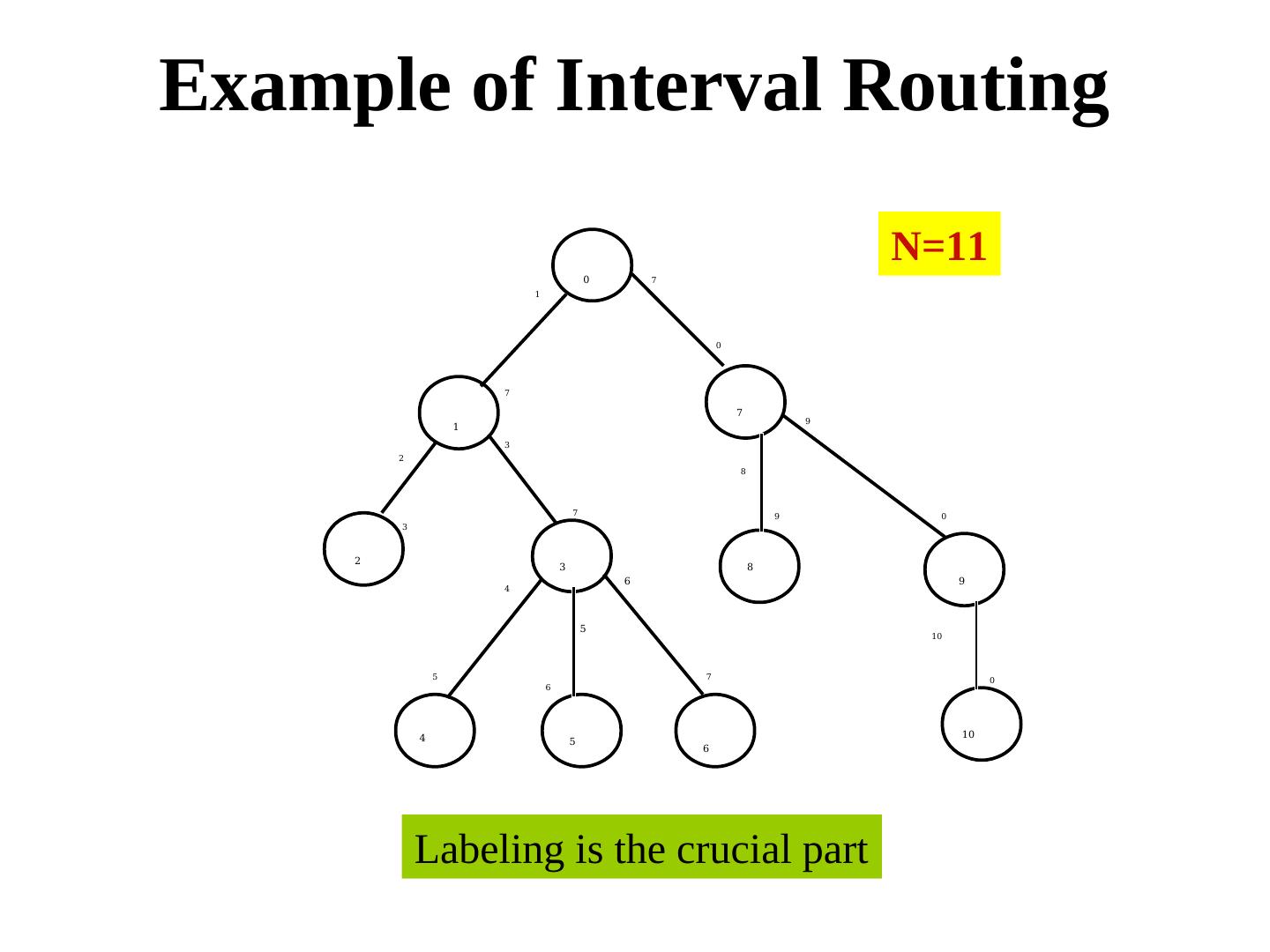
20 .Example of Interval Routing N=11 0 7 1 0 7 7 9 1 3 2 8 7 9 0 3 2 3 8 6 9 4 5 10 5 7 0 6 4 10 5 6 Labeling is the crucial part 

21 . Labeling algorithm Label the root as 0. Do a pre-order traversal of the tree. Label successive nodes as 1, 2, 3 For each node, label the port towards a child by the node number of the child. Then label the port towards the parent by L(i) + T(i) + 1 mod N, where - L(i) is the label of the node i, - T(i) = # of nodes in the subtree under node i (excluding i), Question 1. Why does it work? Question 2. Does it work for non-tree topologies too? YES, but the construction is a bit more complex. 

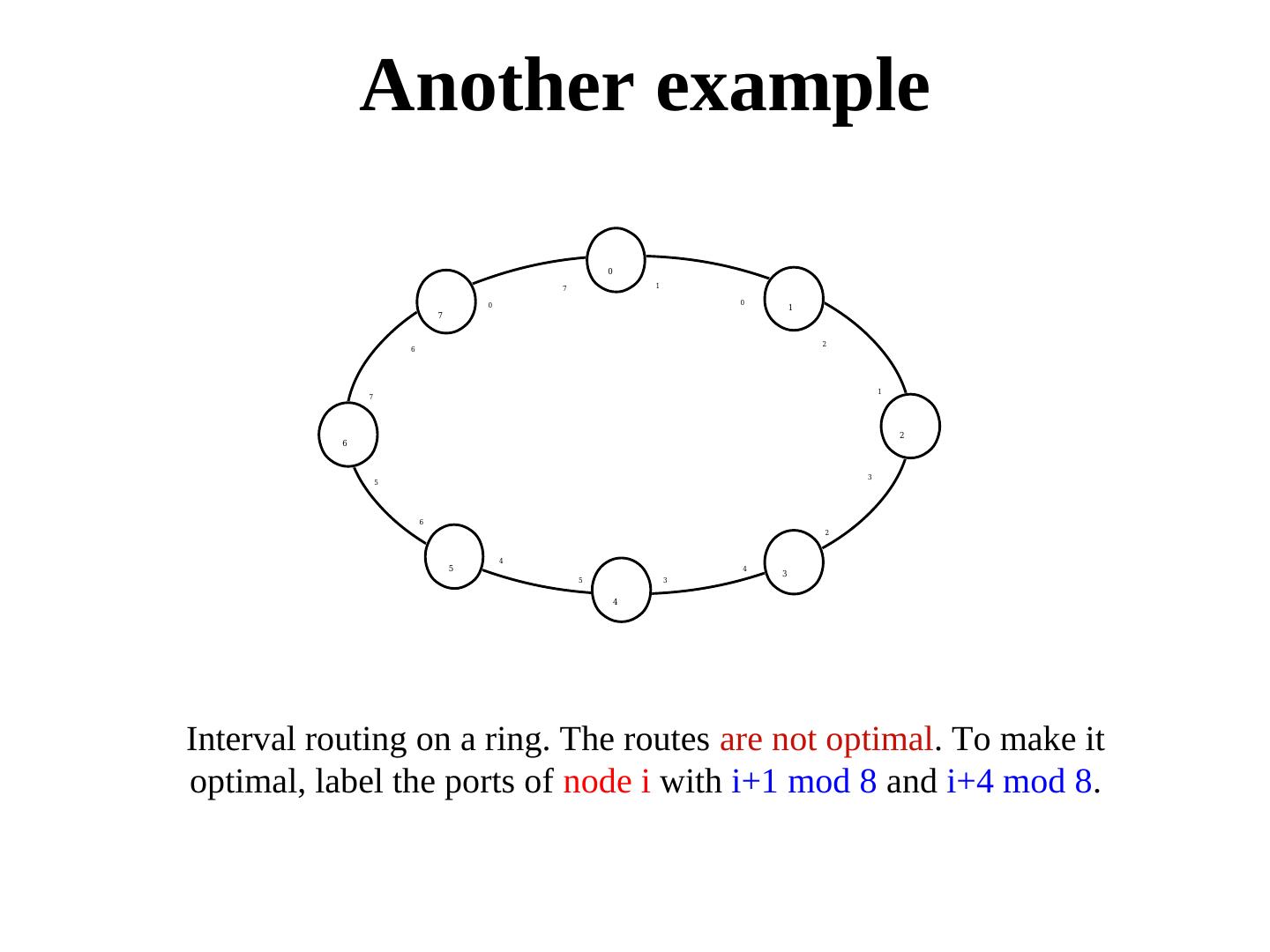
22 . Another example 0 7 1 0 0 1 7 2 6 1 7 2 6 3 5 6 2 4 5 4 3 5 3 4 Interval routing on a ring. The routes are not optimal. To make it optimal, label the ports of node i with i+1 mod 8 and i+4 mod 8. 

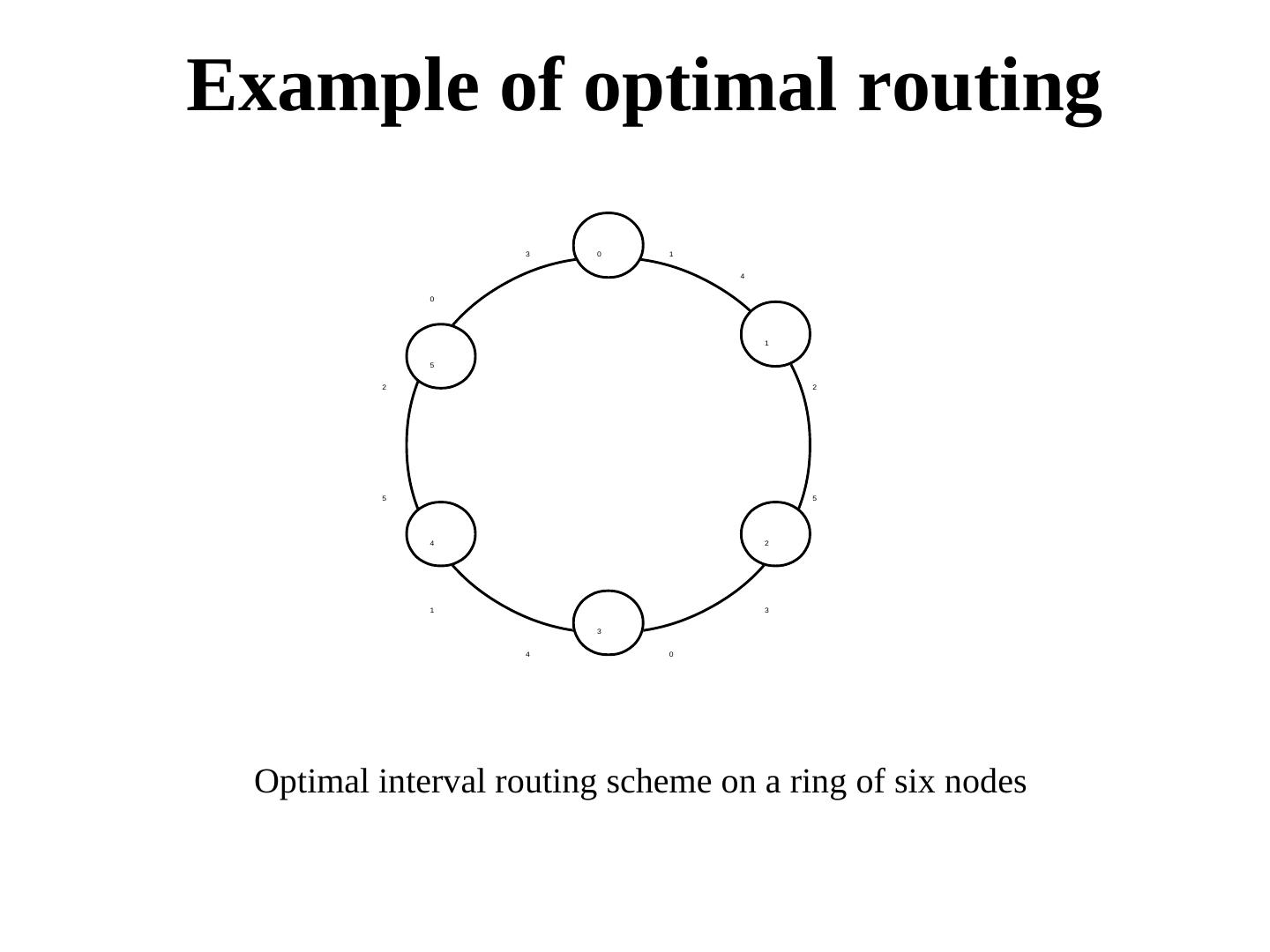
23 .Example of optimal routing 3 0 1 4 0 1 5 2 2 5 5 4 2 1 3 3 4 0 Optimal interval routing scheme on a ring of six nodes 

24 . So, what is the problem? Works for static topologies. Difficult to adapt to changes in topologies. Some recent work on compact routing addresses dynamic topologies (Amos Korman, ICDCN 2009) 

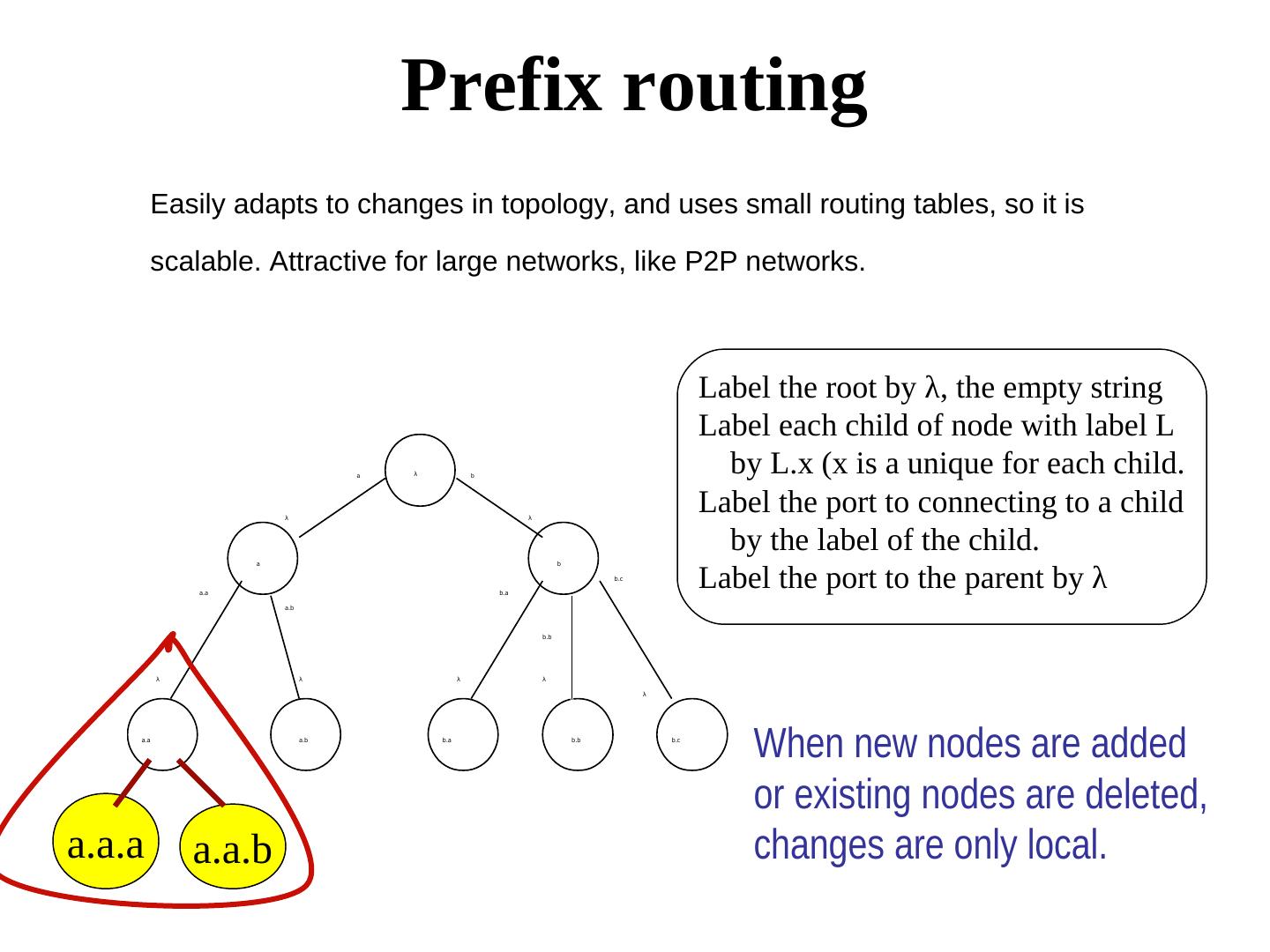
25 . Prefix routing Easily adapts to changes in topology, and uses small routing tables, so it is scalable. Attractive for large networks, like P2P networks. Label the root by λ, the empty string Label each child of node with label L a λ b by L.x (x is a unique for each child. λ λ Label the port to connecting to a child by the label of the child. Label the port to the parent by λ a b b.c a.a b.a a.b b.b λ λ λ λ λ a.a a.b b.a b.b b.c When new nodes are added or existing nodes are deleted, a.a.a a.a.b changes are only local. 

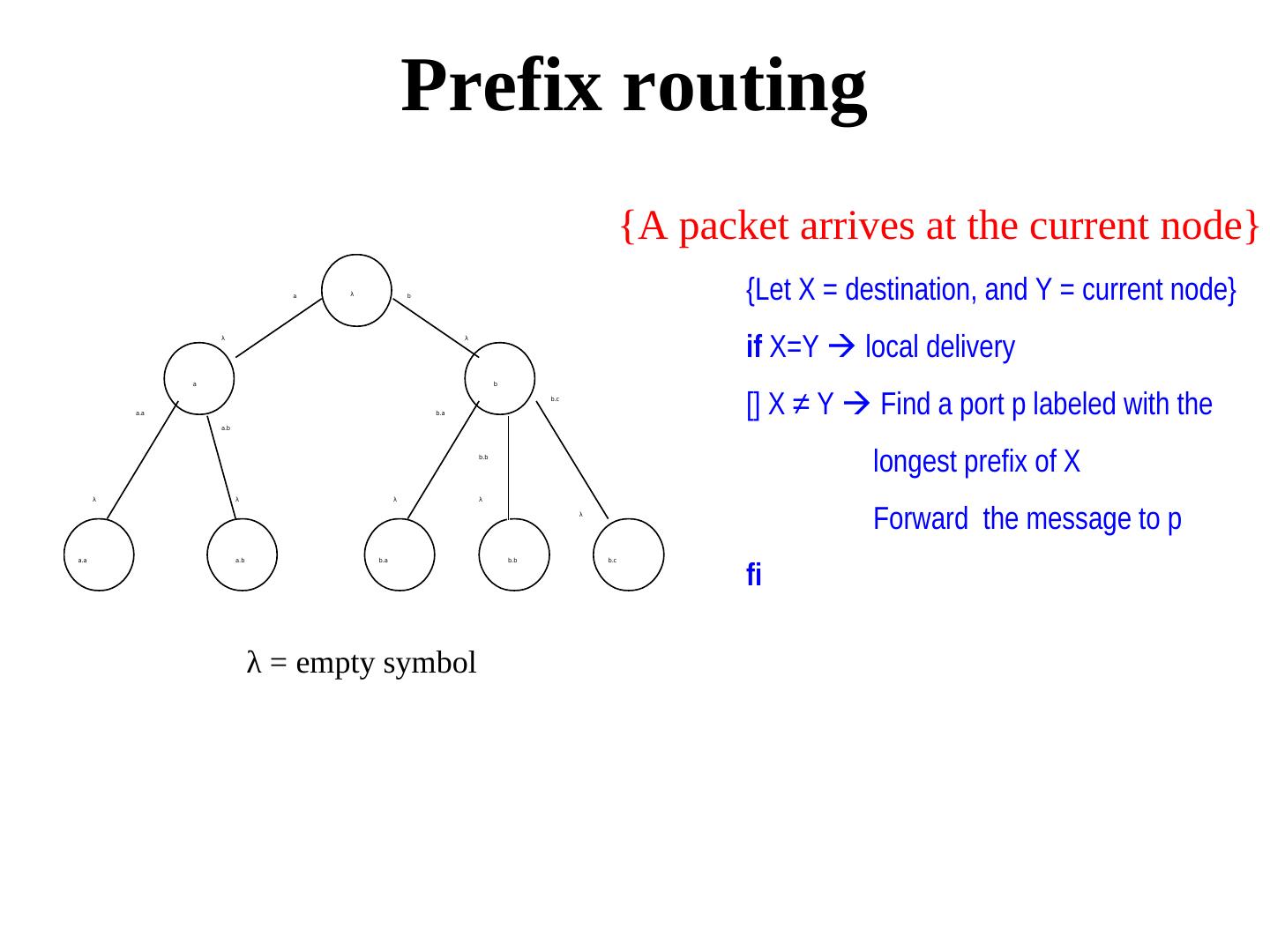
26 . Prefix routing {A packet arrives at the current node} a λ b {Let X = destination, and Y = current node} if X=Y  local delivery λ λ a b a.a b.a b.c [] X ≠ Y  Find a port p labeled with the a.b b.b longest prefix of X λ λ λ λ λ Forward the message to p fi a.a a.b b.a b.b b.c λ = empty symbol 

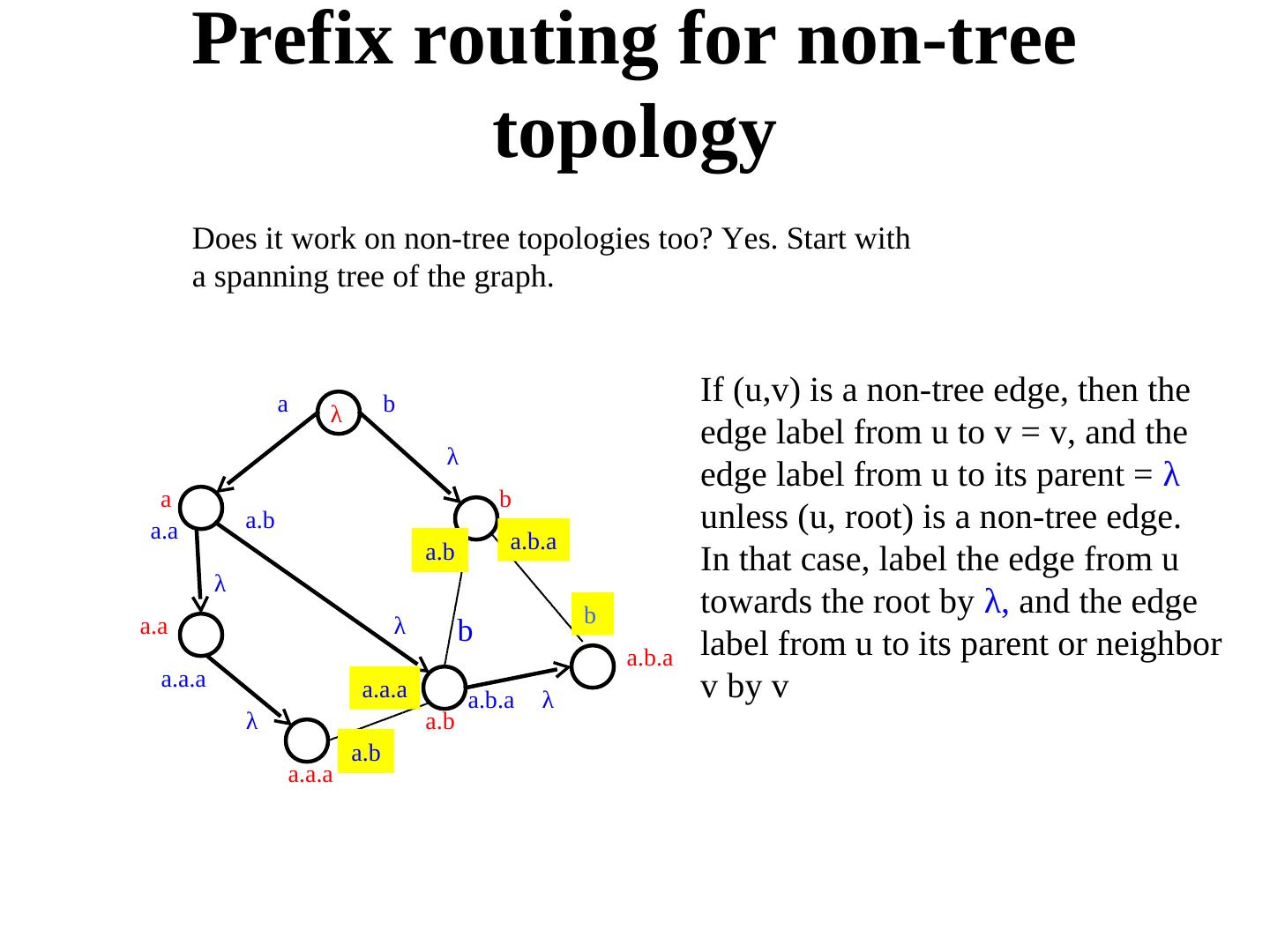
27 . Prefix routing for non-tree topology Does it work on non-tree topologies too? Yes. Start with a spanning tree of the graph. a b If (u,v) is a non-tree edge, then the λ edge label from u to v = v, and the λ edge label from u to its parent = λ a b a.a a.b unless (u, root) is a non-tree edge. a.b a.b.a In that case, label the edge from u λ b towards the root by λ, and the edge a.a λ b a.b.a label from u to its parent or neighbor a.a.a a.a.a v by v a.b.a λ λ a.b a.b a.a.a 

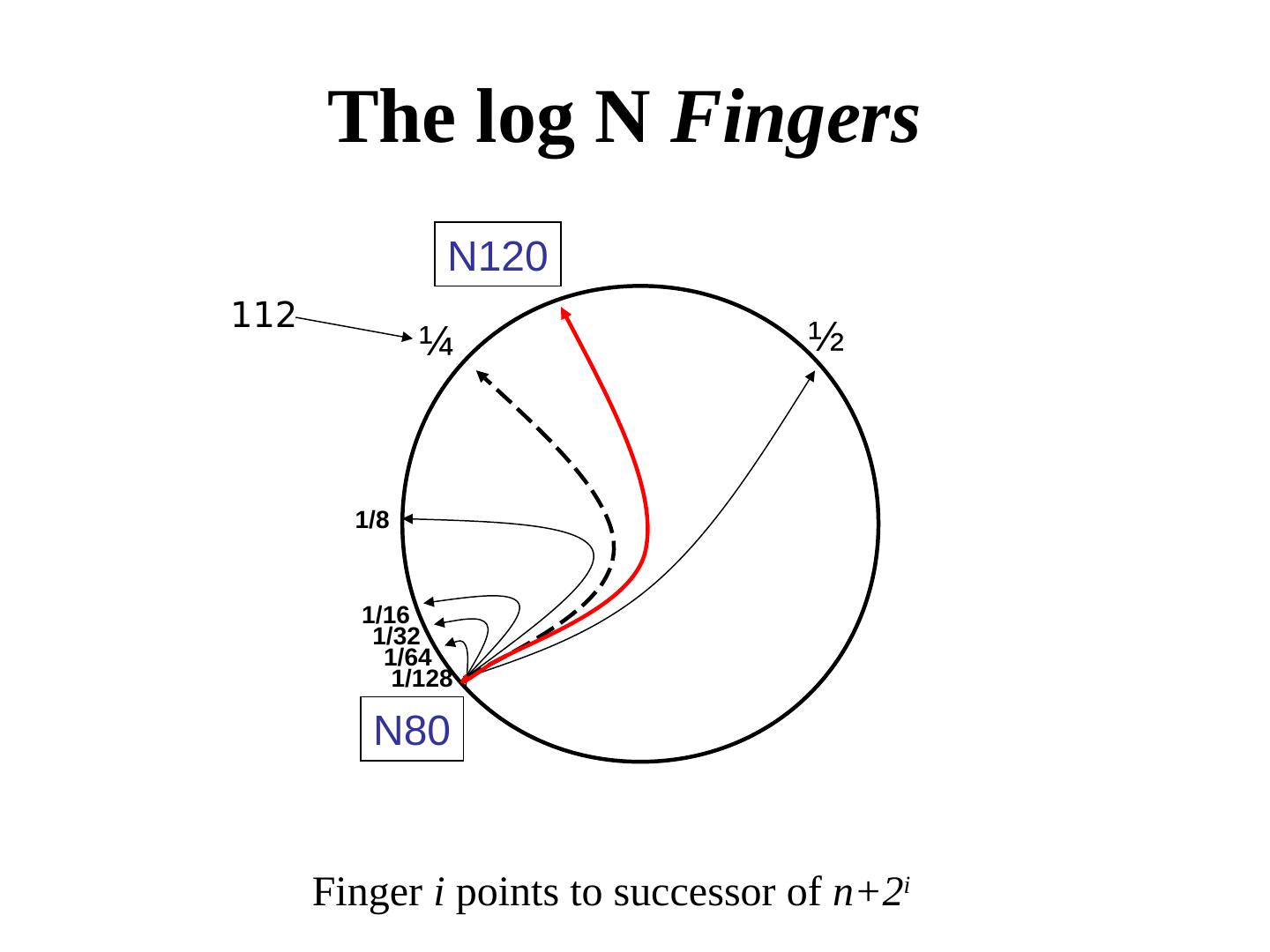
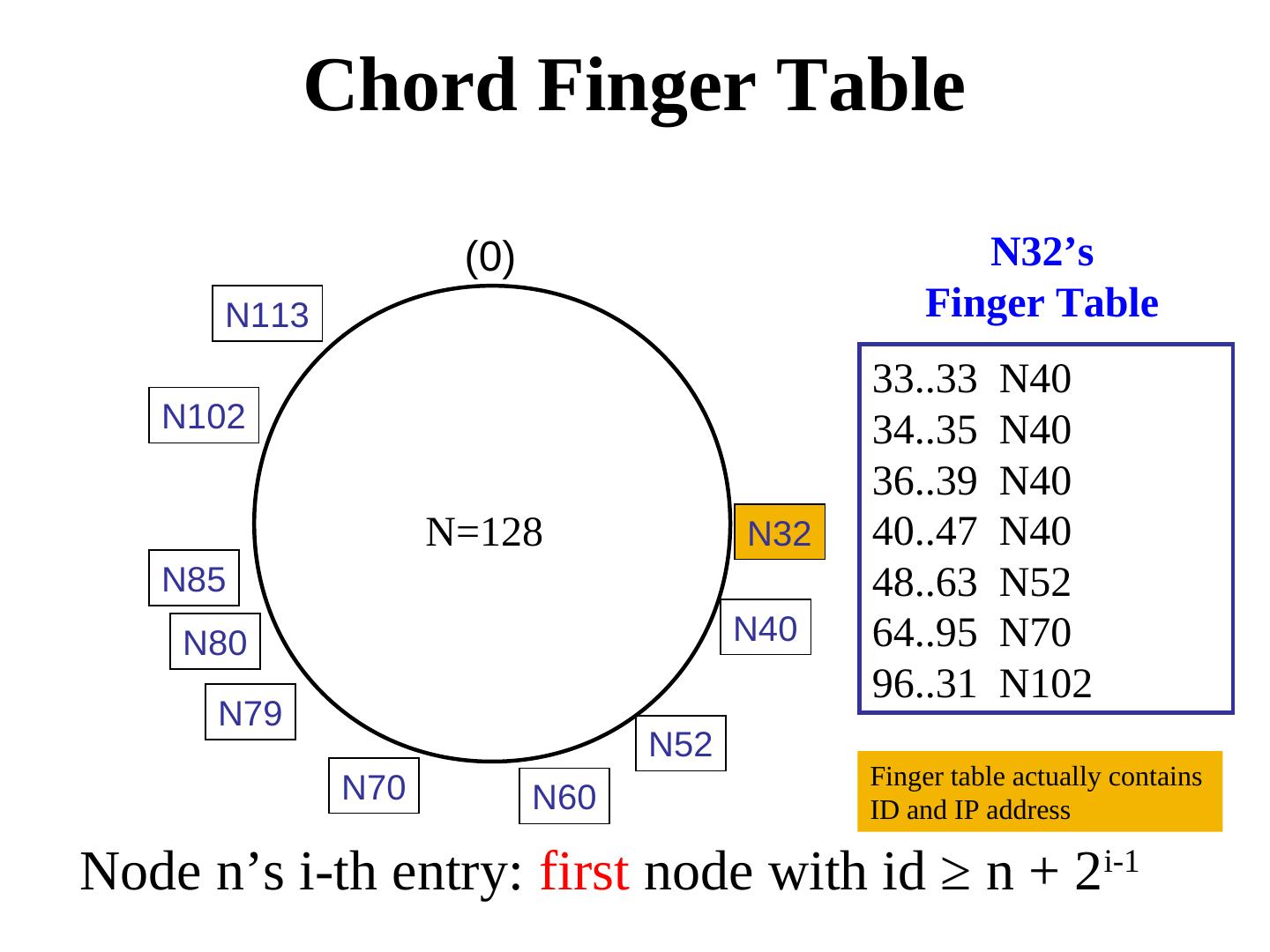
28 . Routing in P2P networks: Example of Chord – Small routing tables: log n – Small routing delay: log n hops – Load balancing via Consistent Hashing – Fast join/leave protocol (polylog time) 

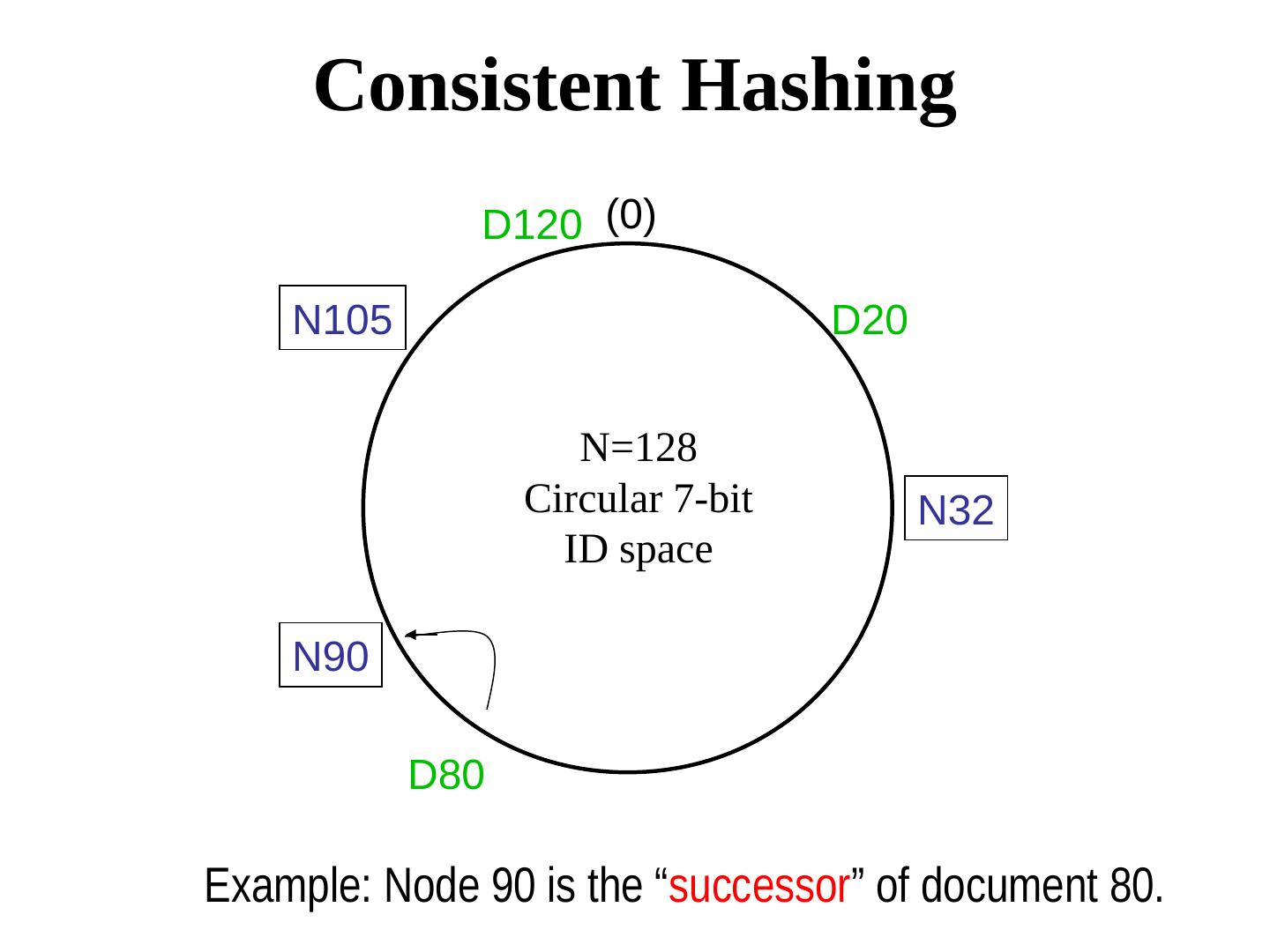
29 . Consistent Hashing Assigns an m-bit key to both nodes and objects from. Order these nodes around an identifier circle (what does a circle mean here?) according to the order of their keys (0 .. 2m-1). This ring is known as the Chord Ring. Object with key k is assigned to the first node whose key is ≥ k (called the successor node of key k)