分布式系统和算法：全局状态搜集

1 .Global State Collection 

2 . Global state collection Some applications - computing network topology - termination detection - deadlock detection Chandy-Lamport algorithm does a partial job. Each process generates a fragment of the global state, but these pieces have to be “stitched together” to form a global state. 

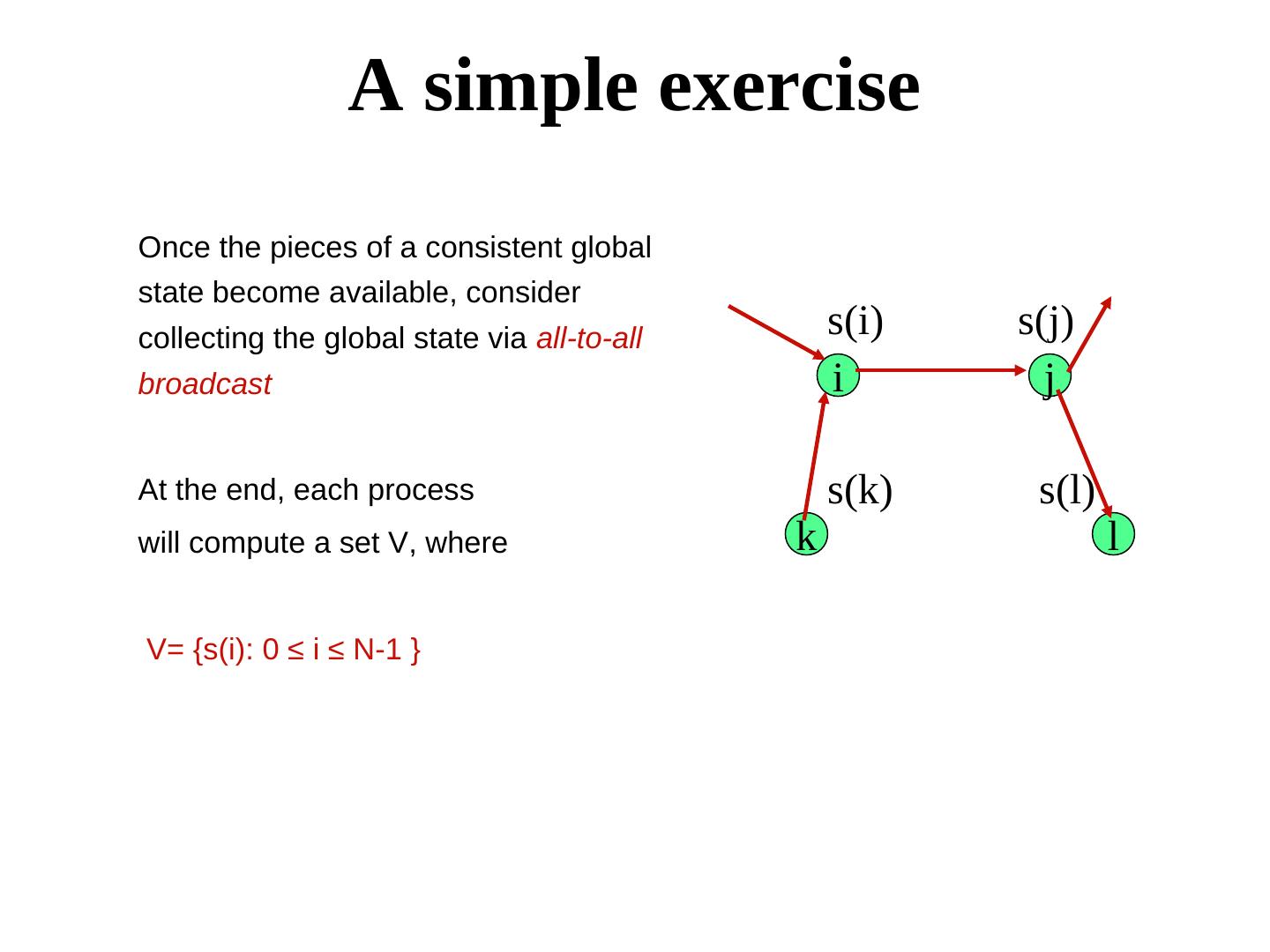
3 . A simple exercise Once the pieces of a consistent global state become available, consider collecting the global state via all-to-all s(i) s(j) broadcast i j At the end, each process s(k) s(l) will compute a set V, where k l V= {s(i): 0 ≤ i ≤ N-1 } 

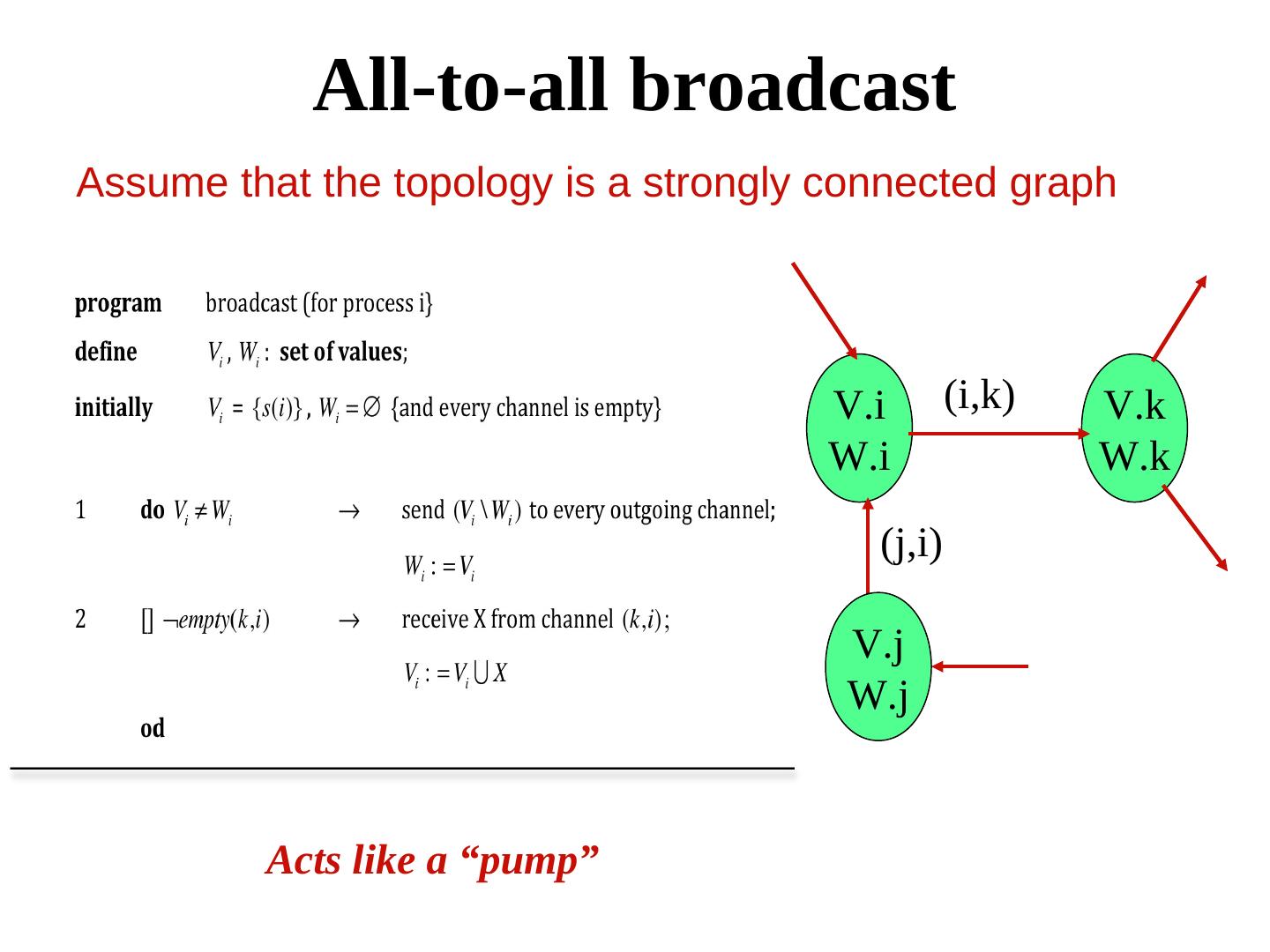
4 . All-to-all broadcast Assume that the topology is a strongly connected graph V.i (i,k) V.k W.i W.k (j,i) V.j W.j Acts like a “pump” 

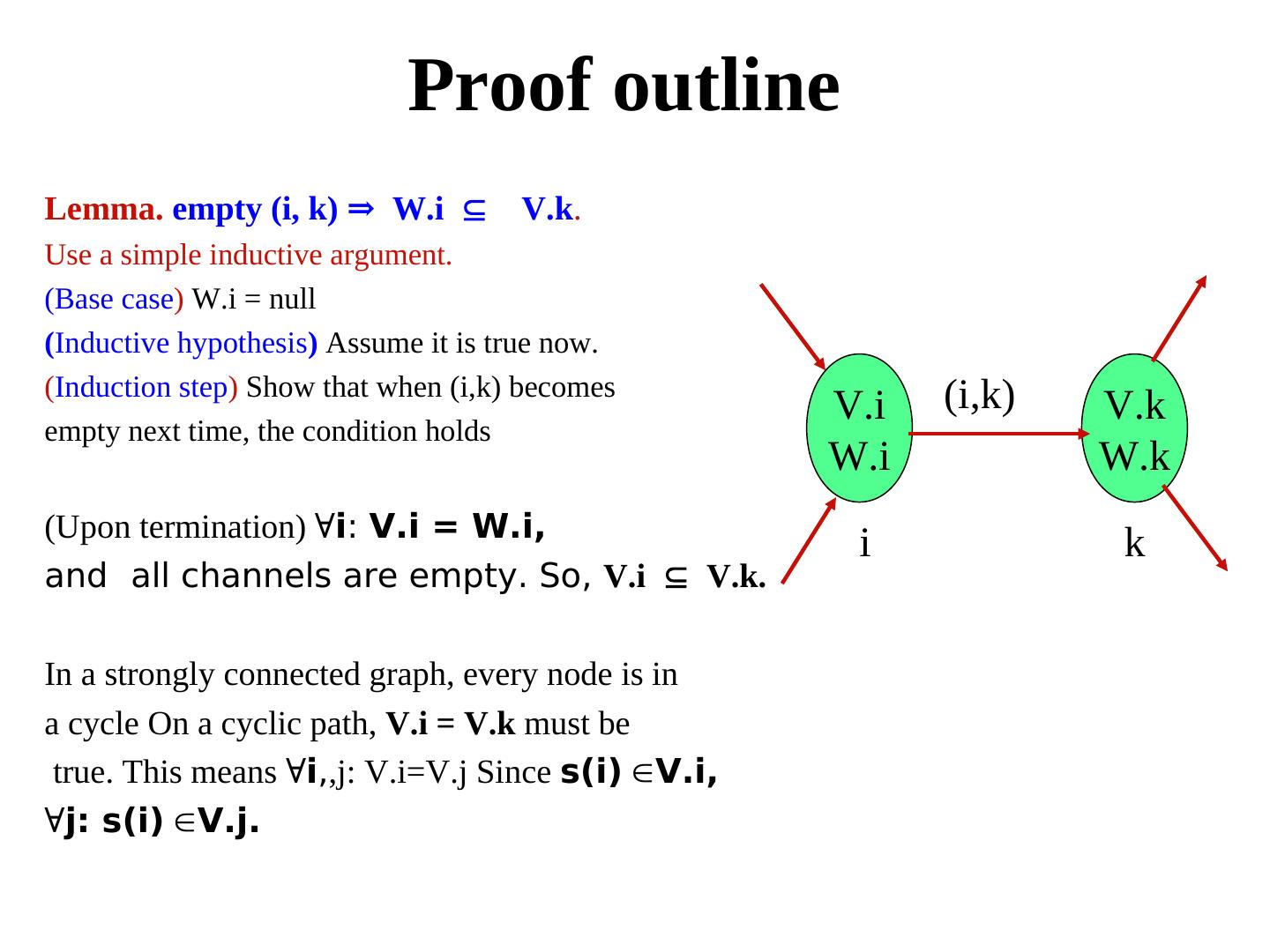
5 . Proof outline Lemma. empty (i, k) ⇒ W.i ⊆V.k. Use a simple inductive argument. (Base case) W.i = null (Inductive hypothesis) Assume it is true now. (Induction step) Show that when (i,k) becomes (i,k) V.i V.k empty next time, the condition holds W.i W.k (Upon termination) ∀i: V.i = W.i, i k and all channels are empty. So, V.i ⊆V.k. In a strongly connected graph, every node is in a cycle On a cyclic path, V.i = V.k must be true. This means ∀i,,j: V.i=V.j Since s(i) ∈V.i, ∀j: s(i) ∈V.j. 

6 . Proof outline Lemma. The algorithm will terminate in a bounded number of steps. Consider the variant function Channel states (i,k) V.i V.k W.i W.k i k Statement 1 and Statement 2 increase Y lexicographically, until the V’s reach their largest value {s(0), s(1), s(2), …, s(n-1)}. So the algorithm terminates in a bounded number of steps. 

7 . Termination detection During the progress of a distributed computation, processes may periodically turn active or passive. A distributed computation terminates when: (a) every process is passive, (b) all channels are empty, and (c) the global state satisfies the desired postcondition 

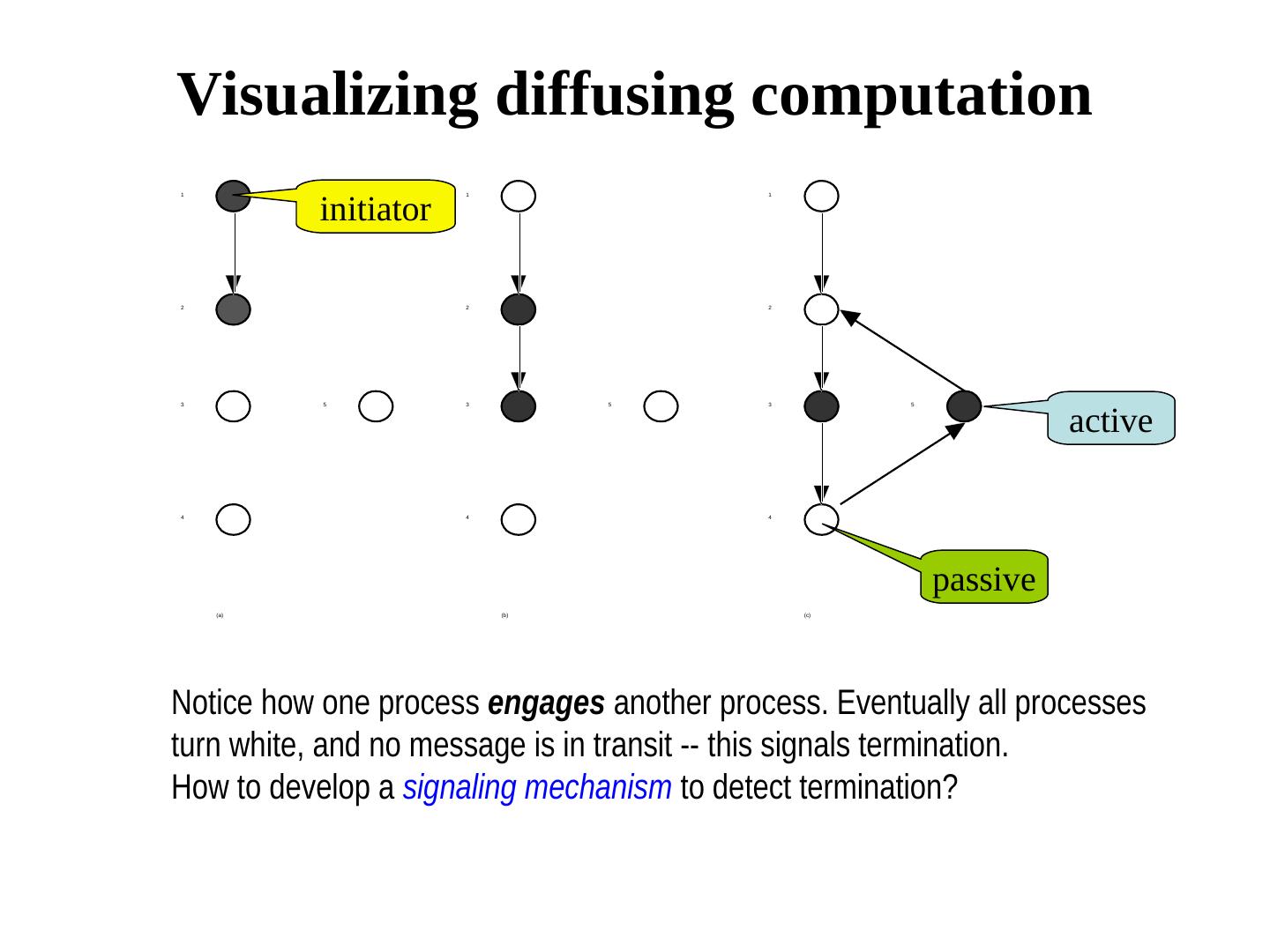
8 .Visualizing diffusing computation initiator 1 1 1 2 2 2 active 3 5 3 5 3 5 4 4 4 passive (a) (b) (c) Notice how one process engages another process. Eventually all processes turn white, and no message is in transit -- this signals termination. How to develop a signaling mechanism to detect termination? 

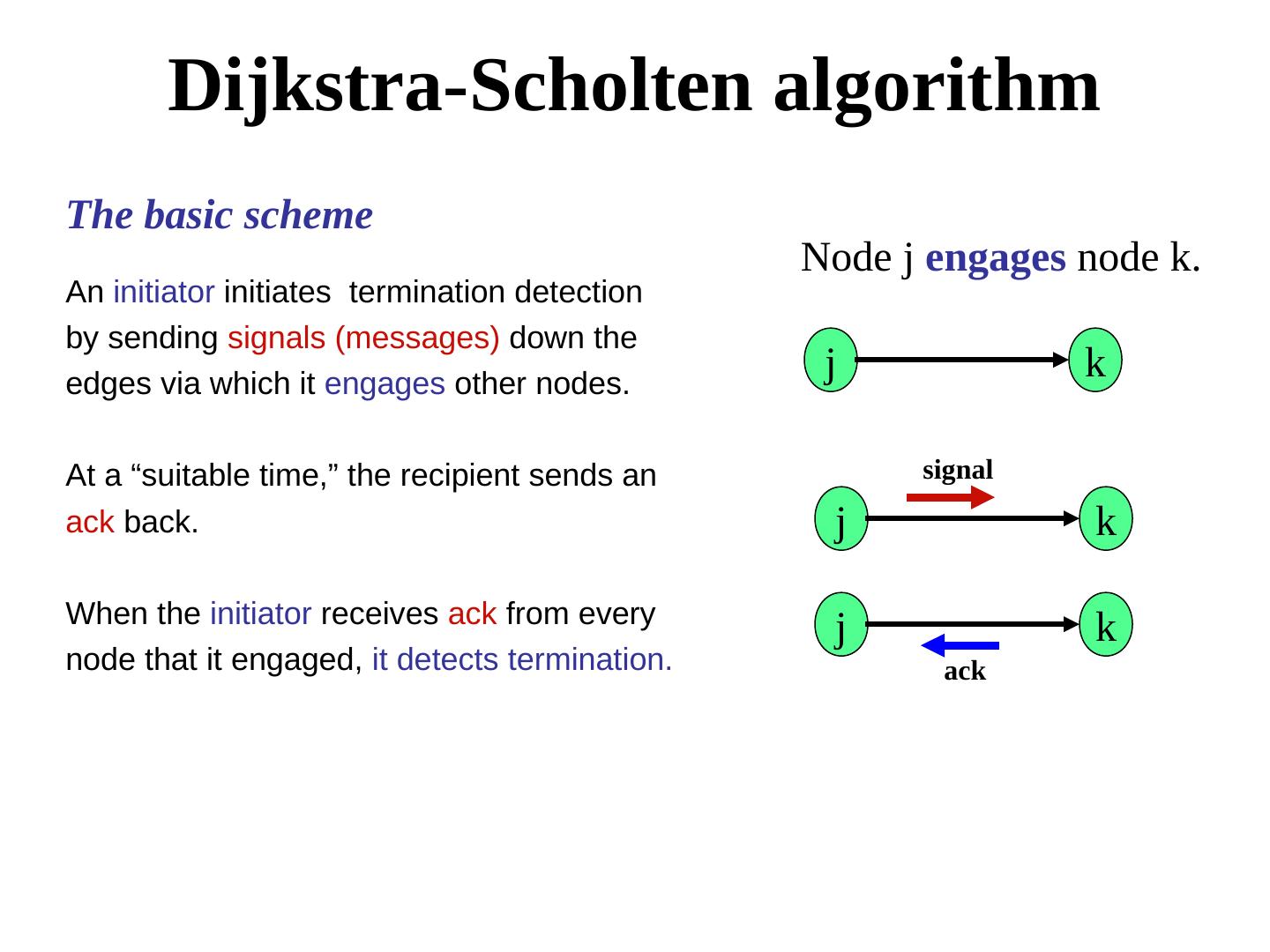
9 . Dijkstra-Scholten algorithm The basic scheme Node j engages node k. An initiator initiates termination detection by sending signals (messages) down the edges via which it engages other nodes. j k At a “suitable time,” the recipient sends an signal ack back. j k When the initiator receives ack from every j k node that it engaged, it detects termination. ack 

10 . Dijkstra-Scholten algorithm Deficit (e) = # of signals on edge e - # of acks on edge e 0 For any node, C = total deficit along incoming edges and D = total deficit along outgoing edges edges 1 For the initiator, by definition, C = 0 2 3 Dijkstra-Scholten algorithm used the following two invariants to develop their algorithm: Invariant 1. (C ≥ 0) ⋀ (D ≥ 0) 4 5 Invariant 2. (C > 0) ⋁ (D = 0) (D = 0) 

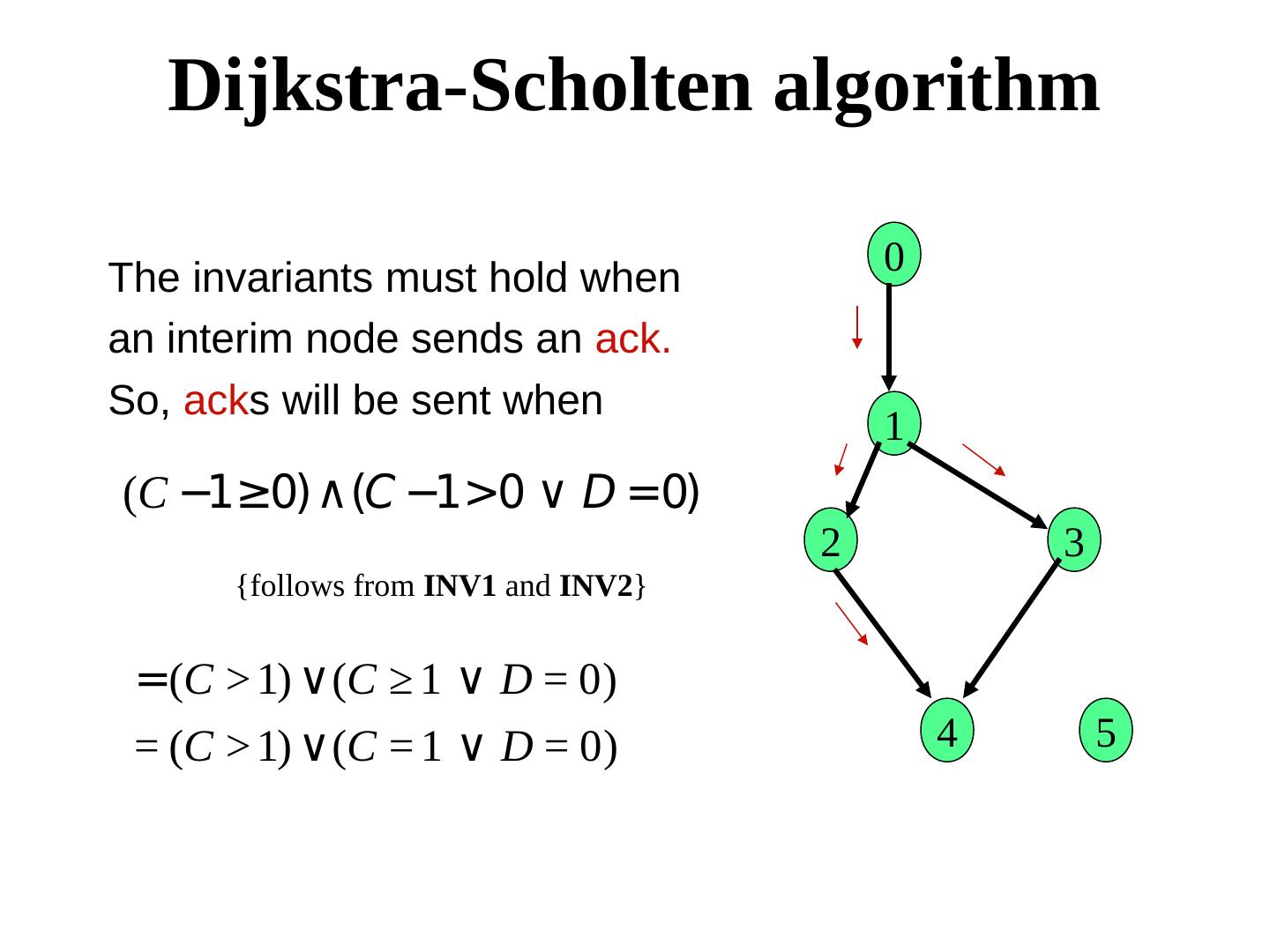
11 . Dijkstra-Scholten algorithm 0 The invariants must hold when an interim node sends an ack. So, acks will be sent when 1 (C −1≥0)∧(C −1>0 ∨ D =0) 2 3 {follows from INV1 and INV2} =(C > 1) ∨(C ≥ 1 ∨ D = 0) = (C > 1) ∨(C = 1 ∨ D = 0) 4 5 

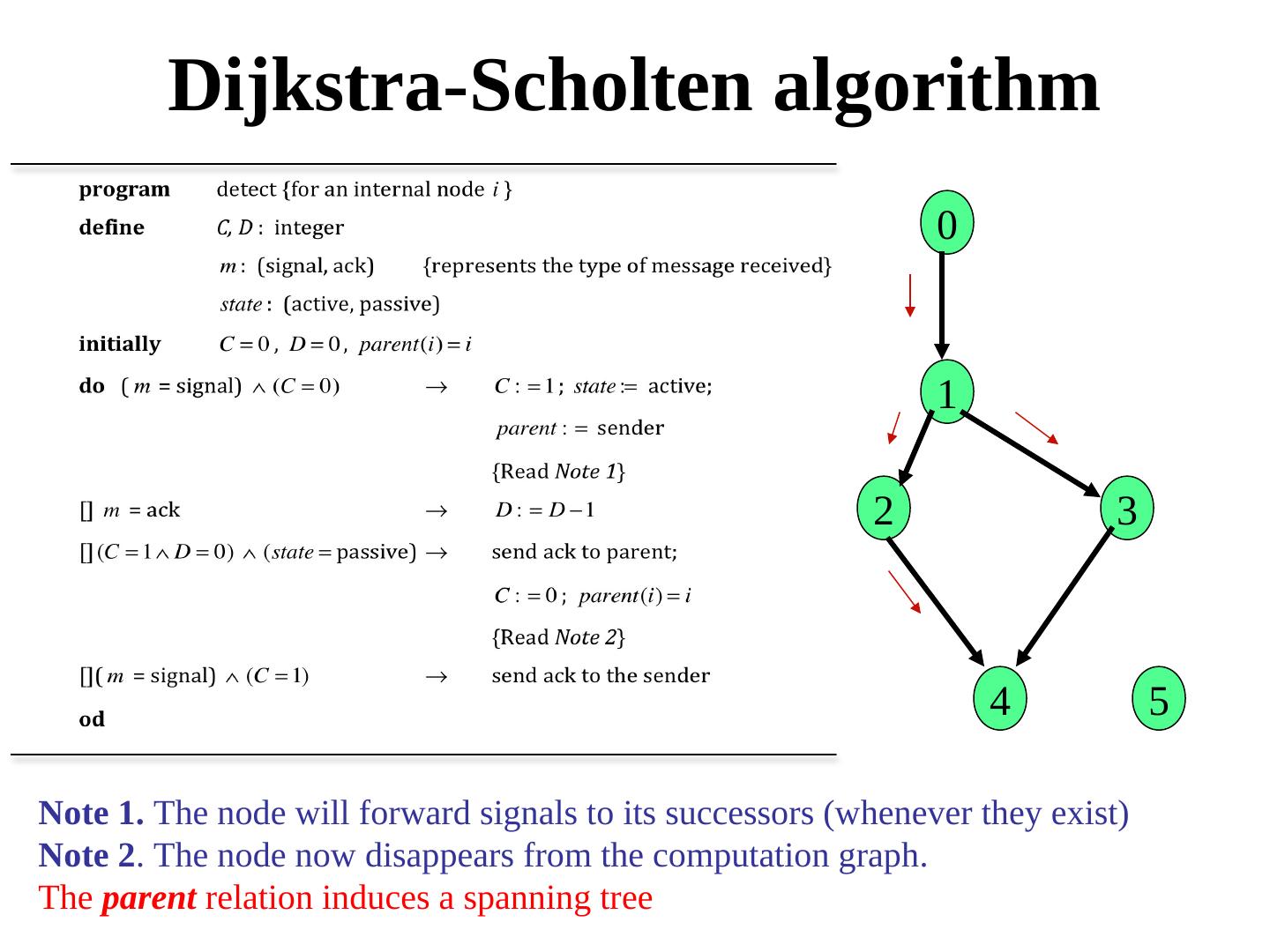
12 . Dijkstra-Scholten algorithm 0 1 2 3 4 5 Note 1. The node will forward signals to its successors (whenever they exist) Note 2. The node now disappears from the computation graph. The parent relation induces a spanning tree 

13 . Distributed deadlock When each process waits for some other process (to do something), a deadlock occurs. Assume each process owns a few resources. Review how resources are allocated, and how a deadlock is created. Three criteria for the occurrence of deadlock - Exclusive use of resources - Non-preemptive scheduling - Circular waiting by all (or a subset of) processes 

14 . Distributed deadlock Three aspects of deadlock – deadlock detection – deadlock prevention – deadlock recovery 

15 . Distributed deadlock • May occur due to bad designs/bad strategy [Sometimes prevention is more expensive than detection and recovery. So designs may not care about deadlocks, particularly if it is rare.] • Caused by failures or perturbations in the system 

16 .Distributed Deadlock Prevention uses pessimistic strategies An example from banker’s problem (Dijkstra) A banker has $10,000. She approves a credit line of $6,000 to each of the three customers A, B, C. since the requirement of each is less than the available funds. 1. The customers can pay back any portion of their loans at any time. Note that no one is required to pay any part of the loan unless (s)he has borrowed up to the entire credit line. 2. However, after the customer has borrowed up to the entire credit line ($6000) (s)he must return the entire money is a finite time. 3. Now, assume that A, B, C borrowed $3000 each. The state is unsafe since there is a “potential for deadlock.” Why? 

17 . Banker’s Problem Questions for the banker Let the current allocations be A = $2000, B = $2400, $C=$1800. 1. Now, if A asks for an additional $1500, then will the banker give the money immediately? 2. Instead, if B asks for $1500 then will the banker give the money immediately? 

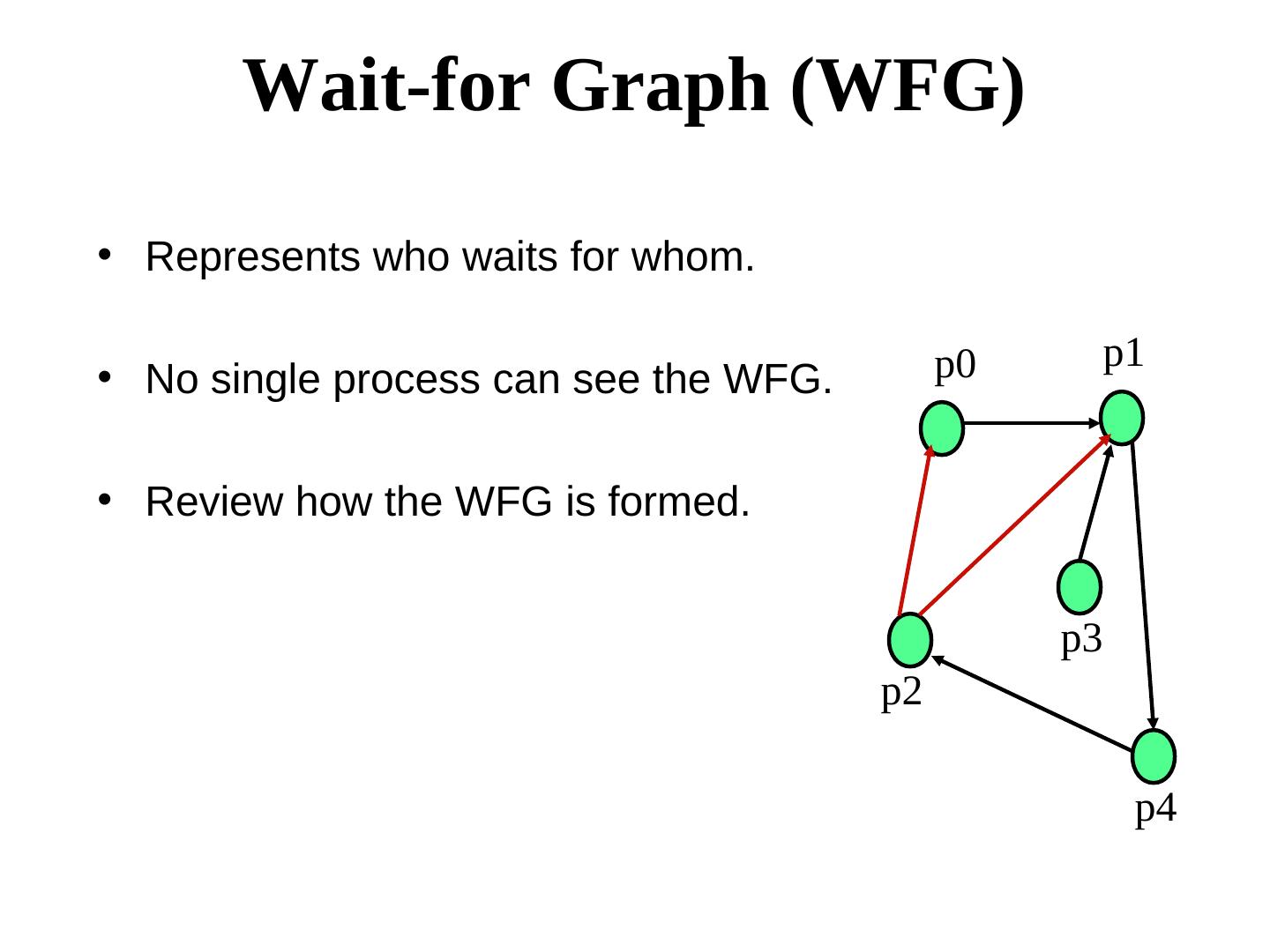
18 . Wait-for Graph (WFG) • Represents who waits for whom. p0 p1 • No single process can see the WFG. • Review how the WFG is formed. p3 p2 p4 

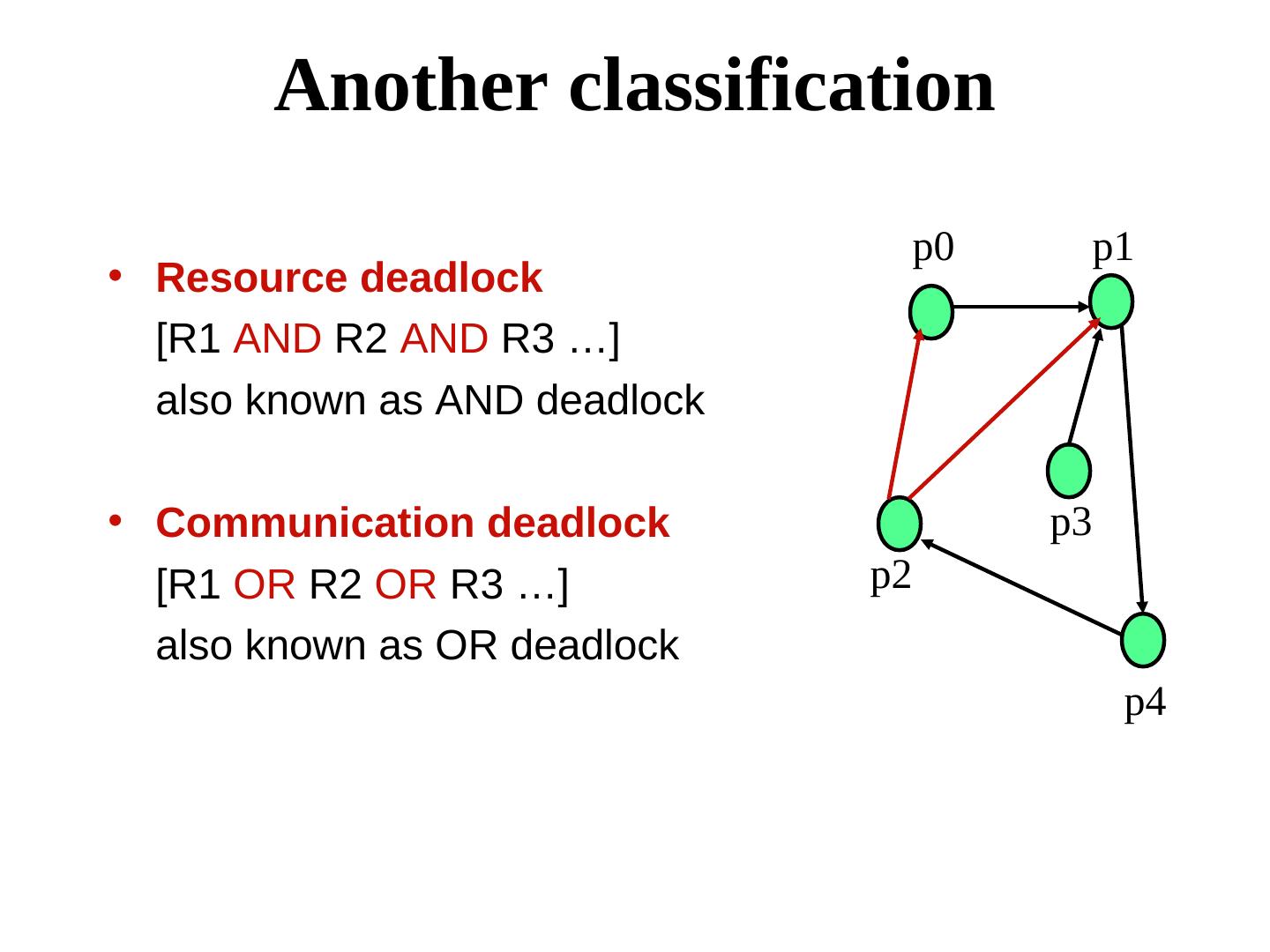
19 . Another classification p0 p1 • Resource deadlock [R1 AND R2 AND R3 …] also known as AND deadlock • Communication deadlock p3 [R1 OR R2 OR R3 …] p2 also known as OR deadlock p4 

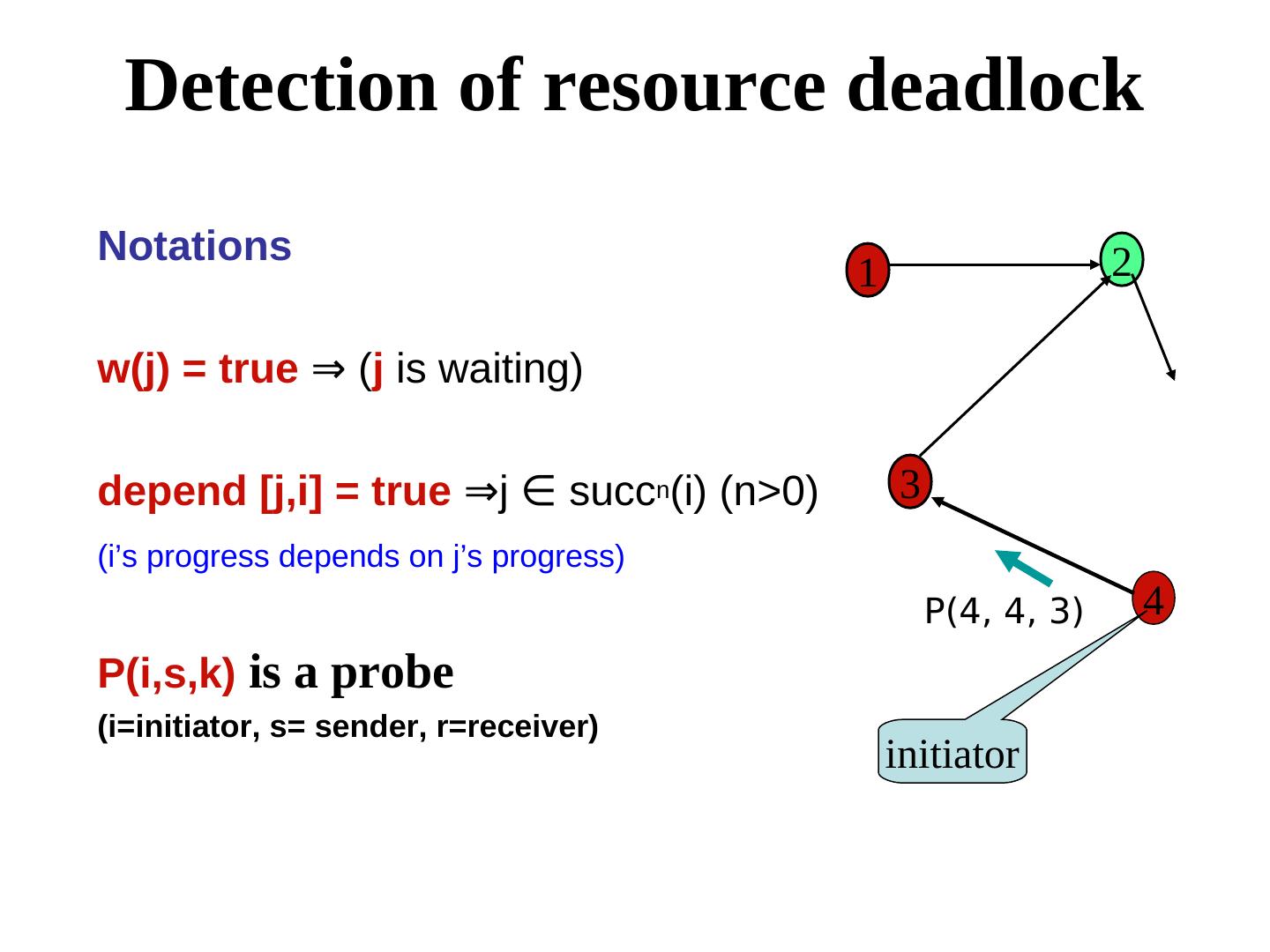
20 . Detection of resource deadlock Notations 2 1 w(j) = true ⇒ ( (j is waiting) depend [j,i] = true ⇒ (j ∈ succ succn(i) (n>0) 3 (i’s progress depends on j’s progress) P(4, 4, 3) 4 P(i,s,k) is a probe (i=initiator, s= sender, r=receiver) initiator 

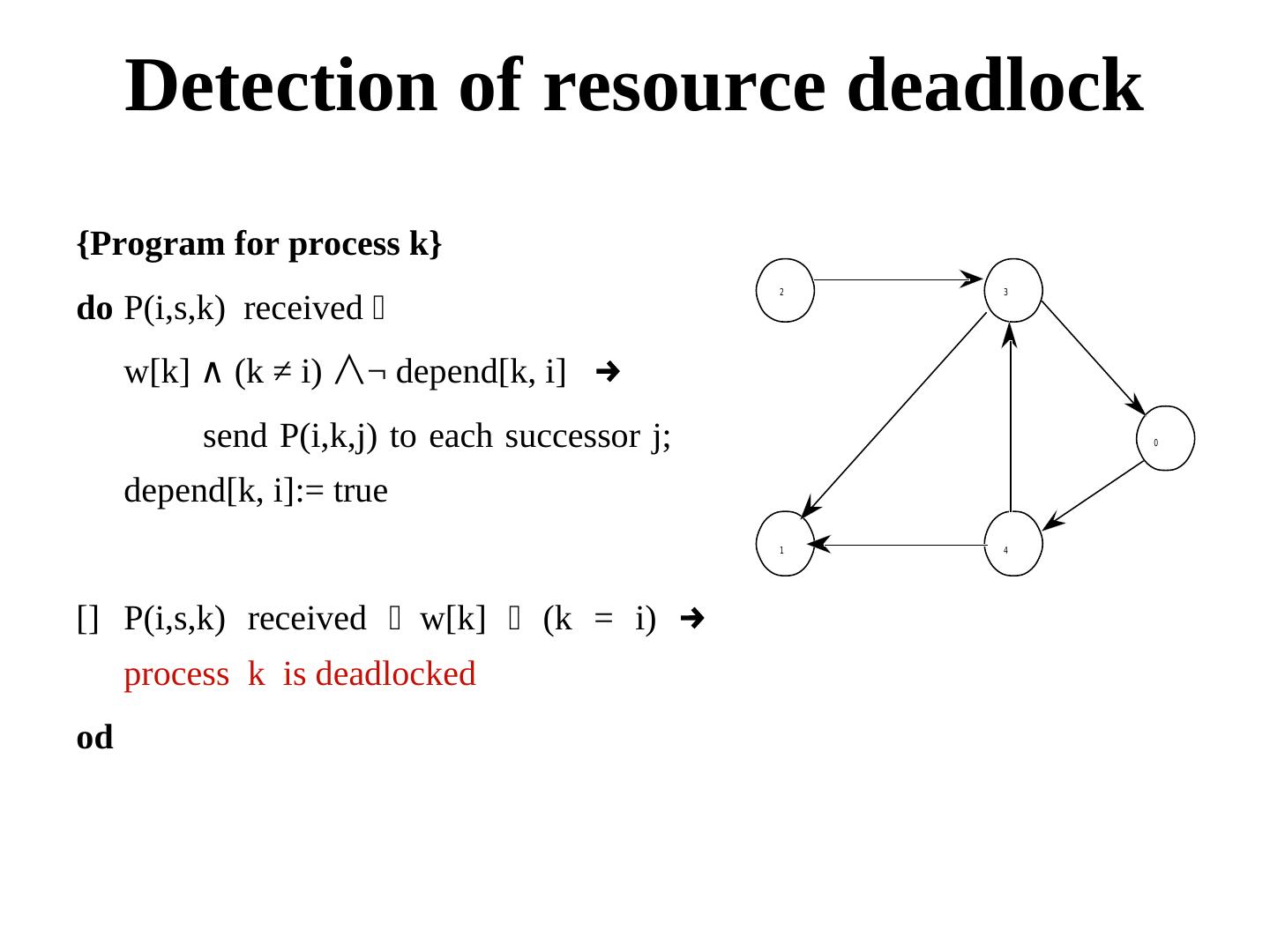
21 . Detection of resource deadlock {Program for process k} do P(i,s,k) received ⋀ 2 3 w[k] ∧ (k ≠ i) ∧¬ depend[k, i] → send P(i,k,j) to each successor j; 0 depend[k, i]:= true 1 4 [] P(i,s,k) received ⋀w[k] ⋀ (k = i) → process k is deadlocked od 

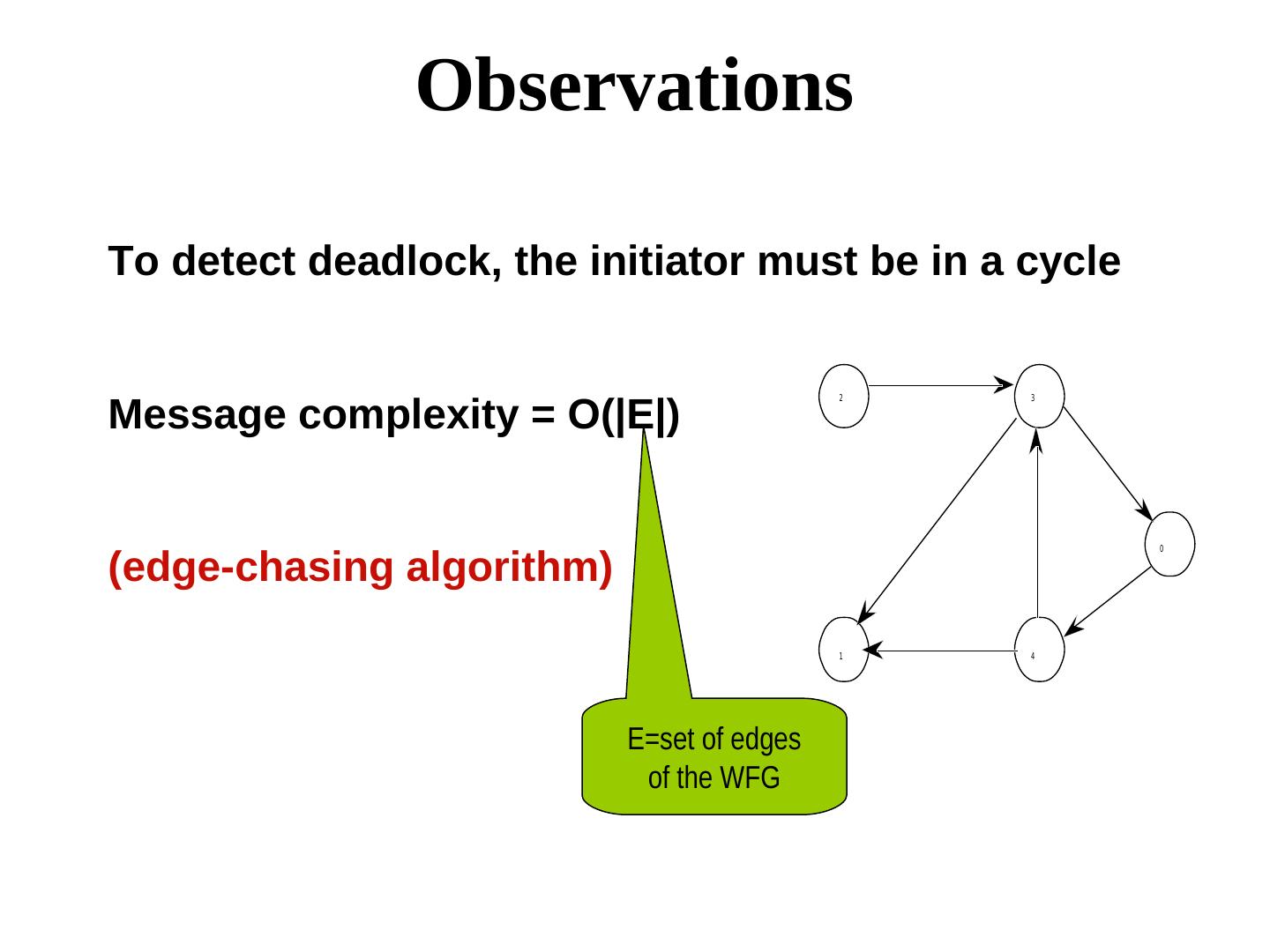
22 . Observations To detect deadlock, the initiator must be in a cycle Message complexity = O(|E|) 2 3 (edge-chasing algorithm) 0 1 4 E=set of edges of the WFG 

23 .Communication deadlock 5 0 1 2 3 4 This WFG has a resource deadlock but no communication deadlock 

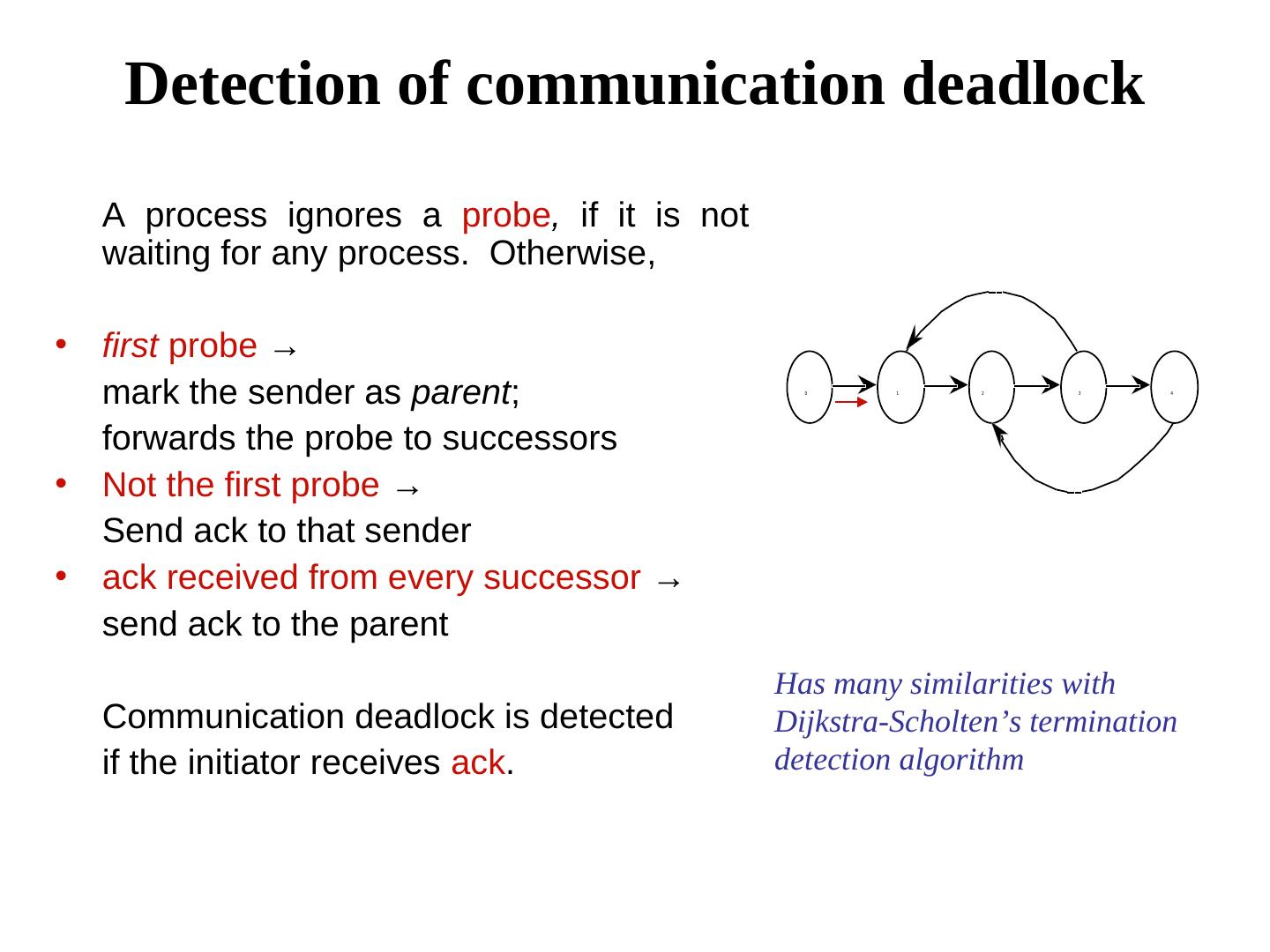
24 . Detection of communication deadlock A process ignores a probe, if it is not waiting for any process. Otherwise, • first probe → mark the sender as parent; 0 1 2 3 4 forwards the probe to successors • Not the first probe → Send ack to that sender • ack received from every successor → send ack to the parent Has many similarities with Communication deadlock is detected Dijkstra-Scholten’s termination if the initiator receives ack. detection algorithm