1 .Time and Clock 

2 . Time and Clock Primary standard of time = rotation of earth De facto primary standard = atomic clock (1 atomic second = 9,192,631,770 orbital transitions of Cesium 133 atom. 86400 atomic sec = 1 solar day – approx. 3 ms (Match up with solar day requires leap second correction each year) Coordinated Universal Time (UTC) does the adjustment for leap seconds = GMT ± number of hours in your time zone 

3 . Global positioning system: GPS Location and precise time computed by triangulation Right now GPS time is nearly 16 seconds ahead of UTC, since It does not use leap sec. correction Per the theory of relativity, an additional correction is needed. Locally compensated by the receivers. A system of 32 satellites broadcast accurate spatial coordinates and time maintained by atomic clocks 

4 . Physical clock synchronization Question 1. Why is physical clock synchronization important? Question 2. With the price of atomic clocks or GPS coming down, should we care about physical clock synchronization? 

5 . Classification Types of Synchronization Types of clocks Unbounded 0, 1, 2, 3, . . .  External Synchronization Bounded 0,1, 2, . . . M-1, 0, 1, . . .  Internal Synchronization  Phase Synchronization Unbounded clocks are not realistic, but are easier to deal with in the design of algorithms. Real clocks are always bounded. 

6 .Terminologies What are these? Drift rate ρ Clock skew δ Resynchronization interval R Max drift rate ρ implies: (1- ρ) ≤ dC/dt < (1+ ρ) Challenges • (Drift is unavoidable) • Accounting for propagation delay • Accounting for processing delay • Faulty clocks 

7 . Internal synchronization Step 1. Leader reads every clock in the Berkeley Algorithm system. Step 2. Discard outliers and substitute A simple averaging algorithm them by the value of the local clock. that guarantees mutual Step 3. Computes the average, and consistency |c(i) - c(j)| < δ. sends the needed adjustment to the - The participants elect a participating clocks leader - The leader coordinates the Resynchronization interval R will depend synchronization on the drift rate. 

8 .Berkeley algorithm 

9 . Internal synchronization with byzantine clocks Lamport and Melliar-Smith’s averaging algorithm handles Assume n clocks, at most t are faulty byzantine clocks too Step 1. Read every clock in the system. Step 2. Discard outliers and substitute them by the c- δ c value of the local clock. i j Step 3. Update the clock using the average of c+ δ c-2 δ these values. k Synchronization is maintained if n > 3t Bad clock A faulty clocks exhibits 2-faced Why? or byzantine behavior 

10 . Internal synchronization Lamport & Melliar-Smith’s algorithm (continued) The maximum difference between the averages computed by two c c- δ non-faulty nodes is (3tδ/ n) i j To keep the clocks synchronized, c-2 δ c+ δ k k 3tδ/ n < δ So, 3t < n Bad clocks 

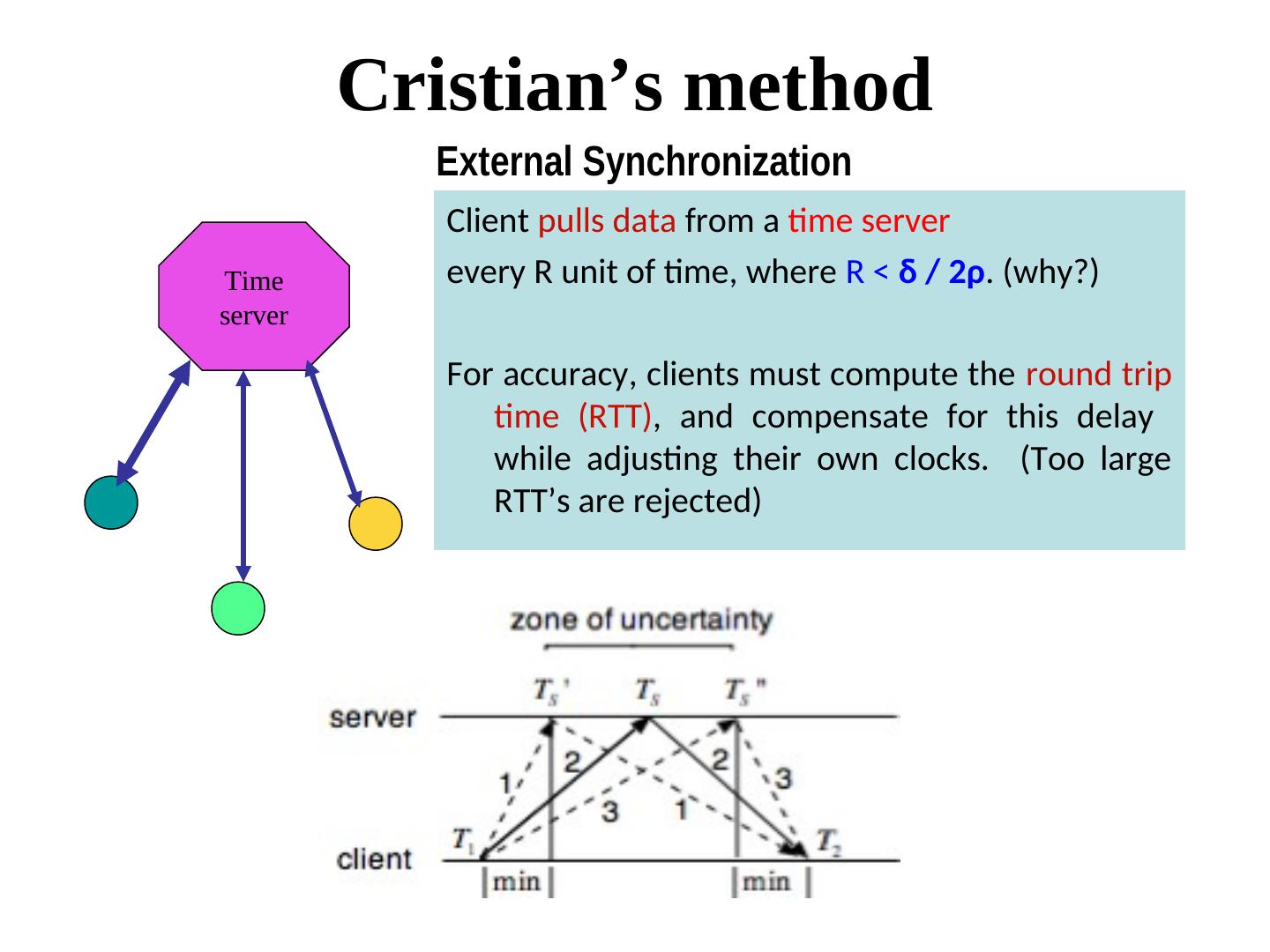
11 . Cristian’s method External Synchronization Client pulls data from a time server Time every R unit of time, where R < δ / 2ρ. (why?)why?)) server For accuracy, clients must compute the round trip time (why?)RTT), and compensate for this delay while adjusting their own clocks. (why?)Too large RTT’s are rejected) 

12 . Network Time Protocol (NTP) Cesium clocks or GPS based clocks Broadcast mode - least accurate Procedure call - medium accuracy Peer-to-peer mode -upper level servers use this for max accuracy A computer will try to synchronize its clock with several servers, and accept the best results to set its time. Accordingly, the synchronization subnet is dynamic. 

13 . Peer-to-peer mode of NTP Let Q’s time be ahead of P’s time by δ. Then T2 = T1 + TPQ + δ T2 T3 Q T4 = T3 + TQP - δ y = TPQ + TQP = T2 +T4 -T1 -T3 (RTT) δ = (T2 -T4 -T1 +T3) / 2 - (TPQ - TQP) / 2 P T1 T4 x Between y/2 and -y/2 So, x- y/2 ≤ δ ≤ x+ y/2 Ping several times, and obtain the smallest value of y. Use it to calculate δ 

14 . Problems with Clock adjustment 1. What problems can occur when a clock value is advanced from 171 to 174? 2. What problems can occur when a clock value is moved back from 180 to 175? 

15 . Sequential and Concurrent events Sequential = Totally ordered in time. Total ordering is feasible in a single process that has only one clock. This is not true in a distributed system, since clocks are never perfectly synchronized. Can we define sequential and concurrent events without using physical clocks, since physical clocks are not be perfectly synchronized? 

16 . What does “concurrent” mean? Simultaneous? Happening at the same time? NO. There is nothing called simultaneous in the physical world. Alice Explosion 2 Explosion 1 Bob 

17 . Causality Causality helps identify sequential and concurrent events without using physical clocks. Joke  Re: joke ( implies causally ordered before or happened before) Message sent  message received Local ordering: a  b  c (based on the local clock) 

18 . Defining causal relationship Rule 1. If a, b are two events in a single process P, and the time of a is less than the time of b then a  b. Rule 2. If a = sending a message, and b = receipt of that message, then a  b. Rule 3. (a  b) ∧ ( (b  c) ⇒ a  c 

19 . Example of causality a  d since (a  b ∧ ( b  c ∧ ( c  d) h d e  d since (e  f ∧ ( f  d) t g c i f (Note that  defines a PARTIAL order). m b e a e Is g f or f g? NO.They are concurrent. P Q R . Concurrency = absence of causal order 

20 . Logical clocks Each process maintains its logical LC is a counter. Its value respects clock as follows: causal ordering as follows LC1. Each time a local event takes a  b ⇒ LC(a) < LC(b) place, increment LC. LC2. Append the value of LC to outgoing But LC(a) < LC(b) does NOT messages. imply a  b. LC3. When receiving a message, set LC to 1 + max (local LC, message LC) 

21 . Total order in a distributed system Total order is important for some Let a, b be events in processes applications like scheduling (first- i and j respectively. Then come first served). But total order does not exist! What can we do? a << b iff -- LC(a) < LC(b) OR -- LC(a) = LC(b) and i < j Strengthen the causal order  to define a total order (<<) among events. Use LC to define total a  b ⇒ a << b, but the converse is not true. order (in case two LC’s are equal, process id’s will be used to break the tie). The value of LC of an event is called its timestamp. 

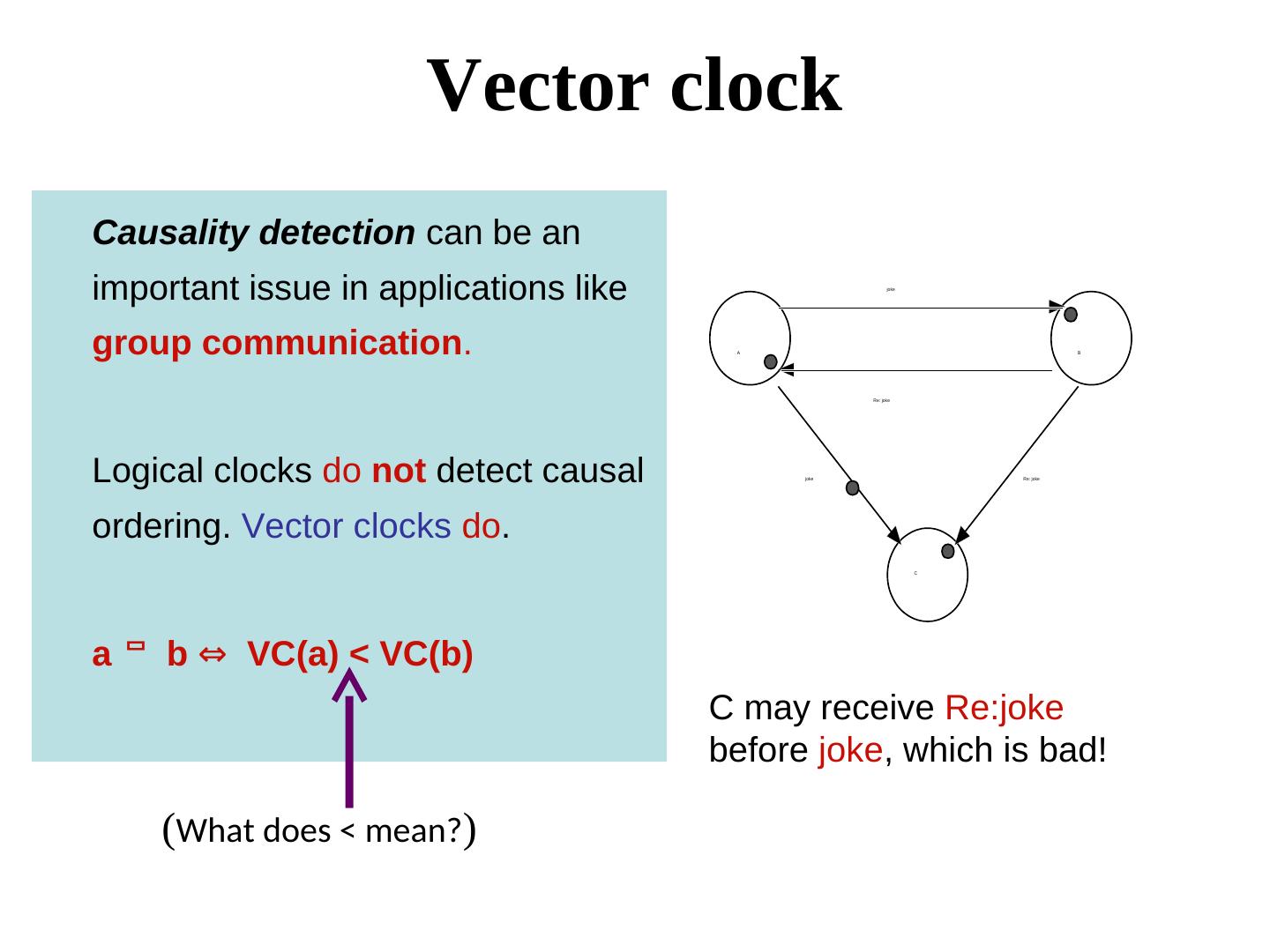
22 . Vector clock Causality detection can be an important issue in applications like joke group communication. A B Re: joke Logical clocks do not detect causal joke Re: joke ordering. Vector clocks do. C a  b ⇔ VC(a) < VC(b) C may receive Re:joke before joke, which is bad! (What does < mean?)) 

23 . Implementing VC {Sender process i} ith component of VC 1. Increment VC[i]. 1,1,0 2,1,0 2. Append the local VC to every outgoing 0,0,0 message. 0,0,0 {Receiver process j} 0,1,0 2,2,4 3. When a message with a vector timestamp T 0,0,0 arrives from i, first increment the jth 0,0,1 0,0,2 2,1,3 2,1,4 component VC[j] of the local vector clock, and then update the local vector clock as follows: ∀k: 0 ≤ k ≤N-1:: VC[k] := max (T[k], VC[k]). 

24 . Vector clocks 0 1 2 3 4 5 6 7 Example Vector Clock of an event in a system of 8 processes [3, 3, 4, 5, 3, 2, 1, 4] < [3, 3, 4, 5, 3, 2, 2, 5] Let a, b be two events. Define. VC(a) < VC(b) iff But, ∀i : 0 ≤ i ≤ N-1 : VC(a)[i] ≤ VC(b)[i], and [3, 3, 4, 5, 3, 2, 1, 4] and ∃ j : 0 ≤ j ≤ N-1 : VC(a)[j] < VC(b)[j], [3, 3, 4, 5, 3, 2, 2, 3] VC(a) < VC(b) ⇔ a  b are not comparable Causality detection