分布式系统和算法：分布式算法

1 .Representing distributed algorithms 

2 . How to represent a distributed algorithm? We will introduce the notions of atomicity, non- determinism, fairness etc that are important issues in specifying distributed algorithms. These concepts are not built into languages like JAVA, C++, python etc! 

3 . Syntax & semantics: guarded actions <guard G>  <action A>> is equivalent to if G then A> (Borrowed from E.W. Dijkstra: A Discipline of Programming) 

4 . Syntax & semantics: guarded actions • Sequential actions S0; S1; S2; . . . ; Sn • Alternative constructs if . . . . . . . . . . fi • Repetitive constructs do . . . . . . . . . od The specification is useful for representing abstract algorithms, not executable codes. 

5 . Syntax & semantics Alternative construct if G1  S 1 [] G2  S 2 … [] Gn Sn fi When no guard is true, skip (do nothing). When multiple guards are true, the choice of the action to be executed is completely arbitrary. 

6 . Syntax & semantics Repetitive construct do G1  S1 [] G2  S2 . [] Gn  Sn od Keep executing the actions until all guards are false and the program terminates. When multiple guards are true, the choice of the action is arbitrary. 

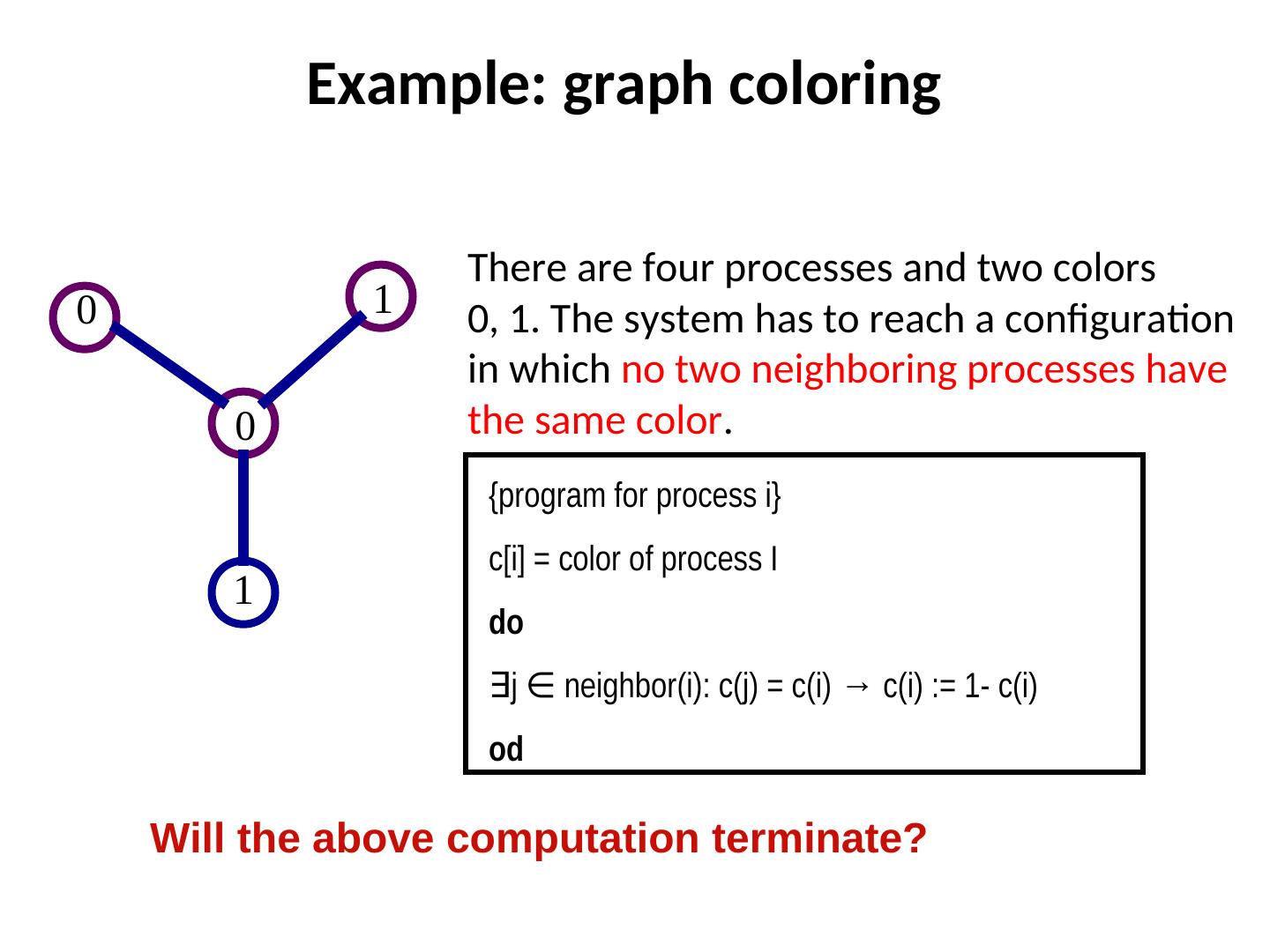
7 . Example: graph coloring There are four processes and two colors 0 1 0, 1. The system has to reach a configuration in which no two neighboring processes have 0 the same color. {program for process i} c[i] = color of process I 1 do ∃j ∈ neighbor(i): c(j) = c(i) → c(i) := 1- c(i) neighbor(i): c(j) = c(i) → c(i) := 1- c(i) od Will the above computation terminate? 

8 . Central vs. Distributed Schedulers Central scheduler implies that at most one process can execute its action at a time. A bit unrealistic, but it simplifies reasoning about program correctness Distributed scheduler allows any number of eligible processes to execute their actions at the same time. It is more realistic, but reasoning about correctness is more difficult. 

9 . Consider another example program uncertain; define x : integer; initially x=0 do x < 4  x := x + 1 [] x = 3  x := 0 od Question. Will the program terminate? (Our goal here is to understand fairness) 

10 . The adversary A distributed computation can be viewed as a game between the system and an adversary. The adversary may come up with feasible schedules to challenge the system (and cause “bad things”). A correct algorithm must be able to prevent those bad things from happening. 

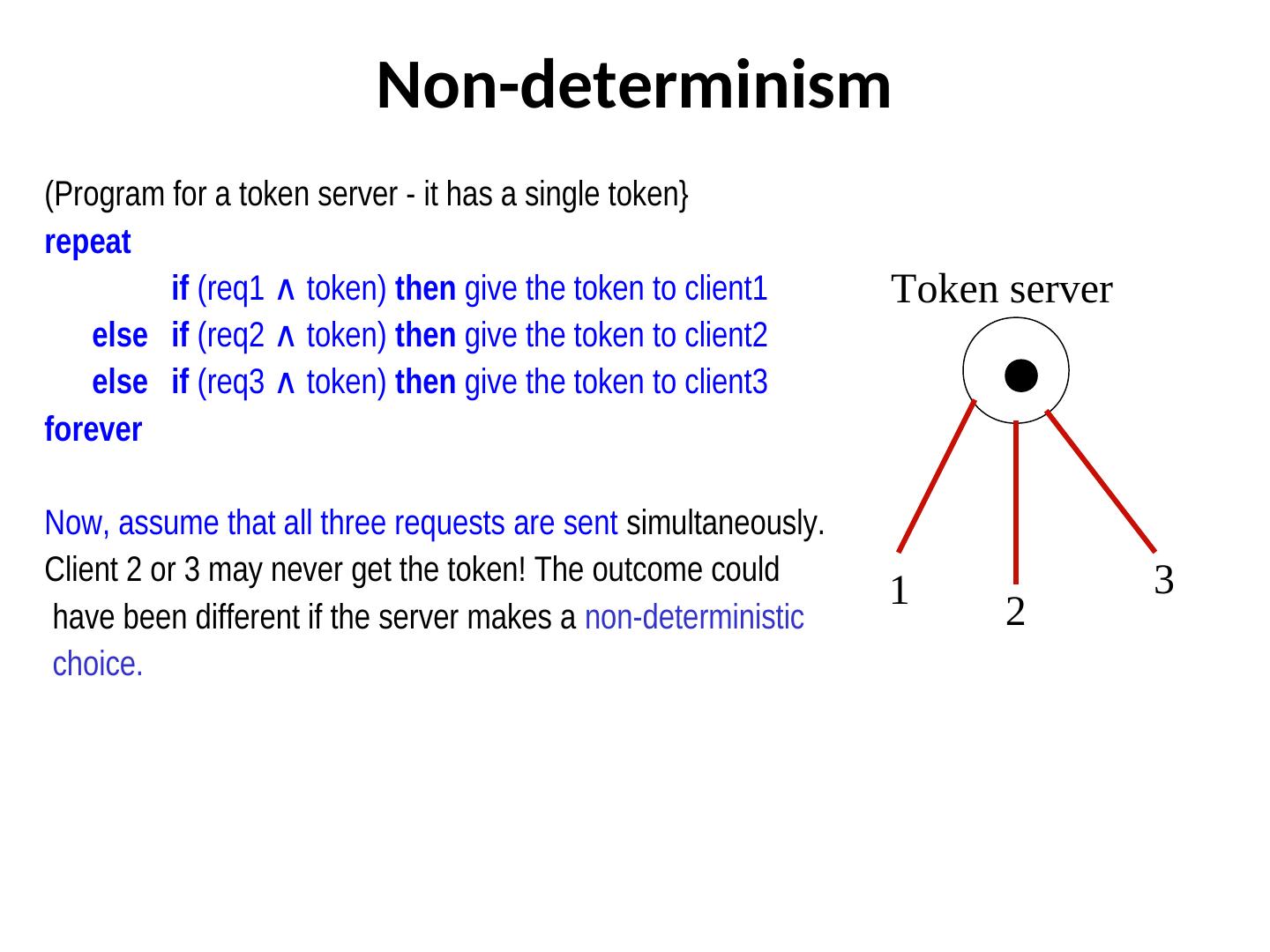
11 . Non-determinism (Program for a token server - it has a single token} repeat if (req1 ∧ token) token) then give the token to client1 Token server else if (req2 ∧ token) token) then give the token to client2 else if (req3 ∧ token) token) then give the token to client3 forever Now, assume that all three requests are sent simultaneously. Client 2 or 3 may never get the token! The outcome could 3 1 have been different if the server makes a non-deterministic 2 choice. 

12 . Examples of non-determinism If there are multiple processes ready to execute actions, then who will execute the action first is nondeterministic. Message propagation delays are arbitrary and the order of message reception is non-deterministic. Determinism caters to a specific order and is a special case of non-determinism. 

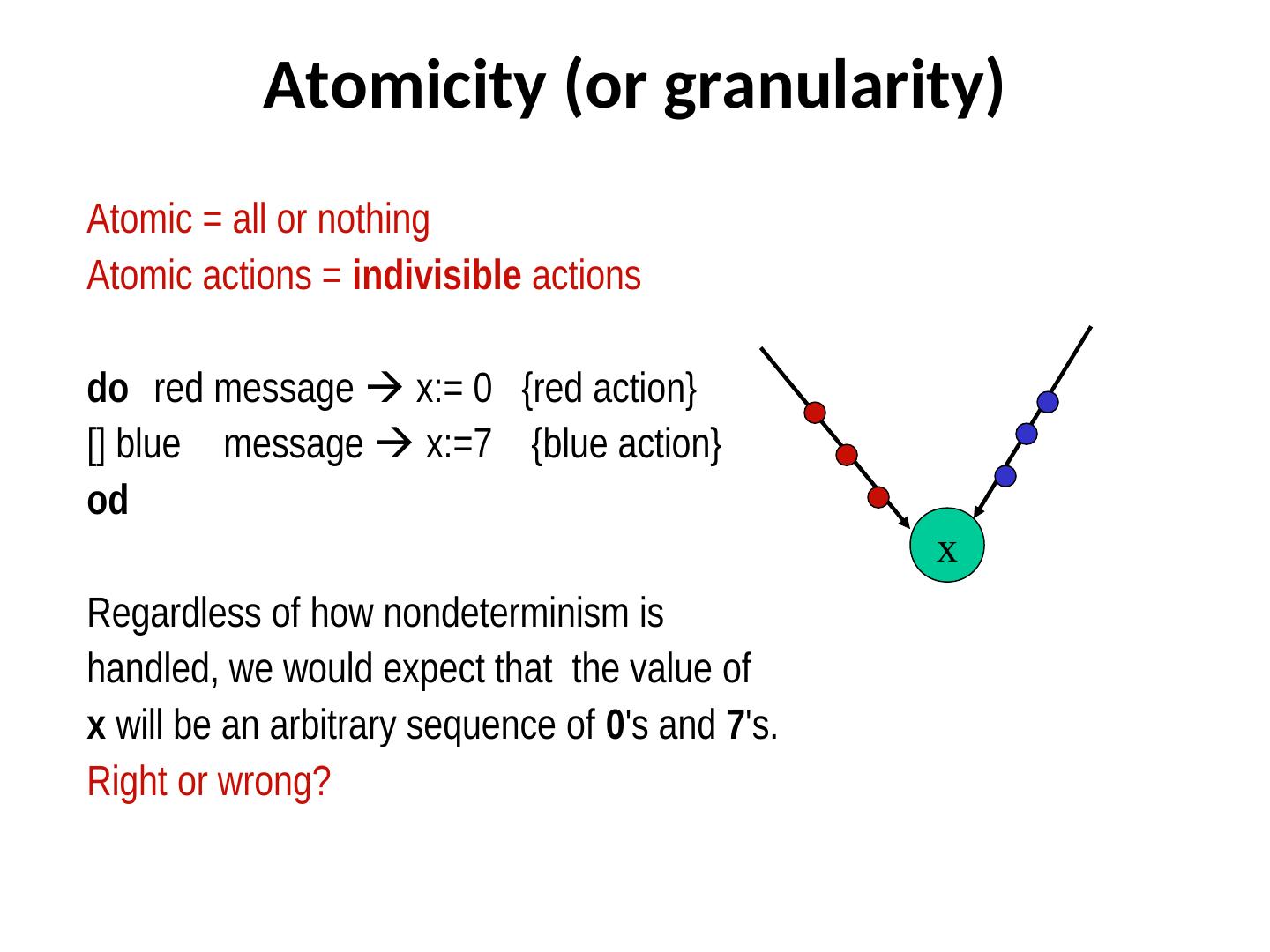
13 . Atomicity (or granularity) Atomic = all or nothing Atomic actions = indivisible actions do red message  x:= 0 {red action} [] blue message  x:=7 {blue action} od x Regardless of how nondeterminism is handled, we would expect that the value of x will be an arbitrary sequence of 0's and 7's. Right or wrong? 

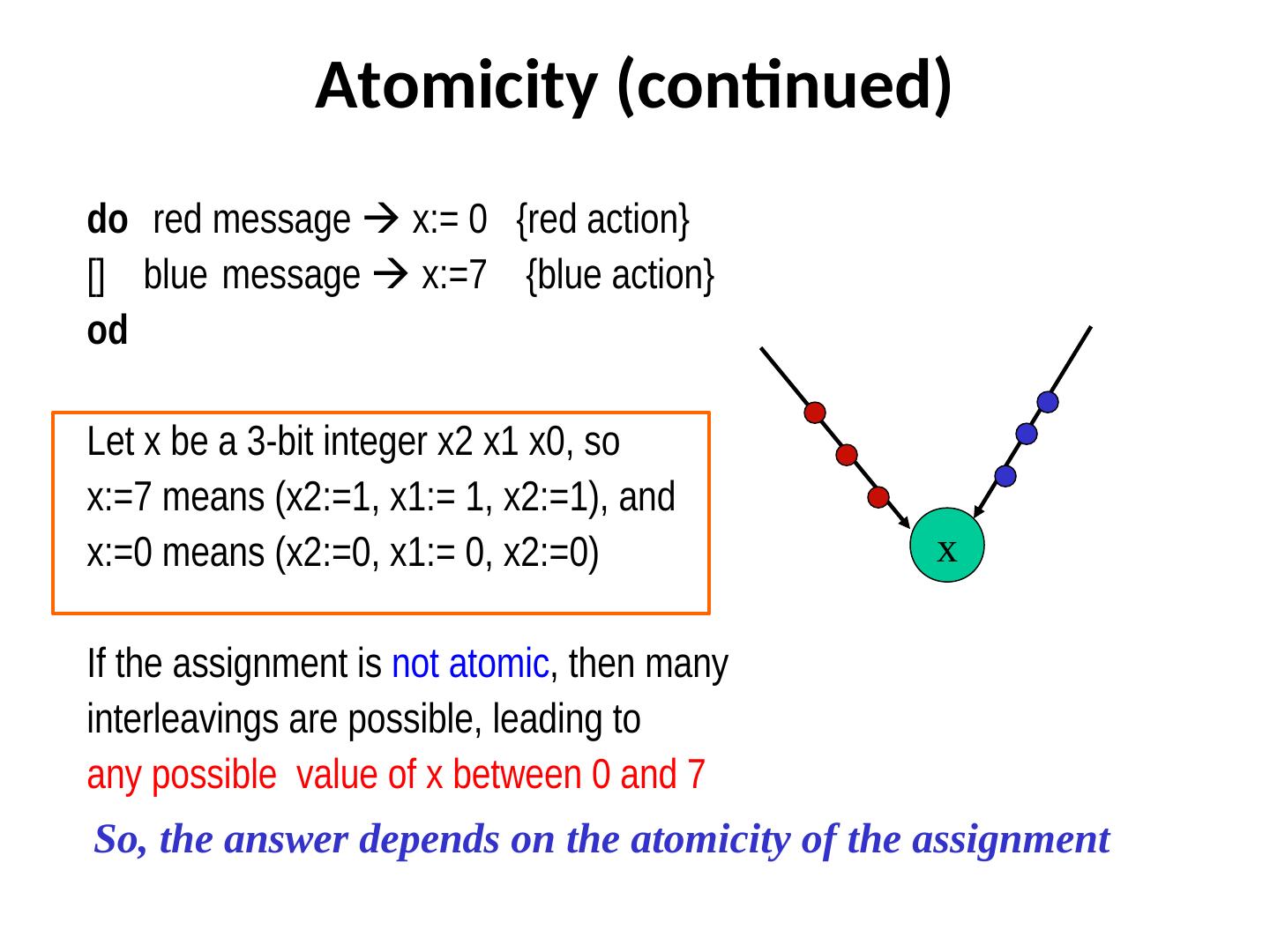
14 . Atomicity (continued) do red message  x:= 0 {red action} [] blue message  x:=7 {blue action} od Let x be a 3-bit integer x2 x1 x0, so x:=7 means (x2:=1, x1:= 1, x2:=1), and x:=0 means (x2:=0, x1:= 0, x2:=0) x If the assignment is not atomic, then many interleavings are possible, leading to any possible value of x between 0 and 7 So, the answer depends on the atomicity of the assignment 

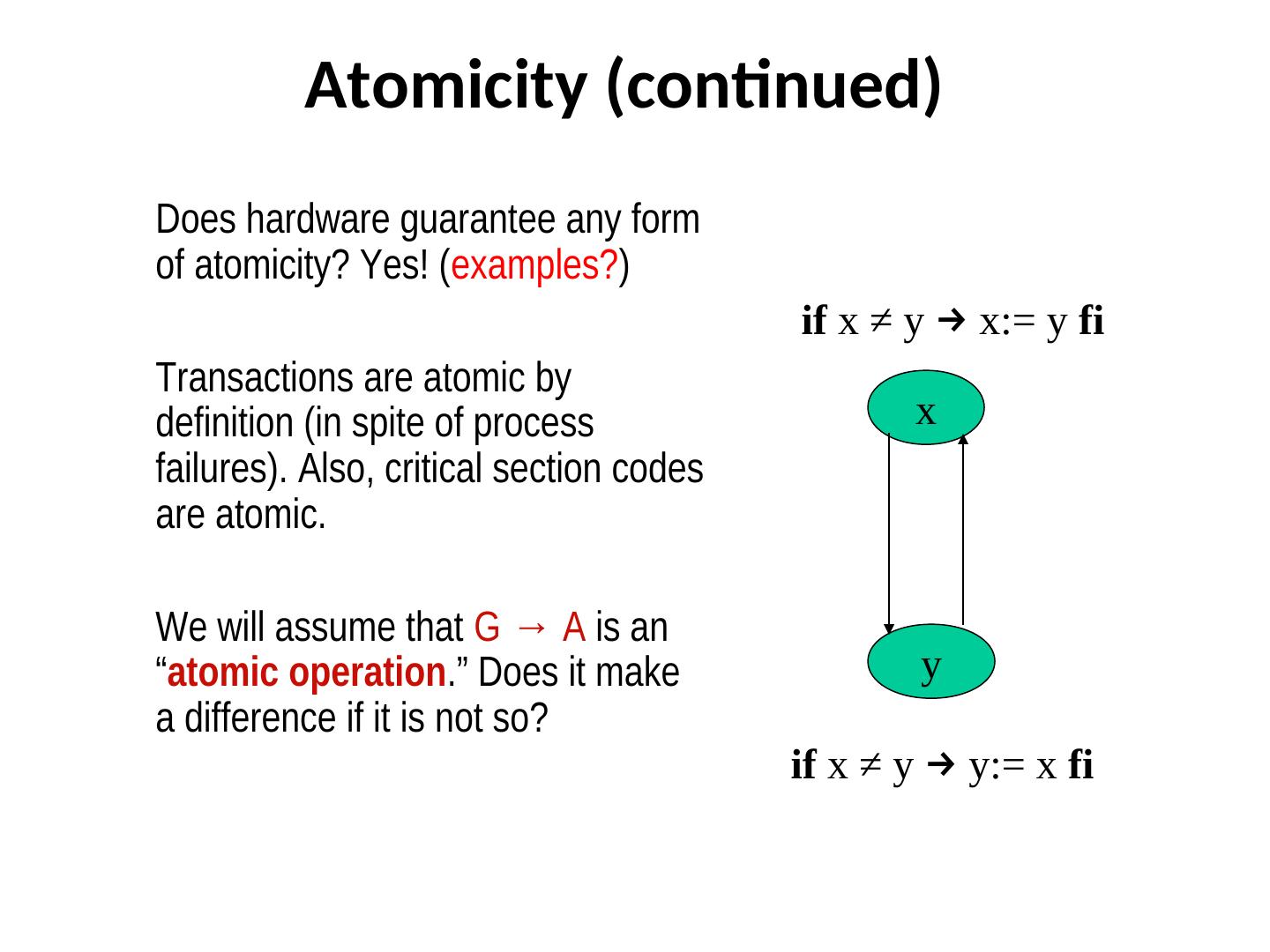
15 . Atomicity (continued) Does hardware guarantee any form of atomicity? Yes! (examples?) if x ≠ y → x:= y fi Transactions are atomic by definition (in spite of process x failures). Also, critical section codes are atomic. We will assume that G → A is an “atomic operation.” Does it make y a difference if it is not so? if x ≠ y → y:= x fi 

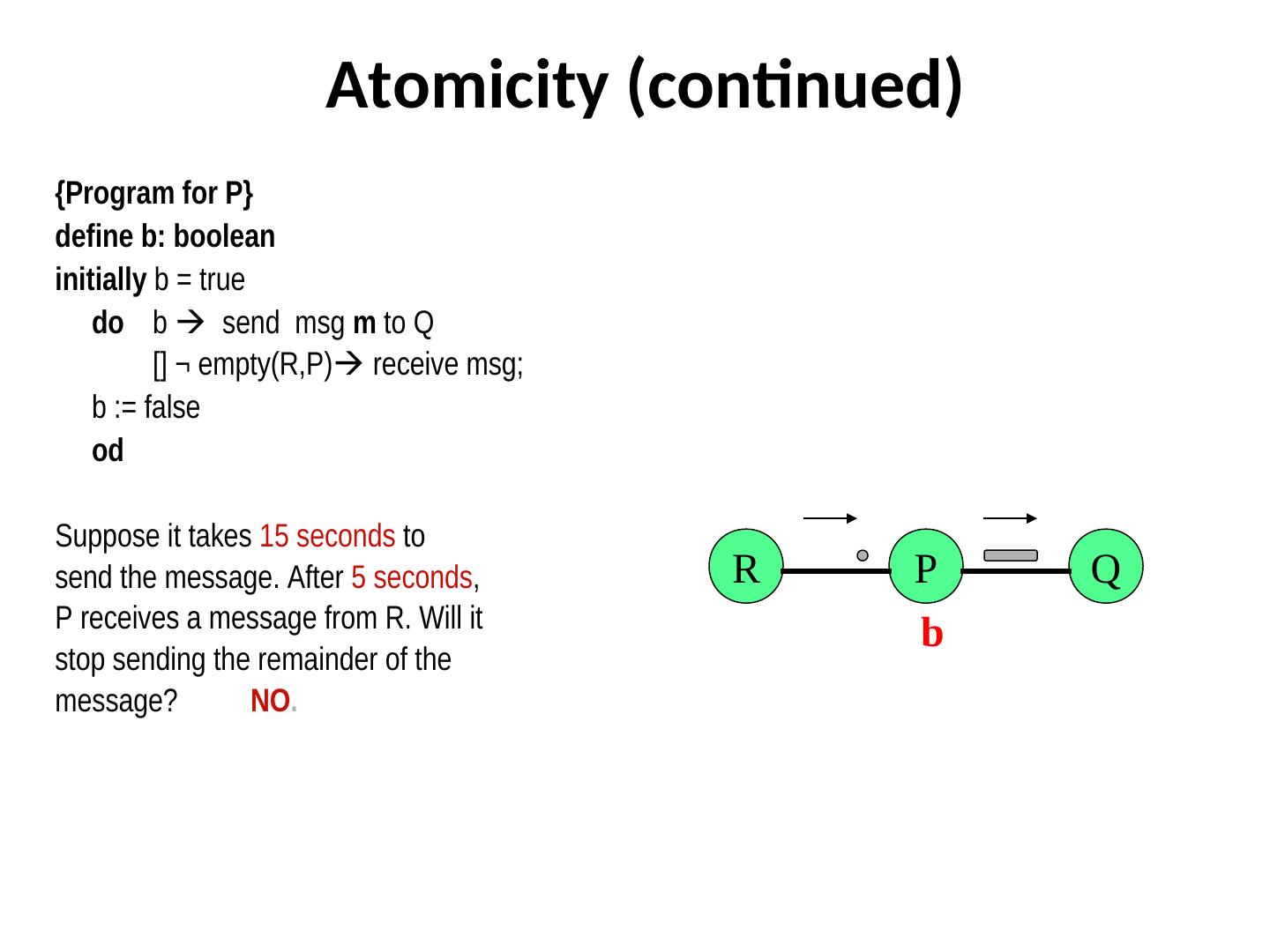
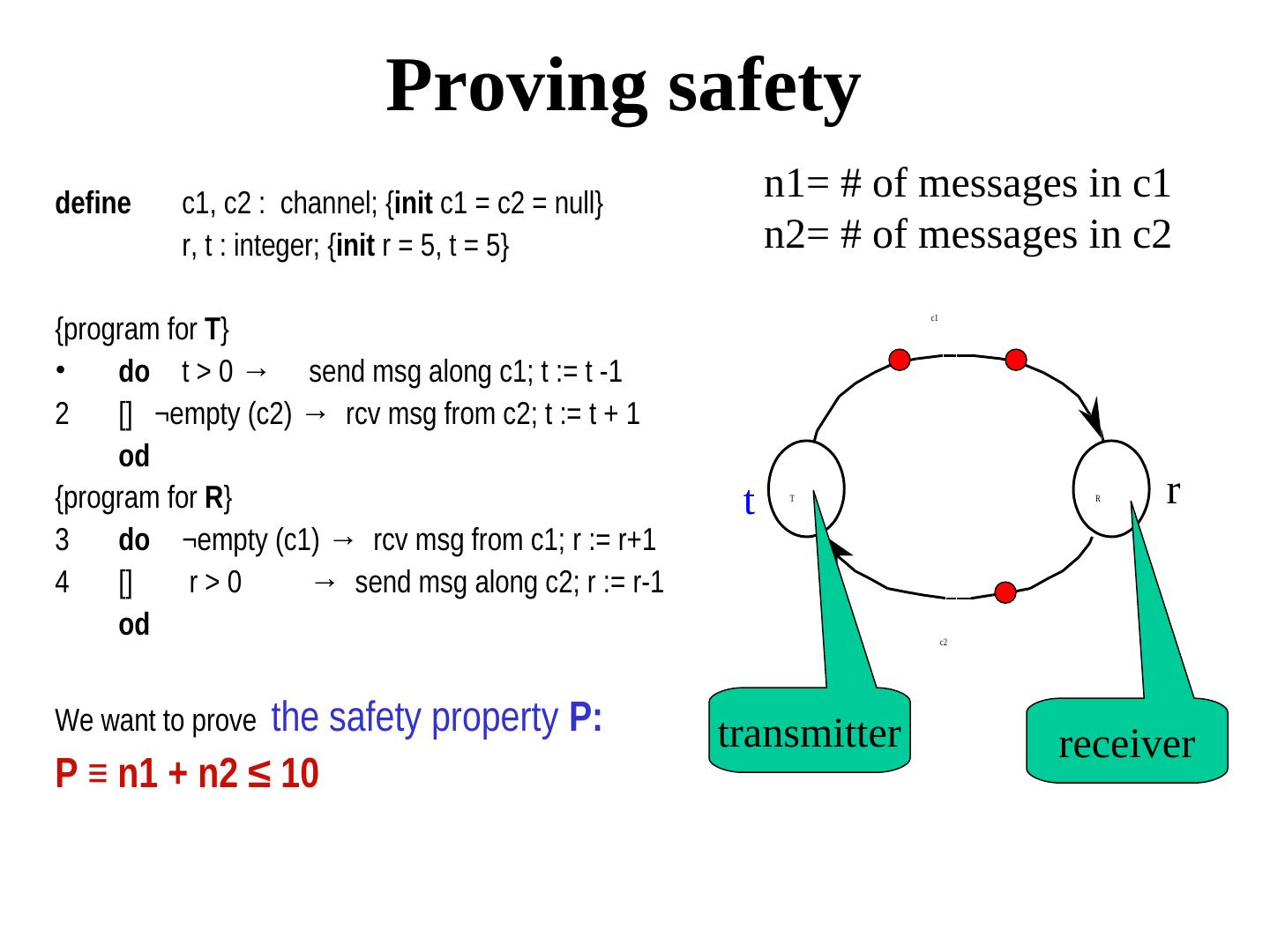
16 . Atomicity (continued) {Program for P} define b: boolean initially b = true do b  send msg m to Q [] ¬ empty(R,P) receive msg; b := false od Suppose it takes 15 seconds to send the message. After 5 seconds, R P Q P receives a message from R. Will it b stop sending the remainder of the message? NO. 

17 . Fairness Defines the choices or restrictions on the scheduling of actions. No such restriction implies an unfair scheduler. For fair schedulers, the following types of fairness have received attention: – Unconditional fairness Scheduler / demon / – Weak fairness adversary – Strong fairness 

18 . Fairness Program test An unfair scheduler may never define x : integer schedule the second (or the third actions). So, x may always be {initial value unknown} equal to zero. do true  x:=0 An unconditionally fair scheduler [] x=0  x:=1 will eventually give every [] x=1  x:=2 statement a chance to execute without checking their eligibility. od (Example: process scheduler in a multiprogrammed OS.) 

19 . Weak Fairness • A scheduler is weakly fair, Program test when it eventually executes define x : integer every guarded action whose guard becomes true, and {initial value unknown} remains true thereafter do true  x : = 0 [] x = 0  x : = 1 • A weakly fair scheduler will [] x=1  x:=2 eventually execute the od second action, but may never execute the third action. Why? 

20 . Strong fairness A scheduler is strongly fair, when it Program test eventually executes every guarded define x : integer action whose guard is true infinitely often. {initial value unknown} do true  x : = 0 [] x=0  x:=1 The third statement will be executed [] x=1  x:=2 under a strongly fair scheduler. Why? od udy more examples to reinforce these concep 

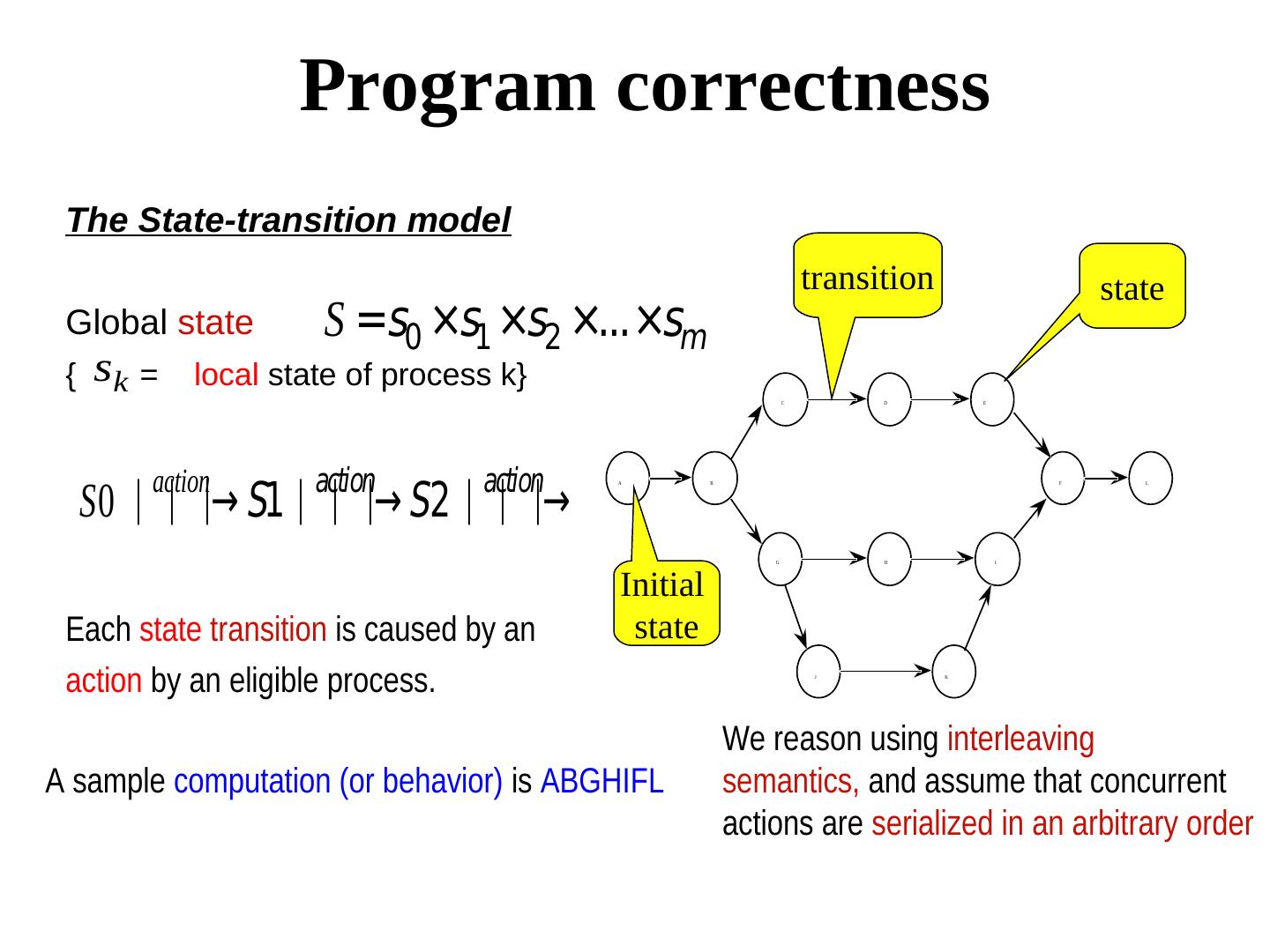
21 . Program correctness The State-transition model transition state Global state S =s0 ×s1 ×s2 ×...×sm { sk = local state of process k} C D E action action action S0 ⏐⏐⏐→ S1⏐⏐⏐→ S2 ⏐⏐⏐→ A B F L G H I Initial Each state transition is caused by an state action by an eligible process. J K We reason using interleaving A sample computation (or behavior) is ABGHIFL semantics, and assume that concurrent actions are serialized in an arbitrary order 

22 . Correctness criteria • Safety properties • Bad things never happen • Liveness properties • Good things eventually happen 

23 . Testing vs. Proof Testing: Apply inputs and observe if the outputs satisfy the specifications. Fool proof testing can be painfully slow, even for small systems. Most testing are partial. Proof: Has a mathematical foundation, and is a complete guarantee. Sometimes not scalable. 

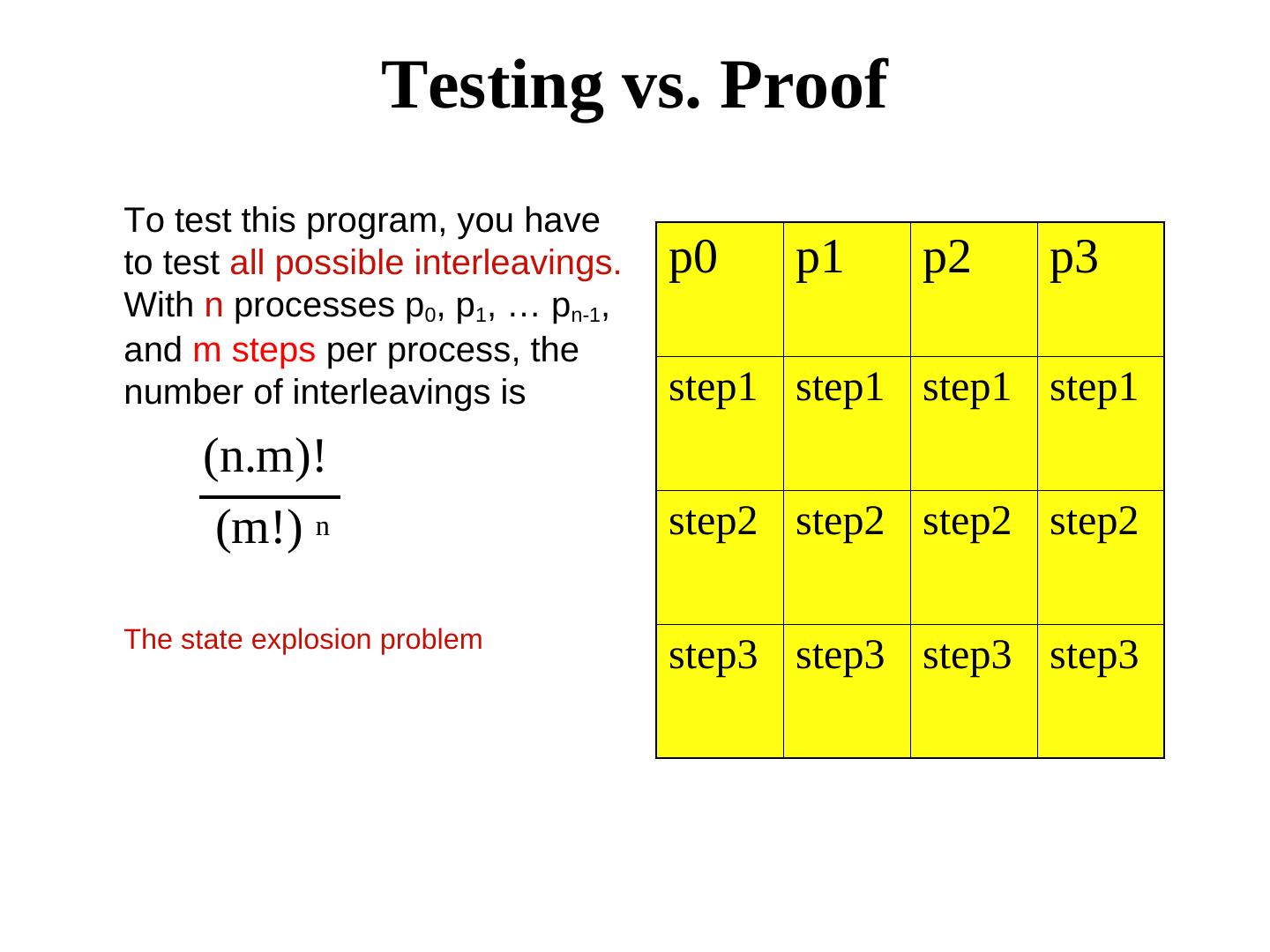
24 . Testing vs. Proof To test this program, you have to test all possible interleavings. p0 p1 p2 p3 With n processes p0, p1, … pn-1, and m steps per process, the number of interleavings is step1 step1 step1 step1 (n.m)! (m!) n step2 step2 step2 step2 The state explosion problem step3 step3 step3 step3 

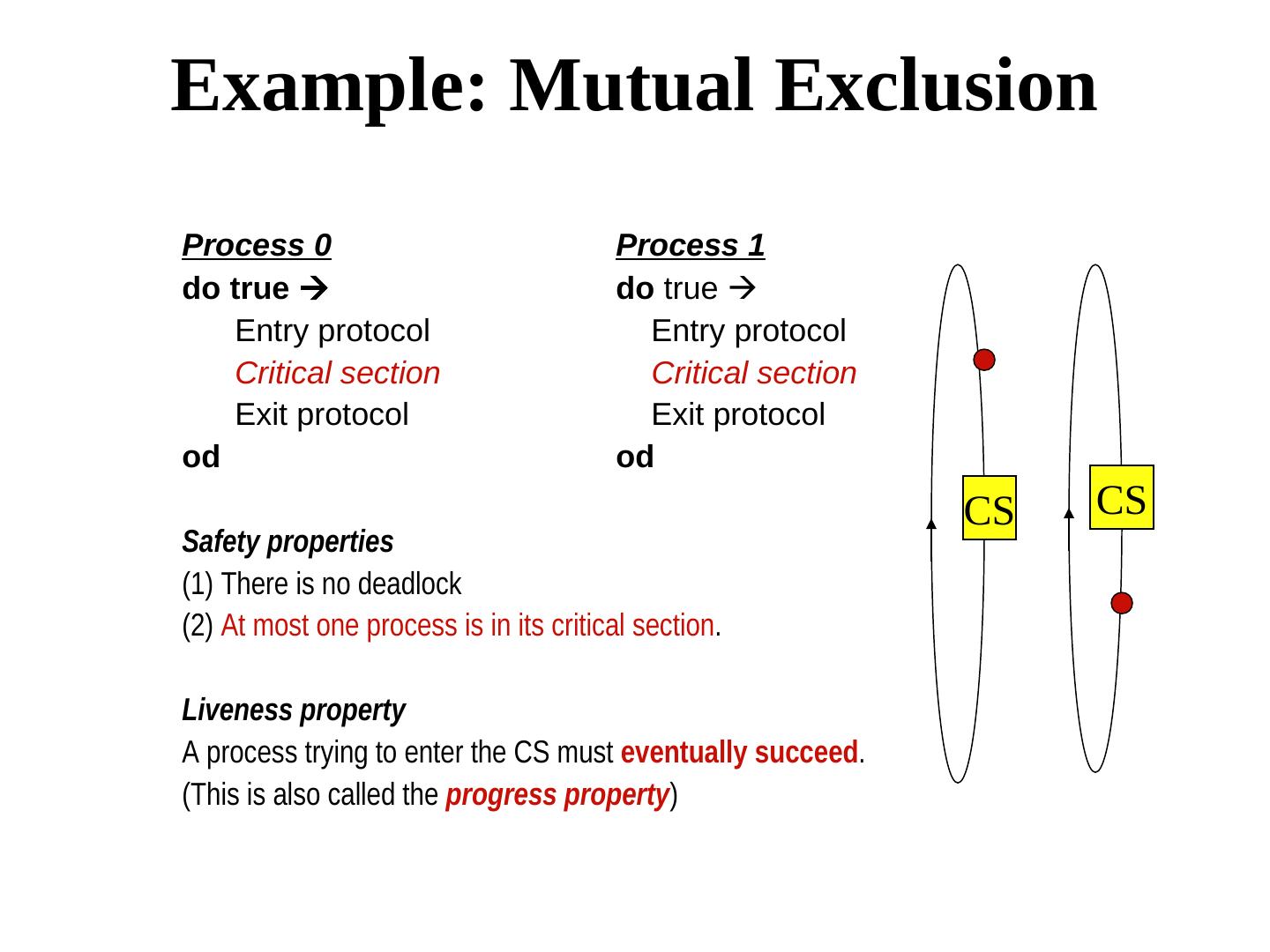
25 .Example: Mutual Exclusion Process 0 Process 1 do true  do true  Entry protocol Entry protocol Critical section Critical section Exit protocol Exit protocol od od CS CS Safety properties (1) There is no deadlock (2) At most one process is in its critical section. Liveness property A process trying to enter the CS must eventually succeed. (This is also called the progress property) 

26 . Exercise program mutex 1 {two process mutual exclusion algorithm: shared memory model} define busy :shared boolean (initially busy = false} {process 0} {process 1} do true  do true  do busy  skip od; do busy  skip od; busy:= true; busy:= true; critical section; critical section busy := false; busy := false {remaining codes} {remaining codes} od od Does this mutual exclusion protocol satisfy liveness and safety properties? 

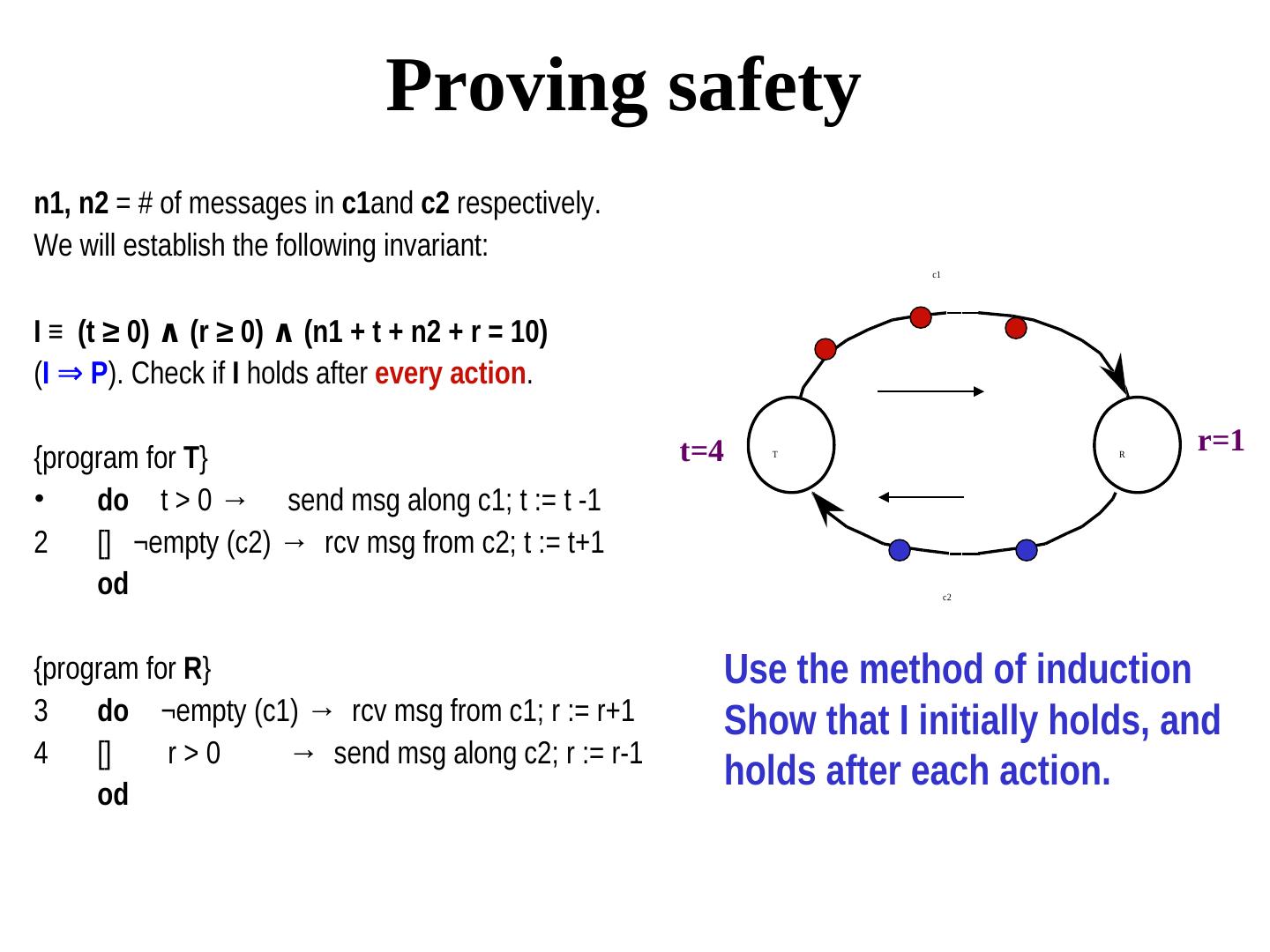
27 . Safety invariants Invariant means: something meaningful should always hold Example: Total no. of processes in CS ≤ 1 (mutual exclusion prob Another safety property is Partial correctness. It implies that “If the program terminates then the postcondition will hold.” Consider the following: do G0  S1 [] G1  S1 [] … [] Gk  Sk od Safety invariant: ¬(G0 ∨ G1 ∨ G2 ∨…∨ Gk) ⇒ postcondition It does not say if the program will terminate. (termination is a liveness property) Total correctness = partial correctness + termination. 

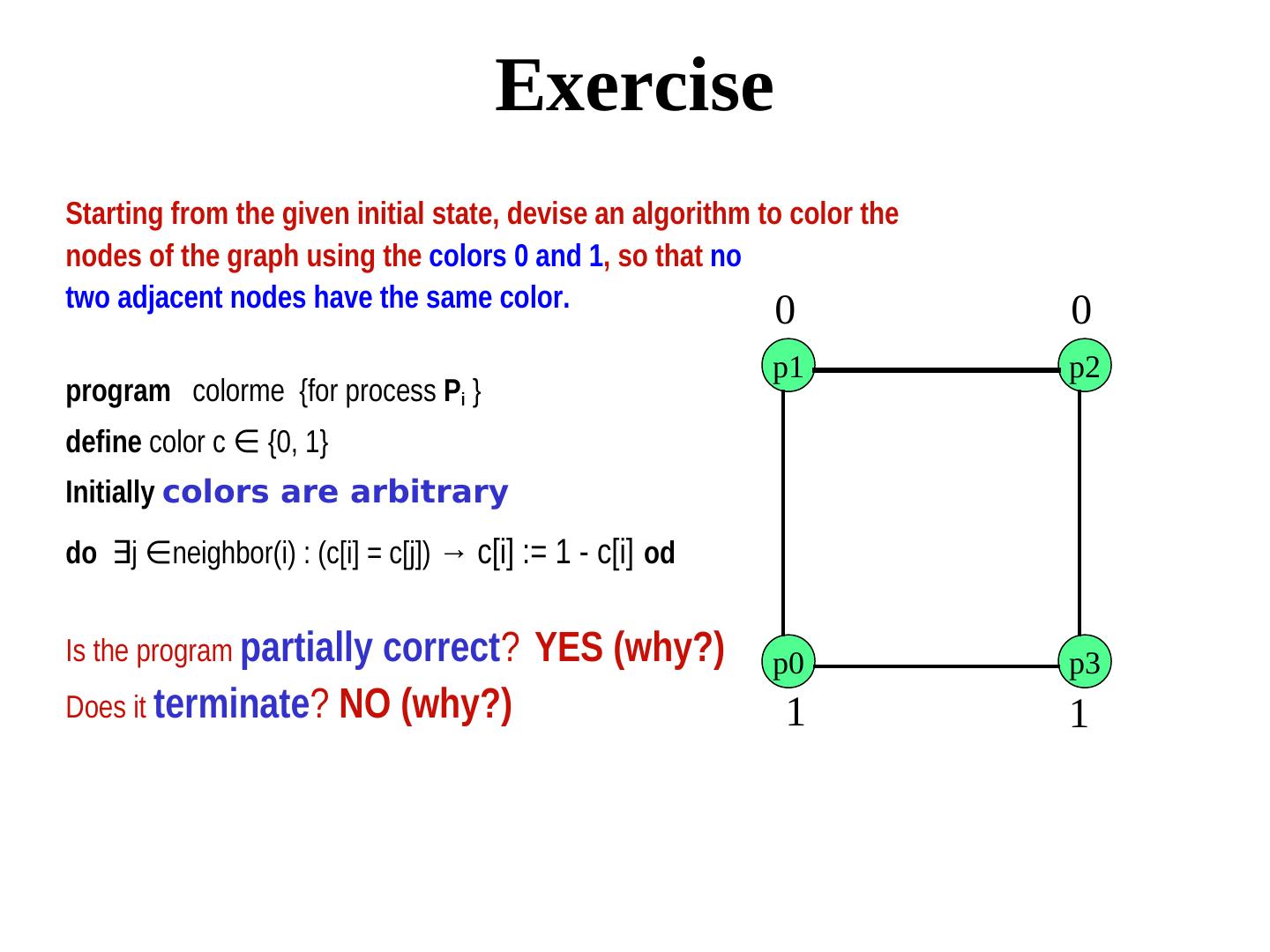
28 . Exercise Starting from the given initial state, devise an algorithm to color the nodes of the graph using the colors 0 and 1, so that no two adjacent nodes have the same color. 0 0 p1 p2 program colorme {for process Pi } define color c ∈ neighbor(i): c(j) = c(i) → c(i) := 1- c(i) {0, 1} Initially colors are arbitrary do ∃j ∈ neighbor(i): c(j) = c(i) → c(i) := 1- c(i)neighbor(i) : (c[i] = c[j]) → c[i] := 1 - c[i] od Is the program partially correct? YES (why?) p0 p3 Does it terminate? NO (why?) 1 1 

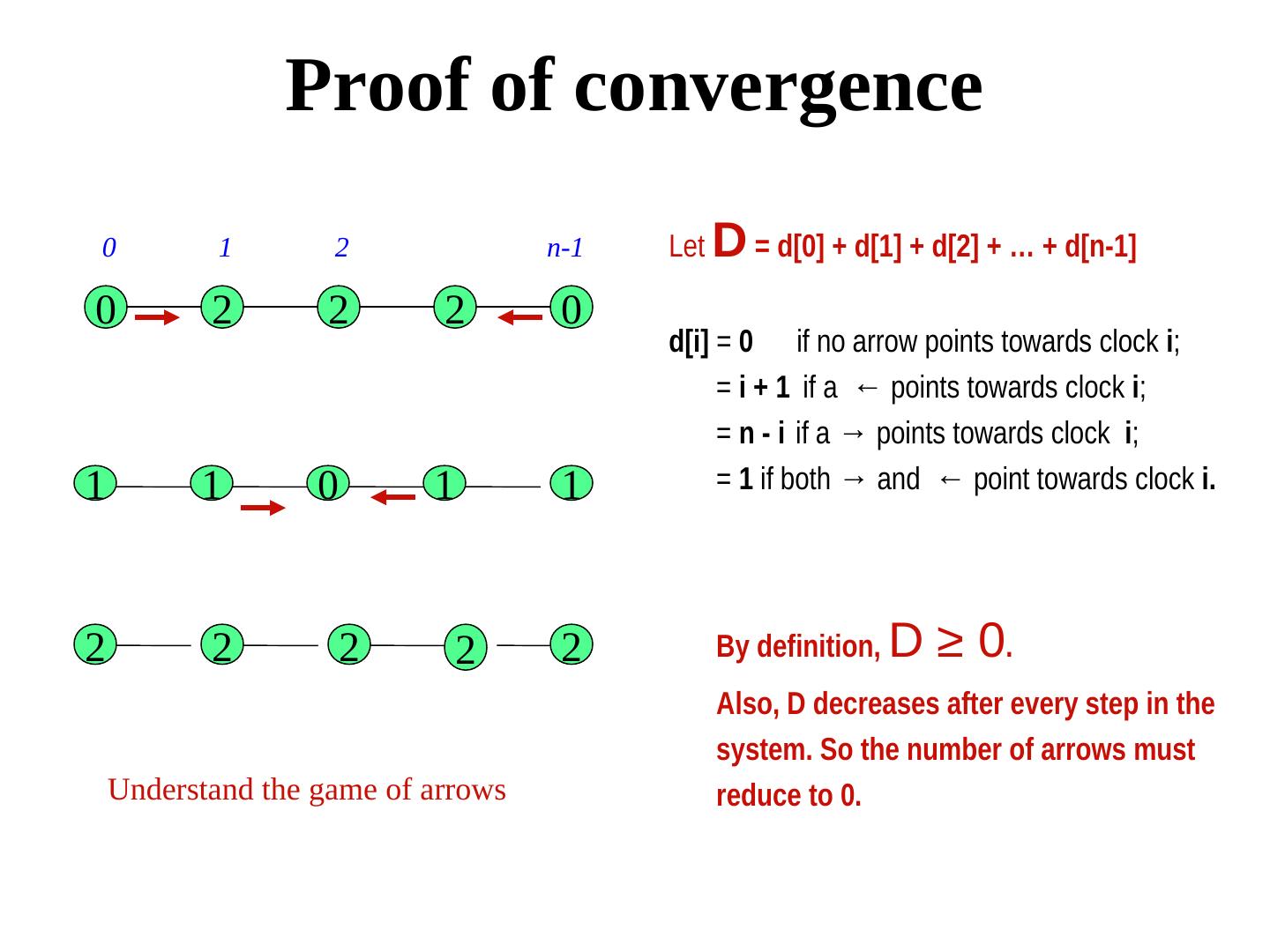
29 . Liveness properties Eventuality is tricky. There is no need to guarantee when the desired thing will happen, as long as it happens.. Some examples  The message will eventually reach the receiver.  The process will eventually enter its critical section.  The faulty process will be eventually be diagnosed  Fairness (if an action will eventually be scheduled)  The program will eventually terminate.  The criminal will eventually be caught. Absence of liveness cannot be determined from finite prefix of the computation