- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
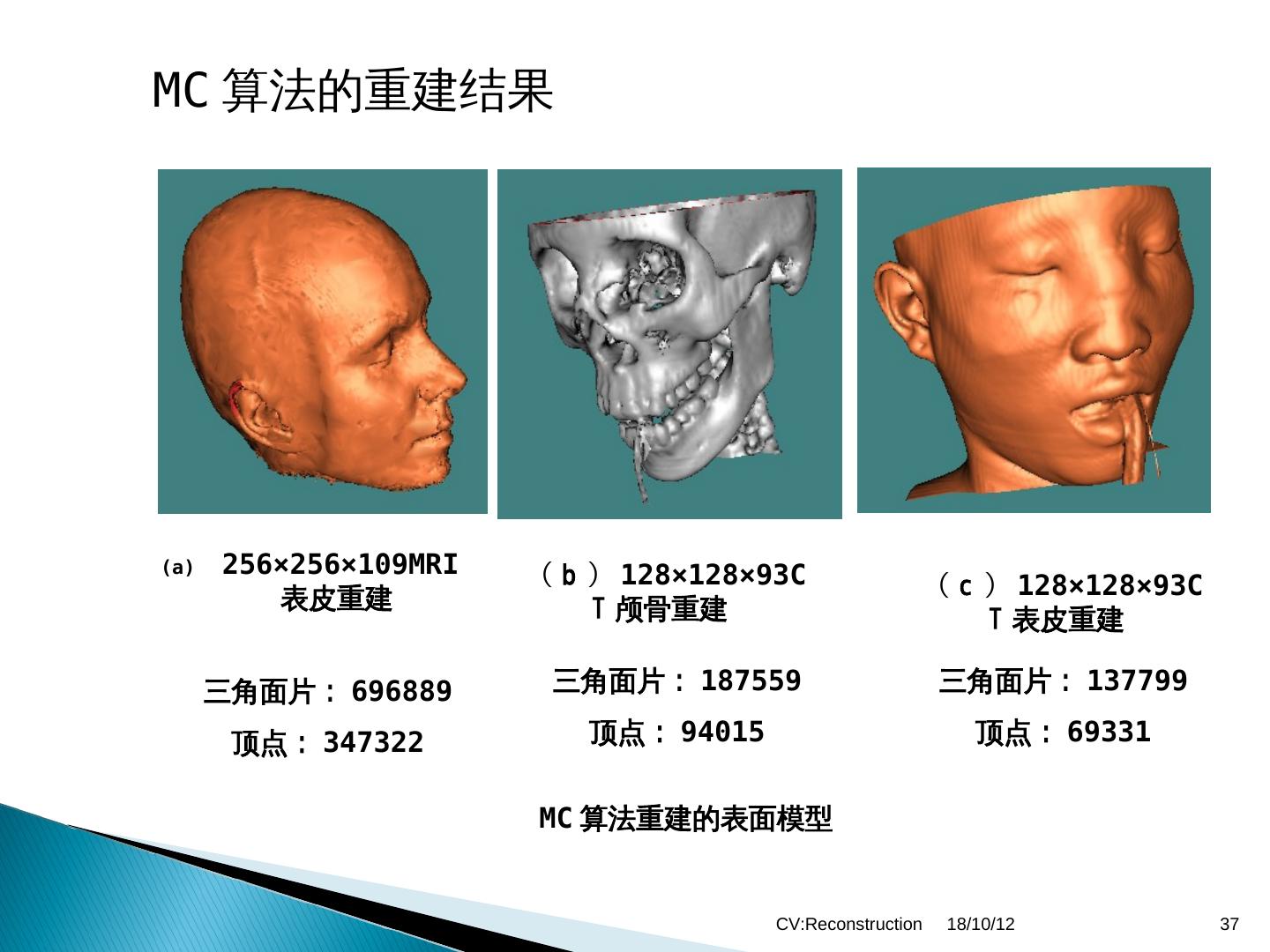
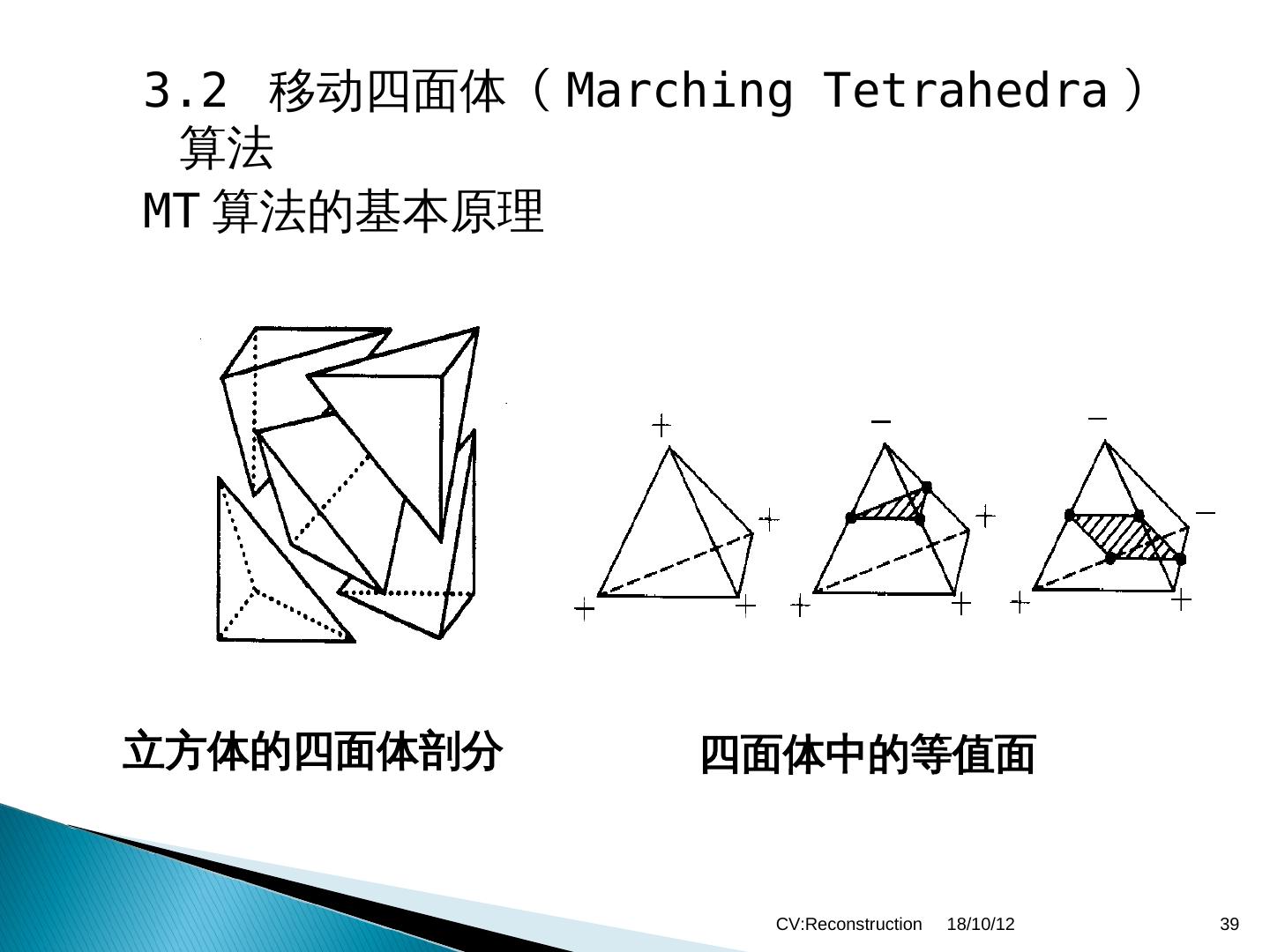
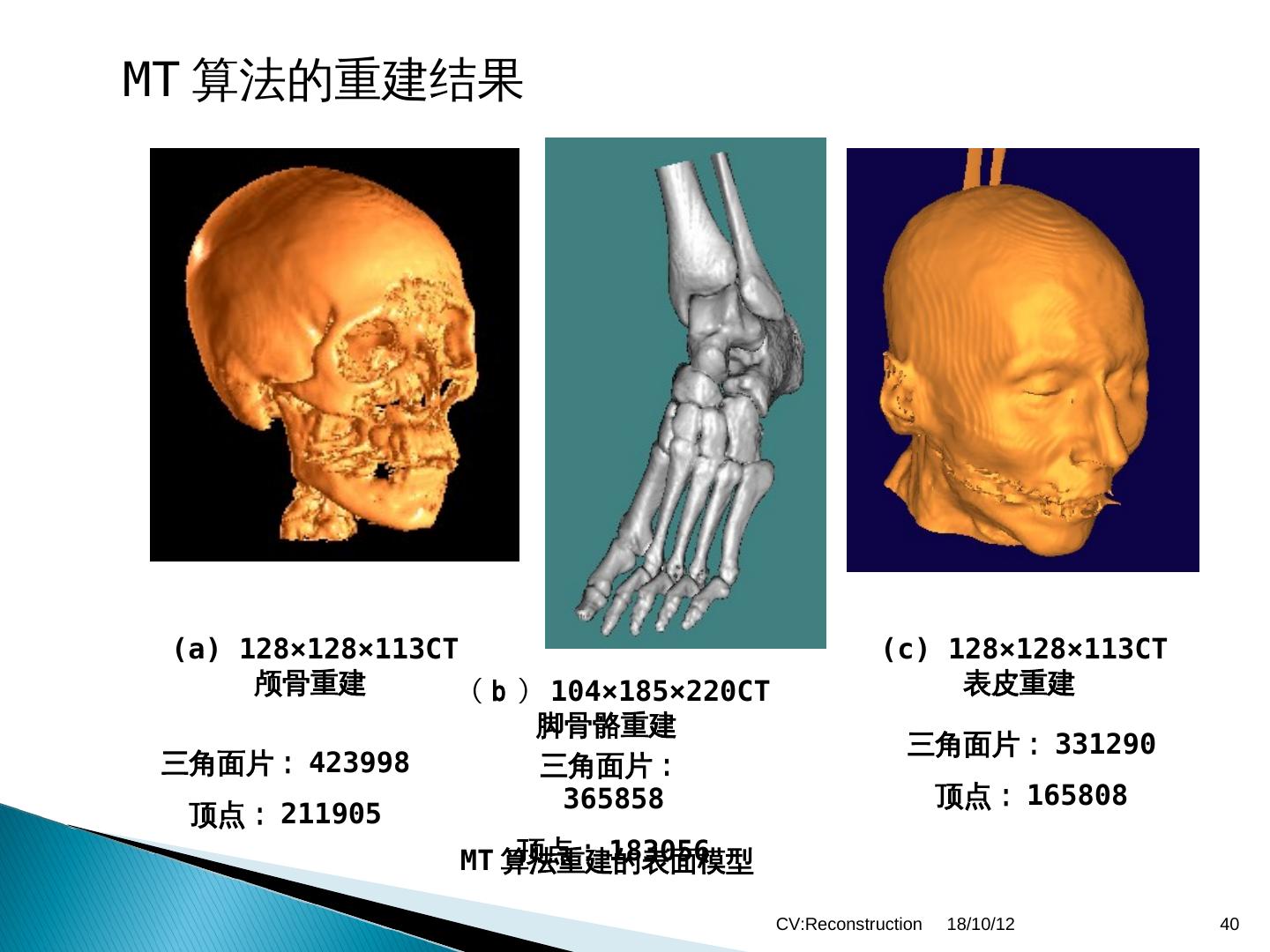
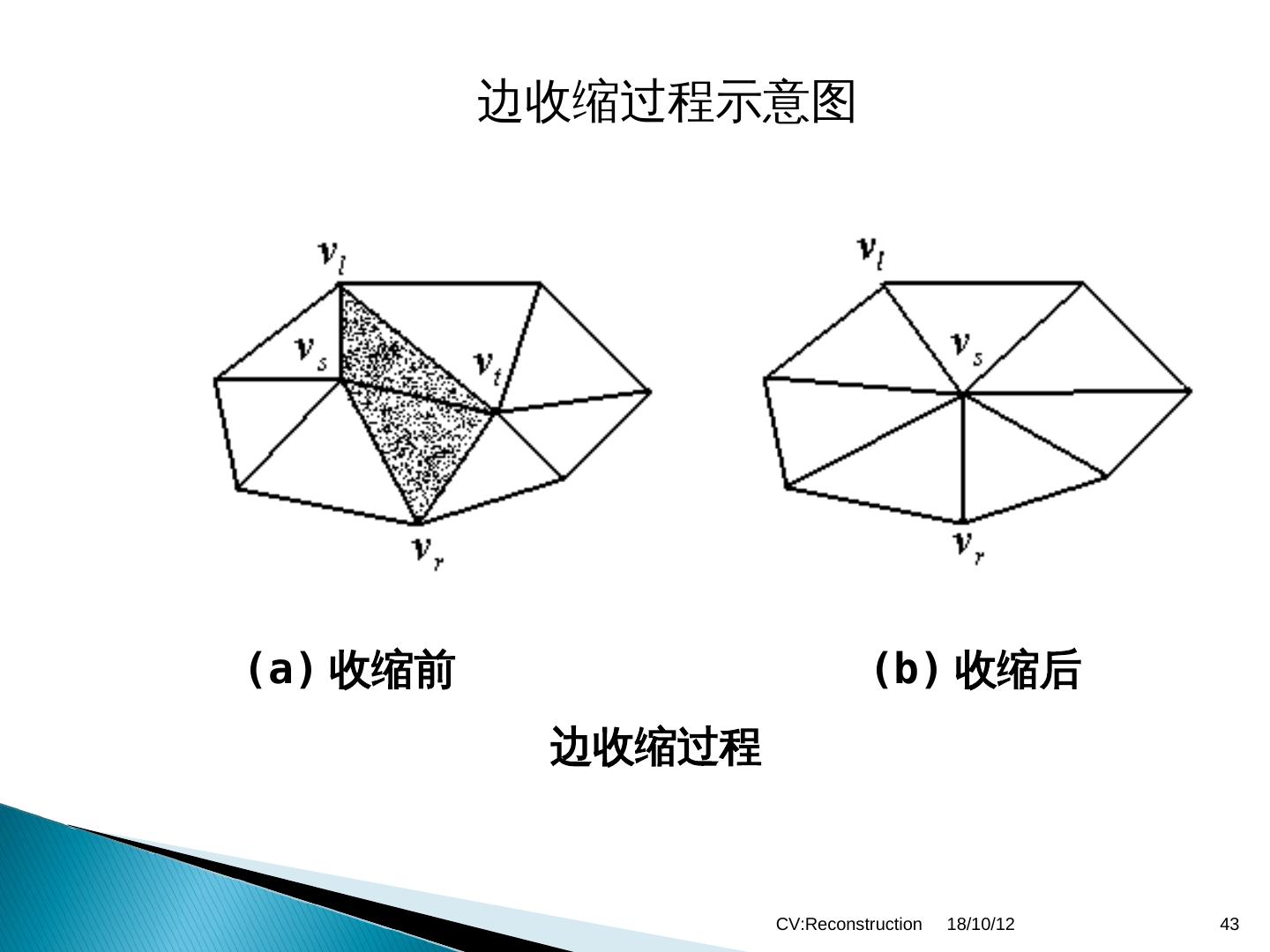
三维重建
展开查看详情
1 .Chapter 11 3D Reconstruction
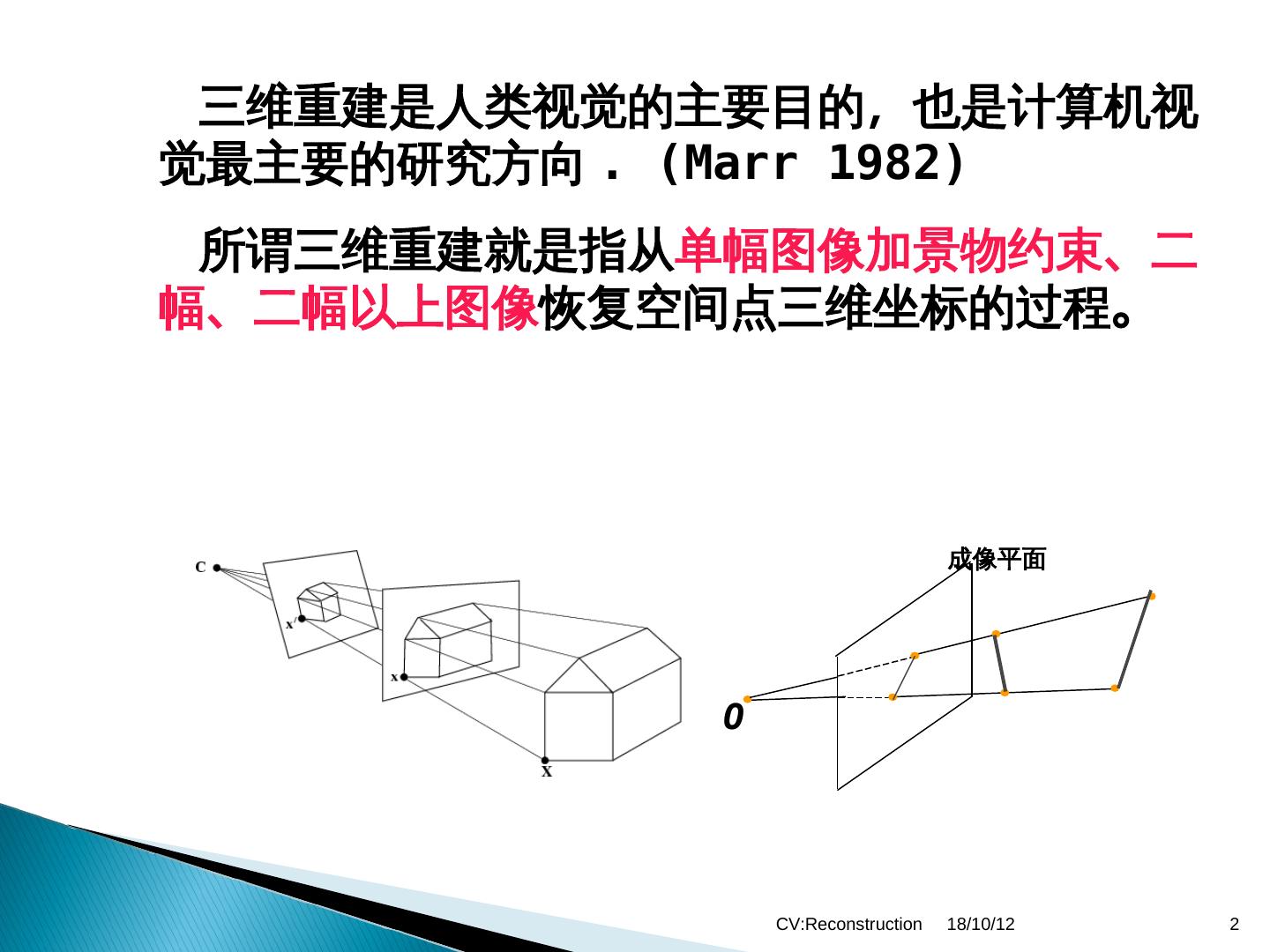
2 . 三维重建是人类视觉的主要目的,也是计算机视 觉最主要的研究方向 . (Marr 1982)Marr 1982)) 所谓三维重建就是指从单幅图像加景物约束、二 幅、二幅以上图像恢复空间点三维坐标的过程。 成像平面 O CV:Reconstruction 18/10/12 2
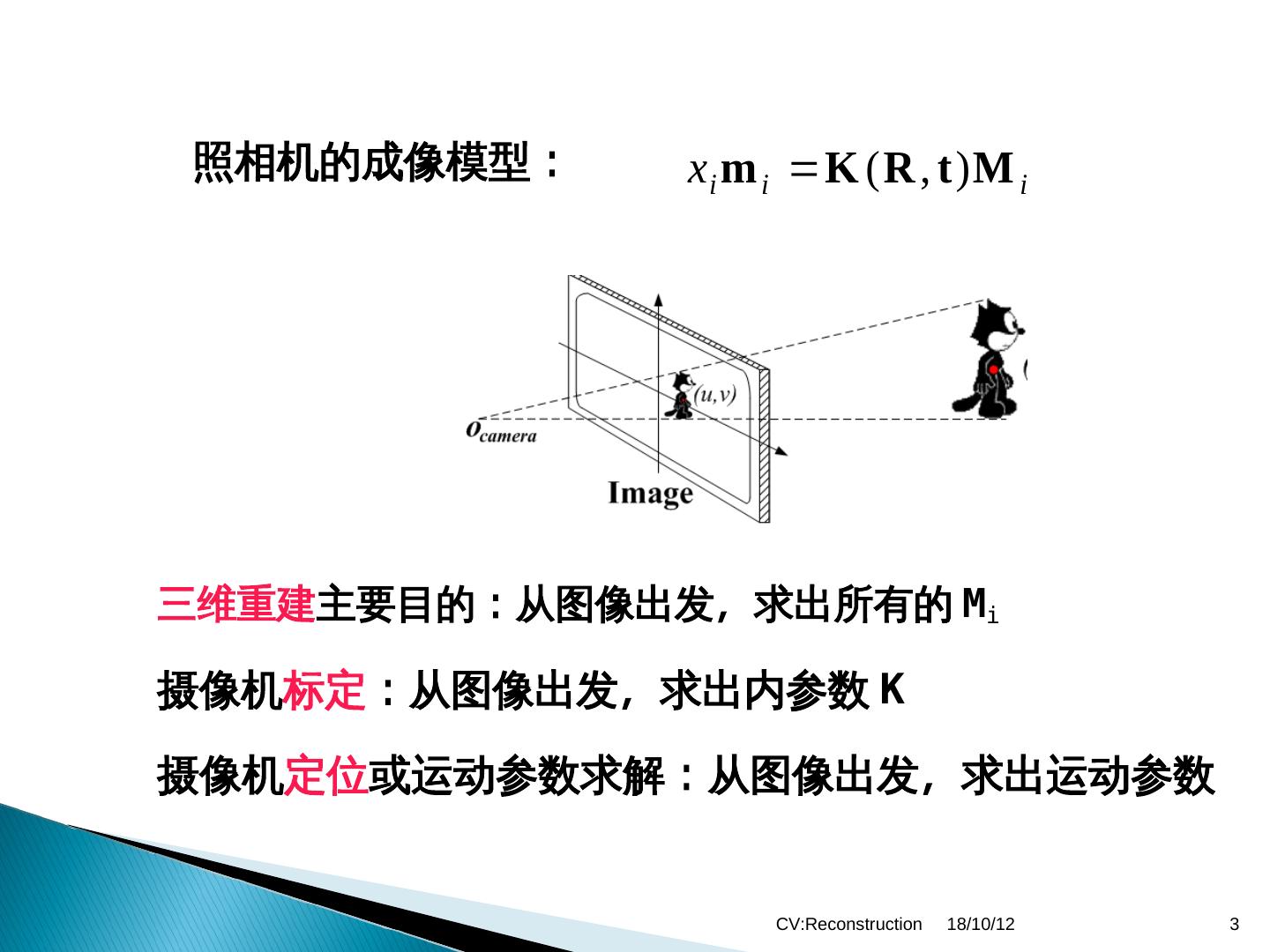
3 .照相机的成像模型: xi m i K ( R , t ) Μ i 三维重建主要目的:从图像出发,求出所有的 Mi 摄像机标定:从图像出发,求出内参数 K 摄像机定位或运动参数求解:从图像出发,求出运动参数 CV:Reconstruction 18/10/12 3
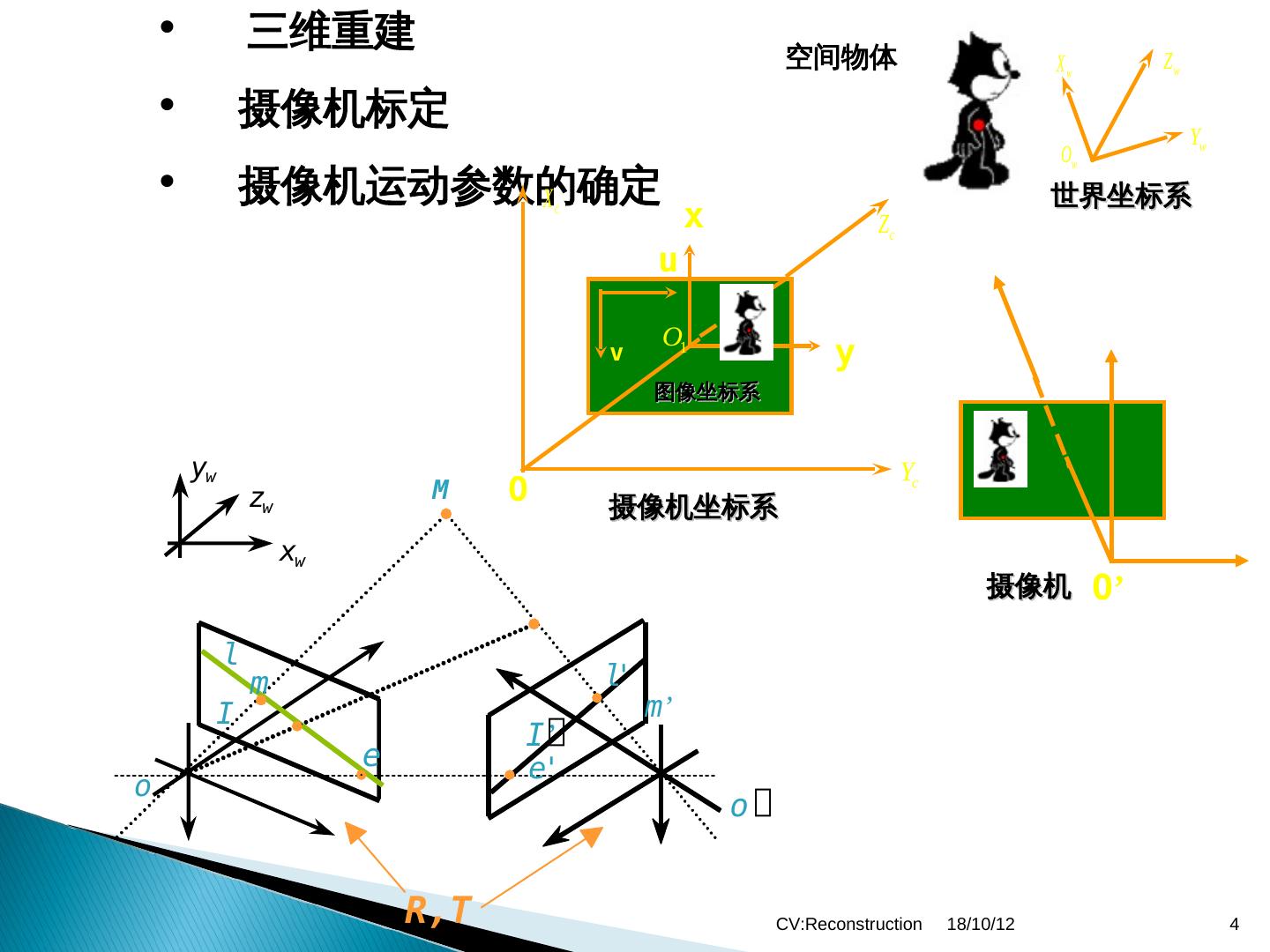
4 . • 三维重建 空间物体 Xw Zw • 摄像机标定 Yw Ow • 摄像机运动参数的确定 X 世界坐标系 c x Zc u O1 v y 图像坐标系 yw Yc zw M O 摄像机坐标系 xw 摄像机 O’ l m l' I m’ I’ e e' o o R,T CV:Reconstruction 18/10/12 4
5 . 深度测量 (measurement)measurement)) 获取物体 (measurement)object)) 或场景 (measurement)scene) 的深度 信息 主动传感器 (measurement)act)ive sensor)->range range dat)a 被动传感器 (measurement)passive sensor)->range image 三维建模 (measurement)modeling) 形成物体 (measurement)object)) 或场景 (measurement)scene) 的三维 三维场景 场景 点云 表示 深度测量 三维建模 poin t clou d CV:Reconstruction 18/10/12 5
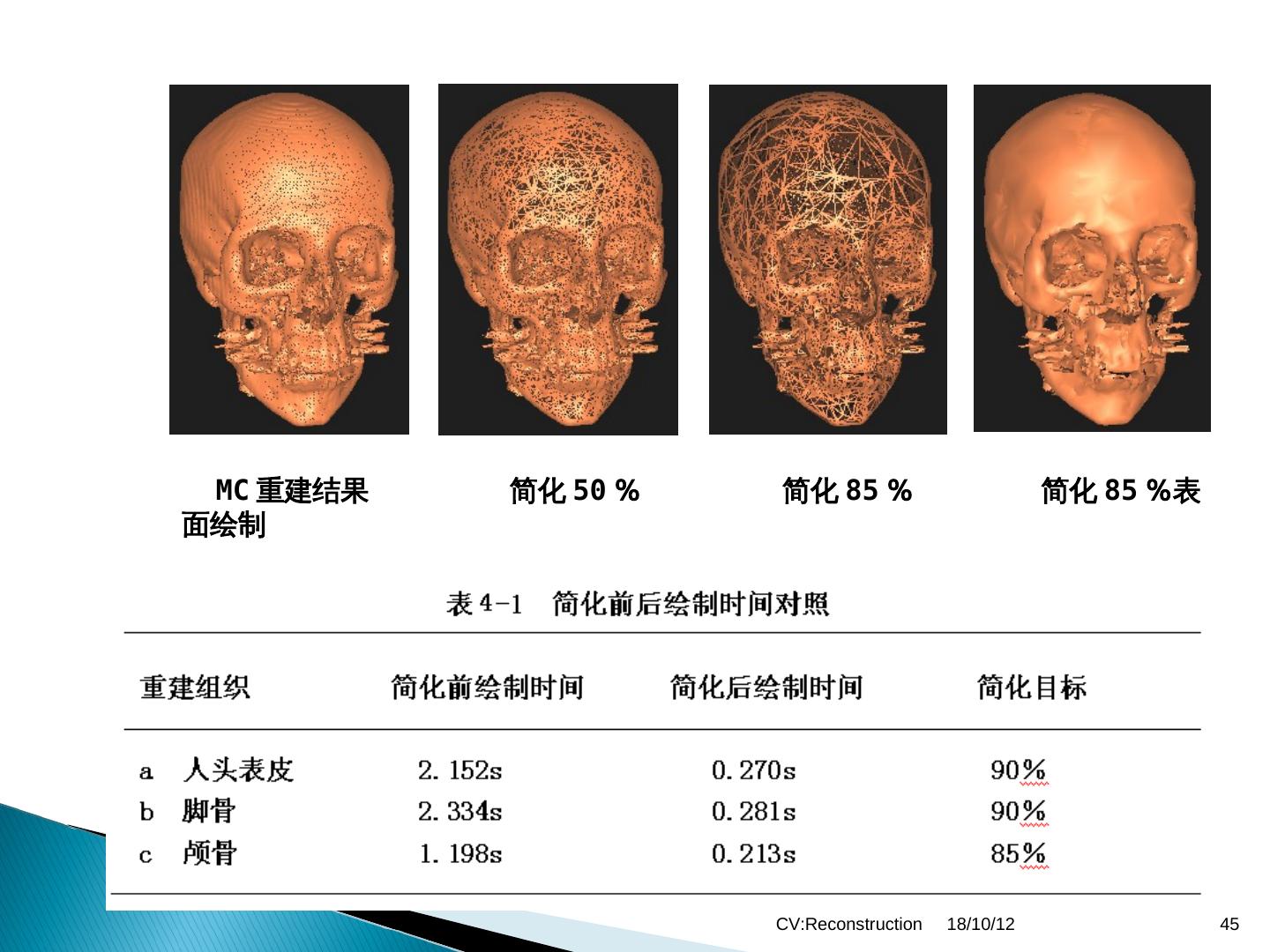
6 . 表面重建 通过几何单元拼接拟合物体表面来描述物体的 三维结构 基于深度图的表面重建 基于三维密度图的表面重建 体重建 直接将体像素以一定的颜色和透明度投影到显 示平面 CV:Reconstruction 18/10/12 6
7 . Connected Set of Polygons (Usually Triangles) ◦ May not be closed 7
8 . Coarse Mesh & Subdivision Rule ◦ Define smooth surface as limit of sequence of refinements 8
9 . Tensor Product Spline Patches ◦ Careful constraints to maintain continuity 9
10 . Points satisfying: F(x,y,z) = 0 Polygonal Model Implicit Model 10
11 . 用平面多边形(也称平面片, planar pat)ch) 组成多边形网面模型( polygon mesh mode l ),表示物体三维形状. CV:Reconstruction 18/10/12 11
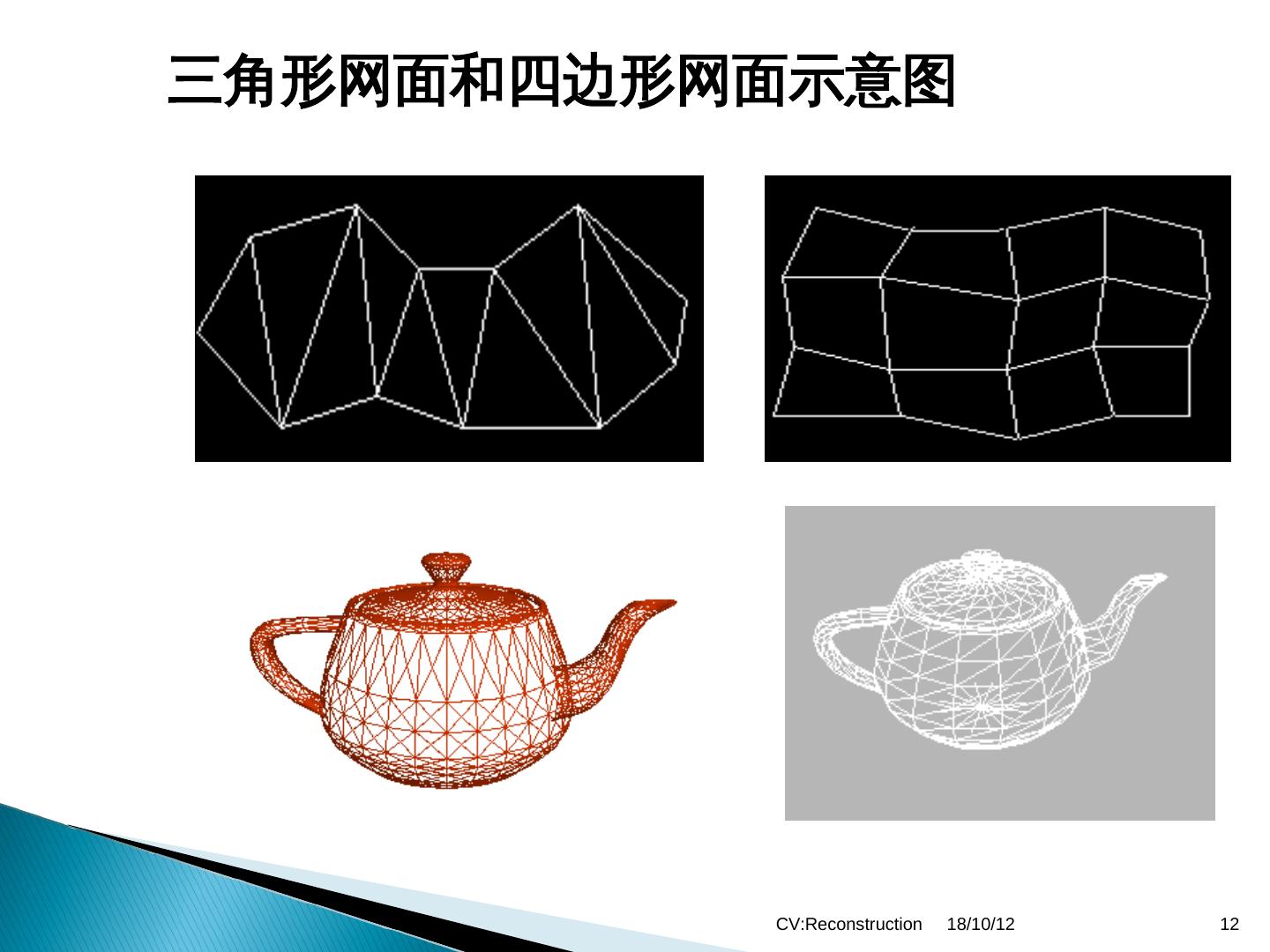
12 .三角形网面和四边形网面示意图 CV:Reconstruction 18/10/12 12
13 . 顶点坐标表示 各个平面表示为顶点三维坐标的集合 问题:顶点重复出现. 顶点序列表示 顶点按序编号,平面中顶点用编号表示 问题:边重复出现,且不能明显表示相邻平面 的边界. CV:Reconstruction 18/10/12 13
14 . 多边形表表示 CV:Reconstruction 18/10/12 14
15 .多边形网面表例 CV:Reconstruction 18/10/12 15
16 . 用双多项式表示曲面 平面: z=a0+a1x+a2y 双线性曲面片: z=a0+a1x+a2y+a3xy 双二次曲面片: z=a0+a1x+a2y+a3xy+a4x2+a5y2 双三次曲面片: z=a0+a1x+a2y+a3xy+a4x2+a5y2 +a6x3+a7x2y+a8xy2+a9y3 双四次曲面片: z=a0+a1x+a2y+a3xy+a4x2+a5y2 +a6x3+a7x2y+a8xy2+a9y3 +a10x4+a11x3y+a12x2y2+a13xy3+a14y4 CV:Reconstruction 18/10/12 16
17 . 1.3 张量积曲面 • 复杂曲面的参数多项式 a 0 v 3 a 2 p(u , v) u 3 u 2 u 1 1 b 0 b1 b 2 b 3 a 2 v v a 3 1 张量积曲面由两条曲线合成,可以认为是两曲 线的积:一条曲线以 u 为坐标,另一条以 v 为坐标 .任何平行于坐标轴的平面和张量积三次多项式曲 面的交线都是三次多项式曲线. p(u , v) U T MV 18/10/12 CV:Reconstruction 17
18 .1.4 超二次曲面 具有参数的二次多项式,通过调整参数可以改变物 体的形状 s 2 x 2 2 y s2 s1 2 z s1 例:超椭球 s2 ( ) ( ) ( ) 1 rx ry rz 18/10/12 CV:Reconstruction 18
19 . 2). 基于深度图的表面拟合 • 根据深度测量值获得连续表面 1. 表面插值 (Marr 1982)interpolation) 通过所有测量点 2). 表面逼近 (Marr 1982)approximation) 不一定包含,但尽可能接近测量 点 回归 (Marr 1982)regression) CV:Reconstruction 18/10/12 19
20 . 2).1 三角形面插值 1. 对于图像中一点( i,j ),计算其图像 平 m 1 n 1 面坐标: xj j y i i 2 2 2). 获得深度图中包含该点的三个非共线的 点 3. 计算三点所对应的平面 4. 确定( i,j z ij )在该平面上的深度值 a 0 a1 x j a 2 y i 18/10/12 CV:Reconstruction 20
21 . 实数域上的三角剖分 定义 1 :假设 V 是二维实数域上的有限点集,边 e 是由点集中的点 作为端点构成的封闭线段 , E 为 e 的集合。那么该点集 V 的一个三角 剖分 T=(V,E) 是一个平面图 G ,该平面图满足条件: 1. 除了端点,平面图中的边不包含点集中的任何点。 2. 没有相交边。 3. 平面图中所有的面都是三角面,且所有三角面的合集就是点集 V 的凸包 Delaunay 边 定义 2 :假设 E 中的一条边 e (两个端点为 a,b ), e 若满足下列 条件,则称之为 Delaunay 边: 存在一个圆经过 a,b 两点,圆内不含点集 V 中任何的点,这一特性 又称空圆特性。 Delaunay 三角剖分 定义 3 :如果点集 V 的一个三角剖分 T 只包含 Delaunay 边,那么 该三角剖分称为 Delaunay 三角剖分。 CV:Reconstruction 18/10/12 21
22 . Delaunay 三角剖分,由于其 独特性,关于点集的很多种几何 图都和 Delaunay 三角剖分相 关,如 Voronoi 图, EMST 树, Gabriel 图等 . Delaunay 三角剖分有几个很 好的特性: 1. 最大化最小角,“最接近于规 则化的“的三角网 . 2. 唯一性(任意四点不能共 圆) . Delaunay 三角剖分的不足 : 在低纬空间下数据量较小时更有 效. 18/10/12 CV:Reconstruction 22
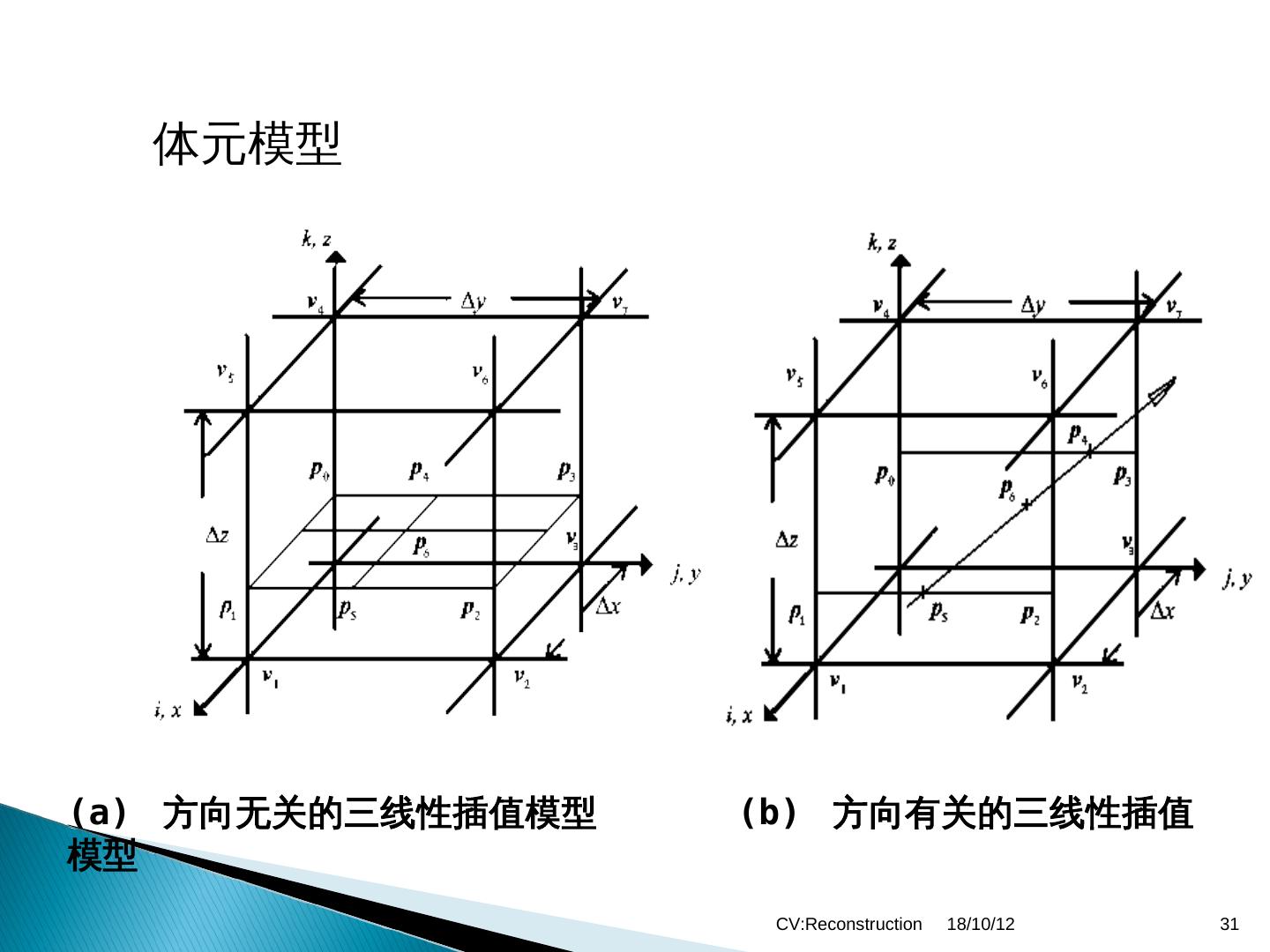
23 .2).2) 线性插值 • 用二元线性函数对曲面片建模 f(Marr 1982)x,y)=a0+a1x+a2)y+a3xy • 用矩形四个顶点计算系数,代入获得深度值 18/10/12 CV:Reconstruction 23
24 .把每一个顶点的坐标代入 z 00 a 0 a1 x 0 a 2 y 0 a3 x 0 y 0 z 01 a 0 a1 x 0 a 2 y1 a 3 x 0 y1 z10 a 0 a1 x1 a 2 y 0 a 3 x1 y 0 z11 a 0 a1 x1 a 2 y1 a3 x1 y1 联立上述四个方程,得到系数求解出: x1 y1 z 00 x1 y 0 z 01 x 0 y1 z10 x 0 y 0 z11 a0 ( x1 x 0 )( y1 y 0 ) y1 z 00 y 0 z 01 y1 z10 y 0 z11 a1 ( x1 x 0 )( y1 y 0 ) x1 z 00 x1 z 01 x0 z10 x 0 z11 a2 ( x1 x 0 )( y1 y 0 ) z 00 z 01 z10 z11 a3 ( x1 x0 )( y1 y 0 ) CV:Reconstruction 18/10/12 24
25 . 2).3 鲁棒插值 最小中值二乘回归 • 用最小中值二乘准则和重采样策略实现 鲁棒回归 arg min { med [( zi f ( xi , yi ; a)) 2 ]} a ( xi , yi )N 1. 取距离当前点最近的 n 个点 m 2). C 在 n 个点中任取 m 个点,共 n 种组合 3. 对每一个组合,作最小中值二乘回归 4. 取各个组合中对应最小平方中值的解 18/10/12 CV:Reconstruction 25
26 . 由于深度测量值存在误差,因此找一个曲面来逼近 深度数据比曲面插值更重要. 设重建曲面的模型为: z f ( x, y; a 0 , a1 , , a m 1 ) 该曲面重建问题实际上成为确定最适合数据的曲面 模型参数的回归问题,回归函数为: n 1 2 ( z i f ( xi , y i ; a0 , a1 ,, a m 1 )) 2 i 0 CV:Reconstruction 18/10/12 26
27 . 不适定 (measurement)ill-posed) 问题,因为许多函数可以 对该数据集实现最佳拟合 可以增加一个逼近约束函数,使得所选择的曲面 拟合函数有唯一解. n 1 2 f f f 2 f ( z i f ( xi , y i )) ( 2 2 2 2 2 2 )dxdy i 0 x x y y 上面方程的第一个项称为问题约束,第二项是加 权光滑约束项,叫做正则项或稳定函数。 在问题约束上通过增加稳定函数将不适定问题变 为适定问题的过程叫正则化 ( regularizat)ion ). CV:Reconstruction 18/10/12 27
28 . 2.4.2 回归样条 • 用张量积 B 样条对表面建模 m 1 n 1 m 1 n 1 f ( x, y ) aij Bij ( x, y ) aij B j ( x) Bi ( y ) i 0 j 0 i 0 j 0 • 用最小二乘法求解回归问题 N1 N1 m 1 n 1 2 ( z (k ) f ( x, y )) 2 [ z (k ) ( aij Bij ( x, y )] 2 k 0 k 0 i 0 j 0 CV:Reconstruction 18/10/12 28
29 . 回归样条 • 计算方法 1. 张量积基函数 Bij ( x, y ) B j ( x) Bi ( y ) 2). 每一个测量点对应一个包含 16 个系数(三次 B 样条)的方程 3. 用最小二乘法解线性方程组得所有系数 CV:Reconstruction 18/10/12 29