单幅图像深度重建:基于纹理的深度图重建

1 .9.4 基于纹理的深度图重建 

2 .包含多个纹理区域的图像 

3 . beeren flower 彩色纹理图像 food water 

4 . 1 纹理（ Texture ）  目前对于纹理的精确定义还未形成统一认识， 多根据应用需要做出不同定义．  两种较常采用的定义： 定义 1 按一定规则对元素（ elements ） 或基元（ primitives ）进行排列所形成的重复 模式 . 定义 2 如果图像函数的一组局部属性是恒 定的，或者是缓变的，或者是近似周期性的， 则图像中的对应区域具有恒定的纹理． 

5 . 纹理（ Texture ）  纹理的基本特征 纹理是区域属性，并且与图像分辨率（或 称尺度， resolution or scale ）密切相 关 重复性 规则性 周期性 方向性 

6 . 空域滤波  局部模板法 设计一组具有频率选择性的模板，与 图像做卷积 .  局部矩法 以每一个像素为中心，计算局部窗口 内的矩特征值，形成特征图像 . 相当于 用一组模板对图像进行滤波 . 

7 . 空域滤波  The filter bank used in texture analysis. Total of 48 filters: 36 oriented filters, with 6 orientations, 3 scales, and 2 phases, 8 center-surround derivative filters and 4 low-pass Gaussian filters. 

8 . Gabor 变换与小波变换  Gabor 变换（高斯窗口）  Fw  u, b   f  x  w x  b e  j 2ux dx  (D. Gabor, 1946) • 小波变换： 窗口宽度随频率变化而变化 1   x b W f ,a  u, b    f  xh   dx a   a  

9 . Gabor 变换纹理特征  二维 Gabor 滤波器具有频率和方向选择 性  Gabor 纹理特征提取的一般步骤： 1. 用不同尺度和方向的 Gabor 滤波器对图 像进行滤波，得到一组子图像； 2. 对各个子图像做一定处理； 3. 根据子图像计算相应特征，形成特征矢 量或特征图像，比如子图像窗口内的标准差 . 

10 .Gabor 变换纹 理特征示例： (a) 纹理图像 (b) 滤波图像 (16,135 度) (c) 滤波图像 (32,0 度) (d) 特征图像 (b) 

11 . 小波变换纹理特征 • 对图像作小波变换 ， 分别得到水平和垂 直方向上的高频和低频 子图像，可以对低频子 图像或每个子图像再作 同样的变换 . 根据最 后得到的每个子图像计 算一个特征，如能量， 墒等，形成纹理特征矢 量. 

12 . Markov 随机场  图像建模的重要工具，应用广泛． (J. Besag, 1974)  预备知识（标注问题， labeling ） 位 (site) 集合： S 1,2,, m 标志 (label) 集合，位上可能发生事件 的集合，可以是连续的，也可以是离散的 ： Lc [ X l , X h ]  R ， Ld [l1 , l 2 ,  , l n ] 

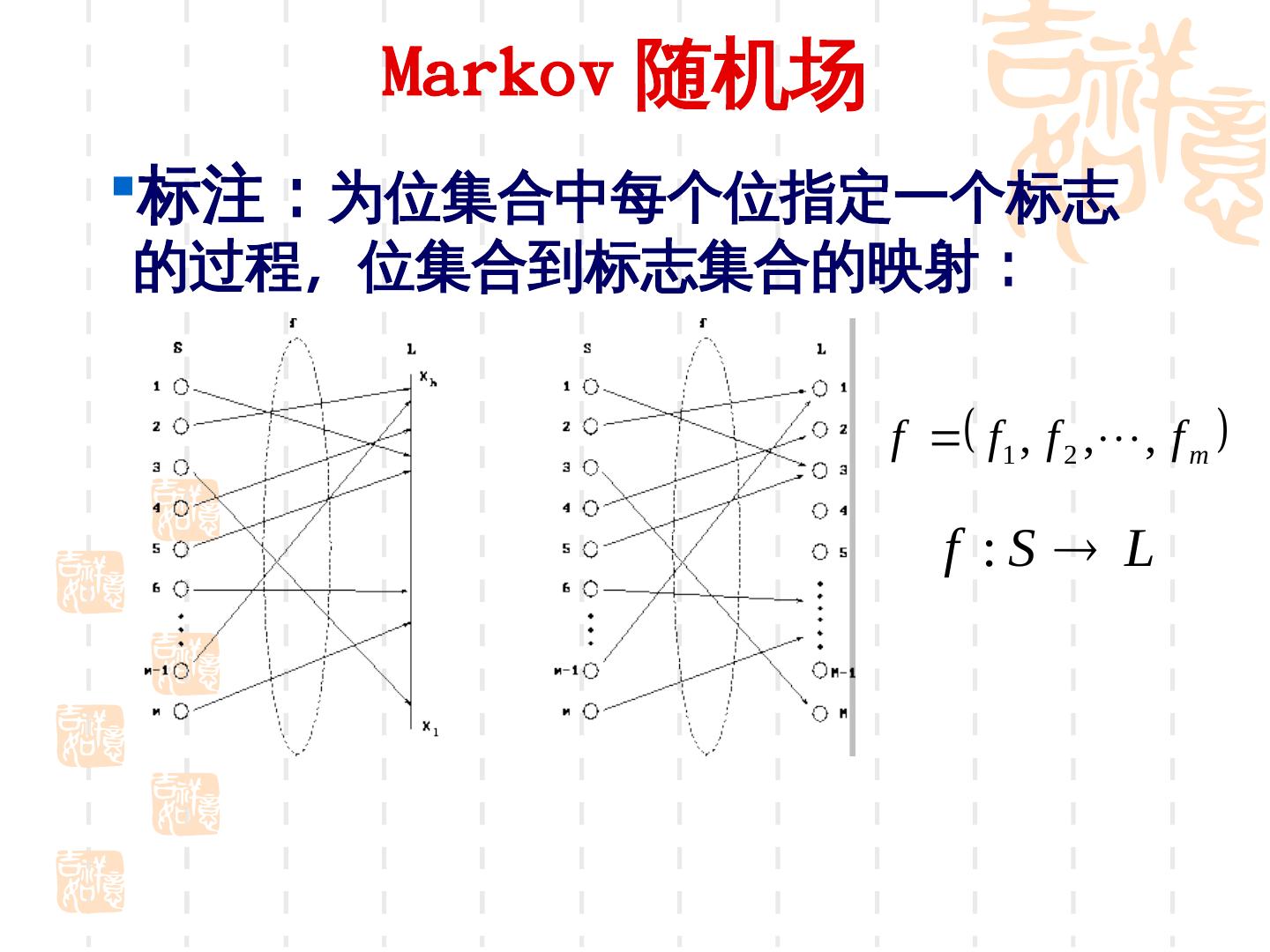
13 . Markov 随机场 标注：为位集合中每个位指定一个标志 的过程，位集合到标志集合的映射： f  f 1 , f 2 ,  , f m  f :S  L 

14 . Markov 随机场  标注：从如下 空间中导出 F 的过程： f m F L1 L2  Lm , 当L1  L2   Lm 时， F  L 在图象领域，可将 f 理解为一幅图象， F 则 是全部可允许图像的集合 . •标注也被称为着色 (coloring ，数学规 划 ) 或配置 (configuration ，随机场 ) •如果各个位为随机变量，则位集合 S 称为随机场 . 

15 . Markov 随机场  在随机场中，从 导出F 的过程就是确定 f 出现的概率 . f  假设各个位的标注是彼此无关的，则有 P ( f )  P  f i  ， P ( f i  f i   )  P  f i  只需单独考虑每个位，问题简单（理想） • 实际应用时，需要考虑上下文约束 (contextual constraints) Markov 随机 场 

16 . Markov 随机场  当且仅当以下两个条件满足时，随 机场为 Markov 随机场： P f   0 正性（ Positivity ）    P f i f S   i  P f i f Ni  Markov 性 (Markovianity) •若 fi 能够独立发生，那么 f 就能够发生 •一个像素点的随机概率只与它邻域的像 素有关 

17 .根据矩阵中各位置与位置 i 的距离，可以将邻域系统表 达为等级形式 邻域系统的等级划分 一个象素点和图像中其他各象素点的相关性就可以通过条 件概率和邻域系统来描述 

18 . Gibbs 随机场  邻域系统 (neighboring system) 邻域集 (neighbor set) ： 一阶邻域（四连通），二阶邻域（八连通）等 团 (cliques) ： 由邻域关系限定的位子集 单位团 (single-site) ，双位团 (pair- site) ，三位团 (triple-site) 等 C1  i , C2   i, i  , C3   i, i, i  , i, i, i互为邻居 团是有序的 : i, i   i , i 

19 . Gibbs 随机场  邻域 团 团具有尺寸 , 形状和方向 

20 . Gibbs 随机场  当且仅当随机场的配置服从 Gibbs 分布时 ，称为 Gibbs 随机场 : 1 1  TU f  T ：温度常量，常取 1 P f   e z 1  U f  规范化常量，称为划分函数 Z  e T f F （ partition function ） U  f    Vc  f  所有团势能之和，称为能量函 cC 数 (energy function) Vc  f  ：团势能 (clique potential) 

21 . Gibbs 随机场  物理意义 配置的能量越小，其概率越大  均匀性 (homogeneity) ： Vc  f  与团在随机场中的位置无关   或者说，P f i f N i 与位 i 无 关 • 各向同性 (isotropic) ： Vc  f  与团的方向无关 • 在纹理领域， Markov(Gibbs) 随机场 具 有均匀性 

22 . Gibbs 随机场  Hammersley-Clifford 定理 Markov 随机场与 Gibbs 随机场等价  意义： 既可以用局部成分的相互影响来建模，也可 以用全局能量来建模 .  如何确定团势能的形式和参数是 Markov(Gibbs) 随机场的主要工作 .  划分函数的计算复杂度很高，是一个难题 ，实际多做一定简化 . 

23 . 3 从纹理恢复形状  根据纹理属性变化与表面形状的关 系恢复表面形状 . • 三种效应： 透视缩小 ( 与表面方向有 关) 缩放和密度变化 ( 与观察 者 和纹理基元的距离有关 ) •基准维 (characteristic dimension) ： 没有发生透视缩小的方向 

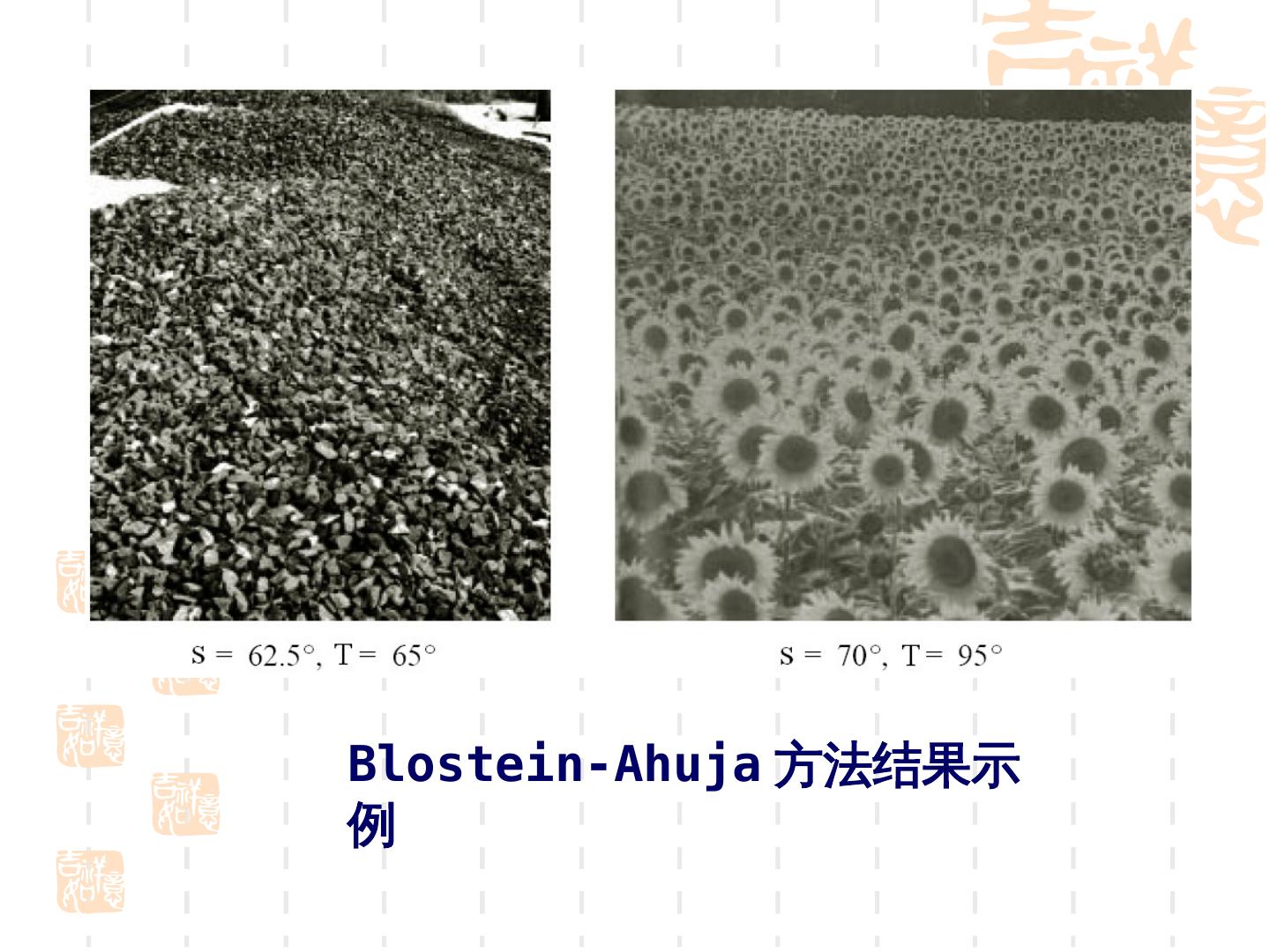
24 . 3. 从纹理恢复形状  几种方法 Bajcsy-Lieberman 方法：利用基元尺 寸梯度，求相对深度 ; Witken 方法：利用边缘方向分布，估 计表面方向 ; Blostein-Ahuja 方法：利用基元面积 梯度，估计表面方向 . 

25 .椭圆长短轴在缩小（缩放效应） 缩小速度长轴为线性，短轴为二次（透视缩小效 应，长轴方向为基准维） 

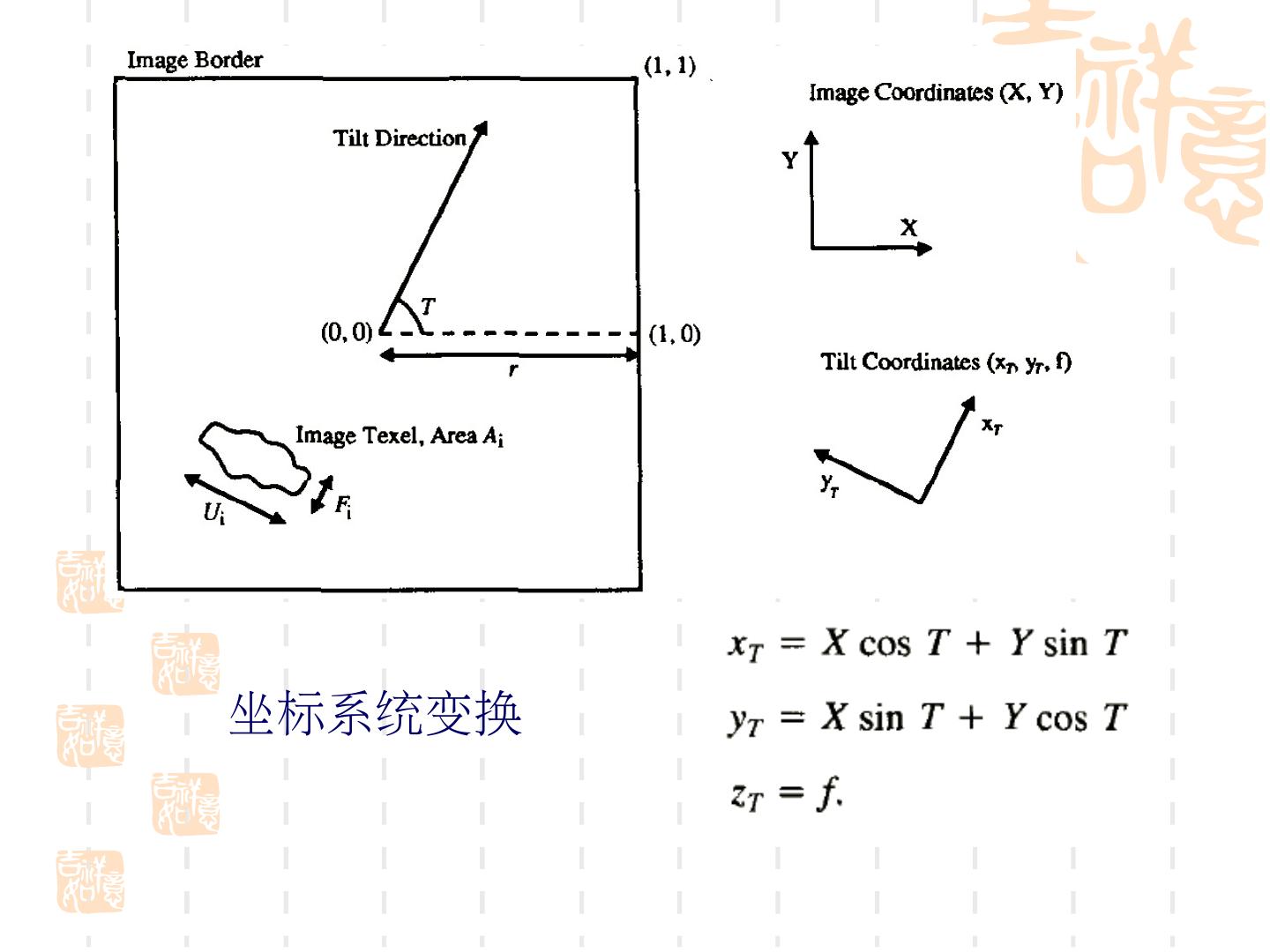
26 . Blostein-Ahuja 方法  假设表面为平面，纹理基元单一且无深度差  恢复公式（依据）的推导 1. 为简化推导，将坐标系统转换到 tilt 方向 2. 根据透视投影模型，建立任意基元长短轴 与中心基元长短轴的长度关系； 3. 将上述关系转化为任意基元与中心基元的 面积关系 . 

27 .坐标系统变换 

28 .透视投影模型 

29 . Blostein-Ahuja 方法  形成表面方向估计依据 → 为未知参数空间，根据纹理图像 从中搜索最佳结果： 将该空间离散化，对于每组值，计算图像中 各个位置上的纹理基元面积，与实际面积比较，获 得拟合度，取最佳拟合度对应的结果 . ( 表面拟 合)