单幅图像深度重建:基于单眼线索的深度重建——灭点和散焦

1 .9.2 基于灭点几何的深度图重建 Vanishing Point (Line) 

2 .从 2DD 图像进入 3DD 世界 

3 .• 基于灭点几何的 深度图重建方法 适用于结构化环 境下 . • 将场景模化为一 系列平面的集合 

4 .基础知识 : 射影几何 Ames Room 

5 .观察这样一个现象 平行线交汇于一点 

6 . 投影平面 齐次坐标系 • 用于表示无穷远处的点，即消失点 • 消失点具有单应性 • 图像中的一个点对应于投影空间的一条射线 y (sx,sy,s) (x,y,1) (0,0,0) ) z x image plane • 图像平面上每个点 (x,y) 对应于一条射线 (sx,sy,s) – 射线上所有点在齐次坐标系下是等价的 : (x, y, 1) )  (sx, sy, s) 

7 . 直线的投影 图像中的一条直线对应于投影空间中的什么呢？ • 直线对应于一个通过初始直线的平面（由无数条射线构成） • 每条射线 (x,y,z) 满足 : ax + by + cz = 0  x in vector notation : 0  a b c   y   z  l p • 一条直线也可以表示为一个三维向量 l 

8 . 点与直线的二元性质 • 直线 l 是一个齐次的三维向量 • 它 于直线上的每个点（射线） p : l p=0 p1) p2 l1) p l l2 可以得出结论： • l  于 p1) 和 p2  l = p1)  p2 • l 是平面的法线 假设有两条直线 l1) and l2 ，其交点对应于平面内一点 P • p  于 l1) 和 l2  p = l1)  l2 所以，点和 直线在投影空间内具有二元性 

9 .理想的点和直线 (a,b,0) y (sx,sy,0) y z image plane z image plane x x 理想点 (“ 无穷远处的点” ) • p  (x, y, 0) – 平行于图像平面 • 坐标无穷大 理想直线 • l  (a, b, 0) – 平行于图像平面 • 对应于图像中的一条直线 ( 坐标空间有限 ) 

10 . 消失点 image plane vanishing point camera center ground plane 消失点 • 无穷远点在图像平面上的投影 • 由理想直线引起 

11 . 消失点（ 2D ） image plane vanishing point camera center line on ground plane 

12 . 消失点 image plane vanishing point V camera center C line on ground plane line on ground plane 性质 • 两条平行线具有同一个消失点 • 由 C 点到 v 点的射线平行于地平面上的直线 • 一幅图像可能含有多个消失点 

13 . 消失线 v1 v2 多个消失点 • 平面上每组平行线定义一个消失点 • 所有消失点的集合构成地平线，也就是消失线 • 不同的平面定义了不同的消失线 

14 . 消失线 多个消失点 • 平面上每组平行线定义一个消失点 • 所有消失点的集合构成地平线，也就是消失线 • 不同的平面定义了不同的消失线 

15 .Computing vanishing points V P0 D P P0  tD  PX  tDX   PX / t  DX   DX  P  tDY   PY / t  DY  D  Pt  Y  t  P   Y   PZ  tDZ   PZ / t  DZ   DZ         1   1/ t   0  Properties v ΠPP • P is a point at infinity, v is its projection • They depend only on line direction • Parallel lines P0 + tD, P1 + tD intersect at P 

16 .Computing vanishing lines C l ground plane Properties • l is intersection of horizontal plane through C with image plane • Compute l from two sets of parallel lines on ground plane • All points at same height as C project to l – points higher than C project above l • Provides way of comparing height of objects in the scene 

17 .

18 .Fun with vanishing points 

19 .“Tour into the Picture” (SIGGRAPH ’97) Create a 3D “theatre stage” of five billboards Specify foreground objects through bounding polygons Use camera transformations to navigate through the scene 

20 .The idea Many scenes (especially paintings), can be represented as an axis-aligned box volume (i.e. a stage) Key assumptions: • All walls of volume are orthogonal • Camera view plane is parallel to back of volume • Camera up is normal to volume bottom How many vanishing points does the box have? • Three, but two at infinity • Single-point perspective Can use the vanishing point to fit the box to the particular Scene! 

21 .Fitting the box volume User controls the inner box and the vanishing point placement (# of DOF???) Q: What’s the significance of the vanishing point location? A: It’s at eye level: ray from COP to VP is perpendicular to image plane. Why? 

22 .Example of user input: vanishing point and back face of view volume are defined High Camera 

23 .Example of user input: vanishing point and back face of view volume are defined High Camera 

24 .Example of user input: vanishing point and back face of view volume are defined Low Camera 

25 .Example of user input: vanishing point and back face of view volume are defined Low Camera 

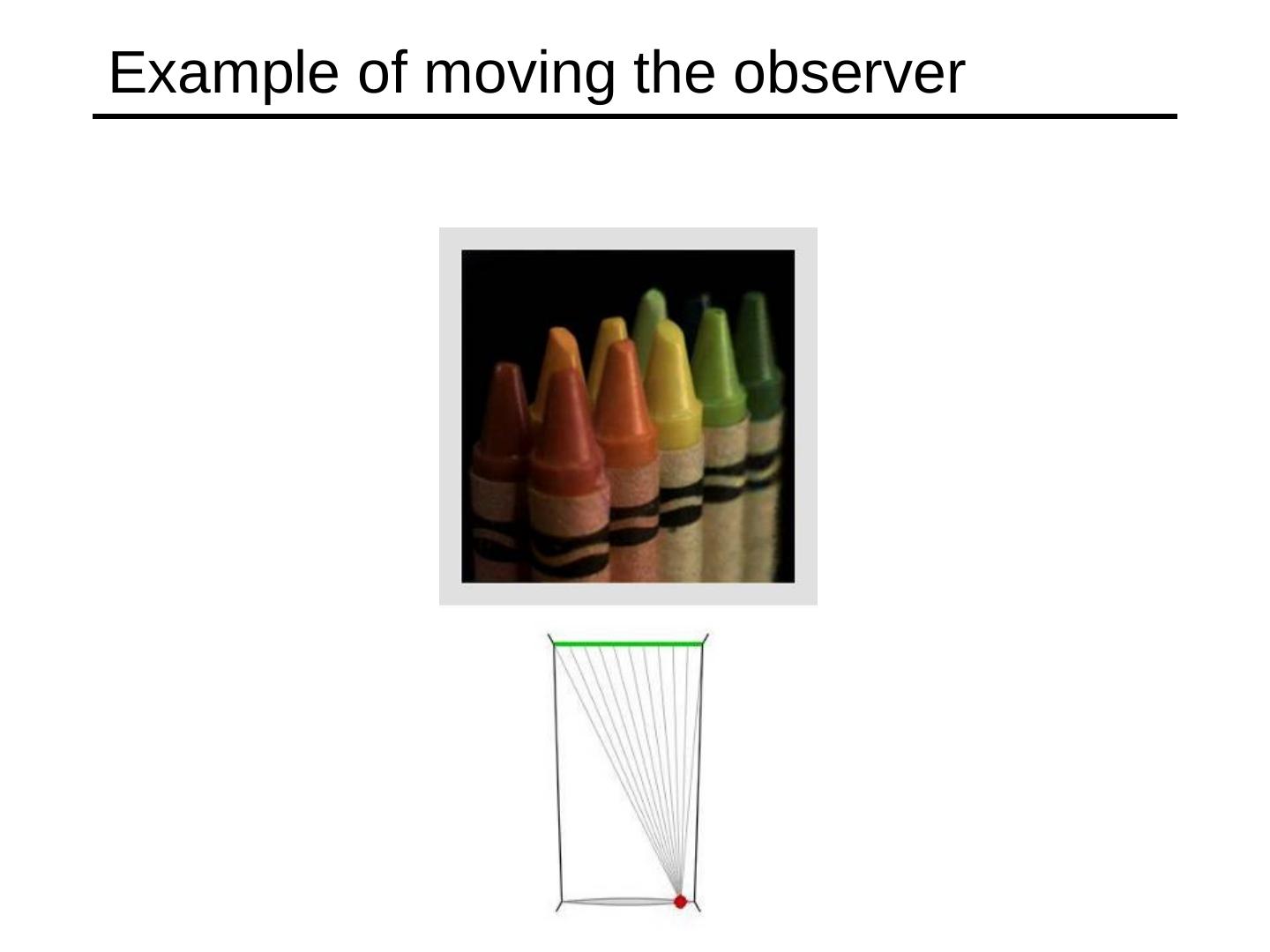
26 .Comparison of how image is subdivided based on two different camera positions. You should see how moving the vanishing point corresponds to moving the eyepoint in the 3D world. High Camera Low Camera 

27 .Another example of user input: vanishing point and back face of view volume are defined Left Camera 

28 .Another example of user input: vanishing point and back face of view volume are defined Left Camera 

29 .Another example of user input: vanishing point and back face of view volume are defined Right Camera