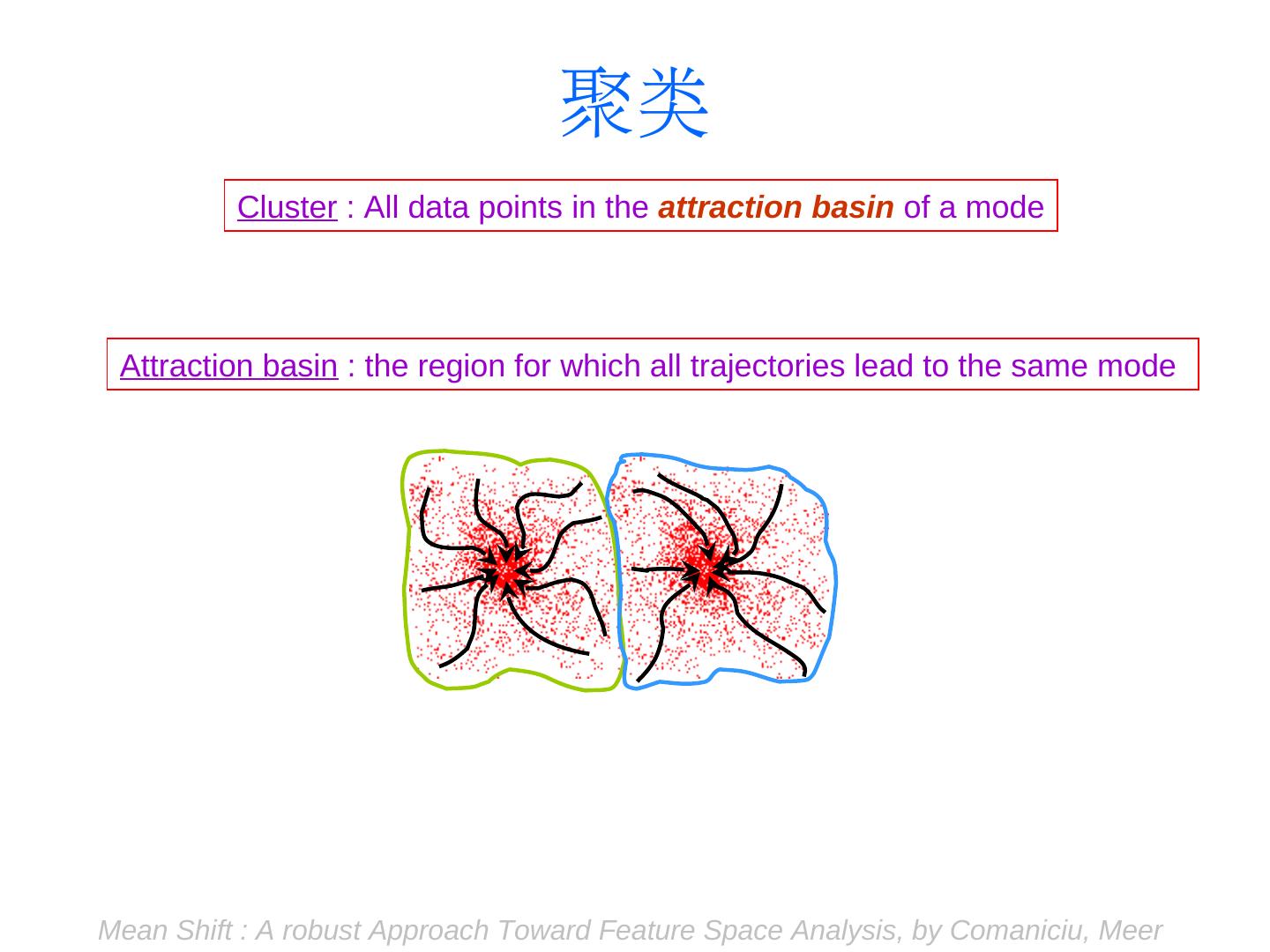
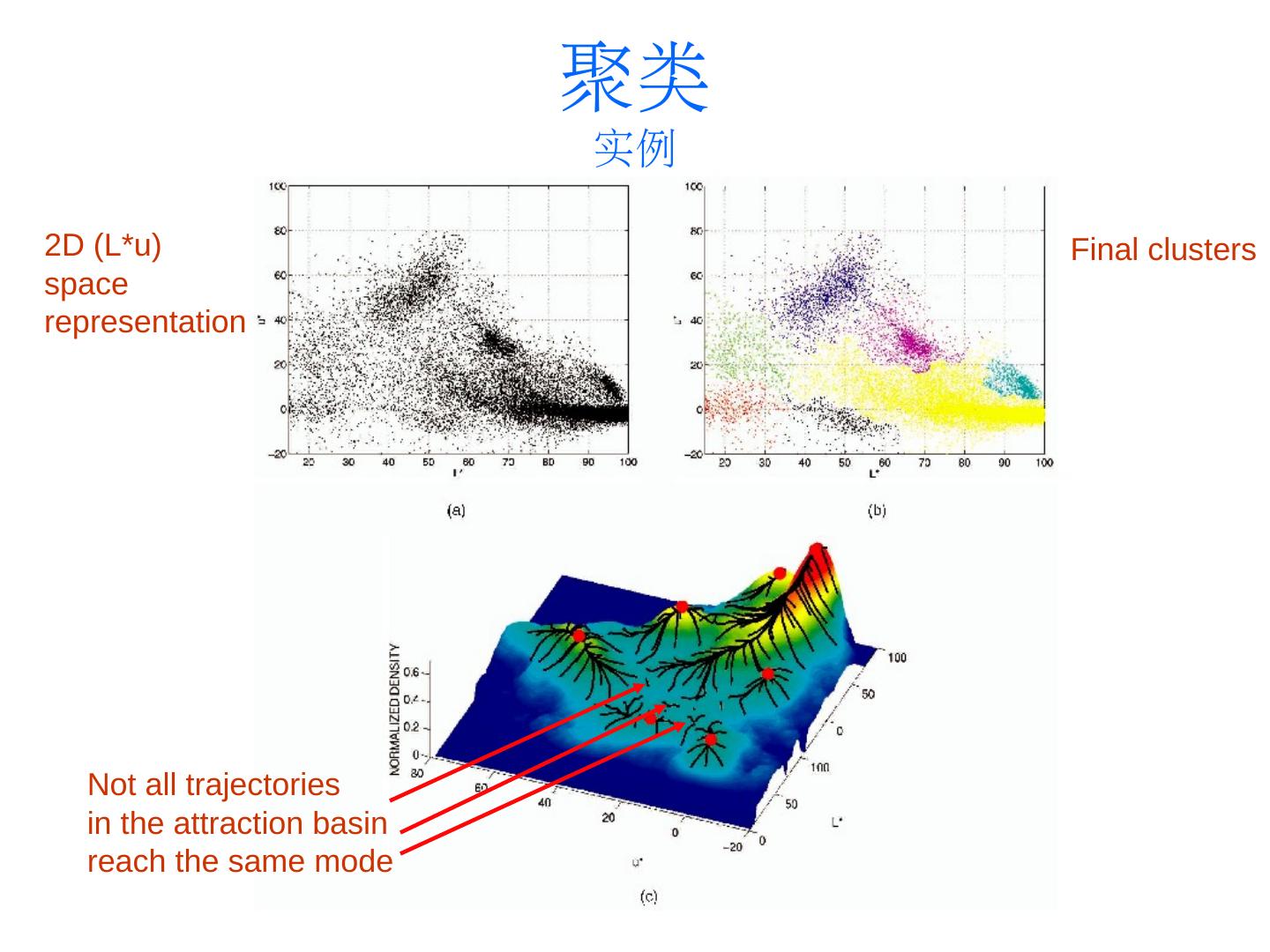
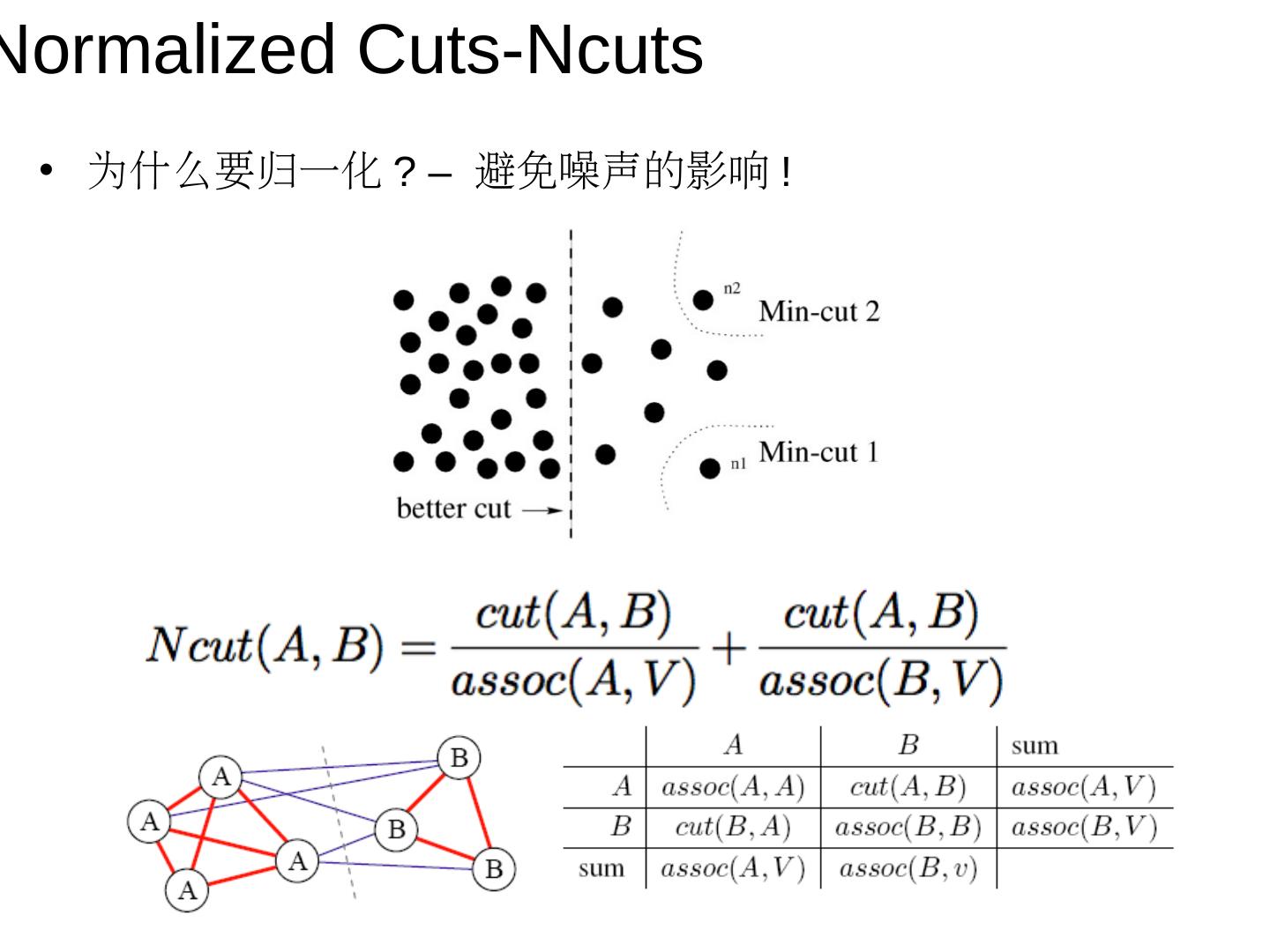
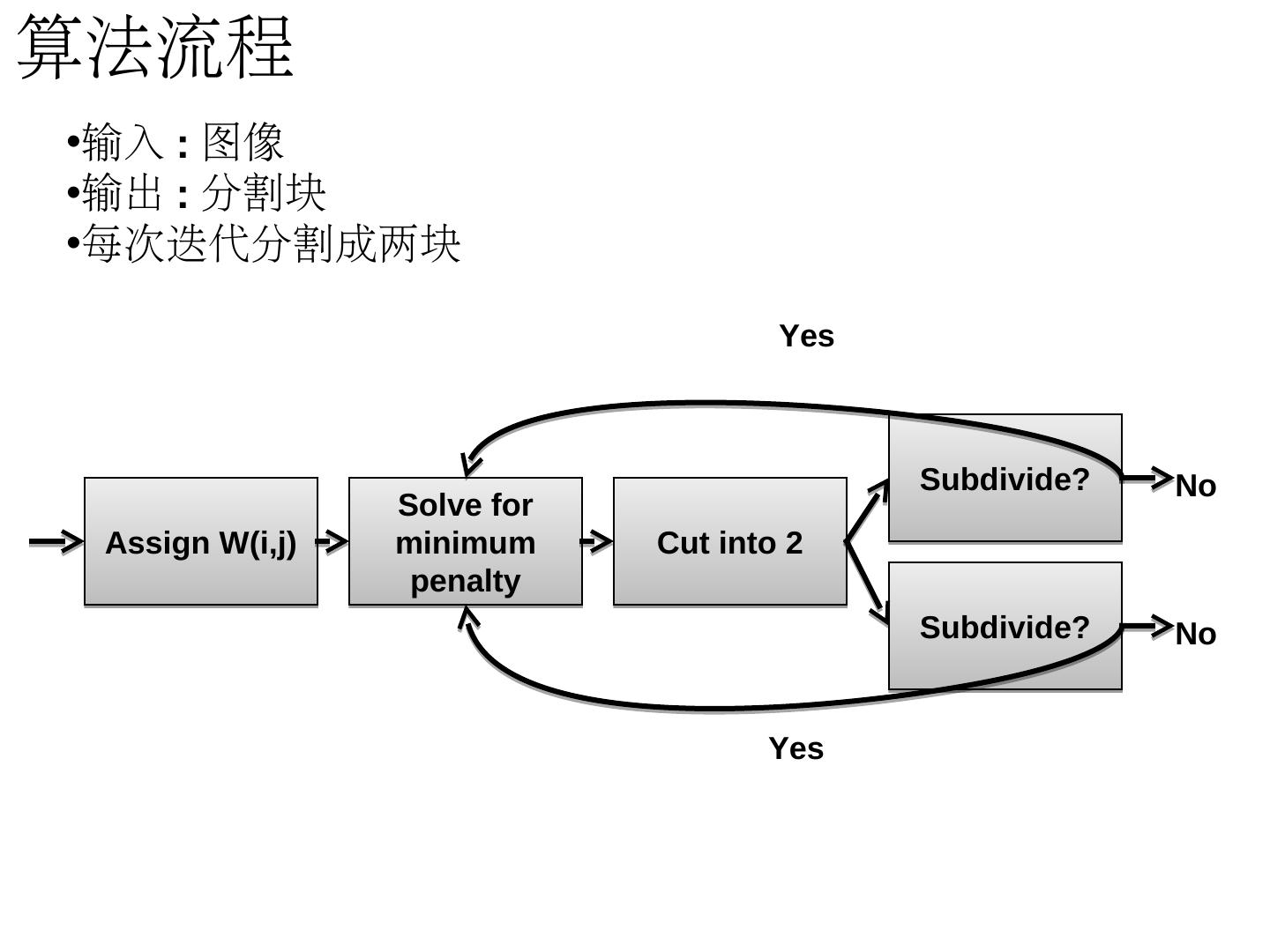
图像分割：Mean shift&Ncuts

1 .Mean Shift Segmentation Algorithm 

2 . 主要内容 • Mean Shift 理论 • What is Mean Shift ? • Density Estimation Methods • Deriving the Mean Shift • Mean shift properties • Mean Shift 的应用 • Clustering • Segmentation 

3 .Mean Shift 理论 

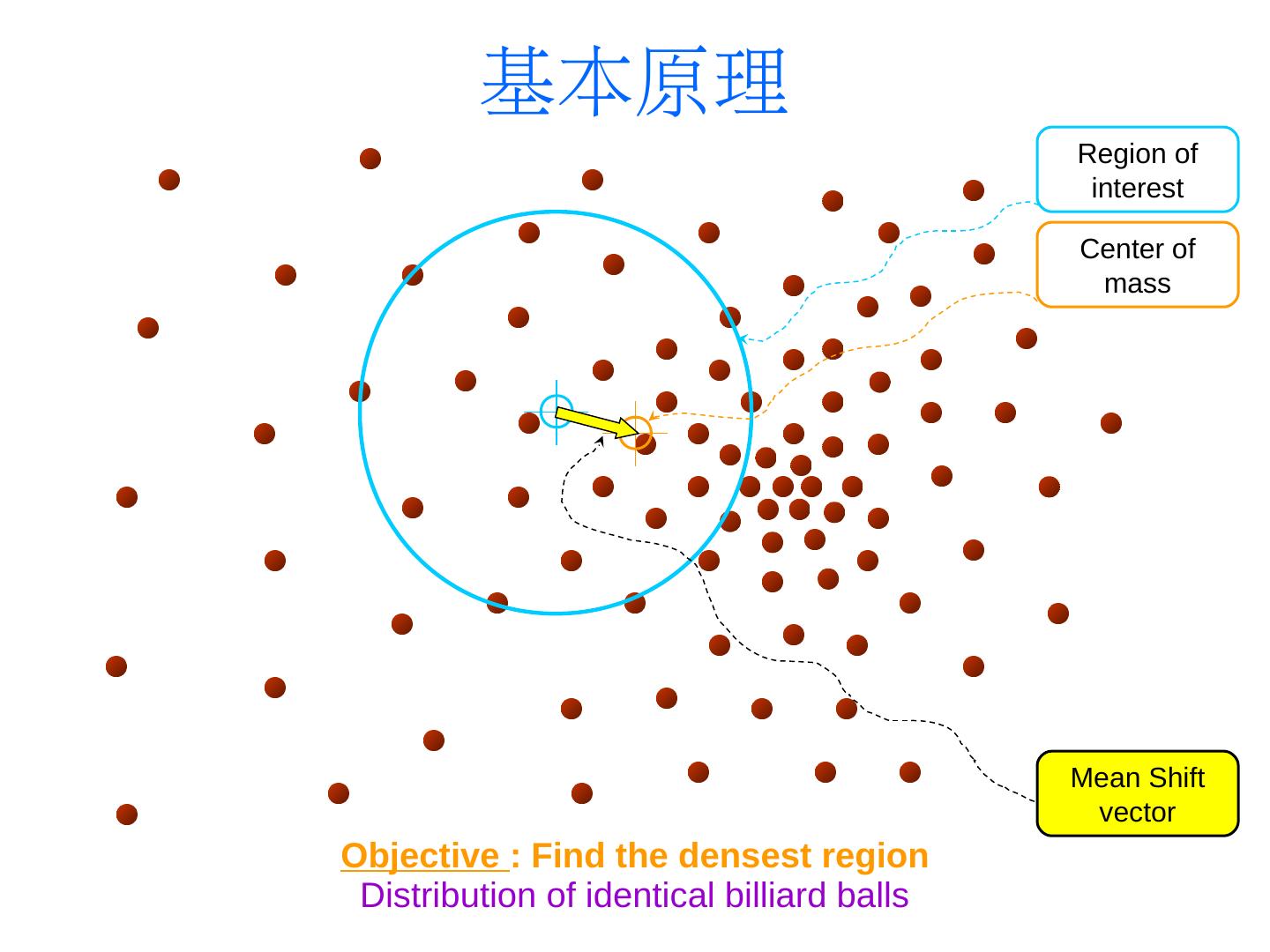
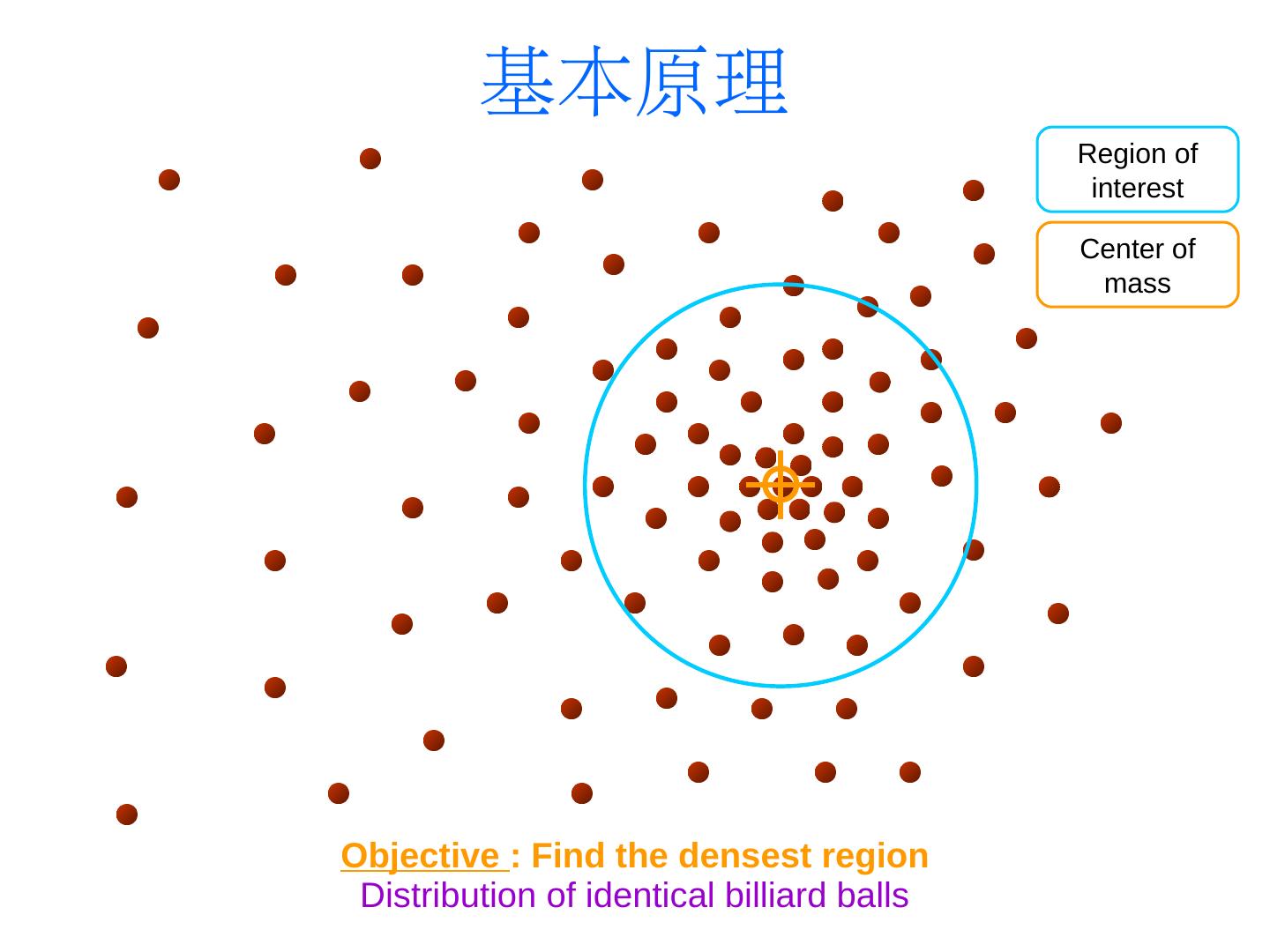
4 . 基本原理 Region of interest Center of mass Mean Shift vector Objective : Find the densest region Distribution of identical billiard balls 

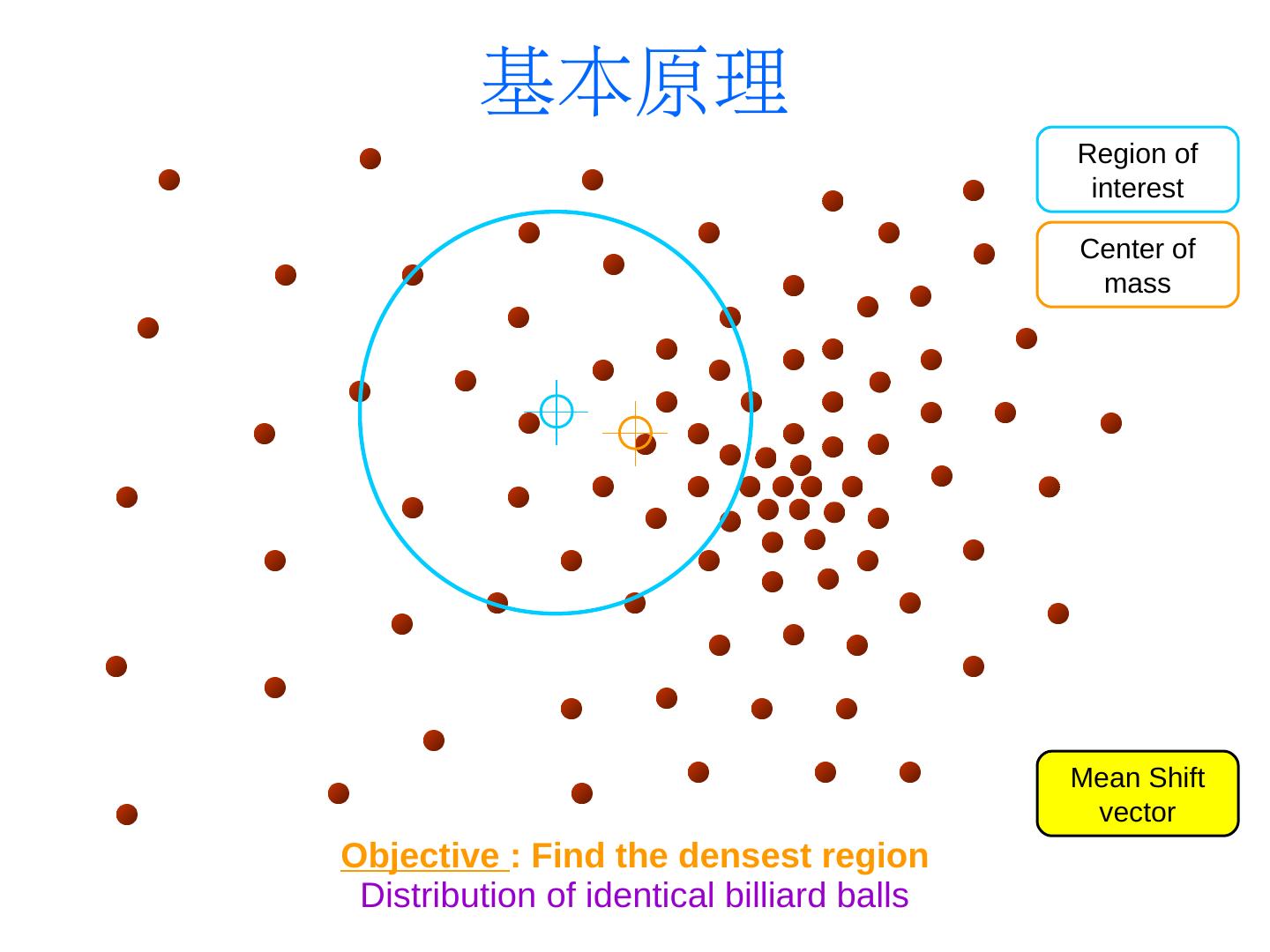
5 . 基本原理 Region of interest Center of mass Mean Shift vector Objective : Find the densest region Distribution of identical billiard balls 

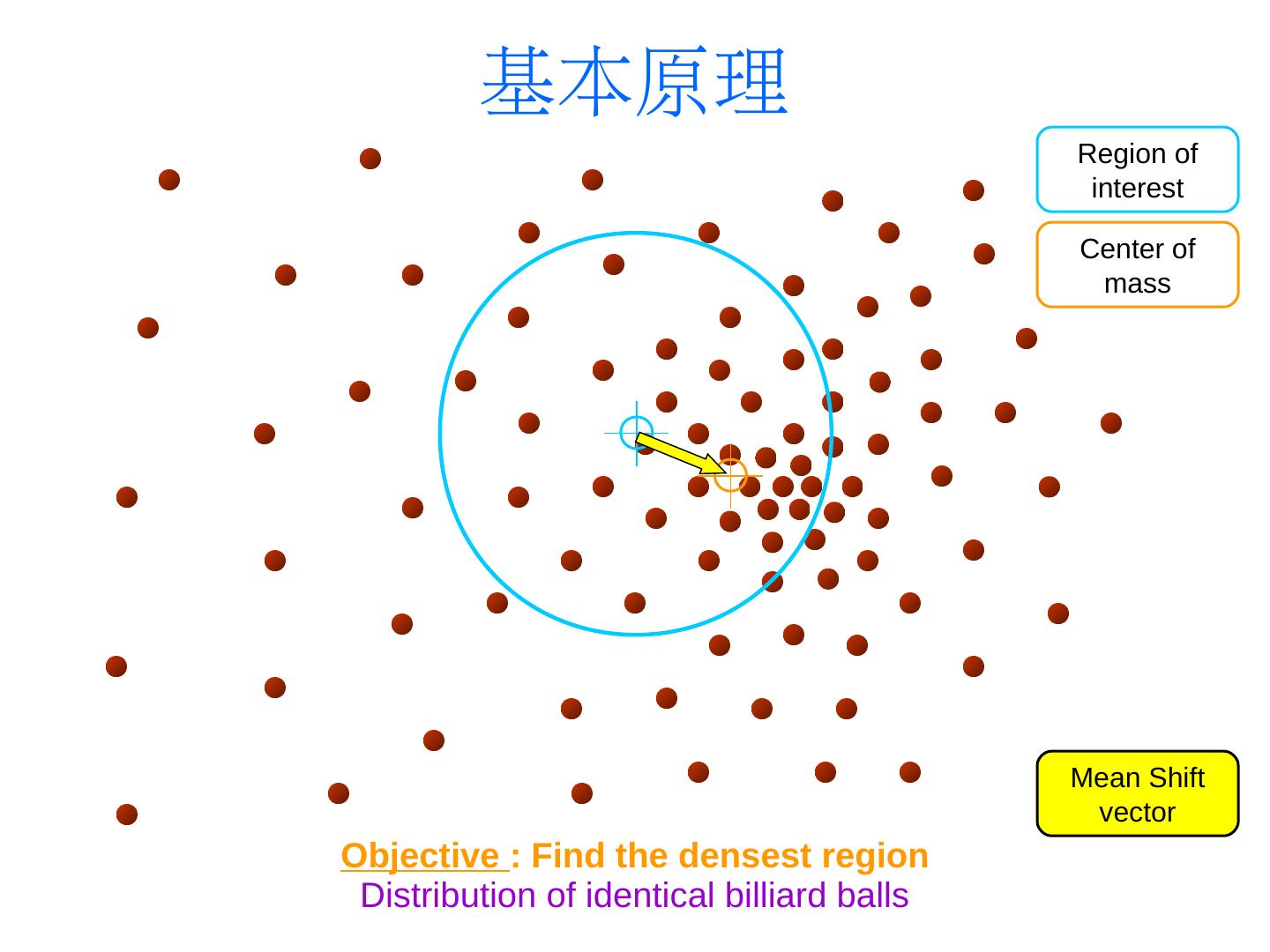
6 . 基本原理 Region of interest Center of mass Mean Shift vector Objective : Find the densest region Distribution of identical billiard balls 

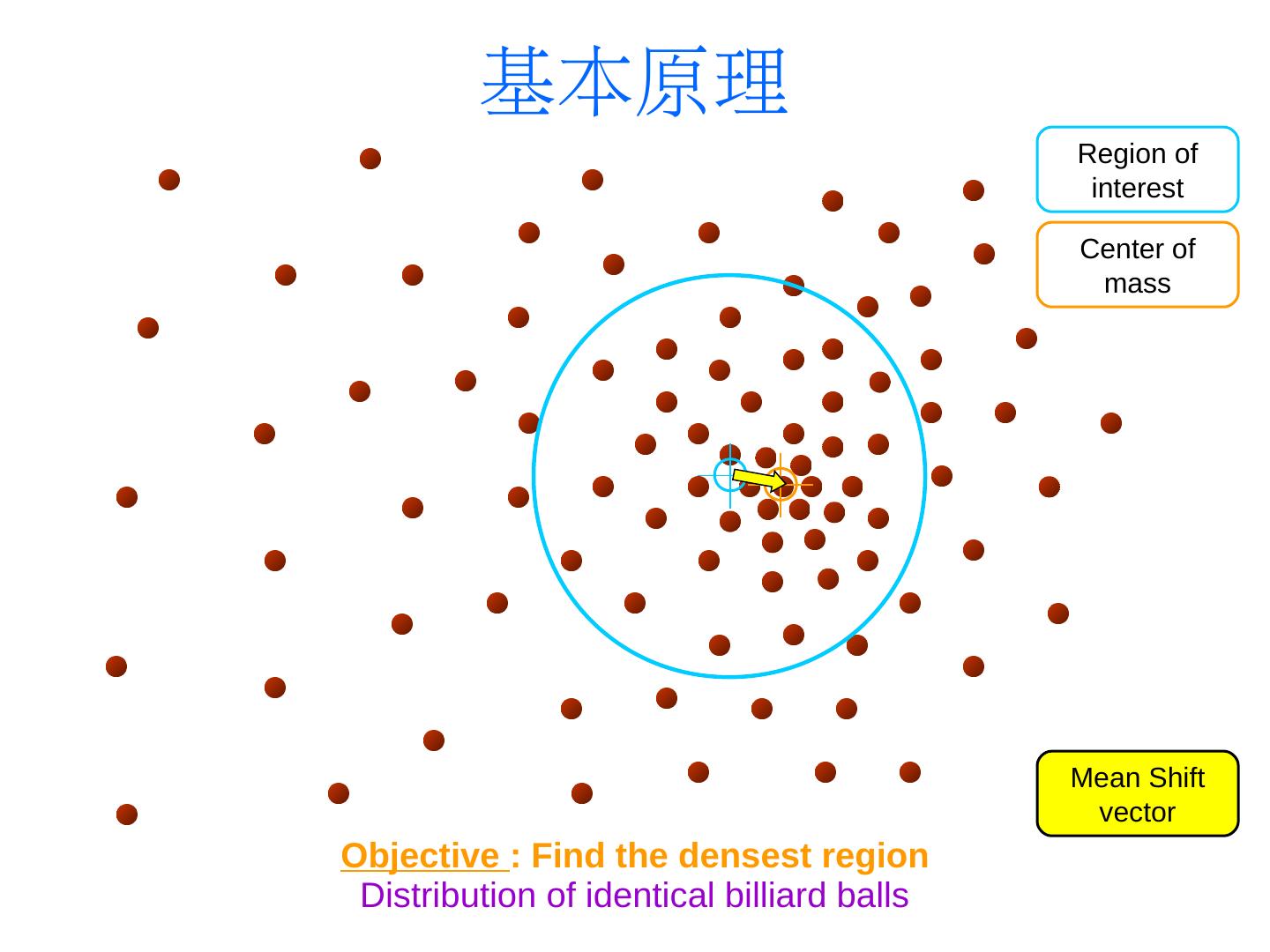
7 . 基本原理 Region of interest Center of mass Mean Shift vector Objective : Find the densest region Distribution of identical billiard balls 

8 . 基本原理 Region of interest Center of mass Mean Shift vector Objective : Find the densest region Distribution of identical billiard balls 

9 . 基本原理 Region of interest Center of mass Mean Shift vector Objective : Find the densest region Distribution of identical billiard balls 

10 . 基本原理 Region of interest Center of mass Objective : Find the densest region Distribution of identical billiard balls 

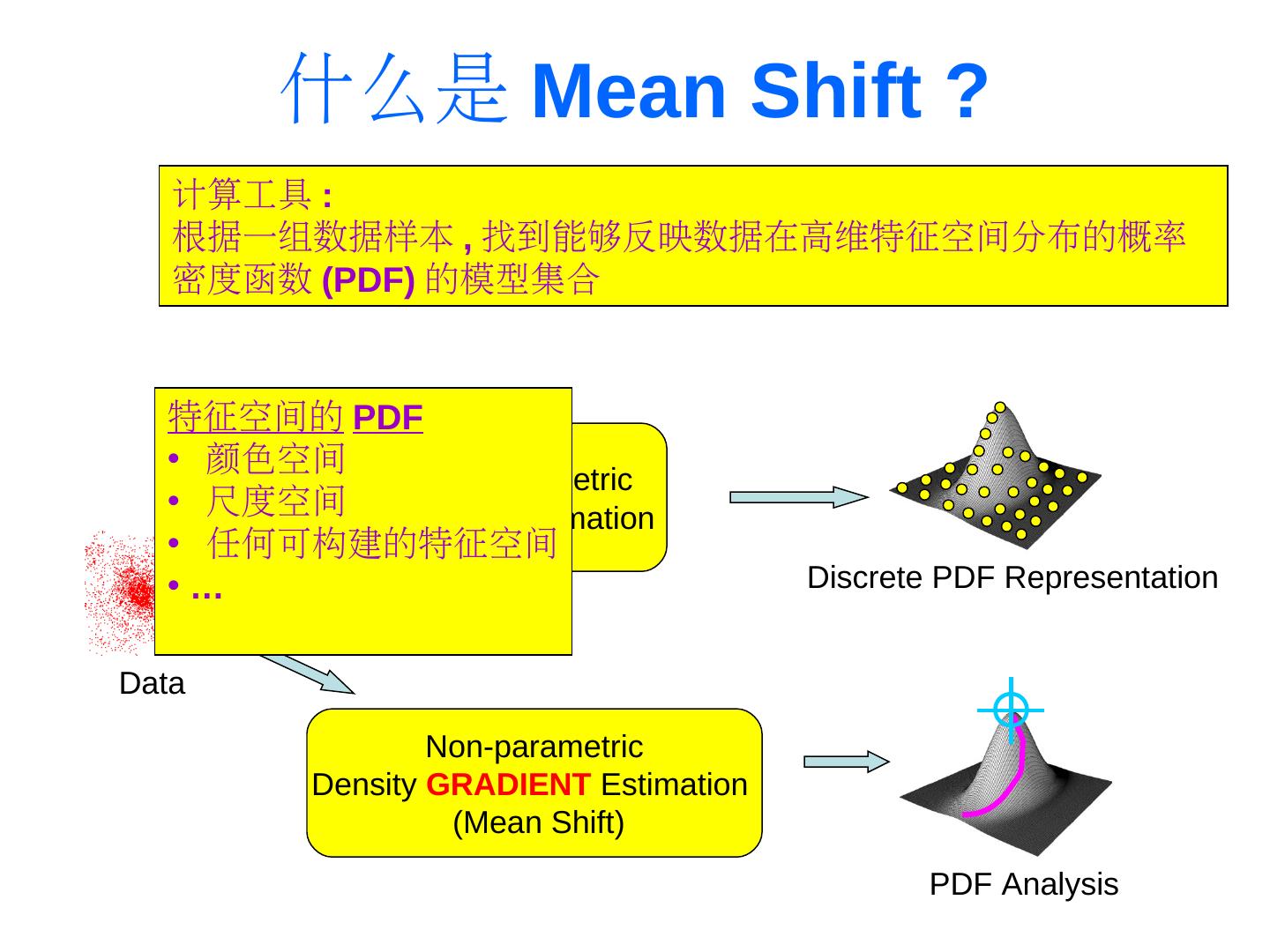
11 . 什么是 Mean Shift ? 计算工具 : 根据一组数据样本 , 找到能够反映数据在高维特征空间分布的概率 密度函数 (PDF)PDF) 的模型集合 特征空间的 PDF • 颜色空间 Non-parametric • 尺度空间 Density Estimation • 任何可构建的特征空间 •… Discrete PDF Representation Data Non-parametric Density GRADIENT Estimation (Mean Shift) PDF Analysis 

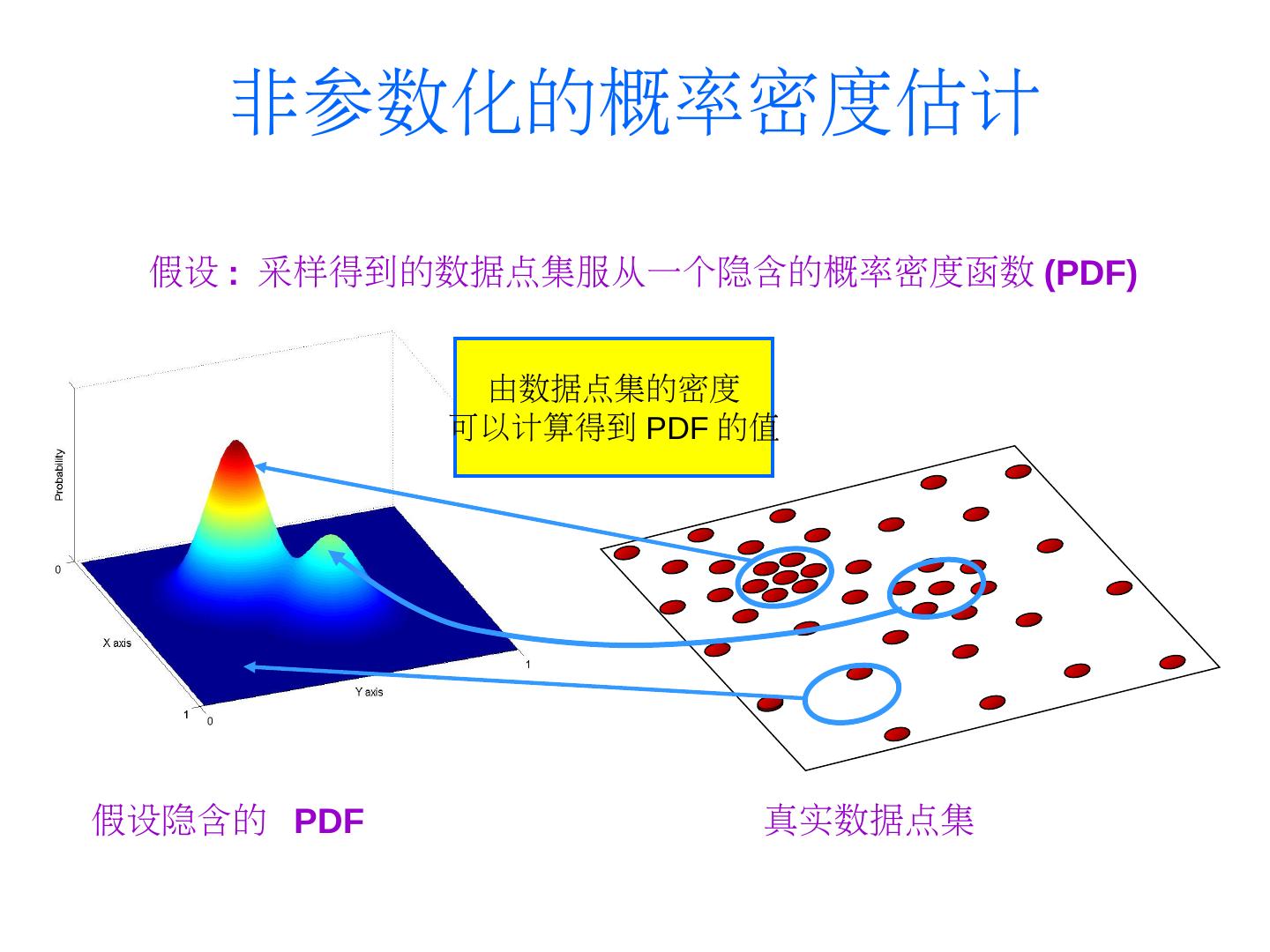
12 . 非参数化的概率密度估计 假设 : 采样得到的数据点集服从一个隐含的概率密度函数 (PDF)PDF) 由数据点集的密度 可以计算得到 PDF 的值 假设隐含的 PDF 真实数据点集 

13 . 非参数化的概率密度估计 假设隐含的 PDF 真实数据点集 

14 . 非参数化的概率密度估计 ? 假设隐含的 PDF 真实数据点集 

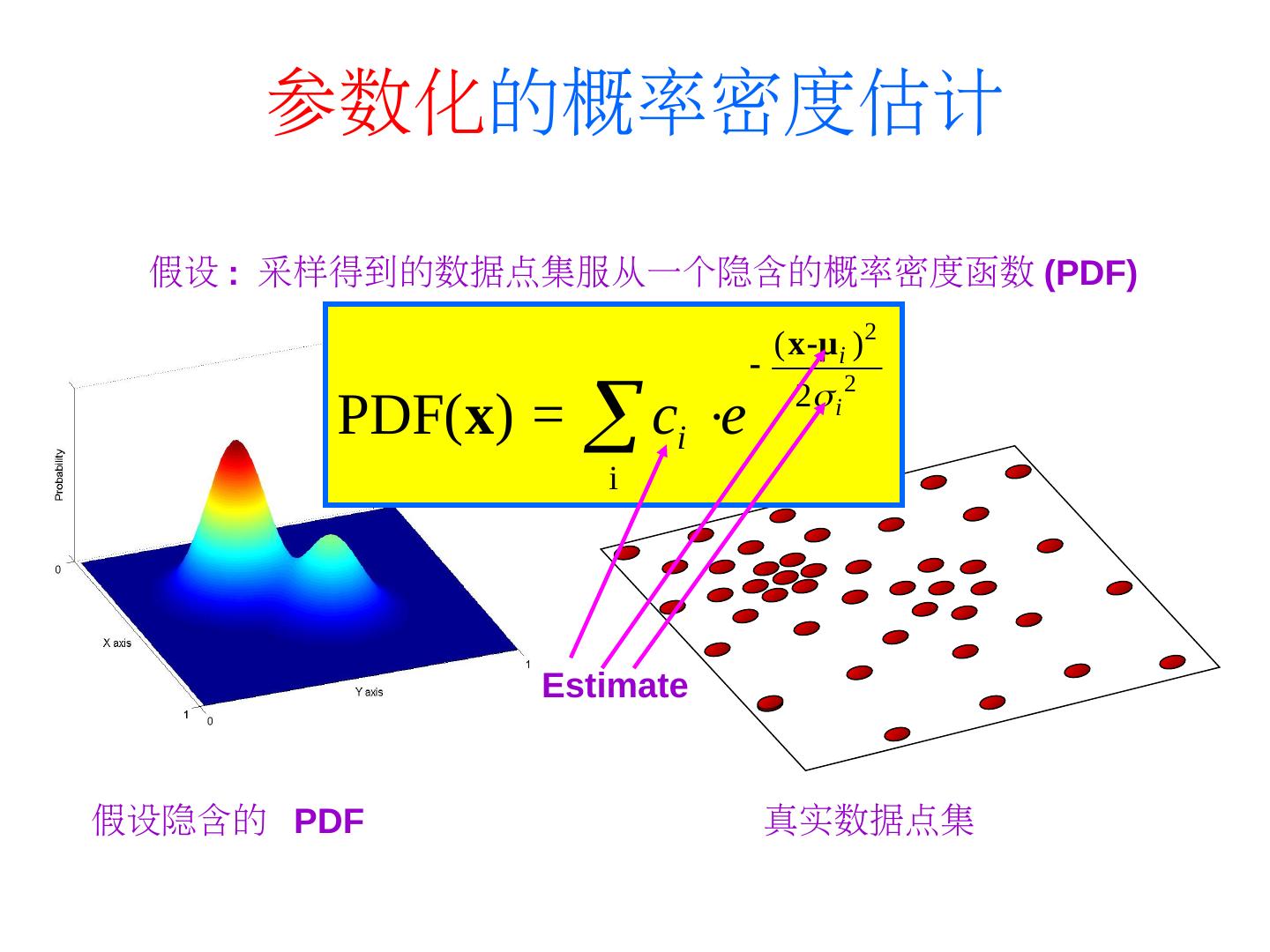
15 . 参数化的概率密度估计 假设 : 采样得到的数据点集服从一个隐含的概率密度函数 (PDF)PDF) ( x-μi )2  PDF(x) =  c e i i 2 i 2 Estimate 假设隐含的 PDF 真实数据点集 

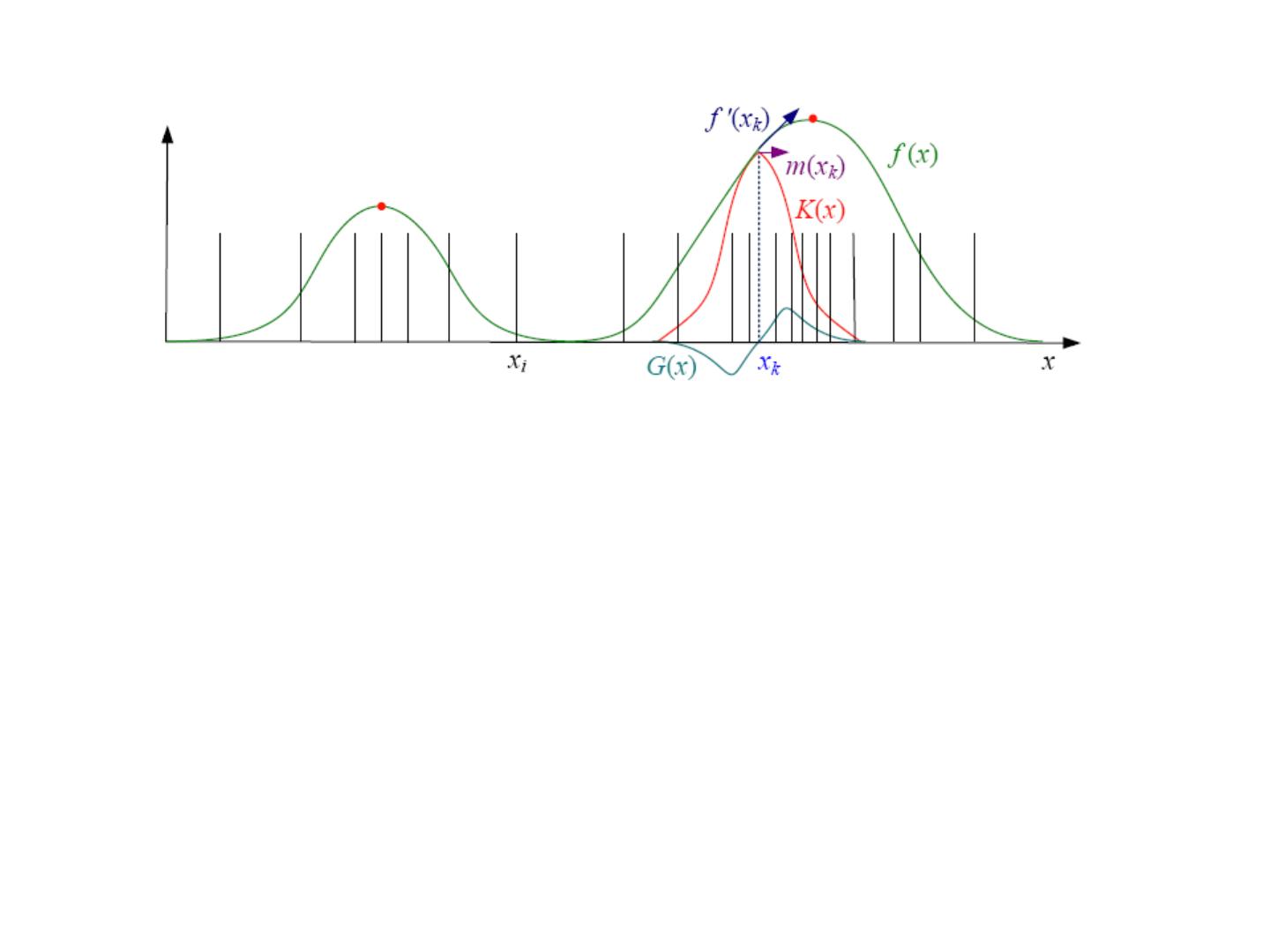
16 .核函数密度估计 (PDF)Kernel Density Estimation) Parzen Windows – 整体框架 1 n P ( x)   K ( x - x i ) 用于描述有限数量数据点集 n i 1 x1…xn 的函数 核函数性质 : Data •归一化的 K (x)dx 1 Rd • 对称的 xK (x)dx 0 Rd •指数衰减 d lim x K (x) 0 • ??? x   K (x)dx cI T xx Rd 

17 .

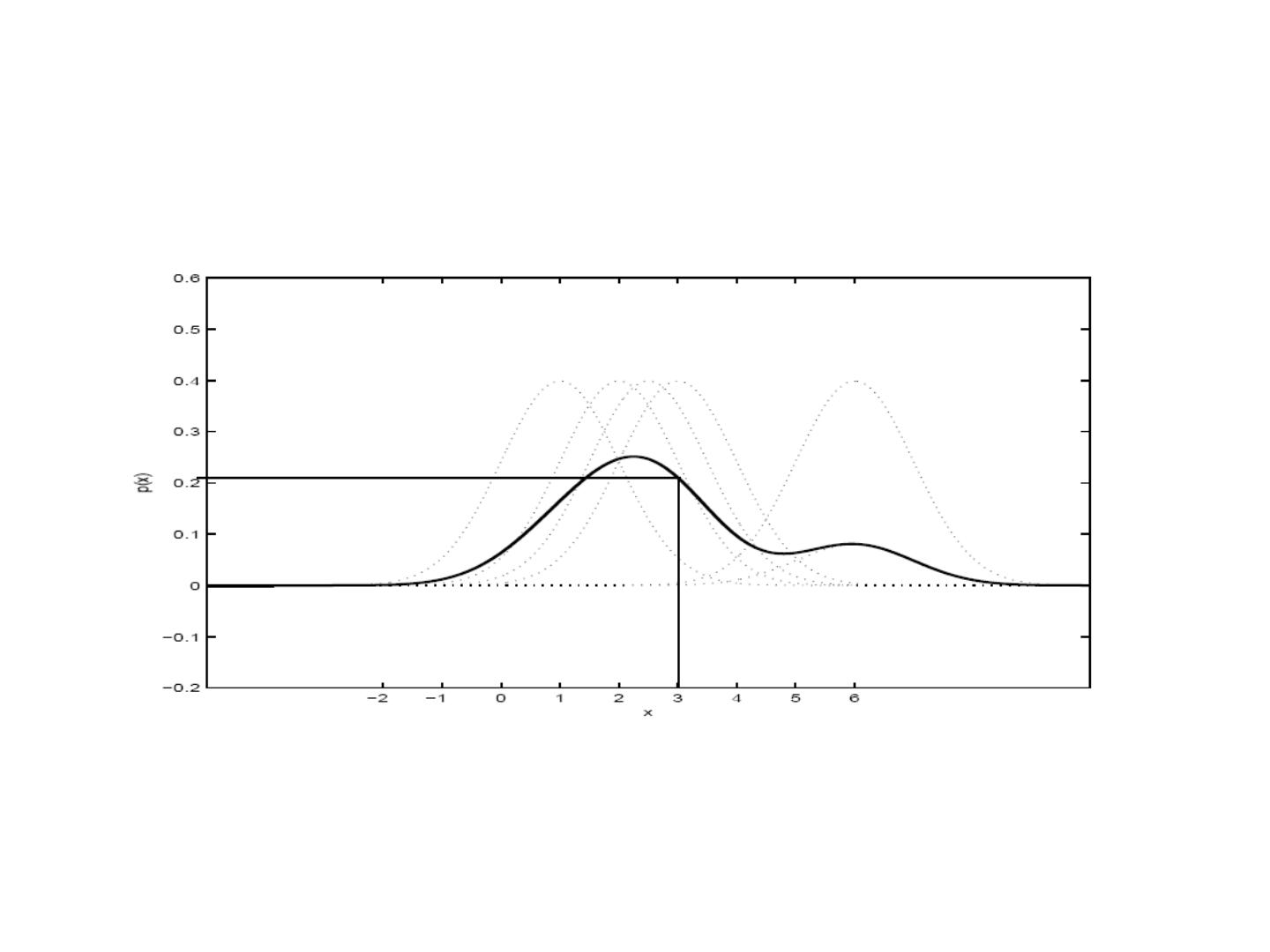
18 .Example: Given a set of five data points x1 = 2, x2 = 2.5, x3 = 3, x4 = 1 and x5 = 6, find Parzen probability density function (pdf) estimates at x = 3, using the Gaussian function with σ = 1 as window function. 

19 .

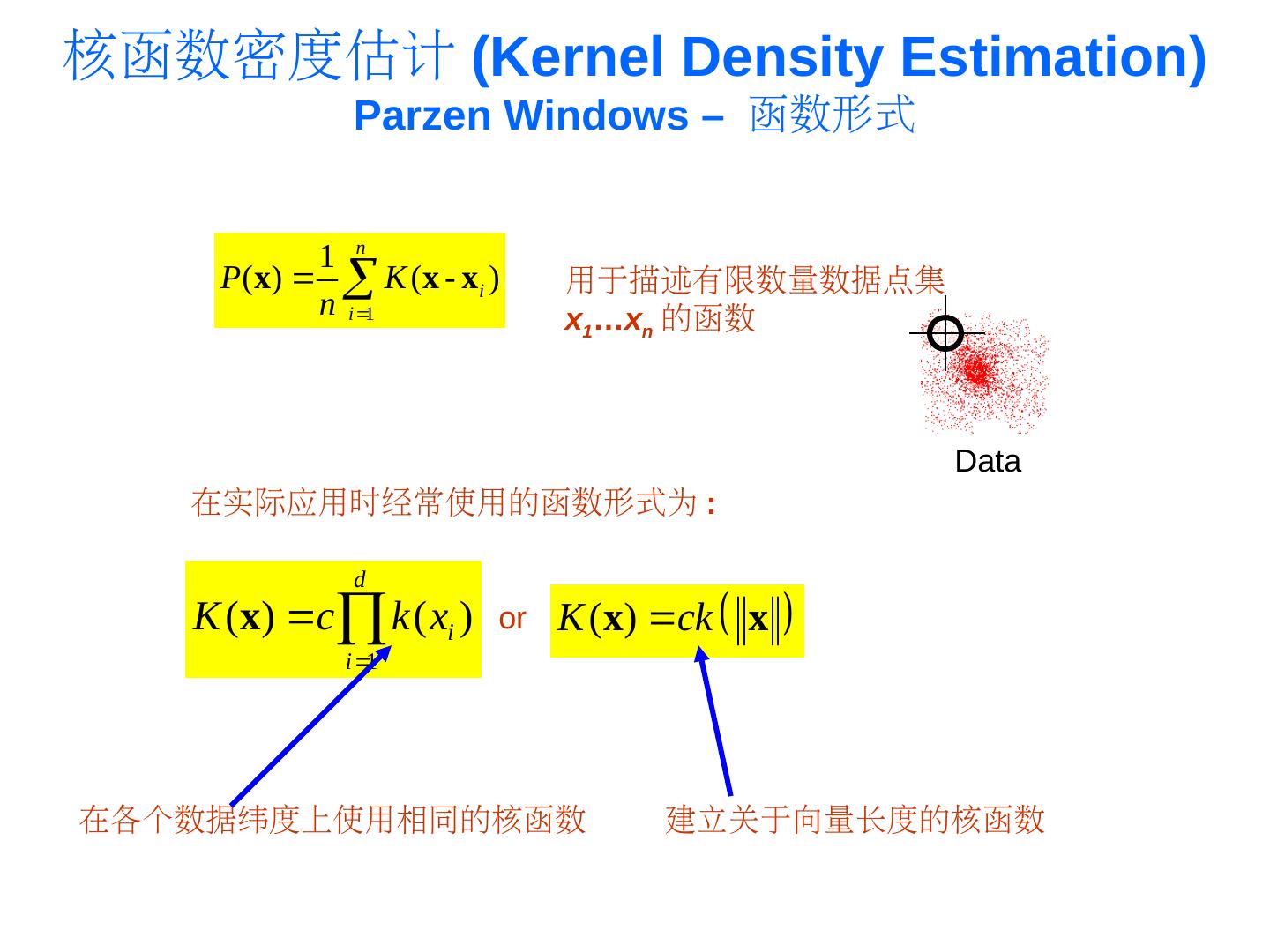
20 .核函数密度估计 (PDF)Kernel Density Estimation) Parzen Windows – 函数形式 1 n P ( x)   K ( x - x i ) 用于描述有限数量数据点集 n i 1 x1…xn 的函数 Data 在实际应用时经常使用的函数形式为 : d K (x) c k ( xi ) or K (x) ck  x  i 1 在各个数据纬度上使用相同的核函数 建立关于向量长度的核函数 

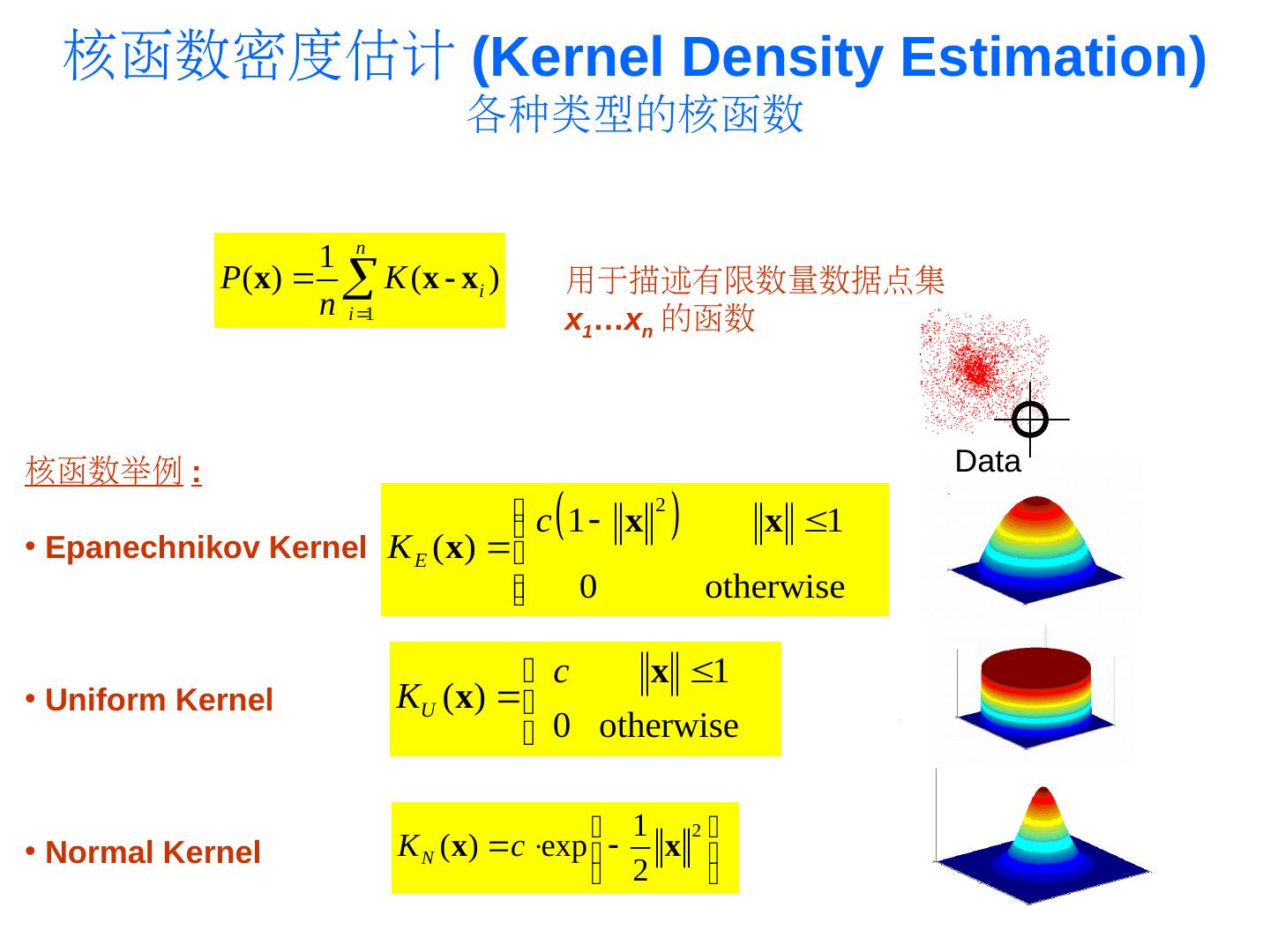
21 . 核函数密度估计 (PDF)Kernel Density Estimation) 各种类型的核函数 1 n P ( x)   K ( x - x i ) 用于描述有限数量数据点集 n i 1 x1…xn 的函数 核函数举例 : Data • Epanechnikov Kernel K E (x)    c 1  x 2  x 1  0 otherwise  c x 1 • Uniform Kernel KU (x)   0 otherwise  1 2 • Normal Kernel K N (x) c exp   x   2  

22 .核函数密度估计 (PDF)Kernel Density Estimation) 梯度 Gradient 1 n 不估计 PDF ! P( x)   K ( x - xi ) n i 1 只估计概率密度的梯度 假设使用的核函数  x - xi 2  形式为 : K (x - xi ) ck    h   可以得到 : Size of window  n    x g i i  c n c n P ( x)   ki    g i    n i 1  x n i 1 n  i 1      i 1 gi  g(x)  k (x) 

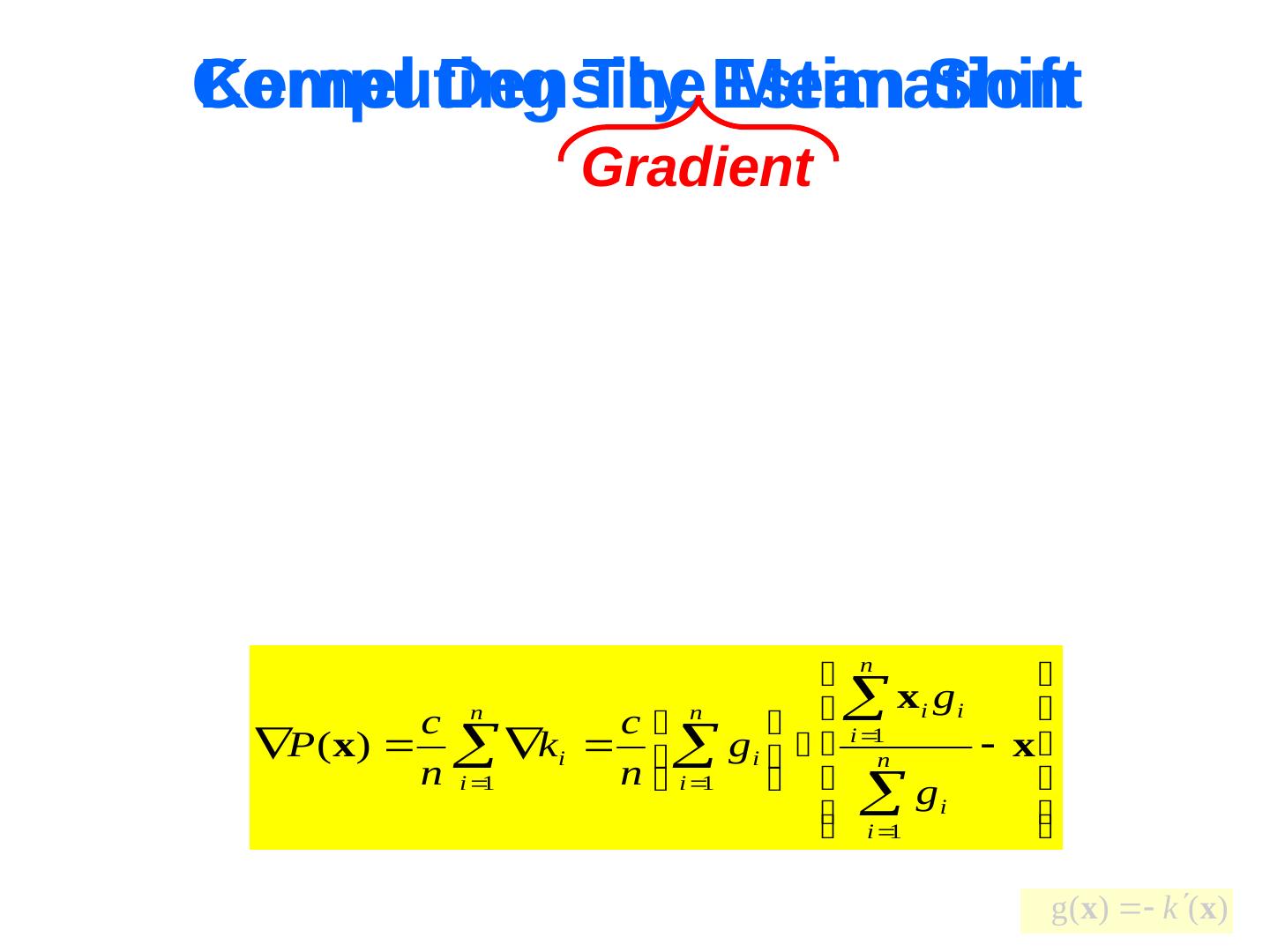
23 .Computing Kernel Density The Estimation Mean Shift Gradient  n    x g i i  c n c n P ( x)   ki    g i    n i 1  x n i 1 n  i 1      i 1 gi  g(x)  k (x) 

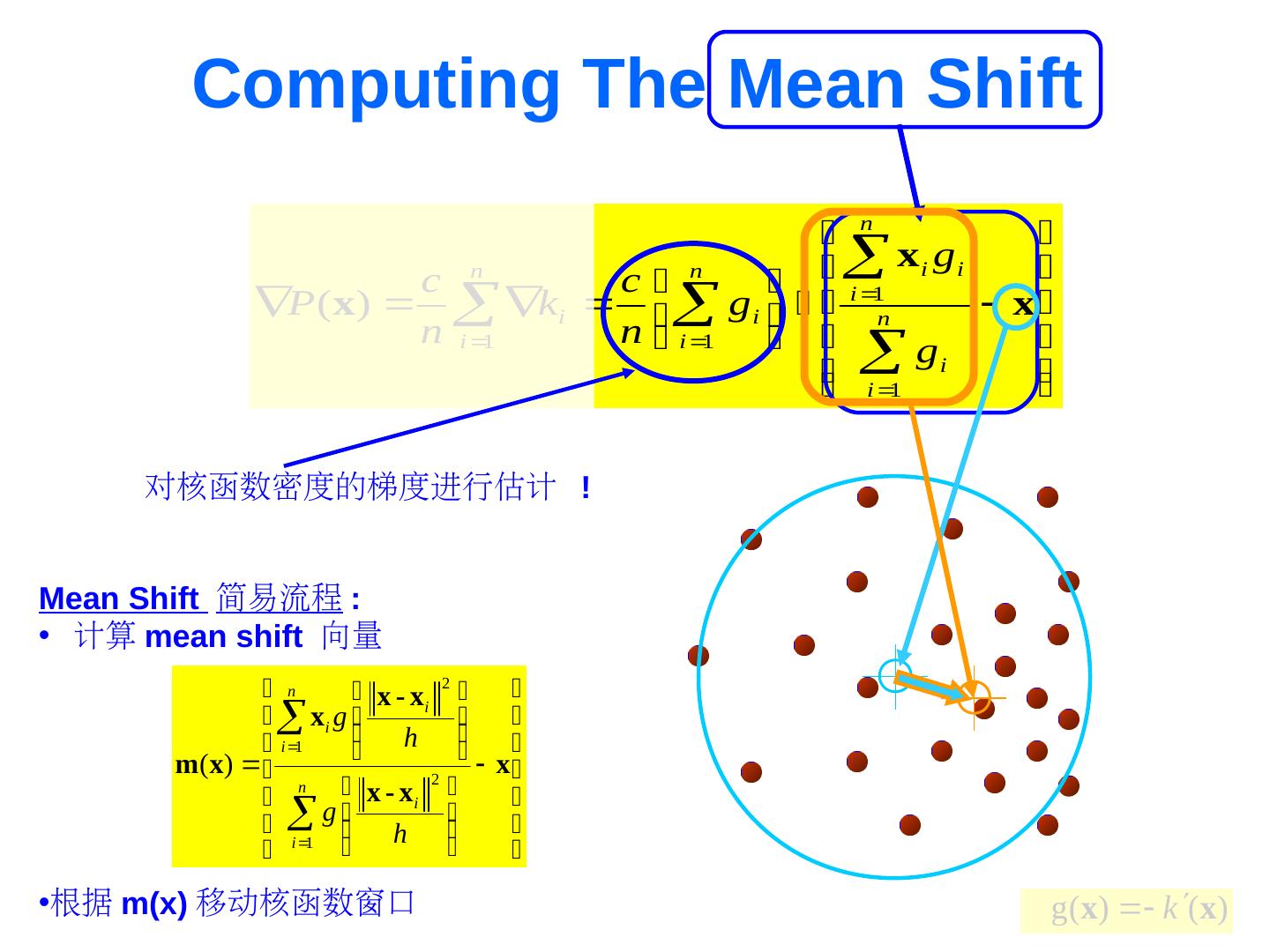
24 . Computing The Mean Shift  n    x g i i  c n c n P ( x)   ki    g i    n i 1  x n i 1 n  i 1      i 1 gi  对核函数密度的梯度进行估计 ! Mean Shift 简易流程 : • 计算 mean shift 向量  n  x - xi 2     xi g     i 1  h   m ( x )    x  n  x - xi  2    g  h    i 1    •根据 m(PDF)x) 移动核函数窗口 g(x)  k (x) 

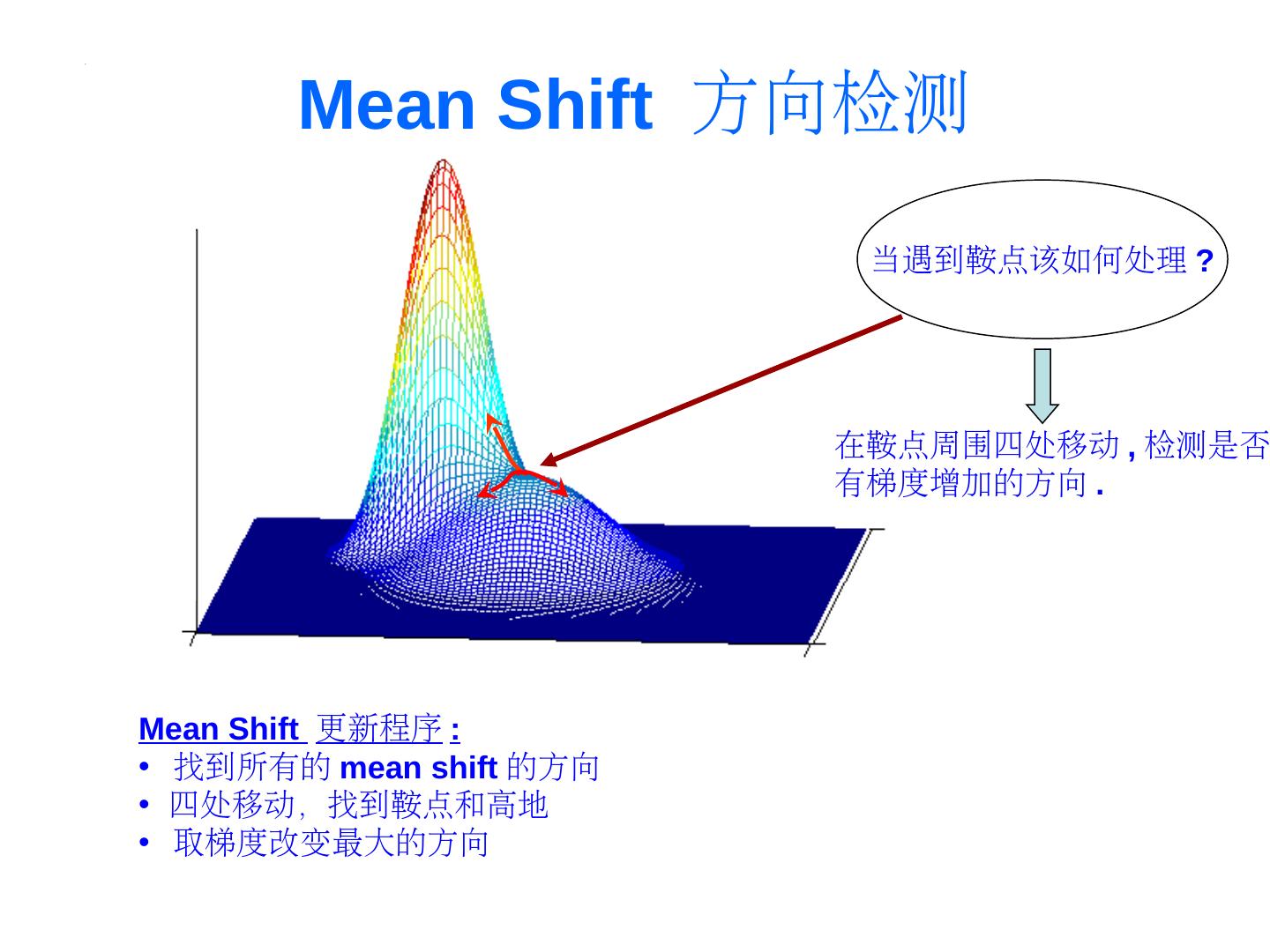
25 . Mean Shift 方向检测 当遇到鞍点该如何处理 ? 在鞍点周围四处移动 , 检测是否 有梯度增加的方向 . Mean Shift 更新程序 : • 找到所有的 mean shift 的方向 • 四处移动，找到鞍点和高地 • 取梯度改变最大的方向 

26 . Mean Shift 特性 • 自动收敛的速度– mean shift 向量的大小取决于 Adaptive 梯度本身 Gradient Ascent • 在最大值附近，步长很小而且非定值 • 理论上需要无限步数 , 因此需要设定一个下界。 • 对于 Uniform Kernel (PDF) ), 可以在有限步数内收 敛 • Normal Kernel (PDF) ) 可以得到平滑轨迹 , 但是收 敛速度慢于 Uniform Kernel (PDF) ). 

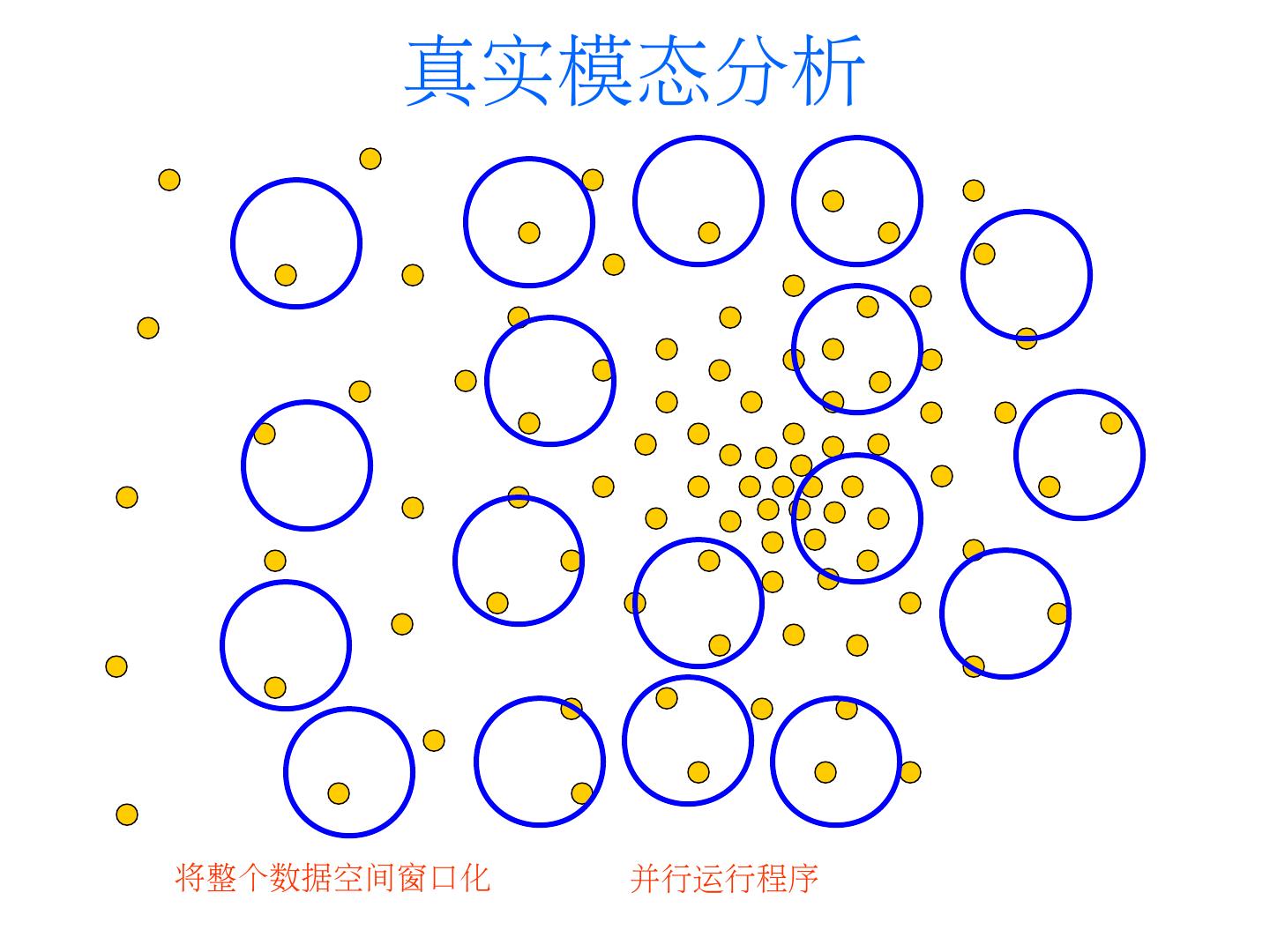
27 . 真实模态分析 将整个数据空间窗口化 并行运行程序 

28 .真实模态分析 蓝色的数据点是被窗口移动时经过的 

29 .真实模态分析 An example 窗口是向着梯度变化最剧烈的方向移动的