- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
图像分割:snake模型
展开查看详情
1 .第五章 图像分割
2 .常见的图像分割算 法: (a)主动轮廓线 (b)水平集 (c)基于图的分割算法 (d)Mean shift (e)Ncuts (f)Graph cut
3 .常见的图像分割算 法: (a)主动轮廓线 (b)水平集 (c)基于图的分割算法 (d)Mean shift (e)Ncuts (f)Graph cut
4 .主动轮廓线模型 (Snake 模型 )
5 . 1. 引言 Marr 视觉计算理论的不足 三个独立的层次 , 底层缺乏约束导致病态问题 自下而上 , 底层的错误将被带给高层无法修正 Snakes: active contour models Kass,1987,ICCV 对传统的视觉计算理论的挑战 设计这样一个能量函数 : 其局部极值组成了可供高层 视觉处理进行选择的方案 , 高层机制可能通过将图像 特征推向一个适当的局部极值点从该组方案中选择最 优的一种
6 . 1.1 Snake 模型的基本原理 基本原理是表征拟合误差的“能量”为最小化的曲线 . 设对于拟合目标有一个待选曲线集 , 定义能量函数 与待选集中每一条曲线相关联 , 能量函数的设计原 则就是 : 有利属性要能导致能量缩小。 有利属性包括 : 曲线连续、平滑、曲线与高梯度区 域接近以及其他一些具体的先验知识。 活动轮廓在取值范围内移动时 , 就能在能量函数的 指导下收敛到局部边界 , 且能保持曲线的连续和平 滑。
7 . 1.1 Snake 模型的基本原理 蛇模型是在曲线本身的内力和图像数据的外部约束力作用 下的移动的变形轮廓线。 作用在蛇模型上的力依据轮廓所在的位置及其形状决定如 何在空间局部的变化。 内力和外力的作用是不同的 : 内力起平滑约束作用 , 外 力则引导蛇模型向图像特征移动。 施加在蛇模型上的外力来自于图像或更高层的处理外力 , 将蛇模型推离不期望的特性。 蛇模型的内力包含两项 . 形象的说 , 可以认为蛇模型是 由两种抽象的弹性材料构成 : 弦与杆。前者使轮廓抵抗 韧性 , 而后者使轮廓抵抗弯曲。
8 .
9 . 1.2 Snake 模型的特点 Snake 模型的优点 图像数据、初始估计、目标轮廓及基于知识的约束统 一于一个特征提取过程中 ; 经适当地初始化后 , 它能够自主地收敛于能量极小值 状态 ; 尺度空间中由粗到精地极小化能量可以极大地扩展捕 获区域和降低计算复杂性 Snake 模型的缺点 对初始位置敏感 , 需要依赖其他机制将 Snake 放 置在感兴趣的图像特征附近 ; 它有可能收敛到局部极值点 , 甚至发散 .
10 . 2.Snake 模型的数学模型 定义 Snake 模型为一可变形曲线 S 为归一化的曲线长度 , 变化范围 (0,1) 蛇模型的总能量函数是
11 . 2.Snake 模型的数学模型 Eint 是内部能量 , 控制蛇模型特性 , 定义为 分别是 v 对 s 的一阶和二阶导数 , 系数 α 、 β 分别是控制蛇模型的弹性和刚性 , 这些参数操纵着模型的物 理行为和局部连续性 外部能量 Eext 决定着向某种固定的特征移动蛇模型 , 吸 引蛇模型到显著的图像特征。因为这些特征只能根据特定 的问题而定义 , 所以一般的外部能量函数不易确定。因 此 , Eext 没有统一的数学表达式 , 必须从问题本身的特 性出发 , 根据实际情况处理
12 . 外部能量 (Eext) 图像能量 定义函数 Eimage(x,y) ,反映的是对图像特征(如反映的是对图像特征(如 边界)的兴趣程度 Eext Eimage (v ( s ))ds s Eimage(x,y) 函数的定义是一个关键问题 . 典型的例子为 Eimage ( x, y ) | x, y )|2 Eimage ( x, y ) | (G ( x, y ) * I ( x, y )) |2
13 . 能量与内外力平衡方程 目标轮廓的确定就被转化成了极小化如下的能量泛函 的问题 1 Esnake ( s ) | vs |2 ( s ) | vss |2 ) Eimage (v( s ))ds s 2 由变分法的原理出发 , 可以将其转化为 Euler 方程 vss vssss Eimage 0 这一方程可以被看作是轮廓内外力的平衡公式 . 每个力都有对应的意义,反映的是对图像特征(如在这些力的作用下轮廓发生 形变。
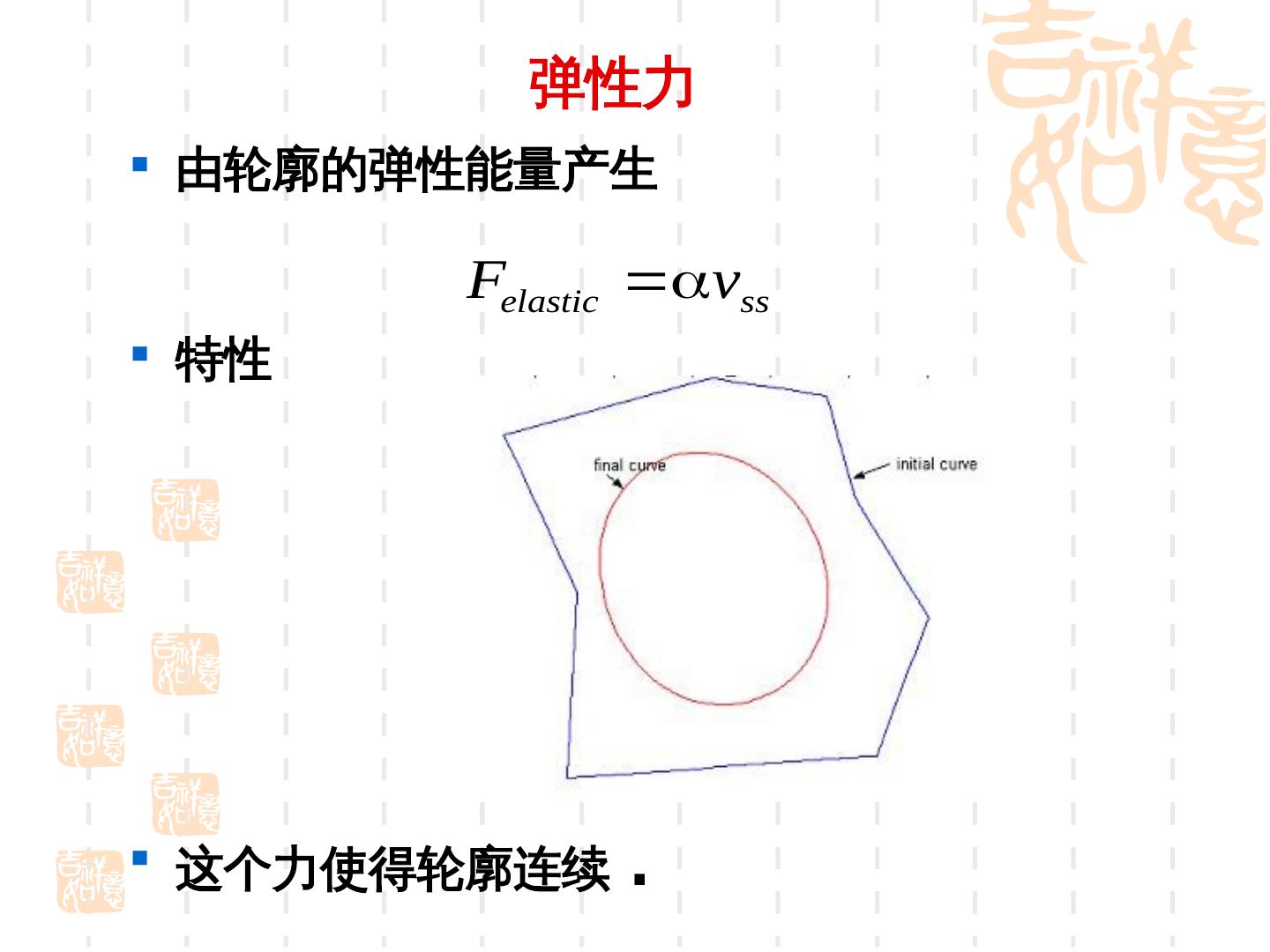
14 . 弹性力 由轮廓的弹性能量产生 Felastic vss 特性 这个力使得轮廓连续 .
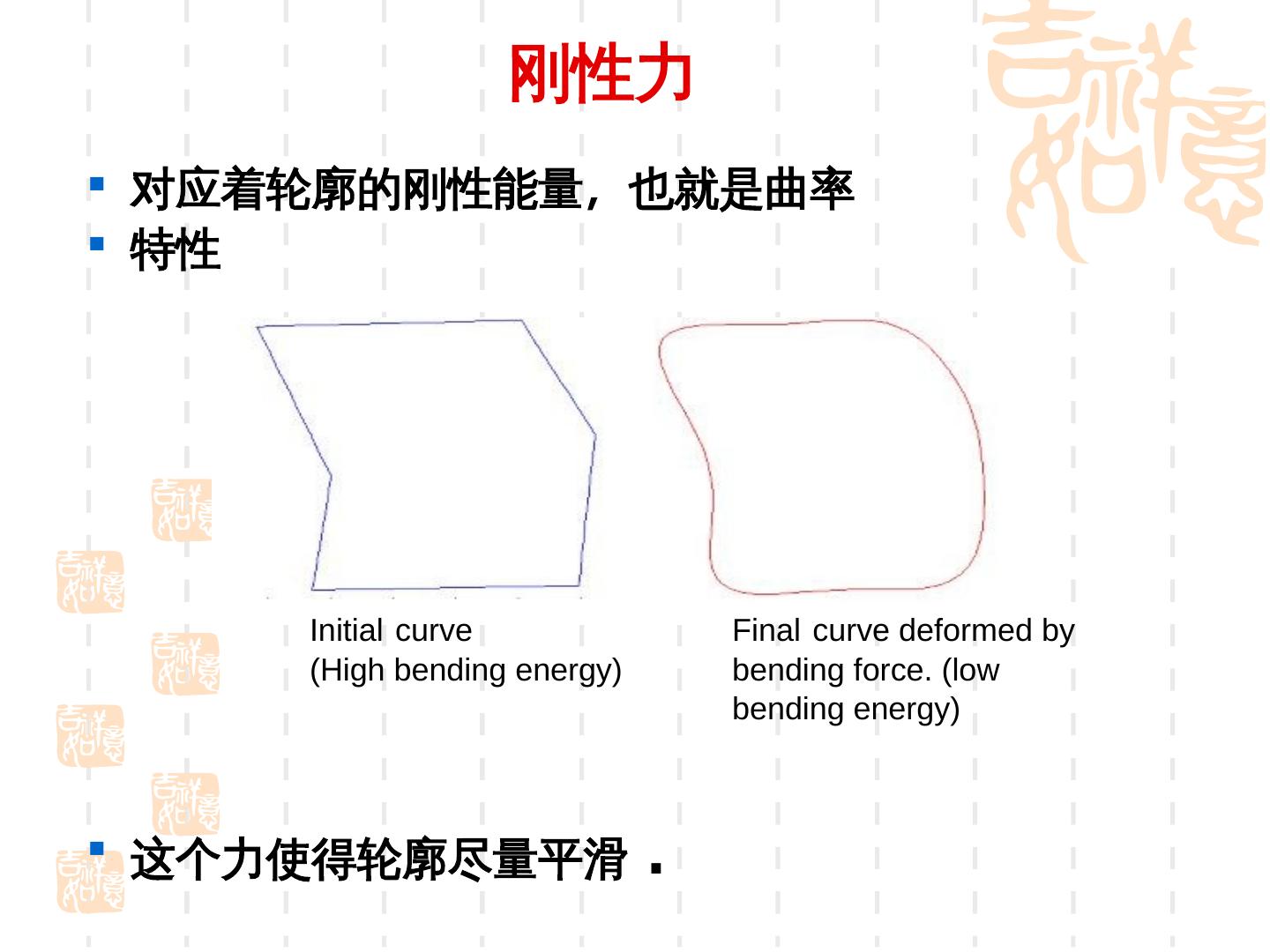
15 . 刚性力 对应着轮廓的刚性能量,反映的是对图像特征(如也就是曲率 特性 Initial curve Final curve deformed by (High bending energy) bending force. (low bending energy) 这个力使得轮廓尽量平滑 .
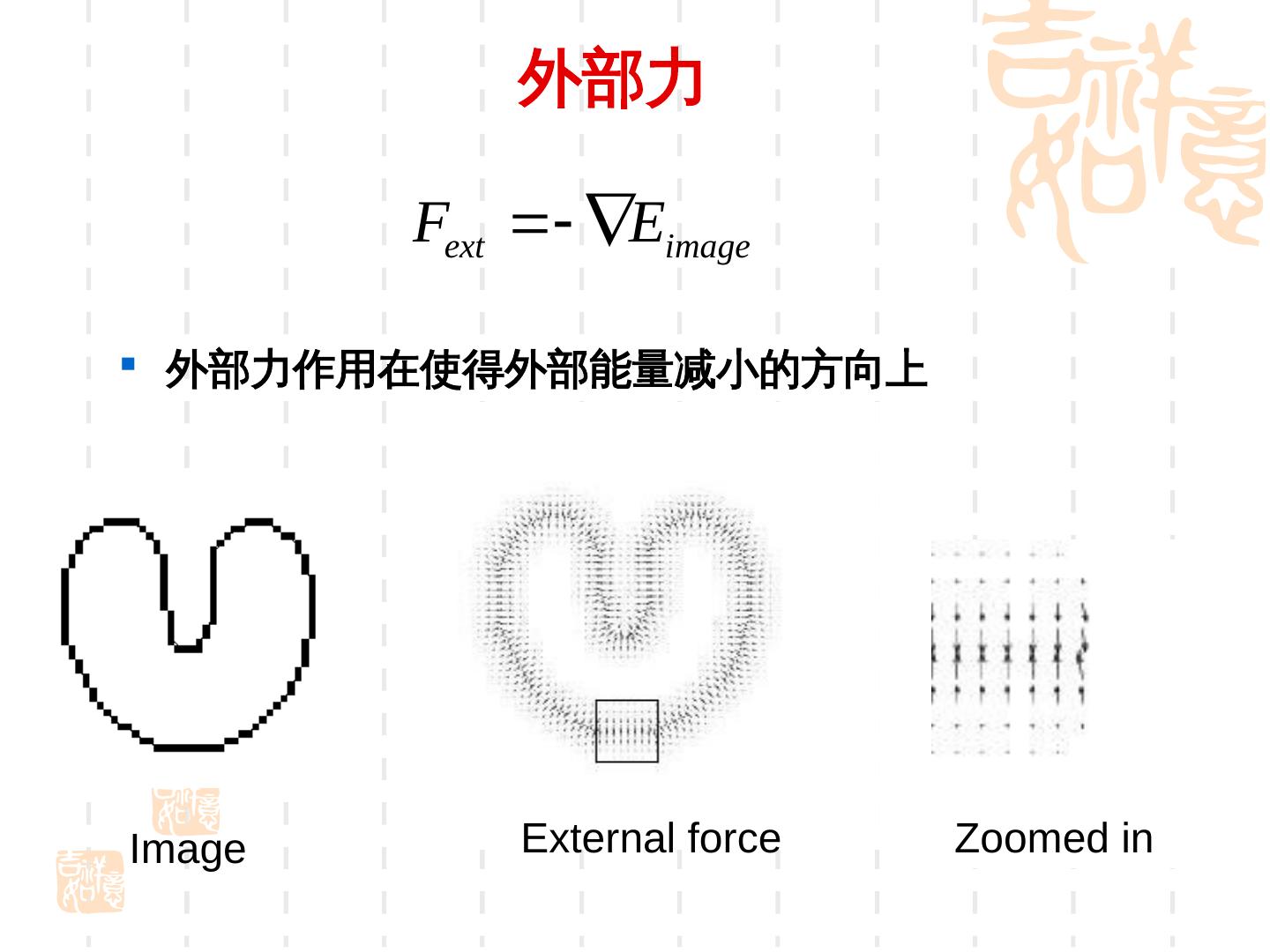
16 . 外部力 Fext Eimage 外部力作用在使得外部能量减小的方向上 Image External force Zoomed in
17 . 离散化 轮廓 v(s) 由一系列控制点组成v0 ,v1 ,.....,vn-1 轮廓通过依次连接更个控制点并分段线性化得到 . 平衡力方程独立作用于各个控制点 每个控制点在内外力的作用下是可以移动的 . 能量以及平衡力的方程均作离散化处理。
18 . 3.Snake 模型用于轮廓提取的实例 在实际应用中 , 我们需要对 Snake 模型离散化 , 计算的是曲线的 各个控制点的能量值 , 定义的能量函数如 (1) 内部能量的连续性项能量 是待考察点的 3 ×3 邻域 dmean 表示曲线上相邻点的平均距离 , 相邻点间的间距与平均值 越接近 , 其能量值越小 , 这样即保证了平滑 , 又避免了堆积。
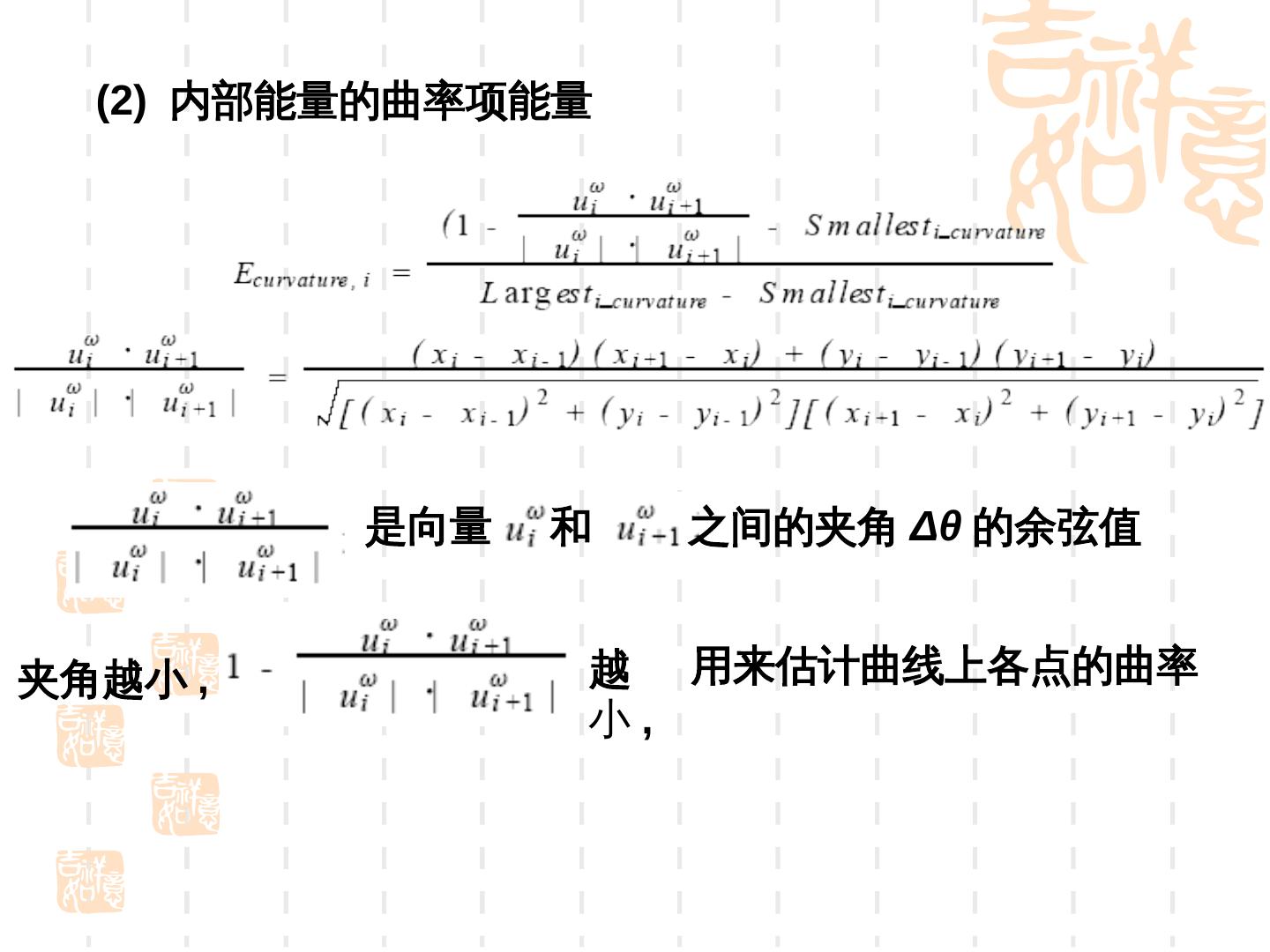
19 . (2) 内部能量的曲率项能量 是向量 和 之间的夹角 Δθ 的余弦值 夹角越小 , 越 用来估计曲线上各点的曲率 小,
20 .(3) 图像能量 这一项表示图像的约束条件 , 根据有利边界点的原则 , 边界点应具 有较小的值 是边缘检测算子 , 是待考察点的 3 ×3 邻域内 的最大值 , 是最大值 .这样的计算用于归一化 (4) 在确定能量函数后 , 对曲线按照能量最小进行迭代 .
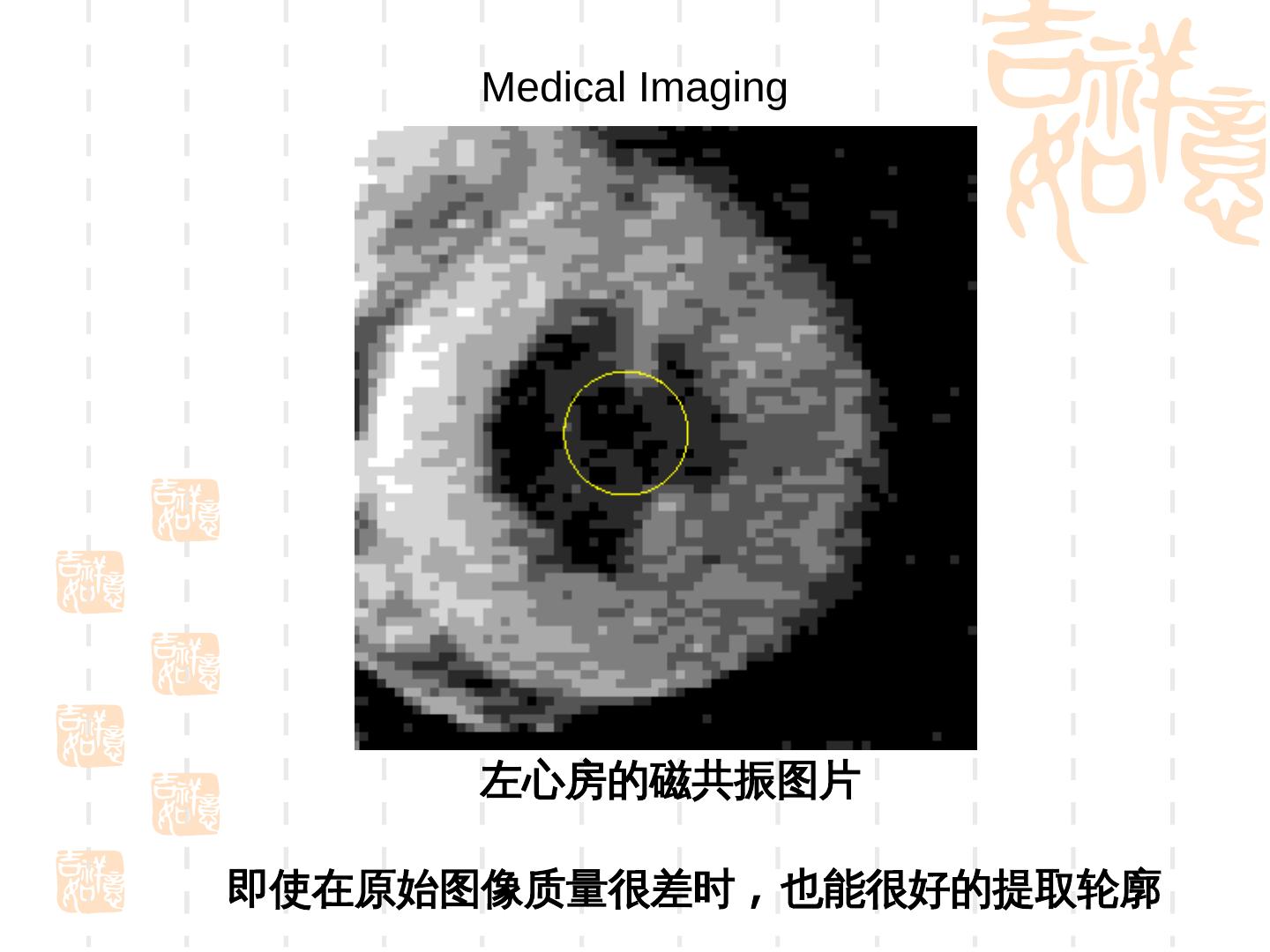
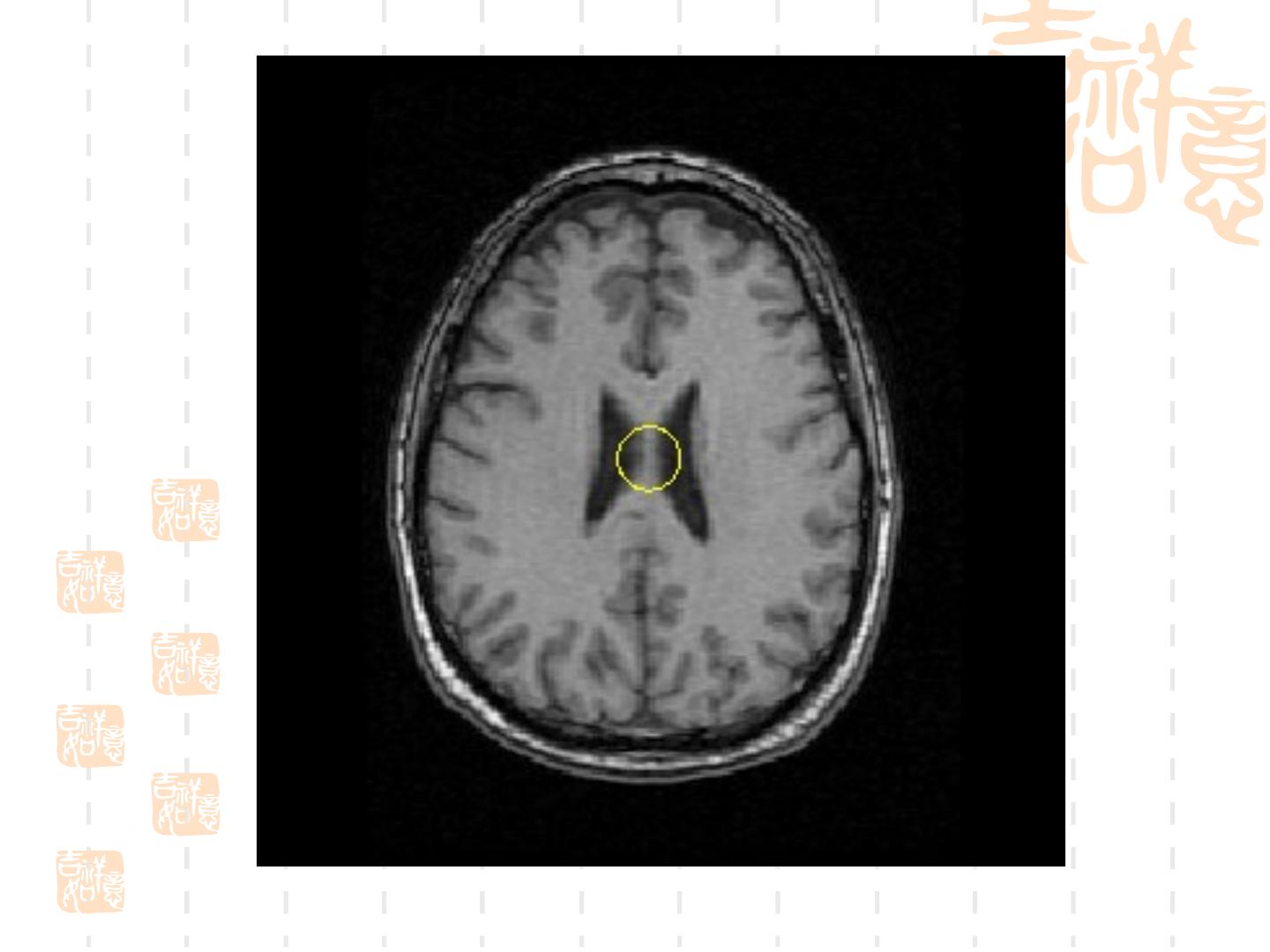
21 . 3.Snake 模型用于轮廓提取的实例
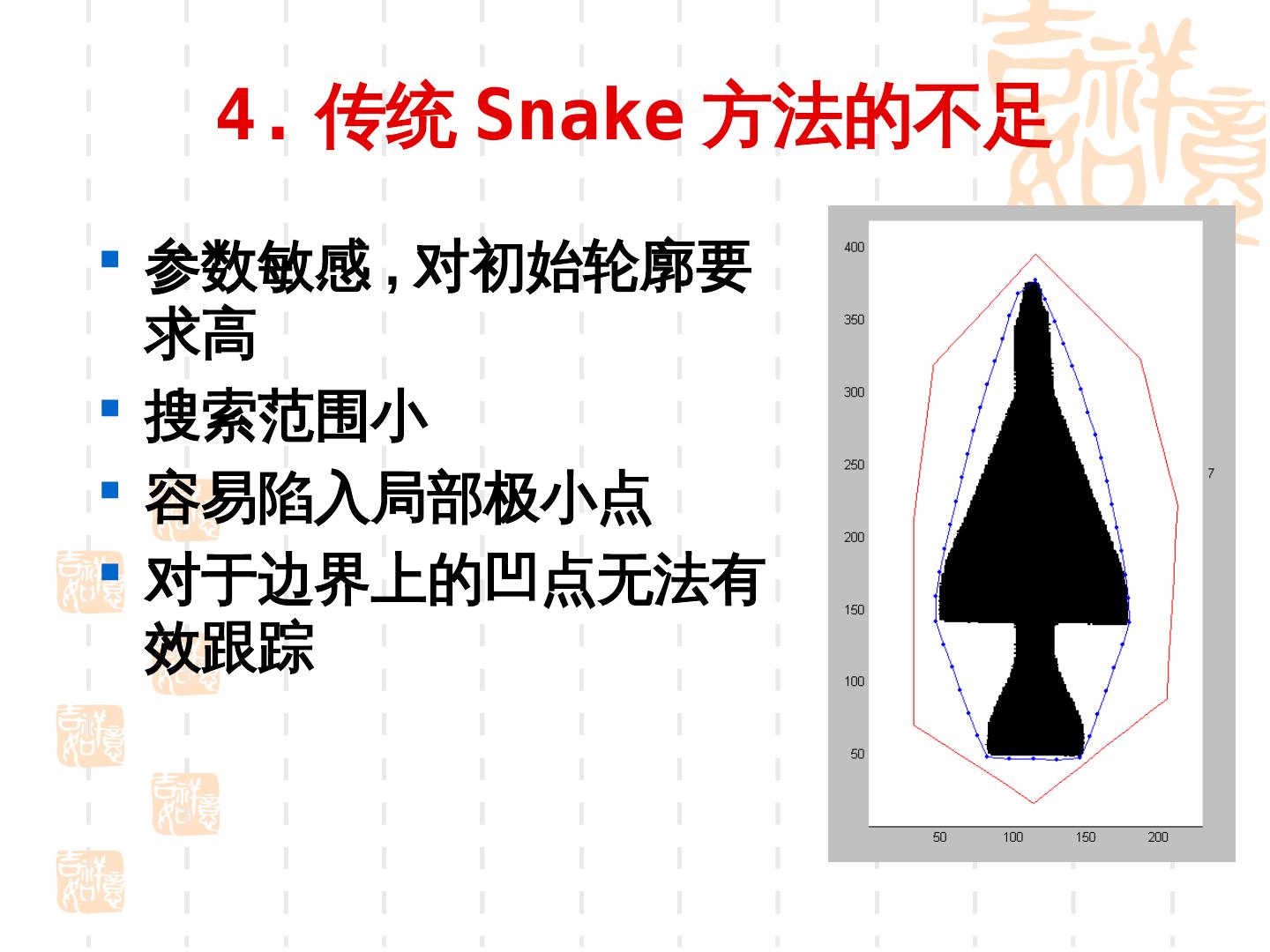
22 . 4. 传统 Snake 方法的不足 参数敏感 , 对初始轮廓要 求高 搜索范围小 容易陷入局部极小点 对于边界上的凹点无法有 效跟踪
23 . 4.Snake 模型的改进 改善 Snake 对初始化轮廓的敏感性 ; 保证 Snake 能够收敛到全局极值 ; 改善 Snake 在能量极小化过程中的收敛 速度或数值稳定性 .
24 . 气球力— balloon force Cohen L D, On active contour models and balloons.1991, Image Understanding 在轮廓线上施加另一外部约束力 , 使轮廓线向目 标靠拢。在该力的作用下轮廓线不断的向外膨胀 , 最终进化到目标轮廓 , 可以形象的称之为气球力 由气球力所构造的能量项 , 在能量函数中的数学 形式可以表达为 : 为以控制点 vi 为中心的大小为 n ×m 的领域内的第 (j ,k) 个邻点 , · 代表矢量间的点乘运算 . ni 是轮廓线上控制点 vi 处的单位法线矢量 , 这样在规定的领 域内 , 在法线矢量 ni 方向上离控制点 vi 最远的点将拥有
25 . 气球力— balloon force 在引入气球力能量项之后 , Snake 模型的外部能量项可以描述为 其中参数 k 用来控制气球力的方向 , 当 k 为负数时 , 气球力使 轮廓线向内收缩 , 相反当 k 为正数时 , 气球力使轮廓向外膨胀 ; 在选择参数 k 和 l 的大小时 , 一般将它们置于同一数量级 , 且 l 稍大于 k , 这是为了在边缘点时轮廓线能够停止运动。 这样 , 原始模型的缺点得到改善 , 对轮廓线的初始化位置要求明 显降低 , 即使在初始位置离希望提取的边缘相当远时 ,Snake 照 样能够进化到目标轮廓。 该模型改善了蛇模型对初始轮廓的敏感性 , 并且能够跨越图像 中的伪边缘点。
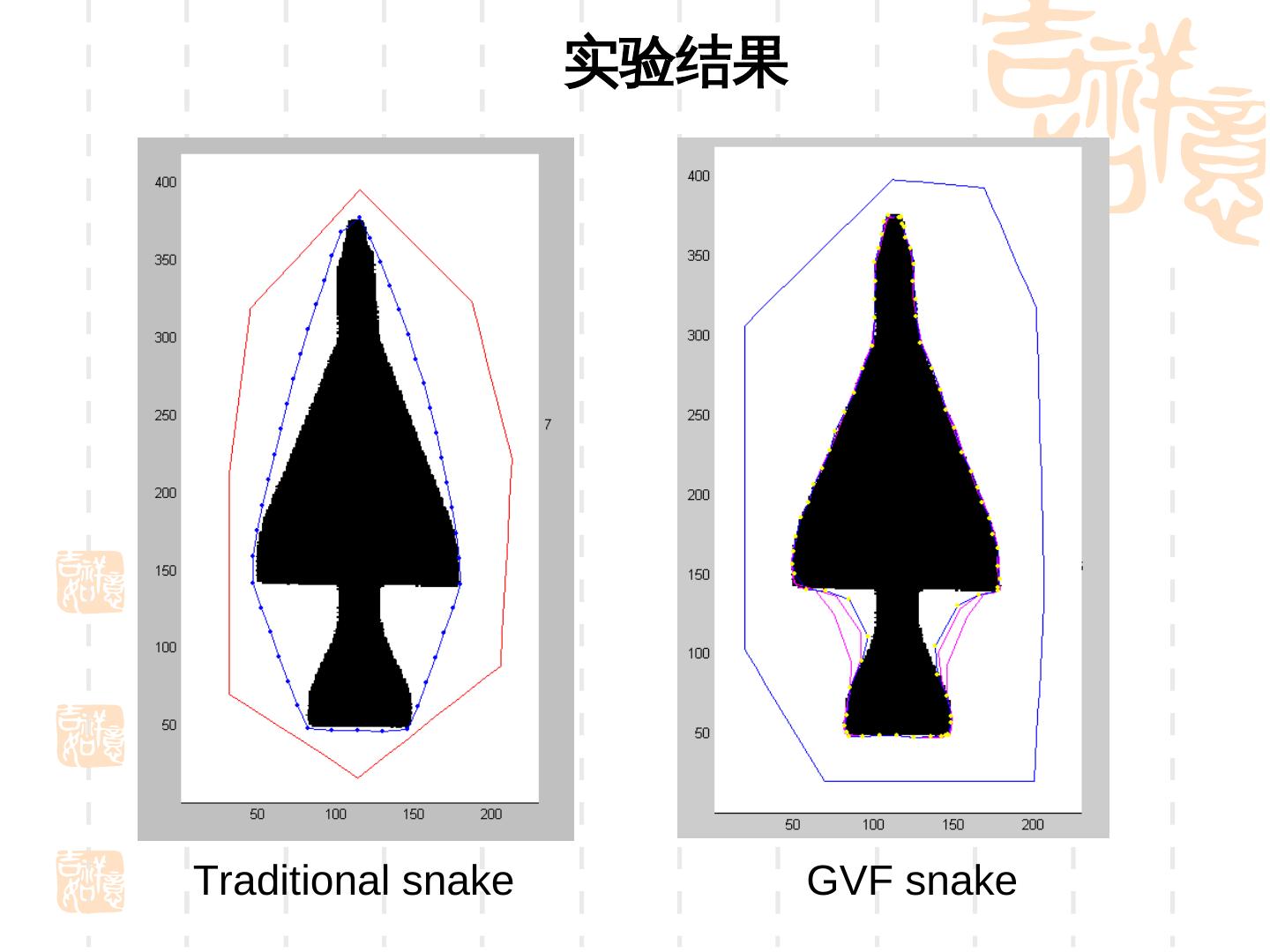
26 .梯度矢量流 -Gradient Vector Flow(GVF) Xu C. and JL Prince. 1998. Snakes, shapes, and gradient vector flow. IEEE Trans Image Processing. 7(3): 359-363 它的数学基础来源于电磁场理论中的亥姆霍兹理 论 , 这种理论阐明了可以将一种普通的静态矢量 场分解为两个组成部分 , 即无旋场部分和有旋场 部分。 在传统的主动轮廓模型中 , 图像梯度信息仅仅是 作为一个静态的无旋场来平衡方程。但是实际上 我们能得到一个更加一般化的静态矢量场 , 它不 仅包含无旋场部分 , 还包含有旋场部分。 GVF 的提取可以有效的解决曲率变化很大的控 制点的收敛效果 , 但是相对的计算会很慢。
27 .梯度矢量流 -Gradient Vector Flow(GVF) GVF 定义一个力的向量场 V(x,y) = (u ( x, y ), v( x, y )) GVF snake 的内外力平衡方程为 vss vssss V 0 GVF snake 定义的能量泛函为 E (u x2 u y2 vx2 v y2 ) | f |2 | V f |2 dxdy
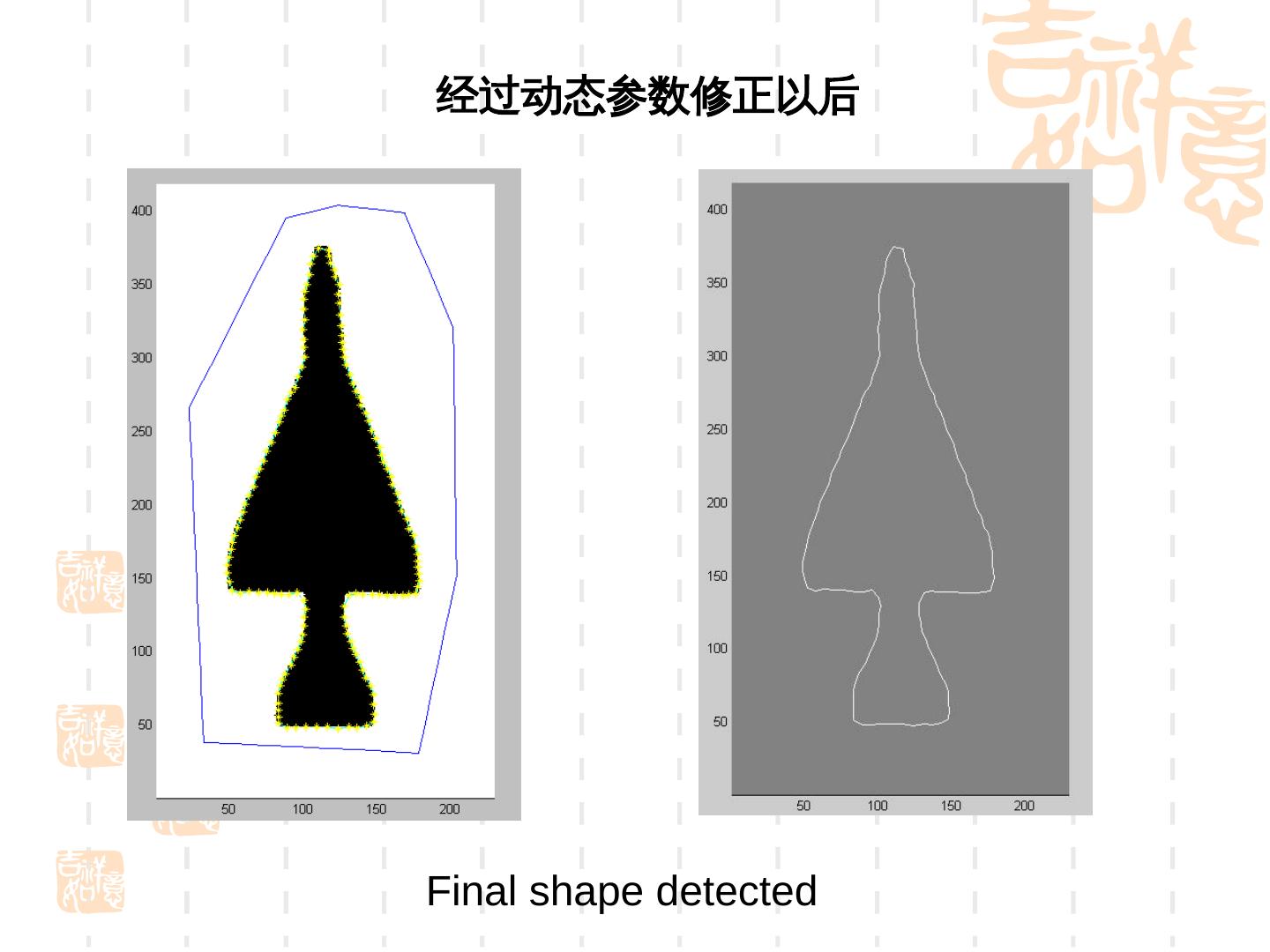
28 . GVF 场可以通过求解下述方程得到 u (u f x )( f x2 f y2 ) 0 v (v f y )( f x2 f y2 ) 0 2 是拉普拉斯算子 . 上述方程的求解是通过顺序迭代 u 和 v 实现的 能够检测边界上凹点的原因 . 使得 f 由 | f| 大的地方向 | f| 小的 地方扩散 , 因而扩大了 Snake 模型的捕捉范 围 , 也能较好地进入深度凹陷区域
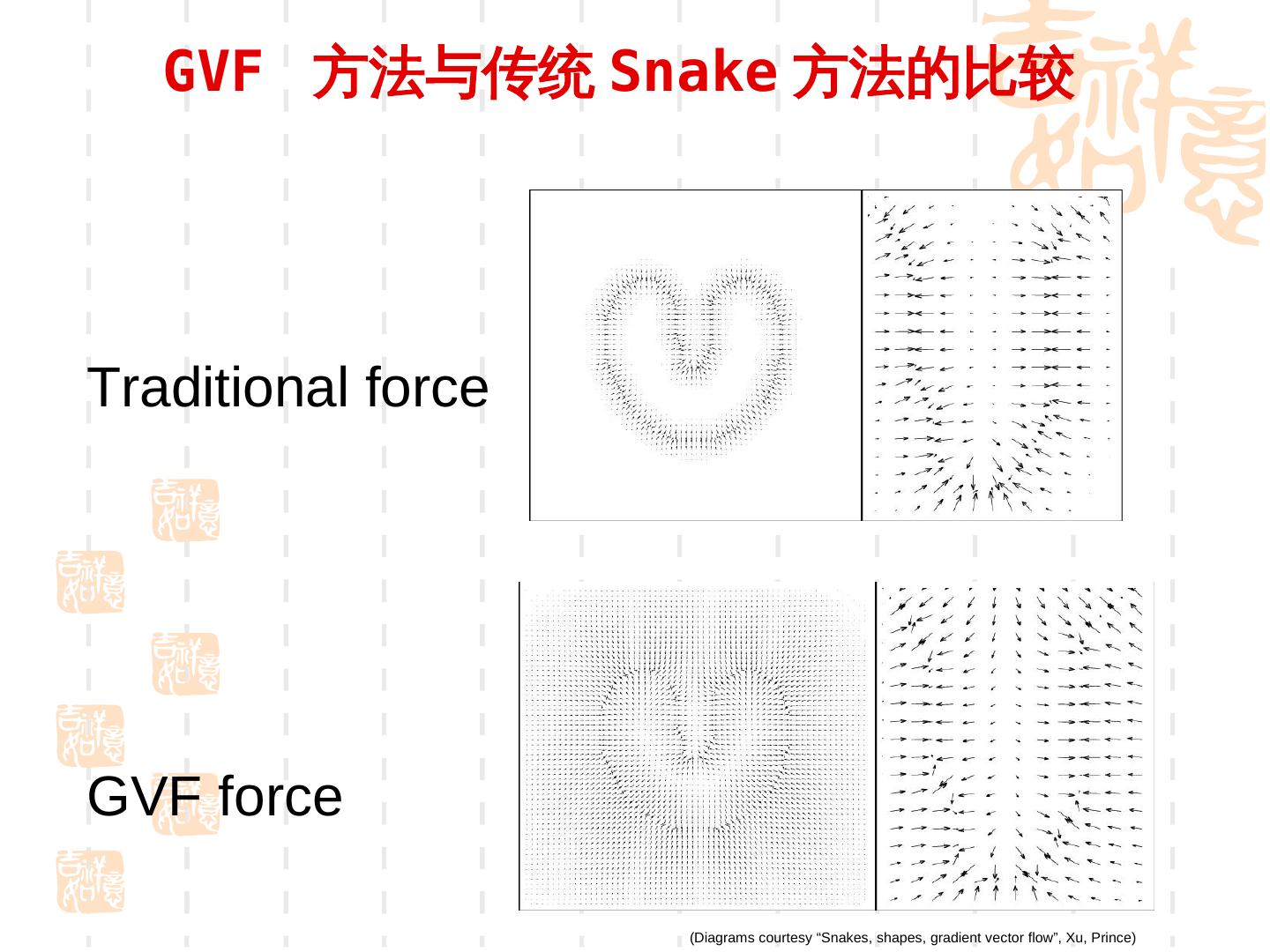
29 . GVF 方法与传统 Snake 方法的比较 Traditional force GVF force (Diagrams courtesy “Snakes, shapes, gradient vector flow”, Xu, Prince)