计算机视觉：特征的提取与匹配

1 .第四章 特征的提取与匹配 

2 .

3 .

4 . 特征的提取和匹配 左图像 角点 线 结构  对于左图像中的每一个特征… 

5 .特征的提取和匹配 右图像 角点 线 结构  在右图像中寻找相似度最大的特征 

6 .基于特征的计算机视觉处理的一般流程  特征提取  确定显著性图像特征（点、线、面）的位置  特征描述  对特征进行紧凑、唯一、可理解的描述  特征匹配  在其它图像中寻找相似度最大的特征  特征跟踪（可选，一般用于视频处理）  仅在原有特征的很小的邻域范围内寻找特征 

7 .主要内容  点特征的处理  面特征的处理  边缘特征的处理  线特征的处理 

8 .点特征提取算法 点特征主要指 明显点，提取 点特征的算子 称为兴趣算子 或有利算子 

9 .点特征的灰度特征 

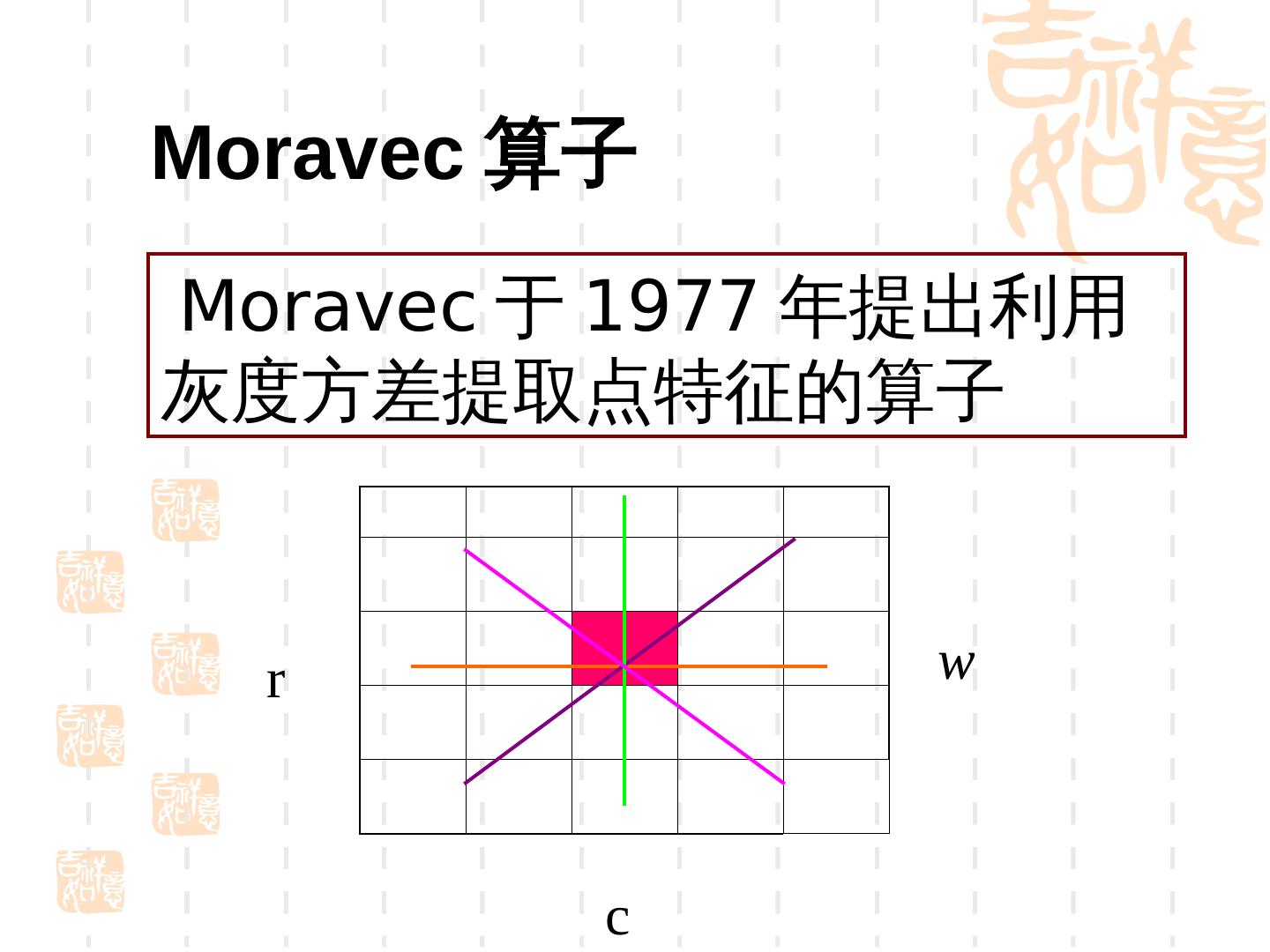
10 .Moravec 算子 Moravec 于 1977 年提出利用 灰度方差提取点特征的算子 r w c 

11 . （ 1 ）计算各像素的兴趣值 IV kk1 1  V11  V  ii    kk ((ggcc  g ii,,rr  gcc ii 11,,rr )) 22    kk1  1 2 V  V22  ii    kk ( g ( gcc i , r  i , r  ii   g g c  i  1, r  c i 1, r i 1i  1 )) 2     kk1  1  V  V33    ( g ( gcc,,rr  g ii  gcc,,rr ii 1) 1 ) 22  ii  kk  kk1 1  K=int V  V44    ( g ( gcc  g ii,,rr ii  gcc ii11 ) 22 1 )  (w/2) ,,rr ii1 ii  kk   IVc ,r min{V1 , V2 , V3 , V4 } 

12 .（ 2 ）给定一经验阈值，将兴趣值 大于阈值的点作为候选点。 （ 3 ）选取候选点中的极值点作为 特征点。 综上所述， Moravec 算子是在四个 综上所述， Moravec 算子是在四个 主要方向上，选择具有最大――最 主要方向上，选择具有最大――最 小灰度方差的点作为特征点。 小灰度方差的点作为特征点。 

13 .Forstner 算子 计算各像素的 Roberts 梯度和像素（ c ， r ）为中 心的一个窗口的灰度协方差矩阵，在图像中寻找具 有尽可能小而接近圆的误差椭圆的点作为特征点。 -1 1 r l Roberts 梯度 1 -1 c 

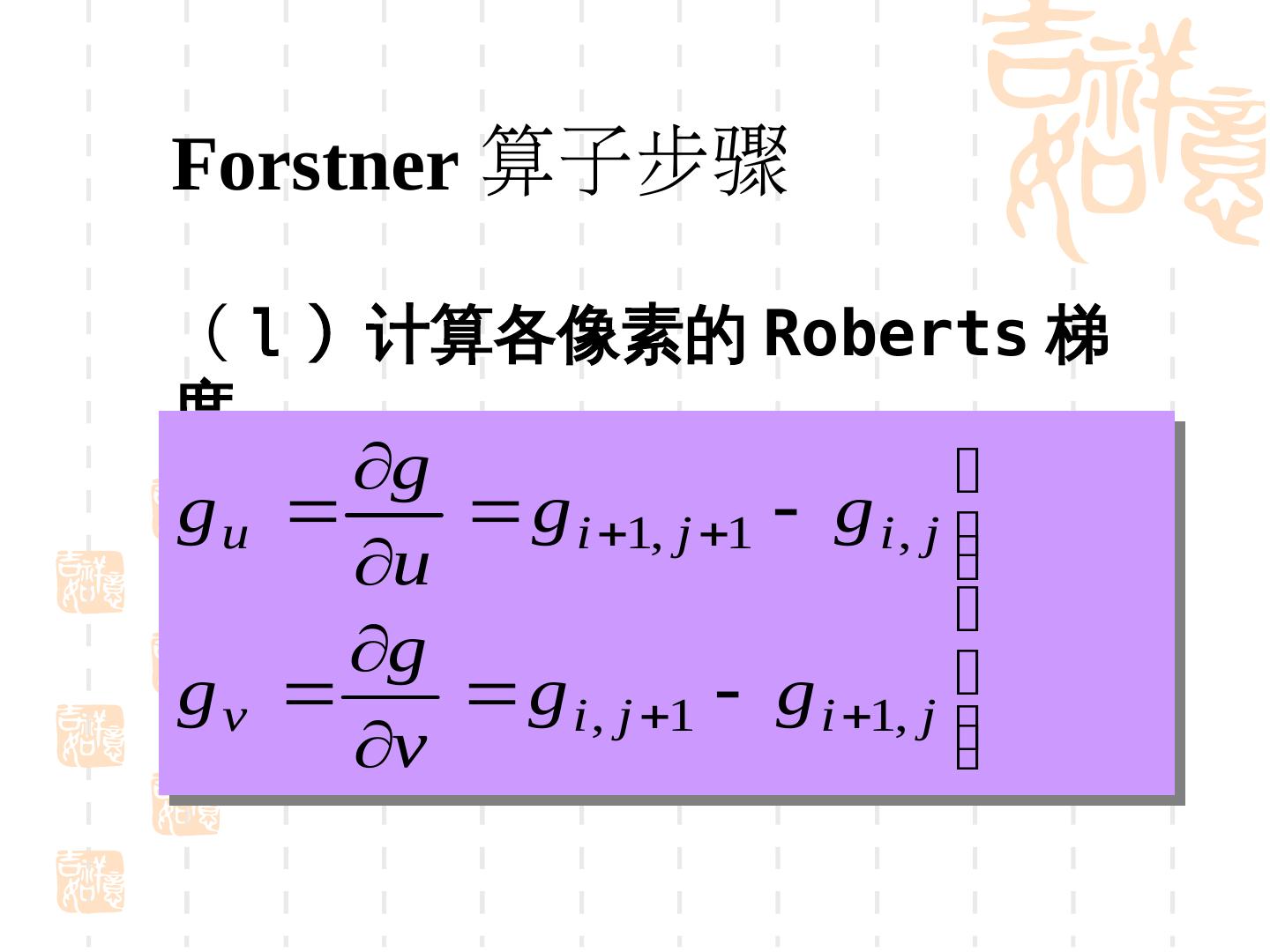
14 .Forstner 算子步骤 （ l ）计算各像素的 Roberts 梯 度 gg  gguu    ggii11,, jj11  ggii,, jj  uu   gg  ggvv    gii,, jj11  gii11,, jj   g  g vv  

15 .（ 2 ）计算 ll （如 55 或更大） 窗口中灰度的协方差矩阵  g guu 22   g g g g uu vv  Q Q N N   22     g g v v gg uu   gg vv   c k  1 r k  1 2 g  u   i 1, j 1 i , j ( g i c  k j r  k  g ) 2 c k  1 r k  1  g v2    i , j 1 i 1, j ( g i c  k j r  k  g ) 2 c k  1 r k  1  gu g v    (g i c  k j r  k i 1, j 1  g i , j )( g i , j 1  g i 1, j ) 

16 .哪个图像块更容易被定位？ 

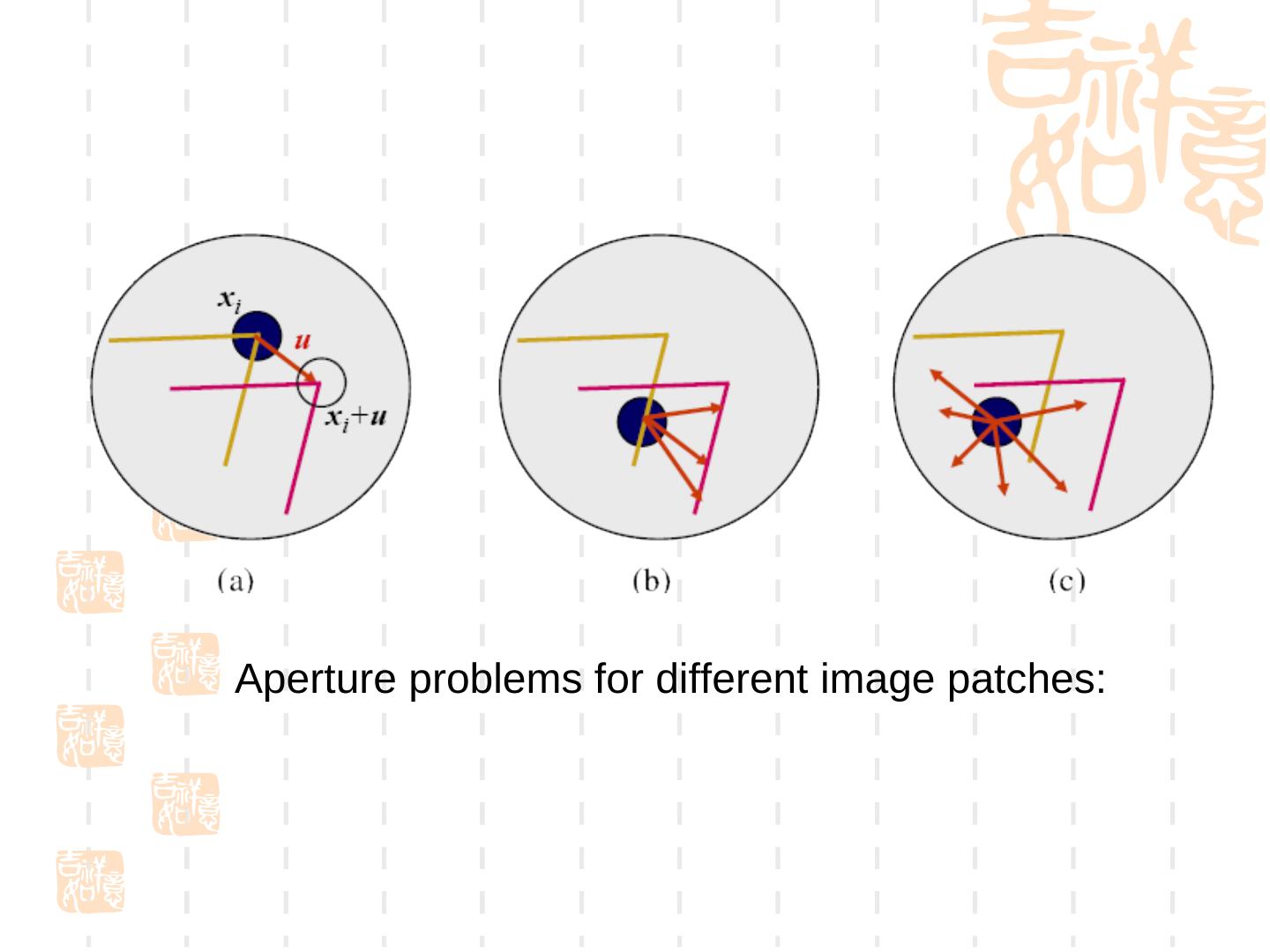
17 .Aperture problems for different image patches: 

18 .判断两幅图像的相似度 由于无法得到另一幅图像，只能在当前图像内寻找 根据泰勒级数展开， 可得， 

19 .图像自相关函数分析 矩阵 A 与信号处理中的自相关函数密切相关 . 设 α ， β 为矩阵 A 的特征值，则 α ， β 与局部自相关函数 的主曲率成比例 . 当两个曲率都低时，局部自相关函数是平坦的，那么窗口图 像区域的灰度值近似为常量；当只有一个曲率高而另一个曲 率低时，局部自相关函数呈脊形，那么 E 只有当沿山脊移动 时变化小，这就表示是边缘；当两个曲率都高时，局部自相 关函数是尖峰，那么 E 在任意方向上移动都会增加，这就表 示是角点 . 因此我们可以由 α ， β 的值判断是否是角点。为了不对 M 进行分解求特征值，可以采用 Tr(A) 和 Det(A) 来代替 α，β， Tr ( A)     A  B A I x 2 B I y 2 Det ( A)   AB  C 2 C I x I y 

20 .

21 .

22 . （ 3 ）计算兴趣值 q 与 w 1 DetN 4 DetN   q 2 trQ trN (trN ) DetN 代表矩阵 N 之行列 trN 代表矩阵 N 之 式 迹 

23 . (4 ）确定待选点 Tqq  T 00..5 5~~0 0..75 75   w (( ff   ffw 00..5 5~~1 1..5 5)) T T    c  ( c   ccc (c 5) 5 )  当 同时 ，该像素为待选点 q  Tq 同时 ，该像素为待选点 w  Tw ，该像素为待选点 （ 5 ）选取极值点 即在一个适当 同时 ，该像素为待选点 窗口中选择最大的待选点 

24 .Harris 算子  角点是景物轮廓线上曲率的局部极大点，对掌握景物 的轮廓特征具有决定作用。一旦找到了景物的轮廓特 征点也就大致掌握了景物的形状。直观的讲，角点就 是图像上所显示的物体边缘拐角所在的位置点。  Harris 角点检测法是一种基于图像灰度的检测方法 ，这类方法主要通过计算点的曲率及梯度来检测角点。 该方法是由 Harris 和 Stephen 于 1988 年提出来 的，也叫 Plessey 角点检测法。其基本思想与 Moravec 角点算子相似，但对其作了许多改进。 

25 .Moravec 角点算子 计算各像素沿同方向的平均灰度变化，选取最小值作为对应 像素点的角点响应函数。定义在一定范围内具有最大角点响 应的像素点为角点。 Moravec 角点算子简单快速，但是它存在一些缺点 : •各向异性 , 只考虑四个方向 •对强边界敏感 , 只考虑了兴趣值的最小值 

26 .Harris 角点算子 这里一阶微分可以由下面的式子近似 因此 ,EE 可以表现成 : 

27 . Harris 角点算子 为消除噪声 , 进行高斯平滑 : 在平移方向 (x ， y) 上的 E 可以表示如下 : ~  gx gx g y  M G ( s )    gx g y g y  M为 2×2 的矩阵 : 

28 .Harris 角点算子 兴趣值的计算公式为 : I Det ( M )  kTrace 2 ( M ), k 0.04 Harris 算法认为，特征点是局部范围内的极大兴趣值对应的 像素。因此，在计算完各点的兴趣值后，要提取出原始图像中 的所有局部兴趣值最大的点。 实际操作中，可以依次取出每个像素的 8 邻域中的 8 个像素， 从中心像素和这 8 个像素中提出最大值，如果中心点像素的兴 趣值就是最大值，则该点就是特征点。 在提取特征点时，凡满足大于某一阈值的像素点均可被认为是 特征点。 阈值选取的方法：通过确定图像中所能提取的最大可能的特征 点数目 N 来选择值最大的若干像素点作为特征点。局部极值点 的数目往往很多，根据 I 值进行排序，取其前 N 个为特征点。 

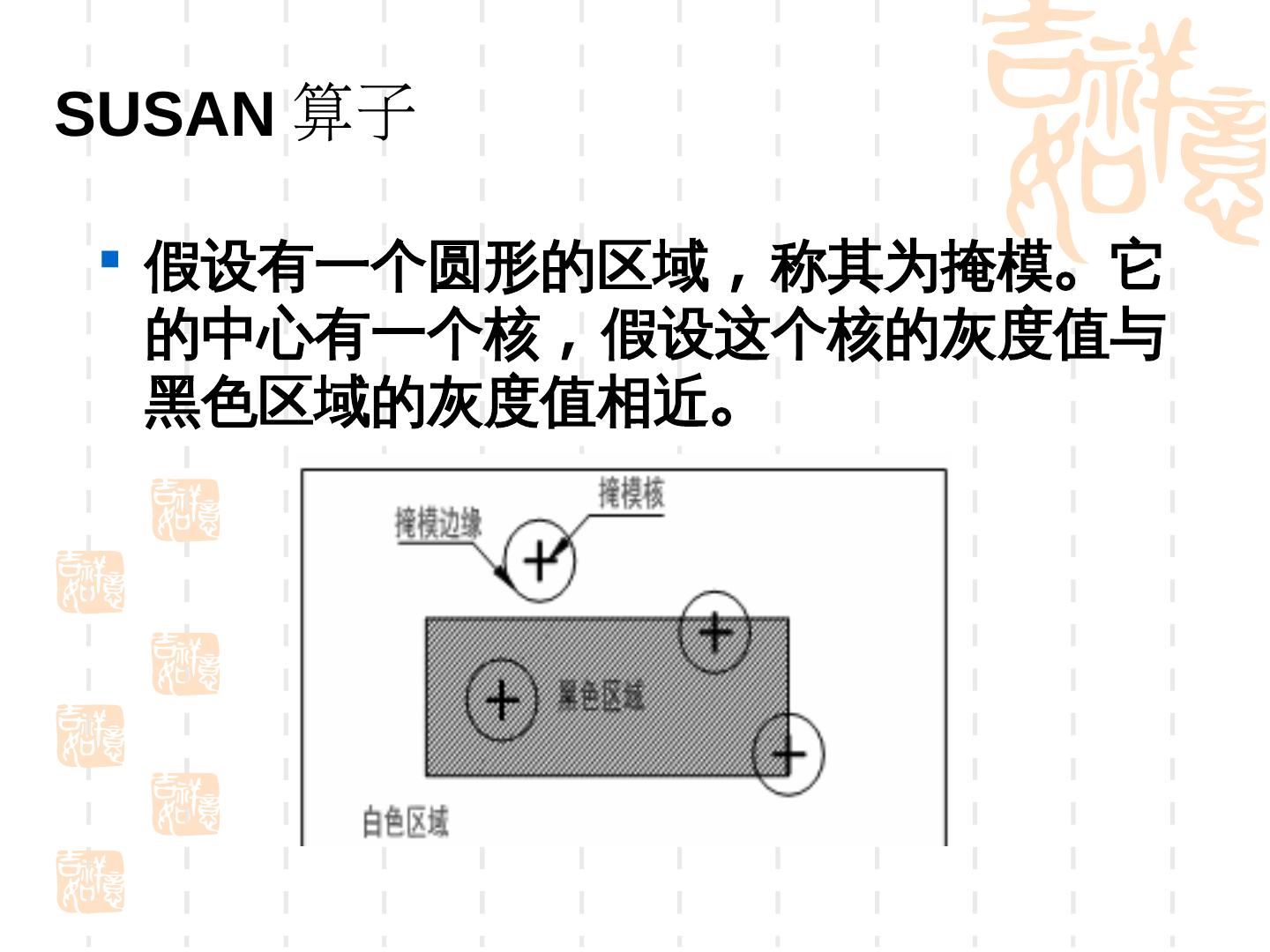
29 .SUSAN 算子  SUSAN 算法由 Smith S M 在 1997 年提 出 , 是一种基于结构元的点特征提取算子 .  SUSAN 是“ Smallest Univalue Segment Assimilating Nucleus” 的 缩写 , 即同化核分割最小值。