计算机视觉：图形处理

1 .第三章 图像处理基础 中国科技大学自动化系 曹 洋 

2 . 3. 空域处理 图像空域处理  a. 线性滤波  b. 非线性滤波  c. 二值图像处理方法  数学形态学  连通成分标记 

3 .空域滤波分类 按照分类方法的不同 数学形态分类 空域滤波器 线性滤波器 非线性滤波器 高通 低通 带通 最大值 最小值 中值 处理效果分类 钝化滤波器 锐化滤波器 

4 .3.1 线性滤波 模板，也常称为：滤波器，掩模，是一个系数矩阵，大小 为 n*n, n 通常为奇数，如 3*3,5*5,9*9. 模板运算：假设原始图像上一点 f(x,y) ，其在变换图 像的映射为 g(x,y) =T[f(x,y)] 。 T 是一种变换操 作，定义在 (x,y) 的邻域，这邻域可能是以 (x,y) 为 中心的一个方形区域，也就是说 T 对 f(x,y) 及其邻 域都作用以产生 g(x,y) 。 在空间滤波、平滑、锐化等处理中，可以通过模板在图像 上作卷积的办法来实现。 

5 .模板运算步骤 : 1. 将模板在图中漫游（卷积） 图像 2. 将模板中系数和图中对应的像素值相乘 卷积 3. 将所有的乘积相加 4. 将和赋值给模板中位置对应的像素 

6 .常用的线性滤波器 均值滤波器（低通） 每一个像素值用其局部邻域内所有像素值的加权均值置换 1 h[i, j ]   M ( k ,l )N f [k , l ] 

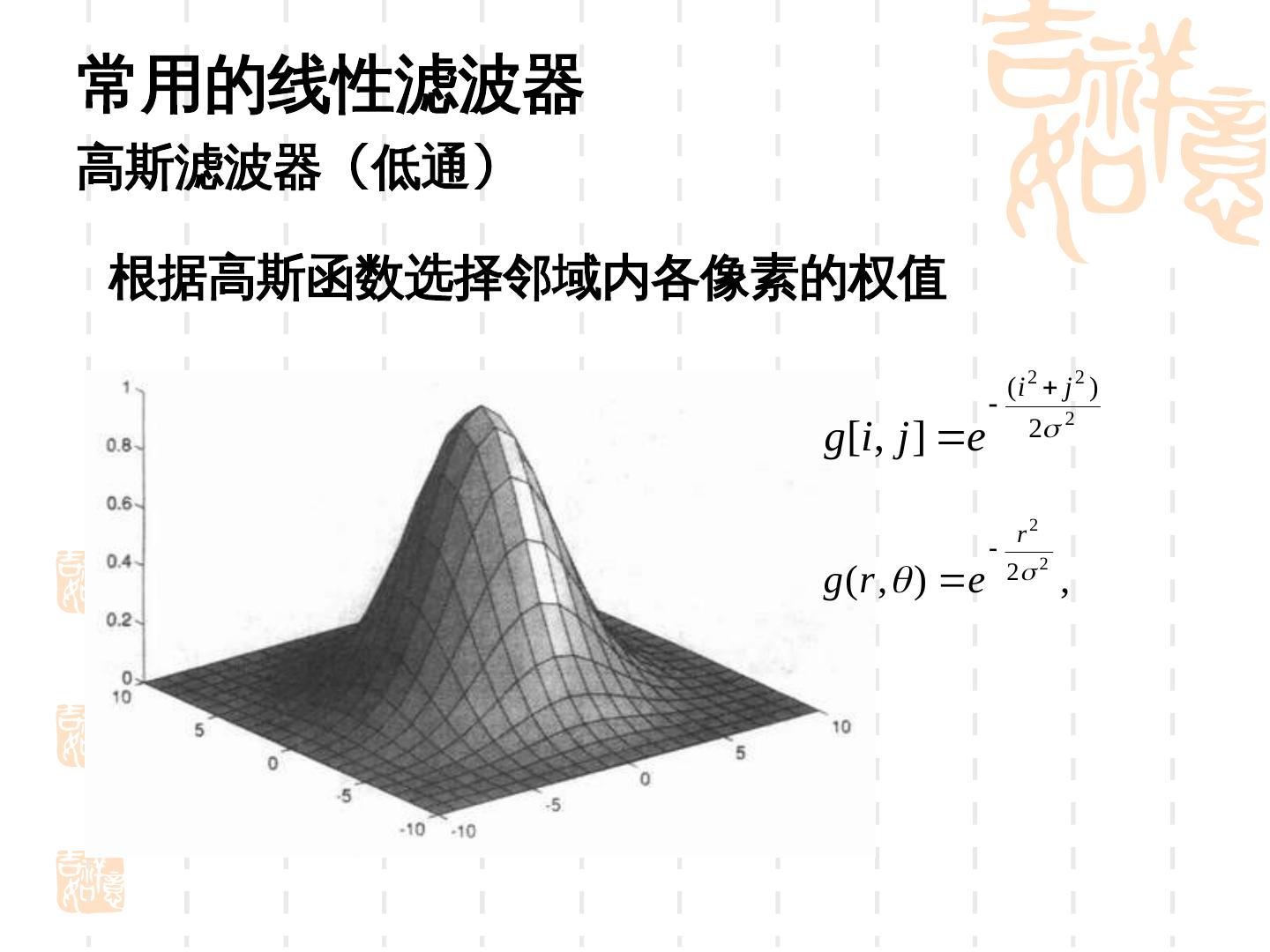
7 .常用的线性滤波器 高斯滤波器（低通） 根据高斯函数选择邻域内各像素的权值 (i 2  j 2 )  2 g[i, j ] e 2 r2  g (r ,  ) e 2 2 , 

8 .高斯平滑滤波器 高斯函数具有五个重要的性质 : • 旋转对称性 在各个方向上的平滑是一致的 • 单调递减 邻域的影响随着距离的增加而减弱 • 傅立叶变换是其本身 保留所需信号 

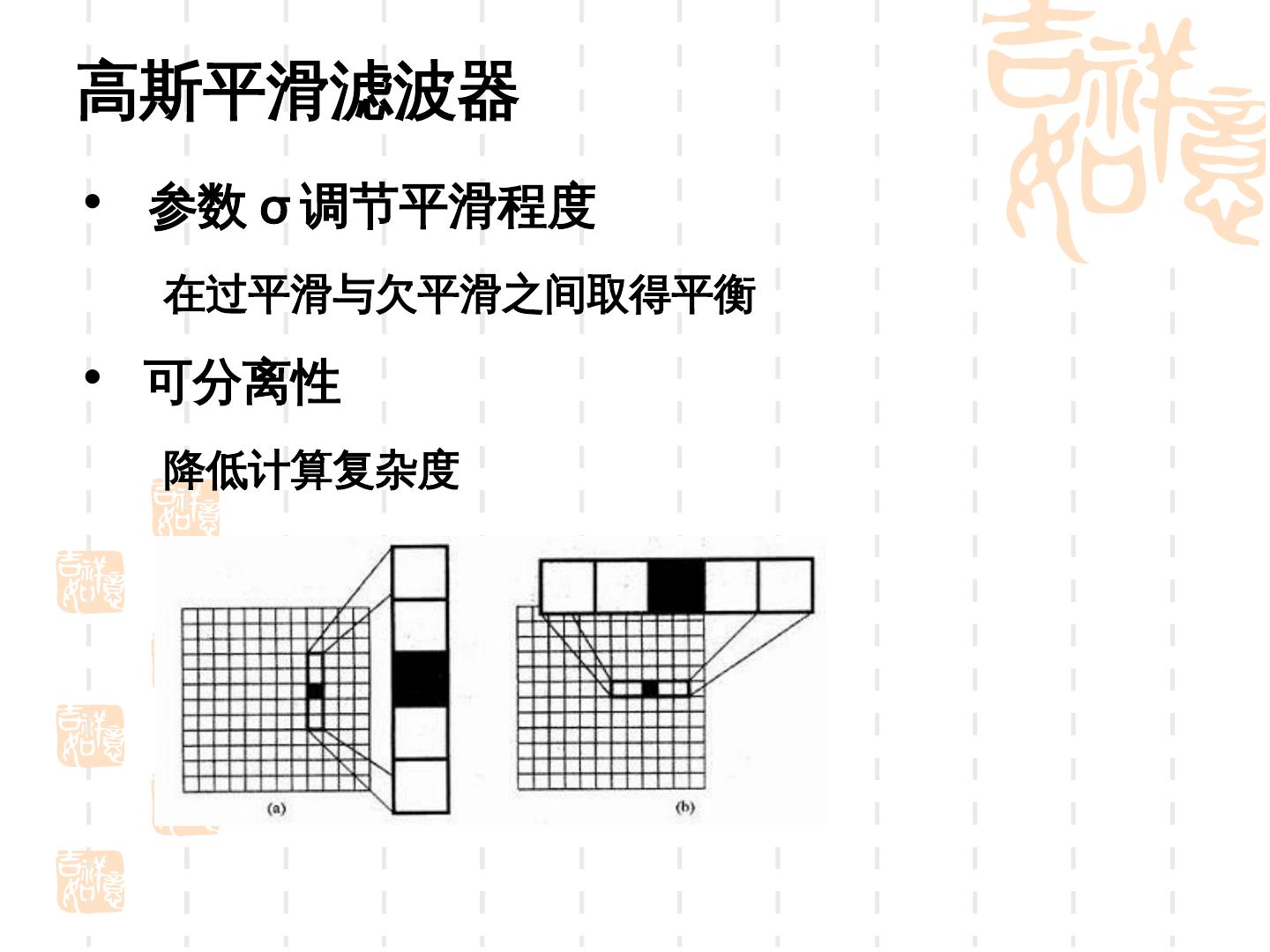
9 .高斯平滑滤波器 • 参数 σ 调节平滑程度 在过平滑与欠平滑之间取得平衡 • 可分离性 降低计算复杂度 

10 .常用的线性滤波器 带通滤波和导向滤波 （ Band-pass and steerable filters ） Gabor Filter 

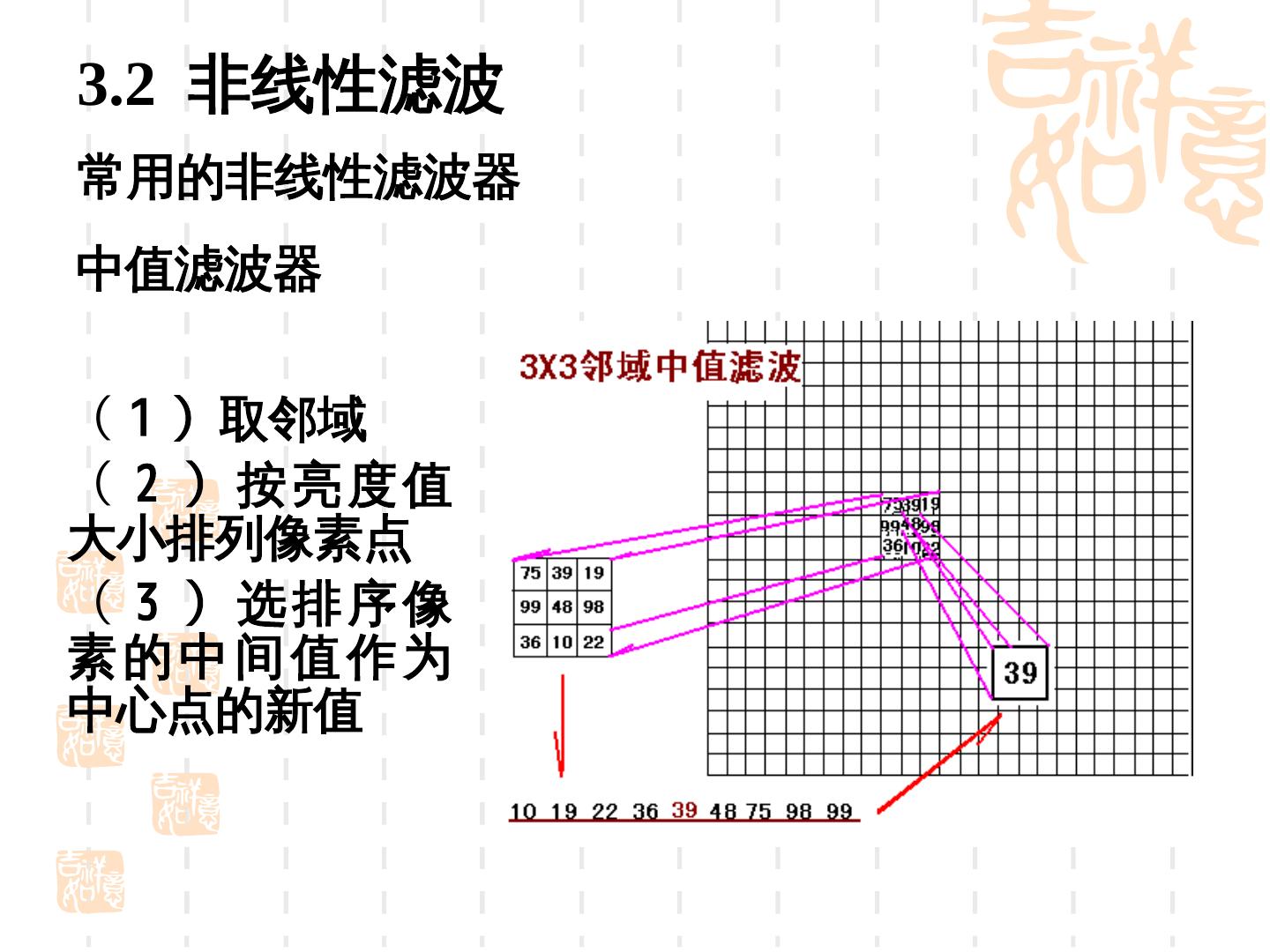
11 .3.2 非线性滤波 常用的非线性滤波器 中值滤波器 （ 1 ）取邻域 （ 2 ）按亮度值 大小排列像素点 （ 3 ）选排序像 素的中间值作为 中心点的新值 

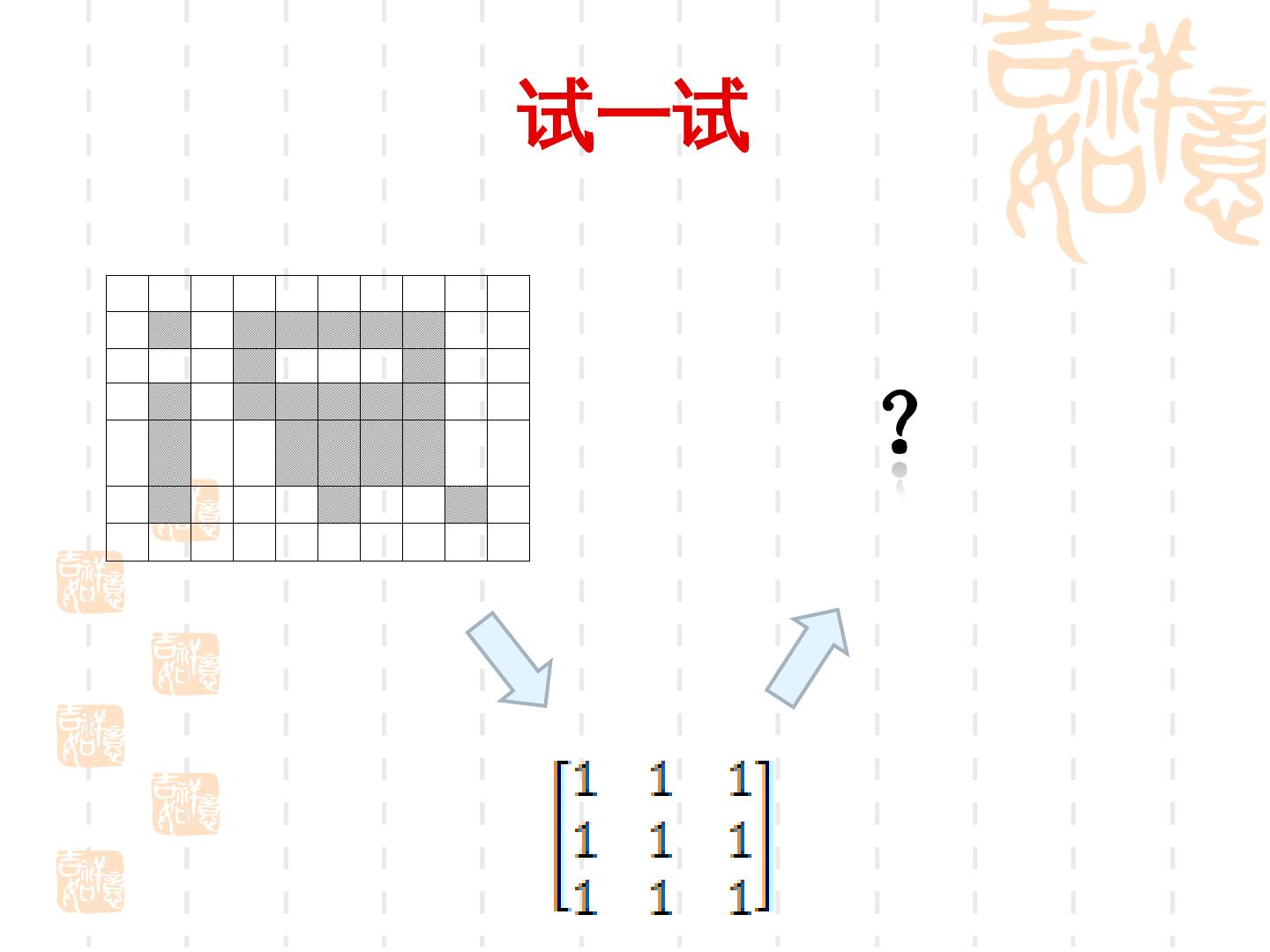
12 .试一试 

13 .试一试 

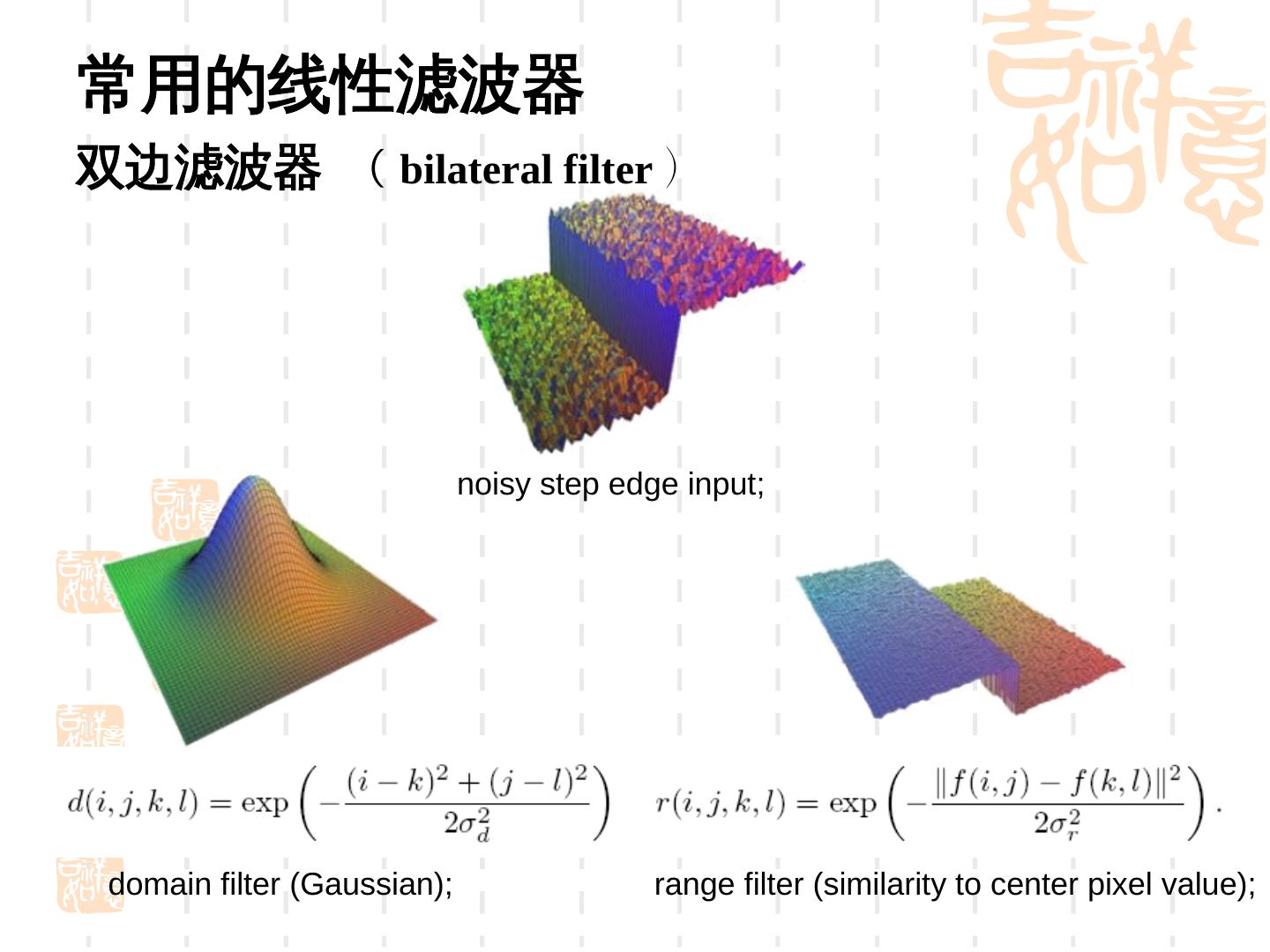
14 .常用的非线性滤波器 双边滤波器（ bilateral filter ） 高斯滤波器的不足 

15 .常用的线性滤波器 双边滤波器 

16 .常用的线性滤波器 双边滤波器 （ bilateral filter ） noisy step edge input; domain filter (Gaussian); range filter (similarity to center pixel value); 

17 .双边滤波器 双边滤波器 滤波结果 

18 . 图像引导滤波器 [6] K. He, J. Sun, and X. Tang. Guided image filtering. In Proc. of ECCV, 2010. 

19 .图像引导滤波器 

20 .图像引导滤波器 

21 .双边滤波器 vs 引导滤波器 

22 .3.3 二值图像处理 二值图像 • 只有黑白两级灰度的图像 • 去掉无关信息的干扰 , 计算速度快 • 所需内存小 , 节省资源 • 算法可应用于灰度图象 • 适用于工业场合 • 

23 .3.3.1 二值图像基本概念 （ 1 ）近邻： 4 邻点 (4-neighbors):neighbors):): 有公共边关系的两个像 素． 8 邻点 (8-neighbors):neighbors):): 两个像素至少共享一个 顶角 . 4 连通 (4-neighbors):connected):): 一个像素与其 4 邻点的关系 8 连通 (4-neighbors):connected):): 一个像素与其 8 邻点的 关系 

24 . (2) 路径 路径 : 从像素到像素的一个像素序列 4 路径 : 像素与其近邻像素是 4 连通关系 8 路径 : 像素与其近邻像素是 8 连通关系 (3) 前景 图像中值为 1 的全部像素的集合，用 S 表示． (4) 连通性 已知像素 p 和 q ，如果存在一条从 p 到 q 的路径， 且路径上的全部像素都包含在 S 中，则称 p 与 q 是连通的 ． 

25 .(5) 连通成份 一个像素集合 S ，如果 S 内的每一个像素与 集合内其它像素连通，则称该集合为一个连通成份 (6) 背景 `S （ S 的补集）中包含图像边界点 的所有连通成份的集合 洞 :`S 中所有非背景其它元 对物体和背景应使用不同的连通 . 如果对 S 使用 8 连通 , 则对 `S 应使用 4 连通 洞 S 

26 .(7) 边界 S 的边界是 S 中与 `S 中有 4 连通关系的像素集合 S ' （ 8) 内部 S 中不属于它的边界的像素集合 . S 的内部等于 S -neighbors): S ' （ 9) 包围 如果从 S 中任意一点到图像边界的 4 路径必须与区域 T 相交，则区域 T 包围区域 S （或 S 在 T 内） 边界 S 图像 内部 边界 S 包围 例：一幅二值图像 

27 .3.3.2 数学形态学（ mathematical mophology ） 图像分析与识别思想：基于形状 理论基础：集合论 作用：保持形状特征，同时简化图像 工具：结构元 

28 .形态学算子 -neighbors):1 • 膨胀（ d):ilation ）：扩张图像区域 结构元原点是指定的，不一定是图像左上角 多种解释：向量、图像位移、结构元位移 A  B { p | p  p  b, p  A, b  B} A  B Ab bB A  B {x | Bˆ x  A  A} 

29 .形态学算子 -neighbors):2 • 腐蚀（ eros):ion ）： 获得表示结构元所有出现位置的图像 AB  p p  b  A, b  B AB   A b bB  AB  p B p  A 