计算机视觉：图像处理

1 .第三章 图像处理基础 中国科技大学自动化系 曹 洋 

2 .图像处理 • 目的 突出感兴趣特征，服务于机器视觉 图像增强 •可能的处理 : 去除噪音、边缘增强、提高对比度、增加亮度、改 善颜色效果、改善细微层次等 —— 通常与改善视觉效果相一致 

3 . 主要内容  图像表示  点操作  空域处理  频域处理 

4 . 1. 图像表示  图像具有二维平面的形式  图像可以存在于多种介质 , 但最后必须以 可视的形式出现  图像是客观世界的真实反映  图像记录的特性可以是光学特性 , 也可以 是非光学特性 , 但可以转为光学特征表达  从信息系统来看 , 图像是一种信息的载体  从数字系统来看 , 图像是一种信号 

5 . 1.1 数字图像生成  数字成像 CCD ：电荷耦合器件电荷耦合器件 , CMOS: 互补金属氧化物半导体 光栅扫描：电荷耦合器件 PAL 制式， NTSC 制式 像素 : 图形系统能够清楚成像的最小单元 分辨率：电荷耦合器件像素的物理尺寸 灰度分辨率：电荷耦合器件灰度 2^kk 灰度级， k 比特数 空间分辨率：电荷耦合器件矩阵 M×N 

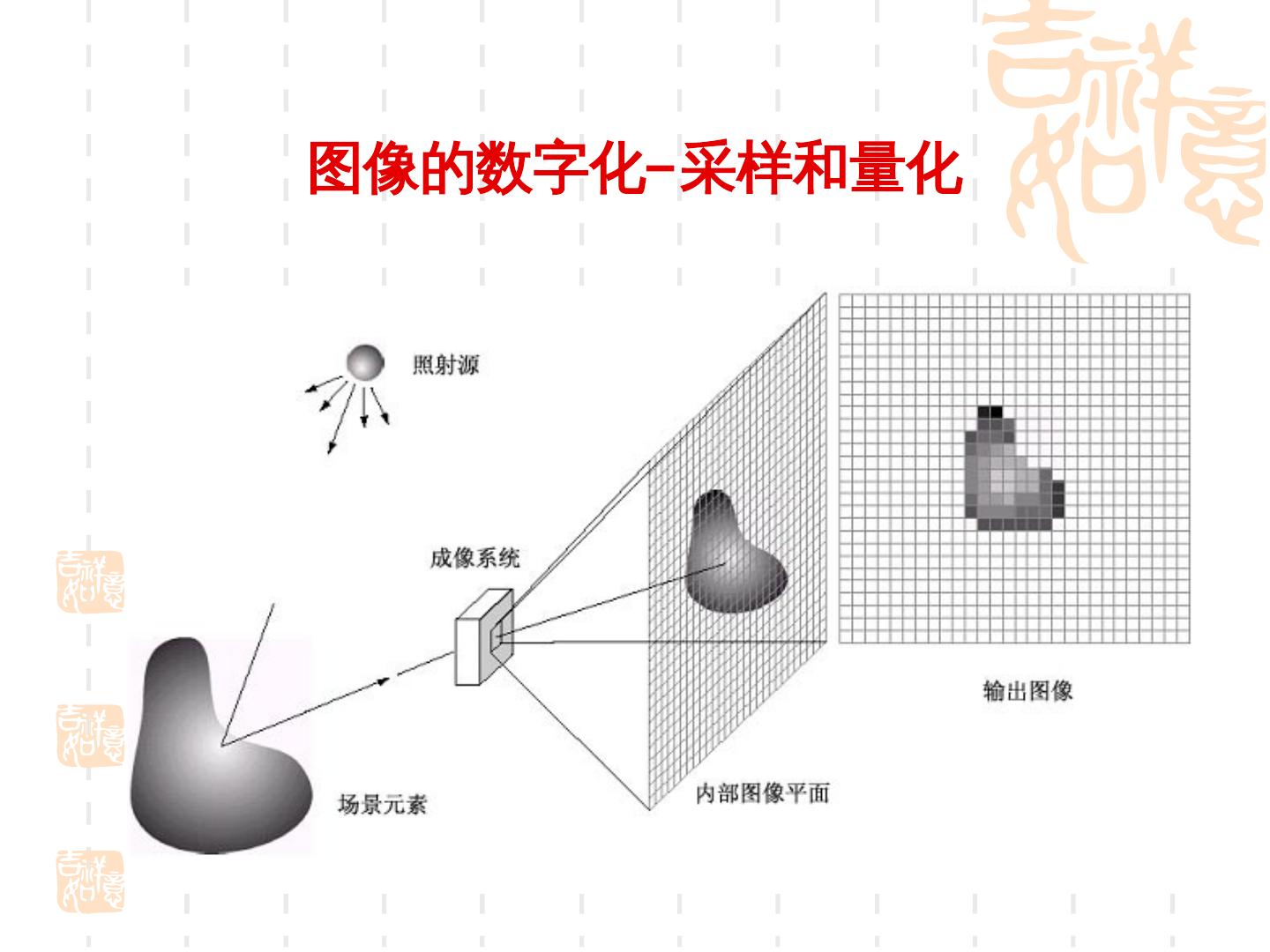
6 .图像的数字化— 采样和量化 

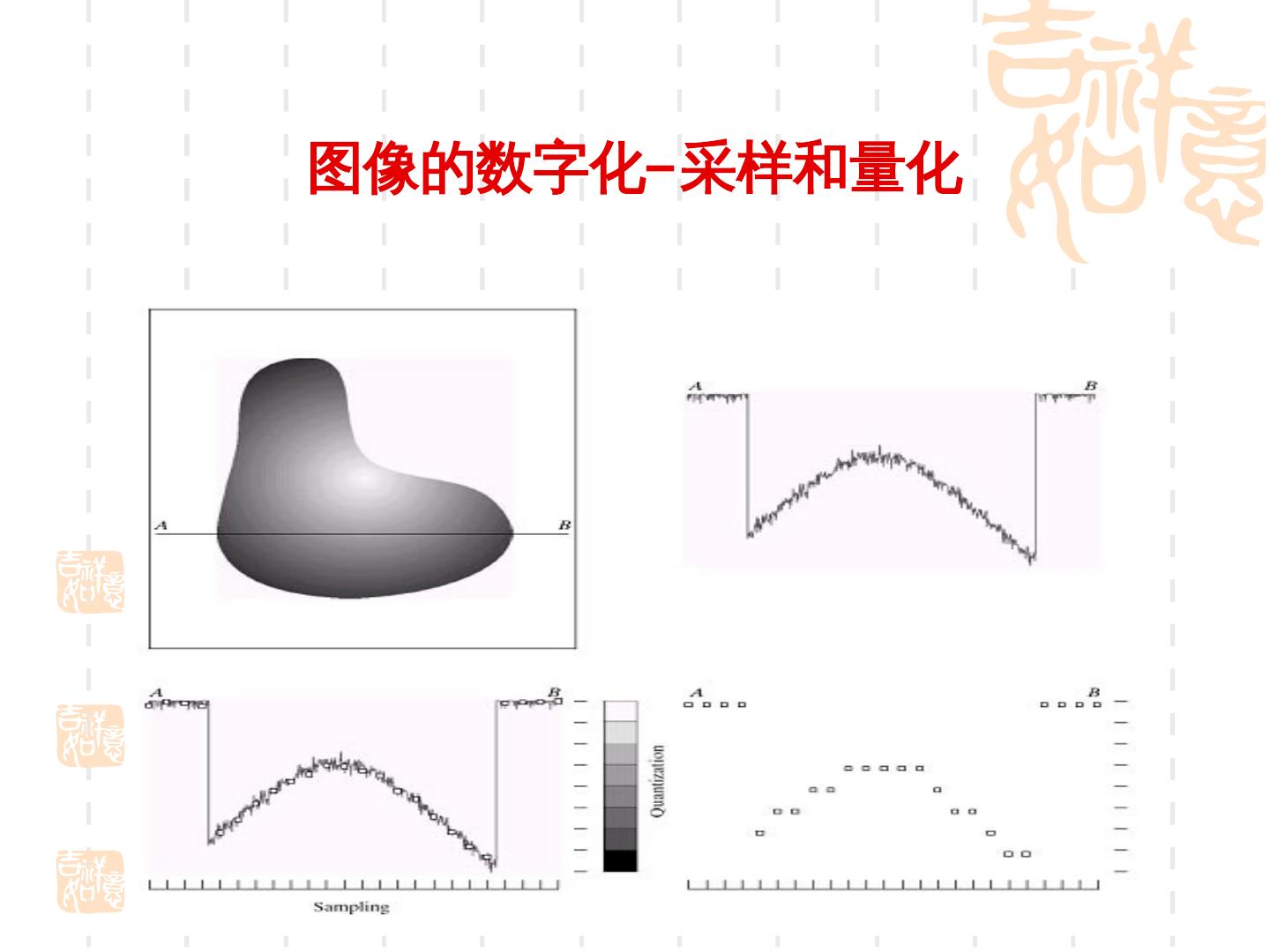
7 .图像的数字化— 采样和量化 

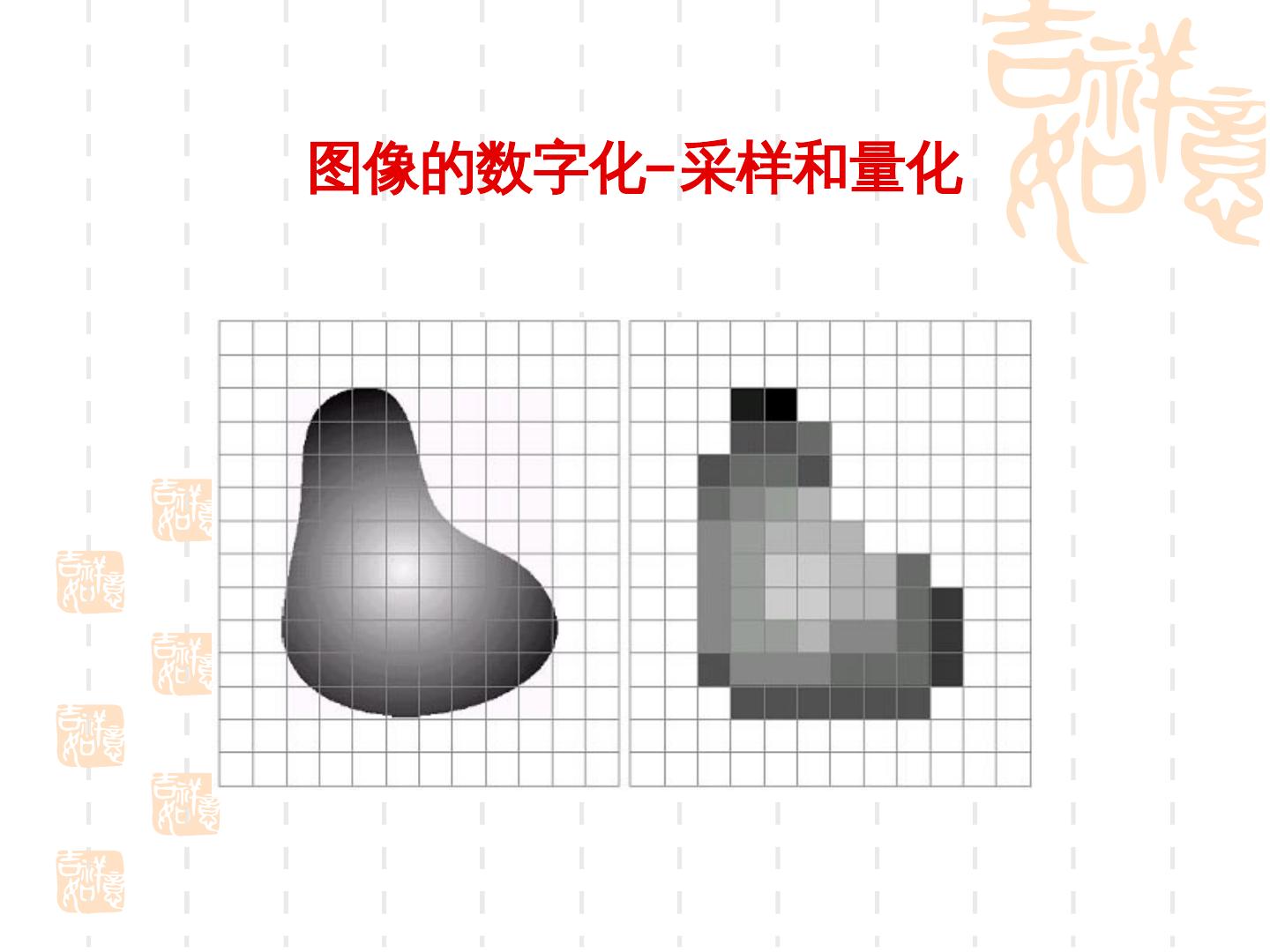
8 .图像的数字化— 采样和量化 

9 .图像的数字化— 采样和量化 

10 . 1.2 图像的表示方法  图像形式  函数形式  信号形式 

11 . 图像形式  2 维灰度图像  3 维密度图像  2.5 维距离图像 

12 .

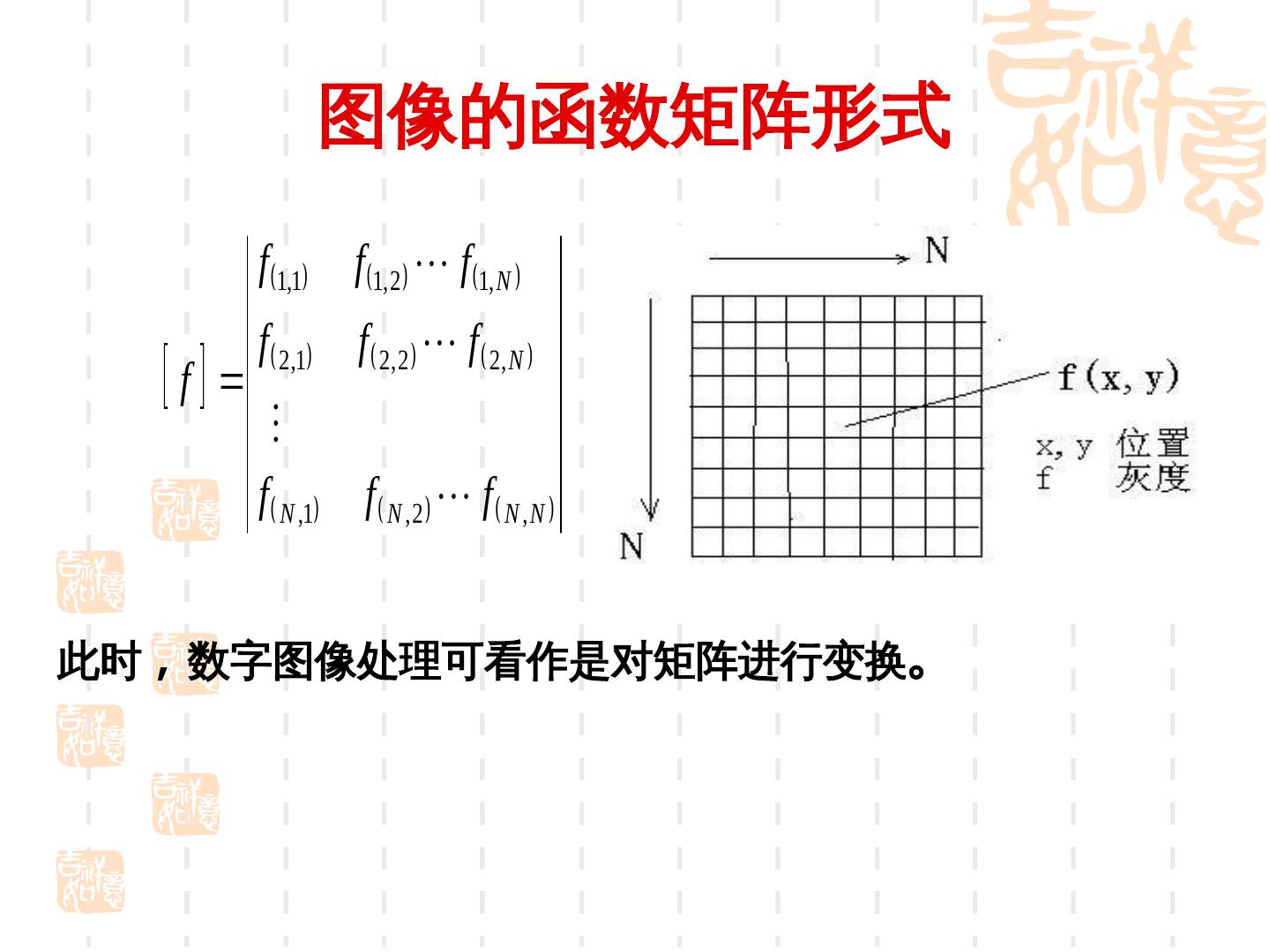
13 . 图像的函数矩阵形式 f 1,1 f 1, 2   f 1, N  f  2,1 f  2, 2   f  2, N  f  f  N ,1 f  N , 2   f  N , N  此时 , 数字图像处理可看作是对矩阵进行变换。 

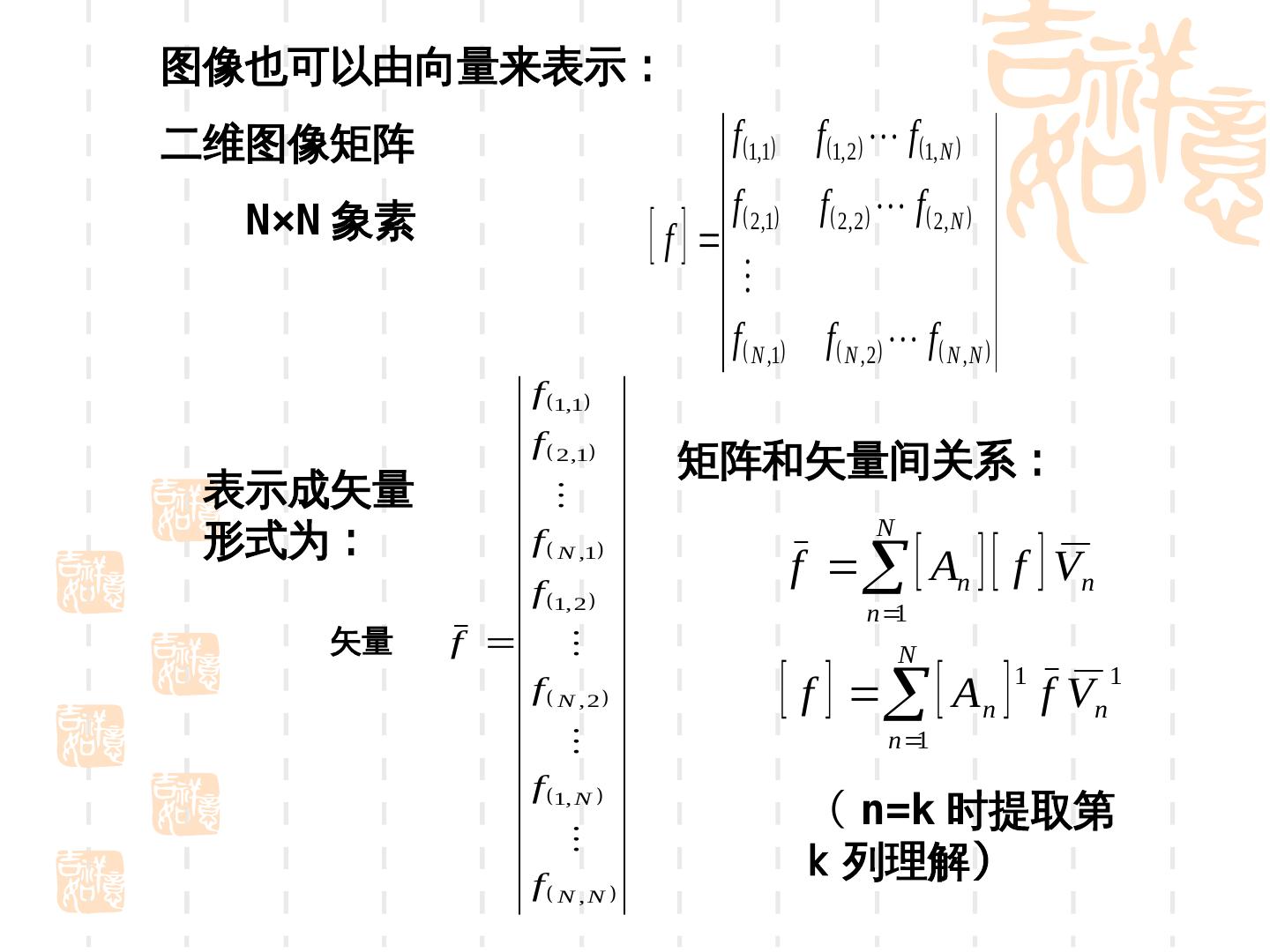
14 .图像也可以由向量来表示：电荷耦合器件 二维图像矩阵 f 1,1 f 1, 2   f 1, N  N×N 象素 f  2,1 f  2,2   f  2, N  f  f  N ,1 f  N , 2   f  N , N  f 1,1 f  2 ,1 矩阵和矢量间关系：电荷耦合器件 表示成矢量  N 形式为：电荷耦合器件 f  N ,1 f   An   f  Vn f 1, 2  n 1 矢量 f   N f N ,2  f    A n  1 f V n 1  n 1 f 1, N  （ n=k 时提取第  f N ,N  k 列理解） 

15 .图像的几何函数形式（流形） 

16 . 信号形式  认知心理学 (psychophysical)psychophysical)) 研究表 明，人类在分析纹理图像时，将图像分解 为不同的频率和方向成分 .  对图像作频率和方向选择性滤波，得到相 应特征 .  空域滤波  频域滤波 Fourier 变换 (psychophysical)Fourier transform)) 

17 .空域频率表示 

18 .空域频率表示 

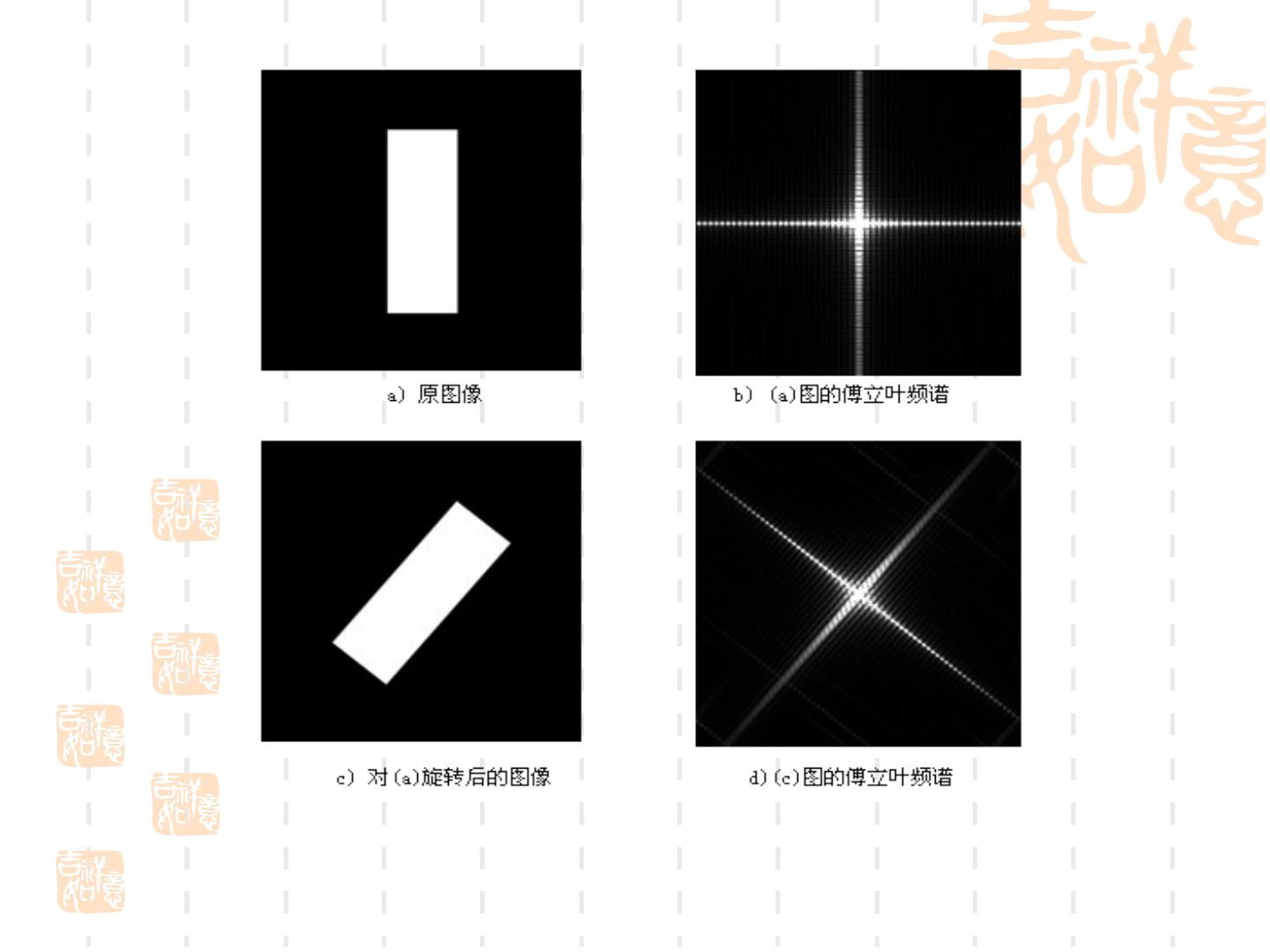
19 . 空域频率表示  图像亮度的变化与图像内容的空域频率成正比  图像的空域频率响应是一种表征锐利度的方法  提取图像空域频率成分的方法：电荷耦合器件傅立叶变换 1 F (u, v)   f ( x, y ) exp( i 2 (ux  vy)) k x y  空域频率随方向变化  空域频率在图像中的分布是变化的  空域内的卷积运算与频域内的乘积运算等价 

20 .傅立叶变换 

21 . 直流部分 二维 DFT 1 2 图像 3 4 二维 IDFT 对应低频 对应高频 成分 成分 图像的二维离散傅立叶变换的频率成分分布示意图 变换结果的左上、右上、左下、右下四个角部分对 应于低频成分，中央部分对应于高频成分。 

22 . （ a ） l)enna 图 （ b ）傅氏变换的频谱图 图像及其频谱图像示意图 对于一幅图像，图像中灰度变化比较缓慢的区域对应 较低的频谱，而灰度变化比较大的边缘地带对应较高 的频谱。而且一幅图像中大部分都是灰度变化缓慢的 区域，只有一小部分是边缘，因此，其变换域的图像 ，能量主要集中在低频部分（对应值较高），只有一 小部分能量集中在高频部分（对应值较低）。 

23 .

24 .

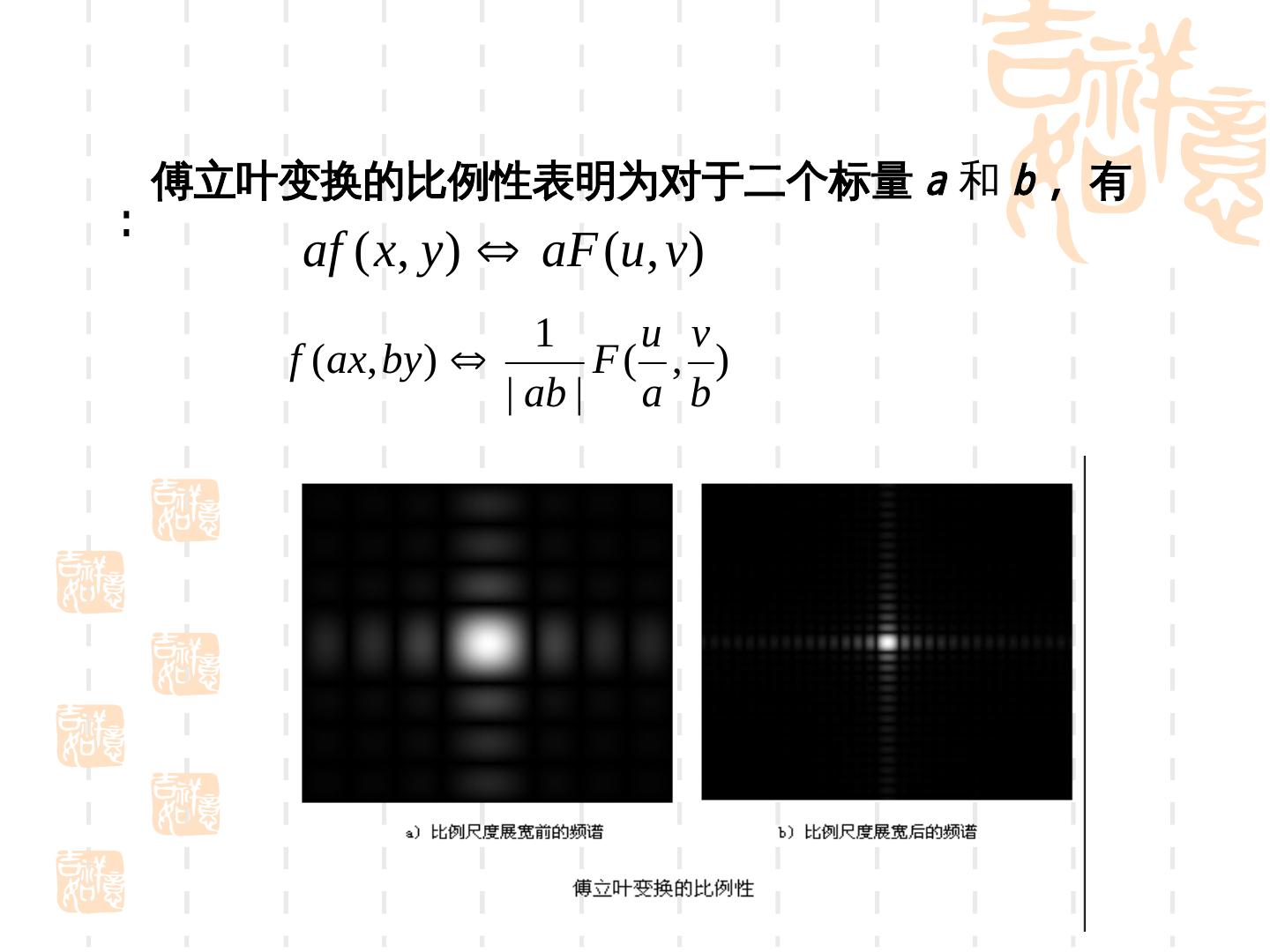
25 . 傅立叶变换的比例性表明为对于二个标量 a 和 b ，有 ：电荷耦合器件 af ( x, y )  aF (u , v) 1 u v f (ax, by )  F( , ) | ab | a b 

26 . 离散图像付氏变换应用 实例 1 正弦波去噪 

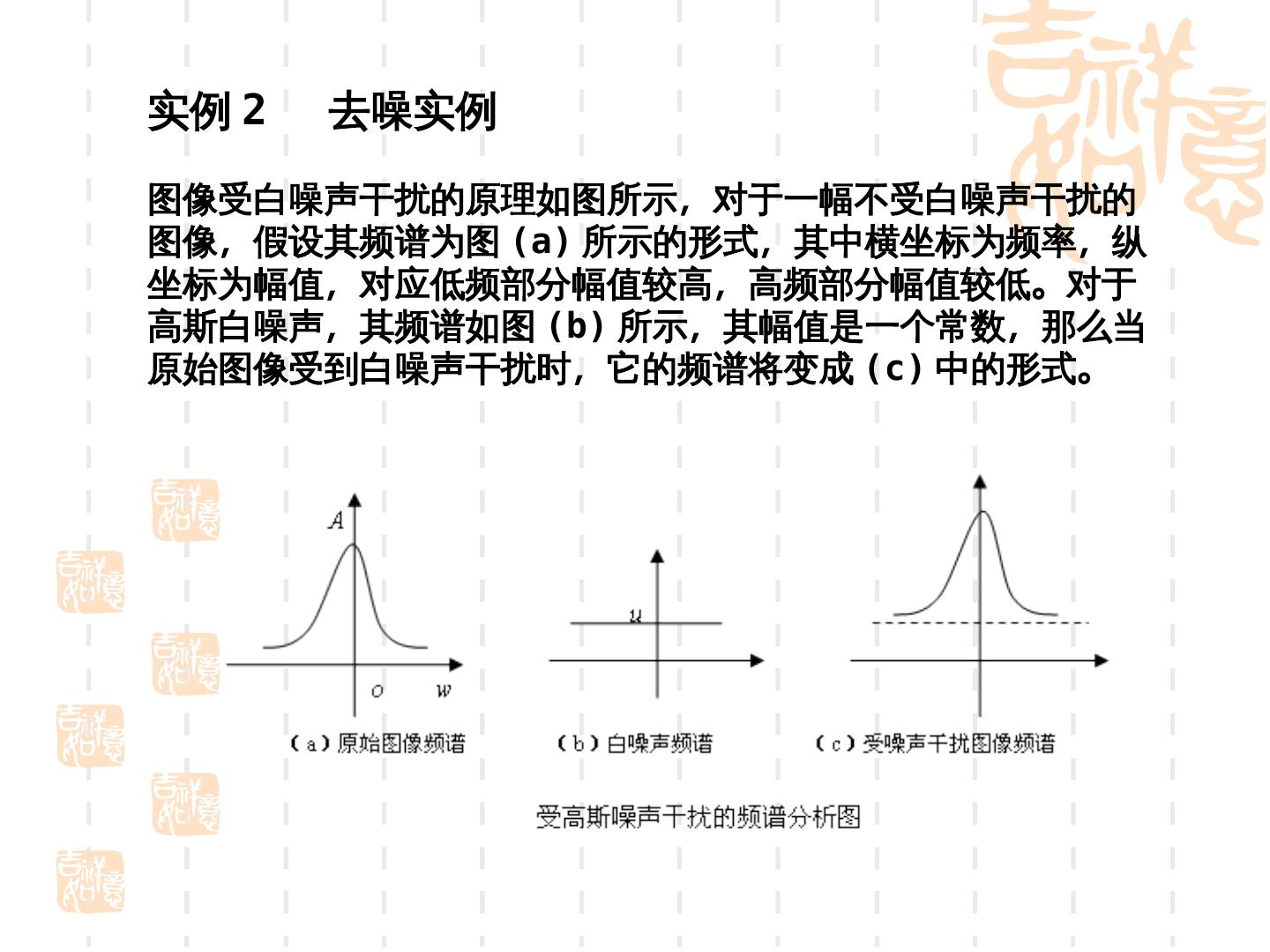
27 .实例 2 去噪实例 图像受白噪声干扰的原理如图所示，对于一幅不受白噪声干扰的 图像，假设其频谱为图 (psychophysical)a) 所示的形式，其中横坐标为频率，纵 坐标为幅值，对应低频部分幅值较高，高频部分幅值较低。对于 高斯白噪声，其频谱如图 (psychophysical)b)) 所示，其幅值是一个常数，那么当 原始图像受到白噪声干扰时，它的频谱将变成 (psychophysical)c) 中的形式。 

28 .要去除图像中的白噪声，在频域中减去白噪声的幅值即可。 理想的方法：电荷耦合器件 知道白噪声的模型，一般情况下很难遇到。在未知噪声幅值 的情况下，可以先对噪声图像求频谱，并计算频谱幅值的平均值 ，用该平均值作为噪声的近似幅值，就可以对图像去噪。 

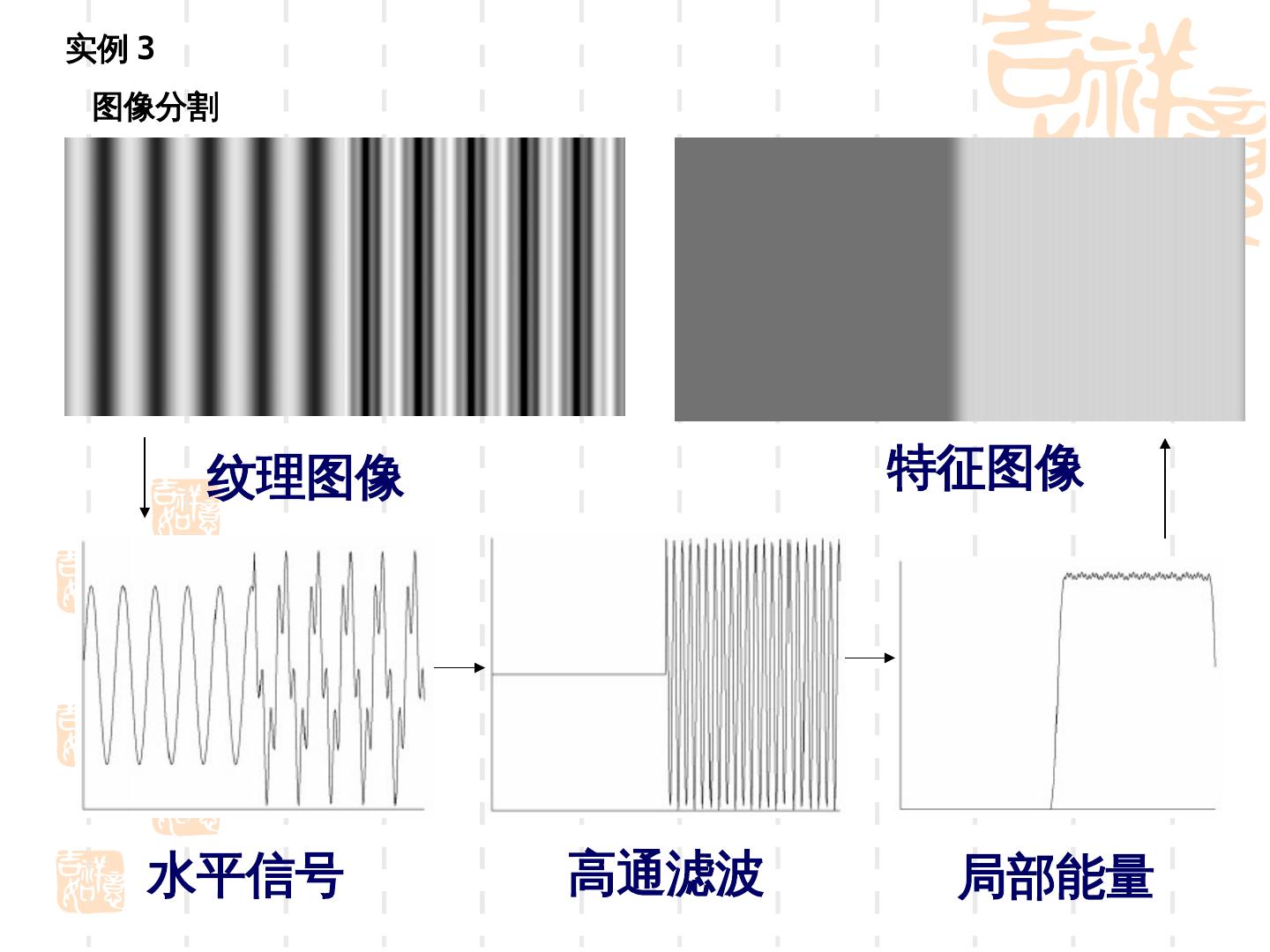
29 .实例 3 图像分割 纹理图像 特征图像 水平信号 高通滤波 局部能量