计算机系统信息安全

1 .计算机系统信息安全 南京大学计算机系 黄皓 教授 2013年9月17日 

2 .开场白 —— 一个电话骗局 中央电视台《今日说法》报道 

3 . 一个电话欺骗（中央电视台今日说法） 第1幕 — 在火车站  一个计划到上海的给孩子看病的旅客到达了上海站。  他到公用电话处，拿起电话听筒，拨打在上海的亲戚的电话。  旅客：“喂，是表哥吗？”  听筒传出：“是，你到了？很不巧，因为交通堵塞，我还没有到车站。你们 到人民路的人民商场门口，我到那里接你吧。”  旅客：“好。” 南京大学计算机系讲义 

4 .一个电话欺骗（中央电视台今日说法） 第2幕 — 在人民商场门口  旅客在人民商场的门口等待。  一个中年人向正在等待的旅客走来。  “我是你表哥委托来接你们的。”  交谈后，在准备回表哥家时：  中年人：“我刚才在前面一个商店看到了我要一直想买的非常紧俏的相机，今 天好不容易看到了，但是我没有带够钱，你们身上有钱吗？借给我一点，回去 马上给你。”  “你要多少？”  ”三千“  “好”  你们稍等，我马上回来。  几个警察迅速抓住了这个快速离开的中年人。  旅客过去跟警察说：“这是我表哥的朋友，你抓错人了吧？” 南京大学计算机系讲义 

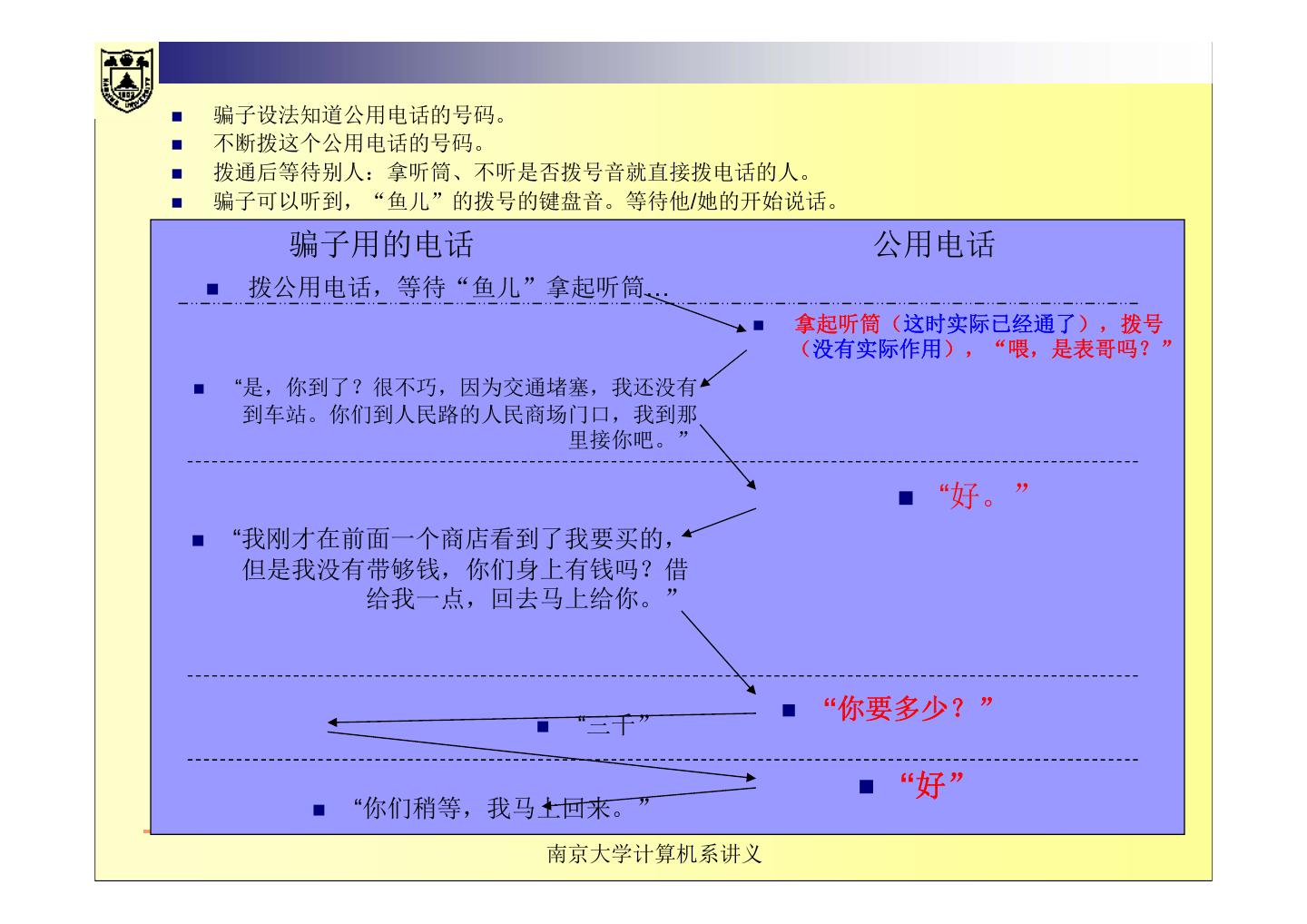
5 . 骗子设法知道公用电话的号码。  不断拨这个公用电话的号码。  拨通后等待别人：拿听筒、不听是否拨号音就直接拨电话的人。  骗子可以听到，“鱼儿”的拨号的键盘音。等待他/她的开始说话。 骗子用的电话 公用电话  拨公用电话，等待“鱼儿”拿起听筒…  拿起听筒（这时实际已经通了），拨号 （没有实际作用），“喂，是表哥吗？”  “是，你到了？很不巧，因为交通堵塞，我还没有 到车站。你们到人民路的人民商场门口，我到那 里接你吧。”  “好。”  “我刚才在前面一个商店看到了我要买的， 但是我没有带够钱，你们身上有钱吗？借 给我一点，回去马上给你。”  “你要多少？”  “三千”  “好”  “你们稍等，我马上回来。” 南京大学计算机系讲义 

6 . 课程内容 1. 对称密码学 8. IP安全 2. 非对称密码学 9. Web安全 3. 密码协议 10. 安全电子交易 4. 公开密钥基础设施 11. 安全邮件 5. 安全模型 12. 网络防火墙技术 6. 安全操作系统 13. 入侵检测技术 7. 安全数据库 14. 安全评估技术 2013/10/15 南京大学计算机系讲义 6 

7 . 参考书 1. 讲稿和各章讲稿所列的参考文献 2. Wenbo Mao(毛文波)，现代密码学理论与实践，电子工 业出版社，2004年7月。 3. 王立斌，黄征译，计算机安全学—安全的艺术与科学， 电子工业出版社，2005年5月。 4. Allen Harper, Shon Harris等著， 杨明军，韩智文，程 文俊译， 灰帽黑客，清华大学出版社，2012年11月，第 1版。 2013/10/15 南京大学计算机系讲义 7 

8 .第1章 对称密码学 

9 . 参考文献 1. Wenbo Mao(毛文波)，现代密码学理论与实践，电子工业出版 社，2004年7月。 2. 吴文玲，冯登国，张文涛，分组密码的设计与分析，清华大学 出版社，2009年10月。 3. 冯登国，密码分析学，清华大学出版社，2000年8月。 4. Bruce Chneier, 应用密码学，机械工业出版社，2000年1月。 2013/10/15 南京大学计算机系讲义 9 

10 . 一个例子  问题  两个朋友Alice和Bob想一起外出，但是他们定不下来是去电影院还是 歌剧院。他们达成一个通过抛掷硬币来决定的协议：  Alice说：“你选择一面，然后我来抛” 。他们约定：如果Bob选择的 一面朝上则有Bob决定，否则有Alice决定。  假想这两个朋友尝试再电话上执行这个协议，如果Alice对Bob说： “你选则一面，然后我来抛，并且告诉你是否你赢了”。 2013/10/15 南京大学计算机系讲义 10 

11 . 一个例子  单向函数  对任意整数x，由x计算f(x)是容易的，而给出f(x)，要找出对应 的原像x是不可能的，不管x是奇数还是偶数。  不可能找出一对整数(x，y)，满足x≠y且f(x)=f(y)。 2013/10/15 南京大学计算机系讲义 11 

12 . 一个例子  协议  Alice和Bob已经同意：  有一个单向函数f  f(x)中的偶数x代表“正面”，奇数x代表“背面” ① Alice选择一个大随机数x并计算f(x)，然后通过电话告诉Bob f(x)的值； 只能是猜测，因为 ② Bob告诉Alice自己对x的奇偶性猜测； f(x)是单向向函数， 无法从函数值计算 ③ Alice告诉Bob x的值； 自变量。 Alice只能如实告诉， ④ Bob验证f(x)，并察看他所做的猜测是正确或错误。 因为Alice无法找到 另一个值y(奇偶性 与x不同)，f(y)=f(x)。 2013/10/15 南京大学计算机系讲义 12 

13 . 一个例子  安全性  首先，Alice无法找到不同的两个数x和y，其中一个是奇数而另一个是偶 数，使其满足f(x)=f(y)。因此，Alice一旦通过电话告诉Bob，f(x)的值(第1 步)，她也就向Bob就x的值做出了承诺，她无法再改变x的值。也就是说 Alice已经完成了其掷硬币过程。  第二，由于，已知f(x)，Bob不能判定出Alice所使用的x是奇数还是偶数， 因周而他不得不把其猜测(第2步)真实地给出。  这样，Alice可给出x的值，令Bob相信其猜测是否正确(第3步)。  如果Bob利用Alice告诉的x来计算对f(x) (第4步)，并与Alice在第1步发送 的结果一样，且Bob相信f所具有的性质，则Bob应该相信最终的输赢。 2013/10/15 南京大学计算机系讲义 13 

14 .1. 基本概念—术语  消息被称为明文（plain text）。  用某种方法伪装消息以隐藏它的内容的过程称为加密 (encryption, encipher)。  加了密的消息称为密文(cipher text)。  而 把 密 文 转 变 为 明 文 的 过 程 称 为 解 密 ( decryption, decipher)。 2013/10/15 南京大学计算机系讲义 14 

15 . 1. 基本概念—术语  使消息保密的技术和科学叫做密码编码学(cryptography)。  从事此行的叫密码编码者（cryptographer）。  破译密文的科学和技术叫做密码分析学（cryptanalysis）。  从事密码分析的专业人员叫做密码分析者（cryptanalyst）。  密码学包括密码编码学和密码分析学两者。现代的密码学家通常也是 理论数学家。 2013/10/15 南京大学计算机系讲义 15 

16 . 1. 基本概念—密码学的其它作用  鉴别 消息的接收者应该能够确认消息的来源；入侵者不 可能伪装成他人。  完整性 消息的接收者应该能够验证在传送过程中消息没 有被修改；入侵者不可能用假消息代替合法消息。  抗抵赖 发送者事后不可能虚假地否认他发送的消息。 2013/10/15 南京大学计算机系讲义 16 

17 . 1. 基本概念—算法和密钥  密码算法也叫密码，是用于加密和解密的数学函数。通常情况下， 有两个相关的函数：一个用作加密，另一个用作解密。  明文用M（消息），密文用C表示，加密函数E作用于M得到密文 C，用数学表示为： E（M）=C.  相反地，解密函数D作用于C产生M D（C）=M.  先加密后再解密消息，原始的明文将恢复出来，下面的等式必须 成立： D（E（M））=M 2013/10/15 南京大学计算机系讲义 17 

18 . 1. 基本概念—受限制的算法  如果算法的保密性是基于保持算法的秘密，这种算法称 为受限制的算法。  如果有人无意暴露了这个秘密，所有人都必须改变他们 的算法。 2013/10/15 南京大学计算机系讲义 18 

19 . 1. 基本概念—现代密码学  现代密码学用密钥解决了这个问题，密钥用K表示。  密钥K的可能值的范围叫做密钥空间。  加密和解密运算都使用这个密钥，加/解密函数现在变 成： EK（M）=C EK1（M）=C DK（C）=M DK2（C）=M DK（EK（M））=M DK2（EK1（M））=M 2013/10/15 南京大学计算机系讲义 19 

20 . 1. 基本概念—对称算法和非对称算法  对称算法 加密密钥能够从解密密钥中推算出来，反过来 也成立。  公开密钥算法 公开密钥算法用作加密的密钥不同于用作 解密的密钥，而且解密密钥不能根据加密密钥计算出来。 2013/10/15 南京大学计算机系讲义 20 

21 . 1. 基本概念—密码分析  密码分析学是在不知道密钥的情况下。恢复出明文的科学。  对密码进行分析的尝试称为攻击。  密码分析的一个基本假设：密码分析者已有密码算法及其实现的全部 详细资料。在实际的密码分析中并不总是有这些详细信息的应该 如此假设。如果其他人不能破译算法，即便了解算法如何工作也是徒 然，如果连算法的知识都没有，那就肯定不可能破译它。 2013/10/15 南京大学计算机系讲义 21 

22 . （1）唯密文攻击  密码分析者有一些消息的密文  这些消息都用同一加密算法加密  密码分析者的任务是恢复尽可能多的明文  或者最好是能推算出加密消息的密钥来  已知：C1=EK（P1），C2=EK（P2），，  推导出：P1，P2，， 2013/10/15 南京大学计算机系讲义 22 

23 . （2）已知明文攻击  密码分析者不仅可得到一些消息的密文，而且也知道这些 消息的明文。  分析者的任务就是用加密信息推出用来加密的密钥或导出一个算 法，此算法可以对用同一密钥加密的任何新的消息进行解密。  已知：P1，C1=Ek（P1），P2，C2=Ek（P2），，Pi，Ci=Ek （Pi）  推导出：密钥k，或从Ci+1= Ek（Pi+1）推出Pi+1的算法。 2013/10/15 南京大学计算机系讲义 23 

24 . （3）选择明文攻击  分析者不仅可得到一些消息的密文和相应的明文，而且他们也可 选择被加密的明文。  这比已知明文攻击更有效。因为密码分析者能选择特定的明文块去 加密，那些块可能产生更多关于密钥的信息，分析者的任务是推出 用来加密消息的密钥或导出一个算法，此算法可以对用同一密钥加 密的任何新的消息进行解密。 2013/10/15 南京大学计算机系讲义 24 

25 . （4）选择密文攻击  密码分析者能选择不同的被加密的密文，并可得到对应的 解密的明文，例如密码分析者存取一个防窜改的自动解密 盒，密码分析者的任务是推出密钥。 选择：C1，P1=Dk（C1），C2，P2=Dk（C2），，Ci， Pi=Dk（Ci）， 推导出： k。 2013/10/15 南京大学计算机系讲义 25 

26 .  最好的算法是那些已经公开的，并经过世界上最好的 密码分析家们多年的攻击，但还是不能破译的算法。  美国国家安全局对外保持他们的算法的秘密，但他们 有很好的密码分析家在内部工作，他们互相讨论他们 的算法，通过执著的审查发现他们工作中的弱点。 2013/10/15 南京大学计算机系讲义 26 

27 . 1. 基本概念— 密码学目标  机密性  完整性  认证  不可抵赖性、公证性 2013/10/15 南京大学计算机系讲义 27 

28 . 2. 古典密码算法  在计算机出现前，密码学由基于字符的密码算法构成。不同的 密码算法是字符之间互相代换或者是互相之间换位，好的密码 算法是结合这两种方法，每次进行多次运算。  现在事情变得复杂多了，但原理还是没变。重要的变化是算法 对比特而不是对字母进行变换，实际上这只是字母表长度上的 改变，从26个元素变为2个元素。大多数好的密码算法仍然是代 替和换位的元素组合。 2013/10/15 南京大学计算机系讲义 28 

29 . 密码体制  P：所有可能的明文组成的有限集。；  C：所有可能的密文组成的有限集；  K：所有可能的密钥组成的有限集； 对任意的k∈K，都存在 一个加密法则ek ∈E 和相应的解密法则dk ∈D ，满足: 对任意的ek: P→C , dk: C→P, 明文x∈P, 均有 dk( ek(x) ) = x 密码体制：( P, C, K, E, D) 2013/10/15 南京大学计算机系讲义 29