人脸识别和特征子空间

1 .Face Recognition and Feature Subspaces Computer Vision Jia-Bin Huang, Virginia Tech Many slides from Lana Lazebnik , Silvio Savarese , Fei-Fei Li, and D. Hoiem

2 .Administrative stuffs Final project Proposal due Oct 27 (Thursday ) Submit via CANVAS Send a copy to Jia-Bin and Akrit via email HW 4 Due 11:59pm on Wed, November 2nd, 2016

3 .The fifth module Face recognition Feature subspace: PCA and LDA Image features and categorization How to extract visual representation? Machine learning crash course What similarities are important ? Object detection Where is the object in the image? Object tracking Where is the object in the next frame?

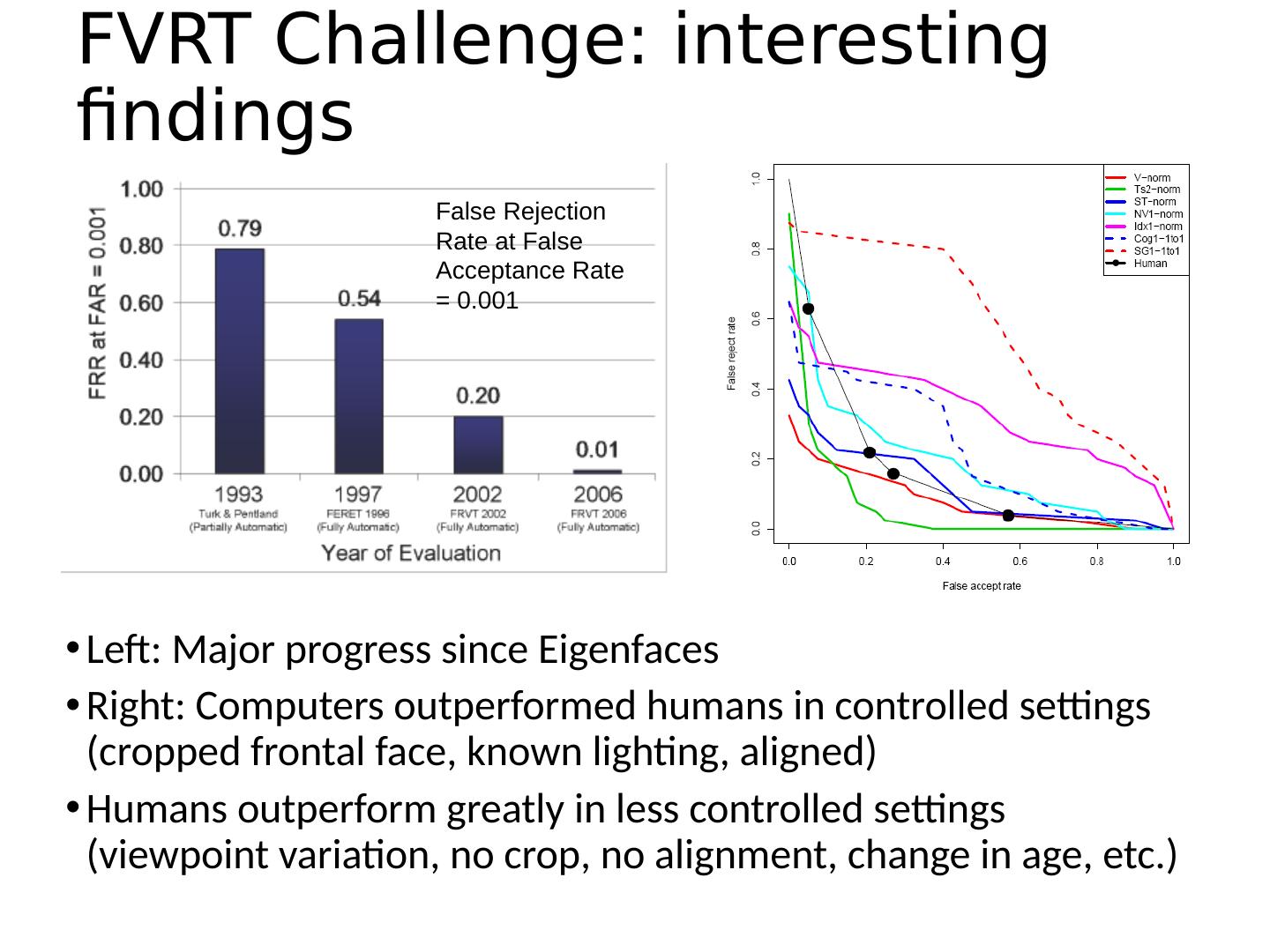
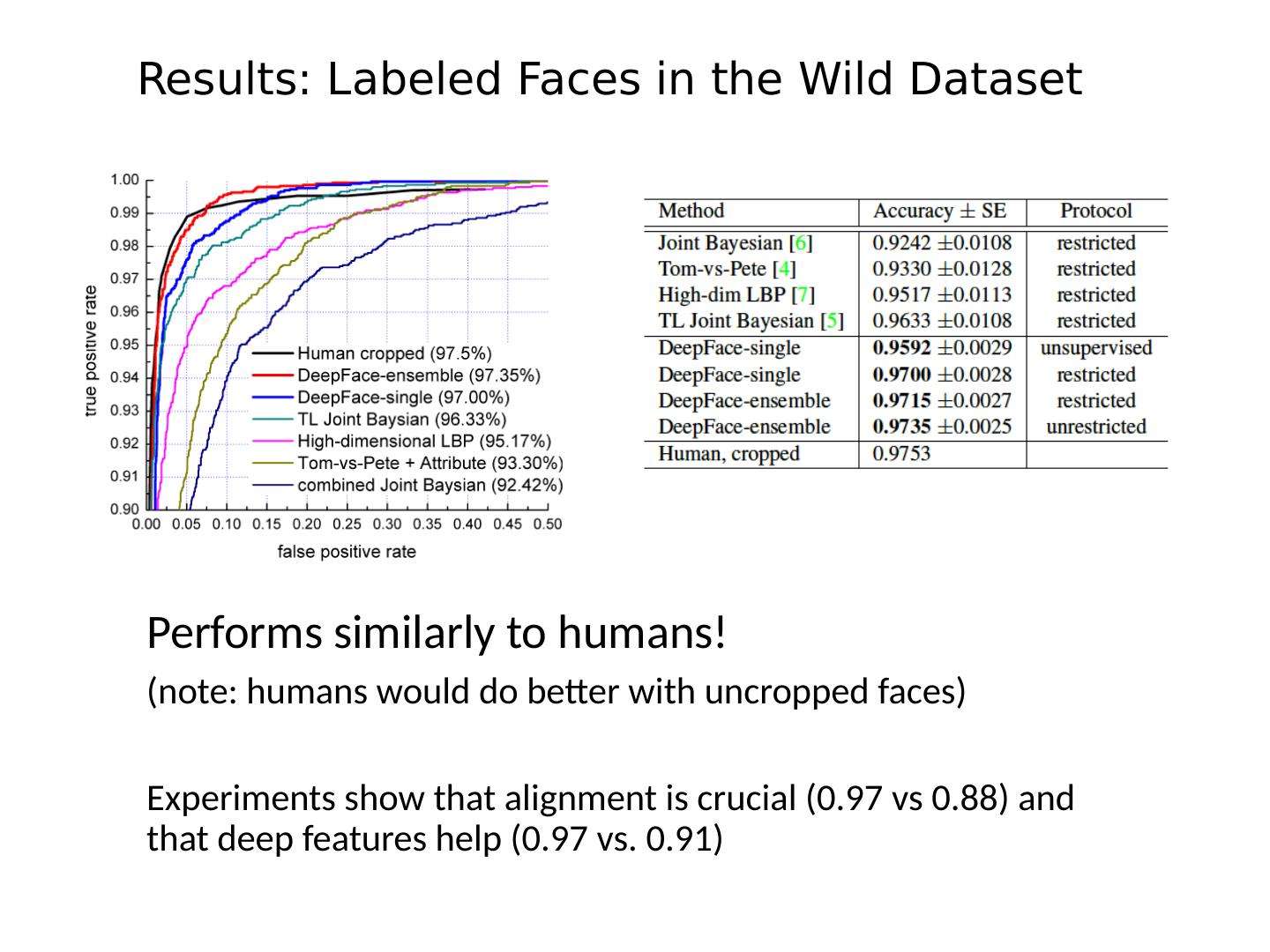
4 .This class: face recognition Two methods: “Eigenfaces” and “ Fisherfaces ” Feature subspaces: PCA and FLD Look at results from recent vendor test Recent method: DeepFace and FaceNet Look at interesting findings about human face recognition

5 .Applications of Face Recognition Surveillance

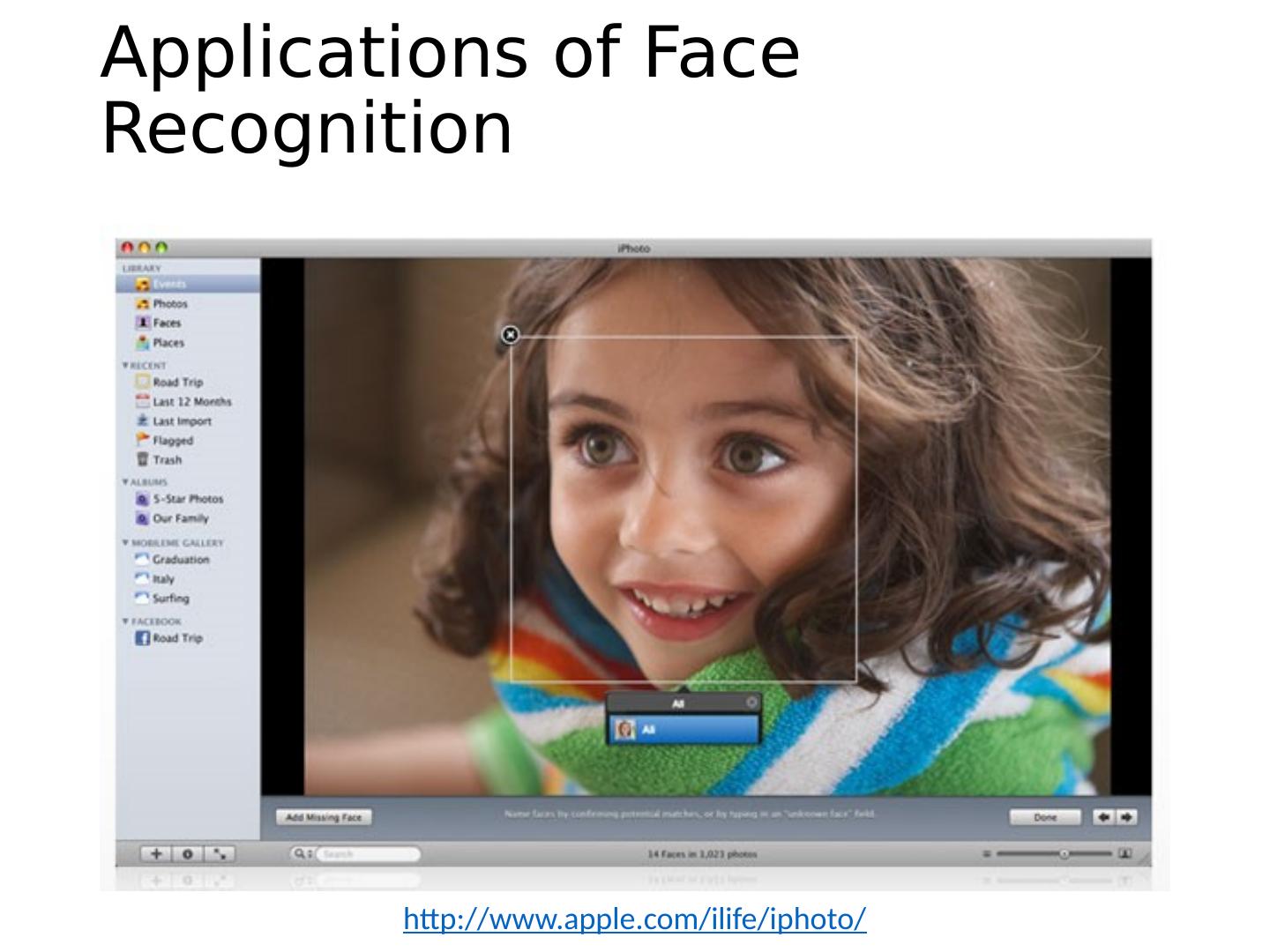
6 .Applications of Face Recognition Album organization: iPhoto 2009 http://www.apple.com/ilife/iphoto/

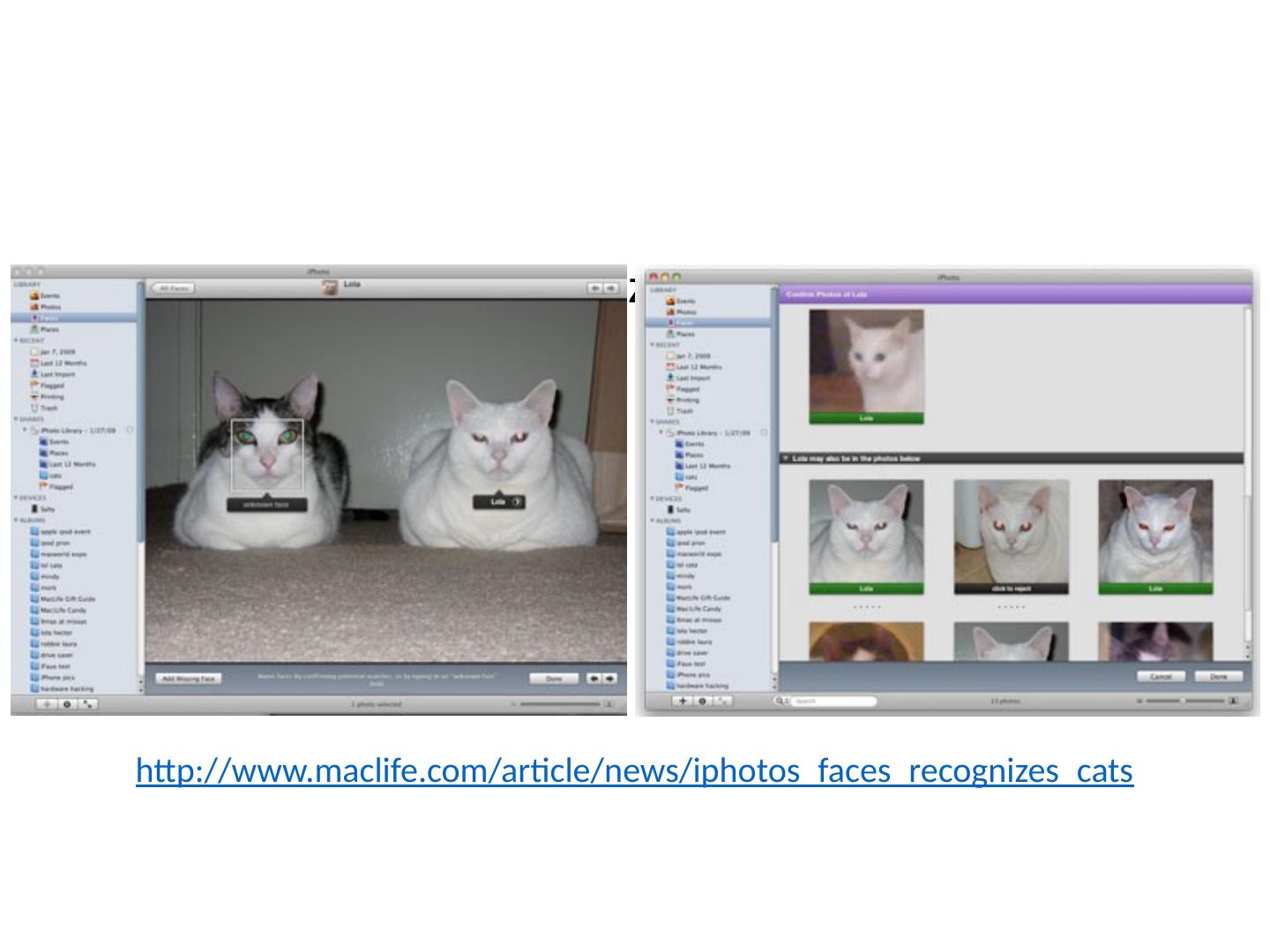
7 .Can be trained to recognize pets! http://www.maclife.com/article/news/iphotos_faces_recognizes_cats

8 .Facebook friend-tagging with auto-suggest

9 .Face recognition: once you’ve detected and cropped a face, try to recognize it Detection Recognition “Sally”

10 .Face recognition: overview Typical scenario: few examples per face, identify or verify test example Why it’s hard? changes in expression, lighting, age, occlusion , viewpoint Basic approaches (all nearest neighbor) Project into a new subspace (or kernel space) (e.g., “ Eigenfaces ”=PCA) Measure face features Make 3d face model, compare shape+appearance , e.g., Active Appearance Model (AAM)

11 .Typical face recognition scenarios Verification : a person is claiming a particular identity; verify whether that is true E.g., security Closed-world identification : assign a face to one person from among a known set General identification : assign a face to a known person or to “unknown”

12 .What makes face recognition hard? Expression

13 .What makes face recognition hard? Lighting

14 .What makes face recognition hard? Occlusion

15 .What makes face recognition hard? Viewpoint

16 .Simple idea for face recognition Treat face image as a vector of intensities Recognize face by nearest neighbor in database

17 .The space of all face images When viewed as vectors of pixel values, face images are extremely high-dimensional 100x100 image = 10,000 dimensions Slow and lots of storage But very few 10,000-dimensional vectors are valid face images We want to effectively model the subspace of face images

18 .The space of all face images Eigenface idea: construct a low-dimensional linear subspace that best explains the variation in the set of face images

19 .Principal Component Analysis (PCA) Given: N data points x 1 , … , x N in R d We want to find a new set of features that are linear combinations of original ones: u ( x i ) = u T ( x i – µ ) ( µ : mean of data points) Choose unit vector u in R d that captures the most data variance Forsyth & Ponce, Sec. 22.3.1, 22.3.2

20 .Principal Component Analysis Direction that maximizes the variance of the projected data: Projection of data point Covariance matrix of data The direction that maximizes the variance is the eigenvector associated with the largest eigenvalue of Σ (can be derived using Raleigh’s quotient or Lagrange multiplier) N N 1/N Maximize subject to || u ||=1

21 .Implementation issue Covariance matrix is huge (M 2 for M pixels) But typically # examples << M Simple trick X is Mx N matrix of normalized training data Solve for eigenvectors u of X T X instead of XX T Then Xu is eigenvector of covariance XX T Need to normalize each vector of Xu into unit length

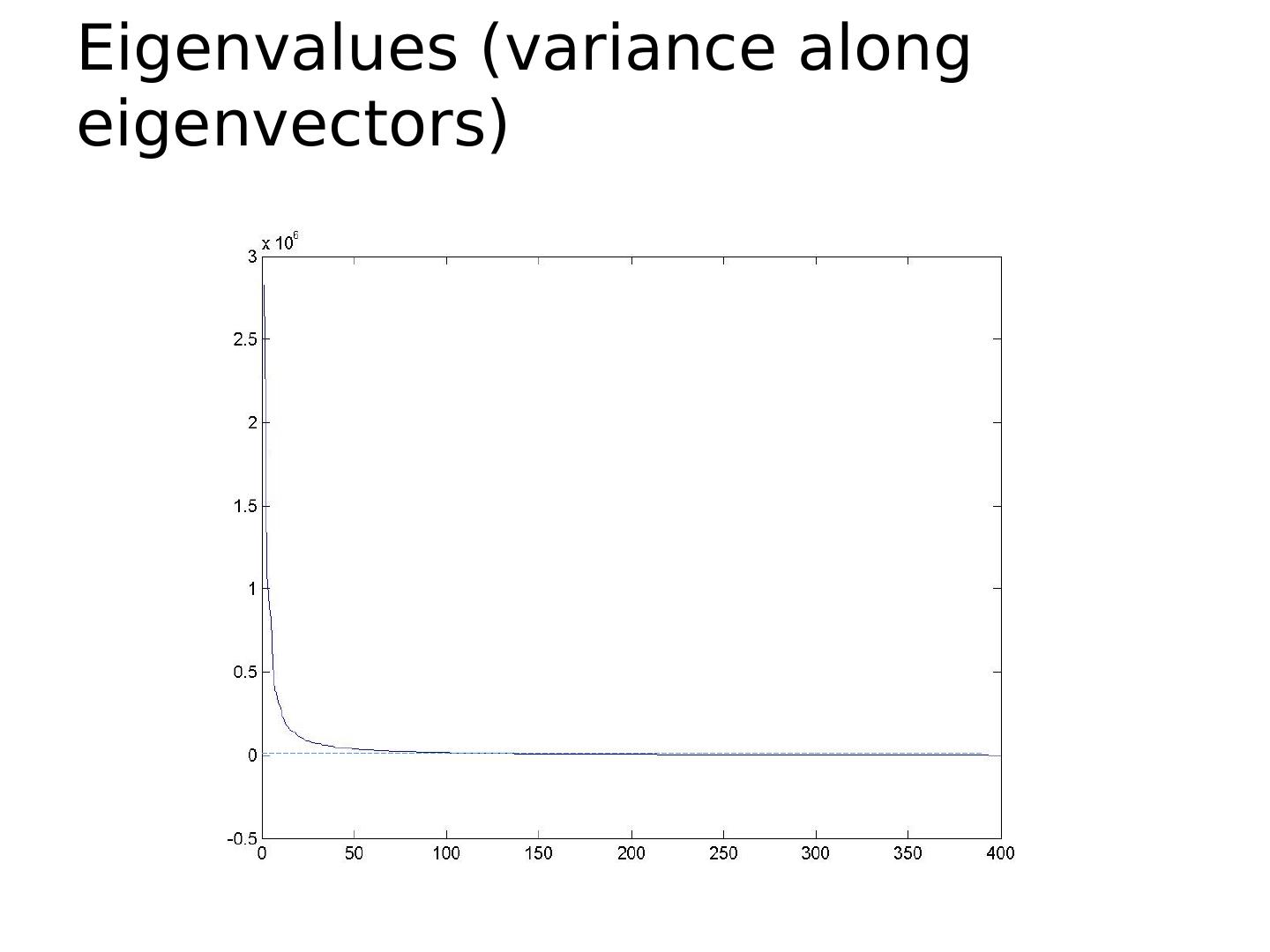
22 .Eigenfaces (PCA on face images) Compute the principal components (“ eigenfaces ”) of the covariance matrix Keep K eigenvectors with largest eigenvalues Represent all face images in the dataset as linear combinations of eigenfaces Perform nearest neighbor on these coefficients M. Turk and A. Pentland , Face Recognition using Eigenfaces , CVPR 1991      

23 .Eigenfaces example Training images x 1 ,…, x N

24 .Eigenfaces example Top eigenvectors: u 1 ,…u k Mean: μ

25 .Visualization of eigenfaces Principal component (eigenvector) u k μ + 3 σ k u k μ – 3 σ k u k

26 .Representation and reconstruction Face x in “face space” coordinates: =

27 .Representation and reconstruction Face x in “face space” coordinates: Reconstruction: = + µ + w 1 u 1 +w 2 u 2 +w 3 u 3 +w 4 u 4 + … = ^ x =

28 .P = 4 P = 200 P = 400 Reconstruction After computing eigenfaces using 400 face images from ORL face database

29 .Eigenvalues (variance along eigenvectors)