- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
EM
展开查看详情
1 .Hidden Variables, the EM Algorithm, and Mixtures of Gaussians Computer Vision Jia-Bin Huang, Virginia Tech Many slides from D. Hoiem
2 .Administrative stuffs Final project proposal due Oct 27 (Thursday ) Tips for final project Set up several milestones Think about how you are going to evaluate Demo is highly encouraged HW 4 out tomorrow
3 .Review: Image Segmentation Gestalt cues and principles of organization Uses of segmentation Efficiency Provide feature supports Propose object regions Want the segmented object Mean-shift segmentation Good general-purpose segmentation method Generally useful clustering, tracking technique Watershed segmentation Good for hierarchical segmentation Use in combination with boundary prediction
4 .HW 4: SLIC ( Achanta et al. PAMI 2012) Initialize cluster centers on pixel grid in steps S - Features: Lab color, x-y position Move centers to position in 3x3 window with smallest gradient Compare each pixel to cluster center within 2S pixel distance and assign to nearest Recompute cluster centers as mean color/position of pixels belonging to each cluster Stop when residual error is small http :// infoscience.epfl.ch/record/177415/files/Superpixel_PAMI2011-2.pdf + Fast 0.36s for 320x240 + Regular superpixels + Superpixels fit boundaries - May miss thin objects - Large number of superpixels
5 .Today’s Class Examples of Missing Data Problems Detecting outliers (HW 4, problem 2 ) Latent topic models Segmentation (HW 4, problem 3) Background Maximum Likelihood Estimation Probabilistic Inference Dealing with “Hidden” Variables EM algorithm, Mixture of Gaussians Hard EM
6 .Missing Data Problems: Outliers You want to train an algorithm to predict whether a photograph is attractive. You collect annotations from Mechanical Turk. Some annotators try to give accurate ratings, but others answer randomly. Challenge: Determine which people to trust and the average rating by accurate annotators. Photo: Jam343 ( Flickr ) Annotator Ratings 10 8 9 2 8
7 .Missing Data Problems: Object Discovery You have a collection of images and have extracted regions from them. Each is represented by a histogram of “visual words”. Challenge: Discover frequently occurring object categories, without pre-trained appearance models. http://www.robots.ox.ac.uk/~vgg/publications/papers/russell06.pdf
8 .Missing Data Problems: Segmentation You are given an image and want to assign foreground/background pixels. Challenge: Segment the image into figure and ground without knowing what the foreground looks like in advance. Foreground Background
9 .Missing Data Problems: Segmentation Challenge : Segment the image into figure and ground without knowing what the foreground looks like in advance . Three steps: If we had labels, how could we model the appearance of foreground and background ? Maximum Likelihood Estimation Once we have modeled the fg / bg appearance, how do we compute the likelihood that a pixel is foreground ? Probabilistic Inference How can we get both labels and appearance models at once ? Expectation-Maximization (EM) Algorithm
10 .Maximum Likelihood Estimation If we had labels, how could we model the appearance of foreground and background? Foreground Background
11 .Maximum Likelihood Estimation data parameters
12 .Maximum Likelihood Estimation Gaussian Distribution
13 .Maximum Likelihood Estimation Log-Likelihood Gaussian Distribution
14 .Maximum Likelihood Estimation Log-Likelihood Gaussian Distribution
15 .Example: MLE >> mu_fg = mean(im(labels)) mu_fg = 0.6012 >> sigma_fg = sqrt(mean((im(labels)-mu_fg).^2)) sigma_fg = 0.1007 >> mu_bg = mean(im(~labels)) mu_bg = 0.4007 >> sigma_bg = sqrt (mean(( im (~labels)- mu_bg ).^2)) sigma_bg = 0.1007 >> pfg = mean(labels(:)); labels im fg : mu=0.6, sigma=0.1 bg : mu=0.4, sigma=0.1 Parameters used to Generate
16 .Probabilistic Inference 2. Once we have modeled the fg / bg appearance, how do we compute the likelihood that a pixel is foreground? Foreground Background
17 .Probabilistic Inference Compute the likelihood that a particular model generated a sample component or label
18 .Probabilistic Inference component or label Compute the likelihood that a particular model generated a sample Conditional probability
19 .Probabilistic Inference component or label Compute the likelihood that a particular model generated a sample Marginalization
20 .Probabilistic Inference component or label Compute the likelihood that a particular model generated a sample Joint distribution
21 .Example: Inference >> pfg = 0.5; >> px_fg = normpdf(im, mu_fg, sigma_fg); >> px_bg = normpdf(im, mu_bg, sigma_bg); >> pfg_x = px_fg*pfg ./ (px_fg*pfg + px_bg*(1-pfg)); im fg : mu=0.6, sigma=0.1 bg : mu=0.4, sigma=0.1 Learned Parameters p( fg | im )
22 .Dealing with Hidden Variables 3. How can we get both labels and appearance parameters at once? Foreground Background
23 .Mixture of Gaussians mixture component component prior component model parameters
24 .Mixture of Gaussians With enough components, can represent any probability density function Widely used as general purpose pdf estimator
25 .Segmentation with Mixture of Gaussians Pixels come from one of several Gaussian components We don’t know which pixels come from which components We don’t know the parameters for the components Problem: Estimate the parameters of the Gaussian Mixture Model. What would you do?
26 .Simple solution Initialize parameters Compute the probability of each hidden variable given the current parameters Compute new parameters for each model, weighted by likelihood of hidden variables Repeat 2-3 until convergence
27 .Mixture of Gaussians: Simple Solution Initialize parameters Compute likelihood of hidden variables for current parameters Estimate new parameters for each model, weighted by likelihood
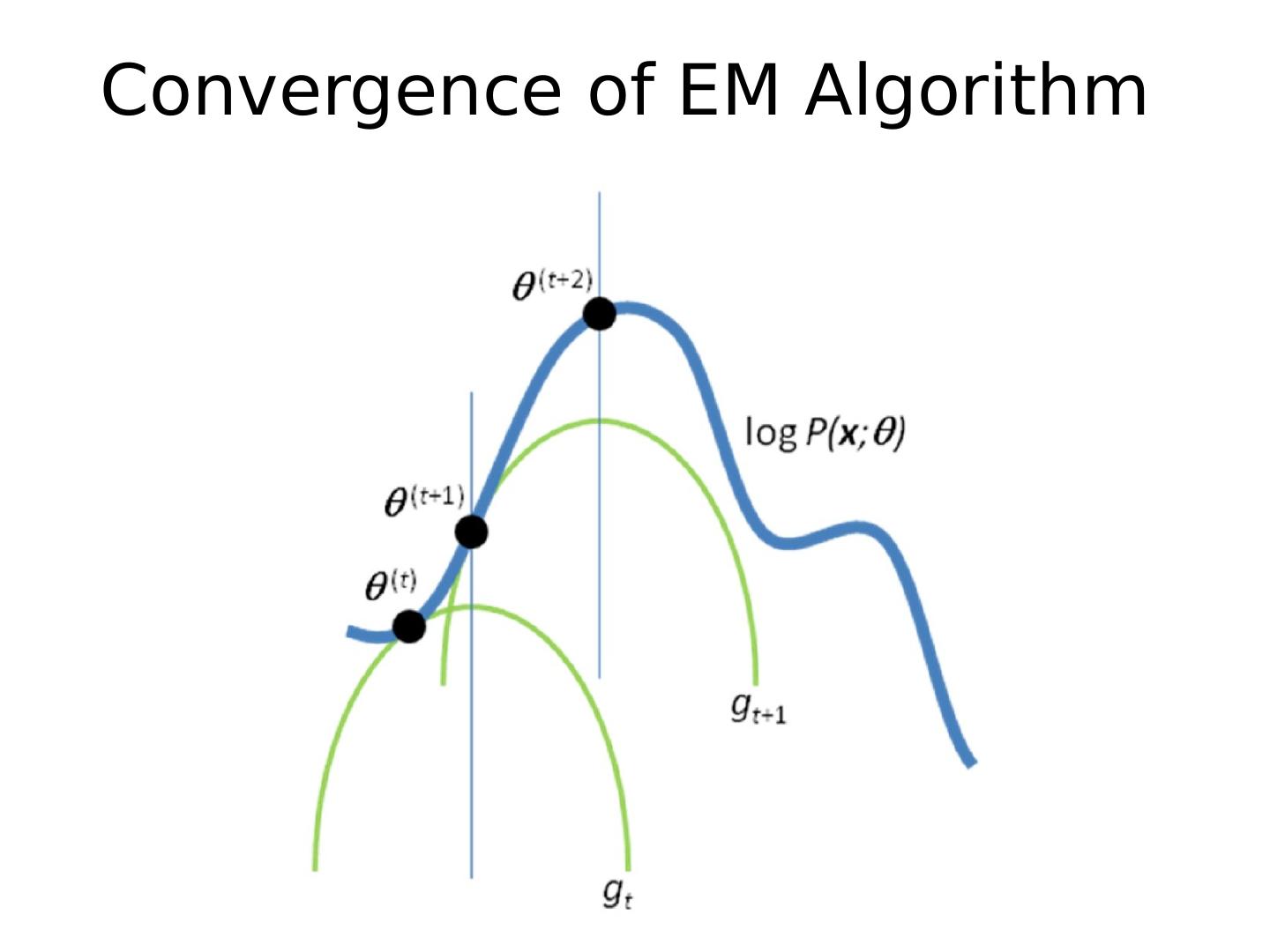
28 .Expectation Maximization (EM) Algorithm Goal: Jensen’s Inequality Log of sums is i ntractable See here for proof: www.stanford.edu/class/cs229/notes/cs229-notes8.ps for concave functions f(x) (so we maximize the lower bound!)
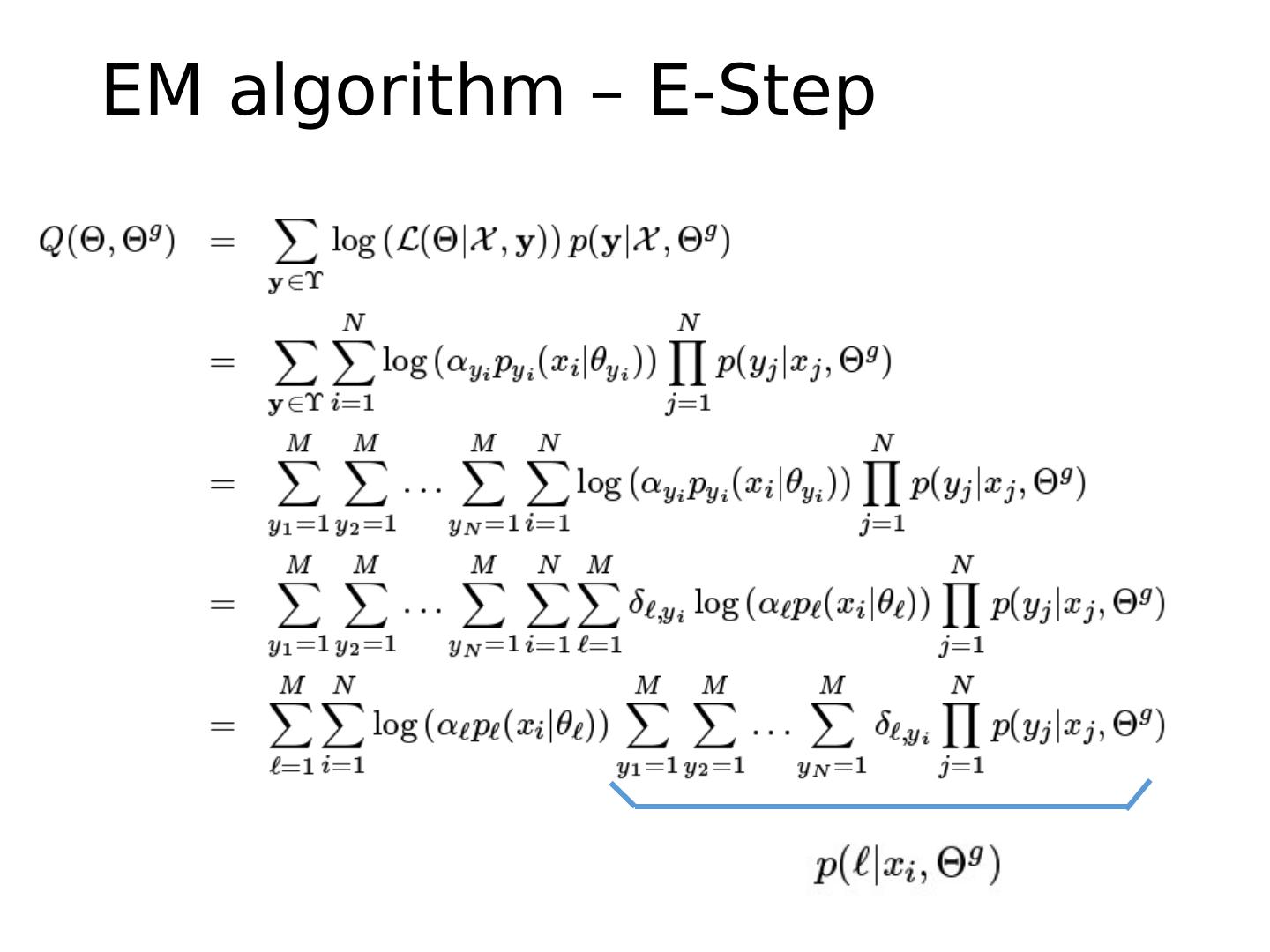
29 .Expectation Maximization (EM) Algorithm E-step: compute M-step: solve Goal: