轮廓检测

1 .Edge Detection Computer Vision Jia-Bin Huang, Virginia Tech Many slides from D. Hoiem and K. Grauman

2 .Administrative Stuffs HW 1 posted, due 11:59 PM Sept 19 Submission through Canvas Questions about HW? Ask me/TA after classes Post questions on Piazza (no emails) Attend office hours

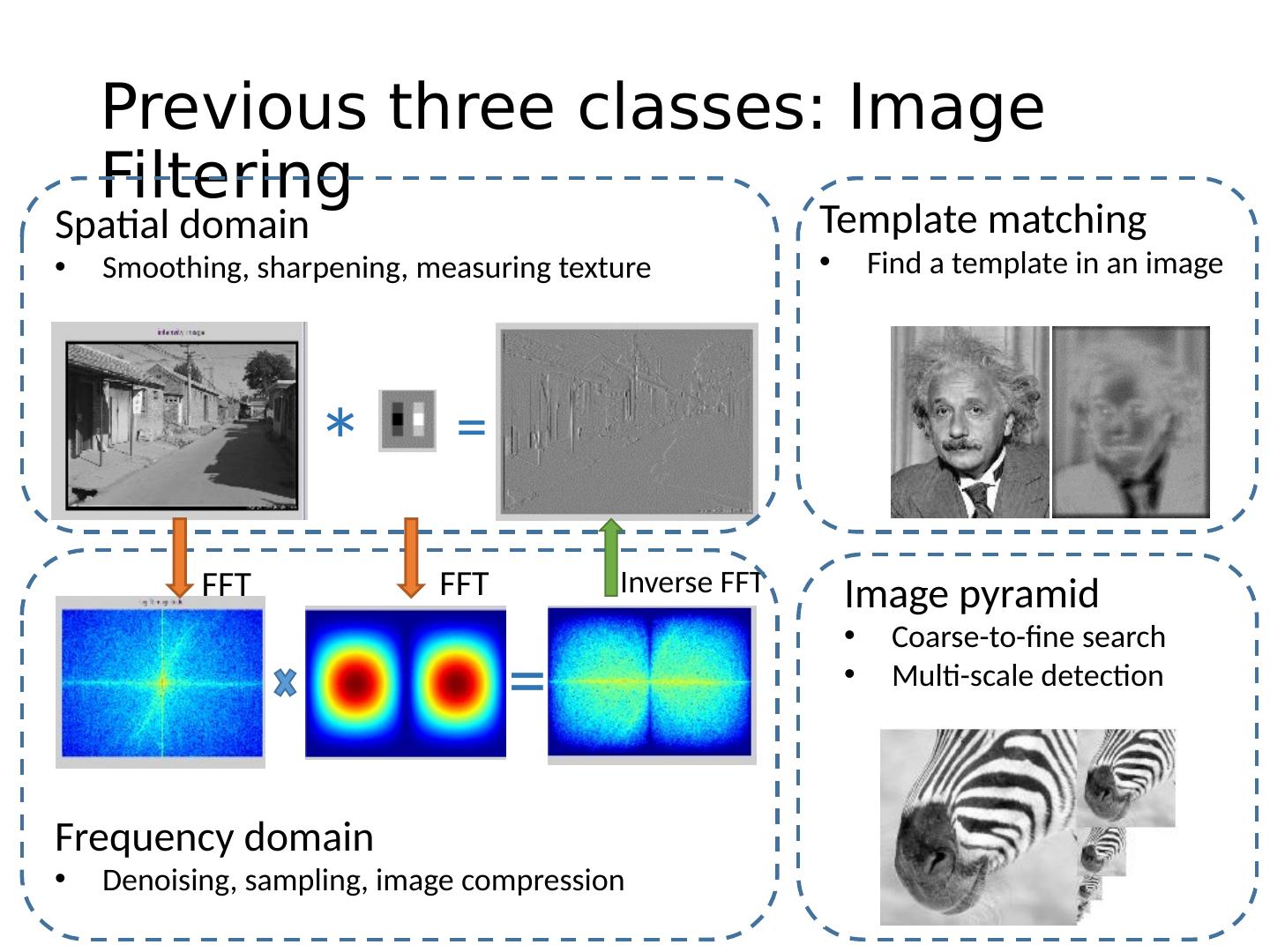
3 .Previous three classes: Image Filtering Spatial domain Smoothing, sharpening, measuring texture * = Frequency domain Denoising , sampling, image compression FFT = Inverse FFT FFT Image pyramid Coarse-to-fine search Multi-scale detection Template matching Find a template in an image

4 .Today’s class Detecting edges Finding straight lines Binary image analysis

5 .Why finding edges is important Cues for 3D shape Group pixels into objects or parts Guiding interactive image editing Recover geometry and viewpoint Vanishing point Vanishing line Vanishing point Vertical vanishing point (at infinity)

6 .Origin of Edges Edges are caused by a variety of factors depth discontinuity surface color discontinuity illumination discontinuity surface normal discontinuity Source: Steve Seitz

7 .Closeup of edges

8 .Closeup of edges

9 .Closeup of edges

10 .Closeup of edges

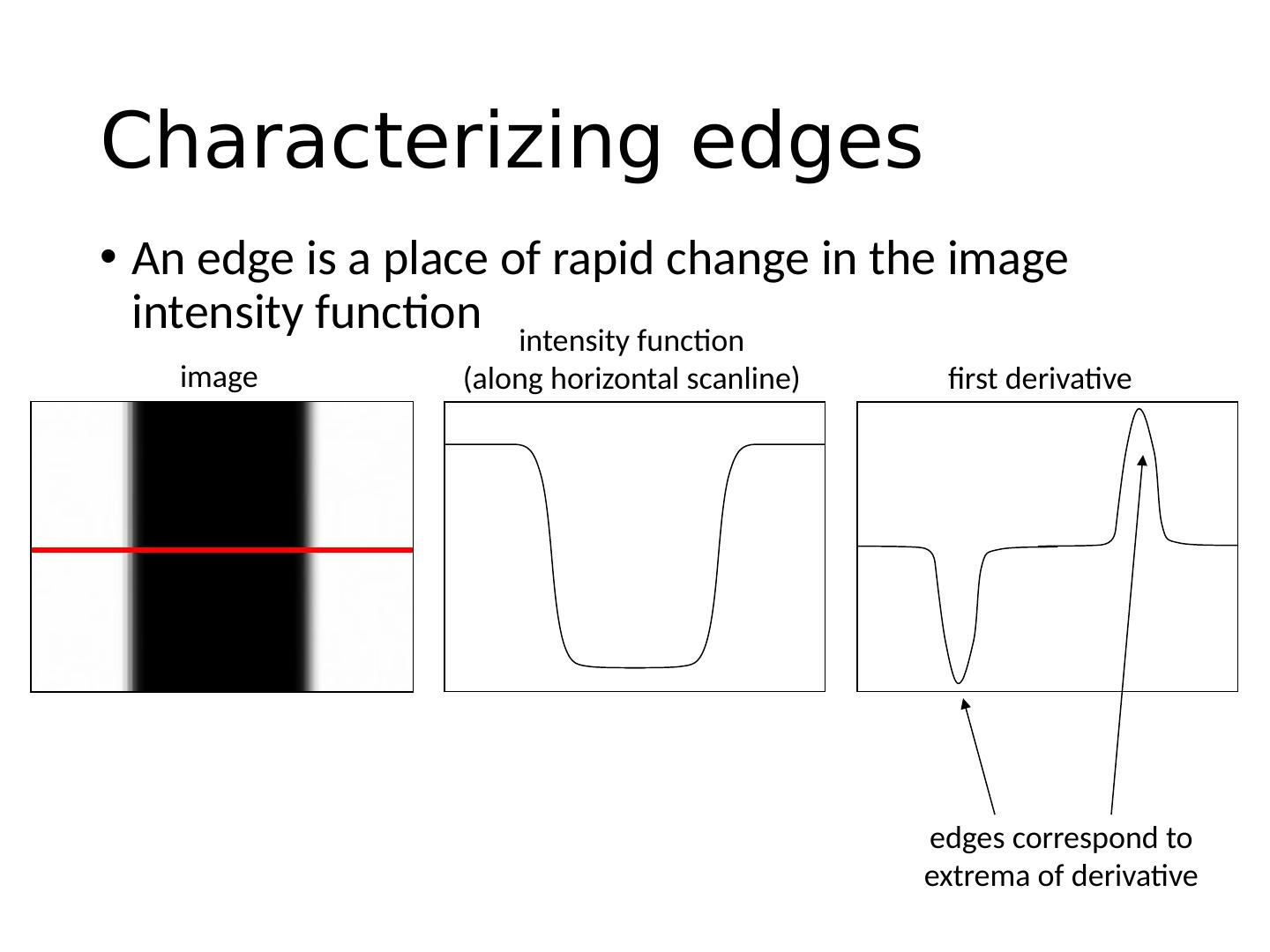
11 .Characterizing edges An edge is a place of rapid change in the image intensity function image intensity function (along horizontal scanline) first derivative edges correspond to extrema of derivative

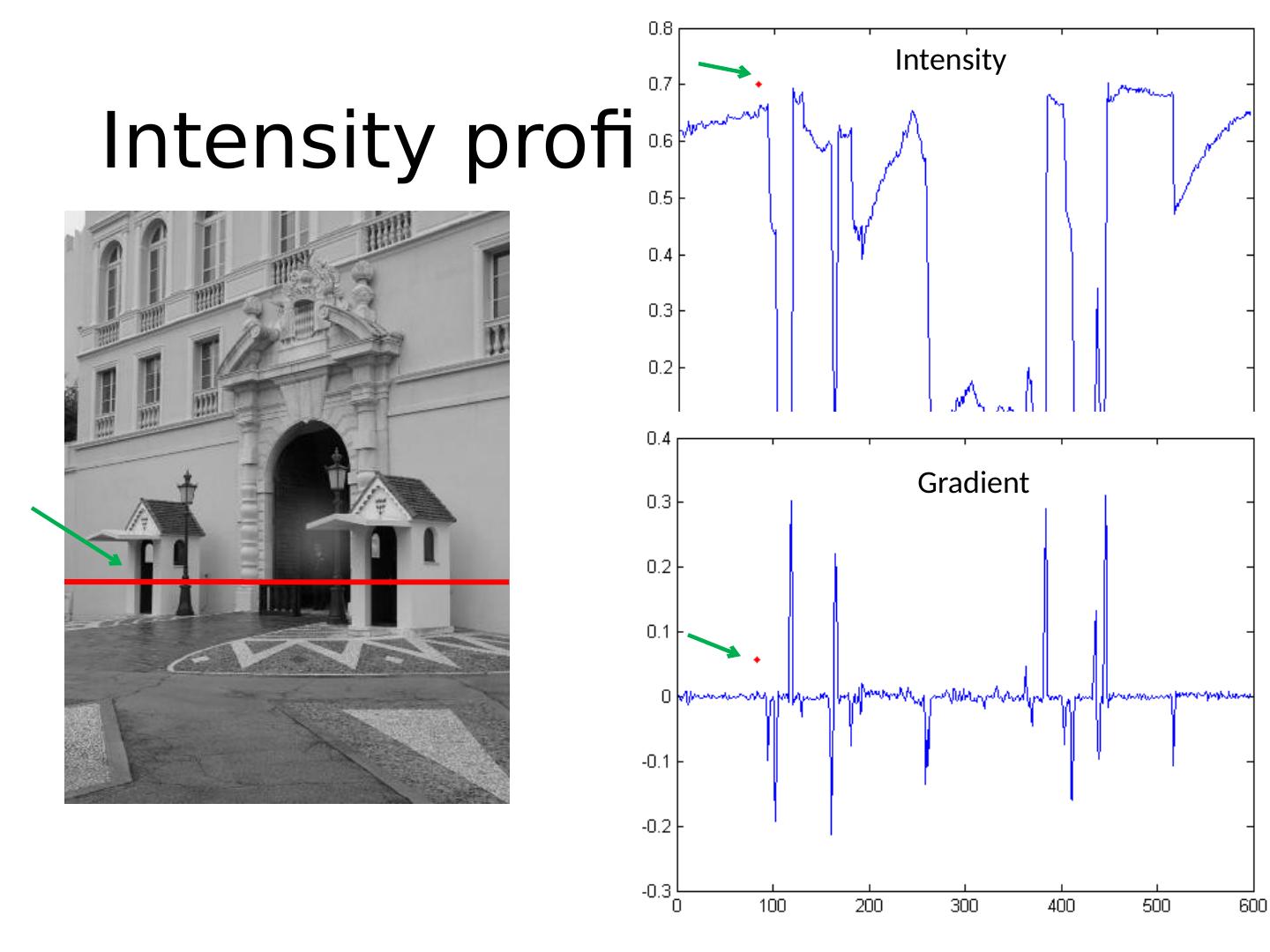
12 .Intensity profile Intensity Gradient

13 .With a little Gaussian noise Gradient

14 .Effects of noise Consider a single row or column of the image Plotting intensity as a function of position gives a signal Where is the edge? Source: S. Seitz

15 .Effects of noise Difference filters respond strongly to noise Image noise results in pixels that look very different from their neighbors Generally, the larger the noise the stronger the response What can we do about it? Source: D. Forsyth

16 .Solution: smooth first To find edges, look for peaks in f g f * g Source: S. Seitz

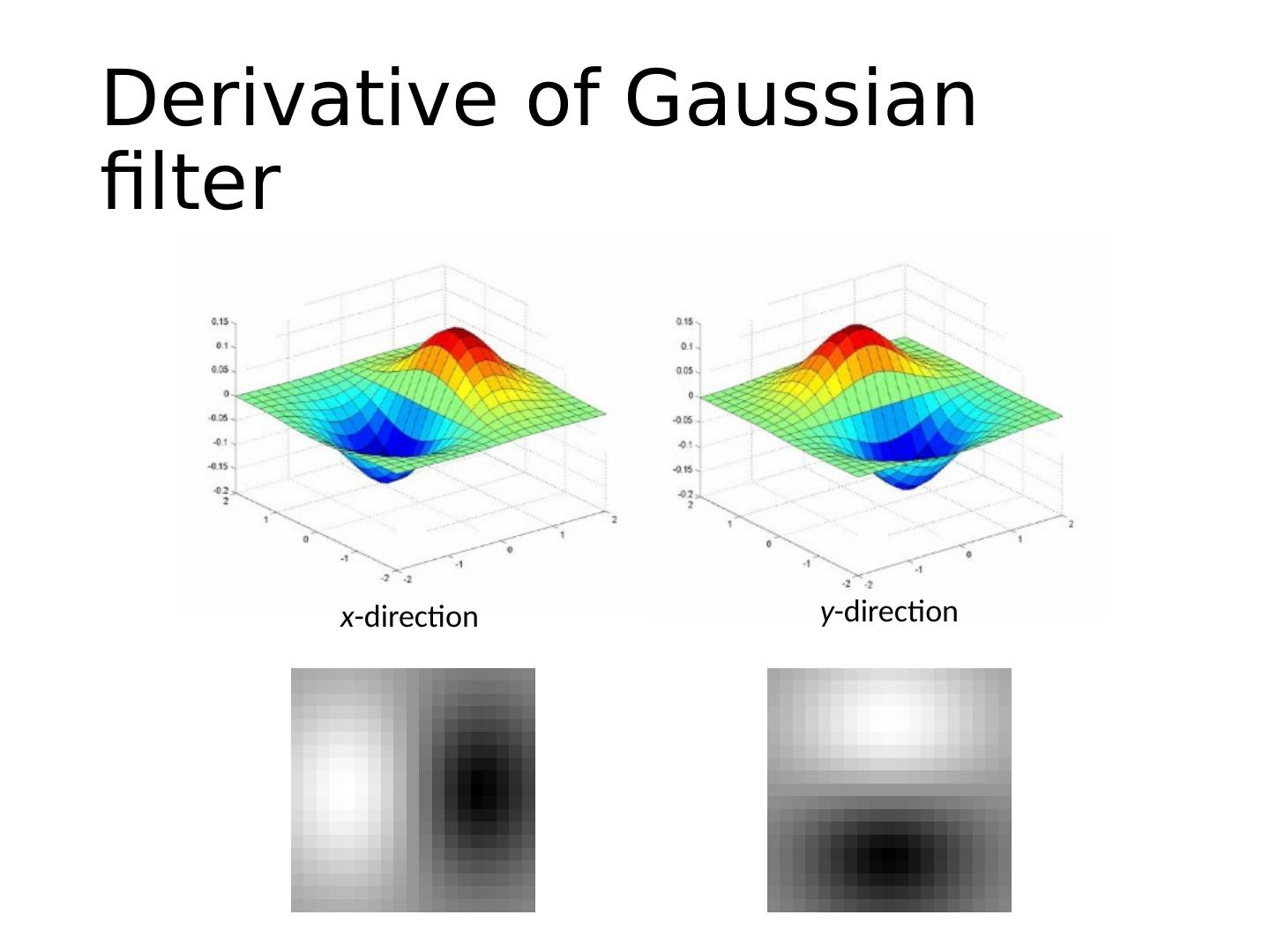
17 .Derivative theorem of convolution Differentiation is convolution, and convolution is associative : This saves us one operation: f Source: S. Seitz

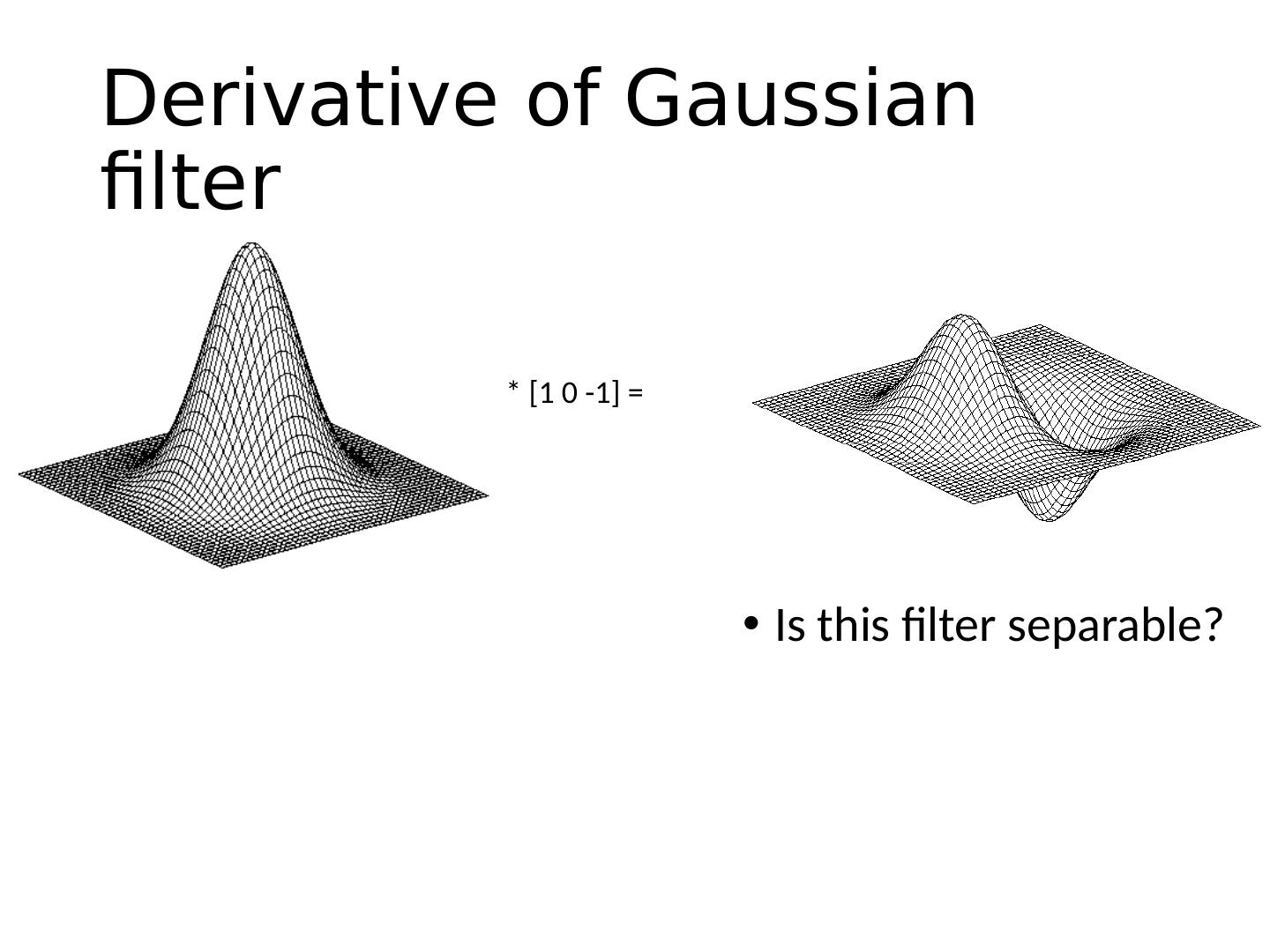
18 .Derivative of Gaussian filter Is this filter separable? * [1 0 -1 ] =

19 .Tradeoff between smoothing and localization Smoothed derivative removes noise, but blurs edge. Also finds edges at different “scales”. 1 pixel 3 pixels 7 pixels Source: D. Forsyth

20 .Implementation issues The gradient magnitude is large along a thick “trail” or “ridge,” so how do we identify the actual edge points? How do we link the edge points to form curves? Source: D. Forsyth

21 .Designing an edge detector Criteria for a good edge detector: Good detection: find all real edges, ignoring noise or other artifacts Good localization detect edges as close as possible to the true edges return one point only for each true edge point Cues of edge detection Differences in color, intensity, or texture across the boundary Continuity and closure High-level knowledge Source: L. Fei-Fei

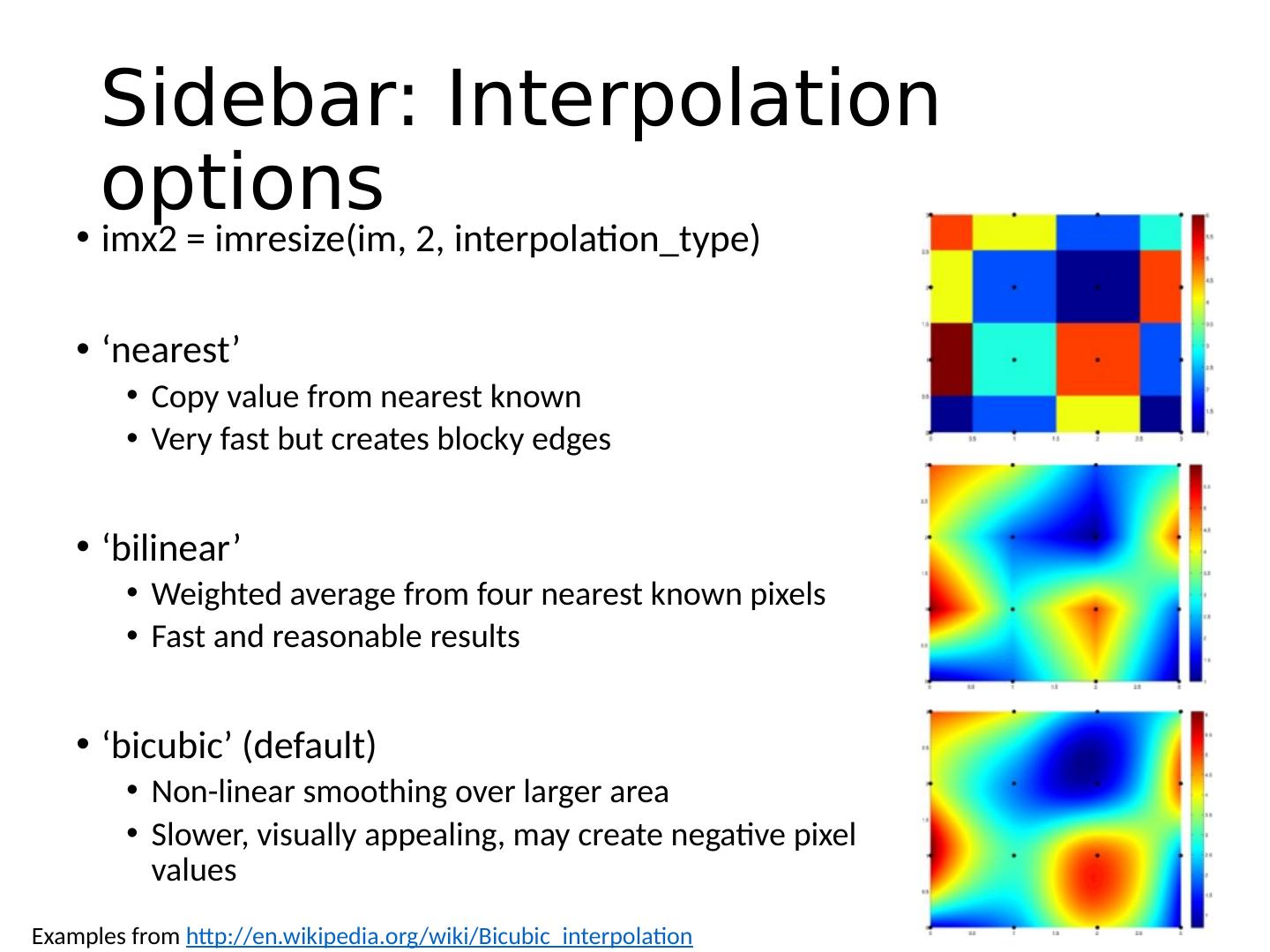
22 .Canny edge detector This is probably the most widely used edge detector in computer vision Theoretical model: step-edges corrupted by additive Gaussian noise Canny has shown that the first derivative of the Gaussian closely approximates the operator that optimizes the product of signal-to-noise ratio and localization J. Canny, A Computational Approach To Edge Detection , IEEE Trans. Pattern Analysis and Machine Intelligence, 8:679-714, 1986. Source: L. Fei-Fei

23 .Example input image (“Lena”)

24 .Derivative of Gaussian filter x -direction y -direction

25 .Compute Gradients (DoG) X-Derivative of Gaussian Y-Derivative of Gaussian Gradient Magnitude

26 .Get Orientation at Each Pixel Threshold at minimum level Get orientation theta = atan2 (- gy , gx )

27 .Non-maximum suppression for each orientation At q, we have a maximum if the value is larger than those at both p and at r. Interpolate to get these values. Source: D. Forsyth

28 .Bilinear Interpolation http://en.wikipedia.org/wiki/Bilinear_interpolation

29 .Sidebar: Interpolation options imx2 = imresize ( im , 2, interpolation_type ) ‘nearest’ Copy value from nearest known Very fast but creates blocky edges ‘bilinear’ Weighted average from four nearest known pixels Fast and reasonable results ‘ bicubic ’ (default) Non-linear smoothing over larger area Slower, visually appealing, may create negative pixel values Examples from http://en.wikipedia.org/wiki/Bicubic_interpolation