- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
影像金字塔及其应用
展开查看详情
1 .Image Pyramids and Applications Computer Vision Jia-Bin Huang, Virginia Tech Golconda, René Magritte , 1953
2 .Administrative stuffs HW 1 posted, due 11:59 PM Sept 19 Anonymous feedback from students Repeat students’ questions and answers T urn on some light in the classroom Post frequently asked questions for HWs
3 .Previous class: Image Filtering Sometimes it makes sense to think of images and filtering in the frequency domain Fourier analysis Can be faster to filter using FFT for large images (N logN vs. N 2 for auto-correlation) Images are mostly smooth Basis for compression Remember to low-pass before sampling
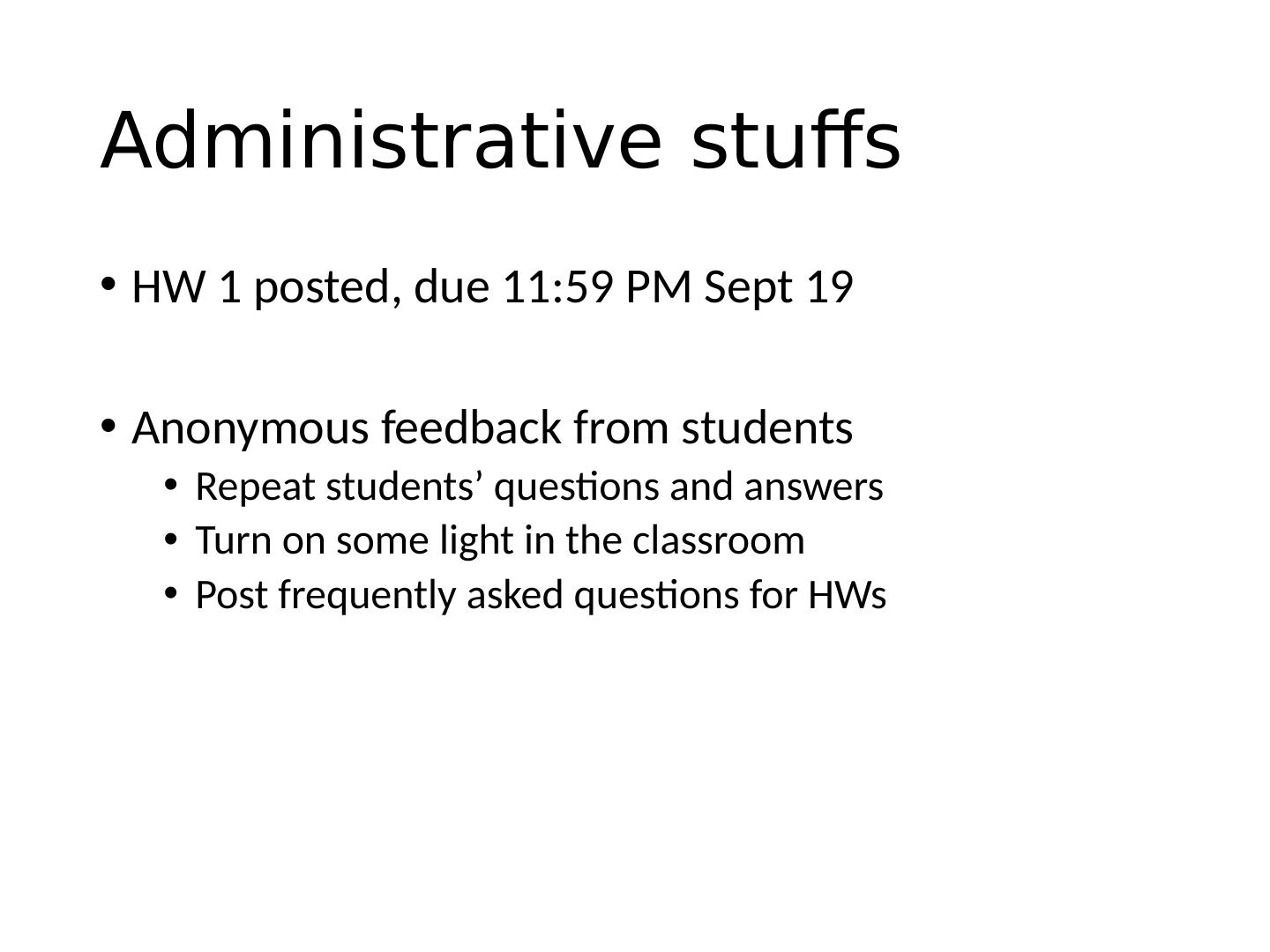
4 .* = Spatial domain Frequency domain FFT FFT = Inverse FFT
5 .Fourier Transform Teases away fast vs. slow changes in the image. Slide credit: A Efros Image as a sum of basis images
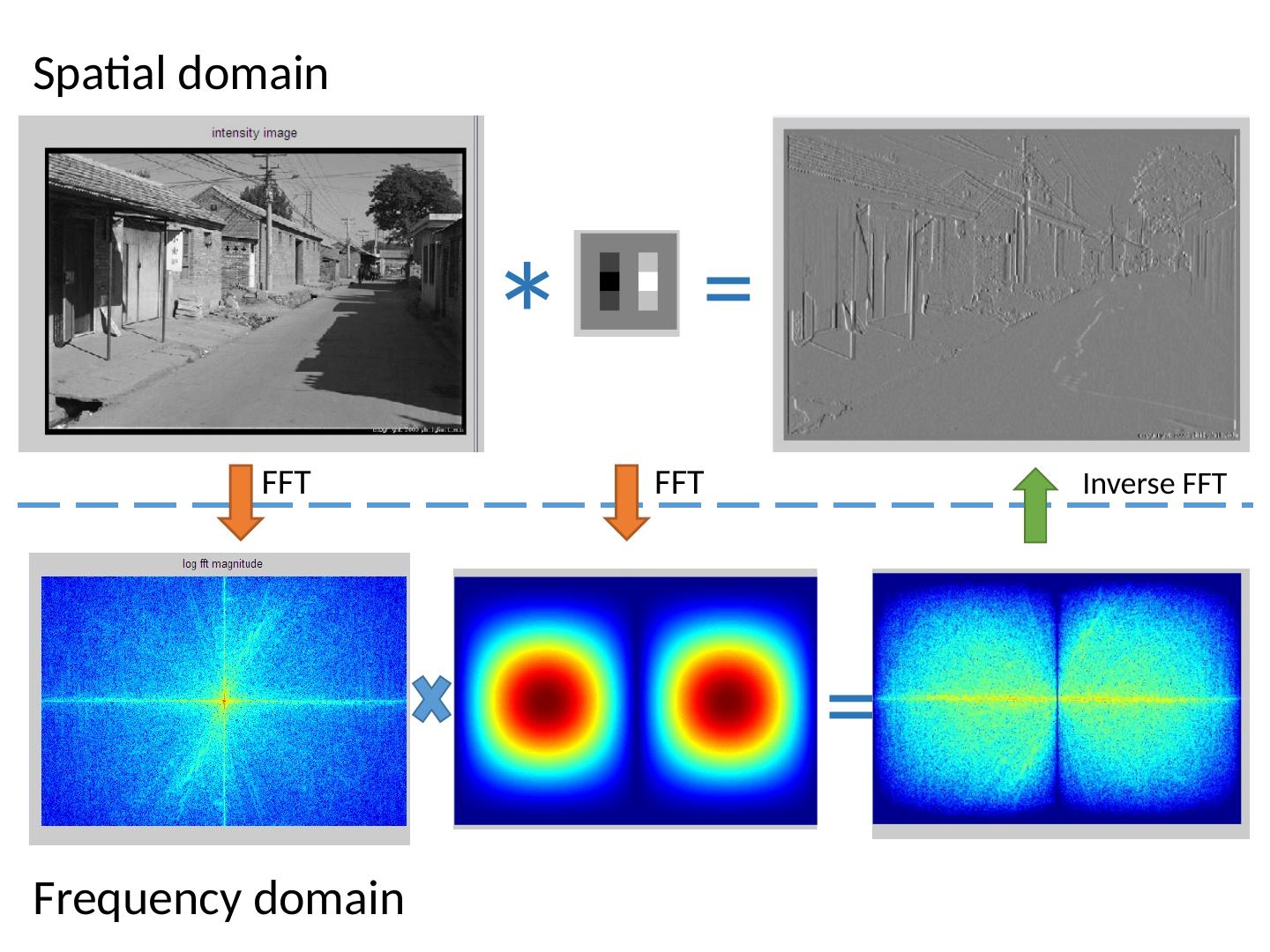
6 .Extension to 2D in Matlab , check out: imagesc (log(abs( fftshift (fft2( im )))));
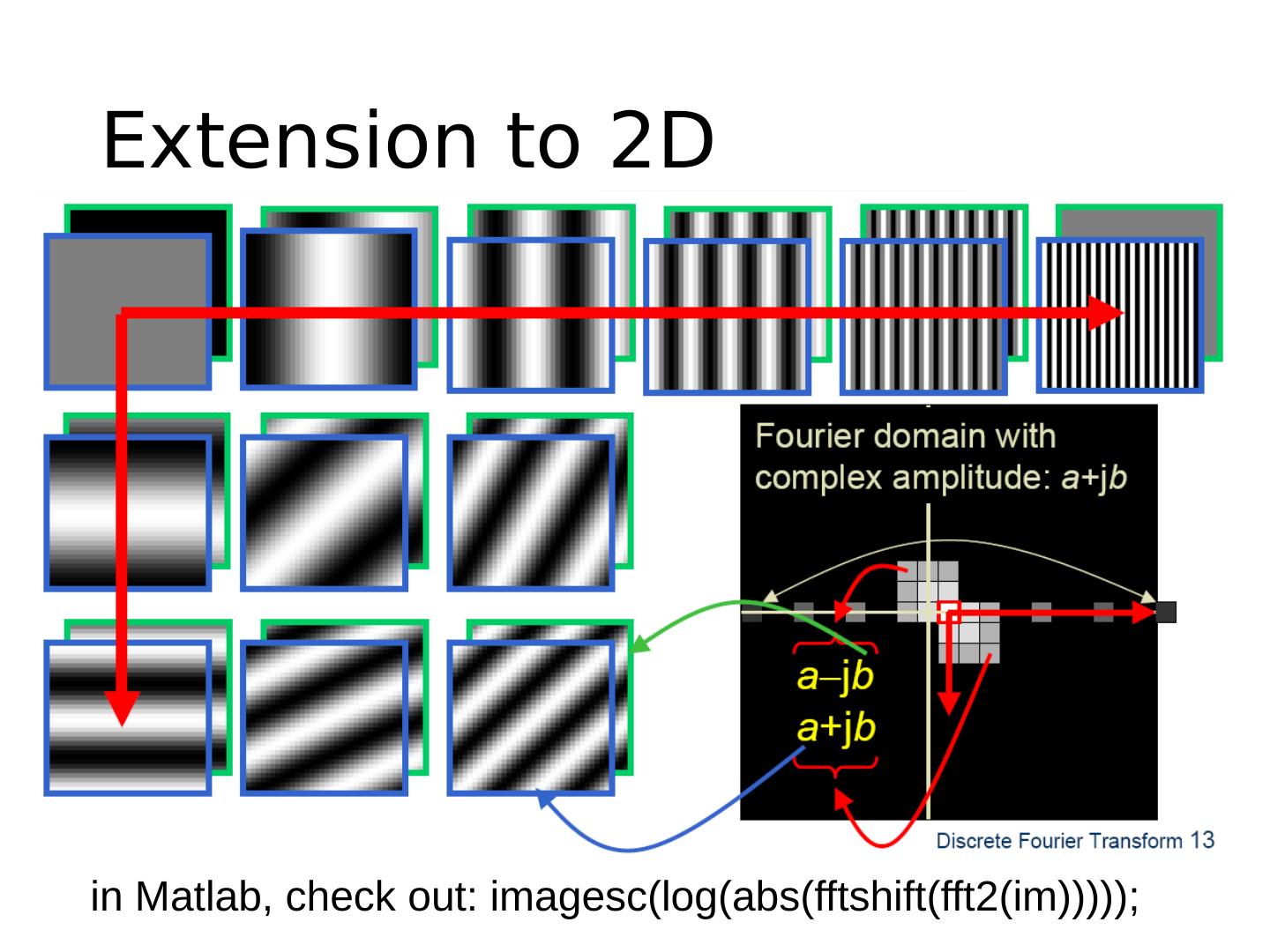
7 .Phase vs. Magnitude Magnitude Phase Intensity image FFT Inverse FFT Use random magnitude Inverse FFT Use random phase
8 .Today’s class Template matching Image Pyramids Compression Introduction to HW1
9 .Template matching Goal: find in image Main challenge: What is a good similarity or distance measure between two patches? D() , ) Correlation Zero-mean correlation Sum Square Difference Normalized Cross Correlation
10 .Matching with filters Goal: find in image Method 0: filter the image with eye patch Input Filtered Image What went wrong? f = image g = filter
11 .Goal: find in image Method 1: filter the image with zero-mean eye Input Filtered Image (scaled) Thresholded Image True detections False detections mean of template g Matching with filters
12 .Goal: find in image Method 2: Sum of squared differences (SSD) Input 1- sqrt(SSD) Thresholded Image True detections Matching with filters
13 . Can SSD be implemented with linear filters? Matching with filters Constant Filtering with g Filtering with box filter
14 .Goal: find in image Method 2: SSD Input 1- sqrt(SSD) What’s the potential downside of SSD? Matching with filters
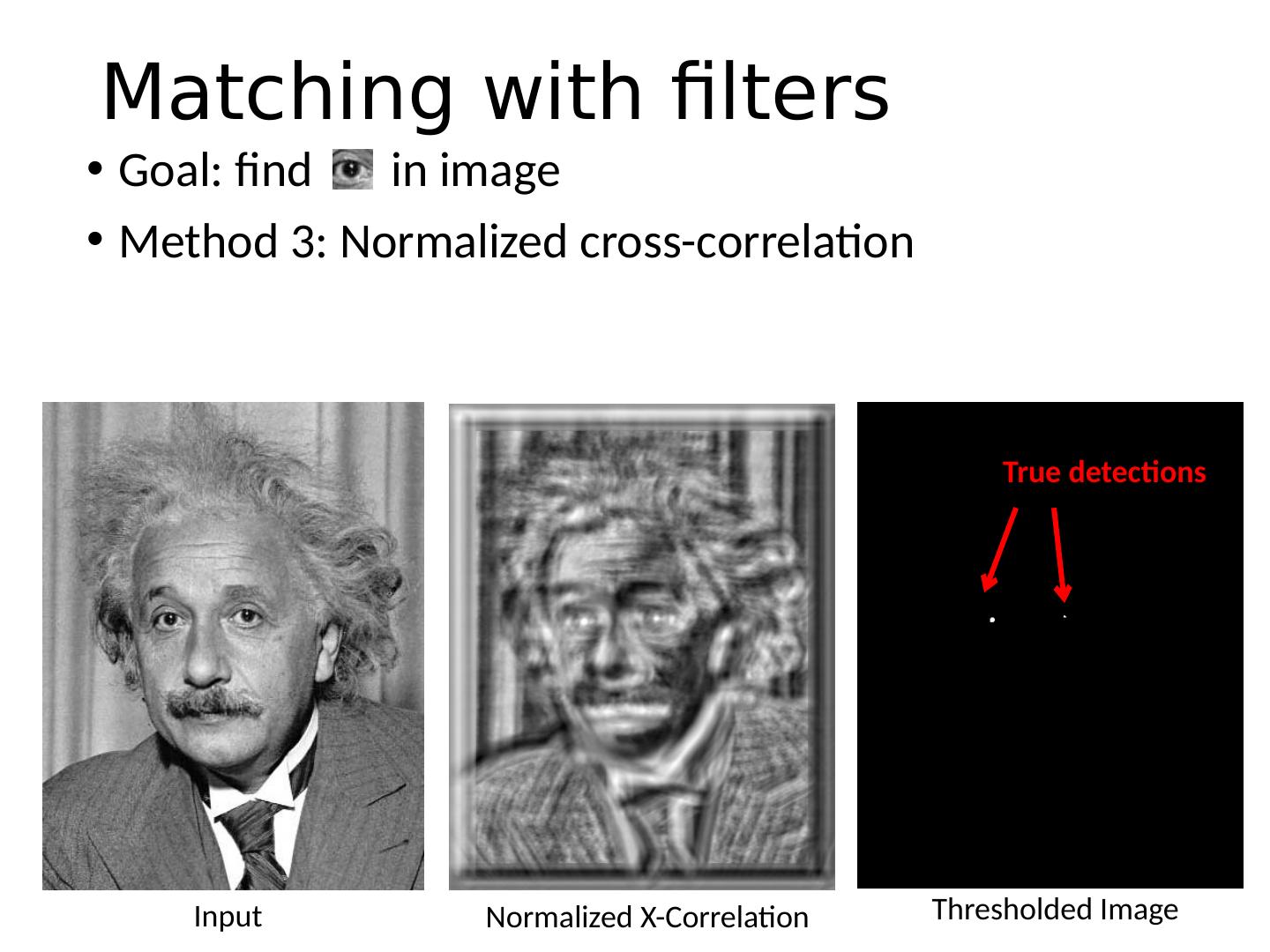
15 .Goal: find in image Method 3: Normalized cross-correlation Matlab: normxcorr2(template, im) mean image patch mean template Matching with filters
16 .Goal: find in image Method 3: Normalized cross-correlation Input Normalized X-Correlation Thresholded Image True detections Matching with filters
17 .Goal: find in image Method 3: Normalized cross-correlation Input Normalized X-Correlation Thresholded Image True detections Matching with filters
18 .Q: What is the best method to use? A : Depends Zero-mean filter: fastest but not a great matcher SSD: next fastest, sensitive to overall intensity Normalized cross-correlation: slowest, invariant to local average intensity and contrast
19 .Q: What if we want to find larger or smaller eyes? A: Image Pyramid
20 .Review of Sampling Low-Pass Filtered Image Image Gaussian Filter Sub-s ample Low-Res Image
21 .Gaussian pyramid Source: Forsyth
22 .Template Matching with Image Pyramids Input: Image, Template Match template at current scale Downsample image In practice, scale step of 1.1 to 1.2 Repeat 1-2 until image is very small Take responses above some threshold, perhaps with non-maxima suppression
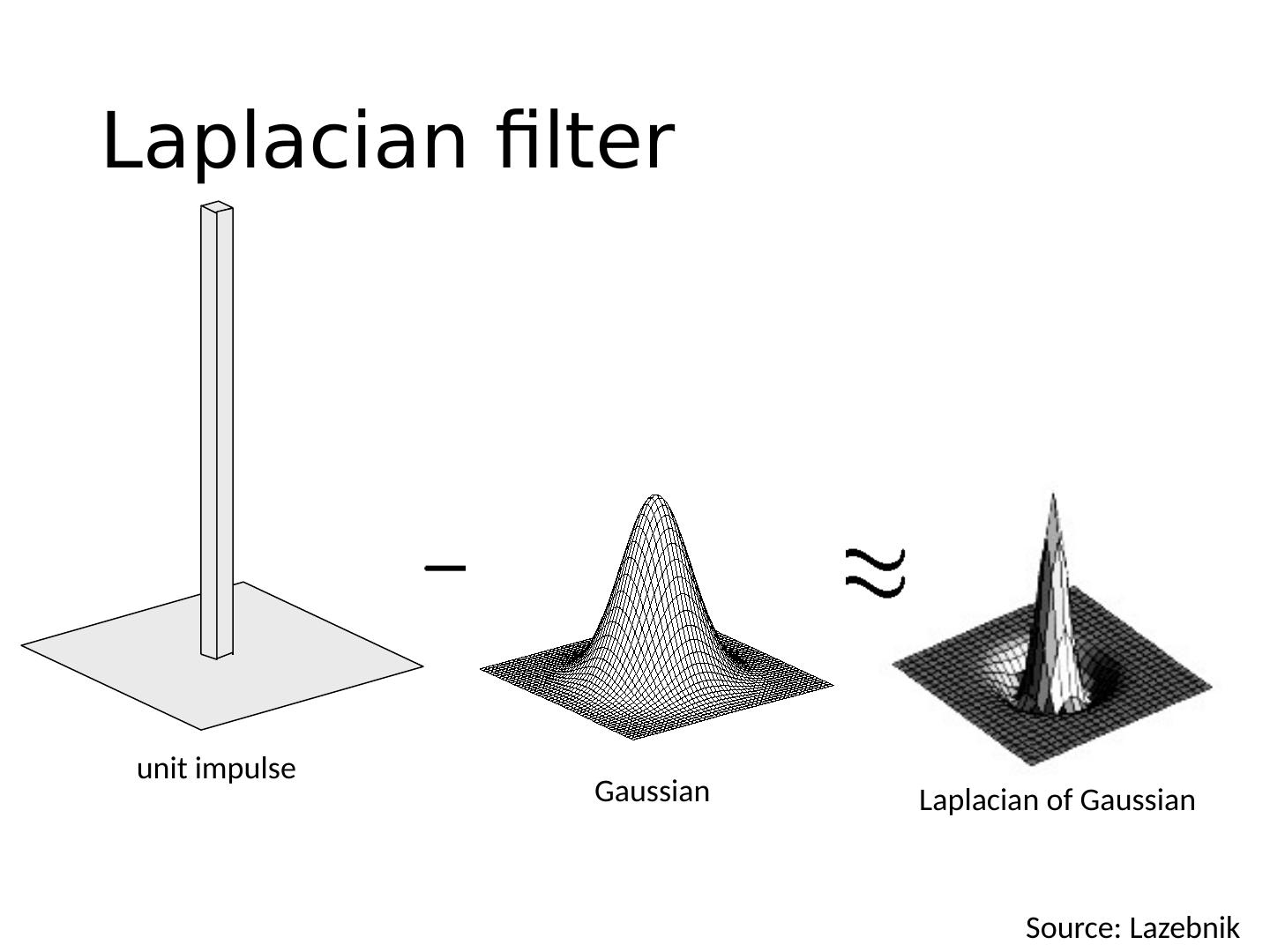
23 .Laplacian filter Gaussian unit impulse Laplacian of Gaussian Source: Lazebnik
24 .Laplacian pyramid Source: Forsyth
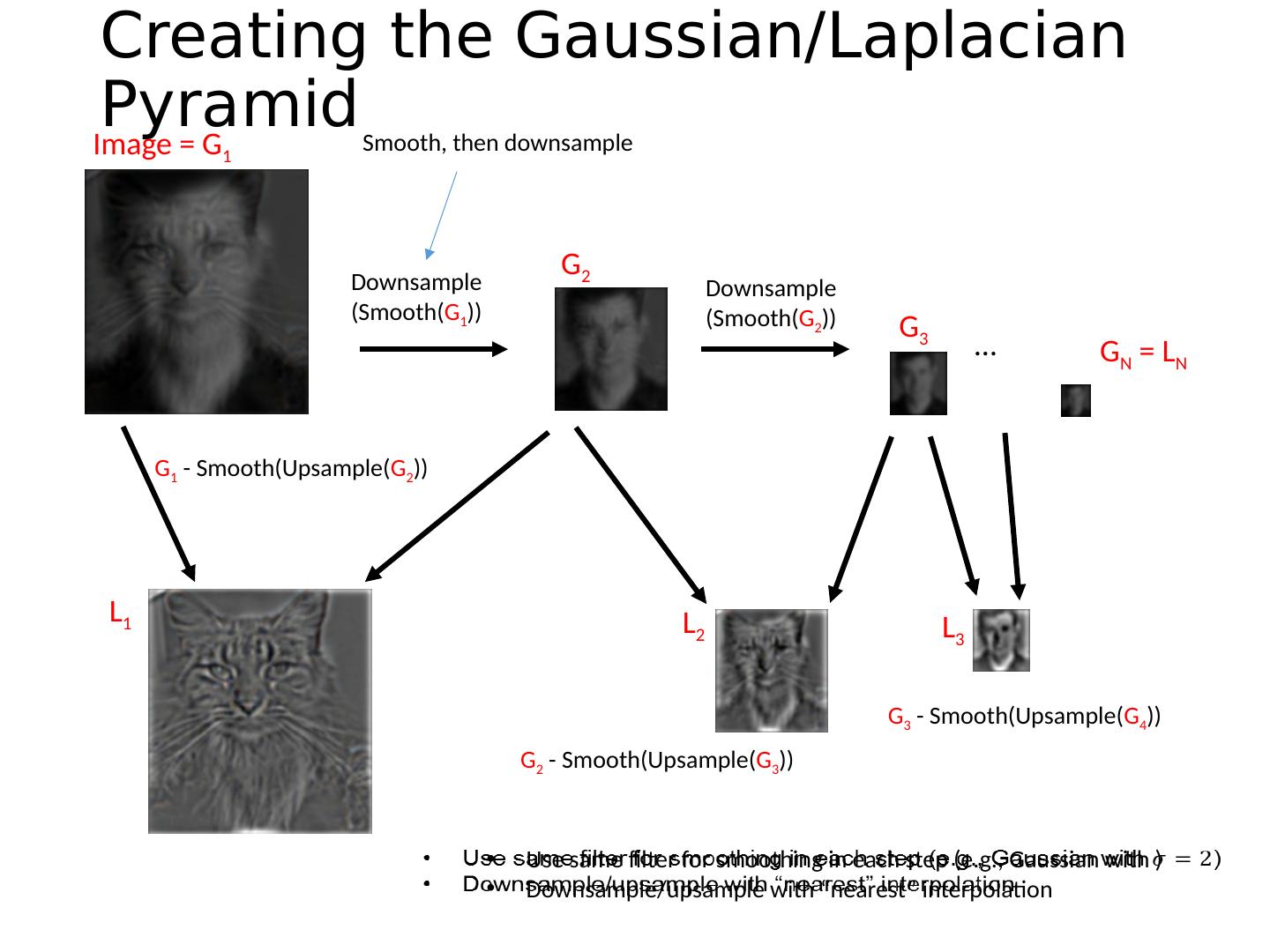
25 .Creating the Gaussian/ Laplacian Pyramid Downsample (Smooth( G 1 )) G 1 - Smooth( Upsample ( G 2 )) Image = G 1 L 1 G 2 … G N = L N G 2 - Smooth( Upsample ( G 3 )) L 2 G 3 - Smooth( Upsample ( G 4 )) L 3 G 3 Use same filter for smoothing in each step (e.g., Gaussian with ) Downsample/upsample with “nearest” interpolation Downsample (Smooth( G 2 )) Smooth, then downsample
26 .Hybrid Image in Laplacian Pyramid High frequency Low frequency
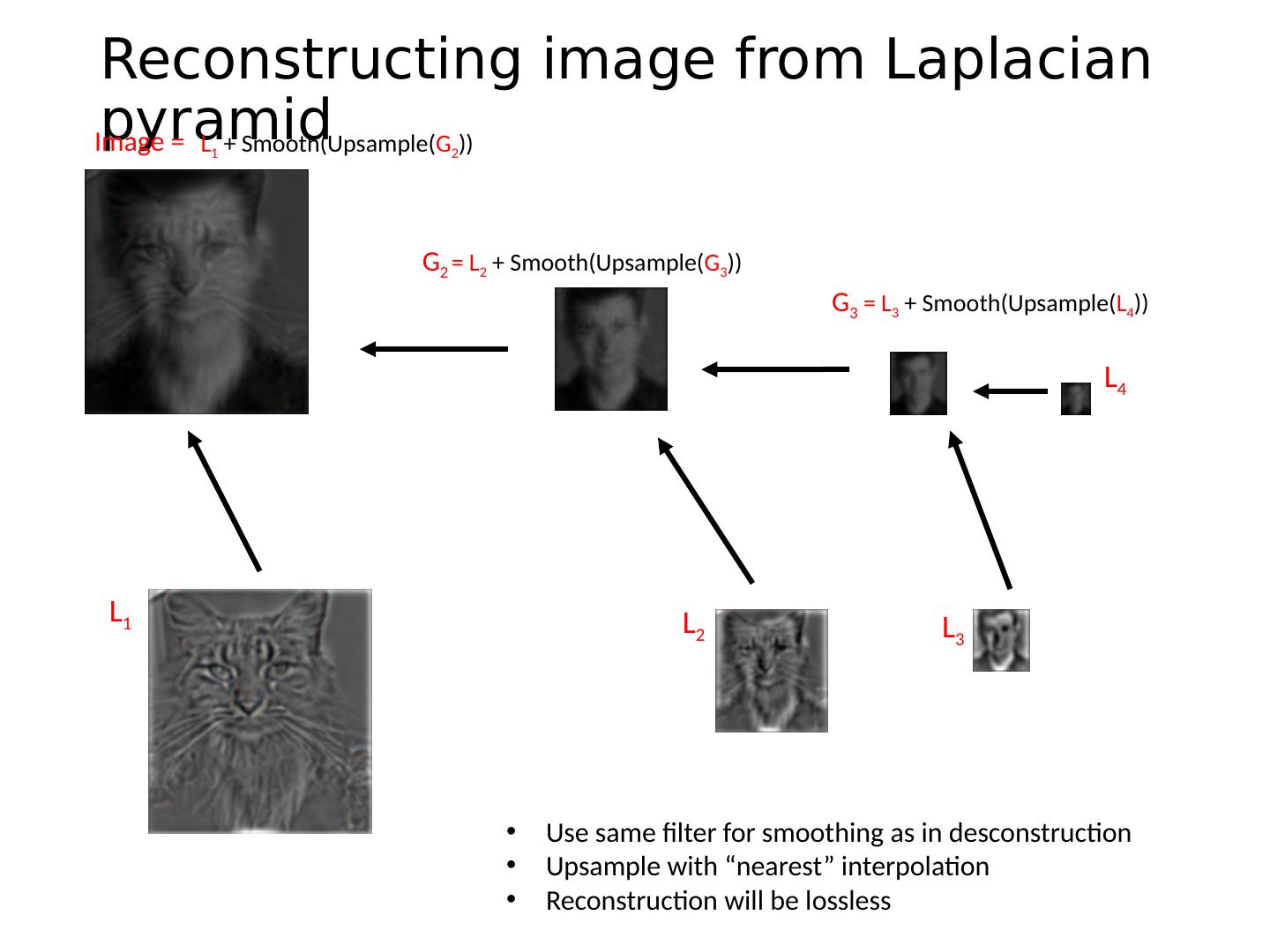
27 .Reconstructing image from Laplacian pyramid Image = L 1 L 4 L 2 G 3 = L 3 + Smooth( Upsample ( L 4 )) L 3 Use same filter for smoothing as in desconstruction Upsample with “nearest” interpolation Reconstruction will be lossless G 2 = L 2 + Smooth( Upsample ( G 3 )) L 1 + Smooth( Upsample ( G 2 ))
28 .Major uses of image pyramids Object detection Scale search Features Detecting stable interest points Course-to-fine registration Compression
29 .