AI：聚类算法

1 . 第五章 聚类方法 内容提要  聚类方法概述  划分聚类方法  层次聚类方法  密度聚类方法  其它聚类方法 2018年11月22日11月22日22日 DMKD Sides By MAO 1 

2 . 聚类分析研究概述  聚类分析源于许多研究领域，包括数据挖掘、统 计学、机器学习、模式识别等。作为一个数据挖 掘中的一个功能，聚类分析能作为一个独立的工 具来获得数据分布的情况，并且概括出每个簇的 特点，或者集中注意力对特定的某些簇做进一步 的分析。  数据挖掘技术的一个突出的特点是处理巨大的、 复杂的数据集，这对聚类分析技术提出了特殊的 挑战，要求算法具有可伸缩性、处理不同类型属 性的能力、发现任意形状的类、处理高维数据的 能力等。根据潜在的各项应用，数据挖掘对聚类 分析方法提出了不同要求。 2018年11月22日11月22日22日 DMKD Sides By MAO 2 

3 . 聚类分析在数据挖掘中的应用分析  聚类在数据挖掘中的典型应用有：  聚类分析可以作为其它算法的预处理步骤：利用聚类进 行数据预处理，可以获得数据的基本概况，在此基础上 进行特征抽取或分类就可以提高精确度和挖掘效率。也 可将聚类结果用于进一步关联分析，以获得进一步的有 用信息。  可以作为一个独立的工具来获得数据的分布情况：聚类 分析是获得数据分布情况的有效方法。通过观察聚类得 到的每个簇的特点，可以集中对特定的某些簇作进一步 分析。这在诸如市场细分、目标顾客定位、业绩估评、 生物种群划分等方面具有广阔的应用前景。  聚类分析可以完成孤立点挖掘：许多数据挖掘算法试图 使孤立点影响最小化，或者排除它们。然而孤立点本身 可能是非常有用的。如在欺诈探测中，孤立点可能预示 着欺诈行为的存在。 2018年11月22日11月22日22日 DMKD Sides By MAO 3 

4 . 聚类概念  定义 5-1 聚类分析的输入可以用一组有序对 (X, s) 或 (X, d) 表示，这里 X 表示一组样本， s 和 d 分别是度量样 本间相似度或相异度（距离）的标准。聚类系统的输出是 一个分区若 C={C1, C2,…, Ck} ，其中 Ci(i=1,2….,K) 是 X 的子集，且满足：  C1 CC2,… C, CCk=X  C1∩C2= CØ, Cij  C 中的成员 C1, C2,…, Ck 叫做类或簇（ Cluster ），每一 个类或簇都是通过一些特征描述的，通常有如下几种表示 方式：  通过它们的中心或类中关系远的（边界）点表示空间的一类点。  使用聚类树中的结点图形化地表示一个类。  使用样本属性的逻辑表达式表示类。  用中心表示一个类是最常见的方式，当类是紧密的或各向 同性时用这种方法非常好，然而，当类是伸长的或向各向 分布异性时，这种方式就不能正确地表示它们了。 2018年11月22日11月22日22日 DMKD Sides By MAO 4 

5 . 聚类分析的目标  聚类分析的目标就是形成的数据簇，并且满足下 面两个条件：  一个簇内的数据尽量相似（ high Cintra-class C similarity ）；  不同簇的数据尽量不相似（ low Cinter-class C similarity ）。  衡量一个聚类分析算法质量，依靠：  相似度测量机制是否合适。  是否能发现数据背后潜在的、手工难以发现的类知识。 2018年11月22日11月22日22日 DMKD Sides By MAO 5 

6 . 聚类分析方法的分类  按照聚类的标准，聚类方法可分为如下两种：  统计聚类方法：这种聚类方法主要基于对象之间的几何距离的。  概念聚类方法：概念聚类方法基于对象具有的概念进行聚类。  按照聚类算法所处理的数据类型，聚类方法可分为三种：  数值型数据聚类方法：所分析的数据的属性只限于数值数据。  离散型数据聚类方法：所分析的数据的属性只限于离散型数据。  混合型数据聚类方法：能同时处理数值和离散数据。  按照聚类的尺度，聚类方法可被分为以下三种：  基于距离的聚类算法：用各式各样的距离来衡量数据对象之间的相似度，如 k- means 、 k-medoids 、 BIRCH 、 CURE 等算法。  基于密度的聚类算法：相对于基于距离的聚类算法，基于密度的聚类方法主要是 依据合适的密度函数等。  基于互连性 (Linkage-Based)Linkage-Based) 的聚类算法：通常基于图或超图模型。高度连通的 数据聚为一类。  按照聚类聚类分析算法的主要思路，可以被归纳为如下几种。  划分法（ Partitioning CMethods ）：基于一定标准构建数据的划分。  属于该类的聚类方法有： k-means 、 k-modes 、 k-prototypes 、 k- medoids 、 PAM 、 CLARA 、 CLARANS 等。  层次法（ Hierarchical CMethods ）：对给定数据对象集合进行层次的分解。  密度法（ density-based CMethods ）：基于数据对象的相连密度评价。  网格法（ Grid-based CMethods ）：将数据空间划分成为有限个单元（ Cell ）的 网格结构，基于网格结构进行聚类。  模型法（ Model-Based CMethods ）：给每一个簇假定一个模型，然后去寻找能够 很好的满足这个模型的数据集。 C C 2018年11月22日11月22日22日 DMKD Sides By MAO 6 

7 . 常见的距离函数  按照距离公理，在定义距离测度时需要满足距离 公理的四个条件自相似性、最小性、对称性以及 三角不等性。常用的距离函数有如下几种：  明可夫斯基距离（ Minkowski ）  二次型距离（ Quadratic ）  余弦距离  二元特征样本的距离度量 2018年11月22日11月22日22日 DMKD Sides By MAO 7 

8 . 明可夫斯基（ Minkowski ）距离距离  假定 x 和 y 是相应的特征， n 是特征的维数。 x 和 y 的 明可夫斯基距离度量的形式如下： 1  n r r d ( x, y )    x i  y i   i 1   当取不同的值时，上述距离度量公式演化为一些特殊的 距离测度 :  当 γ=1 时，明可夫斯基距离演变为绝对值距离： n d ( x, y )  x i  yi i 1  当 γ=2 时，明可夫斯基距离演变为欧氏距离： 1/ 2  n 2 d ( x , y )   x i  yi   i 1  2018年11月22日11月22日22日 DMKD Sides By MAO 8 

9 . 二次型距离  二次型距离测度的形式如下： d ( x, y ) ( x  y ) T A( x  y)  1 2 其中 A 是非负定矩阵。  当取不同的值时，上述距离度量公式演化为一些特殊的距 离测度：  当 A为单位矩阵时，二次型距离演变为欧氏距离。  当 A为对角阵时，二次型距离演变为加权欧氏距离： 1  n 2 2 d ( x, y )   a ii x i  yi   i 1   当为协方差矩阵时，二次型距离演变为马氏距离。 2018年11月22日11月22日22日 DMKD Sides By MAO 9 

10 . 余弦距离  余弦距离的度量形式如下： n x yi 1 i i d ( x, y )  n n x y i 1 2 i i 1 2 i 2018年11月22日11月22日22日 DMKD Sides By MAO 10 

11 . 二元特征样本的距离度量  对于包含一些或全部不连续特征的样本，计算样本间的距 离是比较困难的。因为不同类型的特征是不可比的，只用 一个标准作为度量标准是不合适的。下面我们介绍几种二 元类型数据的距离度量标准。  假定 x 和 y 分别是 n 维特征， xi 和 yi 分别表示每维特征 ，且 xi 和 yi 的取值为二元类型数值 {0 ， 1} 。则 x 和 y 的距离定义的常规方法是先求出如下几个参数，然后采用 SMC 、 Jaccard 系数或 Rao 系数。  设 a ， b ， c 和 d 是样本 x 和 y 中满足 xi=yi=1 ， xi=1 且 yi=0 ， xi=0 且 yi=1 和 xi=yi=0 的二元类型属性的数量，则  简单匹配系数（ Simple Match Coefficient,SMC ）距离 a b  S smc ( x, y )  a b c d  Jaccard 系数 S jc ( x, y )  a a b c a S rc ( x, y )   Rao 系数 a b c d 2018年11月22日11月22日22日 DMKD Sides By MAO 11 

12 . 类间距离  距离函数都是关于两个样本的距离刻画，然而在聚类应用 中，最基本的方法是计算类间的距离。  设有两个类 Ca 和 Cb ，它们分别有 m 和 h 个元素，它们的 中心分别为 γa 和 γb 。设元素 x∈ Ca ， y∈ Cb ，这两个元 素间的距离通常通过类间距离来刻画，记为 D(Ca, Cb) 。  类间距离的度量主要有：  最短距离法：定义两个类中最靠近的两个元素间的距离为类间距离 。  最长距离法：定义两个类中最远的两个元素间的距离为类间距离。  中心法：定义两类的两个中心间的距离为类间距离。  类平均法：它计算两个类中任意两个元素间的距离，并且综合他们 为类间距离： 1 DG (Ca , Cb )    d ( x, y )  离差平方和。 mh xCa yCb 2018年11月22日11月22日22日 DMKD Sides By MAO 12 

13 . 中心法  中心法涉及到类的中心的概念。假如 Ci 是一个聚类， x 是 Ci 内的一个数据点，那么类中心定义如下： 1 xi  ni x xCi 其中 ni 是第 i 个聚类中的点数。因此，两个类 Ca 和 Cb 的类 间距离为： DC (Ca , Cb ) d (ra , rb ) 其中 γa 和 γb 是类 Ca 和 Cb 的中心点， d 是某种形式的距离 公式。 2018年11月22日11月22日22日 DMKD Sides By MAO 13 

14 . 离差平方和  离差平方和用到了类直径的概念：  类的直径反映了类中各元素间的差异，可定义为类中各元素至类 中心的欧氏距离之和，其量纲为距离的平方： m ra  ( xi  x a ) T ( xi  xb ) i 1  根据上式得到两类 Ca 和 Cb 的直径分别为 γa 和 γb ，类 Ca +b= Ca  Cb 的直径为 γa +b ，则可定义类间距离的平方 为： DW2 (C a , C b ) ra b  ra  rb 2018年11月22日11月22日22日 DMKD Sides By MAO 14 

15 . 第五章 聚类方法 内容提要  聚类方法概述  划分聚类方法  层次聚类方法  密度聚类方法  其它聚类方法 2018年11月22日11月22日22日 DMKD Sides By MAO 15 

16 . 划分聚类算法的主要思想  定义 5-2 给定一个有 n 个对象的数据集，划分 聚类技术将构造数据 k 个划分，每一个划分就代 表一个簇， k n 。也就是说，它将数据划分为 k 个簇，而且这 k 个划分满足下列条件：  每一个簇至少包含一个对象。  每一个对象属于且仅属于一个簇。  对于给定的 k ，算法首先给出一个初始的划分方 法，以后通过反复迭代的方法改变划分，使得每 一次改进之后的划分方案都较前一次更好。 2018年11月22日11月22日22日 DMKD Sides By MAO 16 

17 . 聚类设计的评价函数  一种直接方法就是观察聚类的类内差异（ Within cluster variation ）和类间差异 (Between cluster variation ） 。  类内差异：衡量聚类的紧凑性，类内差异可以用特定的距离函数 k k w(C )  w(C )   d ( x, x ) 2 来定义，例如， i i i 1 i 1 xCi  类间差异：衡量不同聚类之间的距离，类间差异定义为聚类中心 间的距离，例如， b(C )   d ( x j , xi ) 2 1j i k  聚类的总体质量可被定义为 w(c) 和 b(c) 的一个单调组合 ，比如 w(c) / b(c) 。 2018年11月22日11月22日22日 DMKD Sides By MAO 17 

18 . k-means 算法  k-means 算法，也被称为 k- 平均或 k- 均值，是一种得到 最广泛使用的聚类算法。相似度的计算根据一个簇中对象 的平均值来进行。 算法 5-1 C Ck-means 算法 输入：簇的数目 k 和包含 n 个对象的数据库。 输出： k 个簇，使平方误差准则最小。 （ 1)assign Cinitial Cvalue Cfor Cmeans; C/* 任意选择 k 个对象作为初始的簇中心； */ xi  C i  xCi x C(Linkage-Based)2) CREPEAT k E i 1  xC x  xi 2 i x C(Linkage-Based)3) C C C CFOR Cj=1 Cto Cn CDO Cassign Ceach C C j C Cto Cthe Cclosest clusters;  算法首先随机地选择 k 个对象，每个对象初始地代表了一 C(Linkage-Based)4个簇的平均值或中心。对剩余的每个对象根据其与各个簇 ) C C C C C C CFOR Ci=1 Cto Ck CDO C C C C C C C C C C C C C C C C C C C C C/ C* 更新簇平均值 */ 中心的距离，将它赋给最近的簇。然后重新计算每个簇的 平均值。这个过程不断重复，直到准则函数收敛。 C(Linkage-Based)5) C C CCompute C C C C C C C C C C C C C C C C C C C C C C C C C C C C C C C/* 计算准则函数 E*/  准则函数试图使生成的结果簇尽可能地紧凑和独立。 C(Linkage-Based)6) CUNTIL C CE 不再明显地发生变化。 2018年11月22日11月22日22日 DMKD Sides By MAO 18 

19 . k-means 例子 样本数据 序号 属性 属性 1 属性 根据所给的数据通过对其实施 k-means ( 设 n=8 ， k=2), ，其主要执行执行步骤： 2 1 1 1 2 2 1 第一次迭代：假定随机选择的两个对象，如序号 属性 1 和序号 属性 3 当作初始点，分别找到离两 3 1 2 点最近的对象，并产生两个簇 {1 ， 2} 和 {3 ， 4 ， 5 ， 6 ， 7 ， 8} 。 4 2 2 对于产生的簇分别计算平均值，得到平均值点。 5 4 3 对于 {1 ， 2} ，平均值点为（ 1.5 ， 1 ）（这里的平均值是简单的相加出 6 5 3 2 ）； 7 4 4 对于 {3 ， 4 ， 5 ， 6 ， 7 ， 8} ，平均值点为（ 3.5 ， 3 ）。 8 5 4 迭代次数 平均值 第二次迭代：通过平均值调整对象的所在的簇，重新聚类，即将所有点按离平均值点 平均值 产生的新簇 新平均值 新平均值 （簇 1 ） （簇 2 ） （簇 1 ） （簇 2 ） （ 1.5 ， 1 ）、（ 3.5 ， 1 ）最近的原则重新分配。得到两个新的簇： 1 （ 1 ， 1 ） （ 1 ， 2 ） {1 ， 2} ， {3 ， 4 ， 5 ， 6 ， 7 ， 8} （ 1.5 ， 1 ） （ 3.5 ， 3 ） 2 {1 ， 2 ， 3 ， 4} 和 {5 ， 6 ， 7 ， 8} 。重新计算簇平均值点，得到新的平均值 （ 1.5 ， 1 ） （ 3.5 ， 3 ） {1 ， 2 ， 3 ， 4} ， {5 ， 6 ， 7 ， 8} （ 1.5 ， 1.5 ） （ 4.5 ， 3.5 ） 点为（ 1.5 ， 1.5 ）和（ 4.5 ， 3.5 ）。 3 （ 1.5 ， 1.5 ） （ 4.5 ， 3.5 ） {1 ， 2 ， 3 ， 4} ， {5 ， 6 ， 7 ， 8} （ 1.5 ， 1.5 ） （ 4.5 ， 3.5 ） 2018年11月22日11月22日22日 DMKD Sides By 1.5 第三次迭代：将所有点按离平均值点（ MAO ， 1.5 ）和（ 4.5 ， 3.5 ）最近的原则重 19 

20 . K-means 1. Ask user how many clusters they’d like. (e.g. k=5) Copyright © 2001, 2004, Andrew W. Moore 

21 . K-means 1. Ask user how many clusters they’d like. (e.g. k=5) 2. Randomly guess k cluster Center locations Copyright © 2001, 2004, Andrew W. Moore 

22 . K-means 1. Ask user how many clusters they’d like. (e.g. k=5) 2. Randomly guess k cluster Center locations 3. Each datapoint finds out which Center it’s closest to. (Thus each Center “owns” a set of datapoints) Copyright © 2001, 2004, Andrew W. Moore 

23 . K-means 1. Ask user how many clusters they’d like. (e.g. k=5) 2. Randomly guess k cluster Center locations 3. Each datapoint finds out which Center it’s closest to. 4. Each Center finds the centroid of the points it owns Copyright © 2001, 2004, Andrew W. Moore 

24 . K-means 1. Ask user how many clusters they’d like. (e.g. k=5) 2. Randomly guess k cluster Center locations 3. Each datapoint finds out which Center it’s closest to. 4. Each Center finds the centroid of the points it owns… 5. …and jumps Copyright © 2001, 2004, Andrew W. there Moore 

25 . K-means Start Advance apologies: in Black and White this example will deteriorate Example generated by Dan Pelleg’s super-duper fast K- means system: Dan Pelleg and Andrew Moore. Accelerating Exact k- means Algorithms with Geometric Reasoning. Proc. Conference on Knowledge Discovery in Databases Copyright © 2001, 1999, 2004, Andrew W. (KDD99) (available on Moore 

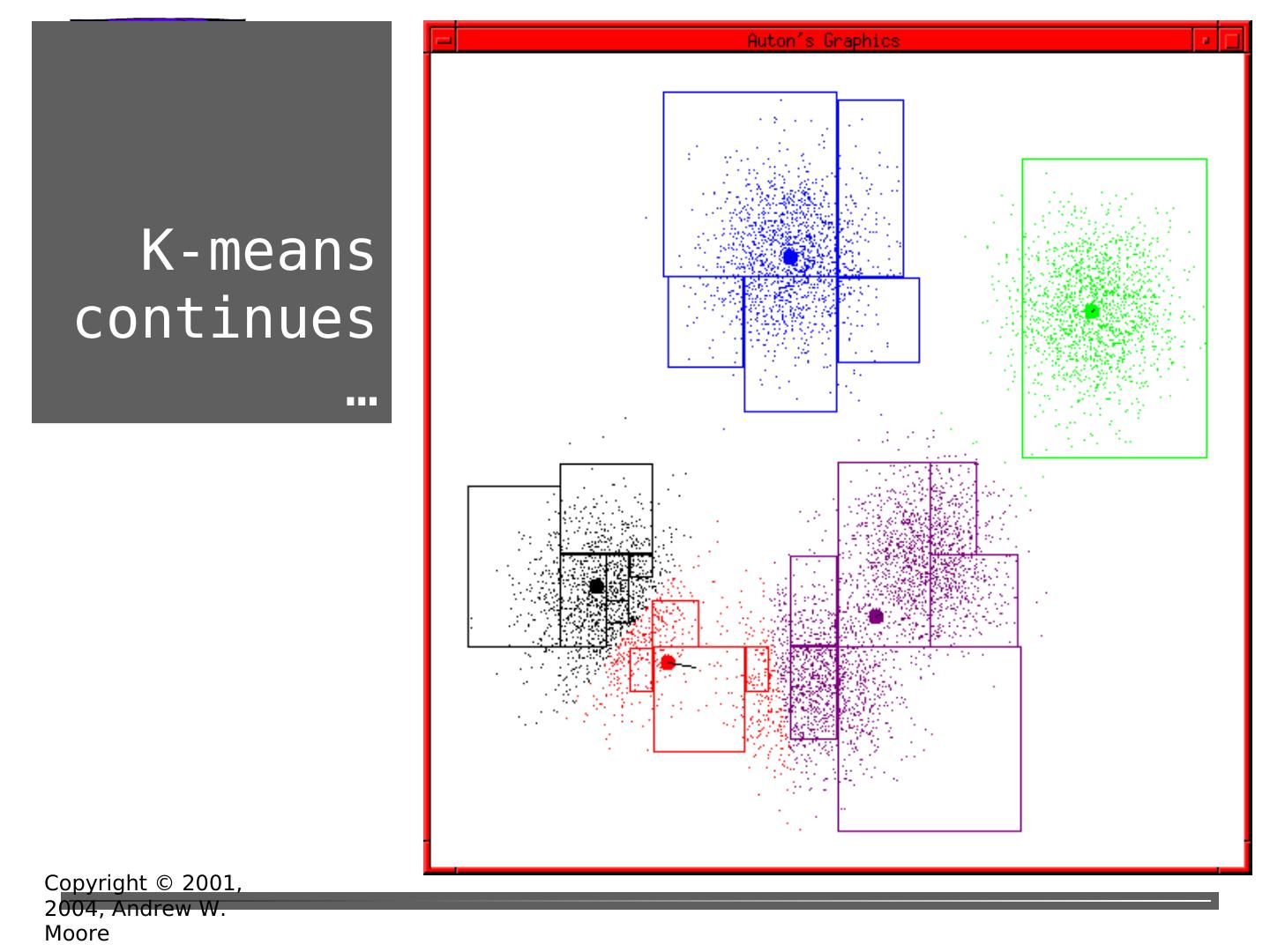
26 . K-means continues … Copyright © 2001, 2004, Andrew W. Moore 

27 . K-means continues … Copyright © 2001, 2004, Andrew W. Moore 

28 . K-means continues … Copyright © 2001, 2004, Andrew W. Moore 

29 . K-means continues … Copyright © 2001, 2004, Andrew W. Moore