AI:时间序列建模

1 .时间序列建模培训  背景及引例  平稳序列  平稳序列建模 

2 .一 背景及引例 概率统计学科中应用性较强的一个分支 广泛的应用领域： 金融经济 气象水文 信号处理 机械振动 ………… 

3 .时间序列的定义  时间序列 : 按时间次序排列的随机变量序列 X 1 , X 2 , (1.1)  n 个观测样本 : 随机序列的n 个有序观测值 x1 , x2 , , xn (1.2)  称序列 x1 , x2 , (1.3) 是时间序列 (1.1) 的一次实现或一条轨道 

4 . 按照时间的顺序把随机事件变化发展的过 程记录下来就构成了一个时间序列。对时 间序列进行观察、研究，找寻它变化发展 的规律，预测它将来的走势就是时间序列 分析。 

5 .太阳黑子对地球的影响  会出现磁暴现象  会引起地球上气候的变化  会影响地球上的地震  会影响树木生长  会影响到我们的身体  ……………………… 

6 .Wolfer 记录的 300 年的太阳黑子 数 

7 .房地产业、房价  关乎国计民生的支柱产业  影响着城镇居民的住房消费  影响着水泥，钢铁，建材，冶金等相关 行业的发展  影响着地方政府财政收入  ……………………………. 

8 .杭州近三年房价走势 

9 .

10 . 股市是经济的晴雨表  从股市本身看，我国股市的确有自己的 特点  股票是一种高风险的资本投资  ……………………………… 

11 .

12 .

13 .1985 至 2000 年广州月平均 气温 

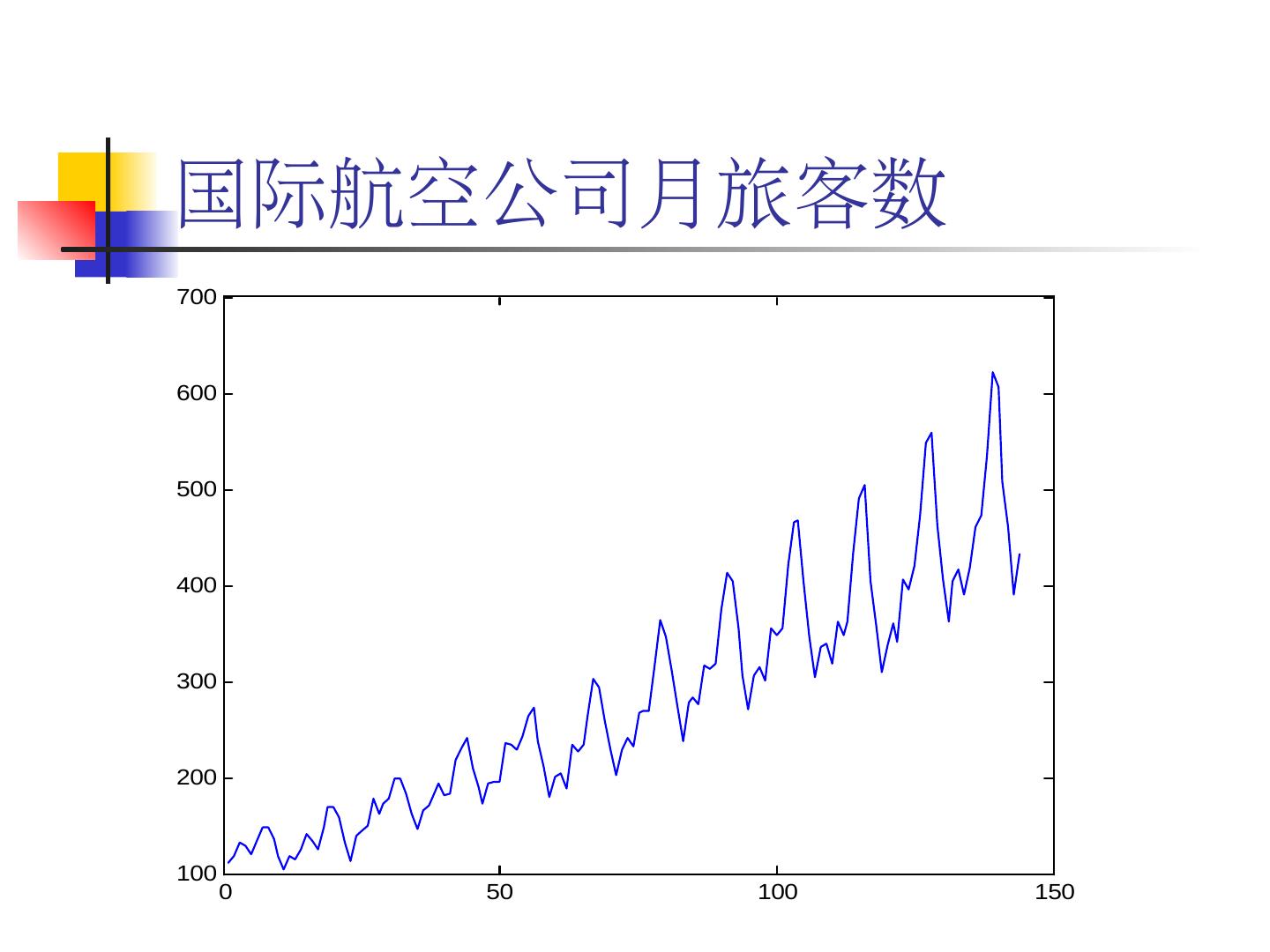
14 .国际航空公司月旅客数 700 600 500 400 300 200 100 0 50 100 150 

15 . 化学反应过程中溶液浓度数据 18.5 18 17.5 17 16.5 16 0 20 40 60 80 100 120 140 160 180 200 

16 .二、平稳序列 

17 .白噪声、白噪声模拟 

18 .

19 . Poisson 白噪声的 60 样本的 产生 1. 随机产生服从 (0,1) 上均匀的 200 个样 本: 2. 给出服从参数为 1 的指数分布的 200 个 独立样本 ; 3. 给出参数为 1 的 Poisson 过程一条样本 轨道在 i=1,…,61 上的取值； 

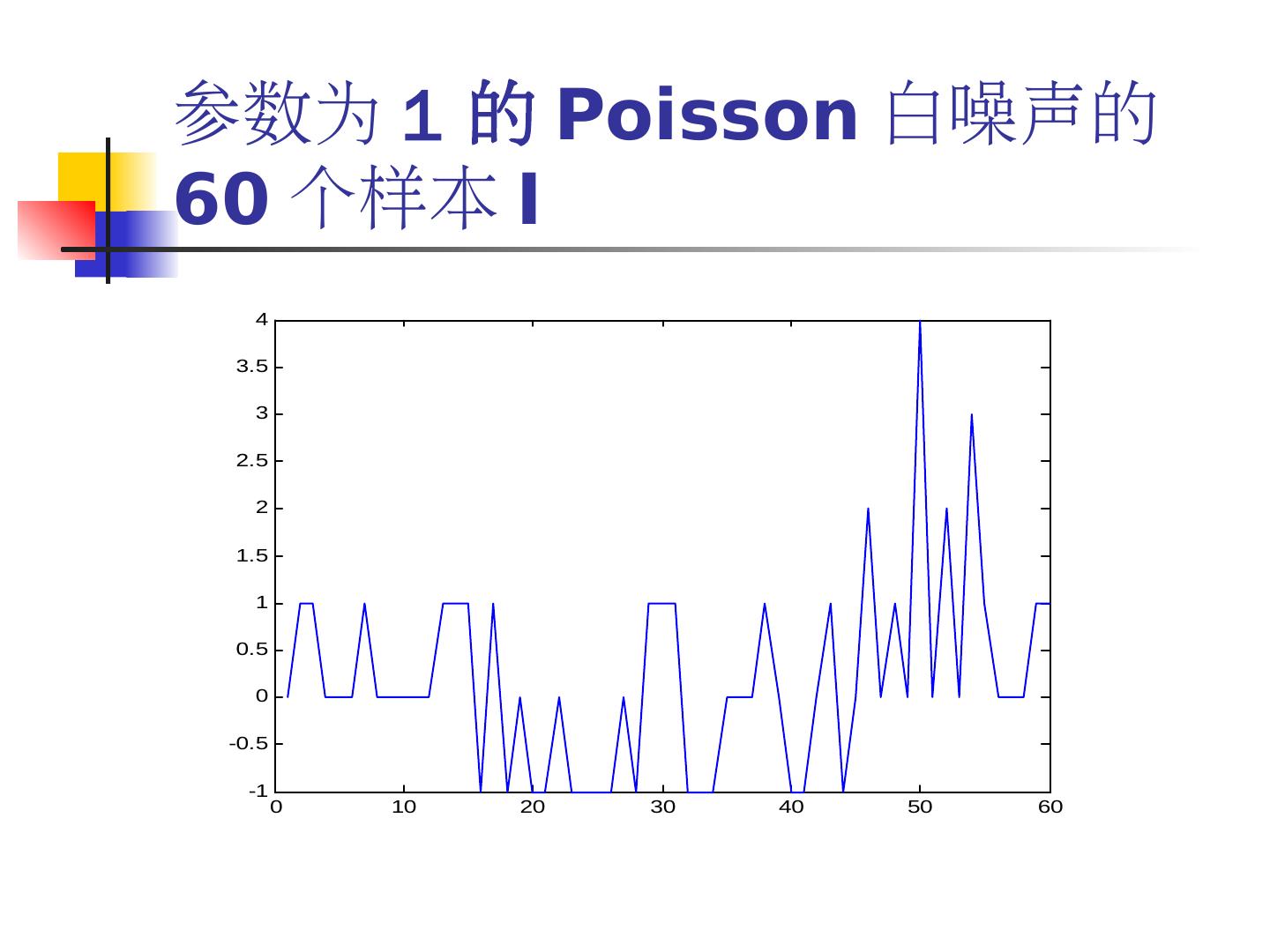
20 .参数为 1 的 Poisson 白噪声的 60 个样本 I 4 3.5 3 2.5 2 1.5 1 0.5 0 -0.5 -1 0 10 20 30 40 50 60 

21 .样本 II 2 1.5 1 0.5 0 -0.5 -1 0 10 20 30 40 50 60 

22 .例：布朗运动 

23 .

24 .标准正态白噪声的 60 个样本 : A=randn(1,60) ； plot(A) 

25 .在经济工作中我们遇到的时间序列通常未必是平 稳的，那么如何检验与鉴别呢？首先我们从图 形上直观地理解一下平稳性与非平稳性： 例 某市 1985-1994 年各月的工业产值： a=[10.93,9.34,11,10.98,11.29,11.84,10.62,10.9,12.77,12.15,12.24,12.3, 9.91,10.24,10.41,10.47,11.51,12.45,11.32,11.73,12.61,13.04,13.14,14.15, 10.85,10.3,12.74,12.73,13.08,14.27,13.18,13.75,14.42,13.95,14.53,14.91, 12.94,11.43,14.36,14.57,14.25,15.86,15.18,15.94,16.54,16.9,16.88,18.1, 13.7,10.88,15.79,16.36,17.22,17.75,16.62,16.96,17.69,16.4,17.51,19.73, 13.73,12.85,15.68,16.79,17.59,18.51,16.8,17.27,20.83,19.18,21.4,23.76, 15.73,13.14,17.24,17.93,18.82,19.12,17.7,19.87,21.17,21.44,22.14,22.45, 17.88,16,20.29,21.03,21.78,22.51,21.55,22.01,22.68,23.02,24.55,24.67, 19.61,17.15,22.46,23.19,23.40,26.26,22.91,24.03,23.94,24.12,25.87,28.25]; 作出其原始数据图形与一阶差分后的图形 

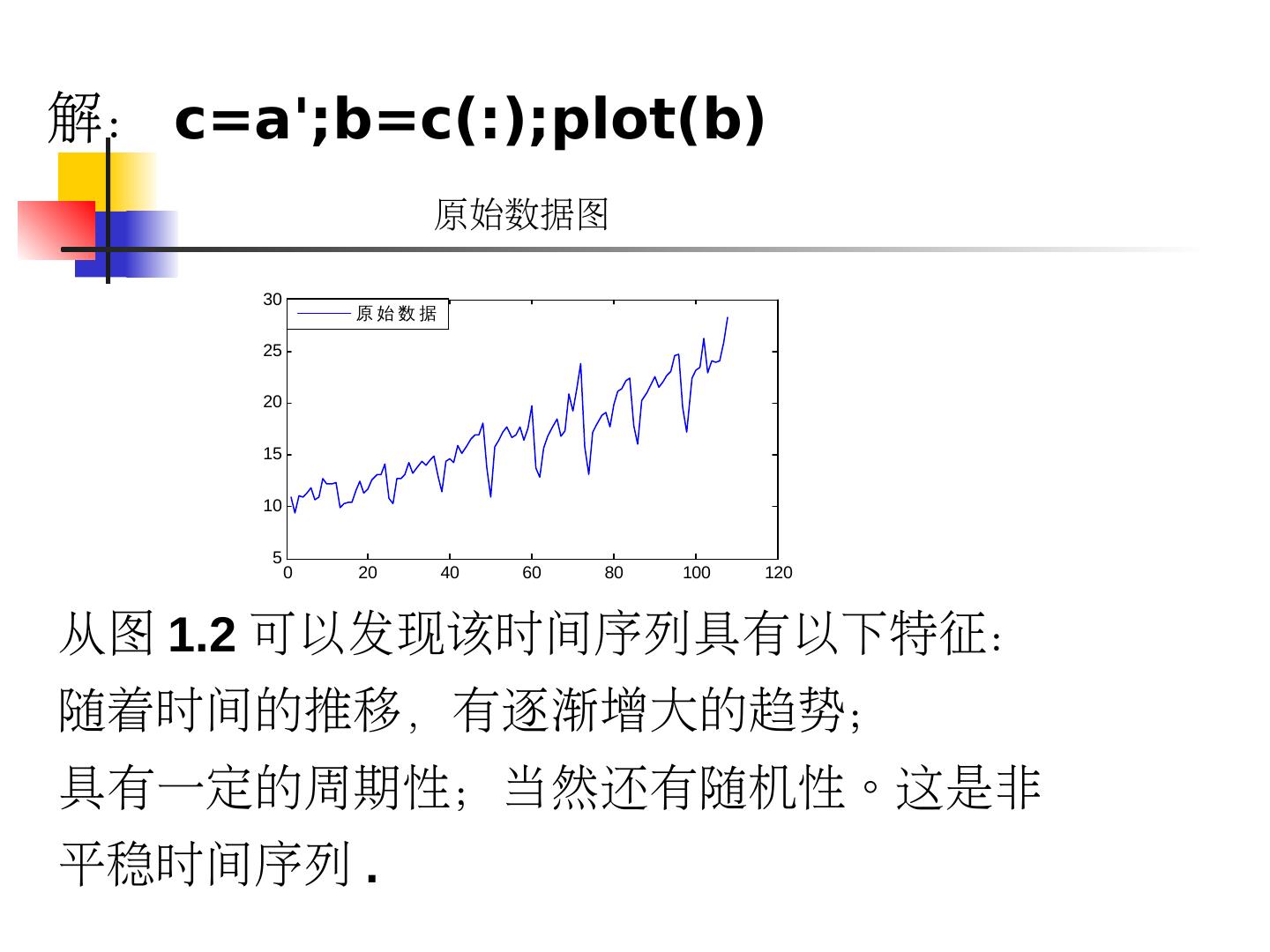
26 .解： c=a';b=c(:);plot(b) 原始数据图 30 原始数据 25 20 15 10 5 0 20 40 60 80 100 120 从图 1.2 可以发现该时间序列具有以下特征： 随着时间的推移，有逐渐增大的趋势； 具有一定的周期性；当然还有随机性。这是非 平稳时间序列 . 

27 . 在时间序列建模的方法中很多都是对平 稳序列作出的，因此对于非平稳时间序列 常常先将其化为平稳序列，差分就是最常 用的一种方法，对于图 1.2 中的数据我们 利用一次差分得到的数据图形如图 1.3 所 示： 10 一 阶 差 分 5 0 -5 -10 0 20 40 60 80 100 120 图 1-3 经过一阶差分处理后的图 

28 .注意：① 时间趋势可以通过差分解决，因为多 时间趋势可以通过差分解决，因为多 项式差分一次，其阶数就降低一次；② 指数 指数 趋势可以通过先取对数，然后再差分。 例如： yt=e2t ，取对数变为 lnyt=2t ，再做一次差分得 lnyt+1-lnyt=2(t+1-t)=2 此时为常数故平稳 

29 . 三 平稳时间序列建模 1. 常见的三类时间序列模型 (1) P 阶自回归模型： AR(p) xt 1 xt  1  2 xt  2    p xt  p   t 其中 t 是白噪声序列，且与 xk 不相关（ k<t ） (2) q 阶移动平均模型： MA(q) xt  t  1 t  1   2 t  2     q t  q 其中 t 是白噪声序列 .