AI：复杂分类器

1 .复杂分类器的简介

2 .复杂分类器 支撑向量机 （ support vector machine ） 神经网络（ Neural Networks ） 模糊逻辑 （ Fuzzy Logic ）

3 .支撑向量机 （ support vector machine ）

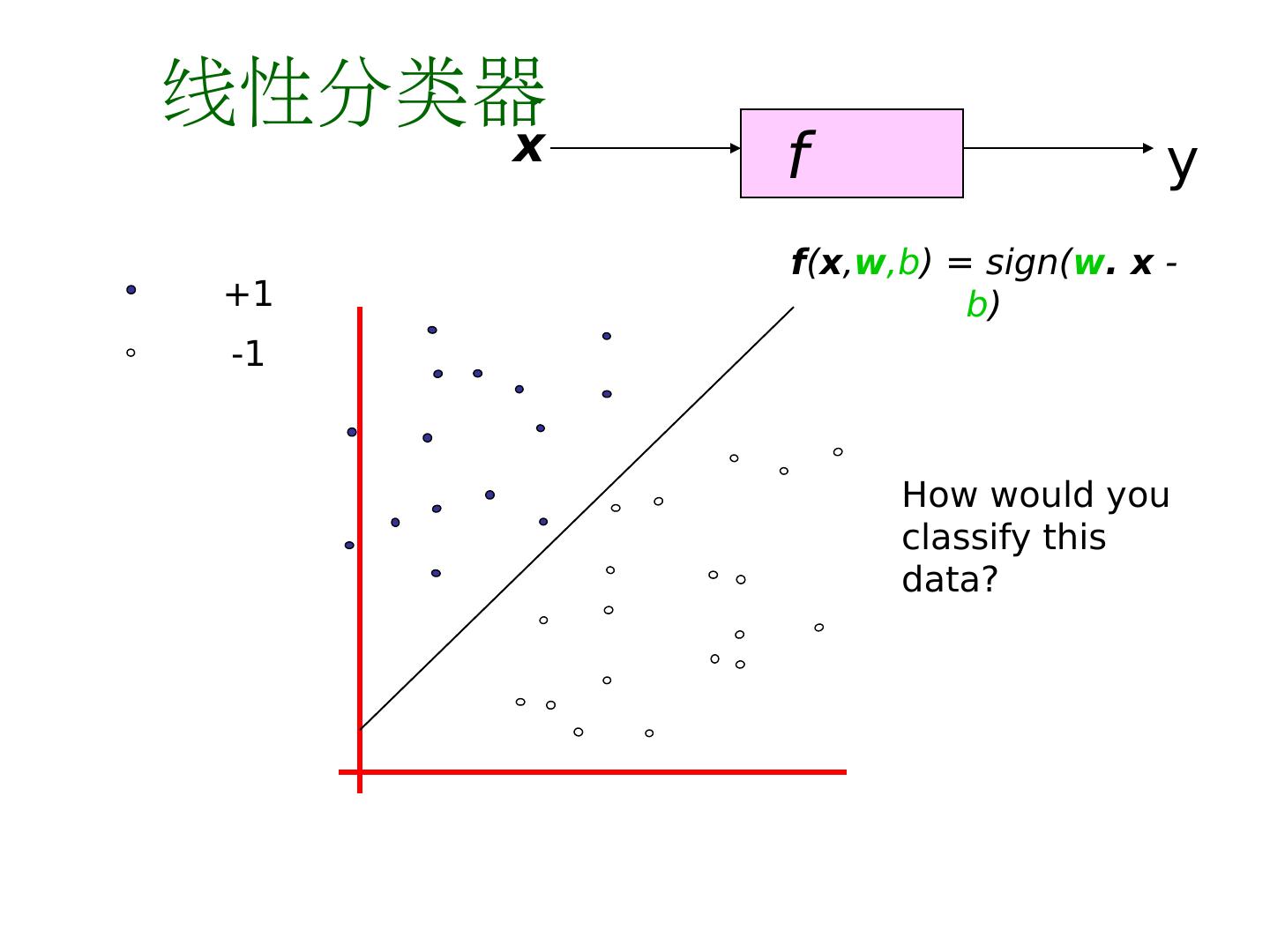
4 .f x y +1 -1 f ( x , w ,b ) = sign( w . x - b ) How would you classify this data? 线性分类器

5 .f x y +1 -1 f ( x , w ,b ) = sign( w . x - b ) How would you classify this data? 线性分类器

6 .线性分类器 f x y +1 -1 f ( x , w ,b ) = sign( w . x - b ) How would you classify this data?

7 .线性分类器 f x y +1 -1 f ( x , w ,b ) = sign( w . x - b ) How would you classify this data?

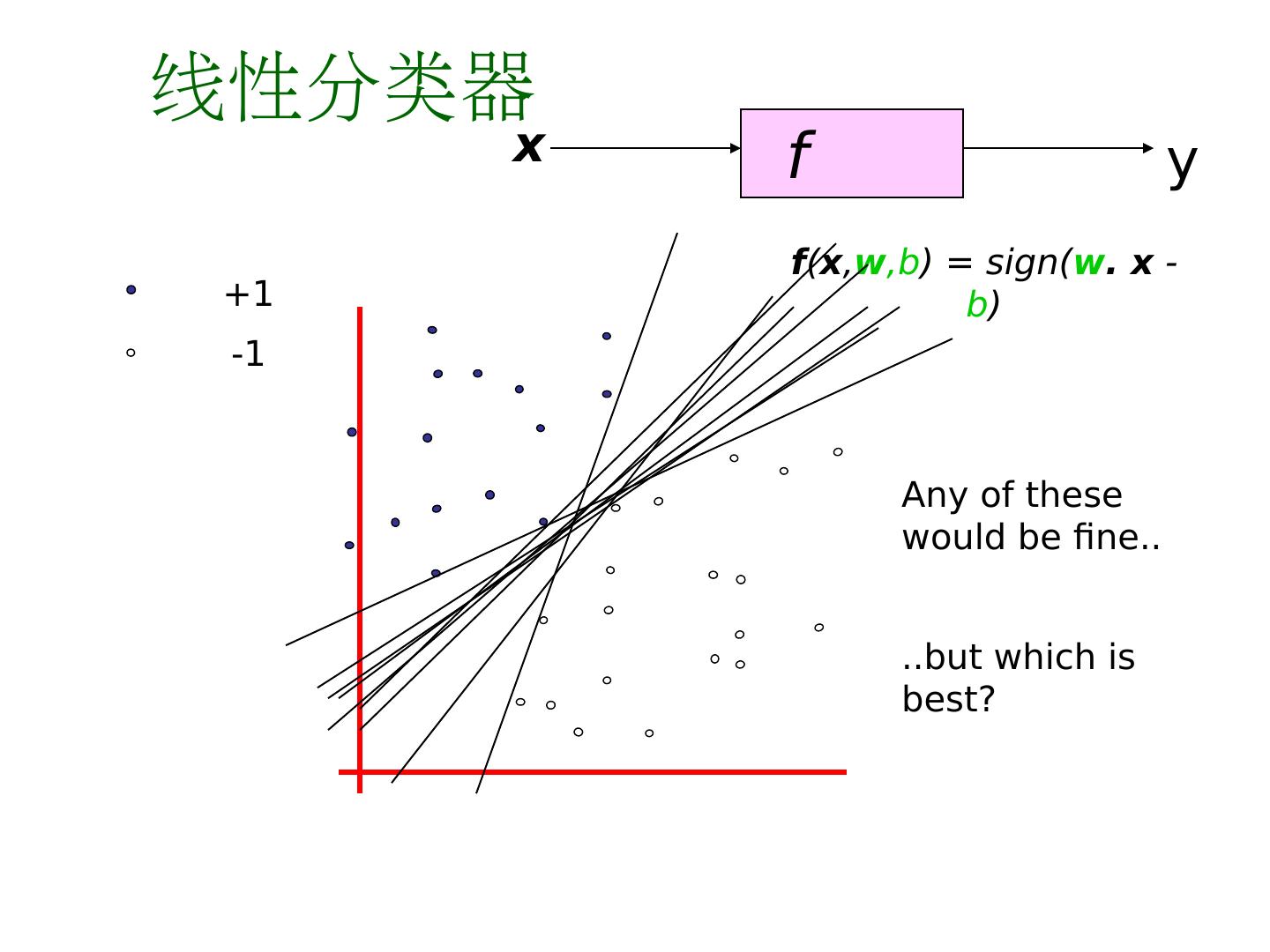
8 .线性分类器 f x y +1 -1 f ( x , w ,b ) = sign( w . x - b ) Any of these would be fine.. ..but which is best?

9 .线性分类器 f x y +1 -1 f ( x , w ,b ) = sign( w . x - b ) 线性分类器的 间隔（ margin） ： 到超平面最近的样本与此超平面之间的距离。

10 .最大间隔 f x y +1 -1 f ( x , w ,b ) = sign( w . x - b ) 具有最大间隔的线性分类器叫做 最大间隔线性分类器 。 其就是一种最简单的支持向量机( SVM) ( 称为线性支持向量机，即 LSVM) 线性支持向量机

11 .f x y +1 -1 f ( x , w ,b ) = sign( w . x - b ) 支持向量( Support Vectors) : 是那些距离超平面最近的点。 具有最大间隔的线性分类器叫做 最大间隔线性分类器 。 其就是一种最简单的支持向量机( SVM) ( 称为线性支持向量机，即 LSVM) 线性支持向量机 最大间隔

12 .Why… 最大间隔? +1 -1 f ( x , w ,b ) = sign( w . x - b ) 支持向量( Support Vectors) : 是那些距离超平面最近的点。 具有最大间隔的线性分类器叫做 最大间隔线性分类器 。 其就是一种最简单的支持向量机( SVM) ( 称为线性支持向量机，即 LSVM) 线性支持向量机 直观上感觉很好. 学习得到的线性分类器.其对未知样本的预测能力与分类器间隔有如下关系：

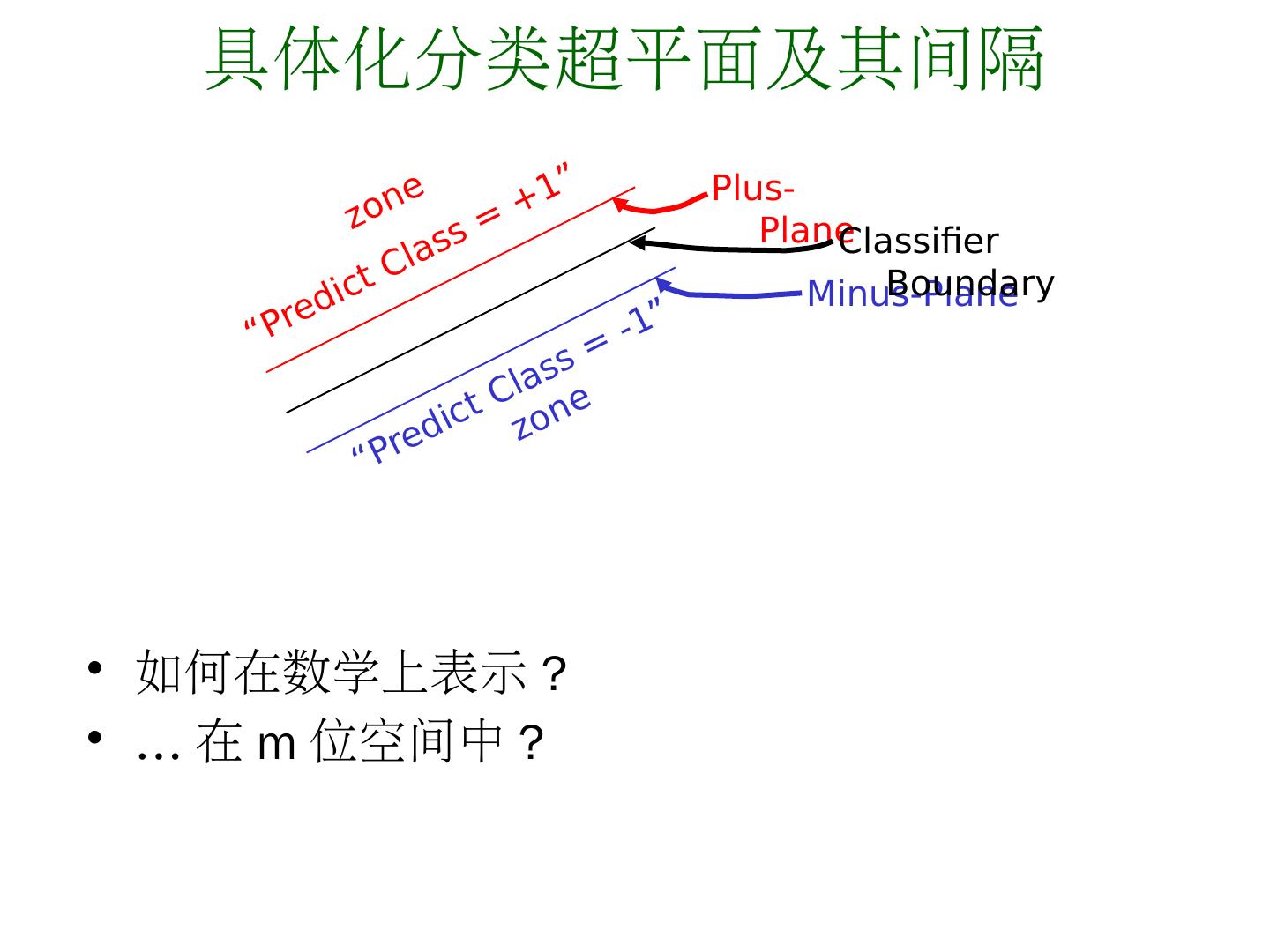
13 .具体化分类超平面及其间隔 如何在数学上表示? … 在 m 位空间中? Plus-Plane Minus-Plane Classifier Boundary zone “ Predict Class = +1” “ Predict Class = -1” zone

14 .Plus-plane = { x : w . x + b = +1 } Minus-plane = { x : w . x + b = -1 } Classify as.. +1 if w . x + b >= 1 -1 if w . x + b <= -1 不可分情况 if -1 < w . x + b < 1 具体化分类超平面及其间隔 Plus-Plane Minus-Plane Classifier Boundary zone “ Predict Class = +1” “ Predict Class = -1” zone

15 .计算间隔 Zone “ Predict Class = +1” “ Predict Class = -1” zone wx+b=1 wx+b=0 wx+b=-1 M = Margin 我们怎样利用 w 与 b 计算 margin? Plus-plane = { x : w . x + b = +1 } Minus-plane = { x : w . x + b = -1 } 注: 向量 w 与 Plus Plane 垂直. 为什么 ?

16 .设 u 和 v 是 Plus Plane 上的两个向量. 则 w . ( u – v ) 是多少? 所以 w 也垂直于 Minus Plane 注: 向量 w 与 Plus Plane 垂直. 为什么 ? Zone “ Predict Class = +1” “ Predict Class = -1” zone wx+b=1 wx+b=0 wx+b=-1 M = Margin 我们怎样利用 w 与 b 计算 margin? Plus-plane = { x : w . x + b = +1 } Minus-plane = { x : w . x + b = -1 } 计算间隔

17 .Plus-plane = { x : w . x + b = +1 } Minus-plane = { x : w . x + b = -1 } 向量 w 与 Plus Plane 垂直 设 x - 是 minus plane 上任意一点 设 x + 是 plus-plane 上距离 x - 最近的点 x - x + 计算间隔 Zone “ Predict Class = +1” “ Predict Class = -1” zone wx+b=1 wx+b=0 wx+b=-1 M = Margin 我们怎样利用 w 与 b 计算 margin?

18 .Plus-plane = { x : w . x + b = +1 } Minus-plane = { x : w . x + b = -1 } 向量 w 与 Plus Plane 垂直 设 x - 是 minus plane 上任意一点 设 x + 是 plus-plane 上距离 x - 最近的点 注: 对于某实数 l， x + = x - + l w . 为什么? x - x + 计算间隔 Zone “ Predict Class = +1” “ Predict Class = -1” zone wx+b=1 wx+b=0 wx+b=-1 M = Margin 我们怎样利用 w 与 b 计算 margin?

19 .Plus-plane = { x : w . x + b = +1 } Minus-plane = { x : w . x + b = -1 } 向量 w 与 Plus Plane 垂直 设 x - 是 minus plane 上任意一点 设 x + 是 plus-plane 上距离 x - 最近的点 注: 对于某实数 l， x + = x - + l w . 为什么? x - x + 计算间隔 Zone “ Predict Class = +1” “ Predict Class = -1” zone wx+b=1 wx+b=0 wx+b=-1 M = Margin 我们怎样利用 w 与 b 计算 margin? x - 与 x + 的连线与 planes 垂直. 于是 x - 在 w 的方向上移动一段距离就可与到达 x + .

20 .现在我们知道: w . x + + b = +1 w . x - + b = -1 x + = x - + l w | x + - x - | = M 于是很容易由 w 和 b 得到 M Zone “ Predict Class = +1” “ Predict Class = -1” zone wx+b=1 wx+b=0 wx+b=-1 M = Margin Width x - x + 计算间隔

21 .现在我们知道: w . x + + b = +1 w . x - + b = -1 x + = x - + l w | x + - x - | = M 于是很容易由 w 和 b 得到 M Zone “ Predict Class = +1” “ Predict Class = -1” zone wx+b=1 wx+b=0 wx+b=-1 M = Margin Width w . ( x - + l w) + b = 1 => w . x - + b + l w . w = 1 => -1 + l w . w = 1 => x - x + 计算间隔

22 .现在我们知道: w . x + + b = +1 w . x - + b = -1 x + = x - + l w | x + - x - | = M Zone “ Predict Class = +1” “ Predict Class = -1” zone wx+b=1 wx+b=0 wx+b=-1 M = Margin Width = M = | x + - x - | =| l w |= x - x + 计算间隔

23 .学习最大间隔分类器 我们现在需要找到一种算法，来求出 w 与 b， 并且 能匹配上所有的样本点 . 怎么做? 梯度下降? 退火算法 ? 矩阵求逆? 牛顿法? Zone “ Predict Class = +1” “ Predict Class = -1” zone wx+b=1 wx+b=0 wx+b=-1 M = Margin Width = x - x +

24 .利用二次优化求解 Minimize subject to y k (w . x k + b )>= 1 k=1,2,…,n

25 .What You Should Know 线性 SVMs 最大间隔分类器 QP 的作用 (但是 , 这里 , 你不必知道如何求解它 ) 最大间隔问题可以转化为一个二次优化( QP) 问题

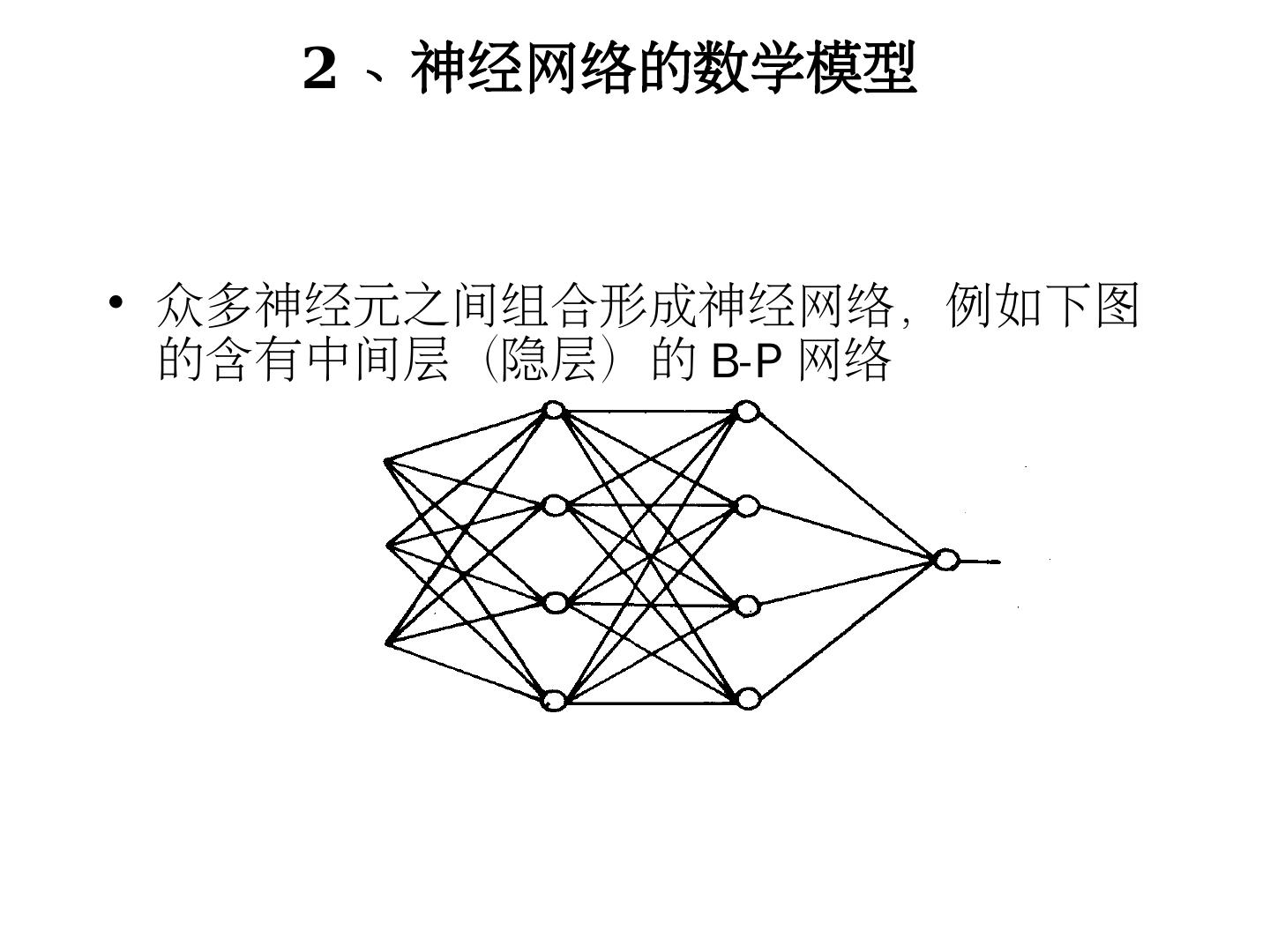
26 .神经网络（ Neural Networks ）

27 .引 言 利用机器模仿人类的智能是长期以来人们认识自然、改造自然和认识自身的理想。 研究 ANN 目的： （ 1 ）探索和模拟人的感觉、思维和行为的规律，设计具有人类智能的计算机系统。 （ 2 ）探讨人脑的智能活动，用物化了的智能来考察和研究人脑智能的物质过程及其规律。

28 .ANN 的研究内容 （ 1 ） 理论研究 ： ANN 模型及其学习算法，试图从数学上描述 ANN 的动力学过程，建立相应的 ANN 模型，在该模型的基础上，对于给定的学习样本，找出一种能以较快的速度和较高的精度调整神经元间互连权值，使系统达到稳定状态，满足学习要求的算法。 （ 2 ） 实现技术的研究 ：探讨利用电子、光学、生物等技术实现神经计算机的途径。 （ 3 ） 应用的研究 ：探讨如何应用 ANN 解决实际问题，如模式识别、故障检测、智能机器人等。

29 .研究 ANN 方法 （ 1 ） 生理结构的模拟： 用仿生学观点，探索人脑的生理结构，把对人脑的微观结构及其智能行为的研究结合起来即人工神经网络（ Artificial Neural Netwroks ，简称 ANN ）方法。 （ 2 ）宏观功能的模拟： 从人的思维活动和智能行为的心理学特性出发，利用计算机系统来对人脑智能进行宏观功能的模拟，即符号处理方法。