展开查看详情
1 .问题归约， 基于归结的演绎推理，基于规则的演绎推理 课本第 2.2 ， 2.3 及 2.4 章
2 .2016/9/24 2 § 问 题归约法 问题归约 (problem reduction) 是另一种问题描述与求解方法。 先把问题分解为子问题和子 - 子问题，然后解决较小的问题。 对该问题的某个具体子集的解答就意味着对原始问题的一个解答。
3 .2016/9/24 3 1. 问题归约描述 问题归约表示的 组成部分 ： 一个初始问题描述； 一套把问题变换为子问题的操作符； 一套本原问题描述。 其中的每一个问题是不证明的，自然成立的，如公理、已知的实事等（本原问题集） 问题归约的 实质 ：从目标 ( 要解决的问题 ) 出发 逆向推理 ，建立子问题以及子问题的子问题，直至最后把初始问题归约为一个平凡的本原问题集合。
4 .2016/9/24 4 梵塔难题 有 3 个柱子 (1 ， 2 和 3) 和 3 个不同尺寸的圆盘（ A ， B 和 C ）。在每个圆盘的中心有一个孔，所以圆盘可以堆叠在柱子上。最初， 3 个圆盘都堆在柱子 1 上：最大的圆盘 C 在底部，最小的圆盘 A 在顶部。要求把所有圆盘都移到柱子 3 上，每次只许移动一个，而且只能先搬动柱子顶部的圆盘，还不许把尺寸较大的圆盘堆放在尺寸较小的圆盘上。这个问题的初始配置和目标配置如图所示。 图 梵塔问题
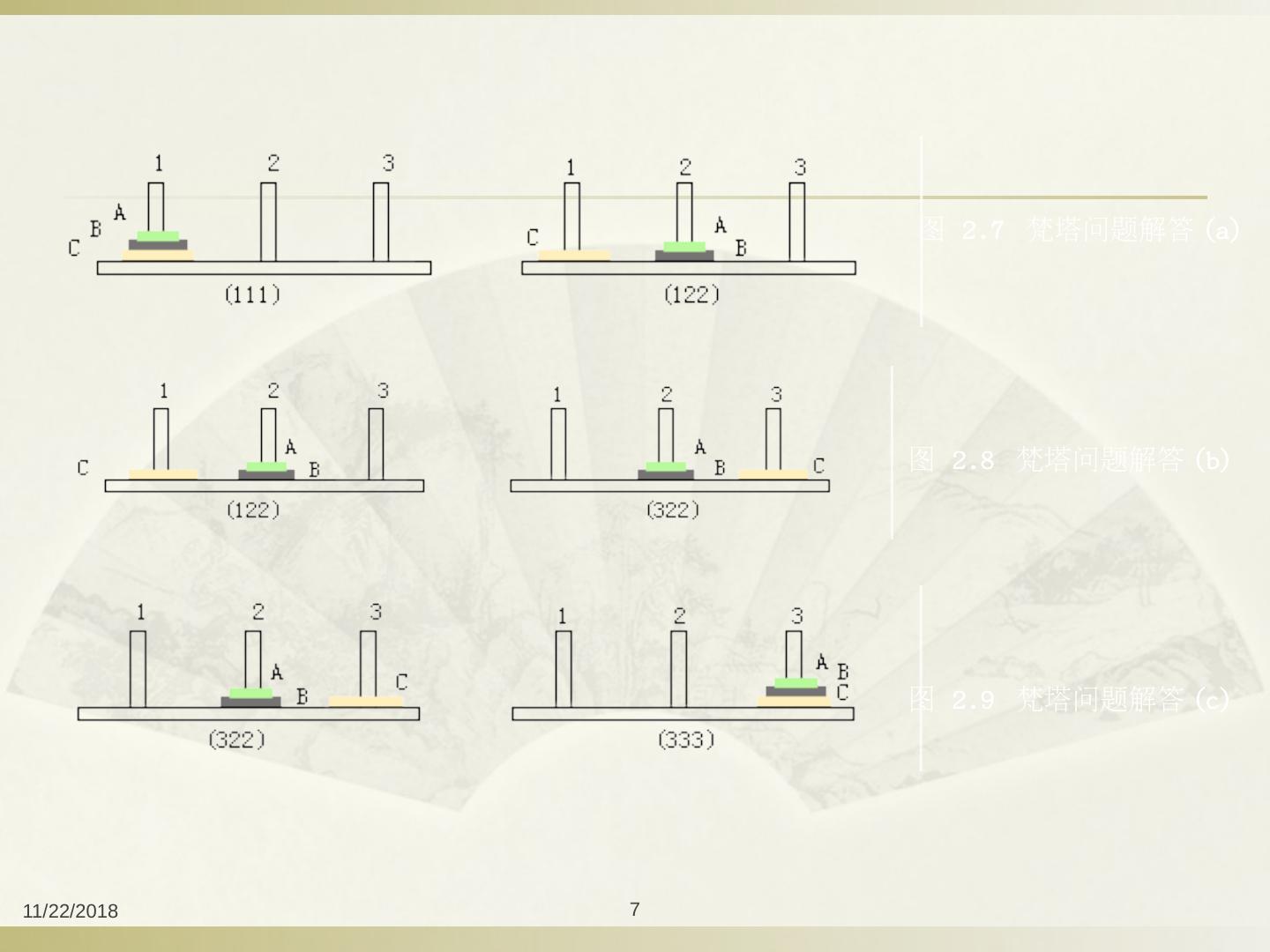
5 .2016/9/24 5 解题过程： 将原始问题归约为一个较简单问题集合，要把所有圆盘都移至柱子 3 ，我们必须首先把圆盘 C 移至柱子 3 ；而且在移动圆盘 C 至柱子 3 之前，要求柱子 3 必须是空的。只有在移开圆盘 A 和 B 之后，才能移动圆盘 C ；而且圆盘 A 和 B 最好不要移至柱子 3 就不能把圆盘 C 移至柱子 3 。因此，首先应该把圆盘 A 和 B 移到柱子 2 上。然后才能够进行关键的一步，把圆盘 C 从柱子 1 移至柱子 3 ，并继续解决难题的其余部分。 将原始难题归约（简化）为下列子难题：移动圆盘 A 和 B 至柱子 2 的双圆盘难题，如图 (a) 所示。
6 .2016/9/24 6 把原始难题归约（简化）为以下三个子难题： 移动圆盘 A 和 B 至柱子 2 的双圆盘难题；如图 (a) 所示 移动圆盘 C 至柱子 3 的单圆盘难题 ；如图 (b) 所示 移动圆盘 A 和 B 至柱子 3 双圆盘难题；如图 (c) 所示
7 .2016/9/24 7 图 2.7 梵塔问题解答 (a) 图 2.8 梵塔问题解答 (b) 图 2.9 梵塔问题解答 (c)
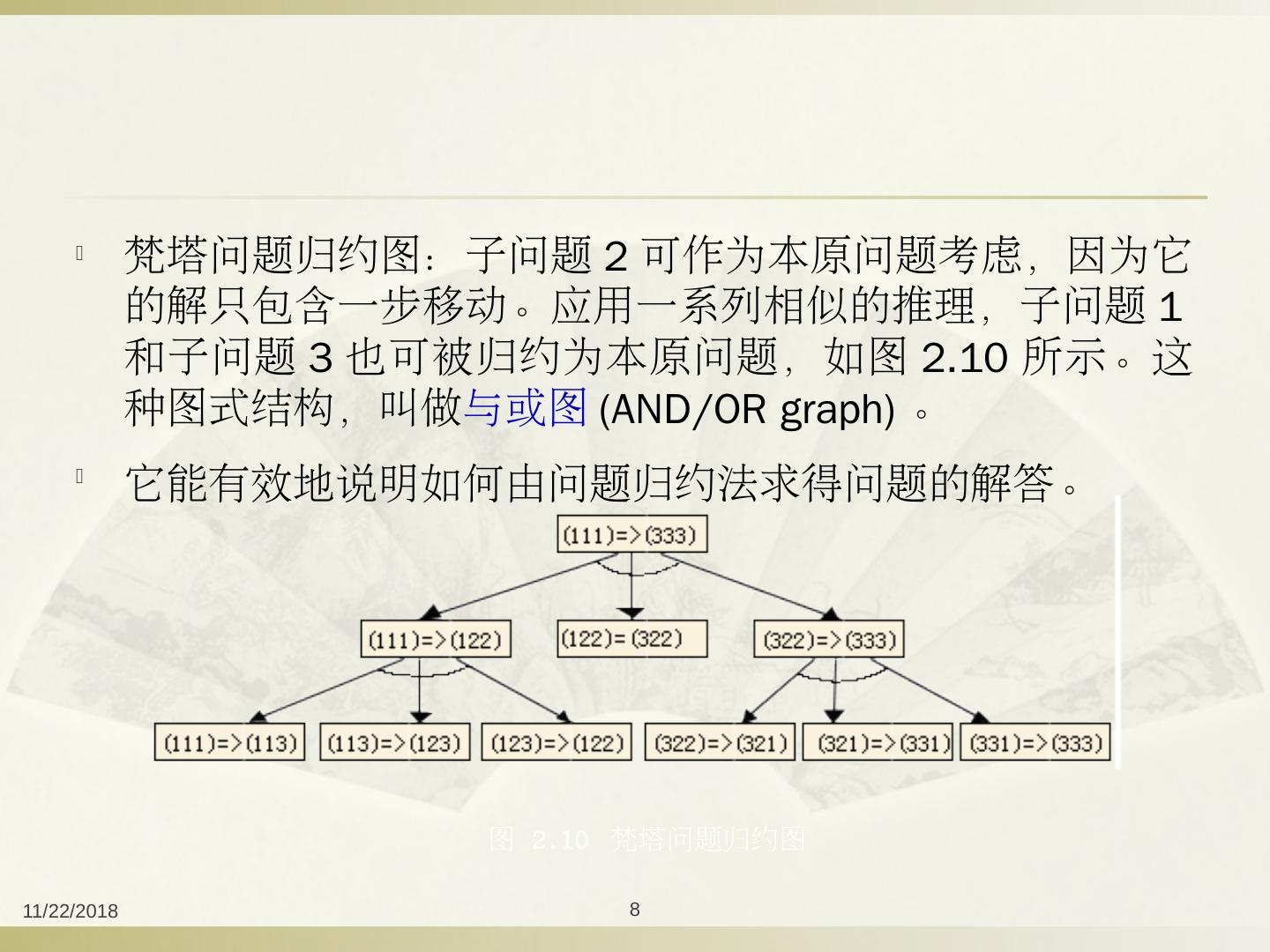
8 .2016/9/24 8 梵塔问题归约图：子问题 2 可作为本原问题考虑，因为它的解只包含一步移动。应用一系列相似的推理，子问题 1 和子问题 3 也可被归约为本原问题，如图 2.10 所示。这种图式结构，叫做 与或图 (AND/OR graph) 。 它能有效地说明如何由问题归约法求得问题的解答。 图 2.10 梵塔问题归约图
9 .2016/9/24 9 把一个问题描述变换为一个归约或后继问题描述的集合，这是由问题归约算符进行的。 变换所得所有后继问题的解就意味着父辈问题的一个解 。 所有问题归约的 目的 是最终产生具有明显解答的本原问题。这些问题可能是能够由状态空间搜索中走动一步来解决的问题，或者可能是别的具有已知解答的更复杂的问题。
10 .2016/9/24 10 2. 与或图表示 一般地，我们用一个类似图的结构来表示把问题归约为后继问题的替换集合，这种结构图叫做 问题归约图 ，或叫 与或图 。如下图所示 : 图 2.13 子问题集合 图 2.14 与或图
11 .2016/9/24 11 一些关于 与或图的术语 ： 父节点 、 子（后继）节点 、 弧线 、 起始节点 。 终叶节点 ：对应于原问题的本原节点。 或节点 ：只要解决某个问题就可解决其父辈问题的节点集合，如（ M ， N ， H ）。 与节点 ：只有解决所有子问题，才能解决其父辈问题的节点集合，如（ B,C) 和（ D,E,F ）各个结点之间用一端小圆弧连接标记。 与或图 ：由 与节点 及 或节点 组成的结构图。
12 .2016/9/24 12 可解节点 的一般定义 (1) 终叶节点是可解节点 ( 因为它们与本原问题相关连 ) 。 (2) 如果某个非终叶节点含有 或后继节点 ，那么只要当其后继节点至少有一个是可解的时，此非终叶节点才是可解的。 (3) 如果某个非终叶节点含有 与后继节点 ，那么只要当其后继节点全部为可解时，此非终叶节点才是可解的。
13 .2016/9/24 13 不可解节点 的一般定义 : (1) 没有后裔的非终叶节点为不可解节点。 (2) 如果某个非终叶节点含有 或后继节点 ，那么只有当其全部后裔为不可解时，此非终叶节点才是不可解的。 (3) 如果某个非终叶节点含有 与后继节点 ，那么只要当其后裔至少有一个为不可解时，此非终叶节点才是不可解的。
15 .15 归结证明过程是一种 反驳程序 ， 即 ： 不是证明一个公式是有效的( valid) ， 而是证明公式之非是不 可满足的 ( dissatisfiable ) 。 这完全是为了方便 ， 并且不失一般性 。 2 .3 归结 演绎推理
16 .16 若欲证明前提条件 P 可推导出结论 Q ，即证明 永真， 该问题的 证明等价于 证明 永假，即 是不可满足的。 2 .3 归结 演绎推理
17 .谓词演算 1 ）符号和符号结构 例如 Inroom (Robot, R1) 是一个符号结构， Robot 和 R1 都是符号， Inroom 是谓词符号 2 ）谓词公式 例如 Married （ father （ L1 ） , x ） ,Married 是谓词符号（简称谓词）， father 是函数， L1 是常量， x 是变量 3 ）连词和量词 连词 量词
18 .合适公式的定义 合适公式的定义（ Important ） Page 41 – 42 合适 公式的解释 通过穷取法确定公式的 Ture or False 解 合适公式的永真性和可满足性 永 真性 可满足性 永 假性 合适 公式的性质
19 .19 双重否定 律( double negation law) : ┓ ( ┓ P (x) ) ≡P (x) 德 · 摩根 定律( Mogen law) : ┓ ( P (x) ∨Q (x) )≡ ┓ P( x )∧ ┓ Q (x) ┓ (P (x) ∧Q (x) ) ≡ ┓ P( x )∨ ┓ Q (x) 1、谓词演算的基本等价式
20 .20 逆否律( inverse-negation law): P( x ) → Q (x) ≡ ┓ Q (x) → ┓ P( x ) 分配律( assignment law): P( x )∧(Q (x) ∨R( x ))≡(P( x )∧Q( x ))∨(P( x) ∧R (x )) P( x )∨(Q (x) ∧R( x ))≡(P( x )∨Q( x ))∧(P( x) ∨R (x)) 1、谓词演算的基本等价式
21 .21 结合律( association law): （ P( x )∧Q (x)) ∧R( x )≡P( x )∧(Q( x )∧R (x)) （ P( x )∨Q (x)) ∨R( x ) ≡P( x )∨(Q( x )∨R (x)) 蕴含等价式( implication law) : P( x )→Q( x )≡ ┓ P( x )∨Q (x) 1、谓词演算的基本等价式
22 .22 易名规则( rename law) : x P(x) ∨ x Q(x)≡ x P(x) ∨ y Q(y) 量词转换律( quantifier transform law) : ┓ x P( x ) ≡ x ┓ P( x ) ┓ x P( x ) ≡ x ┓P ( x ) 1、谓词演算的基本等价式
23 .23 量词分配律( quantifier assignment law) : x (P (x) ∨Q (x) ) ≡ x P (x) ∨ x Q (x) x (P (x )∧Q (x) ) ≡ x P (x) ∧ x Q (x) x (P → Q (x) ) ≡P → x Q (x) x (P → Q (x) ) ≡P → x Q (x) 1、谓词演算的基本等价式
24 .24 量词交换律( quantifier commutative law) : x y (P (x, y)) ≡ y x (P (x, y)) x y (P (x, y) )≡ y x (P (x, y)) x y (P (x, y) ) y x (P (x, y)) x y (P (x, y) ) y x (P (x, y)) 1、谓词演算的基本等价式
25 .25 量词辖域变换等价式 : x P (x) ∨ Q ≡ x (P (x) ∨ Q) x P (x) ∧ Q ≡ x (P (x) ∨ Q) x P (x) ∧ Q ≡ x (P (x) ∨ Q) x P (x) ∧ Q ≡ x (P (x) ∨ Q) Q 中不含变量 1、谓词演算的基本等价式
26 .26 全称量词消去规则 : x P(x)≡P(y) 全称量词引入规则 : P(y)≡ x P(x) 存在量词消去规则 : xQ(x)≡Q(c)(c 为常量 ) 存在量词引人规则 : Q(c)≡ x Q(x) 2、量词消去及引入规则
27 .27 有限域量词消去规则 : 设有限个体域为 D d 1 ， d 2 ， …… d n x P( x )≡P( d 1 )∧P( d 2 ) ， …… ∧P( d n ) x Q (x) ≡Q( d 1 ) ∨Q( d 2 ) ， …… ∨Q( d n ) 2、量词消去及引入规则
28 .28 3 、谓词逻辑中 的标准化 同一个命题或谓词公式可以用不同的命题或谓词公式形式来表达，这些公式形式之间是 相互等值 的。为了把这些公式规范化，下面讨论公式范式问题。 所谓 标准化公 式 就是公式的标准形式 ，公式往往可以转换为和它等价的范式，以便对它们做一般性的处理。 方法是： 对给定公式中的某子公式用与它 “ 等价 ” 的一个公式来代替，并且重复该过程直到得出所需要的形式为止。下面给出一些定义。
29 .29 范式中的 一些定义 : 定义 4.1 文字 (literal) 是原子或原子之非。 定义 4.2 公式 G ， 当且仅当 G 有形式 G 1 ∧…∧ G n (n>=1) 其中每个 G i 都是文字的析取式。则 G 称为 合取范式 (conjunctive normal form) 标准化需求（ pp43-44 ）
热门城市
