AI:棋类游戏与搜索算法

1 .Chess-alike Games Lesson 1

2 .棋类游戏 五子棋 跳棋 围棋 中国象棋 国际象棋 飞行棋 ？

3 .状态空间搜索策略 状态空间表示法 状态空间的图描述

4 .4 状态空间表示法 状态 ：表示系统状态、事实等叙述型知识的一组变量或数组： 操作 ：表示引起状态变化的过程型知识的一组关 系或函数： T

5 .5 状态空间表示法 状态空间 ：利用状态变量和操作符号，表示系统或问题的有关知识的符号体系，状态空间是一个四元组： ：状态集合。 ：操作算子的集合。 ：包含问题的初始状态是 的非空子集。 ：若干具体状态或满足某些性质的路径信息描述。

6 .6 求解路径 ：从 结点到 结点的路径。 ：状态空间的一个解。 状态空间的一个解 ：一个有限的操作算子序列。

7 .7 例 1 八数码问题的状态空间 。 状态集 ：所有摆法 操作算子： 将空格向上移 Up 将空格向左移 Left 将空格向下移 Down 将空格向右移 Right

8 .8 （状态） （操作算子） 状态空间的有向图描述

9 .9 状态空间的图描述 八数码 状态空间图

10 .10 例 2 旅行商问题 （ traveling salesman problem, TSP ）或邮递员路径问题。 （家） （单位： km ） 可能路径： 费用为 375 的路径（ A ， B ， C ， D ， E ， A ）

11 .11 旅行推销员状态空间图（部分） ABCDEA 375 A A A A B B C C C C D D D D A E E E E E E E D 路径 : 路径 : 路径 : 路径 : ABCEDA ABDCE AB DECA 费用 : 费用 : 费用 : 费用 : 425 525 475 525 475 375 325 400 400 300 275 275 250 225 150 100 75 125 175 225 250 100 175 225 425 . . . . . . .

12 .12 盲目的图搜索策略 回溯策略 宽度优先搜索策略 深度优先搜索策略 有界深度优先搜索

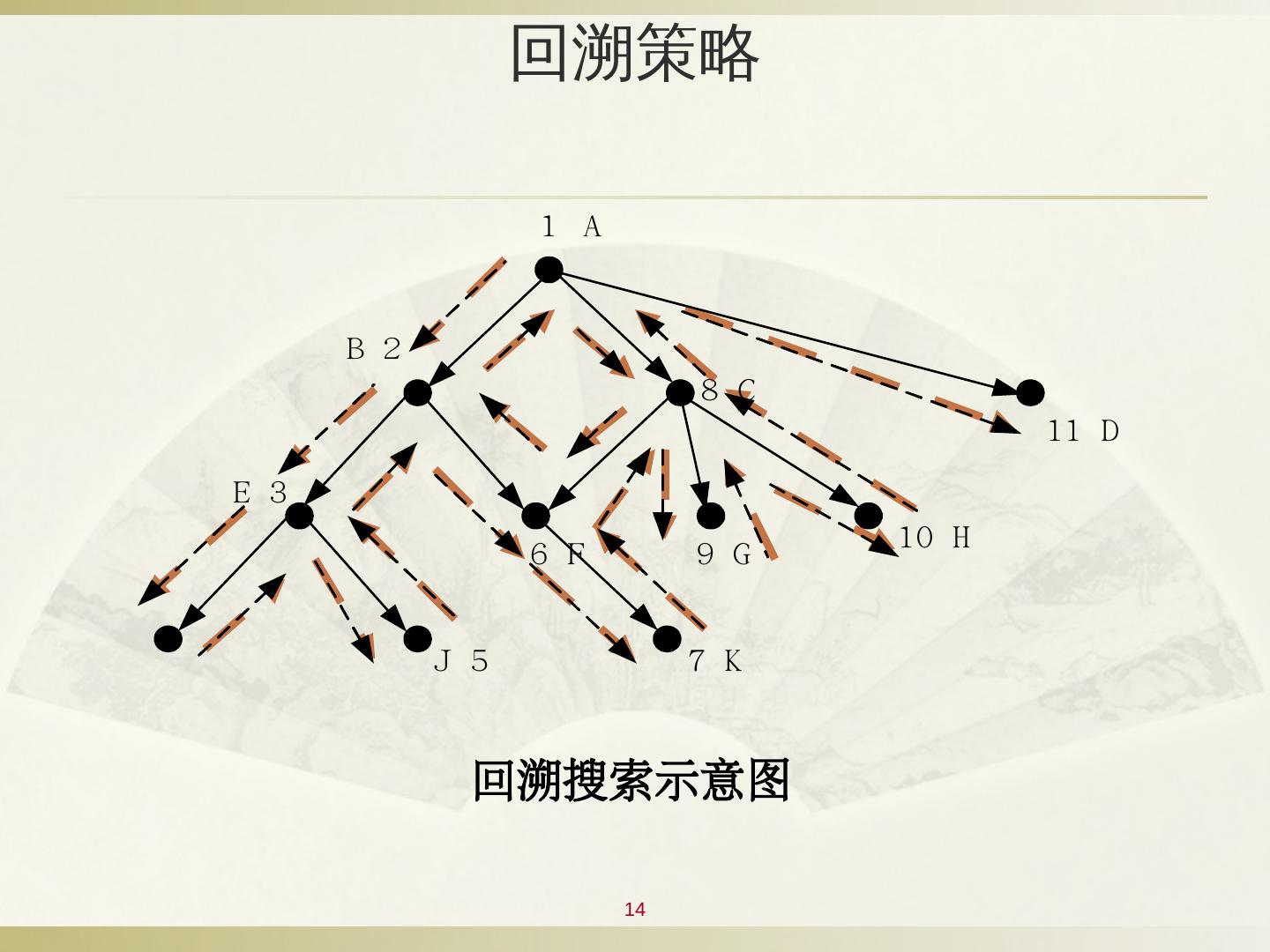
13 .13 回溯策略 带回溯策略的搜索 ： 从初始状态出发，不停地、试探性地寻找路径，直到它到达目的或“不可解结点”，即“死胡同”为止。若它遇到不可解结点就回溯到路径中最近的父结点上，查看该结点是否还有其他的子结点未被扩展。若有，则沿这些子结点继续搜索；如果找到目标，就成功退出搜索，返回解题路径。

14 .14 回溯策略 回溯搜索示意图

15 .15 宽度优先搜索策略 open 表（ NPS 表）：已经生成出来但其子状态未被搜索的状态。 closed 表：记录了已被生成扩展过的状态。 0 S 1 2 3 4 5 6 7 8 9 10 宽度优先搜索法中状态的搜索次序

16 .16 从初始节点开始，按照某种生成规则（算符）逐步生成下一级各子节点，顺序（先生成的子节点优先检查，优先扩展）地检查是否出现目标节点，在该级全部节点中沿广度进行“横向”扫描，即：沿“广度”遍历所有节点，故称“广度优先搜索法”。 宽度优先搜索 策略 基本思想

17 .17 搜索过程中要用到的两个数据结构 状态节点 父节点 OPEN 表 编号 状态节点 父节点 CLOSED 表 盲目搜索策略 • 广度优先搜索 • 深度优先搜索 OPEN 表 CLOSED 表 宽度优先搜索 策略 用于存放刚生成的节点。对于不同的搜索策略，节点在 OPEN 表中的排列顺序是不同的。 （ PS 表和 NSS 表的合并）用于存放将要扩展或者已扩展的节点，所谓对节点进行“扩展”是指：用合适的算符对该节点进行操作，生成一组子节点。

18 .18 把初始节点 S 0 放人 OPEN 表，若 S 0 为目标节点，则得到问题的解，退出； 如果 OPEN 表为空，则问题无解，退出； 把 OPEN 表的第一个节点 ( 记为节点 n) 取出放入 CLOSED 表； 考察节点 n ，若节点 n 不可扩展，则转第 Ⅱ 步； 扩展节点 n ，将其子节点放入 0PEN 表的尾部， 并为每一个子节点都配置指向父节点的指针； 如果 n 的任一个后继节点是目标节点，则找到问题的解，成功退出，否则转向第 Ⅱ 步。 宽度优先搜索 策略 基本过程

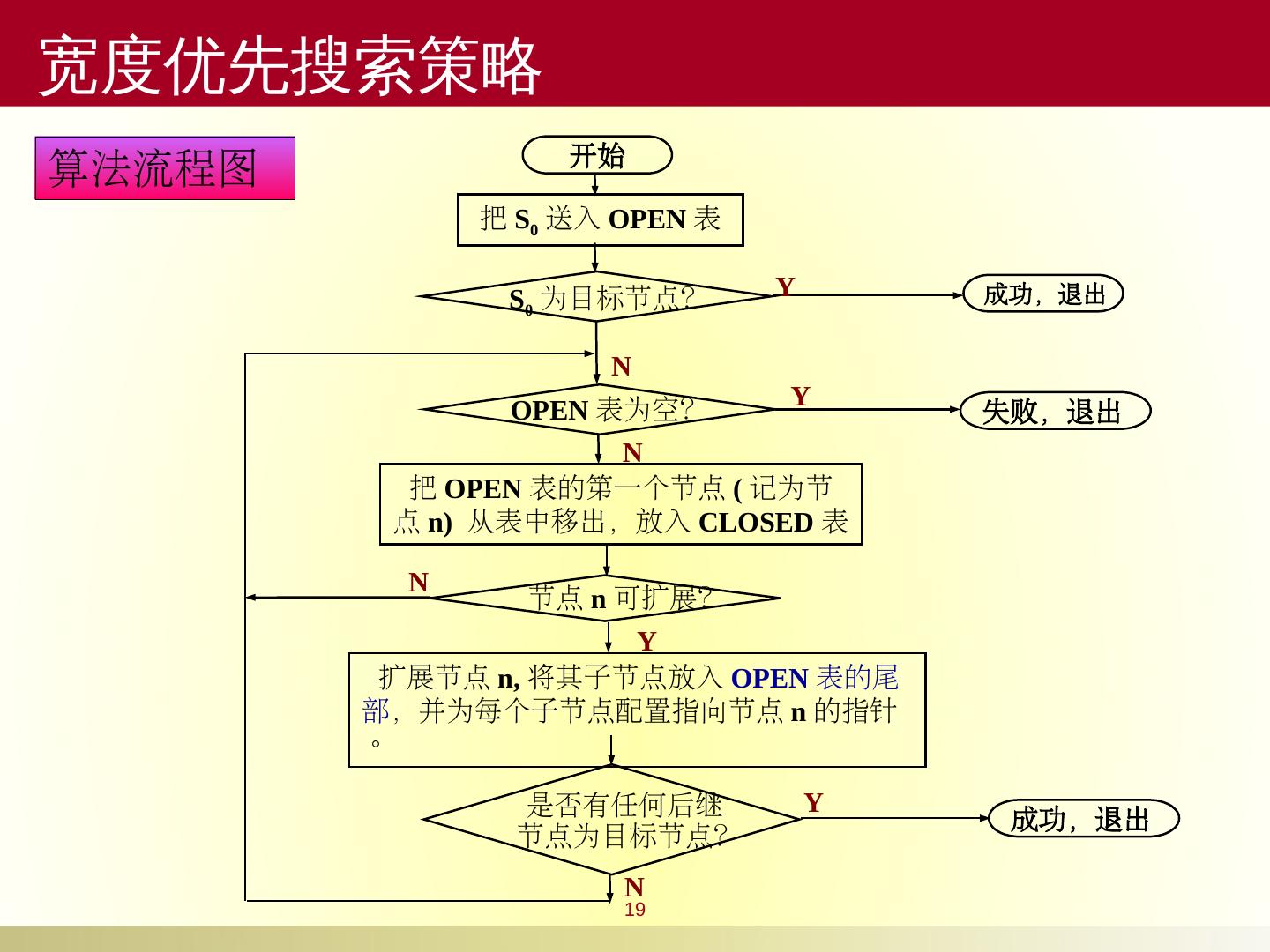
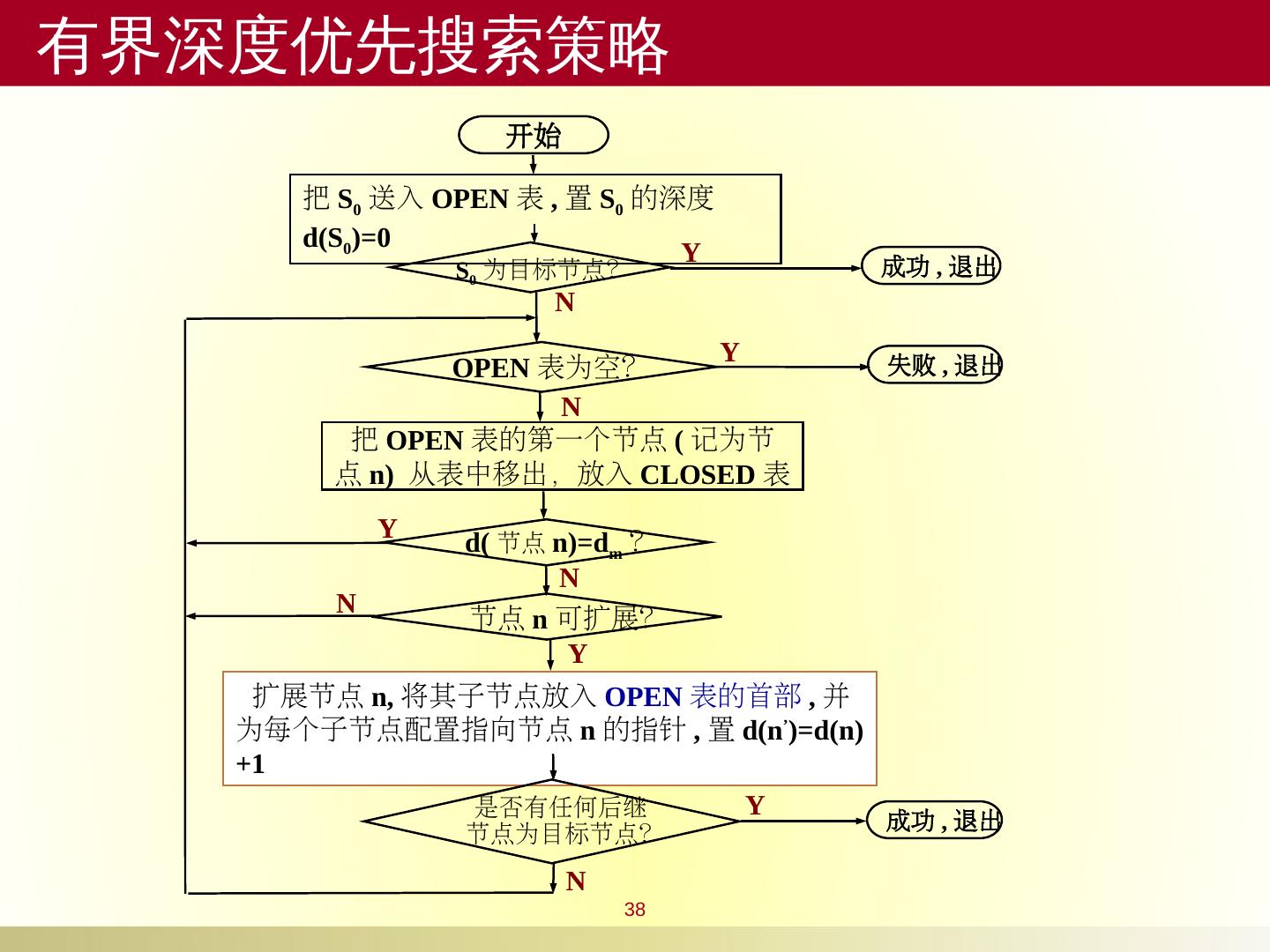
19 .19 开始 把 S 0 送入 OPEN 表 把 OPEN 表的第一个节点 ( 记为节点 n) 从表中移出，放入 CLOSED 表 OPEN 表为空？ 扩展节点 n, 将其子节点放入 OPEN 表的尾部 ，并为每个子节点配置指向节点 n 的指针。 是否有任何后继 节点为目标节点？ 节点 n 可扩展？ 失败，退出 成功，退出 Y N Y N Y N S 0 为目标节点？ 成功，退出 Y N 算法流程图 宽度优先搜索 策略

20 .20 宽度优先搜索策略 Procedure breadth_first_search begin open ： = [start]; closed ： = [ ] * 初始化 while open [ ] do begin 从 open 表中删除第一个状态，称之为 n ； 将 n 放入 closed 表中； if n = 目的状态 then return (success); 生成 n 的所有子状态； 从 n 的子状态中删除已在 open 或 closed 表中出现的状态； 将 n 的其余子状态，按生成的次序加入到 open 表的后段。 end; end; o pen 表：队列结构，即先进先出（ FIFO ）的数据结构

21 .21 状态节点 父节点 OPEN 表 编号 状态节点 父节点 CLOSED 表 S 0 1 2 S 0 1 2 6 3 4 5 S 0 1 2 6 3 4 5 7 8 9 (a) (b) (c) (d) S 0 S 0 1 1 2 1 2 0 0 0 3 4 2 0 3 3 5 6 7 8 9 4 1 1 1 1 2 2 3 3 4 4 5 S 0 1 0 2 0 3 1 4 1 S g (9) S 0 4 9 1 宽度优先搜索能够 保证在搜索树中找到一条通向目标节点的最短途径。 宽度优先搜索 策略 OPEN 表作为“先进先出 (FIFO)” 的队列进行操作

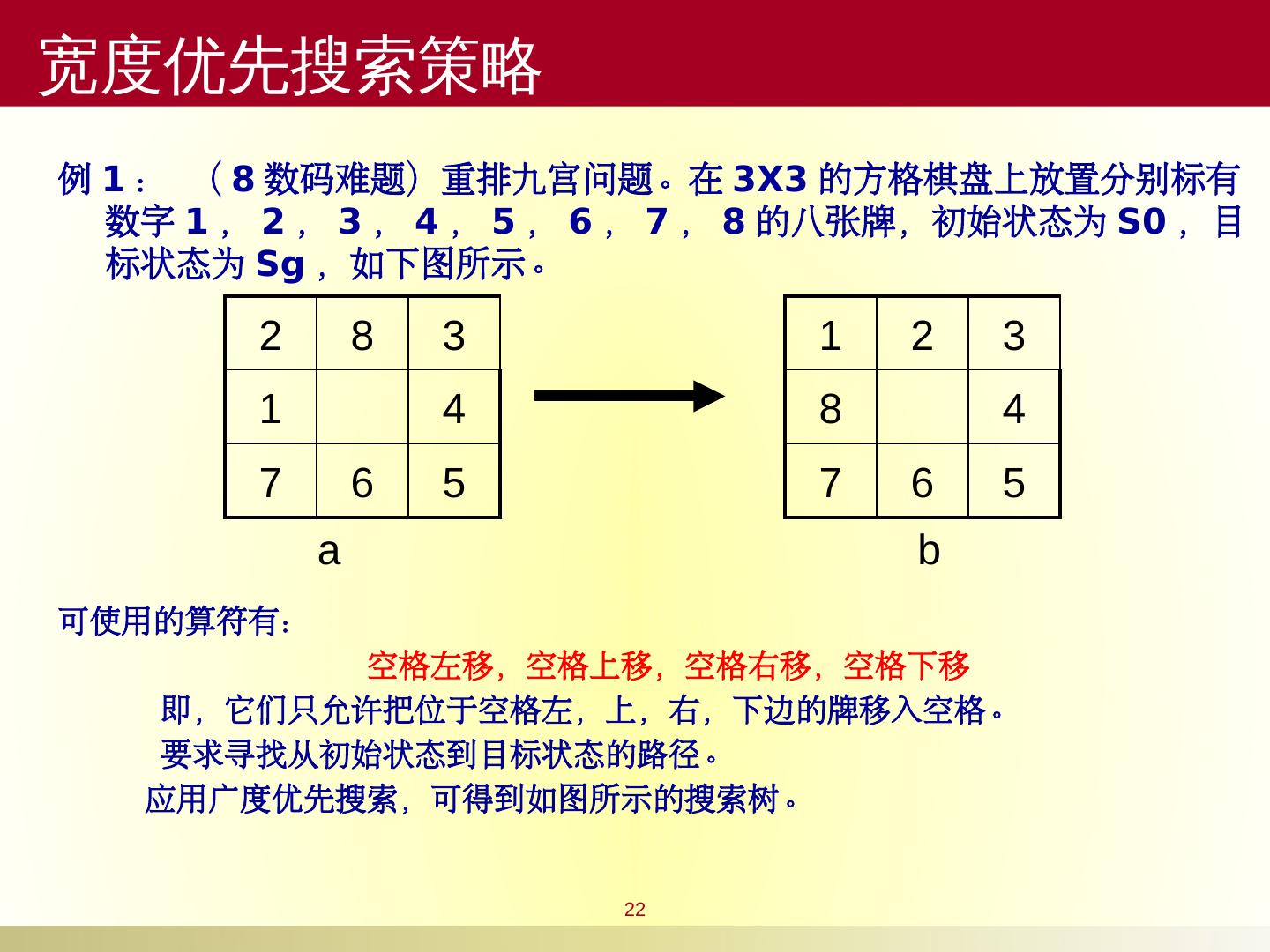
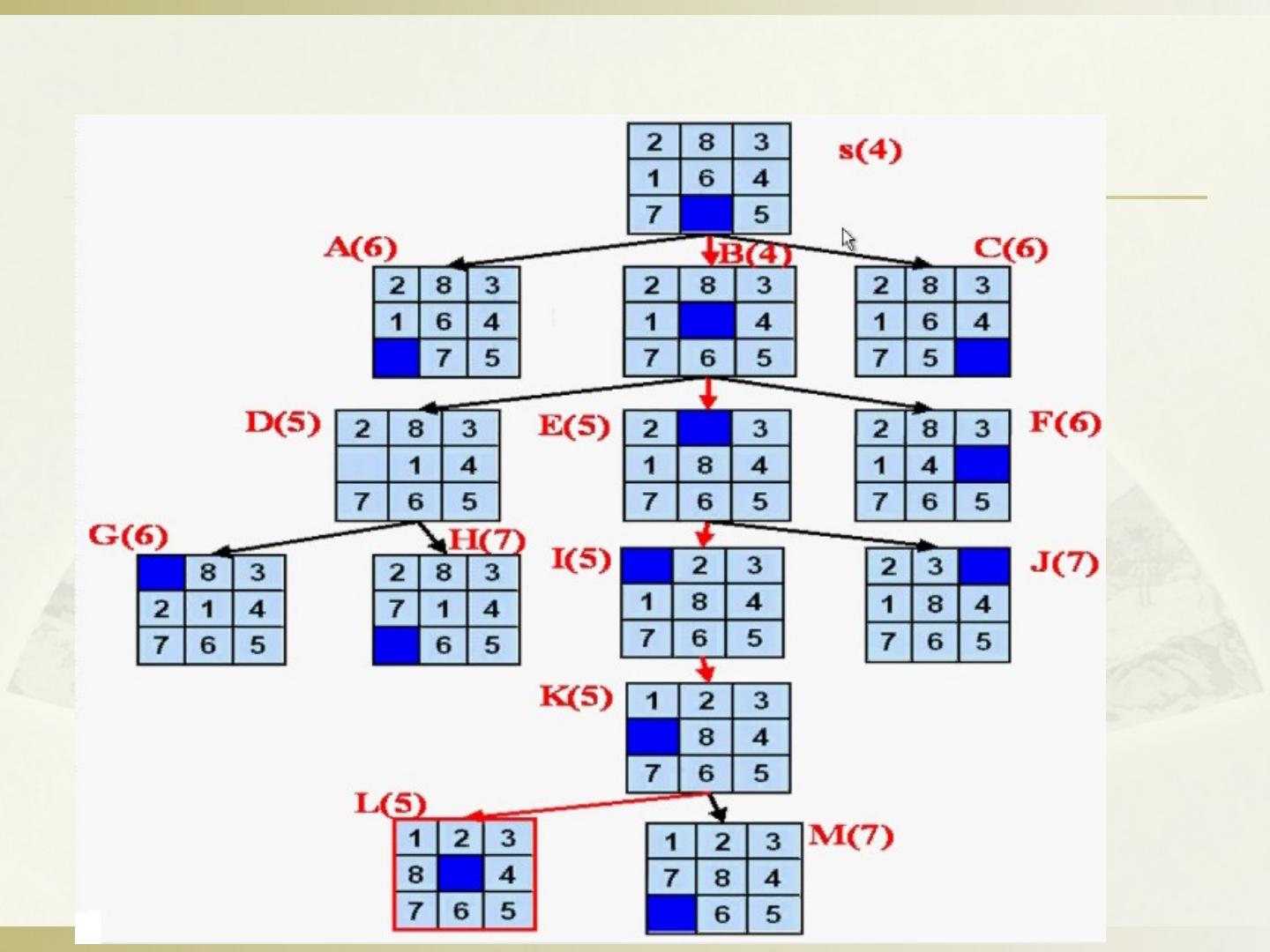
22 .22 例 1 ： （ 8 数码难题）重排九宫问题。在 3X3 的方格棋盘上放置分别标有数字 1 ， 2 ， 3 ， 4 ， 5 ， 6 ， 7 ， 8 的八张牌，初始状态为 S0 ，目标状态为 Sg ，如下图所示。 可使用的算符有： 空格左移，空格上移，空格右移，空格下移 即，它们只允许把位于空格左，上，右，下边的牌移入空格。 要求寻找从初始状态到目标状态的路径。 应用广度优先搜索，可得到如图所示的搜索树。 2 8 3 1 4 7 6 5 1 2 3 8 4 7 6 5 a b 宽度优先搜索 策略

23 .23 八数码难题的宽度优先搜索树 宽度优先搜索 策略

24 .24 宽度优先搜索 策略 解的路径是 : S0 3 8 16 26 (Sg)

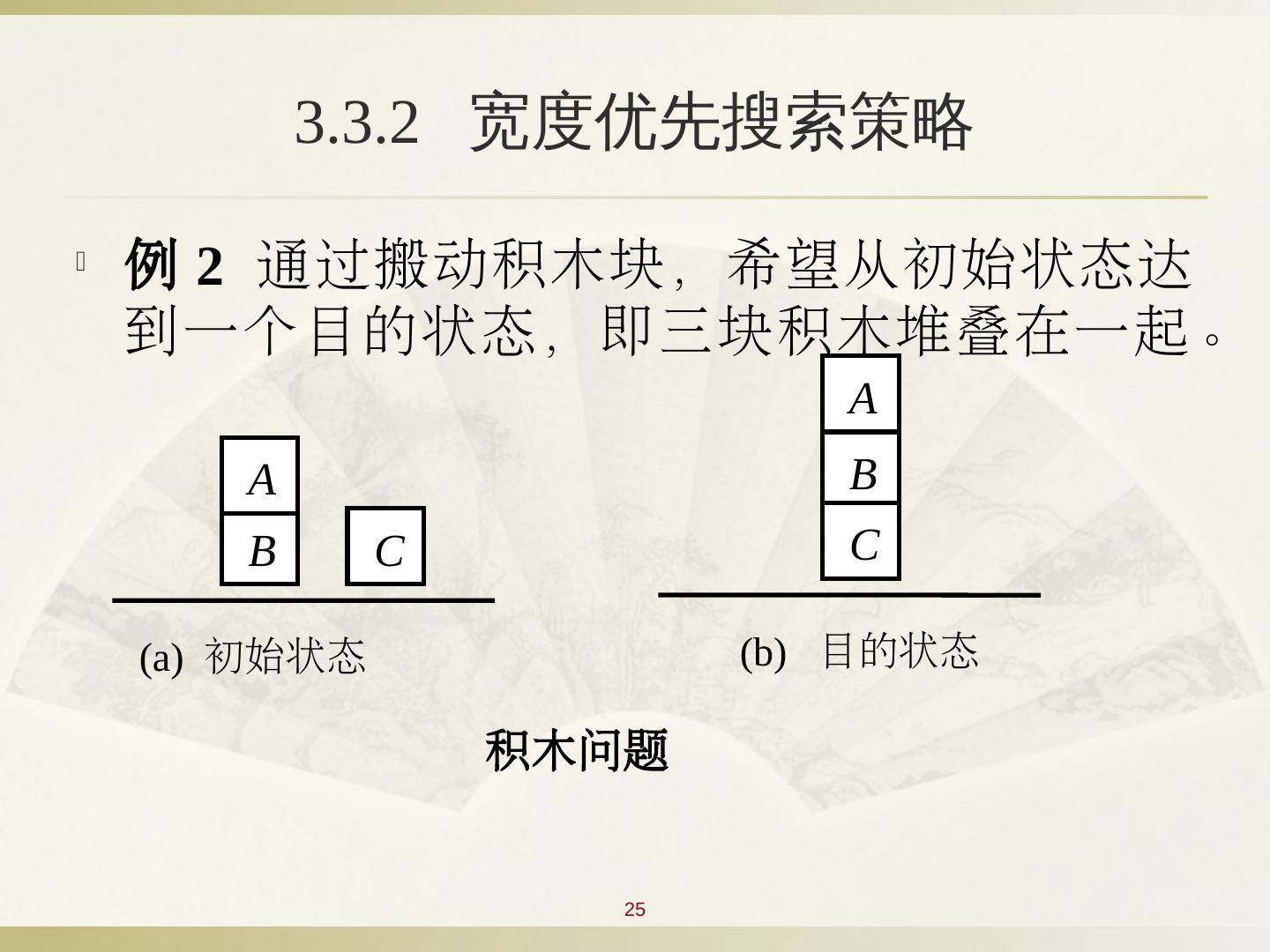
25 .25 例 2 通过搬动积木块，希望从初始状态达到一个目的状态，即三块积木堆叠在一起。 3.3.2 宽度优先搜索策略 B C A A B C (a) 初始状态 (b) 目的状态 积木问题

26 .26 操作算子为 MOVE （ X ， Y ）：把积木 X 搬到 Y （积木或桌面）上面。 3.3.2 宽度优先搜索策略 MOVE （ A ， Table ）：“搬动积木 A 到桌面上”。 操作算子可运用的先决条件： （ 1 ）被搬动积木的顶部必须为空。 （ 2 ）如果 Y 是积木，则积木 Y 的顶部也必须为空。 （ 3 ）同一状态下，运用操作算子的次数不得多于一次。

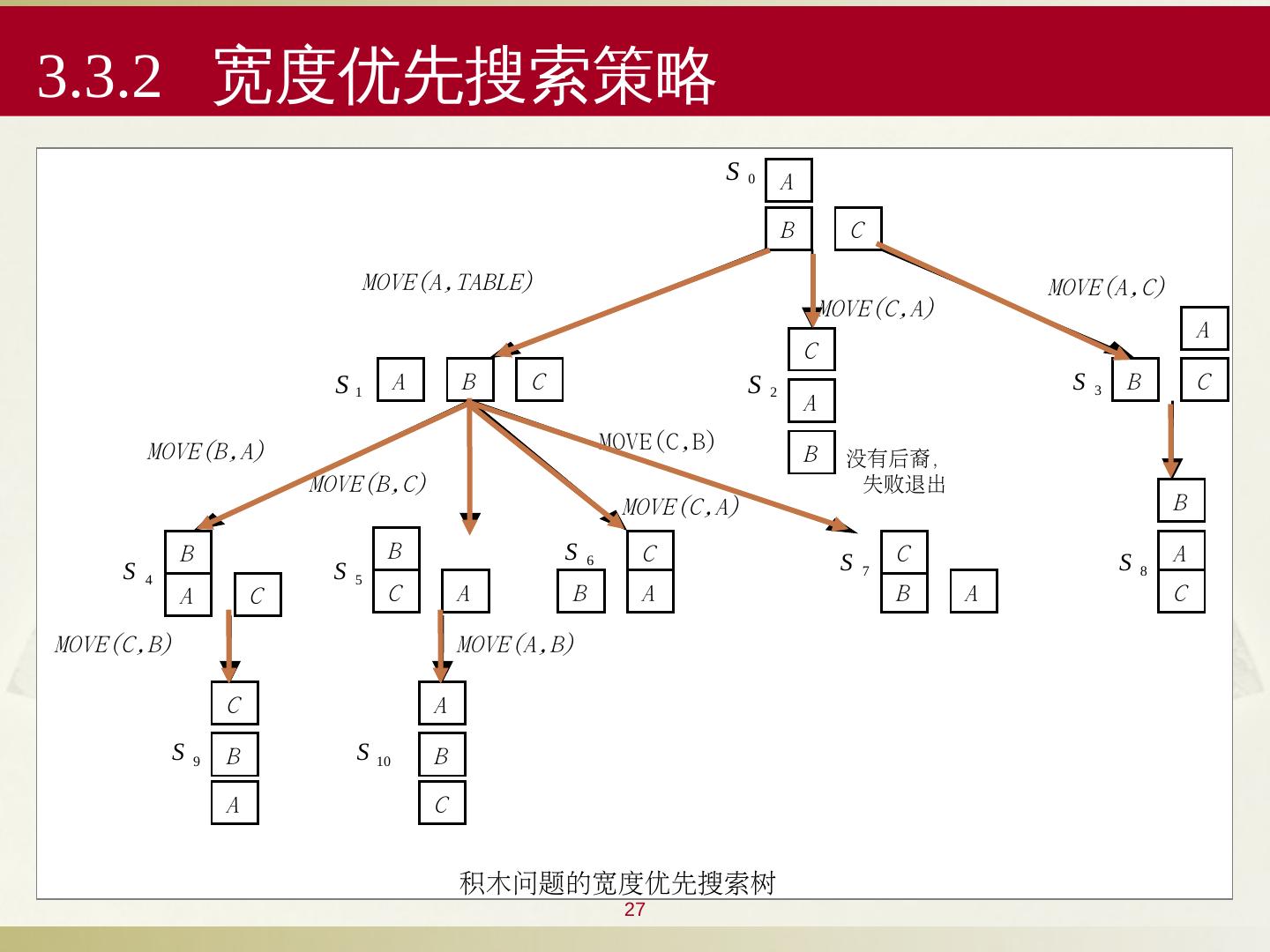
27 .27 A B A B A C C B A C C C B A B C A B A C B A A B C B C B C C A B A MOVE(A,TABLE) MOVE(C,A) MOVE(A,C) MOVE(B,A) MOVE(B,C) MOVE(C,A) MOVE(C,B) MOVE(C,B) MOVE(A,B) 0 S 1 S 2 S 3 S 4 S 5 S 6 S 7 S 8 S 9 S 10 S 没有后裔， 失败退出 积木问题的宽度优先搜索树 3.3.2 宽度优先搜索策略

28 .28 宽度优先搜索 策略 优点： 缺点 盲目性较大 当目标节点距离 初始节点较远时 将会产生许多无 用节点，搜索效 率低。 优点 只要问题有解， 广度优先总可以 得到解，而且得 到的是路径最短 的解。

29 .29 深度优先搜索策略 0 S 1 2 3 4 5 6 7 8 9 10 11 12 13 K K 深度优先搜索法中状态的搜索次序 0 S 1 2 3 4 5 6 7 8 9 10 11 12 13 K K 深度优先搜索法中状态的搜索次序