卷积码

1 . 第四章 卷积码的编码 第四章 卷积码 卷积码与分组码不同，其编码器具有记忆性，即编码器的当前输出不仅与当前输入有关， 还跟以前时刻的输入有关。速率 R=k/n、存储器阶数为 m 的卷积编码器可用 k 个输入、n 个 输出、输入存储器阶数为 m 的线性序贯电路实现，即输入在进入编码器后仍会多呆 m 个时 间单元。通常， n 和 k 都是比较小的整数， 信息序列被分成长度为 k 的分组，码字(codeword) k<n， 被分成长度为 n 的分组。当 k＝1 时，信息序列无需分组，处理连续进行。值得注意的是， 卷积码不象分组码，较大的最小距离和低错误概率不是通过增加 k 和 n 实现的，而是通过增 加存储器阶数 m 实现的。 我们这一章关注卷积编码过程、卷积编码器如何用状态图表示、如何推导卷积码的重量 枚举（weight-enumerating）函数、卷积码的几种距离测量方法。 卷积码是 1955 年由 Elias（1923～2001）首次提出的，随后 Wozencraft 和 Reiffen 提出 了序贯译码方法（对具有较大约束长度的卷积码非常有效） 。1963 年，Massey 提出了一个 效率不高、但易于实现的译码方法――门限译码，这使得卷积码大量应用于卫星和无线信道 的数字传输中。 On December 7, 2001, the field of information theory lost another of its true giants, Peter Elias, who passed away at his home in Cambridge, Massachusetts, a victim of the mysterious and dreadful ailment, Creutzfeld-Jakob Disease. A.J.Viterbi 毕业于麻省理工学院（MIT），分别获博士/硕士 /学士学位,是无线通信领域国际权威专家，被称为 CDMA 之父。现为美国 Qualcomm 公司首席科学家，加州大学 Los Angeles 分校（UCLA）教授，IEEE Fellow（国际电子电气 工程师协会会士）,美国总统国家科学和工程委员会成员。 1967 年，Viterbi 提出了最大似然（ML, Maximum Likelihood）译码算法，易于实现具 有较小约束长度的卷积码的软判决译码。Viterbi 算法配合序贯译码的软判决，使卷积码在 20 世纪 70 年代广泛应用在深空和卫星通信系统。1974 年，Bahl, Cocke, Jelinek 以及 Raviv （BCJR）针对 具有不等先验概率信息比特的卷积码，提出了最大后验概率（MAP，maximum a posteriori probability）译码算法。BCJR 算法近年来广泛应用到软判决迭代译码方案中，其 中信息比特的先验概率在每次迭代时都发生变化。对卷积码描述最详尽的书籍是： R. Johannesson and K.S. Zigangirov, Fundamentals of Convolutional Coding. IEEE Press, Piscataway , N. J., 1999. 1 Copyright by 周武旸 

2 . 第四章 卷积码的编码 4.1 卷积码的编码 卷积码的编码分为两类：前馈和反馈，在每类中又可分为系统和非系统形式。首先考虑 非系统形式的前馈编码器。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.1 速率 R＝1/2 的非系统前馈卷积编码器 图 4.1 为速率 R＝1/2、存储器阶数 m＝3 的非系统前馈卷积编码器框图，该编码器中输 入信息比特 k=1、n＝2 个模 2 加法器、m＝3 个延时单元。由于模 2 加法器是一个线性运算， 因此编码器是一个线性系统，所有卷积码都可用这类线性前馈移位寄存器编码器实现。 v (0) u v (1) 图 4.1 速率 R＝1/2 的非系统前馈卷积编码器 信息序列 u = (u0 , u1 , u2 ,...) 进入编码器，每次 1 比特，由于编码器是一个线性系统，两 个编码器输出序列 v (0) = (v0(0) , v1(0) , v2(0) ,...) 和 v (1) = (v0(1) , v1(1) , v2(1) ,...) 可通过输入序列 u 和两 个编码器脉冲响应的卷积得到。计算脉冲响应时，可设 u=(1 0 0 … )，然后观测两个输出序 列。对一个具有 m 阶存储器的编码器，脉冲响应能够持续最多 m+1 个时间单元，可写为 g (0) = ( g 0(0) , g1(0) , g 2(0) ,..., g m(0) ) 和 g (1) = ( g 0(1) , g1(1) , g 2(1) ,..., g m(1) ) 。对上图的编码器，有 g (0) = (1 0 1 1) （4.1） g (1) = (1 1 1 1) 脉冲响应 g (0) 和 g (1) 称为编码器的生成器序列。这样，编码方程为： v (0)= u ⊗ g (0) （4.2） v (1)= u ⊗ g (1) 其中 ⊗ 表示离散卷积，且所有运算都是模 2 加运算，对于所有 l ≥ 0 ，有： m vl( j ) = ∑ ul −i gi( j ) i =0 （4.3） = ul g ( j) 0 +u g ( j) l −1 1 +  + ul − m g ( j) m ,= j 0,1 其中对于所有 l<i， ul −i  0 ，这样对图 4.1 所示的编码器，有： = ul vl(0) + ul − 2 + ul −3 （4.4） vl(1) =ul + ul −1 + ul − 2 + ul −3 2 Copyright by 周武旸 

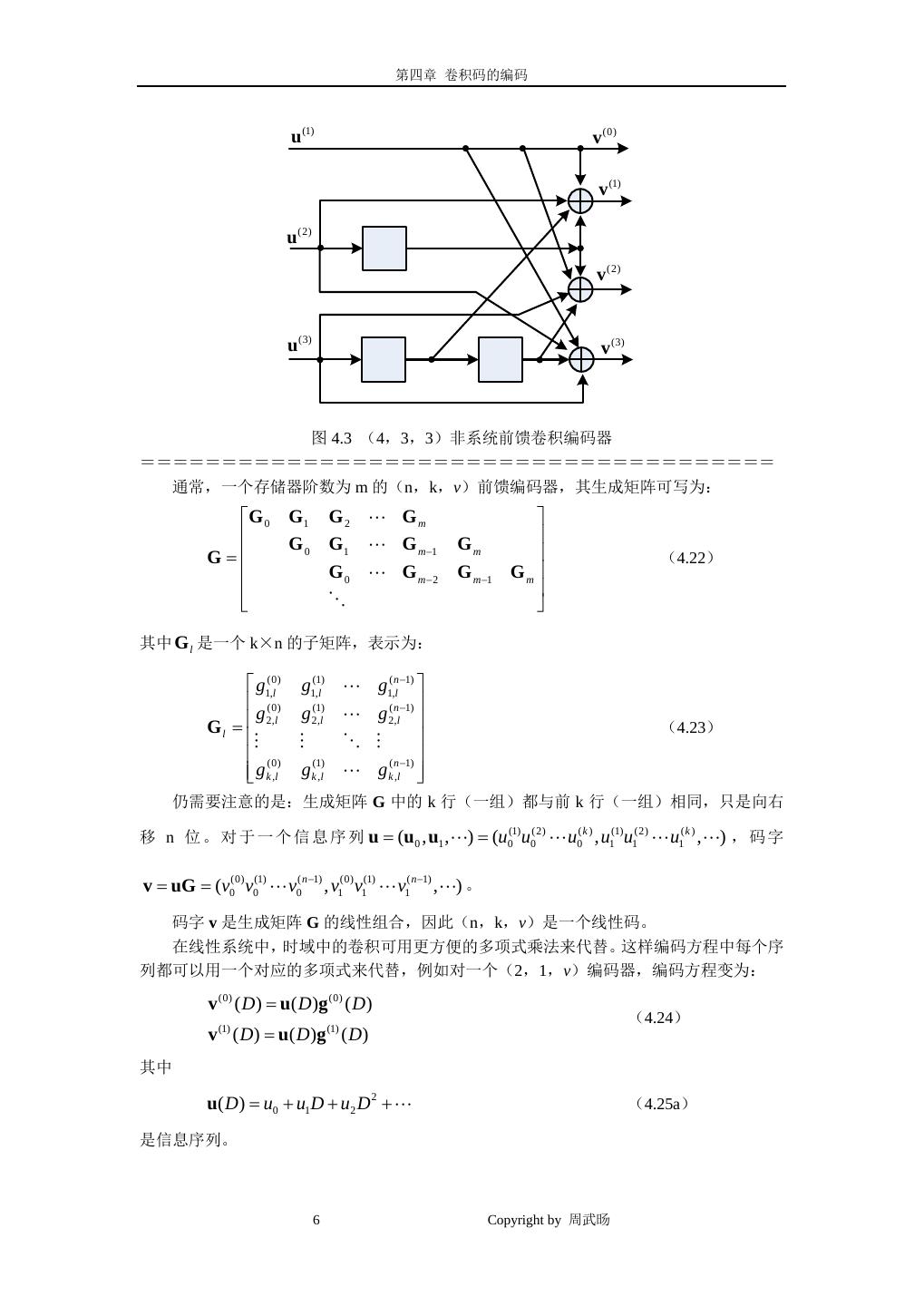
3 . 第四章 卷积码的编码 编码后，两个输出序列复用成一个序列，称为码字（codeword），表示为 v = (v0(0) , v0(1) , v1(0) , v1(1) , v2(0) , v2(1) ,) （4.5） 例如信息序列 u=(1 0 1 1 1)，则输出序列为： v (0)= (1 0 1 1 1) ⊗ (1 0 1 1)= (1 0 0 0 0 0 0 1) （4.6） = (1 0 1 1 1) ⊗ (1 1 1 1) v (1) = (1 1 0 1 1 1 0 1) 复用成一个序列为： v = (11, 01, 00, 01, 01, 01, 00,11) （4.7） 如果将生成器序列 g (0) 和 g (1) 写出矩阵形式，为：  g 0(0) g 0(1) g1(0) g1(1) g 2(0) g 2(1)  g m(0) g m(1)    g 0(0) g 0(1) g1(0) g1(1)  g m(0)−1 g m(1)−1 g m(0) g m(1) G=  （4.8）  g 0(0) g 0(1)  g m(0)− 2 g m(1)− 2 g m(0)−1 g m(1)−1 g m(0) g m(1)        其中空白区域为全 0，这样编码方程可写为矩阵形式： v = uG （4.9） G 称为该编码器的生成矩阵。我们注意到 G 中的每一行都与前一行相同，只是向右移 位了 n=2 位，它是一个半无限矩阵，对应于信息序列 u 是一个任意长度的序列。如果 u 只 有有限长 h，则 G 具有 h 行、2(m+h)列，v 的长度为 2(m+h)。例如上例中 u=(1 0 1 1 1)，则 v = uG 11 01 11 11   11 01 11 11    = (1 0 1 1 1)  11 01 11 11  （4.10）    11 01 11 11   11 01 11 11 = (11 01 00 01 01 01 00 11) 与我们前面的计算一致！ ！ ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.2 速率 R=2/3 的非系统前馈卷积编码器 v (0) u (1) v (1) u (2) v (2) 图 4.2 3 Copyright by 周武旸 

4 . 第四章 卷积码的编码 编码速率 R=2/3、存储器阶数 m=1 的编码器结构如图 4.2 所示，该编码器由 k=2 个移位 寄存器、m=1 个时延单元、n=3 个模 2 加法器组成。信息序列进入编码器时每次进入 k=2 个 比 特 ，= = 0 , u1 ,) (u0 u0 , u1 u1 , u2 u2 ,) ， 或 作 为 两 个 输 入 序 列 (1) (2) (1) (2) (1) (2) 可 写 为 u (u u (1) = (u0(1) , u1(1) , u2(1) ,) 和 u (2) = (u0(2) , u1(2) , u2(2) ,) 。对应于每个输入序列，都有三个生成 器序列。设 g i ( j) = ( gi(,0j ) , gi(,1j ) , , gi(,mj ) ) 表示对应于输入 i 和输出 j 的生成器序列，这样我们可 得到图 4.2 所示编码器的生成器序列为： =g1(0) (1=1) g1(1) (0= 1) g1(2) (1 1) （4.11） =g (0) 2 (0=1) g (1) 2 (1= 0) g (2) 2 (1 0) 这样我们可写出编码方程如下： v (0) = u (1) ⊗ g1(0) + u (2) ⊗ g (0) 2 v = u ⊗ g1 + u ⊗ g 2 (1) (1) (1) (2) (1) （4.12） v (2) = u (1) ⊗ g1(2) + u (2) ⊗ g (2) 2 卷积运算意味着 vl(0) = ul(1) + + ul(1)−1 + ul(2) −1 =vl(1) ul(2) + ul(1)−1 （4.13） vl(2) = ul(1) + ul(2) + ul(1)−1 复用后，码字为： v = (v0(0) v0(1) v0(2) , v1(0) v1(1) v1(2) , v2(0) v2(1) v2(2) ,) (4.14) 例如：如果 u (1) = (1 0 1) 和 u (2) = (1 1 0) ，则 v (0) = (101) ⊗ (11) + (110) ⊗ (01) = (1001) v (1) = (101) ⊗ (01) + (110) ⊗ (10) = (1001) (4.15) v (2) = (101) ⊗ (11) + (110) ⊗ (10) = (0011) 所以输出序列为： v = (110, 000, 001,111) （4.16） 生成矩阵为：  g1,0 (0) (1) (2) g1,0 g1,0 g1,1 g1,1 g1,1  g1,(0)m g1,(1)m g1,(2)m (0) (1) (2)   (0) (1) (2)   g 2,0 g 2,0 g 2,0 g 2,1 g 2,1 g 2,1  g 2,m g 2,m g 2,m (0) (1) (2) (0) (1) (2)  G= (0) (1) (2) g1,0 g1,0 g1,0 (0) (1) (2) g1,m −1 g1,m −1 g1,m −1 g1,m g1,m g1,m(0) (1) (2)  (4.17)  (0) (1) (2)   g 2,0 g 2,0 g 2,0 g 2,(0)m −1 g 2,(1)m −1 g 2,(2)m −1 g 2,(0)m g 2,(1)m g 2,(2)m        编码方程仍写为 v = uG ，注意：G 中每 k＝2 行都与前 2 行相同，只是向右移 n=3 位。 如上例中， u (1) = (101) 和 u (2) = (110) = = ，则 u (u 0 , u1 , u 2 ) (11, 01,10) ，有： 4 Copyright by 周武旸 

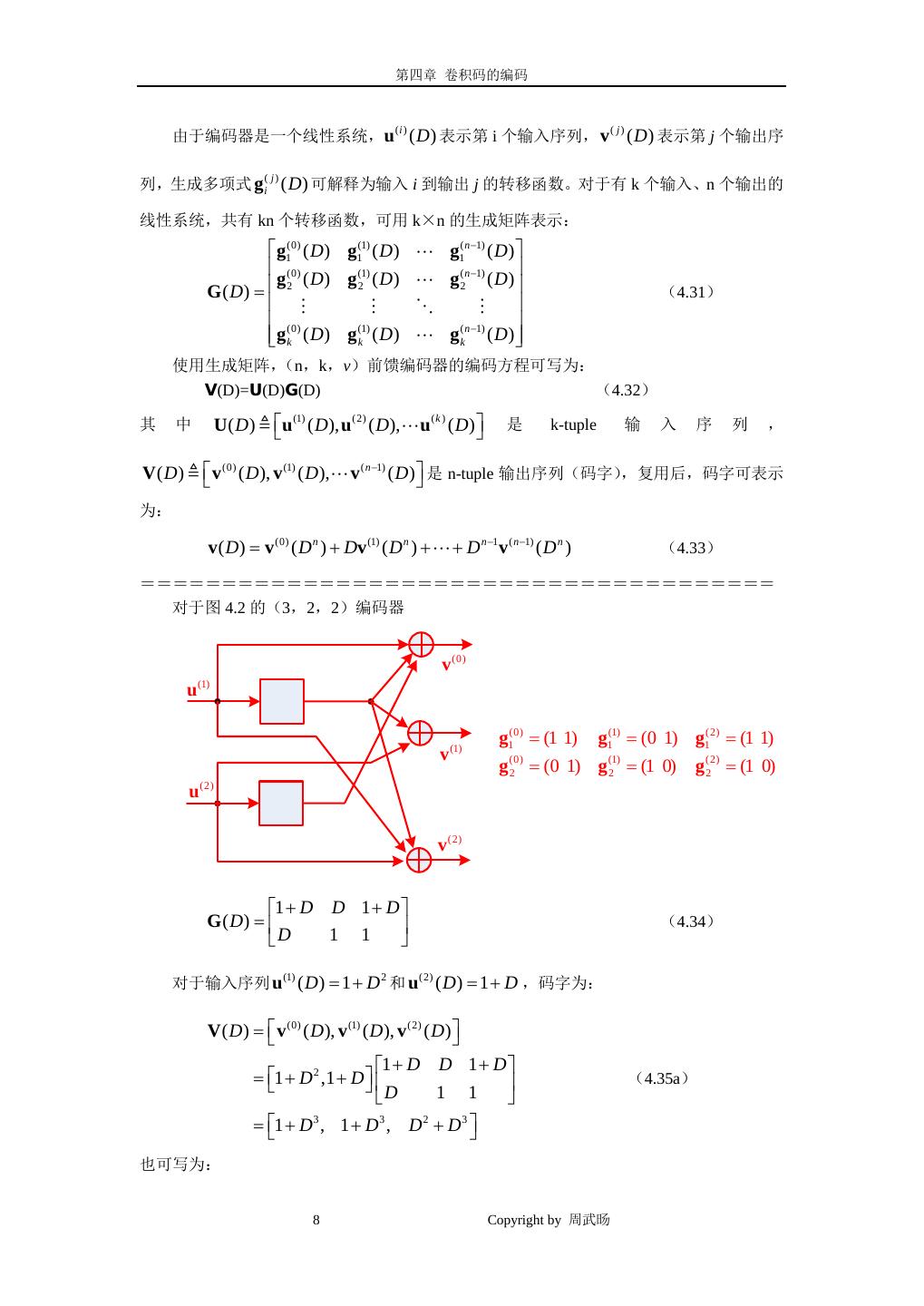
5 . 第四章 卷积码的编码 101 111  011 100     101 111  = v uG = (11, 01,10)    011 100  (4.18)  101 111     011 100  = (110, 000, 001,111) 与我们前面的计算一致！ ！ ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 在上两例中，从存储输入序列的 k 个移位寄存器到 n 个模 2 加法器的连接，直接对应于 在 kn 个生成器序列中的非零项，如式（4.1）和（4.11）所示。从上述的例子中可以看出， 当输入序列数 k>1 时，复杂度明显增加。 下面给出与移位寄存器长度有关的四个定义： 定义 4.1：设 vi 是卷积编码器（有 k 个输入序列）第 i 个移位寄存器的长度，i＝1, 2,…,k。 例如图 4.1 中速率 R＝1/2 的编码器，v＝3；图 4.11 中速率 R＝2/3 的编码器，v1 = v2 =1。 定义 4.2：编码器的存储器阶数 m 定义为： m = max vi （4.19） 1≤i ≤ k 即 m 是所有 k 个移位寄存器的最大值。 m＝v1＝3； 例如图 4.1 中速率 R＝1/2 的编码器， 图 4.11 中速率 R＝2/3 的编码器， m＝max(v1,v2) ＝max(1,1)=1。 定义 4.3：编码器的全局约束长度 v 定义为： v= ∑v 1≤i ≤ k i （4.20） 即，v 是所有 k 个移位寄存器的总和。 例如图 4.1 中速率 R＝1/2 的编码器，v＝v1＝3；图 4.11 中速率 R＝2/3 的编码器，v＝v1+v2=2。 定义 4.4：全局约束长度为 v、编码速率 R＝k/n 的卷积编码器常表示为一个（n,k,v）编码器。 例如图 4.1 中速率 R＝1/2 的编码器是（2，1，3）编码器，图 4.11 中速率 R＝2/3 的编码器 是（3，2，2）编码器。 因此，对于（n，1，v）编码器，全局约束长度 v 就等于存储器阶数 m。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.3：（4，3，3）非系统前馈卷积编码器 （4，3，3）非系统前馈卷积编码器如图 4.3 所示，寄存器长度 v1=0, v2=1, v3=2。存储器 阶数 m＝2，全局约束长度 v＝3，生成器序列为： = = g1(0) (100) = g1(1) (100) = g1(2) (100) g1(3) (100) = = g 2(0) (000) = g 2(1) (110) = g 2(2) (010) g 2(3) (100) （4.21） = = g3(0) (000) = g3(1) (010) = g3(2) (101) g3(3) (101) 5 Copyright by 周武旸 

6 . 第四章 卷积码的编码 u (1) v (0) v (1) u (2) v (2) u (3) v (3) 图 4.3 （4，3，3）非系统前馈卷积编码器 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 通常，一个存储器阶数为 m 的（n，k，v）前馈编码器，其生成矩阵可写为： G 0 G1 G2  Gm   G0 G1  G m −1 Gm  G=  （4.22）  G 0  G m−2 G m −1 Gm       其中 G l 是一个 k×n 的子矩阵，表示为：  g1,(0)l g1,(1)l  g1,( nl −1)   (0)   g 2,l g 2,(1)l  g 2,( nl−1)  Gl = （4.23）       (0)  (1)  g k ,l g k ,l  g k( n,l−1)  仍需要注意的是：生成矩阵 G 中的 k 行（一组）都与前 k 行（一组）相同，只是向右 移 n 位 。 对 于 一 个 信= = 0 , u1 ,) (u0 u0  u0 , u1 u1  u1 ,) ， 码 字 (1) (2) (k ) (1) (2) (k ) 息 序 列 u (u = = (v0(0) v0(1)  v0( n −1) , v1(0) v1(1)  v1( n −1) ,) 。 v uG 码字 v 是生成矩阵 G 的线性组合，因此（n，k，v）是一个线性码。 在线性系统中，时域中的卷积可用更方便的多项式乘法来代替。这样编码方程中每个序 列都可以用一个对应的多项式来代替，例如对一个（2，1，v）编码器，编码方程变为： v (0) ( D) = u( D)g (0) ( D) （4.24） v (1) ( D) = u( D)g (1) ( D) 其中 u( D) =u0 + u1 D + u2 D 2 +  （4.25a） 是信息序列。 6 Copyright by 周武旸 

7 . 第四章 卷积码的编码 v (0) ( D) =v0(0) + v1(0) D + v2(0) D 2 +  （4.25b） v (1) ( D) =v0(1) + v1(1) D + v2(1) D 2 +  是编码后的序列。 g (0) ( D) = g 0(0) + g1(0) D +  + g m(0) D m （4.25c） g (1) ( D) = g 0(1) + g1(1) D +  + g m(1) D m 是生成多项式。 这样码字可写为： V ( D) =  v (0) ( D), v (1) ( D)  （4.26a） 或经过复用后，写为： = v( D) v (0) ( D 2 ) + Dv (1) ( D 2 ) （4.26b） D 可看作为一个时延算子，D 的指数表示相对于序列中的初始 bit 延时了多少时间单元。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 如 图 4.1 所 示 的 （ 2 ， 1 ， 3 ） 编 码 器 ， 生 成 多 项 式 g (0) ( D ) =+ 1 D 2 + D3 及 g (1) ( D) =1 + D + D 2 + D 3 ，对信息序列 u( D) =+ 1 D 2 + D 3 + D 4 ，编码方程为： v (0) ( D) =(1 + D 2 + D 3 + D 4 )(1 + D 2 + D 3 ) =+ 1 D7 （4.27） v (1) ( D) =(1 + D 2 + D 3 + D 4 )(1 + D + D 2 + D 3 ) =+ 1 D + D3 + D 4 + D5 + D 7 码字可写为： V ( D) = 1 + D 7 ,1 + D + D 3 + D 4 + D 5 + D 7  （4.28a） 或 v ( D) =1 + D + D 3 + D 7 + D 9 + D11 + D14 + D15 （4.28b） ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 注意：生成多项式的最低阶项（常数项）对应于移位寄存器连接的最左端，最高阶项对应于 的连接是 g (0) = (1011) ， (0) 移位寄存器连接的最右端。例如图 4.1 中，从移位寄存器到输出 v 对应的生成多项式为 g (0) ( D ) =+ 1 D 2 + D3 。 在（n，1，v）编码器中，由于移位寄存器的最右端必须连接到至少一个输出上，因此 至少有一个生成多项式的阶数必然等于移位寄存器的长度 m，即 m = max deg g ( j ) ( D)  （4.29） 0 ≤ j ≤ n −1 在 k>1 的（n，k，v）编码器中，对于每个输入（共有 k 个输入），都有 n 个生成多项式。 每一组 n 个生成多项式表示着从移位寄存器到 n 个输出的连接序列，因此，有 =vi max deg g i( j ) ( D)  , 1 ≤ i ≤ k （4.30） 0 ≤ j ≤ n −1 ( j) 其中 g i ( D ) 是第 i 个输入到第 j 个输出的生成多项式。 7 Copyright by 周武旸 

8 . 第四章 卷积码的编码 由于编码器是一个线性系统，u ( i ) ( D ) 表示第 i 个输入序列， v ( j ) ( D ) 表示第 j 个输出序 ( j) 列，生成多项式 g i ( D ) 可解释为输入 i 到输出 j 的转移函数。对于有 k 个输入、n 个输出的 线性系统，共有 kn 个转移函数，可用 k×n 的生成矩阵表示： g1(0) ( D) g1(1) ( D)  g1( n −1) ( D)   (0)  g ( D) g (1)2 ( D)  g (2n −1) ( D)  G ( D) =  2 （4.31）        (0)  g k ( D) g k ( D) (1)  g (kn −1) ( D)  使用生成矩阵， （n，k，v）前馈编码器的编码方程可写为： V(D)=U(D)G(D) （4.32） 其 中 U( D)  u (1) ( D), u (2) ( D), u ( k ) ( D)  是 k-tuple 输 入 序 列 ， V ( D)   v (0) ( D), v (1) ( D ), v ( n −1) ( D )  是 n-tuple 输出序列（码字），复用后，码字可表示 为： ( D) v (0) ( D n ) + Dv (1) ( D n ) +  + D n −1 v ( n −1) ( D n ) v= （4.33） ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 对于图 4.2 的（3，2，2）编码器 v (0) u (1) =g1(0) (1= (1) 1) g1(1) (0= 1) g1(2) (1 1) v =g (0) 2 (0=1) g (1) 2 (1= 0) g (2) 2 (1 0) u (2) v (2) 1 + D D 1 + D  G ( D) =   （4.34） D 1 1  对于输入序列 u (1) ( D ) = 1 + D 2 和 u (2) ( D ) = 1 + D ，码字为： V ( D) =  v (0) ( D), v (1) ( D), v (2) ( D)  1 + D D 1 + D  1 D 2 ,1 + D   =+  （4.35a） D 1 1  =1 + D 3 , 1 + D 3 , D 2 + D 3  也可写为： 8 Copyright by 周武旸 

9 . 第四章 卷积码的编码 v ( D) =1 + D + D8 + D 9 + D10 + D11 （4.35b） ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 我们也可以将式（4.31）、 （4.32）、（4.33）的复用码字 v(D)写成： k v ( D ) = ∑ u ( i ) ( D n )g i ( D ) （4.36） i =1 其中 g= i ( D) g i(0) ( D n ) + Dg i(1) ( D n ) +  + D n −1g i( n −1) ( D n ), 1 ≤ i ≤ k （4.37） 是第 i 个输入到输出的复合生成多项式。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例如图 4.1 所示的（2，1，3）编码器，复合生成多项式为： = g ( D) g (0) ( D 2 ) + Dg (1) ( D 2 ) （4.38） =1 + D + D 3 + D 4 + D 5 + D 6 + D 7 当输入信息多项式 u( D ) =+ 1 D 2 + D 3 + D 4 时，码字为： v ( D ) = u ( D 2 )g ( D ) =(1 + D 4 + D 6 + D8 )(1 + D + D 3 + D 4 + D 5 + D 6 + D 7 ) （4.39） =1 + D + D + D + D + D + D + D 3 7 9 11 14 15 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 卷积编码器的一个重要子类是系统编码器，在一个系统编码器中，前 k 个输出序列（称 为系统输出序列）正好是 k 个输入序列的拷贝，即： v (i −1) u= = (i ) , i 1, 2, , k （4.40） 生成器序列满足： 1, if j = i − 1 =g i( j ) = i 1, 2, k （4.41） 0, if j ≠ i − 1 在系统前馈编码器中，生成矩阵可表示为： I P0 0 P1 0 P2  0 Pm   I P0 0 P1  0 Pm −1 0 Pm  G=  （4.42）  I P0  0 Pm − 2 0 Pm −1 0 Pm       其中 I 是 k×k 的单位阵，0 是 k×k 的全 0 阵，Pl 是 k × (n − k ) 的矩阵，为： 9 Copyright by 周武旸 

10 . 第四章 卷积码的编码  g1,( kl ) g1,( kl +1)  g1,( nl −1)   (k )  g g 2,( kl+1)  g 2,( nl−1)  Pl =  2,l （4.43）        (k ) ( k +1) ( n −1)   g k ,l g k ,l  g k ,l  类似地，k×n 的生成矩阵变为： 1 0  0 g1( k ) ( D)  g1( n −1) ( D)    0 1  0 g (2k ) ( D)  g (2n −1) ( D)  G ( D) =  （4.44）           0 0  1 g (kk ) ( D)  g (kn −1) ( D)  由于前 k 个输出序列是系统的，即为 k 个输入序列，它们也被称为输出信息序列，后面 的 n－k 个输出序列被称为输出校验序列。通常，需要 kn 个生成多项式来定义（n，k，v） 非系统前馈编码器，需要 k×(n－k)个生成多项式来定义系统前馈编码器。 对于式（4.42）或（4.44）生成矩阵所示的系统前馈编码器，其对应的系统校验矩阵可 直接表示为：  P0T I   T   P1 0 P0T I   P2T 0 P1T 0 P0T          H= T  （4.45） P 0 PmT −1 0 Pm − 2 0  P0T T I   m   PmT 0 PmT −1 0  P1T 0 P0T I   PmT 0  P2T 0 P1T 0 P0T I      其中 I 是（n－k）×（n－k）的单位阵，0 是（n－k）×（n－k）的全零矩阵，类似地， （n －k）×n 的校验矩阵可表示为： g1( k ) ( D) g (2k ) ( D)  g (kk ) ( D) 1 0  0  ( k +1)  g ( D) g (2k +1) ( D)  g (kk +1) ( D) 0 1  0 H( D) =  1 （4.46a）          ( n −1)  g1 ( D) g (2n −1) ( D)  g (kn −1) ( D) 0 0  1  其中 H(D)的后（n－k）列是（n－k）×（n－k）的单位阵，上式也可写为： h1(0) ( D) h1(1) ( D)  h1( k −1) ( D) 1 0  0   (0)  h ( D) h (1) 2 ( D)  h (2k −1) ( D) 0 1  0  H( D) =  2 （4.46b）          (0) ( k −1)  h n − k ( D) h n−k ( D)  (1) h n − k ( D) 0 0  1  其中与第（i－1）个输出信息序列相联系的第（j－k＋1）个校验多项式定义为 h (ji−−k1)+1 ( D) = g i( j ) ( D) ，j＝k, k+1, …, n-1，i＝1, 2, …, k。为了简化表达，可用 hi( j ) ( D) ，i＝1， 2，…,n－k，j＝0，1，…,k－1 来表达。 任何一个有效的码字 v（或 V(D)）必须满足校验方程： 10 Copyright by 周武旸 

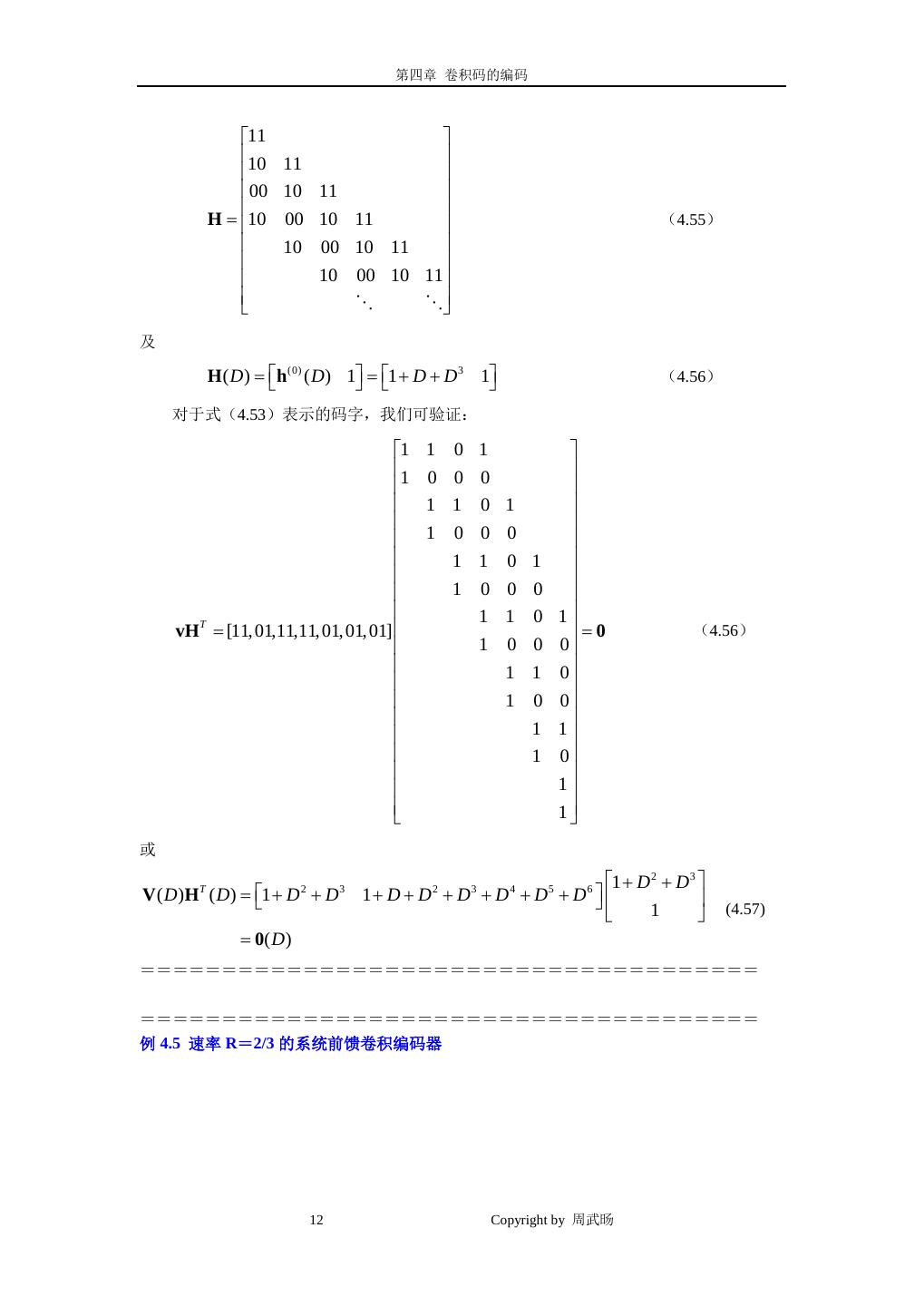
11 . 第四章 卷积码的编码 vHT=0 （4.47） 或 v(D)HT(D)=0(D) （4.48） ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.4 速率 R＝1/2 的系统前馈卷积编码器 v (0) u v (1) 图 4.4 速率 R＝1/2 的系统前馈卷积编码器 （2，1，3）系统前馈编码器如图 4.4 所示，生成器序列为 g(0)=(1000)和 g(1)=(1101)， 生成矩阵为 11 01 00 01   11 01 00 01  G=   （4.49）  11 01 00 01      及 ) 1 1 + D + D 3  G ( D= （4.50） 当输入序列 u( D ) =+ 1 D 2 + D 3 时，输出信息序列为： v (0) ( D) =u( D)g (0) ( D) =(1 + D 2 + D 3 )(1) =+ 1 D 2 + D3 （4.51） 输出校验序列为： v (1) ( D) = u( D)g (1) ( D) = (1 + D 2 + D 3 )(1 + D + D 3 ) （4.52） =+ 1 D + D 2 + D3 + D 4 + D5 + D 6 这样，码字就为： V ( D) =  v (0) ( D) v (1) ( D)  （4.53a） =1 + D 2 + D 3 1 + D + D 2 + D 3 + D 4 + D 5 + D 6  或 = v ( D) v (0) ( D 2 ) + Dv (1) ( D 2 ) （4.53b） =1 + D + D 3 + D 4 + D 5 + D 6 + D 7 + D 9 + D11 + D13 也可写为： v = (11, 01,11,11, 01, 01, 01) （4.54） 利用式（4.45）和式（4.46b），我们可得到校验矩阵： 11 Copyright by 周武旸 

12 . 第四章 卷积码的编码 11  10 11    00 10 11    H = 10 00 10 11  （4.55）  10 00 10 11     10 00 10 11     及 H ( D) = h (0) ( D) 1 = 1 + D + D 3 1 （4.56） 对于式（4.53）表示的码字，我们可验证： 1 1 0 1  1 0 0 0     1 1 0 1     1 0 0 0   1 1 0 1     1 0 0 0   1 1 0 1 vHT = [11, 01,11,11, 01, 01, 01]   0 （4.56）  1 0 0 0  1 1 0    1 0 0    1 1  1 0    1  1  或 1 + D 2 + D 3  V ( D)H ( D) =1 + D + D T 2 3 1 + D + D + D + D + D + D   2 3 4 5 6   1  (4.57) = 0( D ) ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.5 速率 R＝2/3 的系统前馈卷积编码器 12 Copyright by 周武旸 

13 . 第四章 卷积码的编码 v (0) u (1) v (0) u (1) u (2) v (1) v (1) u (2) v (2) v (2) （a） （b） 图 4.5 速率 R＝2/3 的系统前馈卷积编码器的两种表示方式 （a）controller canonical form（b）observer canonical form 生成矩阵： 1 0 1 + D + D 2  G ( D) =   （4.58） 0 1 1 + D  根据式（4.46b） ，校验矩阵可写为： H ( D) = h (0) ( D) h (1) ( D) 1 = 1 + D + D 2 1 + D 1 （4.59） 在图 4.5（a）所示的方式中，编码器需要共 v = v1 + v2 = 3 个时延单元，因此它是一个 （3，2，3）编码器。再者，由于输出信息序列为 v (0) ( D ) = u (1) ( D ) 及 v (1) ( D ) = u (2) ( D ) ， 输出校验序列就为： = v (2) ( D) u (1) ( D)g1(2) ( D) + u (2) ( D)g (2) 2 ( D) （4.60） = (1 + D + D 2 )u (1) ( D) + (1 + D)u (2) ( D) 也可以用图 4.5(b)来表示，注意这种方式只需要 v＝2 个时延单元，因此是一个（3，2，2） 编码器。 因此，对于同样的卷积码，可以用不同的方式表示。我们知道，卷积码可以用状态图表 示（共有 2v 个状态） ，在进行最大似然译码和最大后验概率译码时，其复杂度正比于编码器 状态图中的状态数，因此我们希望寻找具有最小状态数（即最小全局约束长度 v）的编码器 实现。 [在介绍过系统反馈编码器后我们仍将继续讨论最小编码器实现的问题。] ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.6 速率 R＝1/3 的系统反馈卷积编码器 13 Copyright by 周武旸 

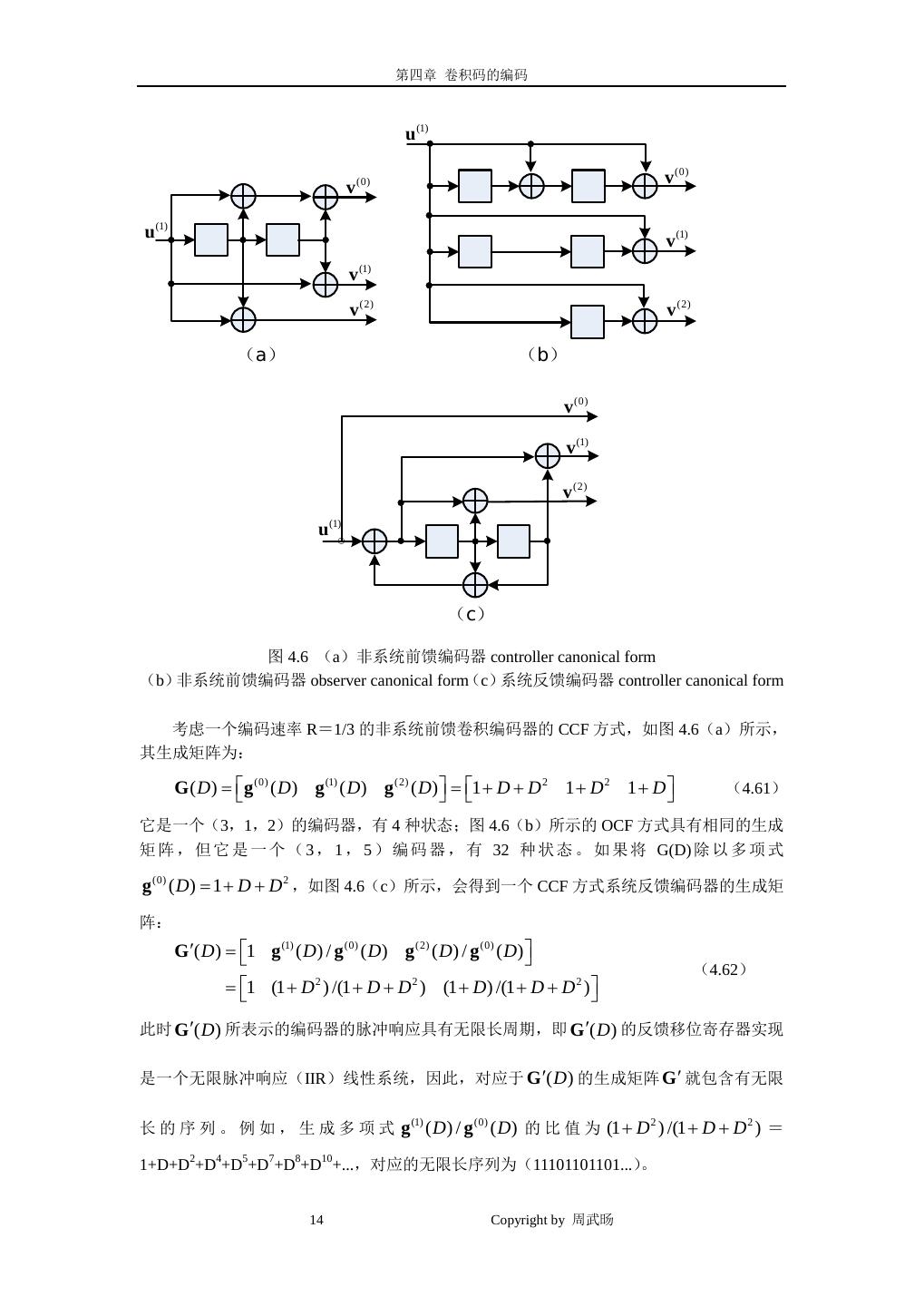
14 . 第四章 卷积码的编码 u (1) v (0) v (0) u (1) v (1) v (1) v (2) v (2) （a） （b） v (0) v (1) v (2) u (1) （c） 图 4.6 （a）非系统前馈编码器 controller canonical form （b）非系统前馈编码器 observer canonical form（c）系统反馈编码器 controller canonical form 考虑一个编码速率 R＝1/3 的非系统前馈卷积编码器的 CCF 方式，如图 4.6（a）所示， 其生成矩阵为： g (0) ( D) g (1) ( D) g (2) ( D)  = G ( D) = 1 + D + D 2 1 + D 2 1 + D  （4.61） 它是一个（3，1，2）的编码器，有 4 种状态；图 4.6（b）所示的 OCF 方式具有相同的生成 矩 阵 ， 但 它 是 一 个 （ 3 ， 1 ， 5 ） 编 码 器 ， 有 32 种 状 态 。 如 果 将 G(D) 除 以 多 项 式 g (0) ( D) =1 + D + D 2 ，如图 4.6（c）所示，会得到一个 CCF 方式系统反馈编码器的生成矩 阵： G ′( D) = 1 g (1) ( D) / g (0) ( D) g (2) ( D) / g (0) ( D)  （4.62） = 1 (1 + D 2 ) /(1 + D + D 2 ) (1 + D) /(1 + D + D 2 )  此时 G ′( D ) 所表示的编码器的脉冲响应具有无限长周期，即 G ′( D ) 的反馈移位寄存器实现 是一个无限脉冲响应（IIR）线性系统，因此，对应于 G ′( D ) 的生成矩阵 G ′ 就包含有无限 长 的 序 列 。 例 如 ， 生 成 多 项 式 g (1) ( D ) / g (0) ( D ) 的 比 值 为 (1 + D 2 ) /(1 + D + D 2 ) ＝ 1+D+D2+D4+D5+D7+D8+D10+...，对应的无限长序列为（11101101101...）。 14 Copyright by 周武旸 

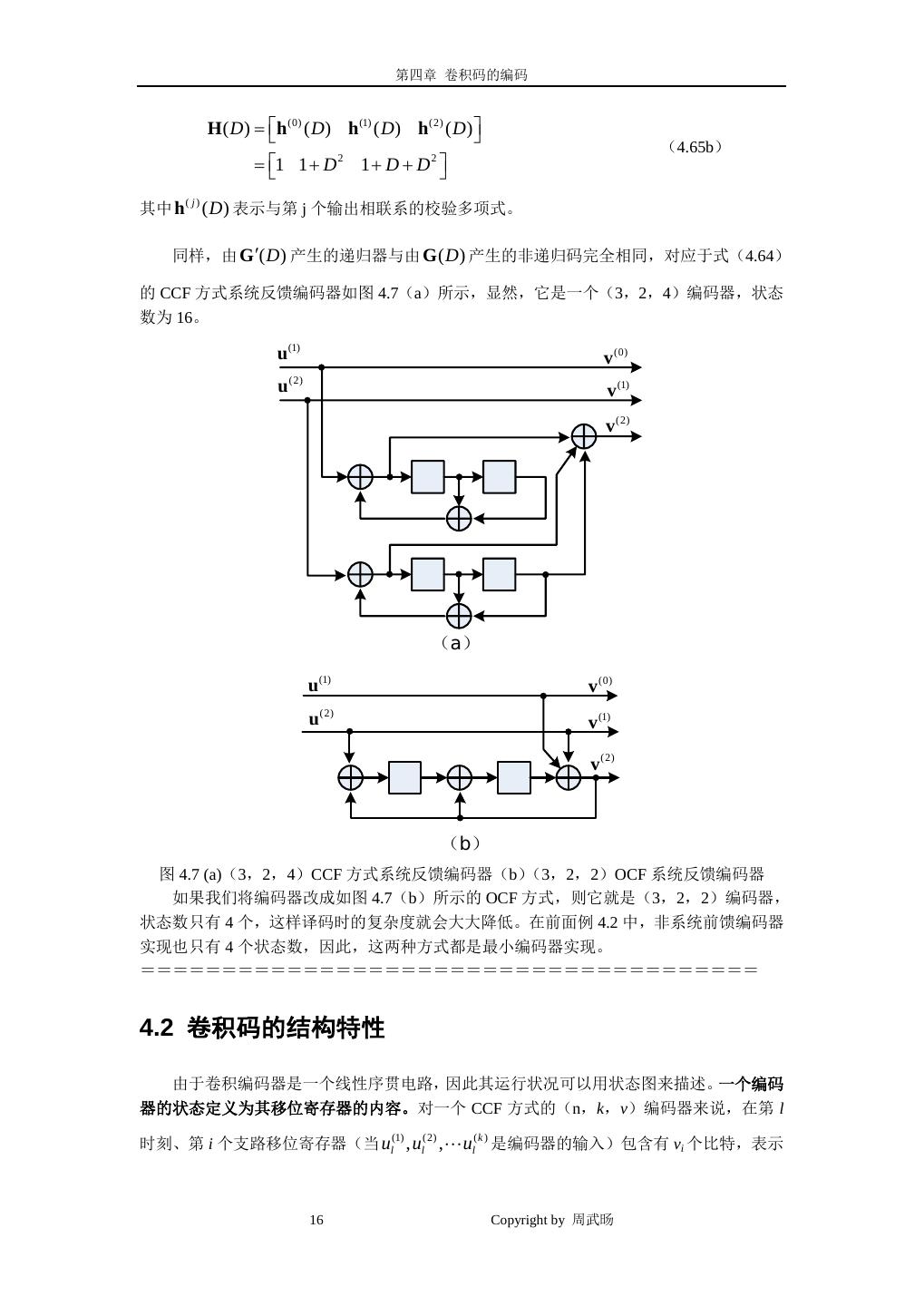
15 . 第四章 卷积码的编码 注意：由 G ′( D ) 产生的编码器输出序列与由 G ( D ) 产生的编码器输出序列完全相同， 因为：在由 G(D)产生的码中，如果由信息序列 u(D)产生码字 V(D)，即 V(D)=u(D)G(D)； 在由 G ′( D ) 产生的码中， u′( D ) = (1 + D + D 2 )u( D ) ，因此产生相同的码字 V(D)，即 V ( D) = u′( D)G ′( D) 。 由于 G ′( D ) 是系统的，我们可用式（4.46a）得到校验矩阵： (1 + D 2 ) /(1 + D + D 2 ) 1 0  H′( D) =   （4.63） (1 + D) /(1 + D + D ) 0 1  2 其中 H′( D ) 对 G ( D ) 和 G ′( D ) 都是有效的校验矩阵。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 通常，如果 k×n 的多项式矩阵 G(D)是一个编码速率 R＝k/n 的非系统卷积编码器的生 成矩阵，则可通过初等行变换把它变为系统生成矩阵 G ′( D ) ，形成系统反馈编码器。在反 馈编码器中，由于单个非零输入的响应具有无限长周期，由反馈编码器产生的码称为递归卷 积码(RCC，Recursive Convolutional Code)。递归码的这种特性是并行级连卷积码（Turbo 码） 具有优异性能的关键因素。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.7：在例 4.2 中所示的非系统前馈卷积码中，其生成矩阵 G(D)如式（4.34）所示，现重 写如下： 1 + D D 1 + D  G ( D) =   （4.34） D 1 1  它是一个（3，2，2）卷积码，状态数为 4。为了将它转化为一个等效的系统反馈编码 器，我们可进行如下的初等行变换： （1）第一行[1/(1+D)][第一行]； （2）第二行第二行＋[D][第一行]； （3）第二行[(1+D)/(1+D+D2)][第二行]； （4）第一行第一行＋[D/(1+D)][第二行]； 这样就可得到系统反馈形式的生成矩阵： 1 0 1/(1 + D + D 2 )  G ′( D) =  2  （4.64） 0 1 (1 + D ) /(1 + D + D )  2 根据式（4.46b）可得到系统校验矩阵： H′( D) = h (0) ( D) / h (2) ( D) h (1) ( D) / h (2) ( D) 1 （4.65a） = 1/(1 + D + D 2 ) (1 + D 2 ) /(1 + D + D 2 ) 1 或等效的非系统校验矩阵多项式： 15 Copyright by 周武旸 

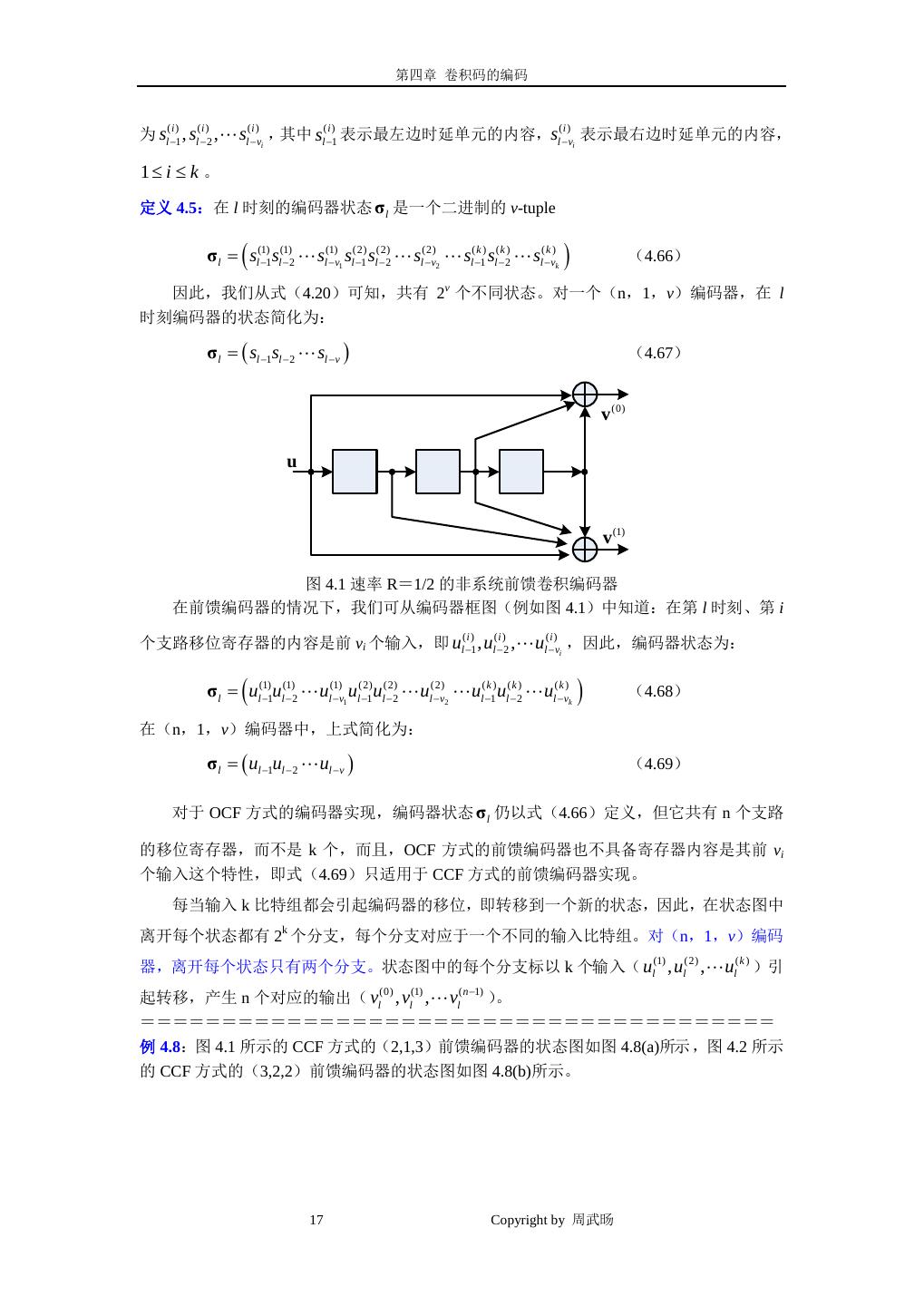
16 . 第四章 卷积码的编码 H ( D) = h (0) ( D) h (1) ( D) h (2) ( D)  （4.65b） = 1 1 + D 2 1 + D + D 2  其中 h ( j ) ( D ) 表示与第 j 个输出相联系的校验多项式。 同样，由 G ′( D ) 产生的递归器与由 G ( D ) 产生的非递归码完全相同，对应于式（4.64） 的 CCF 方式系统反馈编码器如图 4.7（a）所示，显然，它是一个（3，2，4）编码器，状态 数为 16。 u (1) v (0) u (2) v (1) v (2) （a） u (1) v (0) u (2) v (1) v (2) （b） 图 4.7 (a)（3，2，4）CCF 方式系统反馈编码器（b） （3，2，2）OCF 系统反馈编码器 如果我们将编码器改成如图 4.7（b）所示的 OCF 方式，则它就是（3，2，2）编码器， 状态数只有 4 个，这样译码时的复杂度就会大大降低。在前面例 4.2 中，非系统前馈编码器 实现也只有 4 个状态数，因此，这两种方式都是最小编码器实现。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 4.2 卷积码的结构特性 由于卷积编码器是一个线性序贯电路，因此其运行状况可以用状态图来描述。一个编码 器的状态定义为其移位寄存器的内容。对一个 CCF 方式的（n，k，v）编码器来说，在第 l 时刻、第 i 个支路移位寄存器（当 ul , ul , ul 是编码器的输入）包含有 vi 个比特，表示 (1) (2) (k ) 16 Copyright by 周武旸 

17 . 第四章 卷积码的编码 为 sl −1 , sl − 2 , sl −vi ，其中 sl −1 表示最左边时延单元的内容，sl −vi 表示最右边时延单元的内容， (i ) (i ) (i ) (i ) (i ) 1≤ i ≤ k 。 定义 4.5：在 l 时刻的编码器状态 σ l 是一个二进制的 v-tuple ( σ l = sl(1)−1sl(1)− 2  sl(1)−v1 sl(2) −1 sl − 2  sl − v2  sl −1 sl − 2  sl − vk (2) (2) (k ) (k ) (k ) ) （4.66） 因此，我们从式（4.20）可知，共有 2v 个不同状态。对一个（n，1，v）编码器，在 l 时刻编码器的状态简化为： σ l = ( sl −1sl − 2  sl −v ) （4.67） v (0) u v (1) 图 4.1 速率 R＝1/2 的非系统前馈卷积编码器 在前馈编码器的情况下，我们可从编码器框图（例如图 4.1）中知道：在第 l 时刻、第 i 个支路移位寄存器的内容是前 vi 个输入，即 ul −1 , ul − 2 , ul −vi ，因此，编码器状态为： (i ) (i ) (i ) ( σ l = ul(1)−1ul(1)− 2  ul(1)−v1 ul(2) −1 ul − 2  ul − v2  ul −1 ul − 2  ul − vk (2) (2) (k ) (k ) (k ) ) （4.68） 在（n，1，v）编码器中，上式简化为： σ l = ( ul −1ul − 2  ul −v ) （4.69） 对于 OCF 方式的编码器实现，编码器状态 σ l 仍以式（4.66）定义，但它共有 n 个支路 的移位寄存器，而不是 k 个，而且，OCF 方式的前馈编码器也不具备寄存器内容是其前 vi 个输入这个特性，即式（4.69）只适用于 CCF 方式的前馈编码器实现。 每当输入 k 比特组都会引起编码器的移位，即转移到一个新的状态，因此，在状态图中 离开每个状态都有 2k 个分支，每个分支对应于一个不同的输入比特组。对（n，1，v）编码 器，离开每个状态只有两个分支。状态图中的每个分支标以 k 个输入（ ul , ul , ul ）引 (1) (2) (k ) ( n −1) 起转移，产生 n 个对应的输出（ vl , vl , vl (0) (1) ）。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.8：图 4.1 所示的 CCF 方式的（2,1,3）前馈编码器的状态图如图 4.8(a)所示 ，图 4.2 所示 的 CCF 方式的（3,2,2）前馈编码器的状态图如图 4.8(b)所示。 17 Copyright by 周武旸 

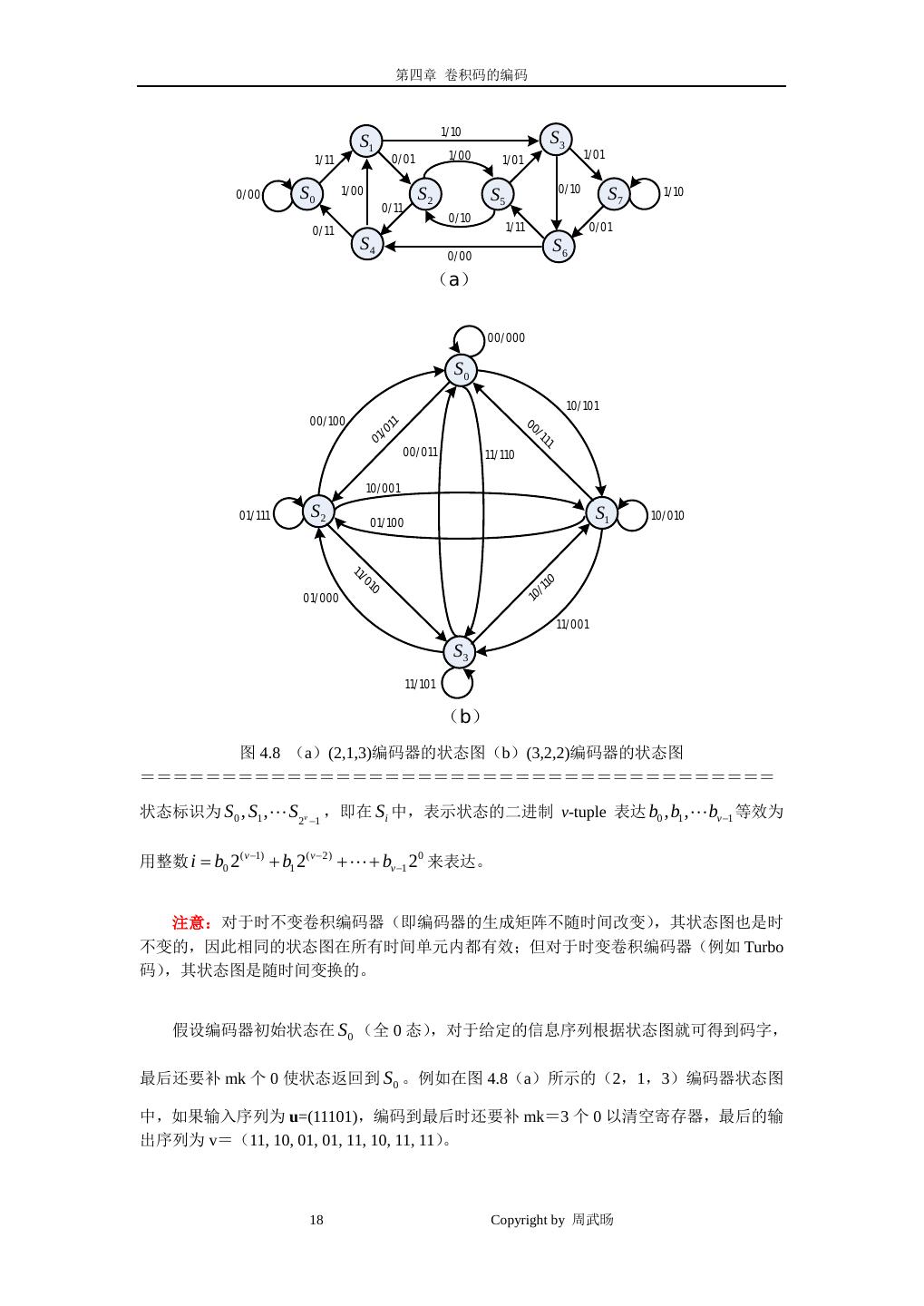
18 . 第四章 卷积码的编码 1/10 S1 S3 1/11 0/01 1/00 1/01 1/01 0/00 S0 1/00 S2 0/10 S7 1/10 S5 0/11 0/10 0/11 1/11 0/01 S4 S6 0/00 （a） 00/000 S0 10/101 00/100 11 00 /0 /1 01 11 00/011 11/110 10/001 01/111 S2 S1 10/010 01/100 11 /0 0 1 1 01/000 /1 0 10 11/001 S3 11/101 （b） 图 4.8 （a）(2,1,3)编码器的状态图（b）(3,2,2)编码器的状态图 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 状态标识为 S0 , S1 , S 2v −1 ，即在 Si 中，表示状态的二进制 v-tuple 表达 b0 , b1 , bv −1 等效为 ( v −1) = 用整数 i b0 2 + b1 2( v − 2) +  + bv −1 20 来表达。 注意：对于时不变卷积编码器（即编码器的生成矩阵不随时间改变），其状态图也是时 不变的，因此相同的状态图在所有时间单元内都有效；但对于时变卷积编码器（例如 Turbo 码），其状态图是随时间变换的。 假设编码器初始状态在 S0 （全 0 态） ，对于给定的信息序列根据状态图就可得到码字， 最后还要补 mk 个 0 使状态返回到 S0 。例如在图 4.8（a）所示的（2，1，3）编码器状态图 中，如果输入序列为 u=(11101)，编码到最后时还要补 mk＝3 个 0 以清空寄存器，最后的输 出序列为 v＝（11, 10, 01, 01, 11, 10, 11, 11） 。 18 Copyright by 周武旸 

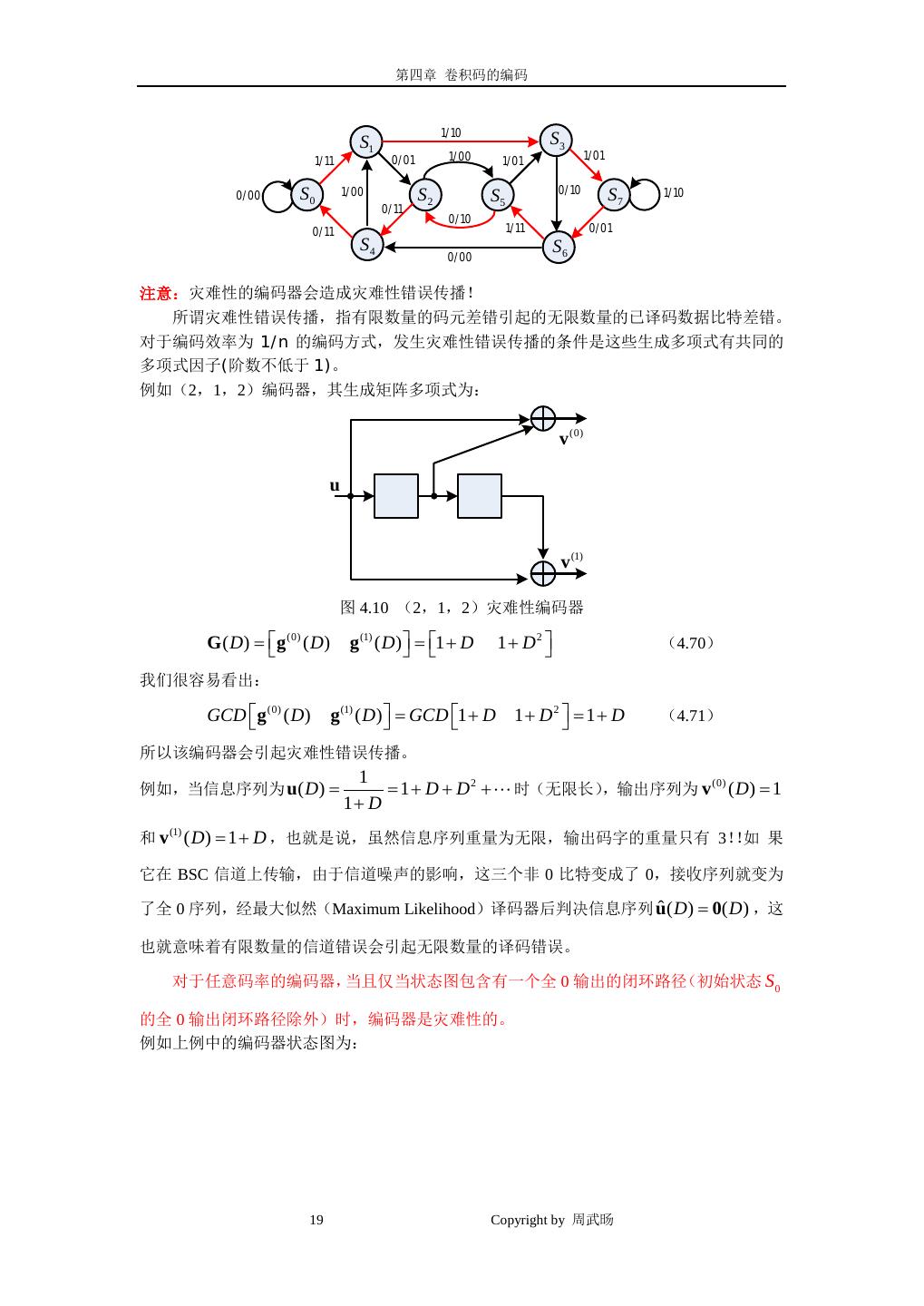
19 . 第四章 卷积码的编码 1/10 S1 S3 1/11 0/01 1/00 1/01 1/01 0/00 S0 1/00 S2 0/10 S7 1/10 S5 0/11 0/10 0/11 1/11 0/01 S4 S6 0/00 注意：灾难性的编码器会造成灾难性错误传播！ 所谓灾难性错误传播，指有限数量的码元差错引起的无限数量的已译码数据比特差错。 对于编码效率为 1/n 的编码方式，发生灾难性错误传播的条件是这些生成多项式有共同的 多项式因子(阶数不低于 1)。 例如（2，1，2）编码器，其生成矩阵多项式为： v (0) u v (1) 图 4.10 （2，1，2）灾难性编码器 g (0) ( D) G ( D) = g (1) ( D)  = 1 + D 1 + D 2  （4.70） 我们很容易看出： GCD g (0) ( D) g (1) ( D)  = GCD 1 + D 1 + D 2  = 1+ D （4.71） 所以该编码器会引起灾难性错误传播。 1 例如，当信息序列为 u( D ) = =1 + D + D 2 +  时（无限长），输出序列为 v (0) ( D) = 1 1+ D 和 v (1) ( D ) = 1 + D ，也就是说，虽然信息序列重量为无限，输出码字的重量只有 3！！如 果 它在 BSC 信道上传输，由于信道噪声的影响，这三个非 0 比特变成了 0，接收序列就变为 了全 0 序列，经最大似然（Maximum Likelihood）译码器后判决信息序列 uˆ ( D ) = 0( D ) ，这 也就意味着有限数量的信道错误会引起无限数量的译码错误。 对于任意码率的编码器，当且仅当状态图包含有一个全 0 输出的闭环路径（初始状态 S0 的全 0 输出闭环路径除外）时，编码器是灾难性的。 例如上例中的编码器状态图为： 19 Copyright by 周武旸 

20 . 第四章 卷积码的编码 0/00 S0 1/ 01 11 0/ 0/10 S2 S1 1/10 01 0/ 1/ 11 S3 1/00 图 4.11 灾难性编码器（2，1，2）的状态图 围绕状态 S3 有一个闭环路径，即 S3 → S3 的输出重量为 0。 对状态图加以修改可得到所有非零码字汉明重量（Hamming weights）的详细描述，即 该码的码字重量枚举函数（WEF，Weight Enumerating Function） 。状态 S0 分为初始态和终止 d 态（围绕 S0 的全 0 输出闭环路径就去掉了），每个分支用分支增益 X 进行标识，其中 d 是 该分支上 n 个编码后的输出比特重量。每条连接着初始态和终止态的路径都表示一个从状态 S0 分开又在状态 S0 汇聚的非零码字。路径增益是一条路径上所有分支增益的乘积。例如图 4.1 和图 4.2 所示编码器的修正状态图如图 4.12(a)和(b)所示。 X S7 X2 X X S3 S3 X S6 X2 X2 X 1 X X2 X2 X S5 X X 1 2 X S0 X S1 X S0 1 S2 2 X S0 X S1 X S2 X2 S X2 S 4 0 X X3 1 X2 X3 （a） （b） 图 4.12 （a）(2,1,3)编码器的修正状态图（b）(3,2,2)编码器的修正状态图 图 4.12 （ a ） 中 ， 表 示 状 态 序 列 S0 S1S3 S7 S6 S5 S 2 S 4 S0 的 路 径 具 有 的 路 径 增 益 为 X 2 ⋅ X1 ⋅ X1 ⋅ X1 ⋅ X 2 ⋅ X1 ⋅ X 2 ⋅ X 2 = X 1 ，即对应的码字重量为 2 12；图 4.12（b）中，表示 状态序列 S0 S1S3 S 2 S0 的路径具有的路径增益为 X ⋅ X ⋅ X ⋅ X = 2 1 0 1 4 X ，即对应的码字重量 为 4，如下图所示。 20 Copyright by 周武旸 

21 . 第四章 卷积码的编码 X S7 X2 X X S3 S3 X S6 X2 X2 X 1 X X2 X2 X S5 X X 1 2 X S0 X S1 X S0 1 S2 2 X S0 X S1 X S2 X2 S X2 S 4 0 X X3 1 X2 X3 （a） （b） 如果将修正状态图作为一个信号流图来考虑，就可得到码字的重量枚举函数（WEF） ， 为： A( X ) = ∑ Ad X d （4.72） d 其中 Ad 是重量为 d 的码字的数目。 在一个状态流图中，连接初始态和终止态的路径且经过任一状态不超过 2 次，则该路径 称为前向路径（forward path），设 Fi 是第 i 个前向路径的增益。如果一个闭环路径，从任一 状态开始，又返回到该状态，且经过任一状态不超过 2 次，则称为一个环（cycle） ，设 Ci 是第 i 个环的增益。在环集合中，如果没有一个状态属于该集合中的多个（≥2）环，则该 环集合是不相交的（nontouching）。设 {i}是所有环集合，{ i′, j ′ }是所有不相交环对（pair） 的集合，{ i′′, j ′′, l ′′ }是所有不相交环三角的集合，依此类推。 我们定义 ∆ = 1 − ∑ Ci + ∑ Ci′C j′ − ∑CC i ′′ j ′′ Cl ′′ +  （4.73） i i′, j ′ i ′′, j ′′,l ′′ 其中 ∑C i i 是 所有环 增益 的和， ∑C C i′, j ′ i′ j′ 是 所 有不相 交环 对（ pair） 增益 乘积 之和， ∑CC i ′′, j ′′,l ′′ i ′′ j ′′ Cl ′′ 是所有不相交环三角增益乘积之和，依此类推。 ∆ i 的定义与 ∆ 类似，表示第 i 个前向路径上的所有状态，以及连接这些状态的分支，在计算 ∆ i 时都要去除掉。这样码字 的重量枚举函数就为： A( X ) = ∑ F∆ i i i （4.74） ∆ 其中分子中的和是所有前向路径上的和。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.9：计算（2，1，3）卷积码的 WEF 21 Copyright by 周武旸 

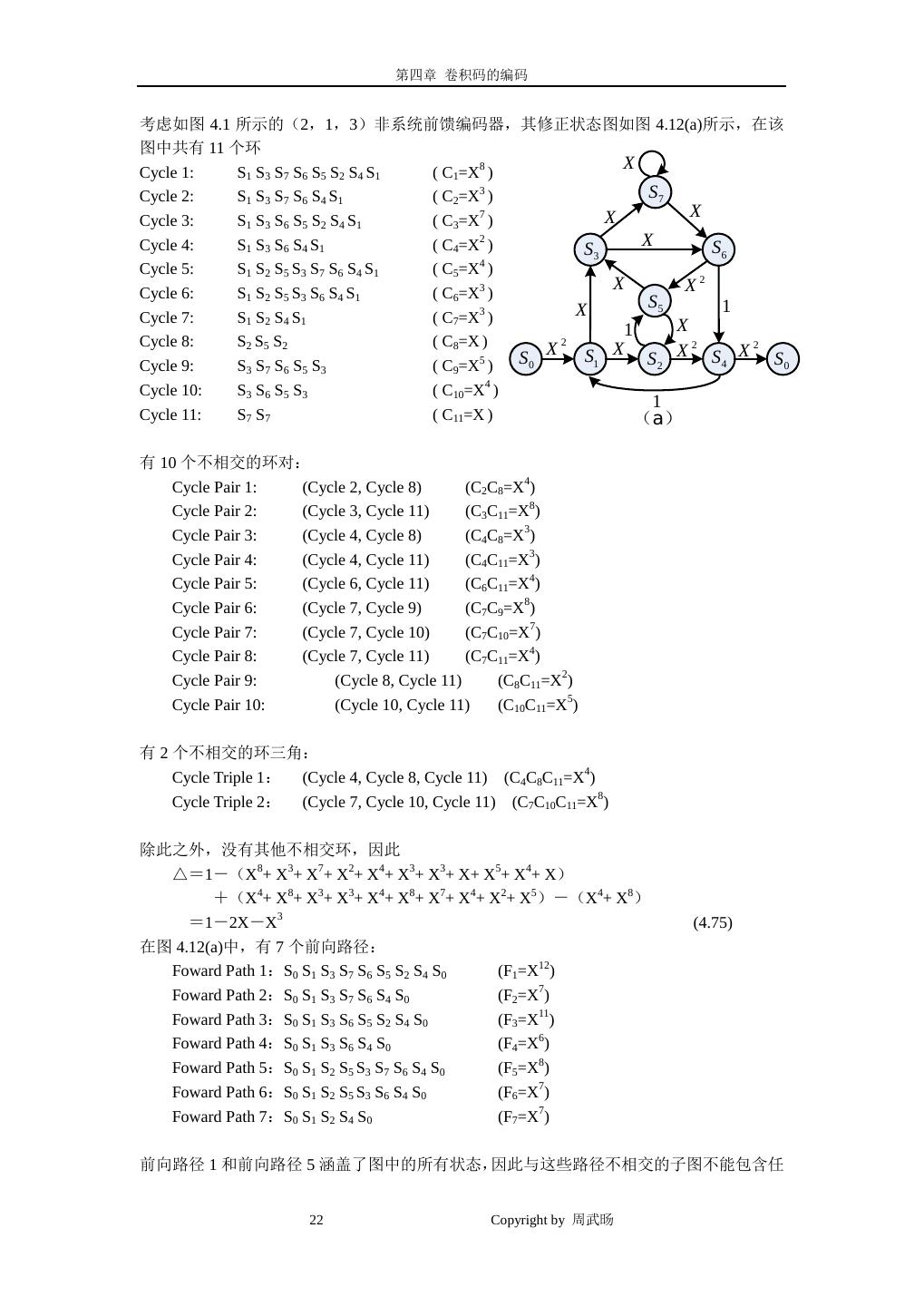
22 . 第四章 卷积码的编码 考虑如图 4.1 所示的（2，1，3）非系统前馈编码器，其修正状态图如图 4.12(a)所示，在该 图中共有 11 个环 Cycle 1: S 1 S 3 S 7 S 6 S 5 S2 S 4 S 1 ( C1=X8 ) X Cycle 2: S 1 S3 S7 S6 S4 S1 ( C2=X3 ) S7 X X Cycle 3: S 1 S 3 S 6 S 5 S 2 S4 S 1 ( C3=X7 ) Cycle 4: S 1 S3 S6 S4 S1 ( C4=X2 ) S3 X S6 4 Cycle 5: S 1 S 2 S 5 S 3 S7 S 6 S 4 S 1 ( C5=X ) Cycle 6: S 1 S 2 S 5 S 3 S6 S 4 S 1 ( C6=X3 ) X X2 X S5 1 Cycle 7: S 1 S2 S4 S1 ( C7=X3 ) X 1 Cycle 8: S 2 S5 S2 ( C8=X ) X 2 X 2 2 Cycle 9: S 3 S7 S6 S5 S3 ( C9=X5 ) S0 S1 S2 X S4 X S0 Cycle 10: S 3 S6 S5 S3 ( C10=X4 ) 1 Cycle 11: S 7 S7 ( C11=X ) （a） 有 10 个不相交的环对： Cycle Pair 1: (Cycle 2, Cycle 8) (C2C8=X4) Cycle Pair 2: (Cycle 3, Cycle 11) (C3C11=X8) Cycle Pair 3: (Cycle 4, Cycle 8) (C4C8=X3) Cycle Pair 4: (Cycle 4, Cycle 11) (C4C11=X3) Cycle Pair 5: (Cycle 6, Cycle 11) (C6C11=X4) Cycle Pair 6: (Cycle 7, Cycle 9) (C7C9=X8) Cycle Pair 7: (Cycle 7, Cycle 10) (C7C10=X7) Cycle Pair 8: (Cycle 7, Cycle 11) (C7C11=X4) Cycle Pair 9: (Cycle 8, Cycle 11) (C8C11=X2) Cycle Pair 10: (Cycle 10, Cycle 11) (C10C11=X5) 有 2 个不相交的环三角： Cycle Triple 1： (Cycle 4, Cycle 8, Cycle 11) (C4C8C11=X4) Cycle Triple 2： (Cycle 7, Cycle 10, Cycle 11) (C7C10C11=X8) 除此之外，没有其他不相交环，因此 △＝1－（X8+ X3+ X7+ X2+ X4+ X3+ X3+ X+ X5+ X4+ X） ＋（X4+ X8+ X3+ X3+ X4+ X8+ X7+ X4+ X2+ X5）－（X4+ X8） ＝1－2X－X3 (4.75) 在图 4.12(a)中，有 7 个前向路径： Foward Path 1：S0 S1 S3 S7 S6 S5 S2 S4 S0 (F1=X12) Foward Path 2：S0 S1 S3 S7 S6 S4 S0 (F2=X7) Foward Path 3：S0 S1 S3 S6 S5 S2 S4 S0 (F3=X11) Foward Path 4：S0 S1 S3 S6 S4 S0 (F4=X6) Foward Path 5：S0 S1 S2 S5 S3 S7 S6 S4 S0 (F5=X8) Foward Path 6：S0 S1 S2 S5 S3 S6 S4 S0 (F6=X7) Foward Path 7：S0 S1 S2 S4 S0 (F7=X7) 前向路径 1 和前向路径 5 涵盖了图中的所有状态，因此与这些路径不相交的子图不能包含任 22 Copyright by 周武旸 

23 . 第四章 卷积码的编码 何状态，即有： △1＝△5＝1 （4.76） 与前向路径 3、前向路径 6 不相交的子图如图 4.13（a）所示，为： △3＝△6＝1－X （4.77） 与前向路径 2 不相交的子图如图 4.13（b）所示，为： △2＝1－X （4.78） 与前向路径 4 不相交的子图如图 4.13（c）所示，为： △4＝1－（X＋X）＋（X2）＝1－2X＋X2 （4.79） 与前向路径 7 不相交的子图如图 4.13（d）所示，为： △7＝1－（X＋X4＋X5）＋（X5）＝1－X－X4 （4.80） X X S7 S7 X X S5 S5 S3 X S6 X 1 X 1 X X X2 S7 S2 S2 S5 （a） （b） （c） （d） 图 4.13 计算△i 时的子图 则 X 12 ⋅1 + X 7 (1 − X ) + X 11 (1 − X ) + X 6 (1 − 2 X + X 2 ) + X 8 ⋅1 + X 7 (1 − X ) + X 7 (1 − X − X 4 ) A( X ) = 1− 2X − X 3 X6 + X7 − X8 = （4.81） 1− 2X − X 3 =X 6 + 3 X 7 + 5 X 8 + 11X 9 + 25 X 10 + 码字的 WEF 提供了所有从状态 S0 分开、又回到状态 S0 的所有非零码字的重量分布的 详细描述，在这个式子中，我们知道，有 1 个码字重量为 6、3 个码字重量为 7、5 个码字重 量为 8，依此类推。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 在修正状态图中，如果对每个分支用 W 来标识对应的非零信息，其中 ω 表示该分支上 ω k 信息 bit 的重量；每经过一个分支标识一个 L 因子，则该码的码字输入－输出重量枚举函 数（IOWEF, Input-Output Weight Enumerating Function）表示为： A(W , X , L) = ∑ Aω ω, d ,l W ω X d Ll , d ,l （4.82） 其中因子 Aω , d ,l 表示具有重量 d、信息重量为 ω 、的经过 l 个分支的码字数。这样图 4.1 所示 编码器的增加修正状态图如图 4.14 所示。 23 Copyright by 周武旸 

24 . 第四章 卷积码的编码 WXL S7 L XL WX XL S6 S3 WX L 2 L WXL S5 WX L WL XL WX 2 L X 2L 2 S0 S1 XL S2 S 4 X L S0 WL 图 4.14 （2，1，3）编码器的增加修正状态图 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.10：对于图 4.14 所示状态图，我们可得到： △＝1－（X8 W4 L7+ X3 W3L5+ X7 W3 L6+ X2 W2 L4+ X4 W4 L7+ X3 W3 L6 + X3 W L3+ X W L2+ X5 W3 L4+ X4 W2 L3+ X W L）＋（X4 W4 L7 + X8 W4 L7+ X3 W3 L6+ X3 W3 L5+ X4 W4 L7+ X8 W4 L7+ X7 W3 L6 + X4 W2 L4+ X2 W2 L3+ X5 W3 L4）－（X4 W4 L7+ X8 W4 L7） ＝1－XW（L+L2）－X2W2（L4－L3）－X3WL3－X4W2（L3－L4） (4.83) 以及 ∑ = i F∆ i i X1 W L ⋅1 + X 7W 3 L6 (1 − XWL2 ) + X 1 W 2 4 8 L (1 − XWL) 1 3 7 + X 6W 2 L5 1 − XW ( L + L2 ) + X 2W 2 L3  + X 8W 4 L8 ⋅1 （4.84） + X W L (1 − XWL) + X WL (1 − XWL − X W L ) 7 3 7 7 4 4 2 3 = X 6W 2 L5 + X 7WL4 − X 8W 2 L5 因此，码字 IOWEF 为： X 6W 2 L5 + X 7WL4 − X 8W 2 L5 A(W , X , L) = 1 − XW ( L + L2 ) − X 2W 2 ( L4 − L3 ) − X 3WL3 − X 4W 2 ( L3 − L4 ) = X 6W 2 L5 + X 7 (WL4 + W 3 L6 + W 3 L7 ) （4.85） + X 8 (W 2 L6 + W 4 L7 + W 4 L8 + 2W 4 L9 ) + 这意味着重量为 6 的码字有 1 个，它经过了 5 个分支，输入的信息重量为 2；重量为 7 的码 字有 3 个，经过 4 个分支的输入信息重量为 1，经过 6 个分支的输入信息重量为 3，经过 7 个分支的输入信息重量为 3，依此类推。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ v +1 在 A(W , X , L) 中的 WL 项对应于输入重量为 1，它表示这是通过增加修正状态图的最 7 4 短路径，但应注意，它并不是输出码字的最小重量路径。如在例 4.10 中，项 X WL 表示最 6 2 5 短路径，但项 X W L 表示最小重量路径。 24 Copyright by 周武旸 

25 . 第四章 卷积码的编码 还应注意的是：WEF A(X)是码（code）的特性，对不同编码器表示它是不变的；而 IOWEF A(W,X,L)是编码器特性，它依赖于输入序列和码字（codeword）之间的映射关系。 IOWEF 的另一个表示方式是只包含输入和输出重量的信息，而不包括路径信息，即将 A(W,X,L)中的 L 变量设为 1： = A(W , X ) ∑ ω = ,d Aω W ω X ,d d A(W , X , L) |L =1 （4.86） 其中 Aω , d = ∑ l Aω ,d ,l 表示输出序列重量为 d、输入信息重量为 ω 的码字数目。 类似地，从 IOWEF 也能够得到 WEF A(X)： = A( X ) ∑= AX d d d A(W= , X ) |W= 1 A(W , X , L) |W= L= 1 （4.87） 其中 Ad = ∑ω Aω ,d 。 在计算 Turbo 码的 WEF 时需要一个重要工具：码字 条件重量枚举函数 （CWEF， ，它列举出与特定信息重量相关的所有码字重量。 Conditional Weight Enumerating Function） 当信息重量为 ω 时，CWEF 为： Aω ( X ) = ∑ Aω ,d X d （4.88） d 直接从式（4.86），IOWEF 可表示为： A(W , X ) = ∑ W ω Aω ( X ) （4.89） ω 很显然，CWEF 也是编码器的特性。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.11：式（4.85）简化的 IOWEF 变为： A(W , X ) =A(W , X , L) |L =1 = W 2 X 6 + (W + 2W 3 ) X 7 + (W 2 + 4W 4 ) X 8 + （4.90） 表明有一个码字输出序列重量为 6，此时的输入信息重量为 2；有 3 个码字输出序列重量为 7，其中 1 个输入信息重量为 1，2 个输入信息重量为 3，依此类推。这样可得到 WEF 为： A( X ) =A(W , X ) |W =1 =X 6 + 3 X 7 + 5 X 8 + （4.91） 这与前面式（4.81）计算的一致！！ 为了计算这种编码器的 CWEF，在状态图中，我们必须找到从初始态到终止态与给定重 量信息序列相关的输出序列重量。 例如，在图 4.14 中，有 1 个重量为 1 的信息序列 u＝ （1000） ； 有 3 个重量为 2 的信息序列 u＝（11000） ，（101000）以及（1001000） ；有 9 个重量为 3 的 信息序列 u＝（111000） ，（1101000） ，（1011000）， （（10101000）， （11001000） ，（10011000） ， （101001000），（100101000）以及（1001001000），等等（信息序列中最后 3 个 0 表示清空 寄存器）。由此，我们可得到： A1(X)＝X7 （4.92a） 6 8 10 A2(X)＝X ＋X ＋X （4.92b） 7 9 11 13 A3(X)＝2X ＋3X ＋3X ＋X （4.92c） 利用式（4.89） ，我们可得到： 25 Copyright by 周武旸 

26 . 第四章 卷积码的编码 A(W , X ) = ∑ W ω Aω ( X ) ω （4.93） = WX + W ( X + X + X ) + W (2 X + 3 X + 3 X + X ) +  7 2 6 8 10 3 7 9 11 13 由于计算的方法不同，所以式（4.90）和式（4.93）不容易一眼看出是相同的，但如果 将式（4.85）的分子和分母按照 W 的升序重新排列，并将 L 设为 1，我们可得到： WX 7 + W 2 ( X 6 − X 8 ) A(W , X ) = 1 − W (2 X + X 3 ) （4.94） = WX + W ( X + X + X ) + W (2 X + 3 X + 3 X + X ) + 7 2 6 8 10 3 7 9 11 13 这样结果就和式（4.93）一致了！ ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 在截断编码器中，输入序列长度限制为 λ= h + m 个 block，即包含 h 个信息 block，m 个终止 block。为了适应这种变化，我们将 IOWEF A(W,X,L)的分子分母按照 L 的升序排列， λ 并在最后的结果中将大于 L 的项忽略掉。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.12：我们将式（4.85）重写为： L4WX 7 + L5W 2 ( X 6 − X 8 ) A(W , X , L) = （4.95） 1 − LWX − L2WX − L3 WX 3 + W 2 ( X 4 − X 2 )  − L4W 2 ( X 2 − X 4 ) 设编码器在输入 λ = 8 个 block 后就终止，即只考虑 h=5 个输入信息 block 和 m=3 个终 止 block，并在最后的结果中去除掉阶数大于 L8 的项，有： A(W , X , L) = L4WX 7 + L5W 2 X 6 + L6 (W 2 X 8 + W 2 X 8 ) + L7 [W 2 X 10 + W 3 ( X 7 + X 11 ) (4.96) +W 4 X 8 ] + L8 [3W 3 X 9 + W 4 ( X 8 + X 10 + X 12 ) + W 5 X 9 ] 在上式中，只有 15 项，这是因为我们只考虑第一个比特是 1 的信息序列，且不考虑信 息序列如 u＝（10001000） 5 ，因为它离开和回到状态 S0 两次。注意： W 是最大输入重量， 因为 λ − m = h = 5 。 现在我们计算该截短编码器的简化 IOWEF、条件重量枚举函数（CWEF）以及重量枚 举函数（WEF） ： A(W , X ) = A(W , X , L) |L =1= WX 7 + W 2 ( X 6 + X 8 + X 10 ) + W 3 (2 X 7 + 3 X 9 + X 11 ) （4.97a） + W 4 (2 X 8 + X 10 + X 12 ) + W 5 X 9 A1 ( X ) = X 7 （4.97b） A2 ( X ) = X 6 + X 8 + X 10 （4.97c） A3 ( X ) = 2 X 7 + 3 X 9 + X 11 （4.97d） A4 ( X ) = 2 X 8 + X 10 + X 12 （4.97e） A5 ( X ) = X 9 （4.97f） 26 Copyright by 周武旸 

27 . 第四章 卷积码的编码 A( X ) = A(W , X ) |W =1 = X 6 + 3 X 7 + 3 X 8 + 4 X 9 + 2 X 10 + X 11 + X 12 （4.97g） 注意：在式（4.97d）中的 CWEF A3 ( X ) 与式（4.92c）中的表达式不同，这是由于在未截 短编码器中，重量 ω = 3 的信息序列长度超过 h＝5 比特，因此在截短编码器中，它们就不 是有效输入序列了。 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 以上计算码字 WEFs 的方法中只考虑离开和回到全 0 态一次的那些非零码字，这是由于 在用最大似然译码（MLD）计算 BER 时所需。 为了确定信息 BER（ML 译码），可将码字 WEFs 表达略加改变，形成比特 WEFs，用 来表示与给定重量的码字相关的非零信息比特数。对于一个重量为 ω 的信息，比特 CWEF 定义为： Bω ( X ) = ∑ Bω ,d X d （4.98） d 其中 Bω , d = (ω / k ) Aω , d ，其含义表示输出序列非零比特总数除以每个时间单元输入的信息 比特数 k（重量为 d 的码字序列是由重量为 ω 的信息序列产生的） 。 比特 IOWEF 可表示为： = B(W , X ) ∑ ω =Bω W ω X ,d ∑ ω W ω Bω ( X ) ,d d （4.99） 比特 WEF 为： = B( X ) ∑= B X d d d B(W , X ) |W =1 （4.100） 其中 Bd = ∑ω Bω ,d 。 这三个比特重量枚举函数 Bω ( X ) 、B（W, X）以及 B（X）都是编码器的特性。 从 Aω ,d 和 Bω ,d 的定义可知，对任意 ω 和 d，有： =Bd ∑ = ω Bω ∑ ω (ω / k ) Aω ,d ,d （4.101） 上式可用于建立码字 IOWEF A（W，X）和比特 WEF B（X）之间的关系： = B( X ) ∑= B X d ∑ ω (ω / k ) Aω d d ,d ,d Xd 1 ∂  ∑ ω ,d Aω ,dW X   ω d （4.102） 1 ∂A(W , X ) = ⋅ = ⋅ k ∂W k ∂W W =1 W =1 也就是说，比特 WEF B（X）可以直接从码字 IOWEF A（W，X）计算得到。 在译码时可以看到，最大似然译码进行的判决在每个时间单元是 k 个信息比特的译码， 因此，为了确定每个信息比特的译码错误概率，我们这里定义的比特 WEFs 中包含了一个 1/k 因子。 27 Copyright by 周武旸 

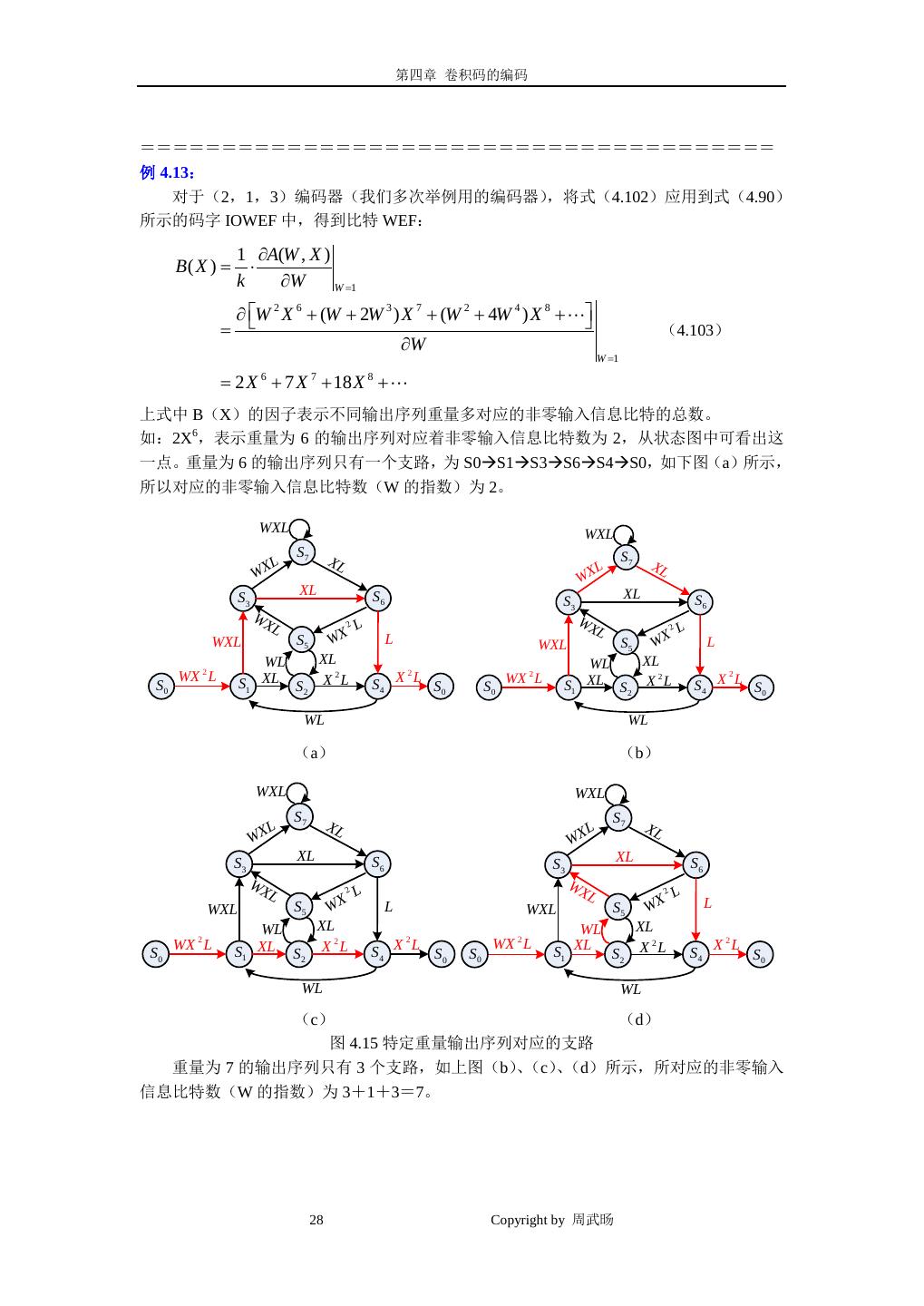
28 . 第四章 卷积码的编码 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 例 4.13： 对于（2，1，3）编码器（我们多次举例用的编码器） ，将式（4.102）应用到式（4.90） 所示的码字 IOWEF 中，得到比特 WEF： 1 ∂A(W , X ) B( X )= ⋅ k ∂W W =1 ∂ W 2 X 6 + (W + 2W 3 ) X 7 + (W 2 + 4W 4 ) X 8 +  = （4.103） ∂W W =1 = 2 X + 7 X + 18 X +  6 7 8 上式中 B（X）的因子表示不同输出序列重量多对应的非零输入信息比特的总数。 如：2X6，表示重量为 6 的输出序列对应着非零输入信息比特数为 2，从状态图中可看出这 一点。重量为 6 的输出序列只有一个支路，为 S0S1S3S6S4S0，如下图（a）所示， 所以对应的非零输入信息比特数（W 的指数）为 2。 WXL WXL S7 S7 L XL XL WX WX L XL S6 XL S3 S3 S6 WX WX L 2 L L 2 L WXL S5 WX L WXL S5 WX L WL XL WL XL WX 2 L X 2L 2 WX 2 L 2 S0 S1 XL S2 S 4 X L S0 S0 S1 XL S2 X 2L S 4 X L S0 WL WL （a） （b） WXL WXL S7 S7 L XL L XL WX WX XL S6 XL S3 S3 S6 WX WX L 2 L L 2 L WXL S5 WX L WXL S5 WX L WL XL WL XL WX 2 L X 2L 2 WX 2 L 2 S0 S1 XL S2 S 4 X L S0 S0 S1 XL S2 X 2L S 4 X L S0 WL WL （c） （d） 图 4.15 特定重量输出序列对应的支路 重量为 7 的输出序列只有 3 个支路，如上图（b） 、（c）、（d）所示，所对应的非零输入 信息比特数（W 的指数）为 3＋1＋3＝7。 28 Copyright by 周武旸 

29 . 第四章 卷积码的编码 4.3 卷积码的距离特性 卷积码的性能取决于所用的译码算法以及该码的距离特性，本节我们介绍几种距离度量 方法，而它们与性能的关系在译码时再介绍。 对卷积码来说，最重要的距离度量是最小自由距离 dfree。 定义 4.6：卷积码的最小自由距离定义为： d free  min {d ( v′, v′′ ) : u′ ≠ u′′} （4.104） u′,u′′ 其中 v′ 和 v′′ 是码字，分别对应于输入序列 u′ 和 u′′ 。 在上式中，假设了码字 v′ 和 v′′ 具有有限长度，且是从全 0 态 S0 开始、在全 0 态 S0 结 束，即会在信息序列 u′ 和 u′′ 后附加 m 个终止 block。如果 u′ 和 u′′ 长度不同，就在短序列后 补 0，使得对应的码字序列有相同的长度。因此，dfree 是该码集合中任意两个有限长度码字 的最小距离。 由于卷积码是线性码，有： = min {ω ( v′ + v′′ ) : u′ ≠ u′′} d free u′,u′′ = min {ω ( v ) : u ≠ 0} （4.105） u = min {ω ( uG ) : u ≠ 0} u 其中 v 是输出码字序列，对应于输入信息序列 u。因此，dfree 是由有限长输入信息序列产生 的输出序列中的最小重量。在状态图中，即为从全 0 态离开、又回到全 0 态的有限长路径的 最小输出重量，因此是 WEF A（X）中的最低阶数。如对于例 4.1 中的（2，1，3）编码器， 其 dfree＝6，例 4.2 中的（3，2，2）编码器，其 dfree＝3。 卷积码另一个重要的距离度量是列距离函数（CDF，Column Distance Function）：dl。设 [ v ]l = ( v0(0) , v0(1)  v0( n −1) , v1(0) , v1(1)  v1( n −1)  vl(0) , vl(1)  vl( n −1) ) （4.106） 表示码字 v 的 l 阶切断。设 [u]l = ( u0(1) , u0(2)  u0( k ) , u1(1) , u1(2)  u1( k )  ul(1) , ul(2)  ul( k ) ) （4.107） 表示输入信息序列 u 的 l 阶切断。 定义 4.7：l 阶的列距离函数（dl）定义为： dl  min {d ([ v′]l ,[ v′′]l ) : [u′]0 ≠ [u′′]0 } [ u′ ]l ,[ u′′ ]l （4.108） = min {ω ([ v ]l ) : [u]0 ≠ 0} [ u ]l 因此，dl 是前（l＋1）个单位时间输入为非 0 信息序列时，输出码字的最小重量。 根据该码的生成矩阵，有： [v]l = [u]l [G]l （4.109） 其中[G]l 是 k(l+1)×n(l+1)的矩阵，是生成矩阵 G（式 4.22）的前 n(l+1)列，表示为： 29 Copyright by 周武旸