- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
热平衡及载流子浓度
展开查看详情
1 . Lecture #3 OUTLINE • Thermal equilibrium • Fermi-Dirac distribution – Boltzmann approximation • Relationship between EF and n, p • Temperature dependence of EF, n, p Finish reading Chapter 2 Spring 2003 EE130 Lecture 3, Slide 1 Review: Energy Band Model and Doping Spring 2003 EE130 Lecture 3, Slide 2 1
2 .Spring 2003 EE130 Lecture 3, Slide 3 Important Constants • Electronic charge, q • Permittivity of free space, εo • Boltzmann constant, k • Planck constant, h • Free electron mass, mo • Thermal voltage kT/q Spring 2003 EE130 Lecture 3, Slide 4 2
3 . Thermal Equilibrium • No external forces applied: – electric field = 0 – magnetic field = 0 – mechanical stress = 0 • Thermal agitation –> electrons and holes exchange energy with the crystal lattice and each other ⇒ Every energy state in the conduction and valence bands has a certain probability of being occupied by an electron Spring 2003 EE130 Lecture 3, Slide 5 Analogy for Thermal Equilibrium Sand particles Dish Vibrating table • There is a certain probability for the electrons in the conduction band to occupy high-energy states under the agitation of thermal energy (vibrating atoms, etc.) Spring 2003 EE130 Lecture 3, Slide 6 3
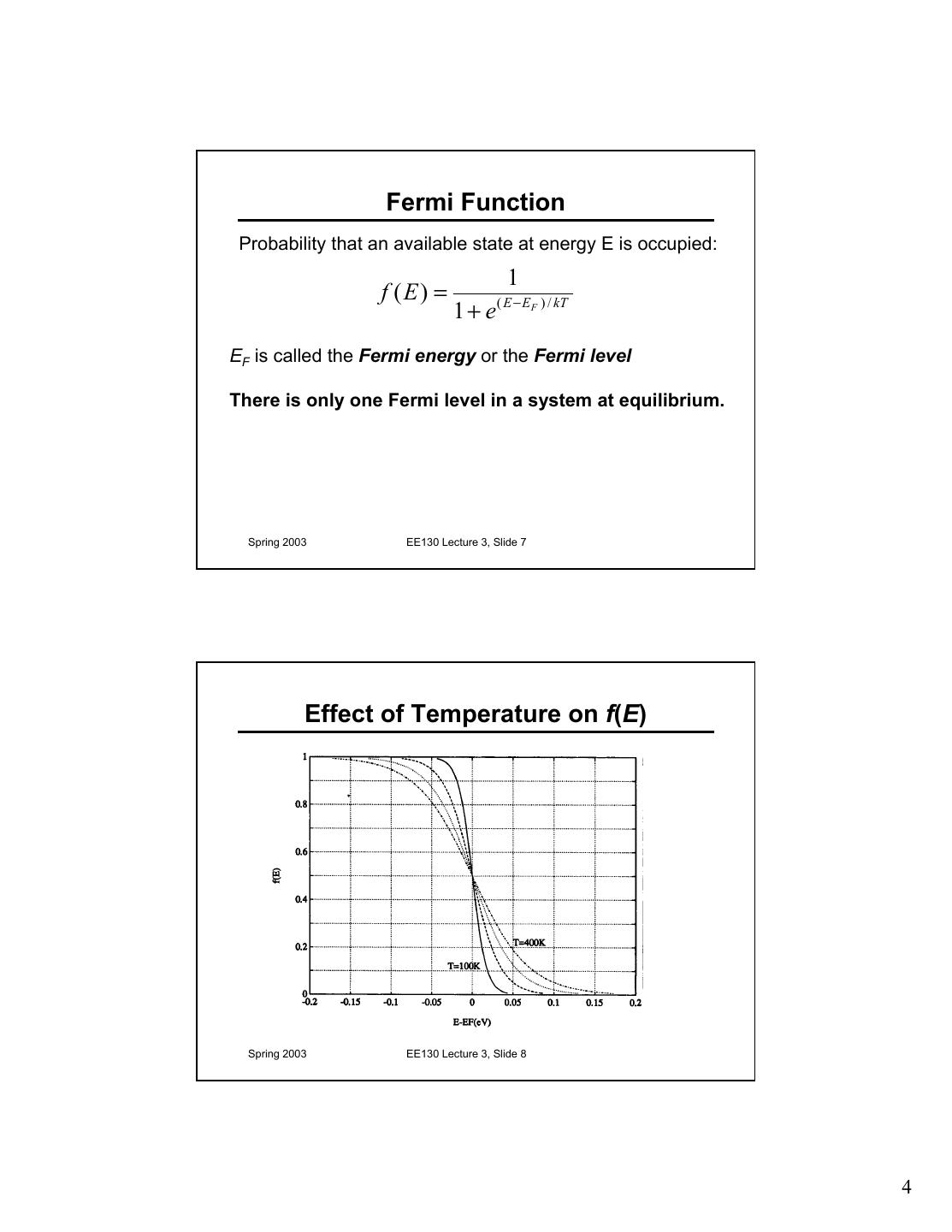
4 . Fermi Function Probability that an available state at energy E is occupied: 1 f (E) = 1 + e( E − EF ) / kT EF is called the Fermi energy or the Fermi level There is only one Fermi level in a system at equilibrium. Spring 2003 EE130 Lecture 3, Slide 7 Effect of Temperature on f(E) Spring 2003 EE130 Lecture 3, Slide 8 4
5 . Boltzmann Approximation If E − E F > 3kT , f ( E ) ≈ e − ( E − EF ) kT If E F − E > 3kT , f ( E ) ≈ 1 − e E − EF kT Spring 2003 EE130 Lecture 3, Slide 9 Density of States E gc(E) ∆Ε Ec Ec Ev Ev gv(E) g(E)dE = number of states per cm3 in the energy range between E and E+dE Near the band edges: mn* 2mn* (E − Ec ) gc ( E ) = E ≥ Ec π 2h 3 m*p 2m*p (Ev − E ) gv ( E ) = E ≤ Ev π 2h 3 Spring 2003 EE130 Lecture 3, Slide 10 5
6 . Equilibrium Distribution of Carriers • Obtain n(E) by multiplying gc(E) and f(E) • Obtain p(E) by multiplying gv(E) and 1-f(E) Spring 2003 EE130 Lecture 3, Slide 11 Equilibrium Carrier Concentrations • Integrate n(E) over all the energies in the conduction band to obtain n top of conduction band n=∫ g c ( E ) f ( E )dE Ec • By using the Boltzmann approximation, and extending the integration limit to ∞, we obtain 3/ 2 2πmn*kT n = N c e −( Ec − EF ) / kT where N c = 2 2 h Spring 2003 EE130 Lecture 3, Slide 12 6
7 .• Integrate p(E) over all the energies in the valence band to obtain p g v ( E )[1 − f ( E )]dE Ev p=∫ bottom of valence band • By using the Boltzmann approximation, and extending the integration limit to -∞, we obtain 3/ 2 2πm*p kT p = N ve − ( E F − Ev ) / kT where N v = 2 2 h Spring 2003 EE130 Lecture 3, Slide 13 Intrinsic Carrier Concentration ni Multiply n = N c e − ( Ec − E F ) / kT and p = N v e − ( EF − Ev ) / kT − E g / kT np = N c N v e − ( Ec − Ev ) / kT = N c N v e 2 Recall that np = ni − E g / 2 kT ni = N c N v e Spring 2003 EE130 Lecture 3, Slide 14 7
8 . Intrinsic Fermi Level • To find EF for an intrinsic semiconductor (n = p = ni): n = N c e( Ei − EC ) / kT = N v e( EV − Ei ) / kT = p EC + EV kT NV Ei = + ln 2 2 N C EC + EV 3kT m p * Ei = + ln * 2 4 mn Spring 2003 EE130 Lecture 3, Slide 15 n(ni, EF) and p(ni, EF) Spring 2003 EE130 Lecture 3, Slide 16 8
9 . Shifting the Fermi Level Spring 2003 EE130 Lecture 3, Slide 17 Example: Energy-band diagram Question: Where is EF for n = 1x1017 cm-3? Spring 2003 EE130 Lecture 3, Slide 18 9
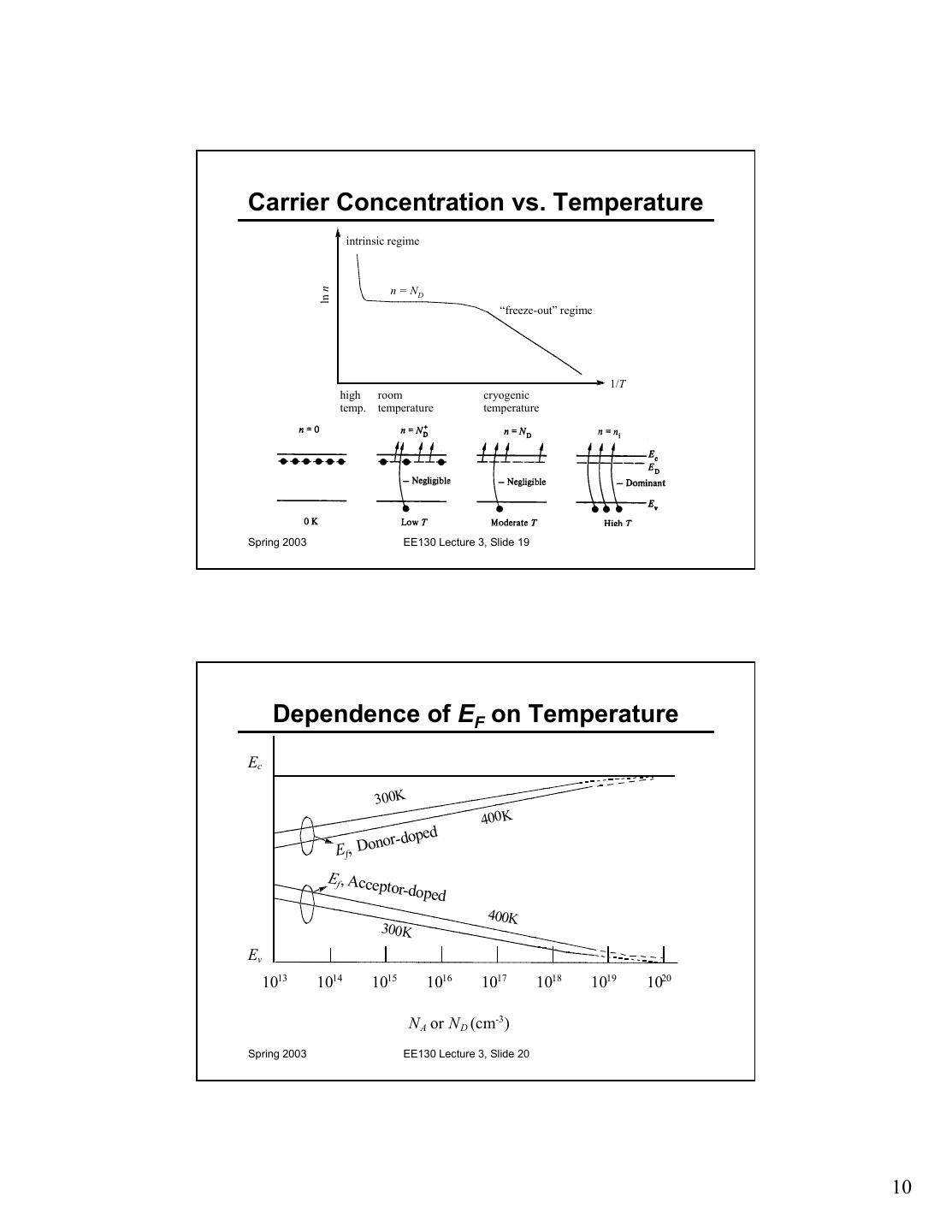
10 .Carrier Concentration vs. Temperature intrinsic regime n = ND ln n “freeze-out” regime 1/T high room cryogenic temp. temperature temperature Spring 2003 EE130 Lecture 3, Slide 19 Dependence of EF on Temperature Ec 300K 400K ed nor-dop Ef, Do Ef , Acce ptor-dop ed 400K 300K Ev 1013 1014 1015 1016 1017 1018 1019 1020 N A or N D (cm-3) Spring 2003 EE130 Lecture 3, Slide 20 10
11 . Dopant Ionization Q: Nd = 1017 cm-3. What fraction of the donors are not ionized? Solution: First assume that all the donors are ionized. n = N D = 1017 cm −3 ⇒ E f = Ec − 146meV 45meV 146 meV Ed Ec EF Ev 1 1 Probability of non-ionization ≈ = = 0.02 1 + e( Ed − EF ) / kT 1 + e((146−45) meV ) / 26 meV Therefore, it is reasonable to assume complete ionization, i.e., n = ND Spring 2003 EE130 Lecture 3, Slide 21 Summary Thermal equilibrium: Balance between internal processes with no external stimulus (no electric field, no light, etc.) => Electron-hole pair (EHP) generation rate = EHP recombination rate • Fermi function: probability that a state at energy E is filled with an electron under equilibrium conditions: 1 f (E) = ( E − E F ) / kT 1+ e – Boltzmann approximation: For high E, i.e. E - EF > 3kT: f ( E ) ≅ e − ( E − EF ) / kT For low E, i.e. EF – E > 3kT: 1 − f ( E ) ≅ e − ( E F − E ) / kT Spring 2003 EE130 Lecture 3, Slide 22 11
12 . n = N c e − ( Ec − EF ) / kT = ni e( EF − Ei ) / kT p = N v e − ( EF − Ev ) / kT = ni e( Ei − EF ) / kT Spring 2003 EE130 Lecture 3, Slide 23 12