传统调度程序的问题

1 .Advanced Operating Systems (CS 202) Scheduling (2) Jan, 23, 2017 

2 .LOTTERY SCHEDULING 2 

3 .Problems with Traditional schedulers •  Priority systems are ad hoc: highest priority always wins •  Try to support fair share by adjusting priorities with a feedback loop –  Works over long term –  highest priority still wins all the time, but now the Unix priorities are always changing •  Priority inversion: high-priority jobs can be blocked behind low-priority jobs •  Schedulers are complex and difficult to control 

4 . More on Priority Scheduling •  For real-time (predictable) systems, priority is often used to isolate a process from those with lower priority. Priority inversion is a risk unless all resources are jointly scheduled. x->Acquire() PH priority x->Acquire() x->Release() time PL x->Acquire() How can this be avoided? PH priority PM x->Acquire() time PL 4 

5 . Lottery scheduling •  Elegant way to implement proportional share scheduling •  Priority determined by the number of tickets each thread has: –  Priority is the relative percentage of all of the tickets whose owners compete for the resource •  Scheduler picks winning ticket randomly, gives owner the resource •  Tickets can be used for a variety of resources 

6 . Example •  Three threads –  A has 5 tickets –  B has 3 tickets –  C has 2 tickets •  If all compete for the resource –  B has 30% chance of being selected •  If only B and C compete –  B has 60% chance of being selected 

7 . Its fair •  Lottery scheduling is probabilistically fair •  If a thread has a t tickets out of T –  Its probability of winning a lottery is p = t/T –  Its expected number of wins over n drawings is np •  Binomial distribution •  Variance σ2 = np(1 – p) 

8 . Fairness (II) •  Coefficient of variation of number of wins σ/np = √((1-p)/np) –  Decreases with √n •  Number of tries before winning the lottery follows a geometric distribution •  As time passes, each thread ends receiving its share of the resource 

9 . Ticket transfers •  How to deal with dependencies? –  Explicit transfers of tickets from one client to another •  Transfers can be used whenever a client blocks due to some dependency –  When a client waits for a reply from a server, it can temporarily transfer its tickets to the server •  Server has no tickets of its own –  Server priority is sum of priorities of its active clients •  Can use lottery scheduling to give service to the clients •  Similar to priority inheritance –  Can solve priority inversion 

10 . Ticket inflation •  Lets users create new tickets –  Like printing their own money –  Counterpart is ticket deflation –  Lets mutually trusting clients adjust their priorities dynamically without explicit communication •  Currencies: set up an exchange rate –  Enables inflation within a group –  Simplifies mini-lotteries (e.g., for mutexes) 

11 . Example (I) •  A process manages three threads –  A has 5 tickets –  B has 3 tickets –  C has 2 tickets •  It creates 10 extra tickets and assigns them to process C –  Why? –  Process now has 20 tickets 

12 . Example (II) •  These 20 tickets are in a new currency whose exchange rate with the base currency is 10/20 •  The total value of the processes tickets expressed in the base currency is still equal to 10 

13 . Compensation tickets (I) •  I/O-bound threads are likely get less than their fair share of the CPU because they often block before their CPU quantum expires •  Compensation tickets address this imbalance 

14 . Compensation tickets (II) •  A client that consumes only a fraction f of its CPU quantum can be granted a compensation ticket –  Ticket inflates the value of all client tickets by 1/f until the client starts gets the CPU 

15 . Example •  CPU quantum is 100 ms •  Client A releases the CPU after 20ms –  f = 0.2 or 1/5 •  Value of all tickets owned by A will be multiplied by 5 until A gets the CPU •  Is this fair? –  What if A alternates between 1/5 and full quantum? 

16 . Compensation tickets (III) •  Compensation tickets –  Favor I/O-bound—and interactive—threads –  Helps them getting their fair share of the CPU 

17 . IMPLEMENTATION •  On a MIPS-based DECstation running Mach 3 microkernel –  Time slice is 100ms •  Fairly large as scheme does not allow preemption •  Requires –  A fast RNG –  A fast way to pick lottery winner 

18 . Example •  Three threads –  A has 5 tickets –  B has 3 tickets –  C has 2 tickets •  List contains –  A (0-4) Search time is O(n) –  B (5-7) where n is list length –  C (8-9) 

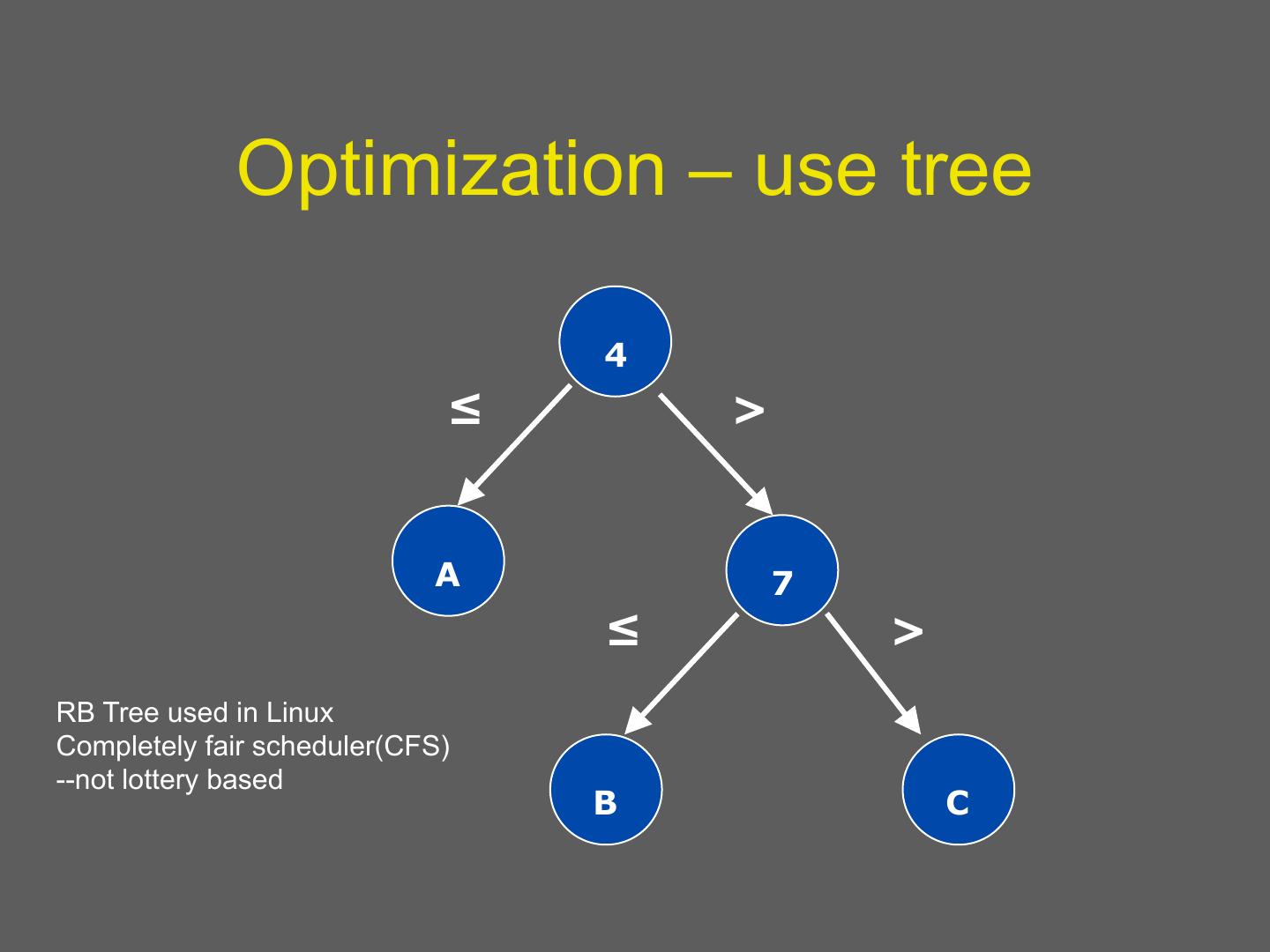
19 . Optimization – use tree 4 ≤ > A 7 ≤ > RB Tree used in Linux Completely fair scheduler(CFS) --not lottery based B C 

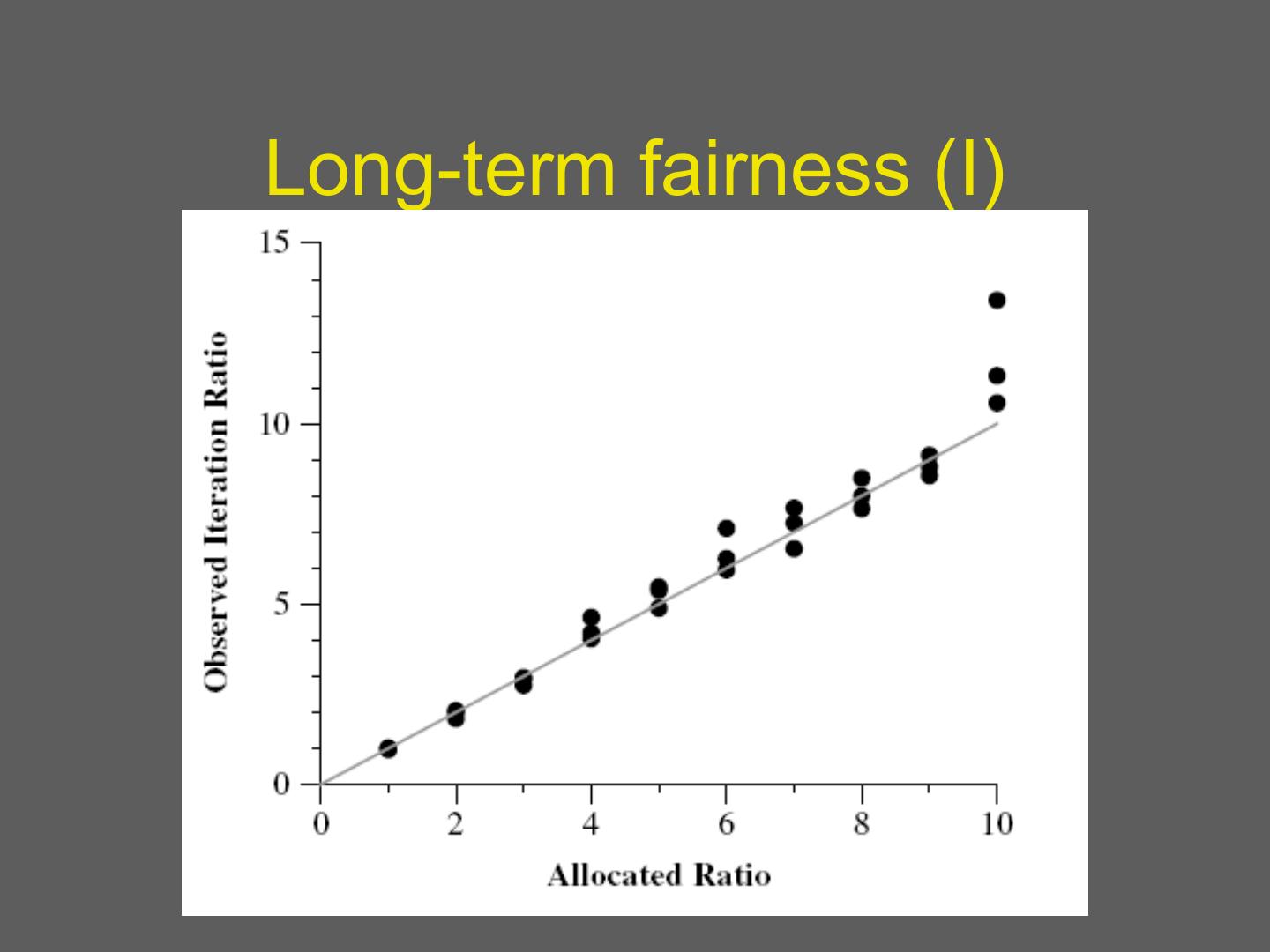
20 .Long-term fairness (I) 

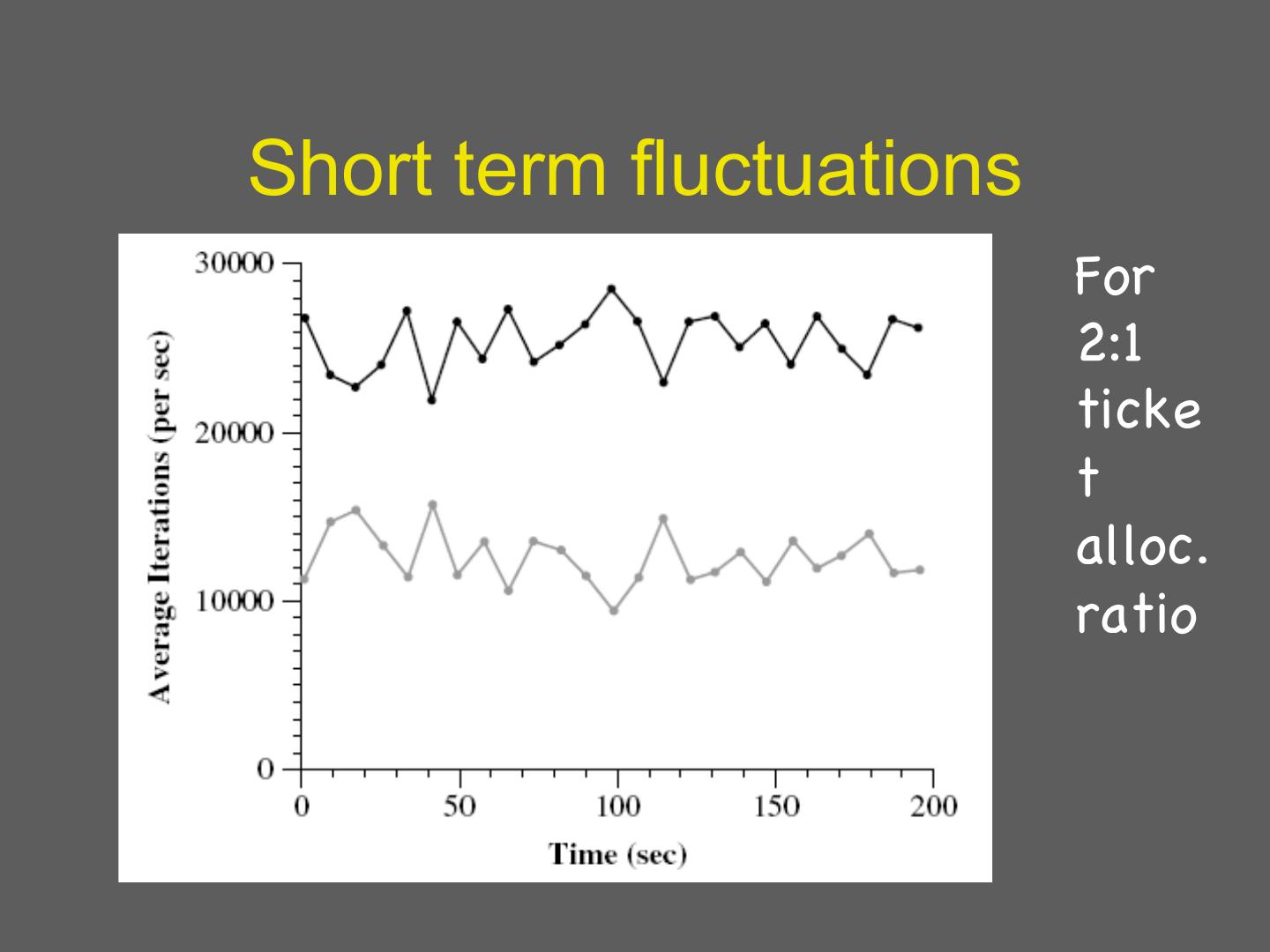
21 .Short term fluctuations For 2:1 ticke t alloc. ratio 

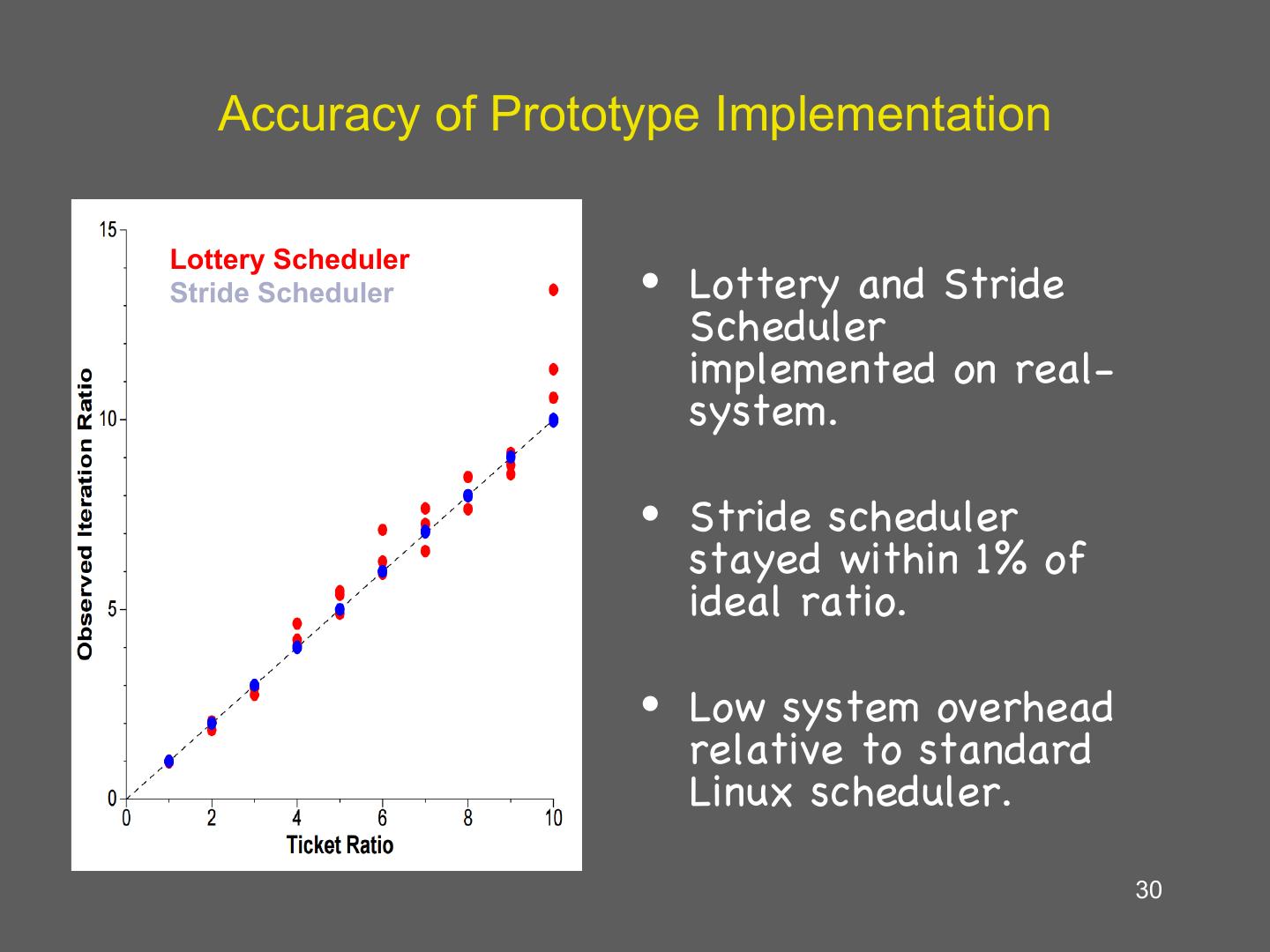
22 . Discussion •  Opinions of the paper and contributions? –  Fairness not great •  Mutex 1.8:1 instead of 2:1 •  Multimedia apps 1.9:1.5:1 instead of 3:2:1 –  Can we exploit the algorithm? •  Consider also indirectly – processes getting kernel cycles by using high priority kernel services –  Real time? Multiprocessor? –  Short term unfairness •  Later this lead to stride scheduling from same authors 22 

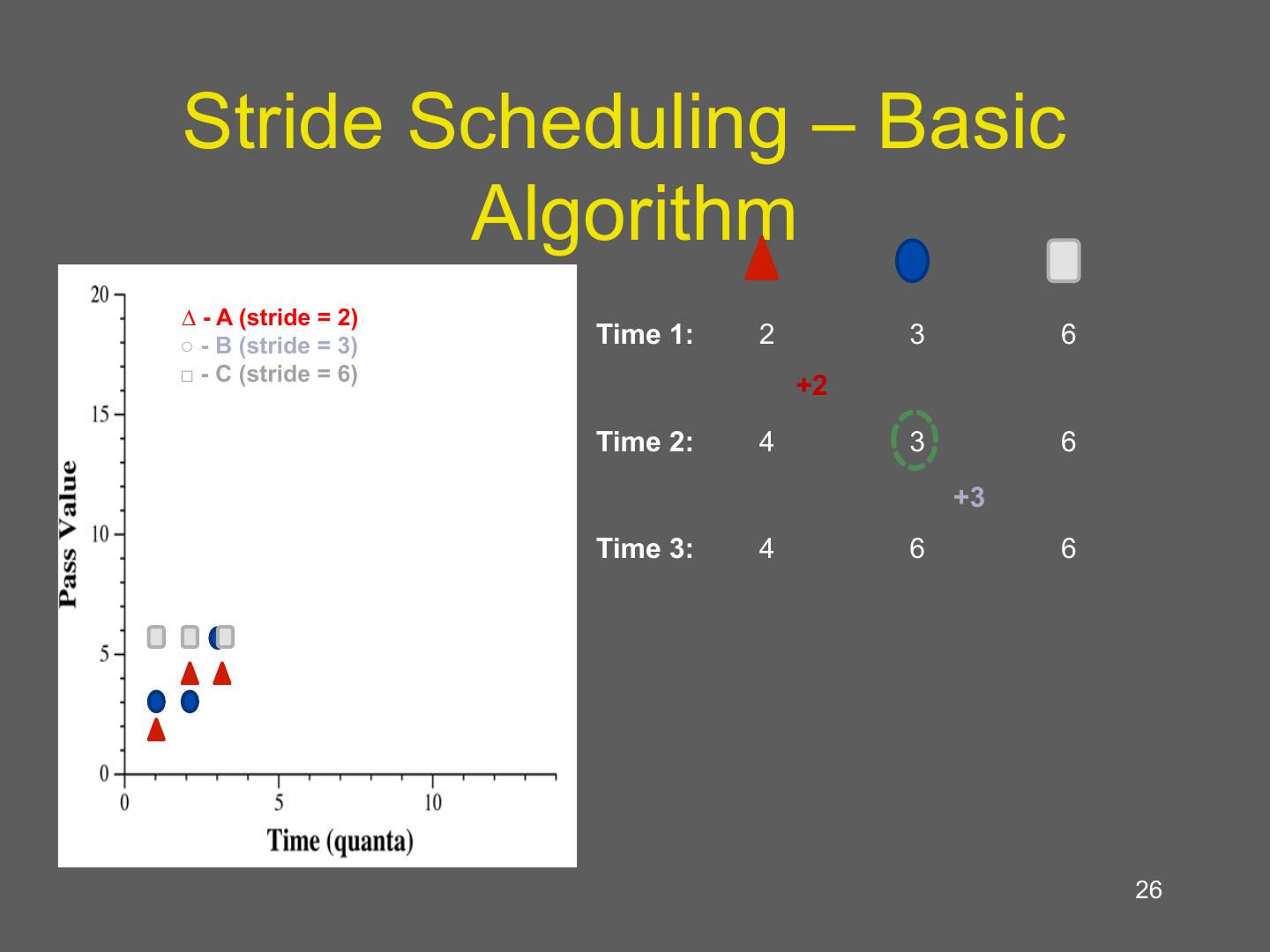
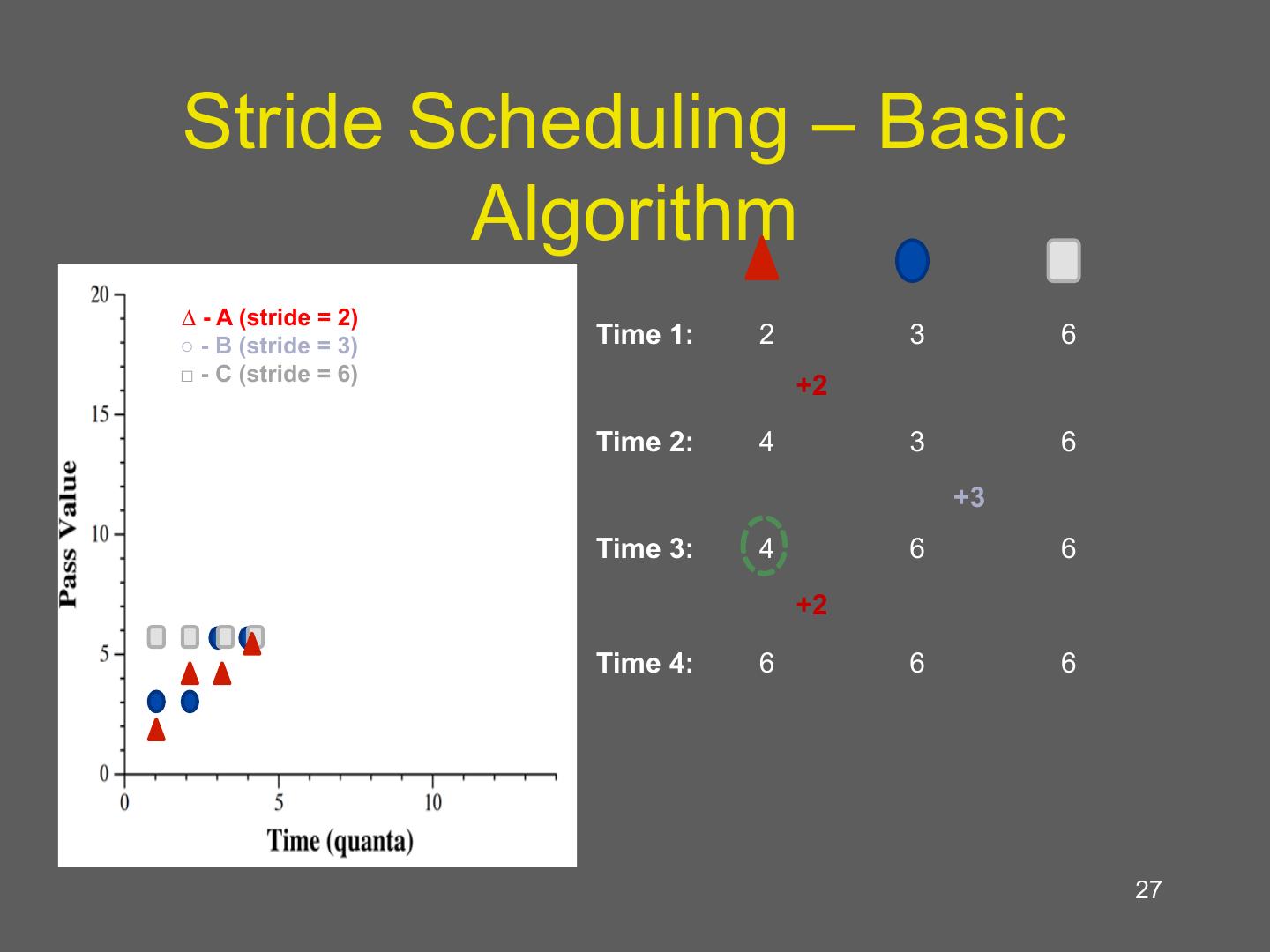
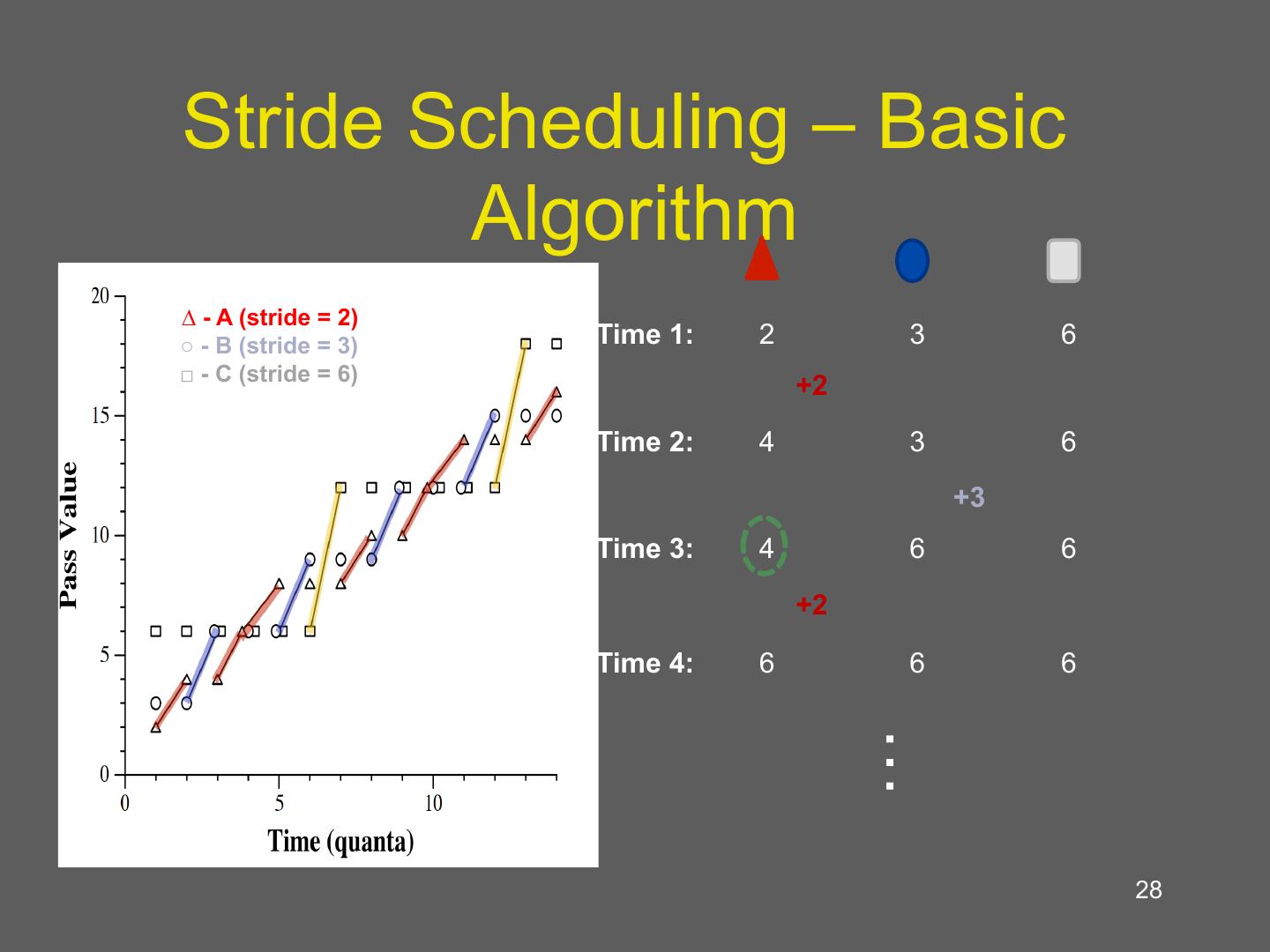
23 . Stride scheduling •  Deterministic version of lottery scheduling •  Mark time virtually (counting passes) –  Each process has a stride: number of passes between being scheduled –  Stride inversely proportional to number of tickets –  Regular, predictable schedule •  Can also use compensation tickets •  Similar to weighted fair queuing –  Linux CFS is similar 23 

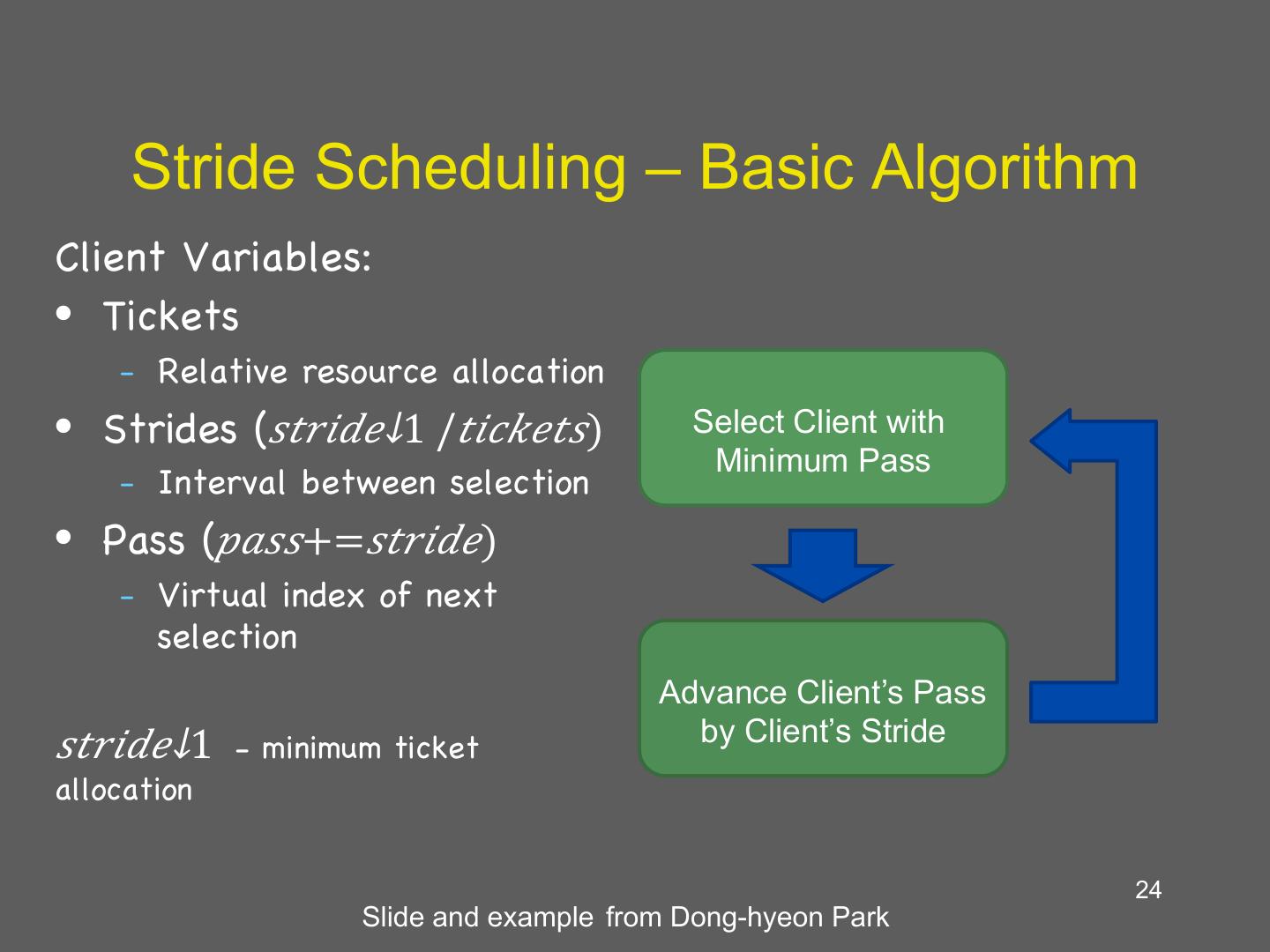
24 . Stride Scheduling – Basic Algorithm Client Variables: •  Tickets –  Relative resource allocation •  Strides (𝑠𝑡𝑟𝑖𝑑​𝑒↓1 /𝑡𝑖𝑐𝑘𝑒𝑡𝑠) Select Client with Minimum Pass –  Interval between selection •  Pass (𝑝𝑎𝑠𝑠+=𝑠𝑡𝑟𝑖𝑑𝑒) –  Virtual index of next selection Advance Client’s Pass 𝑠𝑡𝑟𝑖𝑑​𝑒↓1  - minimum ticket by Client’s Stride allocation 24 Slide and example from Dong-hyeon Park 

25 . Stride Scheduling – Basic Algorithm 3:2:1 Allocation ∆ - A (stride = 2) ○ - B (stride = 3) Time 1: 2 3 6 □ - C (stride = 6) +2 Time 2: 4 3 6 25 

26 . Stride Scheduling – Basic Algorithm 3:2:1 Allocation ∆ - A (stride = 2) ○ - B (stride = 3) Time 1: 2 3 6 □ - C (stride = 6) +2 Time 2: 4 3 6 +3 Time 3: 4 6 6 26 

27 . Stride Scheduling – Basic Algorithm 3:2:1 Allocation ∆ - A (stride = 2) ○ - B (stride = 3) Time 1: 2 3 6 □ - C (stride = 6) +2 Time 2: 4 3 6 +3 Time 3: 4 6 6 +2 Time 4: 6 6 6 27 

28 . Stride Scheduling – Basic Algorithm 3:2:1 Allocation ∆ - A (stride = 2) ○ - B (stride = 3) Time 1: 2 3 6 □ - C (stride = 6) +2 Time 2: 4 3 6 +3 Time 3: 4 6 6 +2 Time 4: 6 6 6 … 28 

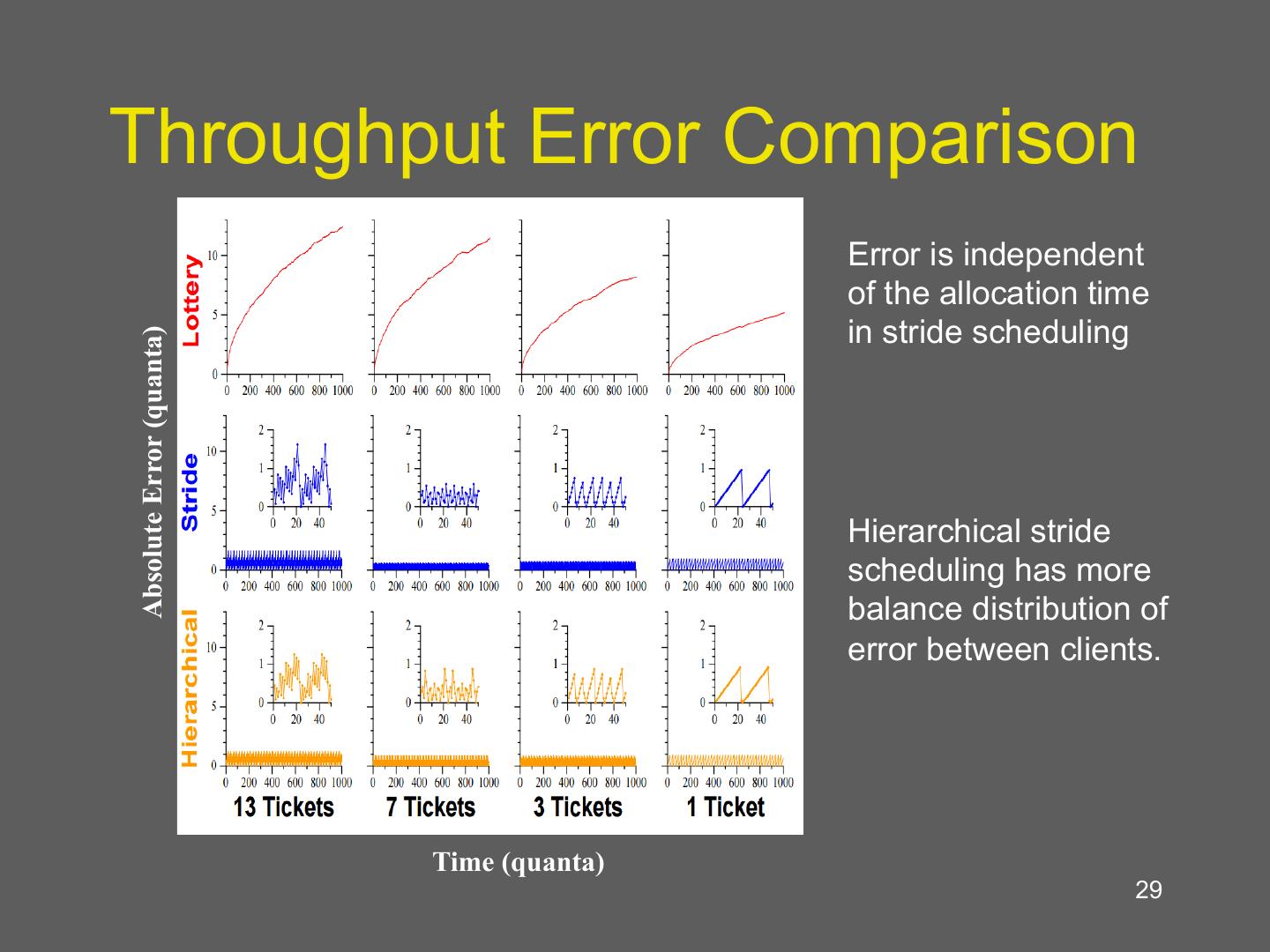
29 .Throughput Error Comparison Error is independent of the allocation time in stride scheduling Absolute Error (quanta) Hierarchical stride scheduling has more balance distribution of error between clients. Time (quanta) 29