编码理论概述

1 . 编码理论 周武旸 wyzhou@ustc.edu.cn 63600485 1 

2 . 课程内容  第一章 绪论  1.1 信道编码的历史及研究现状  1.2 简单编码方式回顾 • 1.2.1 线性分组码 • 1.2.2 循环码  第二章 基础理论  2.1 信道编码定理  2.2 硬判决与软判决  2.3 基本信道模型及其信道容量  2.4 MAP与ML算法  2.5 因子图与和积算法  第三章 BCH码 2 

3 . 课程内容（续）  第四章 卷积码  4.1 卷积码的编码  4.2 卷积码的结构特性  4.3 卷积码的距离特性  4.4 Viterbi译码算法  4.5 SOVA算法  4.6 BCJR算法  第五章 Turbo码  5.1 Turbo码的编码  5.2 Turbo码的迭代译码  5.3 Turbo码的性能界  5.4 交织器设计  5.5 分量码的优化 3 

4 . 课程内容（续）  第六章 编织码  6.1 编织码编码基本原理  6.2 编织码的译码  6.3 编织卷积码的活性距离特性  6.4 基于删余技术的编织码  6.5 编织码的因子图与和积算法分析  第七章 LDPC码  7.1 LDPC码的基本原理  7.2 译码方法  7.3 多进制LDPC码  第八章 Polar码  第九章 优化方法（可选，看进度安排）  8.1 密度进化方法 4  8.2 基于EXIT图的优化方法 

5 . 第一章 序论  编码理论的内容包括三个方面  以保证数字信息传输和处理的可靠性为目的的差错控制编 码（error-control coding），又称为信道编码（channel coding）；  以提高数字信息传输、存储处理的有效性为宗旨的信源编 码（Source coding）；  以增加数字信息传输、存储的安全性为目标的数据加密编 码（data encryption）；  我们主要讨论差错控制编码技术。 5 

6 . 差错控制编码技术是适应数字通信抗噪声干 扰的需要而诞生和发展起来的，它是于1948 年、著名的信息论创始人C. E. Shannon（香 农）在贝尔系统技术杂志发表的“A Mathematical Theory of Communication”一 文，开创了一门新兴学科和理论：信息论和 编码理论。 6 

7 . 1.1 信道编码的历史及研究现状  1948年，Shannon发表的“通信的数学理论”，标志着 信息与编码理论这一学科的创立。该文指出，任何一个通 信信道都有确定的信道容量C，如果通信系统所要求的传 输速率R小于C，则存在一种编码方法，当码长n充分大并 应 用 最 大 似 然 译 码 （ MLD ， Maximum Likelihood Decdoding ） 时 ， 信 息 的 错 误 概 率 可 以 达 到 任 意 小 。 MLD算法的复杂性随n或N的增加呈指数增加，因此当n或 N较大时，MLD在物理上是不可实现的。因此，构造物理 可实现编码方案及寻找有效译码算法一直是信道编码理论 与技术研究的中心任务。  Shannon指出了可以通过差错控制码在信息传输速率不 大于信道容量的前提下实现可靠通信，但却没有给出具体 实现差错控制编码的方法。 7 

8 . 20世纪40年代，R.Hamming提出了第一个实用的差 错控制编码方案。当时他作为一个数学家受雇于贝尔 实验室，主要从事弹性理论的研究。他发现计算机经 常在计算过程中出现错误，而一旦有错误发生，程序 就会停止运行。这个问题促使他编制了使计算机具有 检测错误能力的程序，通过对输入数据编码，使计算 机能够纠正这些错误并继续运行。  Hamming所采用的方法就是将输入数据每4个比特分 为一组，然后通过计算这些信息比特的线性组合来得 到3个校验比特，然后将得到的7个比特送入计算机。 计算机按照一定的原则读取这些码字，通过采用一定 Hamming, 1915-1998 的算法，不仅能够检测到是否有错误发生，同时还可 以找到发生单个比特错误的比特的位置，该码可以纠 正7个比特中所发生的单个比特错误。这个编码方法 就是分组码的基本思想，Hamming提出的编码方案 后来被命名为汉明码。 8 

9 . 虽然汉明码的思想是比较先进的，但是它也存在许多难以接 受的缺点。首先，汉明码的编码效率比较低，它每4个比特 编码就需要3个比特的冗余校验比特。另外，在一个码组中 只能纠正单个的比特错误。  M.Golay研究了汉明码的这些缺点，并提出了两个以他自己 的名字命名的高性能码字：一个是二元Golay码，在这个码 字中Golay将信息比特每12个分为一组，编码生成11个冗余 校验比特，相应的译码算法可以纠正3个错误。另外一个是 三元Golay码，它的操作对象是三元而非二元数字。三元 Golay码将每6个三元符号分为一组，编码生成5个冗余校验 三元符号。这样由11个三元符号组成的三元Golay码码字可 以纠正2个错误。 9 

10 . 汉明码和Golay码都是将q元符号按每k个分为一组．然后通 过编码得到n-k个q元符号作为冗余校验符号，最后组成码长 为n的码字。分组码编码码率为k/n，一般记为(q,n,k,t)码，t 为纠错能力。二元分组码可以简记为(n,k,t)码或者(n,k)码。  Golay码之后最主要的一类分组码就是Reed-Muller码。它是 Muller在1954年提出的，此后Reed在Muller提出的分组码的 基础上得到了一种新的分组码，称为Reed-Muller码，简记 为RM码。在1969年到1977年之间，RM码在火星探测方面 得到了极为广泛的应用。即使在今天，RM码也具有很大的 研究价值，其快速的译码算法非常适合于光纤通信系统。 10 

11 . RM码之后人们又提出了循环码的概念。循环码是分组码的 一种，但它的码字具有循环移位特性，即码字比特经过循环 移位后仍然是码字集合中的码字。这种循环结构大大简化了 编译码结构。循环码的另一个特点就是它可以用一个幂次为 n-k的多项式来表示，这个多项式记为g(D)，称为生成多项 式，其中D为延迟算子。  循环码也 称为循环 冗余校验(CRC，Cyclic Redundancy Check)码，并且可以用Meggitt译码器来实现译码。由于 Meggitt译码器的译码复杂性随着纠错能力t的增加而呈指数 形式的增加，因此通常CRC码用于纠正只有单个错误的应用 情况，常用做检错而非纠错。 11 

12 . 循环码的一个非常重要的子集就是分别由 Hocquenghem 在 1959 年 、 Bose 和 Ray- Chaudhuri研究组在1960年几乎同时提出 的BCH码，BCH码的码字长度为n＝qm-1， 其中m为一个整数。二元BCH码（q=2）的 纠错能力限为t<(2m-1)/2。  1960 年 ， Reed 和 Solomon 将 BCH 码 扩 展 到 非 二 元 （ q>2） 的 情 况 ， 得 到 了 RS （ Reed-Solomon）码 。 1967年，Berlekamp给出了一个非常有效的译码算法后， RS码得到了广泛的应用。此后，RS码在CD播放器、 DVD播放器中得到了很好的应用。 12 

13 . 虽然分组码在理论分析和数学描述方面已经非常成熟，并且 在实际的通信系统中也已经得到了广泛的应用，但分组码固 有的缺陷大大限制了它的进一步发展。首先，由于分组码是 面向数据块的，因此，在译码过程中必须等待整个码字全部 接收到之后才能开始进行译码。在数据块长度较大时，引入 的系统延时是非常大的。分组码的第二个缺陷是它要求精确 的帧同步，即需要对接收码字或帧的起始符号时间和相位精 确同步。另外，大多数基于代数的分组码的译码算法都是硬 判决算法，而不是对解调器输出未量化信息的软译码，从而 造成了一定程度的增益损失。 13 

14 . 卷积码改善了分组码存在的缺点，卷积码是Elias 在1955年提出的。卷积码与分组码的不同在于： 它充分利用了各个信息块之间的相关性。通常卷 积码记为(n，k，N)码。卷积码的编码过程是连续 进行的，依次连续将每k个信息元输入编码器，得 到n个码元，得到的码元中的检验元不仅与本码的 信息元有关，还与以前时刻输入到编码器的信息 元有关。同样，在卷积码的译码过程中，不仅要 从本码中提取译码信息，还要充分利用以前和以 Elias, 1923-2001 后时刻收到的码组．从这些码组中提取译码相关 信息，而且译码也是连续进行的，这样可以保证 卷积码的译码延时相对比较小。 14 

15 . 卷积码的译码通常有如下几个比较流行的译码算 法：  由Wozencraft和Reiffen在1961年提出，Fano 和Jelinek分别在1963年和1969年进行改进了 的序贯译码算法。该算法是基于码字树图结构 的一种次优概率译码算法。  由Massey在1963年提出的门限译码算法。这 个算法利用码字的代数结构进行代数译码。  由Viterbi在1967年提出的Viterbi算法。该算法 是基于码字格图结构的一种最大似然译码算法， 是一种最优译码算法。 Viterbi, CDMA之父  在Viterbi译码算法提出之后，卷积码在通信系统 中得到了极为广泛的应用。如GSM、3G、商业卫 星通信系统等。 15 

16 . 在信道编码定理的指引下，人们一直致力 于寻找能满足现代通信业务要求、结构简 单、性能优越的好码，并在分组码、卷积 码等基本编码方法和最大似然译码算法的 基础上提出了许多构造好码及简化译码复 杂性的方法，提出了乘积码、代数几何码、 低 密 度 校 验 码 (LDPC ， Low Density Parity Check)、分组-卷积级联码等编码 方法和逐组最佳译码、软判决译码等译码 Gallager 方法以及编码与调制相结合的网格编码调 制(TCM，Trellis Coded Modulation)技 术。其中对纠错码发展贡献比较大的有级 联码、软判决译码和TCM技术等。 16 

17 . 虽然软判决译码、级联码和编码调制技术都对信 道码的设计和发展产生了重大影响，但是其增益 与Shannon理论极限始终都存在2～3dB的差距。  在 1993 年 于 瑞 士 日 内 瓦 召 开 的 国 际 通 信 会 议 (ICC‘93)上，法国不列颠通信大学教授C.Berrou 提出了Turbo码，由于它很好地应用了Shannon 信道编码定理中的随机性编、译码条件，从而获 得了几乎接近Shannon理论极限的译码性能。仿 真结果表明，在采用长度为65536的随机交织器并 译码迭代18次情况下，在信噪比Eb/N0>=0.7dB并 采用二元相移键控(BPSK)调制时，码率为1/2的 Turbo码在AWGN信道上的误比特率(BER)<=10-5， Berrou and Forney 达到了与Shannon极限仅相差0.7dB的优异性能。 (1/2码率的Shannon极限是0dB)。 17 

18 . 1997年，Host、Johannesson、Ablov提出了编织卷级码 （Woven Convolutional Code,WCC）的概念，随后编织 码（Woven code）便发展起来了。它是一种组合码，其系 统结构可完全包容传统分组码、卷级码以及各类Turbo码， 开创了编码领域的一个新天地。  编织码的结构综合了并行级联卷级码（Turbo码）和串行级 联卷级码的结构特点，当外编码器个数足够多时，该码型完 全拥有了Shannon编码定理中随机长码的特性，因此，其 纠错性能理论上比Turbo码要优异。  但编织码的编码结构复杂性较高，编码效率也不高，目前研 究最多的是1/3的编织卷级码，译码采用BCJR算法的迭代 译码。 18 

19 . 2007年，土耳其毕尔肯大学Erdal Arikan教授提出了极化码（Polar code ），从理论上第一次严格证明了在BSC 信道下，极化码可以“达到”香农容量 ，且编译码复杂度低。从某种意义上说 ，极化码“理论上”解决了近60年来信 息论和编码领域一直想要解决的问题。 Arikan教授（右）  Polar码的理论基础就是信道极化。信道极化包括信道组合和信道分解部分。当组 合信道的数目趋于无穷大时，则会出现极化现象：一部分信道将趋于无噪信道， 另外一部分则趋于全噪信道，这种现象就是信道极化现象。无噪信道的传输速率 将会达到信道容量 I (W )，而全噪信道的传输速率趋于零。  但极化码实际性能刚出现时不理想（“理论上”是指当码长趋向于无穷时的性能 ；“实际”是指有限长度码长），近年来，极化码实际构造方法和列表连续消去 译码算法（ Successive Cancellation List Decoding）等技术的提出，极化码 的整体性能在某些应用场景中取得了和当前最先进的信道编码技术Turbo码和 LDPC码相同或更优的性能。 19 

20 . 2016年11月18日，在3GPP RAN1 87次会议 中，华为倡导的Polar码成为5G eMBB场景控 制信道编码方案，高通倡导的LDPC码为数据 信道编码方案。  注：ITU-R（国际电信联盟无线电通信局）确定未来的5G具 有以下三大主要的应用场景：（1）增强型移动宽带（eMBB ），如3D/超高清视频等大流量移动宽带业务；（2）超高可 靠与低延迟的通信（URLLC），如无人驾驶、工业自动化等 需要低时延、高可靠连接的业务；（3）大规模机器类通信 （eMTC），如大规模物联网业务。 20 

21 . 发展概括  1948年，Shannon发表开创性文章“通信的数学理论”；  1950年，Hamming发明了汉明码；  1955年，Elias引入了卷级码；  1957年，Prange提出了循环码；  1960年，Bose/Chaudhuri/ Hocquenghem发明了BCH码；Reed和Solomon提 出了RS码；  1962年，Gallager提出了LDPC码；  1967年，Berlekamp引入了BCH/RS码的快速译码算法；  1968年，Gallager著书《Information theory and reliable communication》；  1971年，Viterbi引入卷级码的最大似然译码；  1972年，BCJR算法的提出；  1981年，Tanner提出了用于理解信道编码理论的Tanner图；  1982年，Ungerboeck引入编码调制；  1993年，Berrou/Glaveieux/Thitimajshima提出了Turbo码；  1995年，MacKay重新发现了LDPC码；  1997年， Host/Johannesson/Ablov提出了编织卷级码。  2000年，Aji与McEliece总结了应用消息传递思想进行译码的码型；  2003年，Koetter与Vardy提出了RS码的代数软判决译码； 21  2007年， Arikan教授提出了极化码； 

22 . 高效纠错编码的研究现状  20世纪90年代以后，以迭代译码为基础的高效纠错码成为主要研 究对象，不再将精力放在以代数为基础的代数码上，而是寻找新的 纠错码的认识方式，其中有以Tanner图为基础发展起来的编译码 的可视化方法，如因子图，以及基于图中双边上信息传递的和积算 法，还有用于评估码字性能限的数值化方法－－密度进化、典型集 合界理论等。  由于最大似然译码性能最好，但复杂度随码长指数增加（物理上不 可实现），因此必须研究新的编译码方案，期望在性能和复杂度之 间取得平衡。LDPC和Polar是当前的研究热点。  总之，为实现高效纠错，不是采用级联方式构造随机长码，就是采 用迭代译码，或两者均采用，以逼近Shannon限。 22 

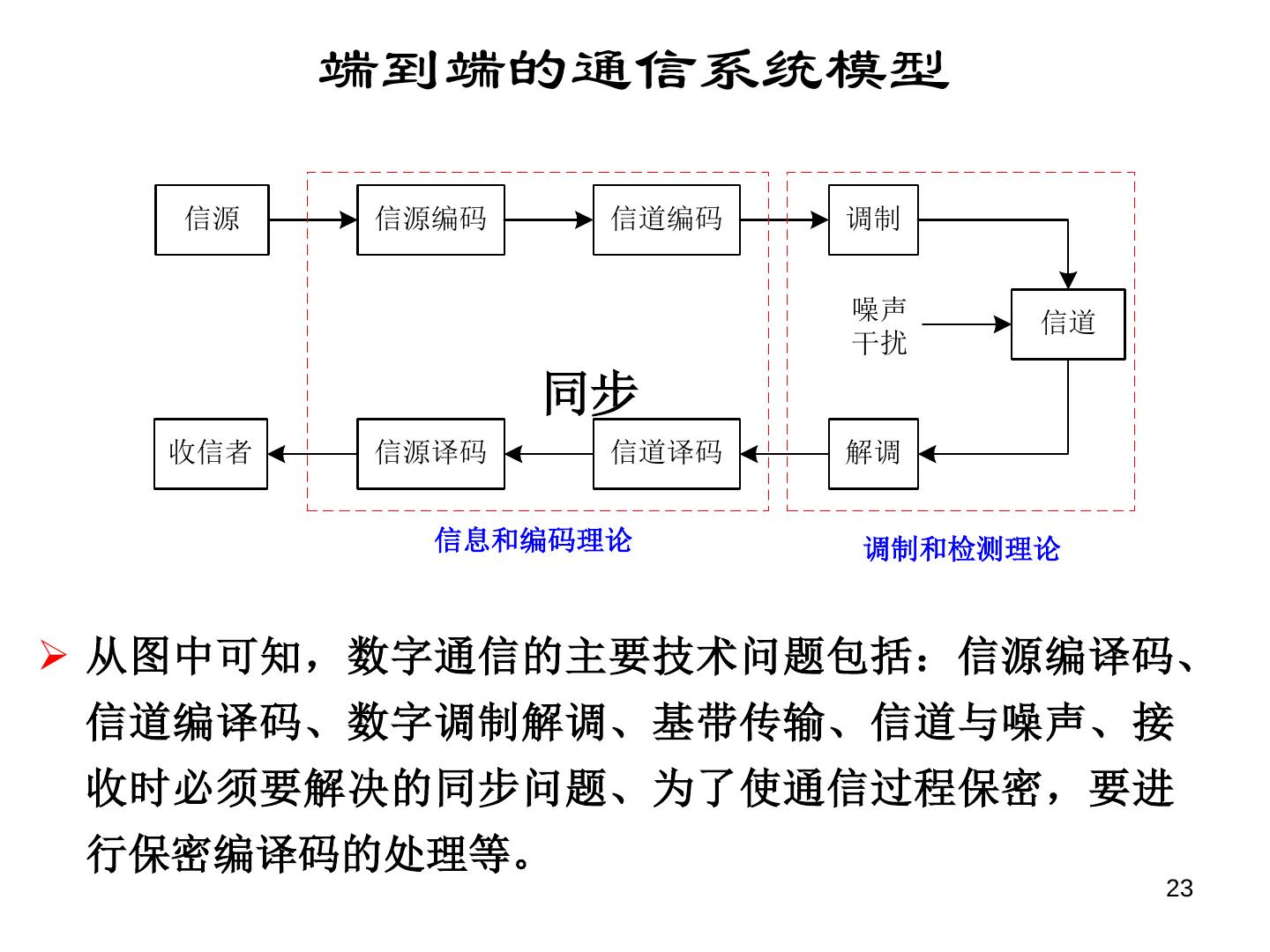
23 . 端到端的通信系统模型 信源 信源编码 信道编码 调制 噪声 信道 干扰 同步 收信者 信源译码 信道译码 解调 信息和编码理论 调制和检测理论  从图中可知，数字通信的主要技术问题包括：信源编译码、 信道编译码、数字调制解调、基带传输、信道与噪声、接 收时必须要解决的同步问题、为了使通信过程保密，要进 行保密编译码的处理等。 23 

24 . 无线信道 比有线信道要恶劣的多！ 

25 . 1.2 简单的编码方式回顾  在设计数字通信系统时，首先应从合理地选择调制解调方法 、合适的发射功率等方面考虑，若仍不能满足系统误码率要 求，则要考虑采用本章所讲的差错控制编码措施。  纠错码，是当消息经过有噪信道传输或要恢复存储的数据时 用来纠错的。用来传输消息的物理介质叫做信道（如电话线 、卫星连接、用于移动通信的无线信道等）。因为纠错码试 图克服信道中噪声造成的损害，因此其编码过程又称为信道 编码，它是提高数字信号传输可靠性的有效方法之一。 25 

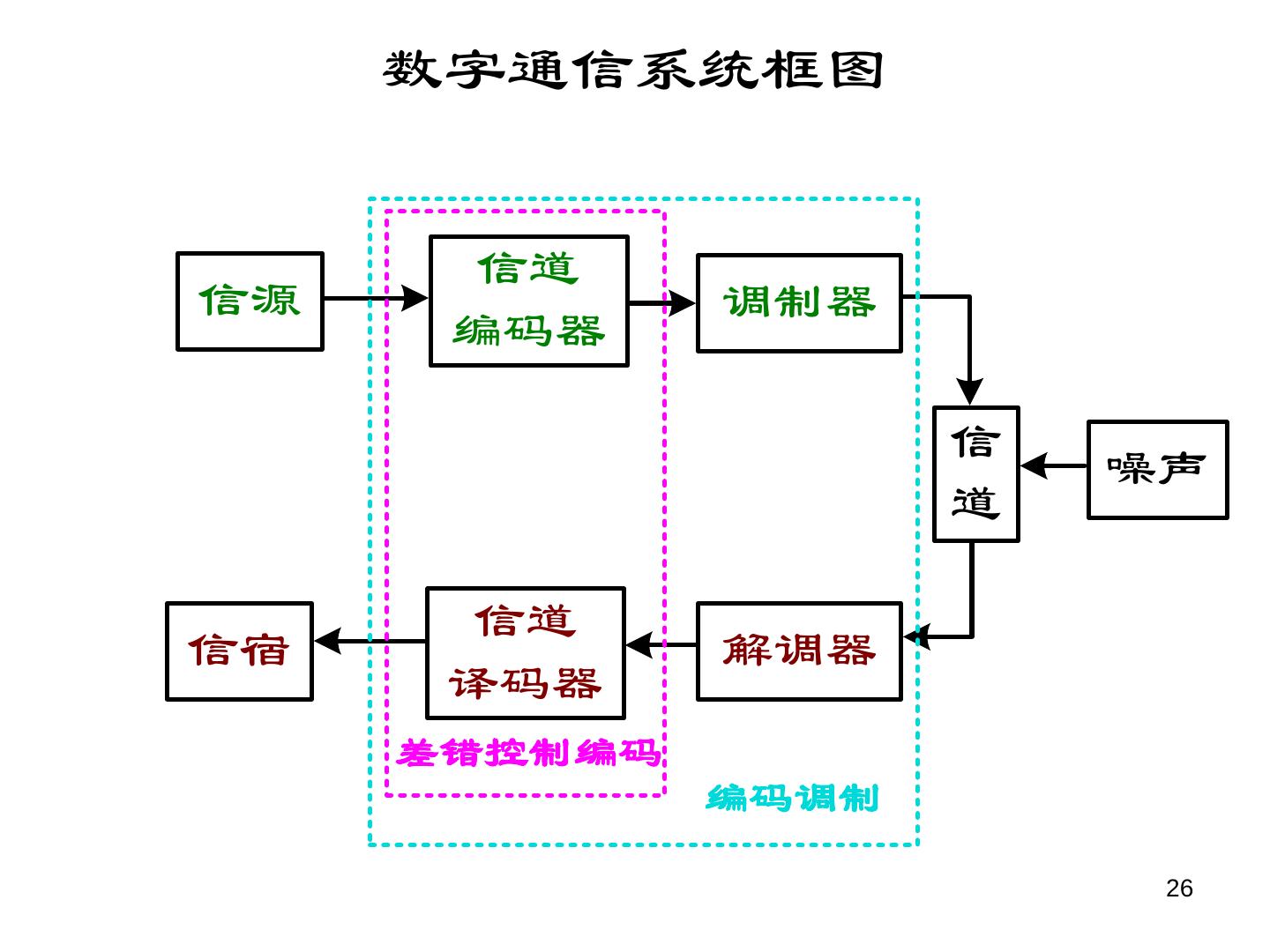
26 . 数字通信系统框图 信道 信源 调制器 编码器 信 噪声 道 信道 信宿 解调器 译码器 差错控制编码 编码调制 26 

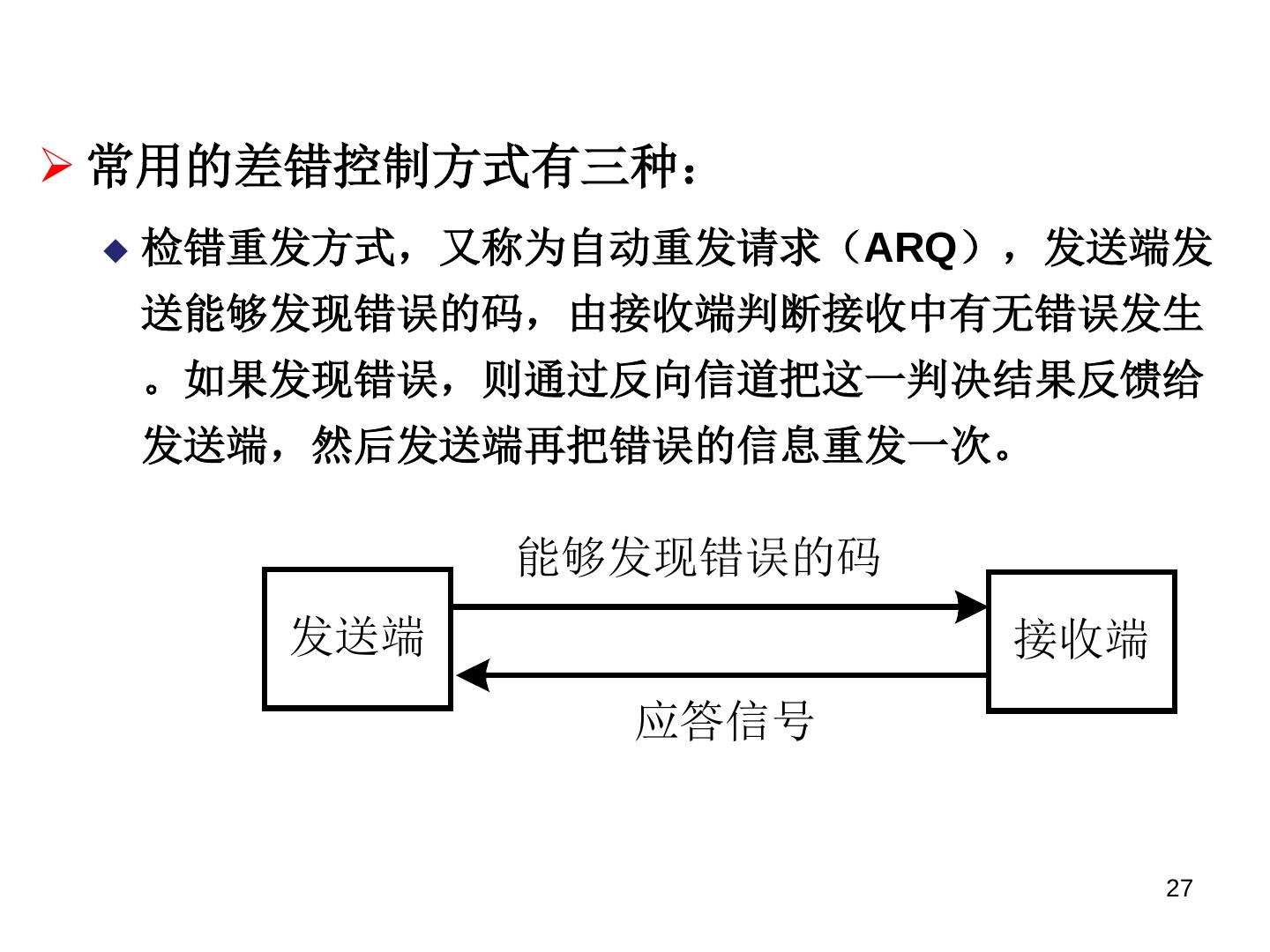
27 . 常用的差错控制方式有三种：  检错重发方式，又称为自动重发请求（ARQ），发送端发 送能够发现错误的码，由接收端判断接收中有无错误发生 。如果发现错误，则通过反向信道把这一判决结果反馈给 发送端，然后发送端再把错误的信息重发一次。 能够发现错误的码 发送端 接收端 应答信号 27 

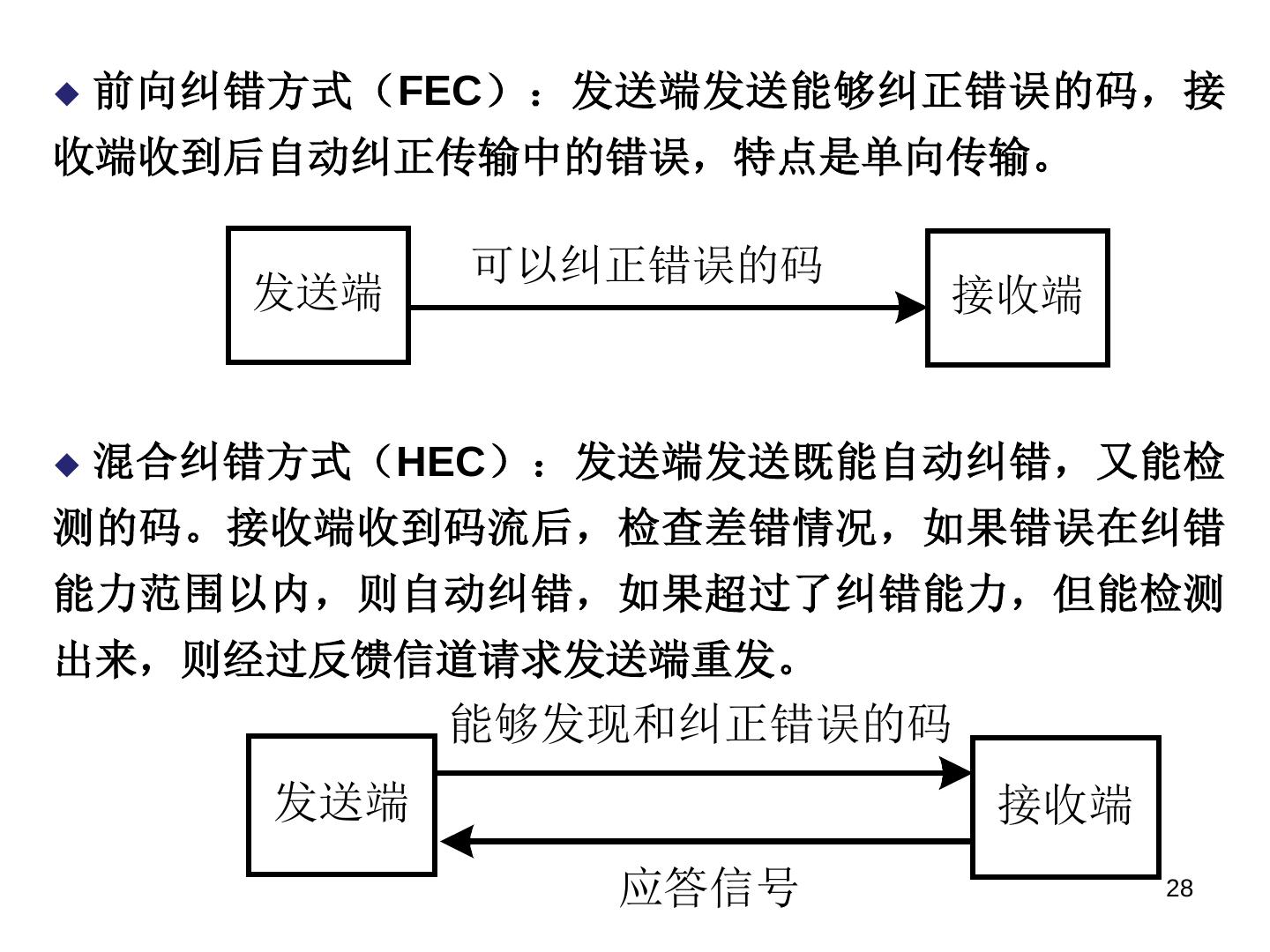
28 . 前向纠错方式（FEC）：发送端发送能够纠正错误的码，接 收端收到后自动纠正传输中的错误，特点是单向传输。 可以纠正错误的码 发送端 接收端  混合纠错方式（HEC）：发送端发送既能自动纠错，又能检 测的码。接收端收到码流后，检查差错情况，如果错误在纠错 能力范围以内，则自动纠错，如果超过了纠错能力，但能检测 出来，则经过反馈信道请求发送端重发。 能够发现和纠正错误的码 发送端 接收端 应答信号 28 

29 . 差错控制编码的基本原理  在信息码元序列中附加一些监督码元，在两者之间 建立某种校验关系，当这种校验关系因传输错误而 受到破坏时，可以被发现和纠正。不同的编码方法 ，有不同的检错和纠错能力。一般来说，付出的代 价越大，检（纠）错的能力就越强。这里所说的代 价，指增加的监督码元的多少。例如，若编码序列 中，平均每两个信息码元就有一个监督码元，则这 种编码的多余度为1/3，或者说，这种编码的编码速 率为2/3，可见，差错控制编码是以降低信息传输速 率来换取信息传递的可靠性提高。 29