有噪信道编码定理

1 .信息论与编码技术 第 6 章 有噪信道编码定理 苗付友 mfy@ustc.edu.cn 2017 年 11 月

2 .在有噪信道中， 怎么能使消息 通过传输后发生的错误最少？ 在有噪信道中，无错误传输的可达的最大信息传输率是多少？

3 .6.1 错误概率和译码规则 6.2 错误概率与编码方法 6.3 联合 𝜀 典型序列 6.4 有噪信道编码定理 6.5 联合信源信道编码定理 主要内容

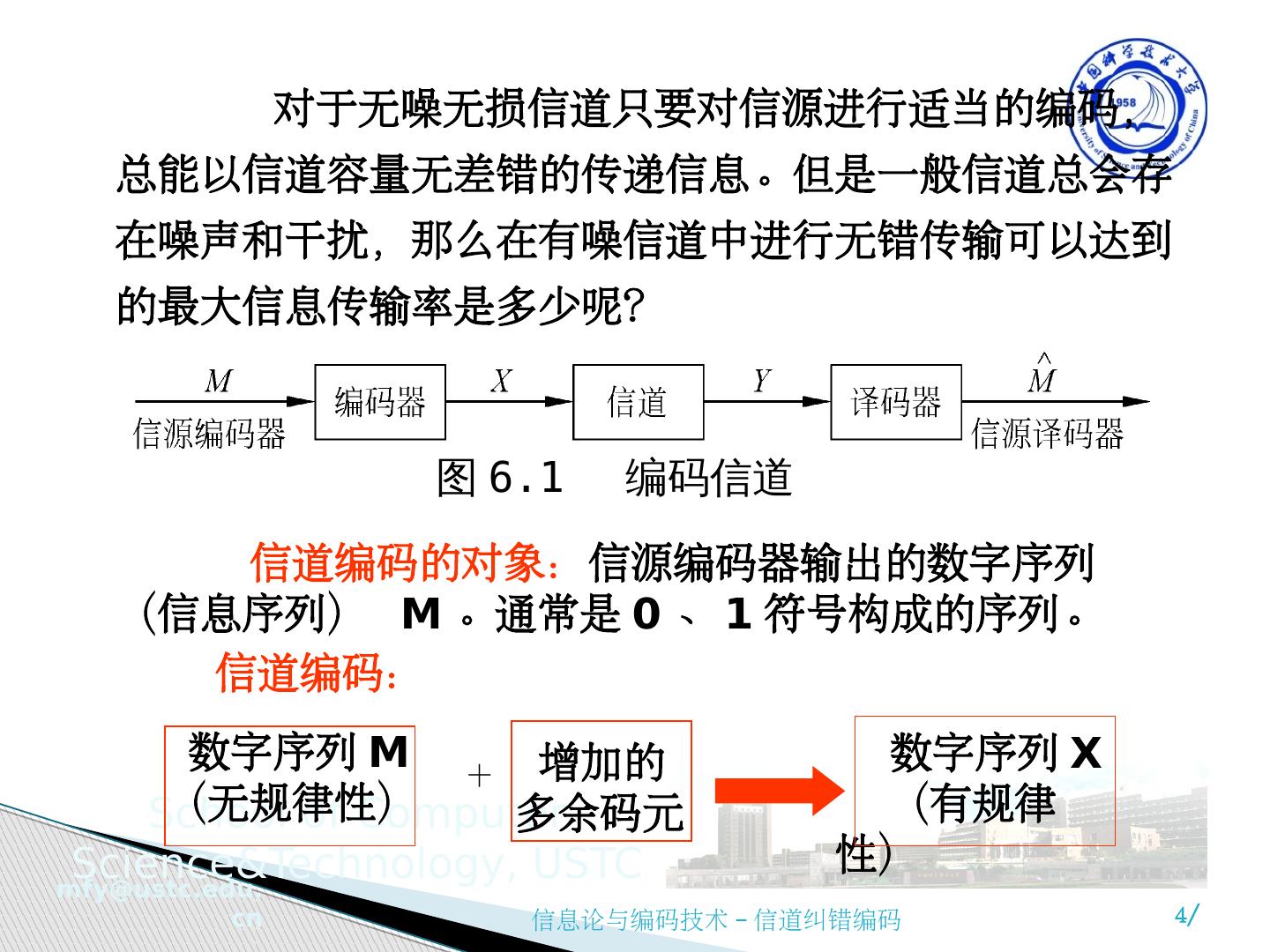
4 .图 6.1 编码信道 信道编码的对象： 信源编码器输出的数字序列（信息序列） M 。通常是 0 、 1 符号构成的序列。 信道编码： 数字序列 M （无规律性） 增加的 多余码元 数字序列 X （有规律性） ＋ 对于无噪无损信道只要对信源进行适当的编码，总能以信道容量无差错的传递信息。但是一般信道总会存在噪声和干扰，那么在有噪信道中进行无错传输可以达到的最大信息传输率是多少呢？

5 .6.1 错误概率和译码规则 为了减少错误，提高通信的可靠性，就必须分析 错误概率 与哪些因素有关，有没有办法控制，能控制到什么程度。 在有噪信道中传输消息是会发生错误的。错误概率与信道统计特性有关。信道的统计特性可由信道的转移矩阵来描述。 0 1 0 1 1/3 1/3 2/3 2/3 例：有一个 BSC 信道，如图所示 若收到 “ 0 ” 译作 “ 0 ” ，收到 “ 1 ” 译作 “ 1 ” ，则平均错误概率为：

6 .6.1 错误概率和译码规则 反之，若收到“ 0” 译作“ 1” ，收到“ 1” 译作“ 0” ，则平均错误 概率 为 1/3 ，可见错误概率与 译码准则 有关。 可见，错误概率既与 信道的统计特性 有关，又与 译码 规则 有关。 译码规则 设离散单符号信道的输入符号集为 输出符号集 。 若 对每一个输出符号 都有一个确定的数 使 对应于惟一的一个输入符号 ，则这样的函数称为译码规则，记为

7 .6.1 错误概率和译码规则 例 6.1 （ p200 ） 可以设计译码准则： 译码规则的选择应该有一个依据，一个自然的依据就是使平均错误概率最小。 有了译码规则以后，收到 的情况下，译码的条件正

8 .6.1 错误概率和译码规则 确概率为： 而错误译码的概率为收到 后，推测发出除了 之外其它符号的概率： 可以得到平均错误译码概率为： 它表示经过译码后平均接收到一个符号所产生错误的大小，也称 平均错误概率 。 如何设计译码规则 最小 ？

9 .6.1 错误概率和译码规则 由前边的讨论可以看出，为使 最小，就应选择 为最大，即选择译码函数 并使之满足条件： 也就是说，收到一个符号以后译成具有最大后验概率的那个输入符号。这种译码准则称为 “ 最大后验概率准则 ” 或 “ 最小错误概率准则 ” 。 根据贝叶斯定律，上式也可以写成

10 .6.1 错误概率和译码规则 即： 当 信源等概分布 时，上式为： 这称为最大似然译码准则，方法是收到一个 后，在信道矩阵的第 j 列，选择最大的值所对应的输入符号作为译码输出。 可进一步写出平均错误概率：

11 .6.1 错误概率和译码规则 也可写成： 上式也可写成对行求和： 如果先验概率相等，则： 例 6.2 （ p201 ）

12 .6.1 错误概率和译码规则 根据最大似然准则可选择译码函数为 B ： 若采用前边讲到的译码函数 A ，则平均错误率为： 若输入不等概分布，其概率分布为：

13 .6.1 错误概率和译码规则 若采用最小错误概率译码准则，则联合矩阵为： 所得译码函数为 C ： 平均错误率为：

14 .6.1 错误概率和译码规则 平均错误概率 与译码规则有关，而译码规则又由信道特性决定。于是，平均错误概率 与信道疑义度 是有一定关系的，满足 费诺不等式 证明： 条件熵

15 .6.1 错误概率和译码规则 故有 应用不等式 得 移项证得费诺不等式

16 .6.1 错误概率和译码规则 图 6.2 费诺不等式的曲线图 接收到 Y 后关于 X 的平均不确定性分为两部分：①是否产生 错误的不确定性 ； ②输入符号发送而造成的最大不确定性 。 函数 随 变化曲线为

17 .6.2 错误概率与编码方法 一般信道传输时都会产生错误，而选择译码准则并不会消除错误，那么如何减少错误概率呢？下边讨论通过优选信道编码方法来降低错误概率。 例：对于如下二元对称信道 （输入等概率） 图 6.3 二元对称信道

18 .6.2 错误概率与编码方法 如何提高信道传输的正确率呢？可以尝试用下面的方法 没有使用的码字 001 010 011 100 101 110 用作消息的码字 α 1 = 000 α 2 = 111 输出端接收序列 000= 𝛽 1 001 = 𝛽 2 010 = 𝛽 3 011 = 𝛽 4 100 = 𝛽 5 101 = 𝛽 6 110 = 𝛽 7 111 = 𝛽 8 二元对称信道的三次扩展信道 图 6.4 简单的重复编码

19 .6.2 错误概率与编码方法 根据最大似然译码准则，可得译码函数为： F(000)=000 F(001)=000 F(010)=000 F(011)=111 F(100)=000 F(101)=111 F(110)=111 F(111)=111 此时，译码可以采用 “ 择多译码 ” ，即根据接收序列中 0 多还是 1 多， 0 多就判作 0 ， 1 多就判作 1 。错误概率降低了两个数量级，这种编码可以纠正码字中的一位码元出错。若重复多次可进一步降低错误率。 信道矩阵 000 001 010 011 100 101 110 111 111 000

20 .6.2 错误概率与编码方法 当 n 很大时，使 很小是可能的。但是又出现了一个新的问题， n 很大时，信息传输率会降低很多。 在上例中 ：消息数 M =2 当 n=1 时 R=1 ；当 n=3 时 R=1/3 ；当 n=5 时 R=1/5...... 结论 ： 利用简单重复编码来减少平均错误概率是以降低信息传输率 R 作为代价的 , 即 “ 牺牲有效性，换取可靠性 ” 。 =

21 .6.2 错误概率与编码方法 分析上边的例子 ：我们只用了扩展信源的两个字符，因此信息率降低了，如果我们把 8 个字符全用上，信息传输率就会回到 1 。但是只有每个符号都正确传输时，才不会发生错误，正确率： (1-p) 3 . 所以此时 错误率 为 1- (1-p) 3 = 比 单符号时还大三倍。我们可以总结如下： 在二元信道的 n 次扩展信道中，选取其中的 M 个作为消息， 则 M 大一些， 跟着大， R 也大， M 小一些， 跟着 小， R 也小。 如果在上例中，取 M ＝ 4 （ 000 011 101 110 ），其他的不用，则 , 与 M=8 比较，错误率 这显然是一个矛盾，有没有解决的办法呢？香农第二定理可以解决这一问题。

22 . 还存在另外一个问题， M=4 时，有 70 种选取方法，而选取方法不同，错误率也不同。我们比较下面两种选取方法：第一种： 000 011 101 110 第二种： 000 001 010 100 按 最大似然准则 ， 第一种方法的错误率为 第二 种方法的错误率为 第一种方法好：如果 000 有一位出错，我们就可以判定出错了；而在第二种方法中，如果 000 中任何一位出错，就变成了其他的合法的码字，无法判断是否出错。仔细观察发现第二种方法中，码字之间太 “ 象 ” 了，或者说太 “ 近 ” 了。 降低了，而信息率也降低了。

23 . 我们再讨论一个例子，取 M ＝ 4 ， n ＝ 5 ，这 4 个码字按如下规则选取： 设输入序列为 : 满足方程： 若译码采取最大似然准则：

24 .优点：①能纠一位或二位码元的错误 ② 增大 n 和 M 的同时，既能降低错误译码概率，又能使传输率不减少。 我们引进这样一个概念： 汉明距离 。

25 .如： 则 在某一 码 C 中 ，任意两个码字的汉明距离的最小值称为 该码 C 的最小距离 。 我们来讨论前边的 5 种码的距离： 设 为两个长度为 n 的二元序列（码字），则 和 之间的 汉明距离 定义为

26 . 码 A 码 B 码 C 码 D 码字 000 111 000 011 101 110 000 001 010 100 000 001 010 011 100 101 110 111 消息数 M 2 4 4 8 最小距离 d min 3 2 1 1 信息传输率 R 1/3 2/3 2/3 1 错误概率 很明显， 越大， 越小，在 M 相同的情况下也是一样。

27 . 在二元对称信道的情况下，译码规则可以如下： 选择 使之满足 它称为 最小距离译码准则 ，它等价于 最大似然译码准则 （ 在二 元 对称信道情况下 ）， 也就是收到一个码字后，把它译成与它最近的输入码字，这样可以使平均错误率最小。 编码选择方法 ： 应尽量设法使选取的 M 个码字中任意两个不同码字的距离尽量大。 于是，最大似然译码规则可用汉明距离表示为：当接收到码字 后，在输入码字集 C 中寻找一个 使之与 的汉明距离为最短。

28 .定义 （ 联合 𝜀 典型序列 ） n 长的序列对（ x ， y ）满足： （ 1 ） x 是 𝜀 典型序列，即对于任意小的整数 𝜀存在 n 使 (2) y 是 𝜀 典型序列，即对于任意小的整数 𝜀存在 n 使 (3) 对于任一下小的正数 𝜀 ，存在 n 使 则成序列对 （ x ， y ） 为 联合 𝜀 典型序列 6.3 联合 𝜀 典型序列

29 .G 𝜀 n (X): 表示 X n 中 x 的典型序列集 G 𝜀 n (Y): 表示 Y n 中 y 的典型序列集 G 𝜀 n (XY): 表示 X n Y n 联合空间中 xy 的典型序列集 , 即： 联合𝜀典型序列指 平均联合自信息以 𝜀 任意小地接近联合熵的 n 长序列对的集合。 6.3 联合 𝜀 典型序列