无失真信源编码定理

1 .信息论与编码技术 第 4 章 无失真信源编码定理 苗付友 mfy@ustc.edu.cn 2016 年 9 月

2 .本章介绍对离散信源进行无失真信源编码的要求、方法及理论极限，并引出香农第一定理。进一步加深对熵的物理意义的理解

3 .信源编码 码符号集 ： X = ｛ x 1 ， x 2 … x q ｝ 信源符号集： S = ｛ s 1 ,…, s q ｝ 码字集： C = ｛ W 1 ,…, W q ｝ 信道编码 信道译码 信源译码 信源 信宿 信 道 干扰

4 .5.1 编码器 5.2 几个概念 5.3 等长码 5.4 渐进等分割性和 𝜀 典型序列 5.5 等长信源编码定理 5.6 变长码 5.7 变长信源编码定理 主要内容

5 .编码的实质 是对信源的原始符号按一定的数学规则进行的一种变换， 以码字代替原始信源符号，使变换后得到的码符号接近等概率分布，从而提高信息的传输有效性 5.1 编码器 编码器 码源符号集 ： X = ｛ x 1 ， x 2 … x q ｝ 信源符号集： S = ｛ s 1 …s q ｝ 码字集： C = ｛ W 1 … W q ｝ 信源 信宿

6 .5.1 编码器 信源编码：从信源符号到码符号的一种映射。 信源编码器 ： 编码器 X = ｛ x 1 ， x 2 … x q ｝ S = ｛ s 1 …s q ｝ C = ｛ W 1 … W q ｝ 定义： 信源编码器的输入信源符号集 , 是输入消息单元也可以是未编码的信号单元 . S 的元素 s i ， i=1 ， 2 … q 叫做信号单元或消息（共有 q 个信源符号）。 编码器输出的码 ,W 的元素 W i ,i =1,2,…q 叫做码字。 构成码字的符号集 , 其元素 x i 一般是适合信道传输的 , 称为码元 . 信源 信宿

7 .5.1 编码器 编码器 X = ｛ x 1 ， x 2 … x q ｝ S = ｛ s 1 …s q ｝ C = ｛ W 1 … W q ｝ 将信源符号集中的符号 s j ， i =1 ， 2…q （或者长为 N 的信源符号序列）变换成由基本符号 x j ,j =1,2…r 组成的长度为 L i 的一一对应的输出符号序列 , 即 C = ｛ W 1 ,W 2 ， … ， W q ｝， W i 称为码字， l i 称为码字长度或简称码长 , 所有这些码字的集合 C 称为码 . 可见编码就是从信源符号到码符号的一种映射 , 若要实现无失真编码 , 这种映射必须是一一对应的 , 可逆的。 信源 信宿

8 .5.1 编码器 例：二元信道基本符号集为 {0,1}, 将信源符号 s 变换成由 0 和 1 符号组成的码符号序列 ( 码元 ), 即编码。 编码器 X= ｛ x 1 =0 ， x 2 =1 ｝ S= ｛ s 1 …s q ｝ C= ｛ W 1 … W q ｝

9 .5.1 编码器 例：下表为信源编码所使用的码表，信源输出序列的长度为 L=1 ，信源共有 4 个符号，对应的概率空间为 信源符号 s i 信源符号出现概率 p ( s i ) 码表 码 1 码 2 s 1 p ( s 1 ) 00 1 s 2 p ( s 2 ) 01 10 s 3 p ( s 3 ) 10 101 s 4 p ( s 4 ) 11 111

10 .5.1 编码器 以码 1 为例，将信源输出的符号按照固定的规则进行变换，即信源编码器输出共有 4 个码字，分别为 00 ， 01 ， 10 和 11 ，码字的长度都为 2 ，即 l i =2 ，（ i =1 ， 2 ， 3 ， 4 ）每个码字都是由取值于码符号集合 {0 ， 1} 的两位二元码组成。也就是说，该码表将信源输出的每个符号映射成二元码。 信源符号 s i 信源符号出现概率 p ( s i ) 码表 码 1 码 2 s 1 p ( s 1 ) 00 1 s 2 p ( s 2 ) 01 10 s 3 p ( s 3 ) 10 101 s 4 p ( s 4 ) 11 111

11 .各种码的定义 5.1 编码器 1. 二元 ( 代 ) 码 : 码符号集为 X={0,1}, 所得码字都是一些二元序列 , 则为二元码 . 它是数字通信和计算机系统中最常用的一种码。 2. 同价 ( 代 ) 码 : 若 码 符号 集 X:{x 1 ,x 2 ,…, x r } 中每个 码符号 x 所占的传输时间相同 , 则所得的码 C 为同价码 . 一般二元码是同价码 . 电报中常用的摩尔 斯码 是非同价码 ，其 码符号 (·) 和划 ( － ) 所占的传输时间不同 .

12 .3 . 等长 码 ( 固定长度码 或定长 码 ): 若一组码中所有 ( 码字的 ) 码长都相等 ,( 即 L i =L( i =1,2,…,q)), 则 称为等长 码 。如下表中的码 1 。 4. 变长码 : 码中的码字长短 不一， 如上图中的码 2 。 信源符号 s i 信源符号出现概率 p ( s i ) 码表 码 1 码 2 s 1 p ( s 1 ) 00 1 s 2 p ( s 2 ) 01 10 s 3 p ( s 3 ) 10 101 s 4 p ( s 4 ) 11 111

13 .5. 非奇异码： 一组 码中所有 的码字都不相同。 即 6. 奇异码：一组码中有相同的码字，即 码 1 奇异，码 2 非奇异。 信源符号 s i 符号出现的概率 p ( s i ) 码 1 码 2 码 3 码 4 s 1 1/2 0 0 1 1 s 2 1/4 11 10 10 01 s 3 1/8 00 00 100 001 s 4 1/8 11 01 1000 0001

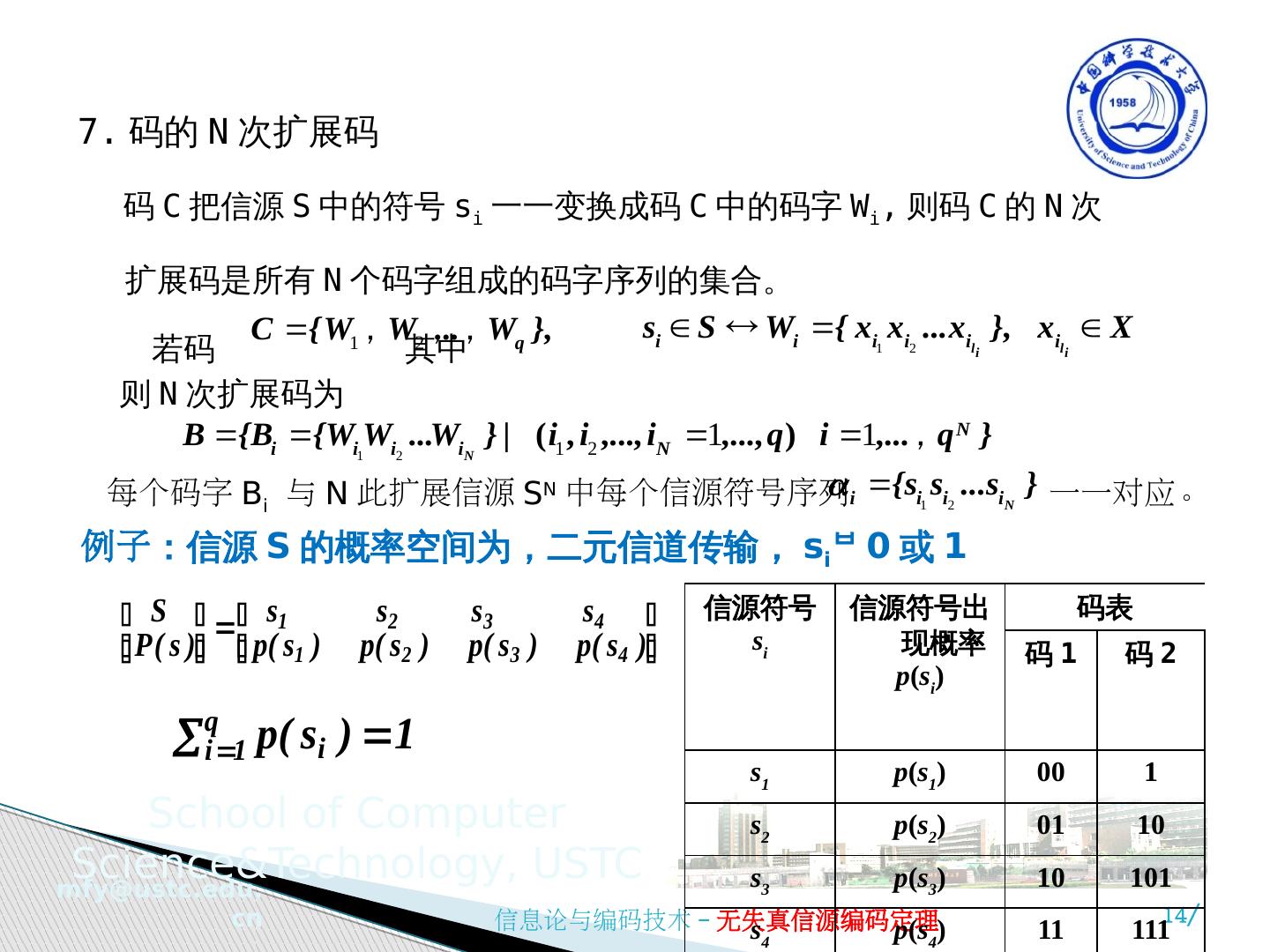
14 .7. 码的 N 次扩展码 码 C 把信源 S 中的符号 s i 一一变换成码 C 中的码字 W i , 则码 C 的 N 次扩展码是所有 N 个码字组成的码字序列的集合。 若码 其中 则 N 次扩展码为 每个码字 B i 与 N 此扩展信源 S N 中每个信源符号序列 一一对应。 例子 ：信源 S 的概率空间为，二元信道传输， s i 0 或 1 信源符号 s i 信源符号出现概率 p ( s i ) 码表 码 1 码 2 s 1 p ( s 1 ) 00 1 s 2 p ( s 2 ) 01 10 s 3 p ( s 3 ) 10 101 s 4 p ( s 4 ) 11 111

15 .可以求得信源 S 的任意 N 次扩展码。 码 1 的二次扩展码 : 1) 信源 S 的二次扩展信源 S 2 ={ 𝛽 1 =s 1 s 1 , 𝛽 2 =s 1 s 2 , 𝛽 3 =s 1 s 3 ,… 𝛽 16 =s 4 s 4 } ，共 q N =4 2 =16 个符号 2 ） S 的二次扩展码 信源符号 𝛽 i 码 字 B i 信源符号 𝛽 i 码 字 B i 𝛽 1 00 00 =W 1 W 1 =B 1 …… …… 𝛽 2 00 01 =W 1 W 2 =B 2 𝛽 5 𝛽 3 00 10 =W 1 W 3 =B 3 𝛽 5 𝛽 4 00 11 =W 1 W 4 =B 4 𝛽 16 11 11 =W 4 W 4 =B 16 信源符号 s i 信源符号出现概率 p ( s i ) 码表 码 1 s 1 p ( s 1 ) 00 s 2 p ( s 2 ) 01 s 3 p ( s 3 ) 10 s 4 p ( s 4 ) 11

16 .注 : 奇异码不是唯一可译码 ; 非奇异码 有唯一可译码 , 又有非唯一可译码 。 唯一可译码 又分为非即时译码和即时码 . 非即时译码 : 接收端收到一个完整的码字后 , 不能立即译码 , 而等下一码字开始接收后才判断是否 可以译码 . 8. 唯一可译码 若码的任意一串有限长的码符号序列 , 只能被唯一的译成所对应的信源符号序列 , 则称为唯一可译码。

17 . 码 1: 如码符号序列为码符号序列为 0010 s 1 s 3 唯一可译码 s i 码 1 码 2 s 1 00 0 s 2 01 01 s 3 10 001 s 4 11 111 s 1 s 2 s 1 s 3 s 1 是非唯一可译码 码 2. 0010 可能译为

18 .注 : 奇异码不是唯一可译码 ; 非奇异码有 唯一可译码 , 又有非唯一可译码。 唯一可译码又分为非即时译码和即时码 . 非即时译码 : 接收端收到一个完整的码字后 , 不能立即译码 , 而等下一码字开始接收后才判断是否可以码 .

19 .表中码 3 是非即时码 , 码 4 是即时码 . 只要收到 1 就表示码意完整。 信源符号 s i 符号出现的概率 P( s i ) 码 1 码 2 码 3 码 4 s 1 1/2 0 0 1 1 s 2 1/4 11 10 10 01 s 3 1/8 00 00 100 001 s 4 1/8 11 01 1000 0001 即时码 ( 非延长码或非续长码 ): 任意一个码子都不是其它码字的前缀部分 . 在延长码中有的是唯一可译 , 有的不是 . 如码 3 是唯一可译码。

20 .综上所述，码的分类有： （非延时码）

21 .信源符号 X i 符号出现概率 P(X i ) 码 1 码 2 码 3 码 4 X 1 1/2 0 0 1 1 X 2 1/4 11 10 10 01 X 3 1/8 00 00 100 001 X 4 1/8 11 01 1000 0001 表 5-2 不同的码字 1 是奇异码，码 2 是非奇异码。 码 3 是唯一可译码，码 2 不是唯一可译码 码 3 是非即时码。码 4 中只要收到符号 1 就表示该码字已完整，可以立即译码，所以码 4 是即时码 , 又称为非延长码，任意一个码字都不是其他码字的前缀部分构 .

22 .码树 平均码长 信息传输率 编码效率 克劳夫特不等式 5.2 几个基本概念

23 .1. 码树 通常情况下可以用码树来表示各个码字的构成，如果码字序列符号为 m 进制的，可以用 m 个符号的码树来构造码字，每个码树有一个树根 A, 树根有 m 个树枝，树枝的尽头称为叶节点 , 中间每个节点生出的树枝的数量等于码符号的数量 m ，从而形成 m 进制的码树。 5.2.1 几个基本概念 - 码树

24 .图 4-3 （ a ）二进制码树 图 4-3 （ b ）图是三进制码树 b 图为非满树，是一个三进码树，有三个支，码是不定长的。码树一定是即时码，反之，任何即时码都是用码树来表示。即时码的码树可以用来译码 A 为根分为两个支，有 n=3 级节点，其终端结点为 2 3 =8 个表示信源符号， a 图为满树 .

25 .5.2.1 几个基本概念 - 码树 【 例 5.2-1】 某地二月份天气的概率分布统计如下：雨天的概率是 1/8 ，雪天的概率也是 1/8 ，阴天的概率是 1/4 ，晴天的概率是 1/2 。设 x 1 表示雨天， x 2 表示雪天， x 3 表示阴天， x 4 表示晴天，则其离散无记忆信源的概率空间为

26 .5.2.1 几个基本概念 - 码树 表 5-3 两种信源编码方案 信源符号 概率 方案 1 的码字 方案 2 的码字 X 1 1/8 00 000 X 2 1/8 01 001 X 3 1/4 10 01 X 4 1/2 11 1 采用两种信源编码方案编成的码字 如下表所 示。绘出方案一和方案二的码树，试比较方案 1 和方案 2 的码字哪个有效性更好一些？

27 .5.2.1 几个基本概念 - 码树 表 5-3 两种信源编码方案 信源符号 概率 方案 1 的码字 方案 2 的码字 X 1 1/8 00 000 X 2 1/8 01 001 X 3 1/4 10 01 X 4 1/2 11 1

28 .5.2.2 几个基本概念 - 平均码长 编码后 的每个信源符号平均所需的码元（码符号）个数。 单位为 “ 码元 / 信源符号 ” 。 对单个信源符号进行编码，设信源为 2 、平均码长 若每个 码字对应的码长为 K i （ i ＝ 1 ， 2 …… q ） 则该 码的平均码长为 （码元 / 信源符号）

29 .5.2.1 几个基本概念 - 平均码长 方案 1 的平均码长 方案 2 的平均码长 （码元 / 信源符号） （码元 / 信源符号） 信源符号 概率 方案 1 的码字 方案 2 的码字 X 1 1/8 00 000 X 2 1/8 01 001 X 3 1/4 10 01 X 4 1/2 11 1