信道纠错编码

1 .信息论与编码技术 第 4 章 信道纠错编码 苗付友 mfy@ustc.edu.cn 2016 年 9 月

2 .本章介绍对离散信源进行无失真信源编码的要求、方法及理论极限，并引出香农第一定理。进一步加深对熵的物理意义的理解

3 .7.1 差错控制的基本形式 7.2 纠错码分类及基本概念 7.3 线性分组码 7.4 循环码 7.5 卷积码 主要内容

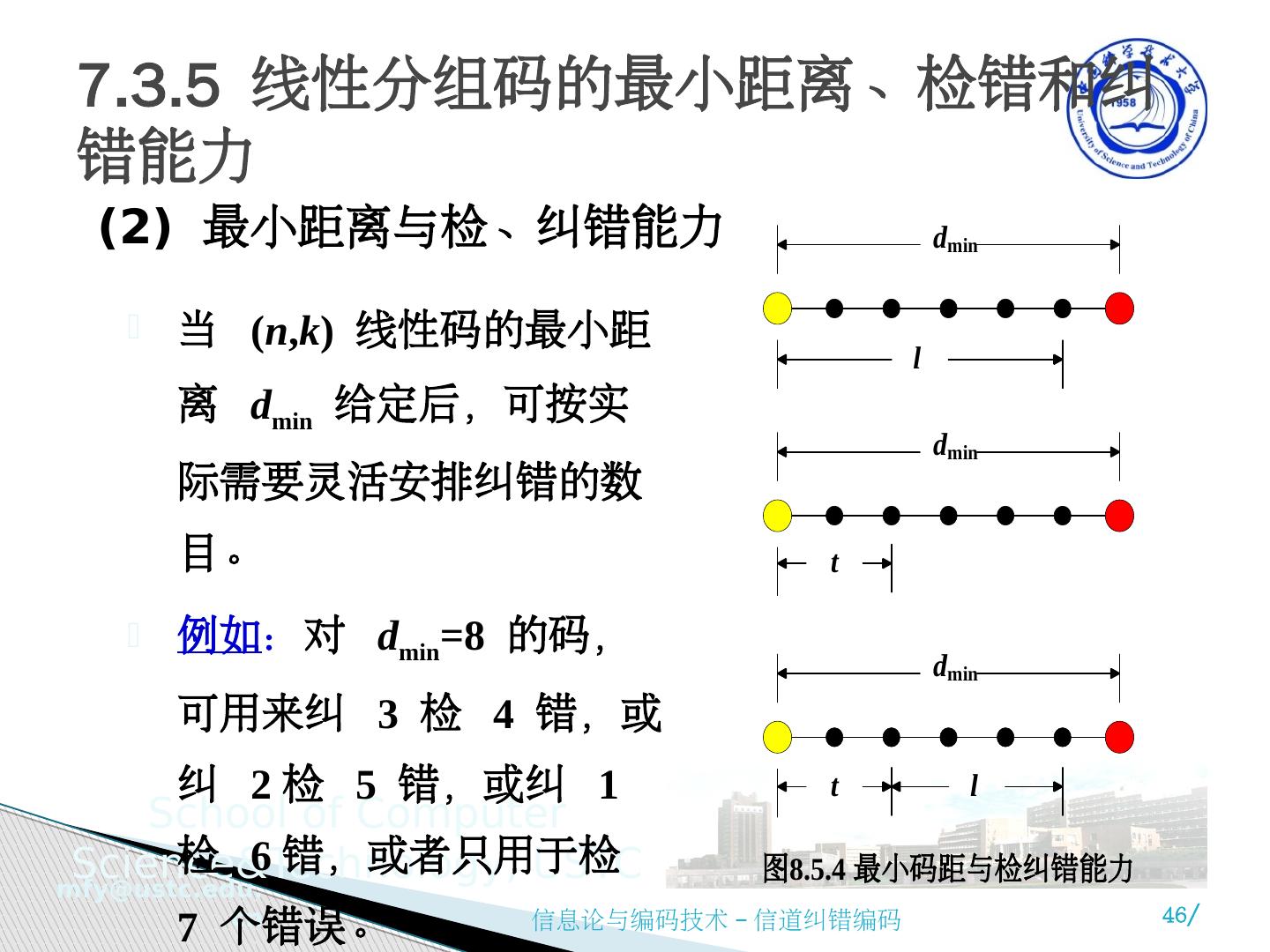
4 .7.3.1 一般概念 7.3.2 一致监督方程和一致 监督矩阵 7.3.3 线性分组码的 生成矩阵 7.3.4 线性分组码的编码 7.3.5 线性分组码的 最小距离 、检错和纠错能力 7.3.6 线性分组码的 译码 7.3.7 线性分组码的性能 7.3.8 汉明码 7.3.9 由已知码构造新码的方法 7.3.10 GSM 的信道编码总体方案 7.3.11 线性分组码的码限 7.3 线性分组码

5 .(1) 线性分组码的编码： 编码过程分为两步： 把信息序列按一定长度分成 若干 信息码组 , 每组由 k 位 组成 ; 编码器按照预定的 线性规则 （可由线性方程组规定），把信息码组变换成 n 重（ n > k ）码字，其中 ( n － k ) 个附加码元是由信息码元的 线性运算 产生的。 (2) 线性分组码的码字数： 信息码组长 k 位 ，有 2 k 个不同的信息码组，有 2 k 个码字与它们一一对应。 7.3.1 一般概念

6 .(3) 术语 线性分组码： 通过预定的线性运算将长为 k 位的信息码组变换成 n 重的码字 ( n > k ) 。由 2 k 个信息码组所编成的 2 k 个码字集合，称为 线性分组码 。 码字： 一个 n 重的码字可以用矢量来表示： C =( c n － 1 , c n － 1 ,…, c 1 , c 0 ) ( n , k ) 线性码： 信息位长为 k ，码长为 n 的线性码。 编码效率 / 编码速率 / 码率 / 传信率： R = k / n 。它说明了信道的利用效率， R 是衡量码性能的一个重要参数。 7.3.1 一般概念 返回目录

7 .7.3.2 一致监督方程和一致监督矩阵 (1) 一致监督方程 (2) 举 例 (3) 一致监督矩阵 (4) 一致监督矩阵特性

8 .(1) 一致监督方程 构成码字的方法： 编码是给已知信息码组按预定规则添加监督码元，构成码字。 在 k 个信息码元之后附加 r ( r = n － k ) 个监督码元，使每个监督元是其中某些信息元的模 2 和。 举例： k =3, r =4 ，构成 (7,3) 线性分组码。设码字为： ( c 6 , c 5 , c 4 , c 3 , c 2 , c 1 , c 0 ) c 6 , c 5 , c 4 为信息元， c 3 , c 2 , c 1 , c 0 为监督元，每个码元取“ 0” 或“ 1” 监督元按下面方程组计算： 7.3.2 一致监督方程和一致监督矩阵

9 .(1) 一致监督方程 一致监督方程 / 一致校验方程：确定信息元得到监督元规则的一组方程称为监督方程 / 校验方程。由于 所有码字都按同一规则确定， 又称为一致监督方程 / 一致校验方程。 为什么叫线性分组码？ 由于一致监督方程是 线性 的，即监督元和信息元之间是线性运算关系，所以由线性监督方程所确定的分组码是 线性分组码。 7.3.2 一致监督方程和一致监督矩阵

10 .(2) 举例 信息码组 ( 101 ) ，即 c 6 =1, c 5 =0, c 4 =1 代入 (7.2.1) 得： c 3 =0, c 2 =0, c 1 =1, c 0 =1 由信息码组 ( 101 ) 编出的码字为 ( 101 0011 ) 。其它 7 个码字如表 8.2.1 。 7.3.2 一致监督方程和一致监督矩阵

11 .7.3.2 一致监督方程和一致监督矩阵 (3) 一致监督矩阵 为了运算方便，将式 (7.2.1) 监督方程写成矩阵形式，得： 将式 (8.2.2) 可写成： H · C T = 0 T 或 C · H T = 0 C T 、 H T 、 0 T 分别表示 C 、 H 、 0 的转置矩阵。

12 .7.3.2 一致监督方程和一致监督矩阵 (3) 一致监督矩阵 系数矩阵 H 的后四列组成一个 (4×4) 阶单位子阵，用 I 4 表示， H 的其余部分用 P 表示：

13 .(3) 一致监督矩阵 推广到一般情况： 对 ( n , k ) 线性分组码，每个码字中的 r ( r = n － k ) 个监督元与信息元之间的关系可由下面的线性方程组确定： 7.3.2 一致监督方程和一致监督矩阵

14 .(3) 一致监督 矩阵 令上式的系数矩阵为 H ，码字行阵列为 C ： 7.3.2 一致监督方程和一致监督矩阵

15 .(4) 一致监督矩阵特性 对 H 各行实行初等变换，将后面 r 列 化为 单位子阵 ，得到下面矩阵，行变换所得方程组与原方程组同解。 监督矩阵 H 的标准形式 ： 后面 r 列 是一 单位子阵 的监督矩阵 H 。 7.3.2 一致监督方程和一致监督矩阵

16 .(4) 一致监督矩阵特性 H 标准形式的特性 H 阵的每一行都代表一个监督方程，它表示与该行中“ 1” 相对应的码元的模 2 和为 0 。 H 的标准形式表明了相应的监督元是由哪些信息元决定的。例如 (7,3) 码的 H 阵的第一行为 ( 101 1000 ) ，说明第一个监督元等于第一个和第三个信息元的模 2 和，依此类推。 H 阵的 r 行代表了 r 个监督方程， 由 H 所确定的码字有 r 个监督元。 为了得到确定的码， r 个监督方程（或 H 阵的 r 行）必须是 线性独立 的，这要求 H 阵的秩为 r 。 若把 H 阵化成标准形式，只要检查单位子阵的秩，就能方便地确定 H 阵本身的秩。 7.3.2 一致监督方程和一致监督矩阵 参见方程

17 .7.3.3 线性分组码的生成矩阵 (1) 线性码的封闭性 (2) 线性分组码的生成矩阵 (3) 生成矩阵与一致监督矩阵的关系 (4) 对偶码

18 .(1) 线性码的封闭性 线性码的封闭性： 线性码任意两个码字之和仍是一个码字。 定理 7.3.1 ： 设二元线性分组码 C I ( C I 表示码字集合 ) 是由监督矩阵 H 所定义的，若 U 和 V 为其中的任意两个码字，则 U + V 也是 C I 中的一个码字 . [ 证明 ] ： 由于 U 和 V 是码 C I 中的两个码字，故有： HU T = 0 T HV T = 0 T ，那么 H ( U + V ) T = H ( U T + V T )= HU T + HV T = 0 T 即 U + V 满足监督方程，所以 U + V 一定是一个码字。 一个长为 n 的二元序列可以看作是 GF (2) ( 二元域 ) 上的 n 维线性空间中的一点。所有 2 n 个矢量集合构成了 GF (2) 上的 n 维线性空间 V n 。把线性码放入线性空间中进行研究，将使许多问题简化而比较容易解决。 ( n , k ) 线性码是 n 维线性空间 V n 中的一个 k 维子空间 V k 。 7.3.3 线性分组码的生成矩阵

19 .(2) 线性分组码的生成矩阵 生成矩阵的来由 ： 在由 ( n , k ) 线性码构成的线性空间 V n 的 k 维子空间中，一定存在 k 个线性独立的码字： g 1 , g 2 ,…, g k 。码 C I 中其它任何码字 C 都可以表为这 k 个码字的一种线性组合，即： 7.3.3 线性分组码的生成矩阵

20 .(2) 线性分组码的生成矩阵 生成矩阵定义 ： 由于矩阵 G 生成了 ( n , k ) 线性码，称矩阵 G 为 ( n , k ) 线性码的生成矩阵。 7.3.3 线性分组码的生成矩阵

21 .(2) 线性分组码的生成矩阵 生成矩阵 G 的特性 G 中每一行 g i =( g i 1 , g i 2 ,…, g in ) 都是一个码字； 对每一个信息组 m ，由矩阵 G 都可以求得 ( n , k ) 线性码对应的码字。 ( n , k ) 线性码的每一个码字都是生成矩阵 G 的行矢量的线性组合，所以它的 2 k 个码字构成了由 G 的行张成的 n 维空间的一个 k 维子空间 V k 。 7.3.3 线性分组码的生成矩阵

22 .(2) 线性分组码的生成矩阵 线性 系统 分组码 线性系统分组码的构成 ： 通过行初等变换，将 G 化为前 k 列是单位子阵的标准形式。 7.3.3 线性分组码的生成矩阵

23 .(2) 线性分组码的生成矩阵 线性 系统 分组码 线性系统分组码定义 ： 用标准生成矩阵 G k × n 编成的码字，前面 k 位为信息位，后面 r = n － k 位为校验位，这种信息位在前校验位在后的线性分组码称为线性系统分组码。 当生成矩阵 G 确定之后， ( n , k ) 线性码也就完全被确定了，只要找到码的生成矩阵，编码问题也同样被解决了。 7.3.3 线性分组码的生成矩阵

24 .(2) 线性分组码的生成矩阵 举例 ： (7,4) 线性码的生成矩阵为： 7.3.3 线性分组码的生成矩阵

25 .(3) 生成矩阵与一致监督矩阵的关系 由于生成矩阵 G 的每一行都是一个码字，所以 G 的每行都满足： H r × n ( C 1× n ) T =( 0 1× r ) T ，则有： H r × n ( G k × n ) T =( 0 k × r ) T 或 G k × n ( H r × n ) T = 0 k×r 线性系统码的监督矩阵 H 和生成矩阵 G 之间可以直接互换 。 7.3.3 线性分组码的生成矩阵

26 .(3) 生成矩阵与一致监督矩阵的关系 举例 ： 已知 (7,4) 线性系统码的监督矩阵为： 7.3.3 线性分组码的生成矩阵 Q Q T

27 .7.3.3 线性分组码的生成矩阵 (4) 对偶码 对偶码 ： 对一个 ( n , k ) 线性码 C I ，由于 H r × n ( G k × n ) T =( 0 k × r ) T ，如果以 G 作监督矩阵，而以 H 作生成矩阵，可构造另一个码 C Id ， C Id 是一个 ( n , n － k ) 线性码，称码 C Id 为原码的对偶码 . 例如 ： (7,4) 线性码的对偶码是 (7,3) 码： (7,3) 码的生成矩阵 G (7,3) 是 (7,4) 码监督矩阵 H (7,4)

28 .7.3.3 线性分组码的生成矩阵 ( n , k ) 线性码的编码 ： 根据线性码的监督矩阵或生成矩阵 将长为 k 的信息组变换成长为 n ( n > k ) 的码字。 利用监督矩阵构造 (7,3) 线性分组码的编码电路 设码字为： C =( c 6 c 5 c 4 c 3 c 2 c 1 c 0 ) 码的监督矩阵为：

29 .7.3.4 线性分组码的生成矩阵 利用监督矩阵构造 (7,3) 线性分组码的编码电路： 根据上面方程组可直接画出 (7,3) 码的并行编码电路和串行编码电路 :