离散信道及其信道容量

1 .信息论与编码技术 第 3 章 离散信道及其信道容量 苗付友 mfy@ustc.edu.cn 2016 年 9 月

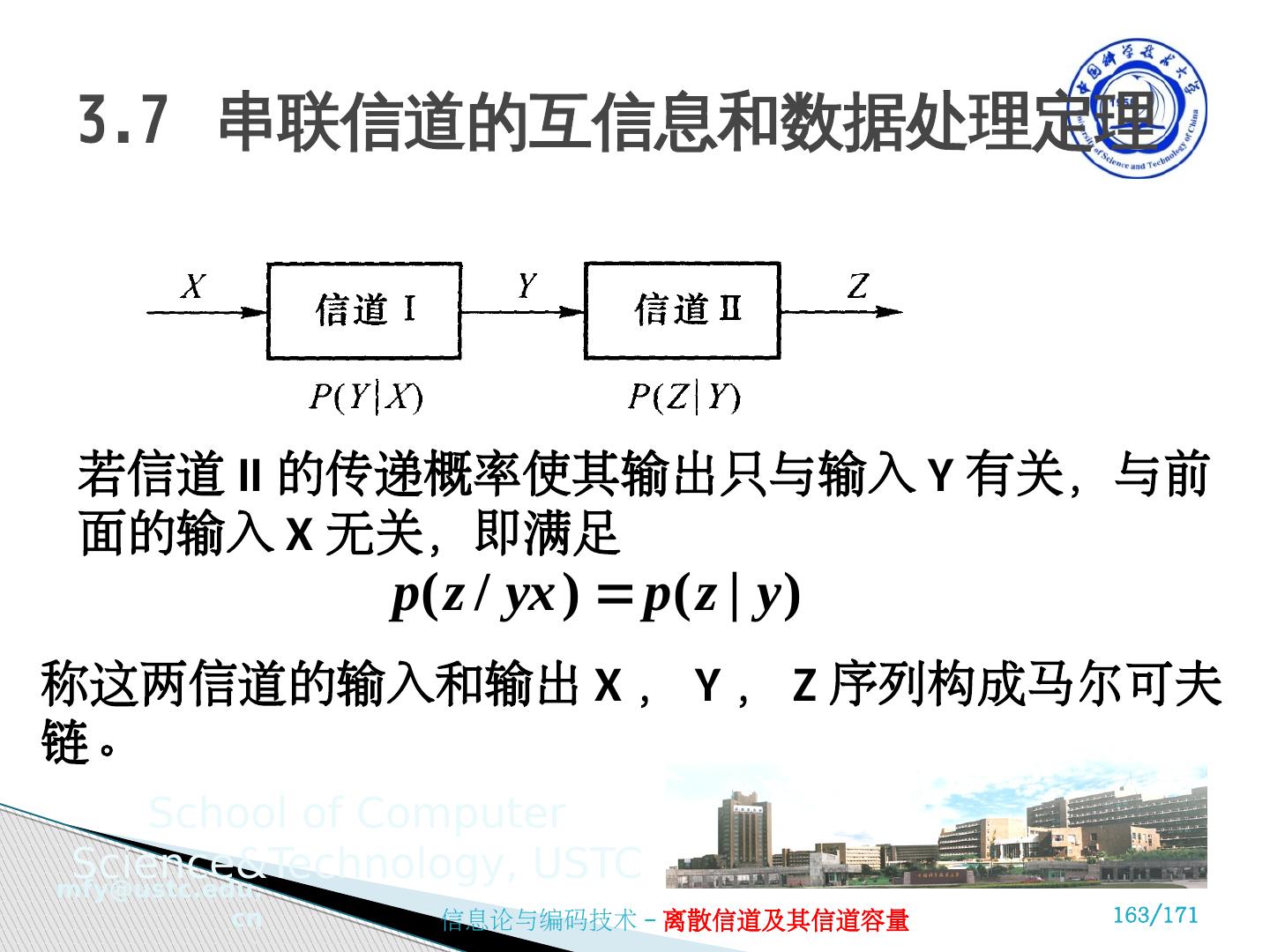
2 .3.1 信道的数学模型及分类 3.2 平均互信息及平均条件互信息 3.3 平均互信息的特性 3.4 信道容量及其一般计算方法 3.5 离散无记忆扩展信道及其信道容量 3.6 独立并联信道及其信道容量 3.7 串联信道的互信息和数据处理定理 3.8 信源与信道的匹配 本章内容

3 .(1) 一般信道的数学模型 (2) 信道的分类 (3) 实际的信道 3.1 信道的数学模型及分类

4 .(1) 一般信道的数学模型 ① 信道的广义性 ② 一般信道的数学模型 3.1 信道的数学模型及分类

5 .(1) 一般信道的数学模型 ① 信道的广义性 信息论把任何一个有输入、输出的系统都可以看成是一个信道 （物理信道多种多样：简单：滤波器；复杂：国际通信线路）。 信号在信道中传输会引入噪声或干扰，它使信号通过信道后产生错误和失真。 信道的输入和输出之间一般不是确定的函数关系，而是 统计依赖关系。 知道了信道的输入信号、输出信号以及它们之间的依赖关系，信道的全部特性就确定了。 3.1 信道的数学模型及分类

6 .(1) 一般信道的数学模型 ② 一般信道的数学模型 信息论对信道的研究： 对具体物理信道抽象，建立与各种通信系统相适应的信道模型，研究信息在这些模型信道上传输的普遍规律，指导通信系统的设计。 信道模型： 不研究信号在信道中传输的 物理过程 ，把信道模型看作黑匣子。 3.1 信道的数学模型及分类

7 .(1) 一般信道的数学模型 ② 一般信道的数学模型 一般，输入和输出信号都是广义的时间连续的随机信号，可用随机过程来描述。 数学模型的数学符号表示： { X P ( Y / X ) Y } 3.1 信道的数学模型及分类

8 .(2) 信道的分类 ① 根据输入输出随机信号的特点分类 ② 根据输入输出随机变量个数的多少分类 ③ 根据输入输出个数分类 ④ 根据信道上有无干扰分类 ⑤ 根据信道有无记忆特性分类 3.1 信道的数学模型及分类

9 .(2) 信道的分类 ① 根据输入输出随机信号的特点分类 离散信道： 输入和输出的随机序列的取值都是离散的信道。 连续信道： 输入和输出的随机序列的取值都是连续的信道。 半离散／ 半连续信道 ： 输入变量取离散值而输出变量取连续值，或反之 . 波形信道： 信道的输入和输出都是一些时间上连续的随机信号 { x ( t )} 和 { y ( t )} ，即信号输入和输出的随机变量是连续的，并且还随时间连续变化。一般可用随机过程来描述其输入和输出。 波形信道可分解成离散信道、连续信道或半离散信道来研究。 3.1 信道的数学模型及分类

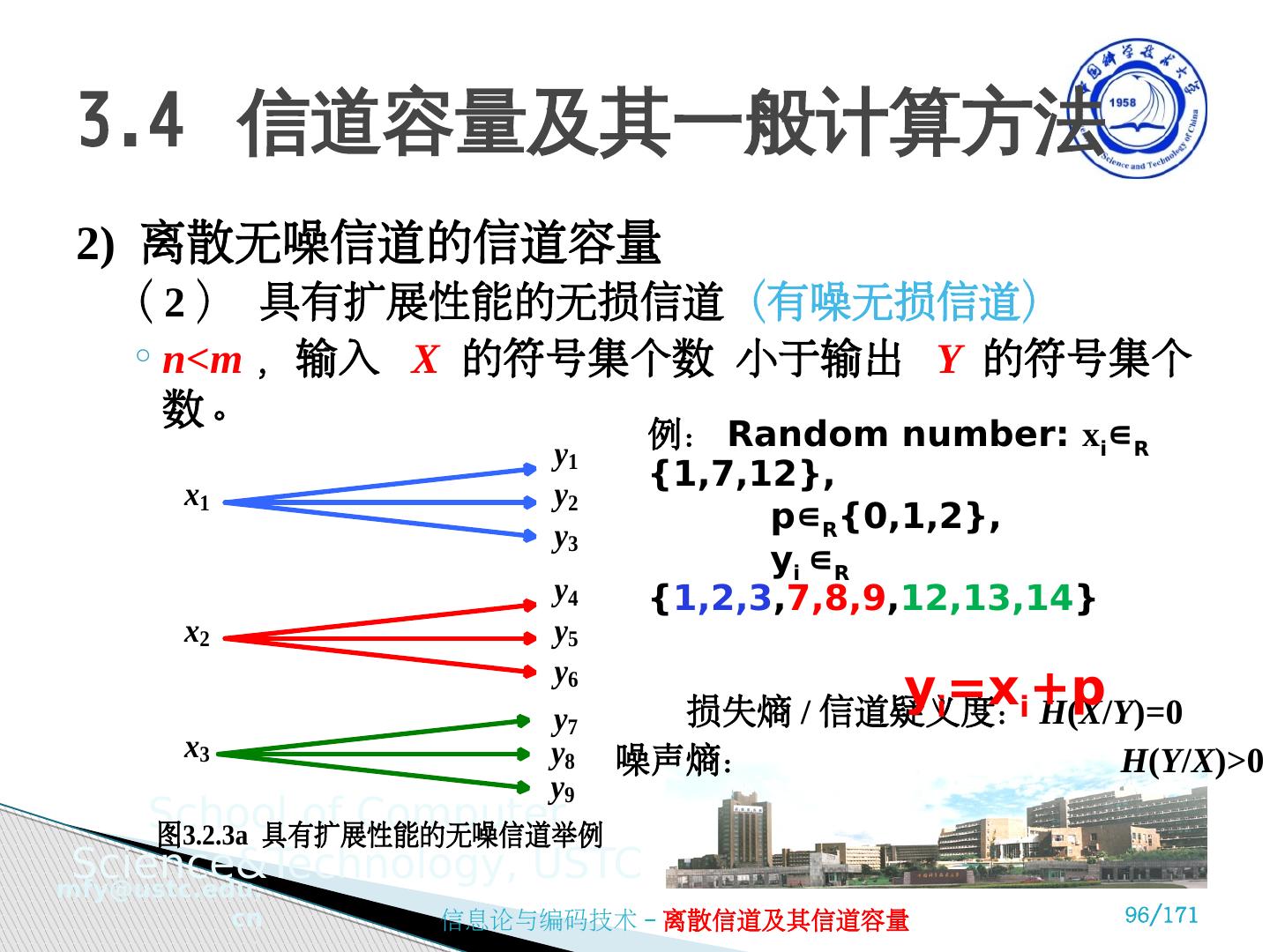
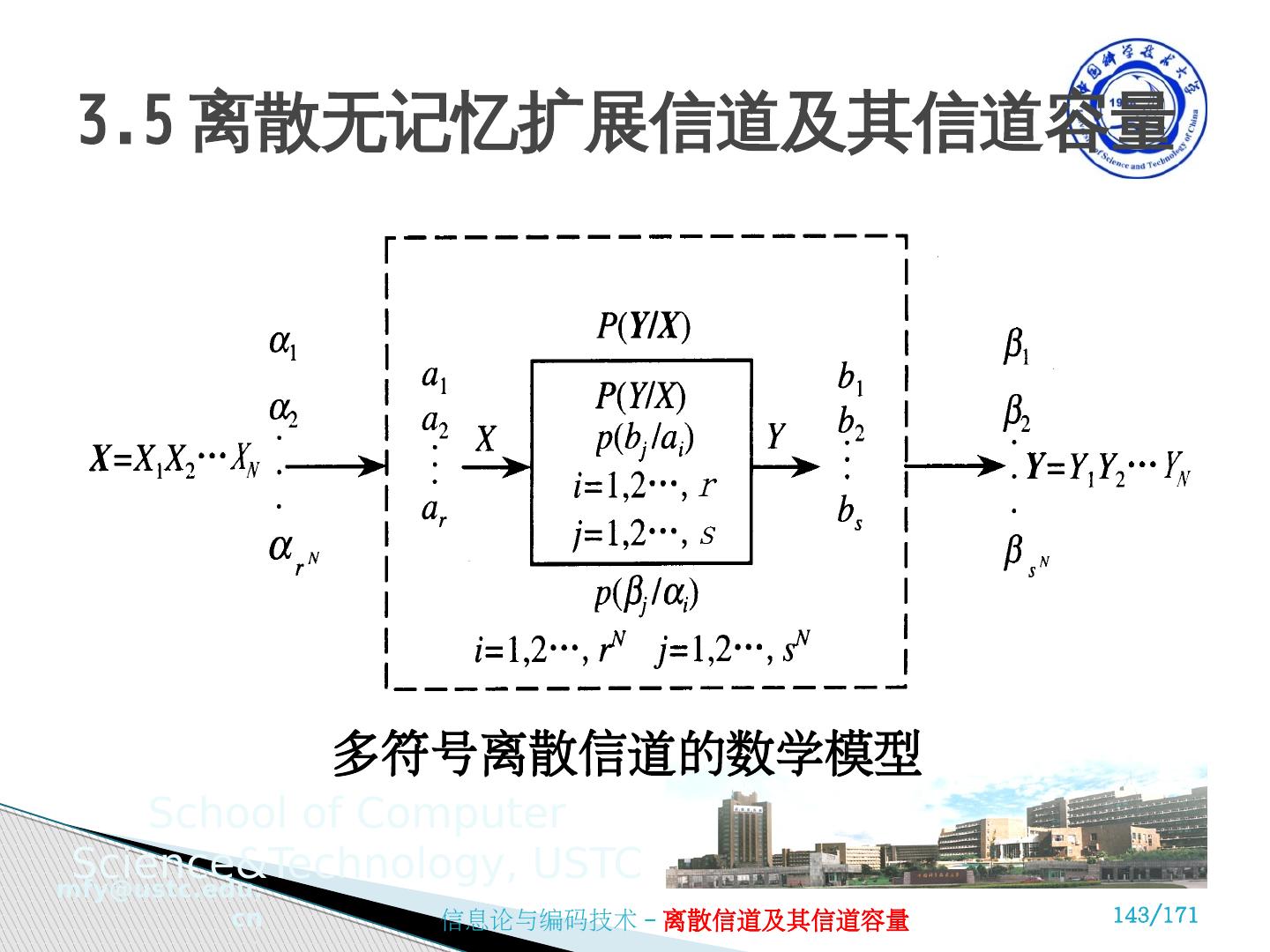
10 .(2) 信道的分类 ② 根据输入输出 随机变量个数 的多少分类 单符号信道： 输入和输出端都只用一个 随机变量 来表示。 离散无记忆扩展信道 （多符号信道） ： 输入和输出端用 随机变量序列（随机矢量） 来表示。 ③ 根据 输入输出个数 分类 单用户信道： 只有一个输入和一个输出的信道。 多用户信道： 有多个输入和多个输出的信道。 单符号与单用户的区别，不要搞混 ! 3.1 信道的数学模型及分类

11 .(2) 信道的分类 ④ 根据信道上有无干扰分类 有干扰信道： 存在干扰或噪声或两者都有的信道。 实际信道一般都是有干扰信道。 无干扰信道： 不存在干扰或噪声，或干扰和噪声可忽略不计的信道。 计算机和外存设备之间的信道可看作是无干扰信道。 ⑤ 根据信道有无记忆特性分类 无记忆信道： 输出仅与当前输入有关，而与过去输入无关的信道。 有记忆信道： 信道输出不仅与当前输入有关，还与过去输入和（或）过去输出有关。 3.1 信道的数学模型及分类

12 .(3) 实际的信道 实际信道的带宽总是有限的，所以输入和输出信号总可以分解成随机序列来研究。随机序列中每个随机变量的取值可以是可数的离散值，也可以是不可数的连续值。 一个实际信道可同时具有多种属性。 最简单的信道是单符号离散信道。 3.1 信道的数学模型及分类

13 .(4) 单符号离散信道的数学模型 ① 信道模型 ② 信道统计特性 3.1 信道的数学模型及分类

14 .(4) 单符号离散信道的数学模型 ① 信道模型 设输入： X ∈{ x 1 , x 2 ,…, x i ,…, x n } 输出： Y ∈{ y 1 , y 2 ,…, y j ,…, y m } 其信道模型： 3.1 信道的数学模型及分类

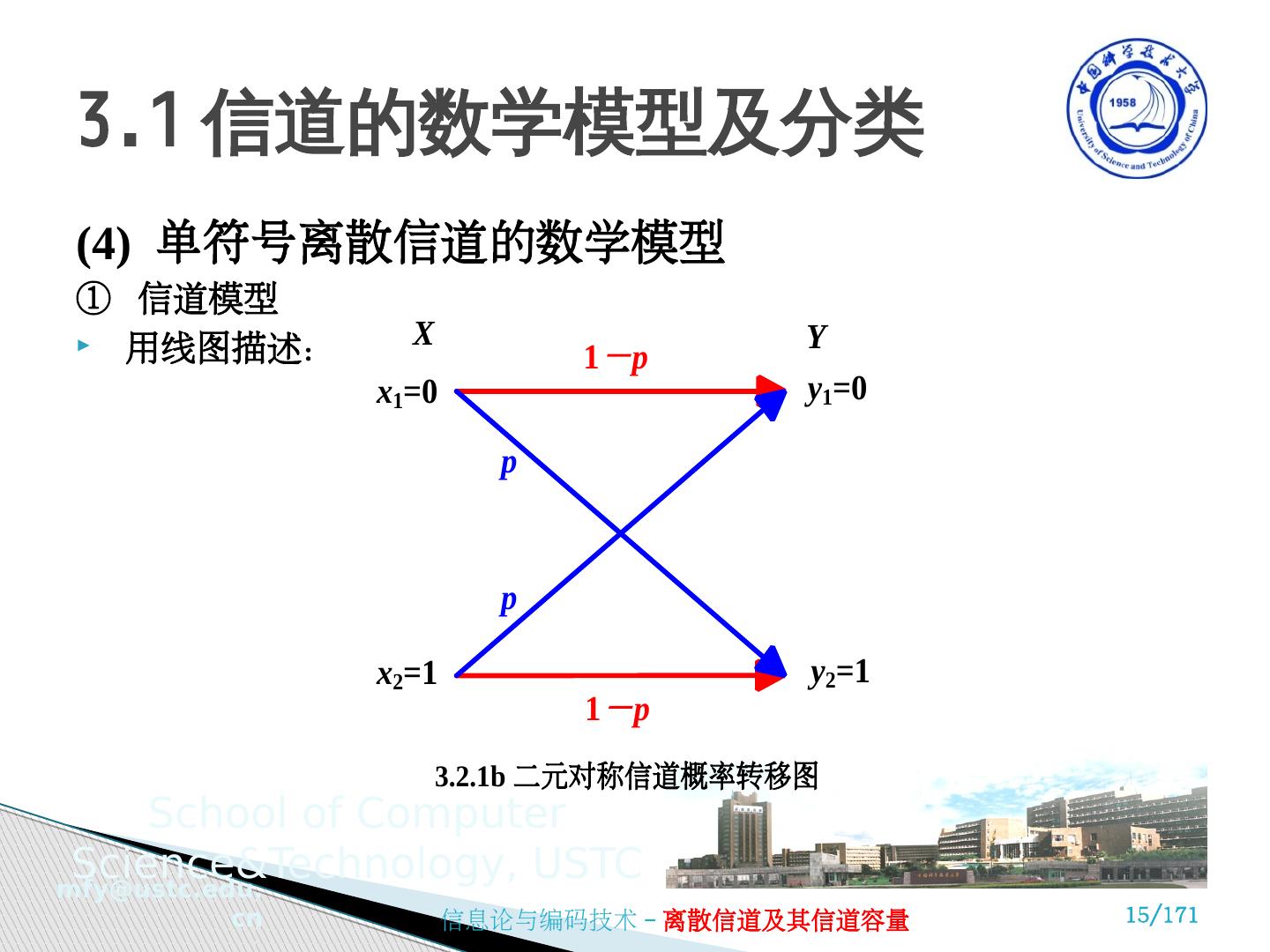
15 .(4) 单符号离散信道的数学模型 ① 信道模型 用线图描述： 3.1 信道的数学模型及分类

16 .(4) 单符号离散信道的数学模型 ② 信道统计特性 信道统计特性： 由信道转移概率描述。 信道转移概率（信道传递概率）： 条件概率 p ( y j / x i ) 。 信道特性表示： 用信道转移概率矩阵，简称 信道矩阵。 3.1 信道的数学模型及分类

17 .反信道矩阵： 由条件概率 p ( x i / y j ) 表示。 3.1 信道的数学模型及分类

18 .（ 5 ）一般离散信道的数学模型 3.1 信道的数学模型及分类 信 道 离散信道的数学模型

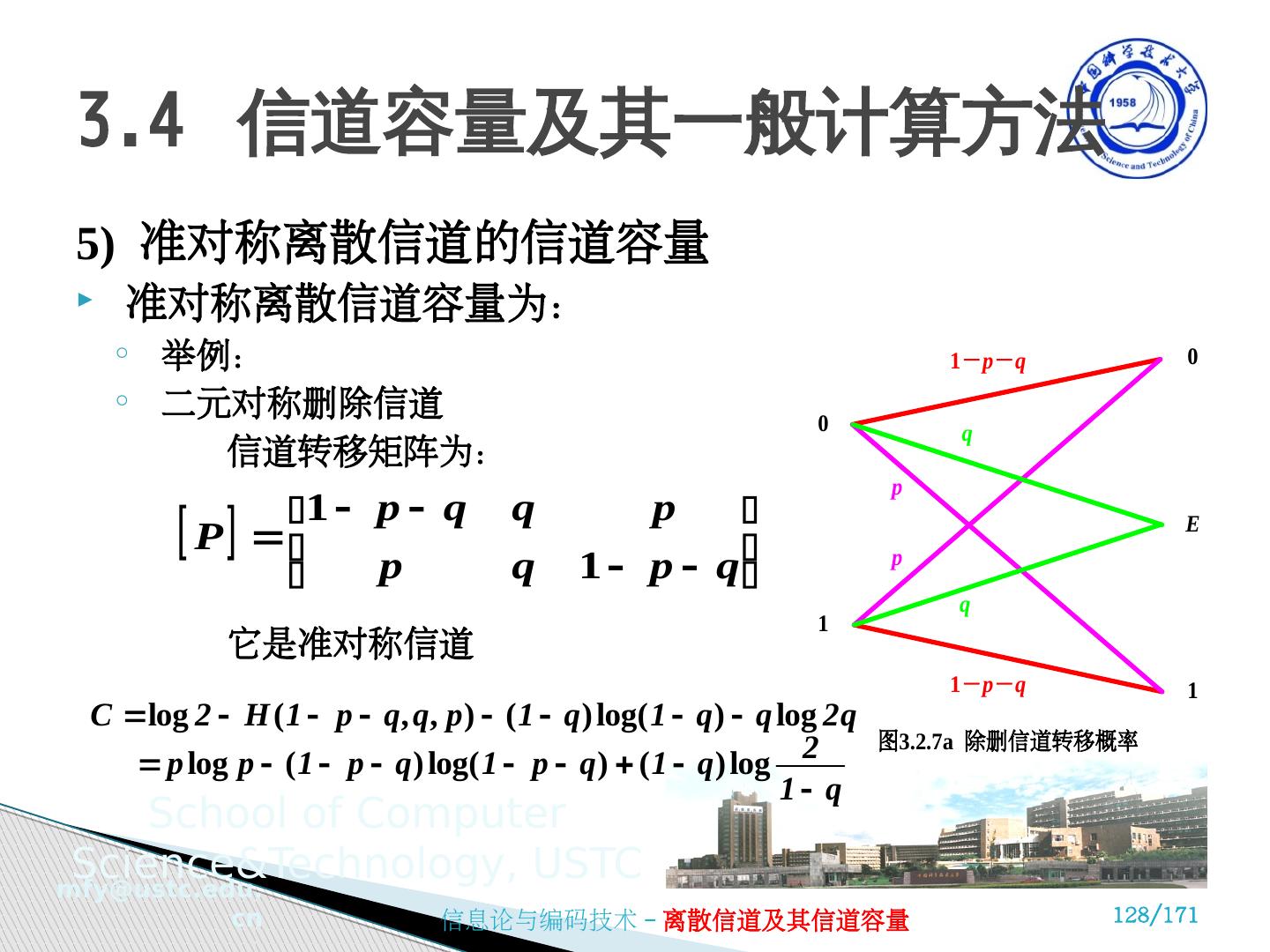
19 .（ 5 ）离散信道的分类 根据信道统计特性（即 p(x/y) ） , 离散信道又分为 : 无干扰（无噪）信道 有干扰无记忆信道 有干扰有记忆信道 3.1 信道的数学模型及分类

20 .（ 5 ）离散信道的分类 — 无干扰信道 信道中没有干扰，输出 Y 与输入 X 之间有确定的一一对应关系 例： X:{x 1 =2,x 2 =4,x 3 =6}; Y: {y 1 =1,y 2 =2,y 3 =3} p(x 1 )=p(x 2 )=1/4; p(x 3 )=1/2; y i =f(x i )=x i /2 3.1 信道的数学模型及分类 P( y i / x j ) y 1 =1 y 2 =2 y 3 =3 X 1 =2 1 0 0 x 2 =4 0 1 0 x 3 =6 0 0 1

21 .（ 5 ）离散信道的分类 -- 有干扰无记忆信道 有干扰：信道输出符号与输入符号间无确定的对应关系 无记忆：任意时刻输出符号只依赖于对应时刻的输入符号，而与以前时刻的输入符号、输出符号无关，与以后的输入符号也无关。 3.1 信道的数学模型及分类 例： X:{x 1 =0,x 2 =1,x 3 =2}; p(x 1 )=p(x 2 )=1/4; p(x 3 )=1/2; Y: {y 1 =0,y 2 =1,y 3 =2} k:{1, 2} p(k=1)=1/3, p(k=2)=2/3 y i =f(x i )=x i + k mod 3 P( y i / x j ) y 1 =0 y 2 =1 y 3 =2 X 1 =0 0 1/3 2/3 x 2 =1 2/3 0 1/3 x 3 =2 1/3 2/3 0

22 .（ 5 ）离散信道的分类 -- 有干扰有记忆信道 是更一般的信道情况 处理方式： 将记忆性较强的 N 个符号作为一个矢量符号处理，各矢量符号间认为是无记忆的 马尔科夫链 3.1 信道的数学模型及分类

23 .平均互信息量 平均条件互信息 3.2 平均互信息及平均条件互信息

24 . 将信道的发送和接收端分别看成是 两个“信源” ，则两者之间的统计依赖关系（信道输入和输出之间）描述了信道的特性。 (1) 互信息量和条件互信息量 (2) 平均互信息量的定义 (3) 平均互信息量的物理含义 3.2.1 平均互信息

25 .(1) 互信息量和条件互信息量 ① 互信息量 ② 互信息的性质 ③ 条件互信息量 3.2.1 平均互信息

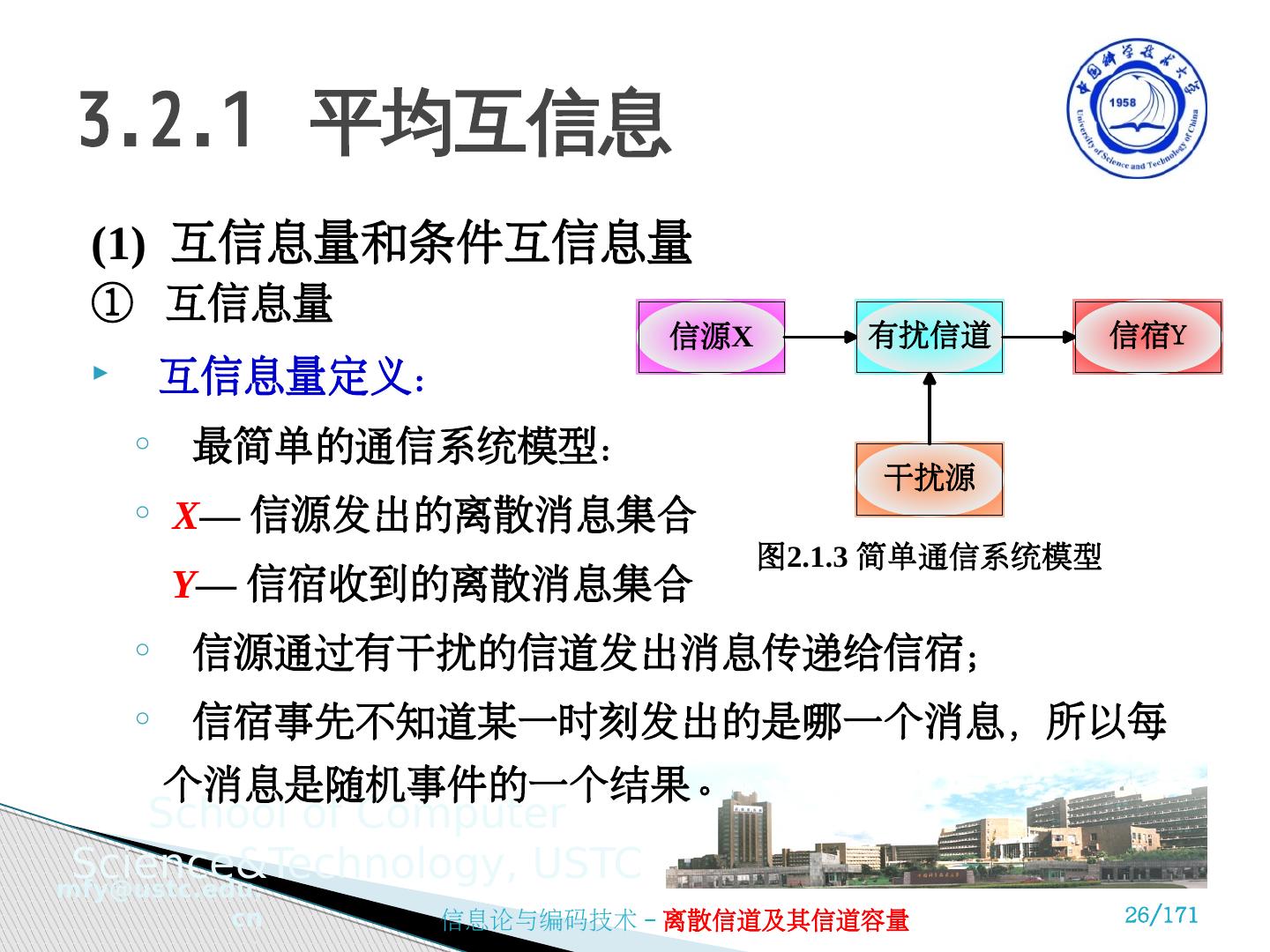
26 .(1) 互信息量和条件互信息量 ① 互信息量 互信息量定义： 最简单的通信系统模型： X — 信源发出的离散消息集合 Y — 信宿收到的离散消息集合 信源通过有干扰的信道发出消息传递给信宿； 信宿事先不知道某一时刻发出的是哪一个消息，所以每个消息是随机事件的一个结果。 3.2.1 平均互信息

27 .(1) 互信息量和条件互信息量 ① 互信息量 互信息量定义： 信源 X 、信宿 Y 的数学模型为： 3.2.1 平均互信息 例： Random number: x i ∊ R {3,4,5,6,7}, p(x i )=1/5, i =0,1,2,3,4; y j ∊ { 0,1,2 } , j=0,1,2; y i mod 3 =x i mod 3

28 .(1) 互信息量和条件互信息量 ① 互信息量 互信息量定义： 先验概率： 信源发出消息 x i 的概率 p ( x i ) 。 后验概率： 信宿收到 y j 后推测信源发出 x i 的概率： p ( x i / y j ) 3.2.1 平均互信息 例： Random number: x i ∊ R {3,4,5,6,7}, p(x i )=1/5, i =0,1,2,3,4; y j ∊ { 0,1,2 } , j=0,1,2; y i mod 3 =x i mod 3

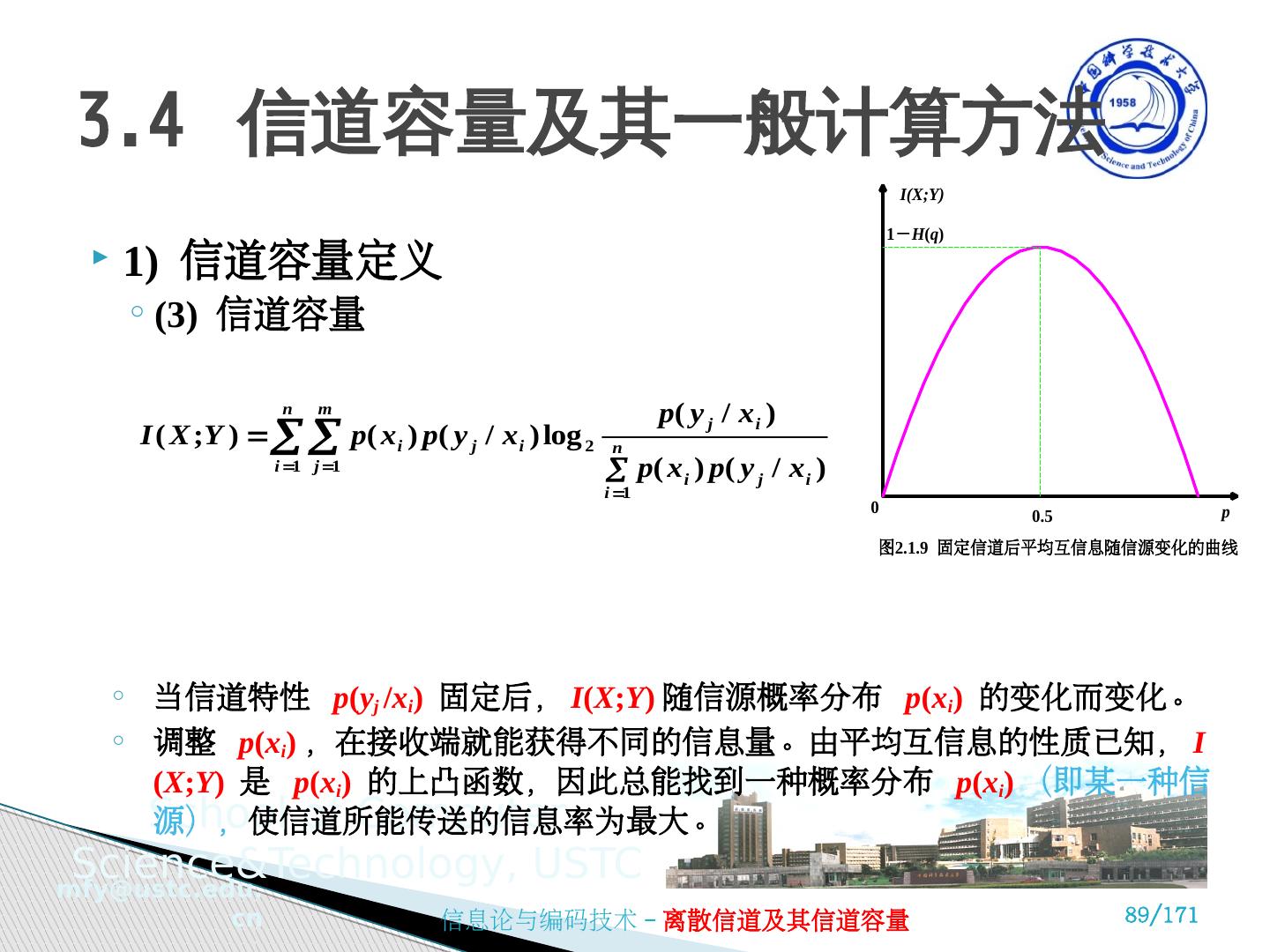
29 .(1) 互信息量和条件互信息量 ① 互信息量 互信息量定义： 互信息量： y j 对 x i 的互信息量定义为后验概率与先验概率比值的对数。 3.2.1 平均互信息