1.Implementing Consistency -- Paxos Some slides from Michael Freedman 

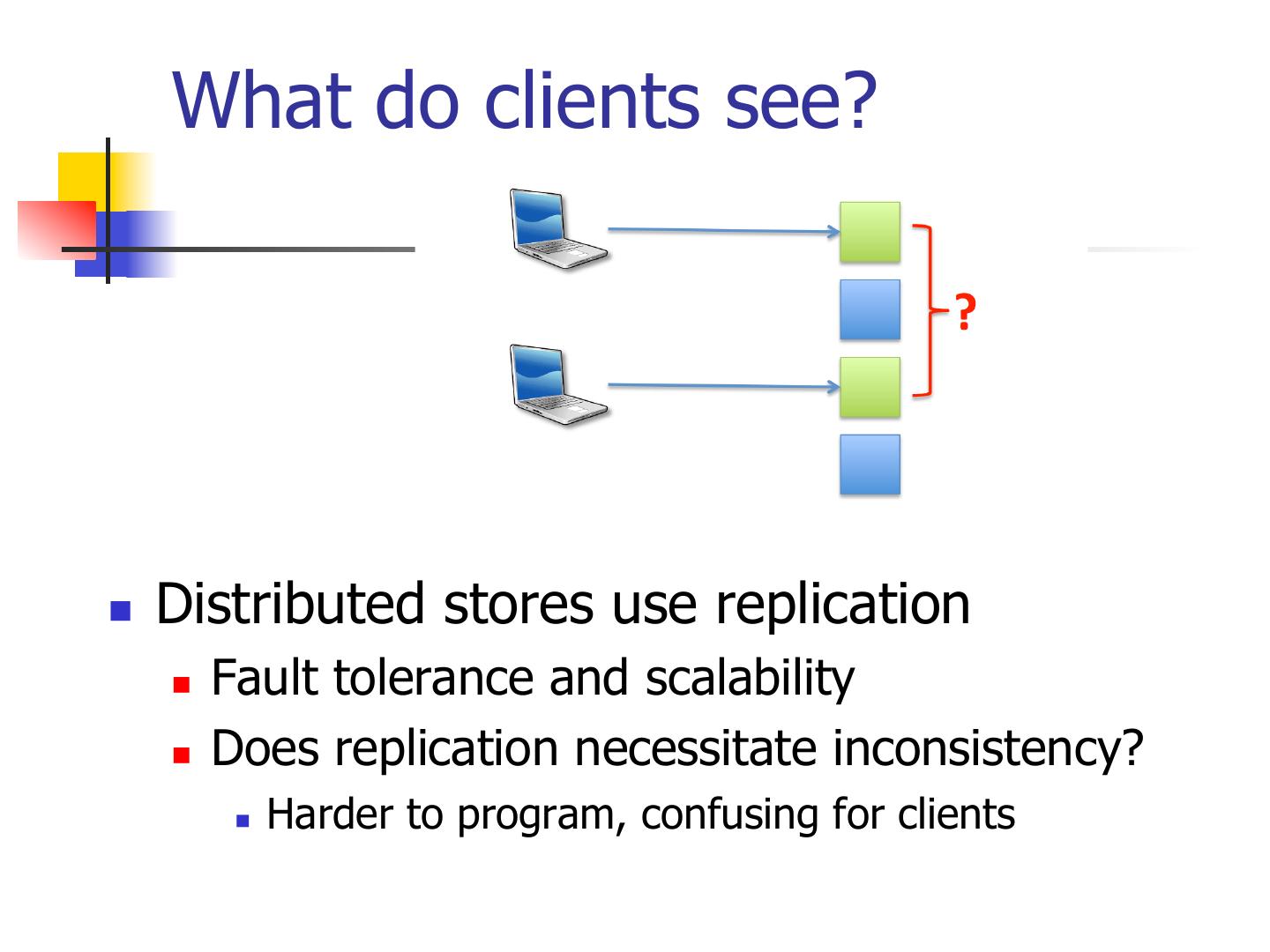
2. What do clients see? n  Distributed stores use replication n  Fault tolerance and scalability n  Does replication necessitate inconsistency? n  Harder to program, confusing for clients 

3.Problem n  How to reach consensus/data consistency in distributed system that can tolerate non-malicious failures? n  We saw some consistency models – how to implement them? 

4.Another perspective n  Lock is the easiest way to manage concurrency n  Mutex and semaphore. n  Read and write locks. n  In distributed system: n  No master for issuing locks. n  Failures. 

5.Recall, consistency models 

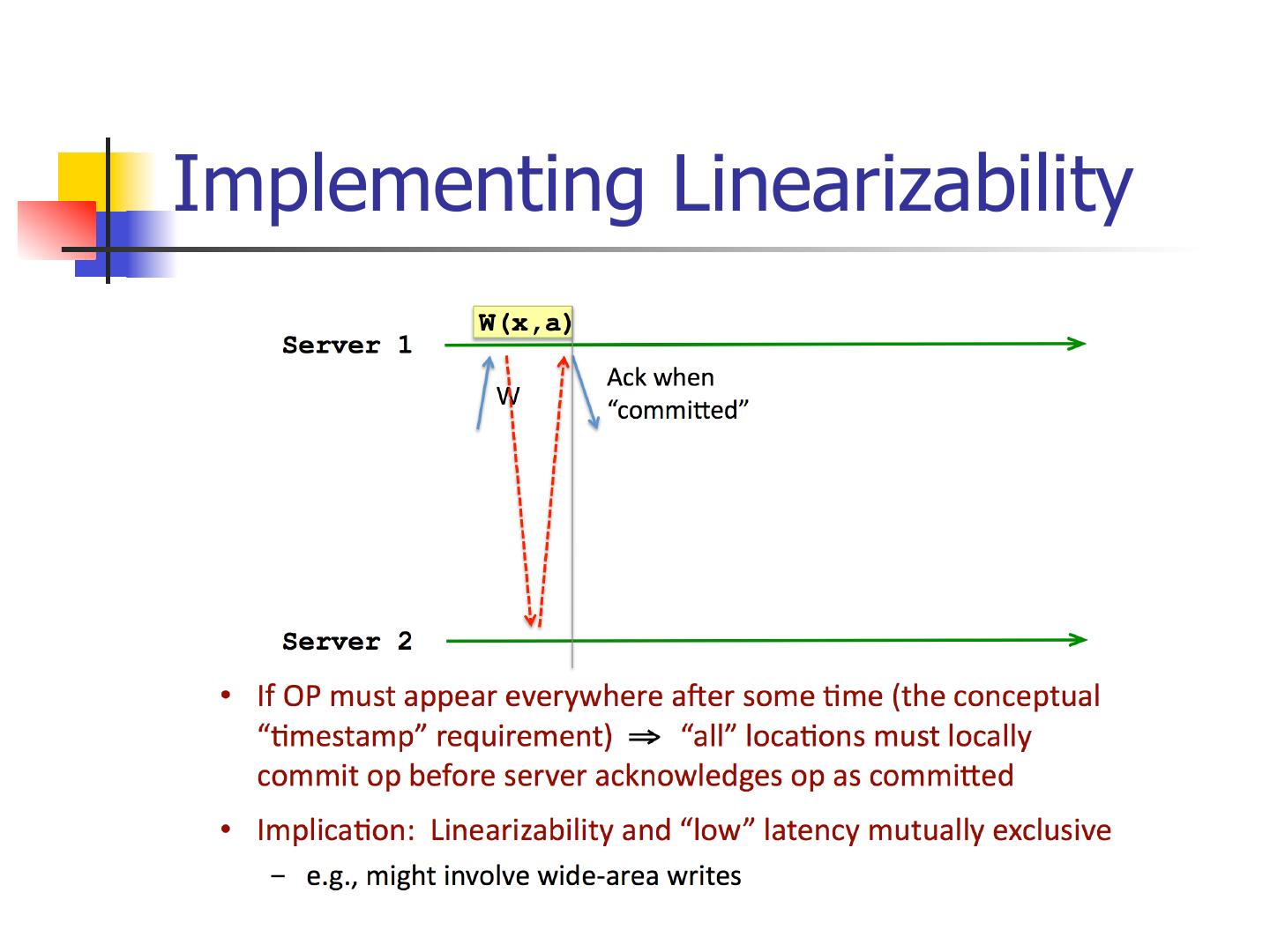
6.Implementing Linearizability 

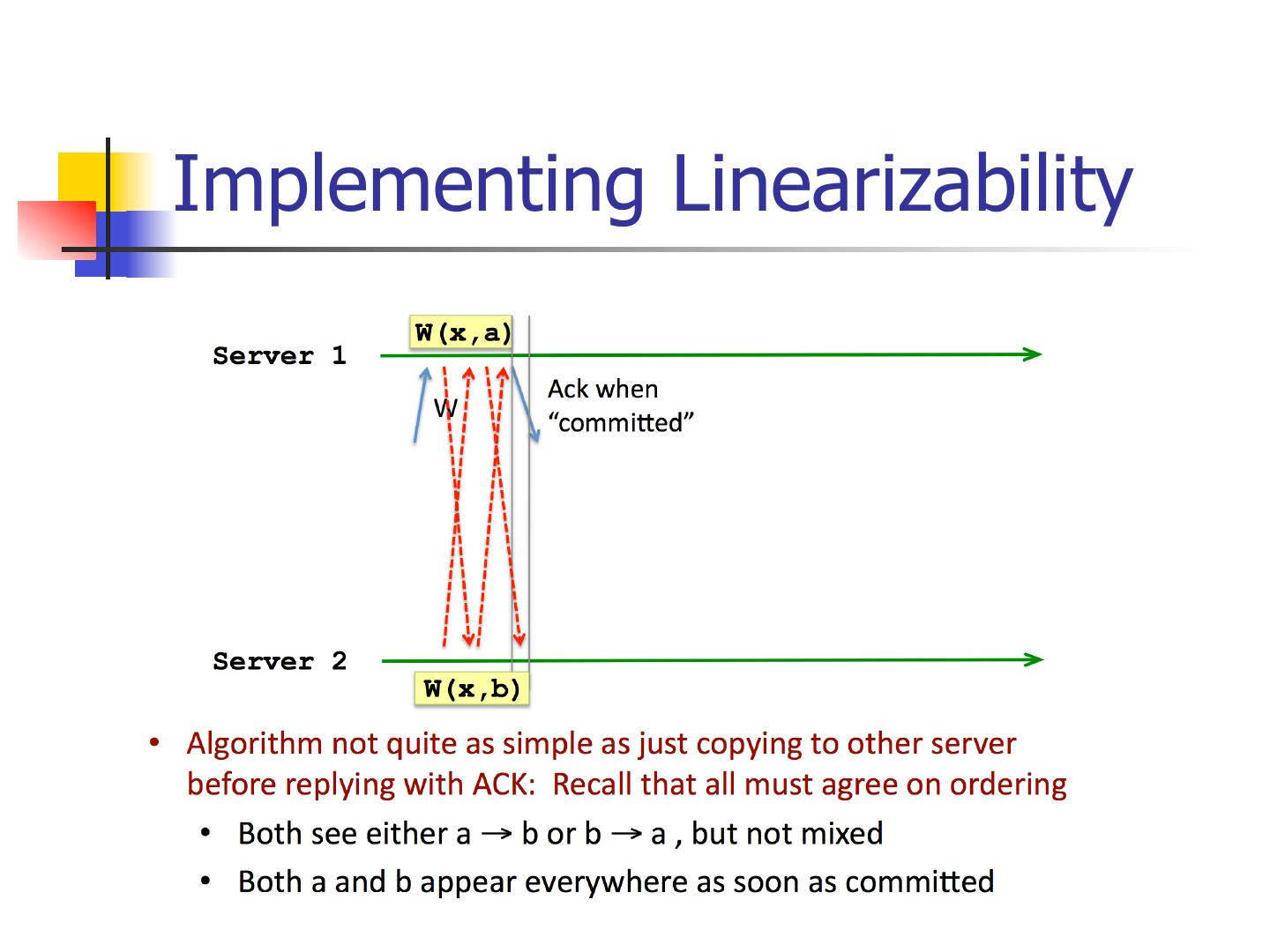
7.Implementing Linearizability 

8. Ok, what to do? n  We want consistency and availability n  Two options 1.  Master Replica Model n  All operations and ordering happen on a single master n  Replicates to secondary copies 2.  Multi-master model n  Read/write anywhere n  Replicas order and replicate content before returning 

9.Coordination protocols 

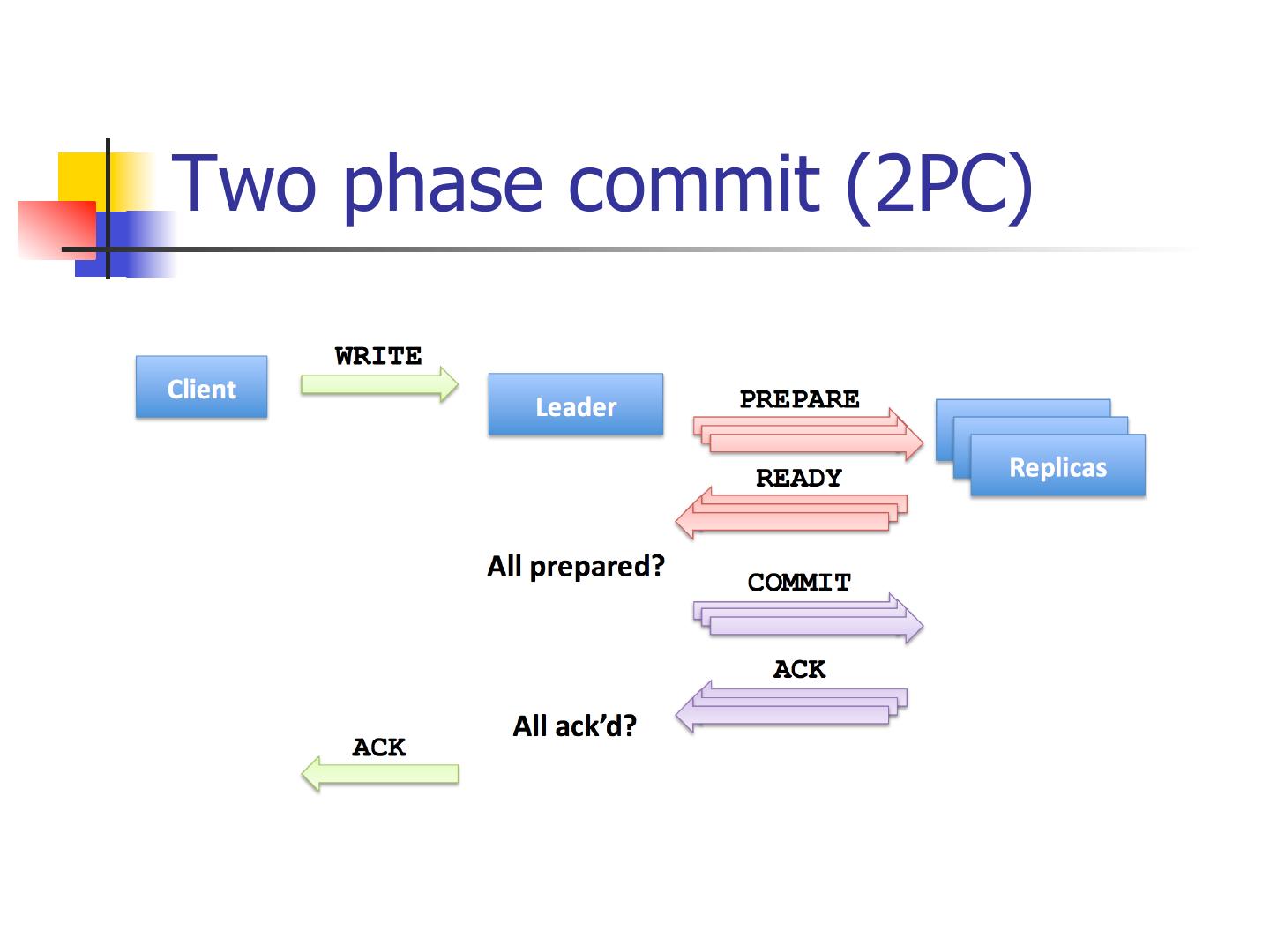
10.Two phase commit (2PC) 

11.What about failures? n  If one or more acceptors fail: n  Still ensure linearizability if |R|+|W|>N+F n  Read and write quoroms of acceptors overlap in at least one non-failed node n  Leader fails? n  Bye bye J: system no longer live n  Pick a new leader? n  How do we agree? n  Need to make sure that group is know 

12.Consensus protocol: Requirements n  Safety n  One value accepted n  It was proposed by some node n  All N nodes agree on the same value n  Liveness n  Some proposed value is eventually chosen n  Each node eventually learns it n  Fault tolerance n  If <= F faults in a window, consensus reached eventually n  Liveness not guaranteed: if >F no consensus 

13.Given desired F, what is N? n  Crash faults need 2F+1 processes n  Byzantine faults (malicious) need 3F+1 processes n  i.e., some replicas are trying to intentionally lie to prevent consensus or change the value 

14.Why is agreement hard? n  What if more than one node is leader? n  What if network is partitioned? n  What if leader crashes in middle? n  What if new leader proposes different values than those committed? n  Network is unpredictable, delays are unbounded 

15.Strawman solution I n  One node X designated as acceptor n  Each proposer sends its value to X n  X decides one value and announces it n  Problem? n  Failure of acceptor halts decision n  Breaks fault-tolerance requirement! 

16.Strawman II n  Each proposer (leader) proposes to all acceptors (replicas) n  Acceptor accepts first proposal, rejects rest n  Acks proposer n  If leader receives acks from majority, picks that value and sends it to replicas n  Problems? n  Multiple proposals – may not get a majority n  What if leader dies before chosing value? 

17.Paxos! n  Widely used family of algorithms for asynchronous consensus n  Due to Leslie Lamport n  Basic approach n  One or more nodes decide to act like a leader n  Proposes a value, tries to get it accepted n  Announces value if accepted 

18.Paxos has three phases 

19.Example 

20.Paxos Properties n  Paxos is guaranteed safe. n  Consensus is a stable property: once reached it is never violated; the agreed value is not changed. 

21.Paxos Properties n  Paxos is not guaranteed live. n  Consensus is reached if “a large enough subnetwork...is non-faulty for a long enough time.” n  Otherwise Paxos might never terminate. 

22.Combining Paxos and 2pc n  Use paxos for view-change n  If anybody notices current master or one or more replicas unavailable n  Propose view change to paxos to establish new group n  Forms the new group for 2pc n  Use 2PC for actual data n  Writes go to master for 2pc n  Reads from any replica or master n  No liveness if majority of nodes from previous view unreachable n  What if a node comes back/joins? 

23.Example system n  Apache zookeeper n  Used by a large number of Internet scale projects n  Locking/barriers n  Leader election n  Consistency n  … 

24.CAP Conjecture n  System can have two of: n  C: Strong consistency n  A: Availability n  P: Tolerance to network partition n  2PC: CA n  Paxos: CP n  Eventual consistency: AP